Dynamic Bankruptcy Prediction Models for European Enterprises
Abstract
1. Introduction
2. Literature Review
- Intensity of competition,
- Life cycle of products,
- The demand,
- Changes in consumer preferences,
- Technological change,
- Reducing entry barriers into the industry,
- Susceptibility of the industry to business cycle.
- Riskiest sectors—industry: Metal, mining, automotive, aerospace, housing, paper,
- Medium risk industries—restaurants, retail, medical sector, tourism, transport,
- Least risky sectors—journalistic, military, pharmaceutical industry, and agriculture.
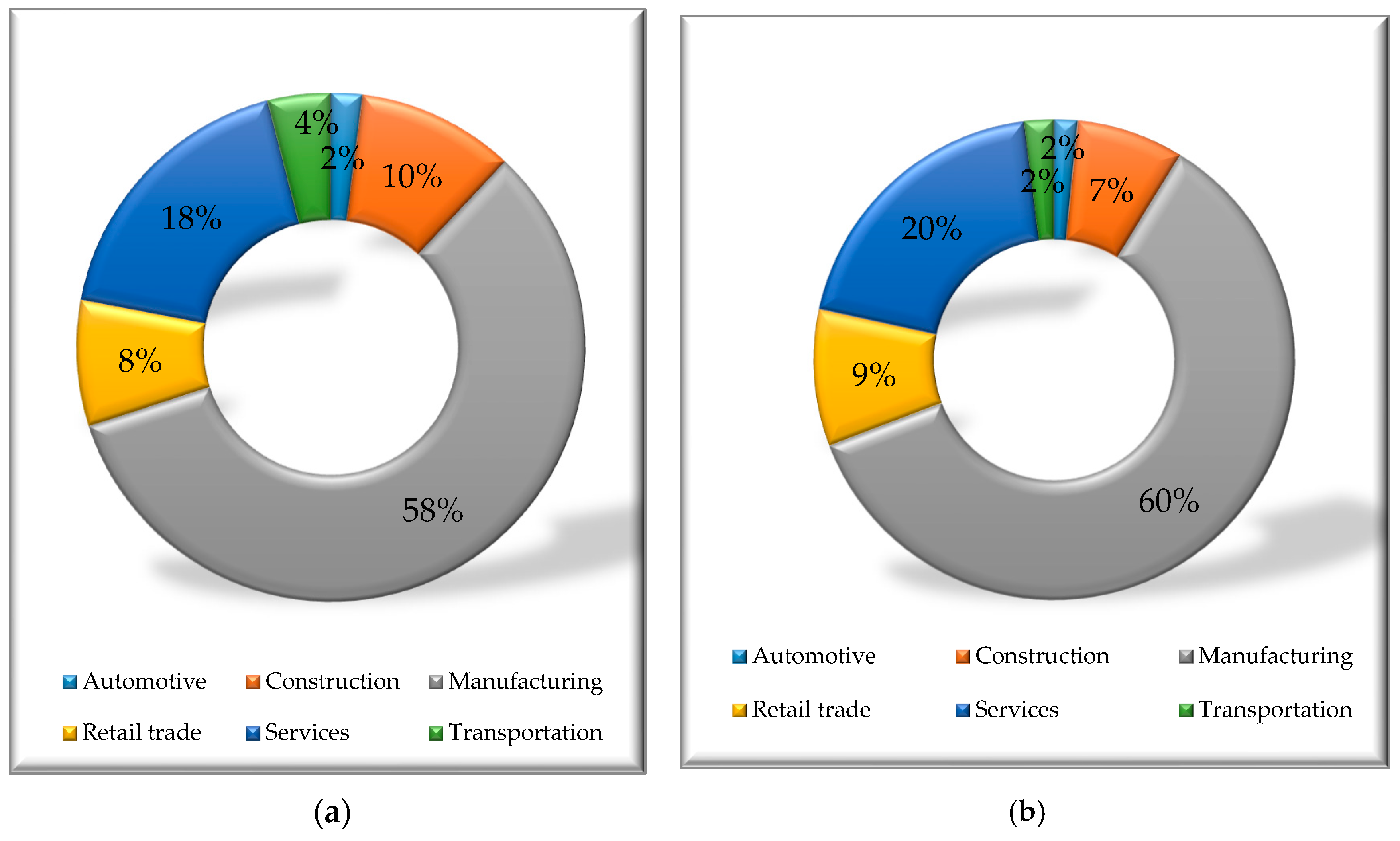
3. Data, Samples, and Modeling Methods
- Has chosen a clear definition of “bankrupt” enterprises. The enterprises at risk of bankruptcy were chosen based on the following three criteria: Information from the firm’s authorities about the risk of financial failure, court judgments declaring bankruptcy, and liquidation of the company;
- Has chosen four prediction methods that do not allow manipulation of thresholds—multilayer neural network, recurrent neural network, fuzzy sets, and decision trees;
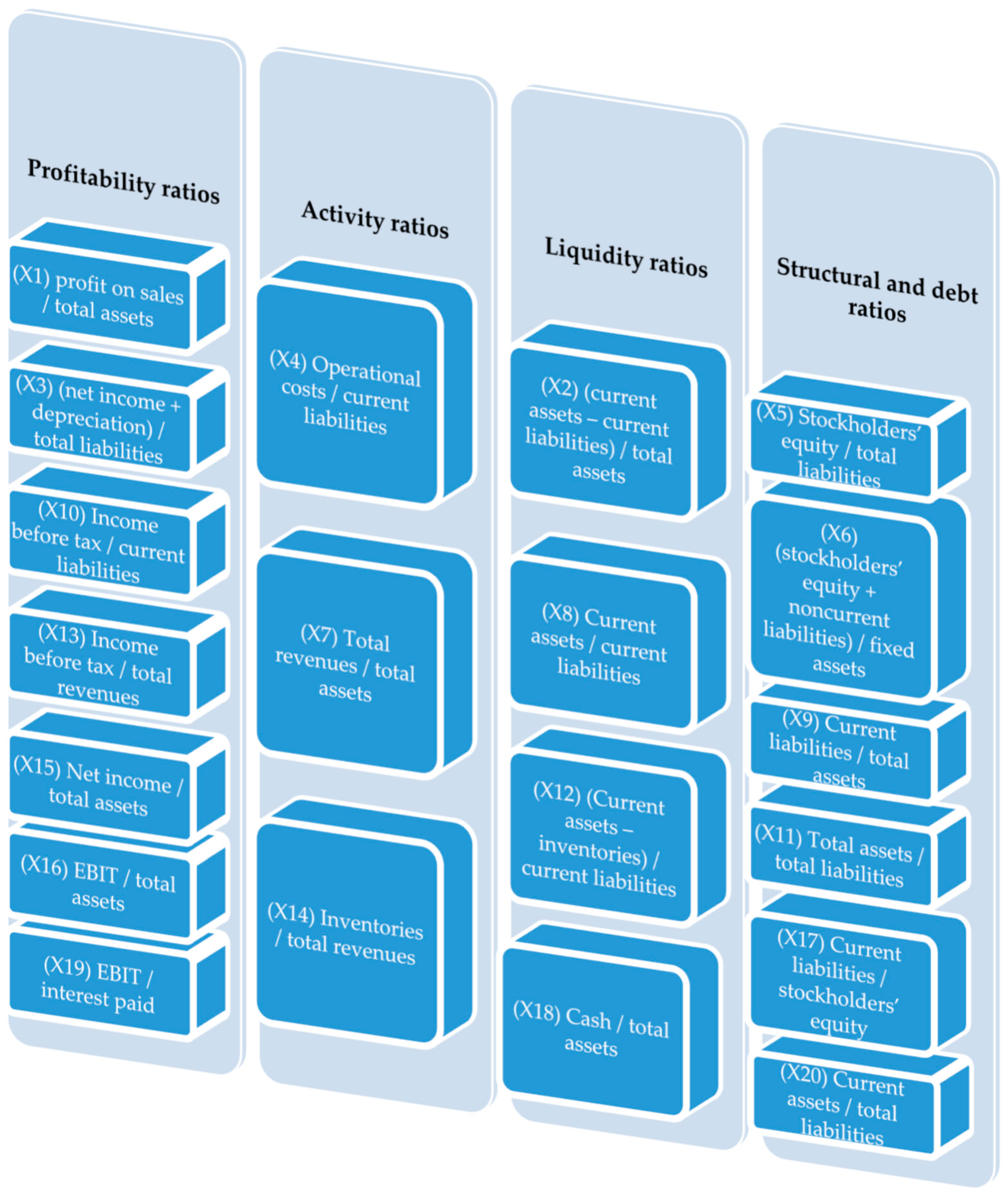
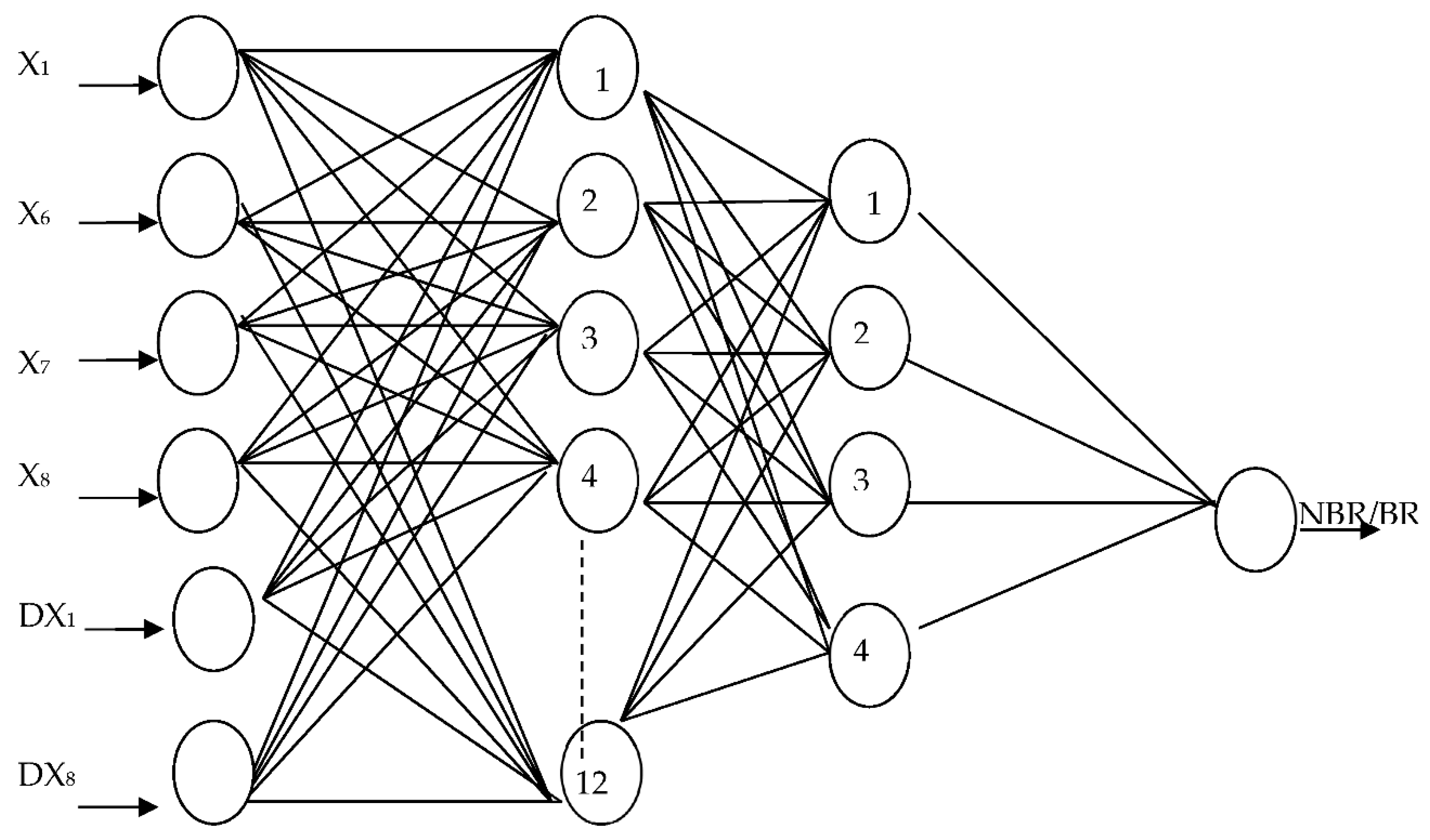
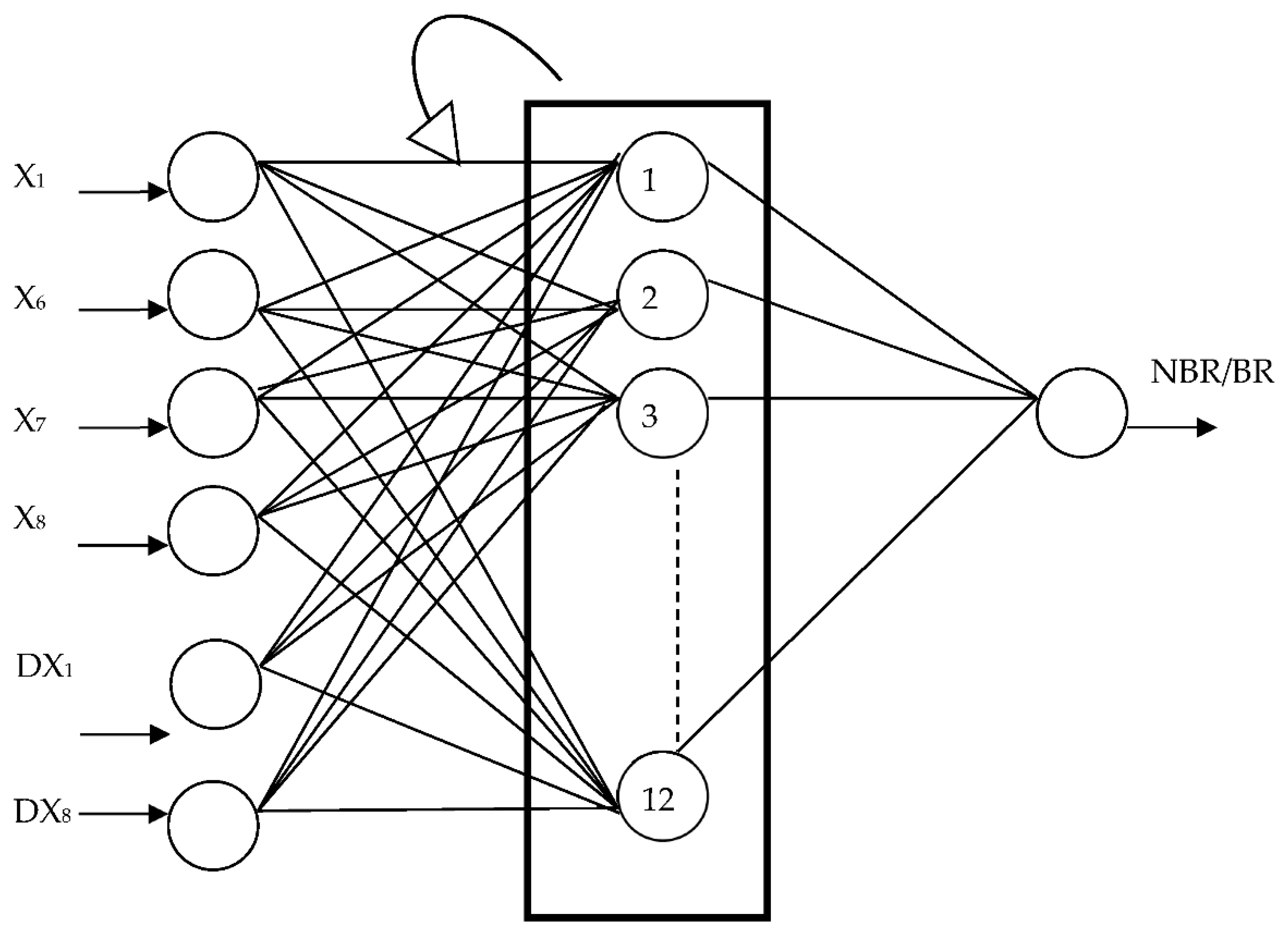
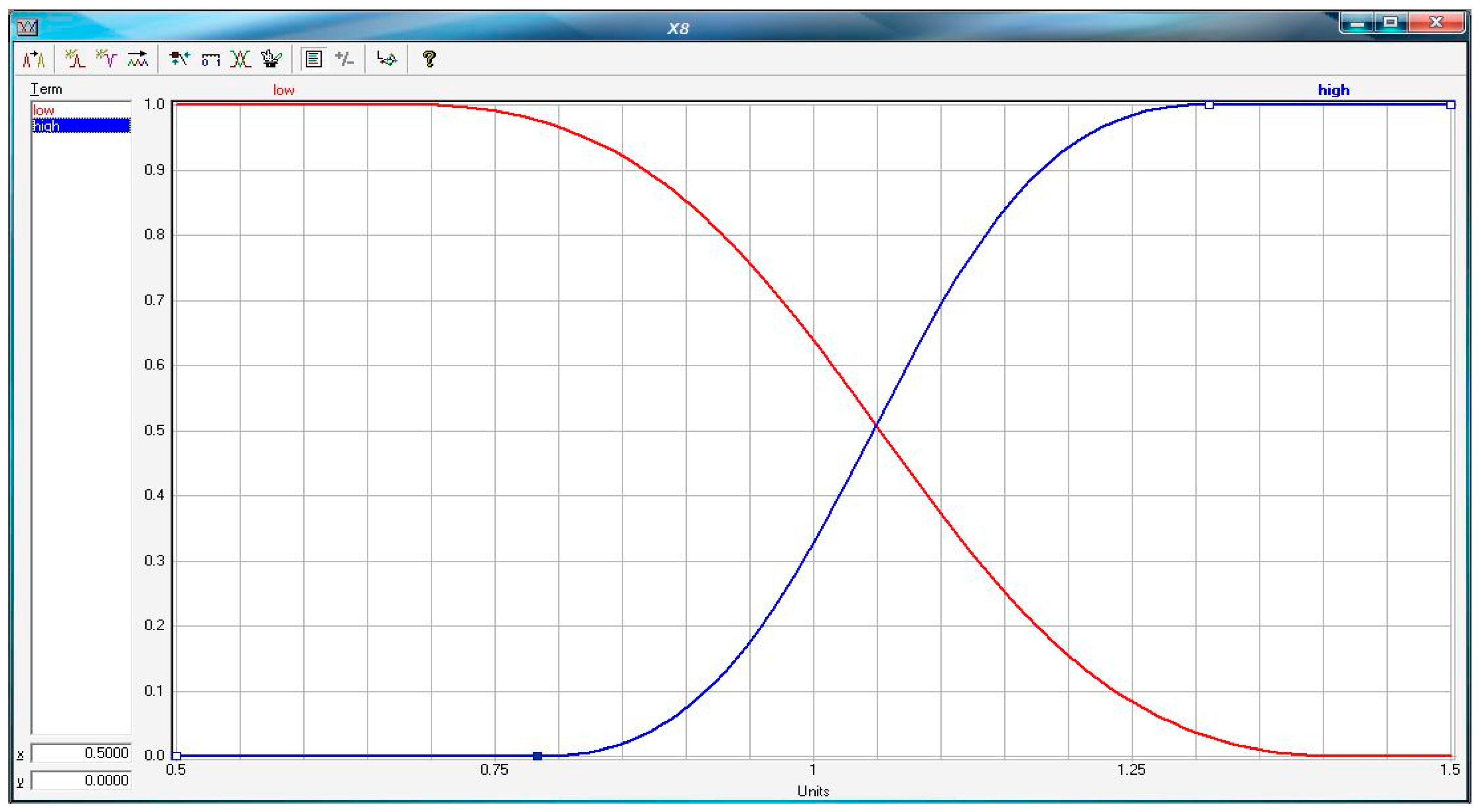
- Has calculated 20 financial ratios (Figure 3) for all the enterprises (bankrupt and non-bankrupt) for whole analyzed period of 10 years prior to bankruptcy and the dynamics for all ratios. The assumption was to build the models with at least two variables representing the change of value of financial ratio to avoid stationarity of the created models;
- Has selected enterprises that were operating in the market for at least 10 years (to avoid the selection of new, young companies characterized with higher bankruptcy risk).
4. Results and Discussion
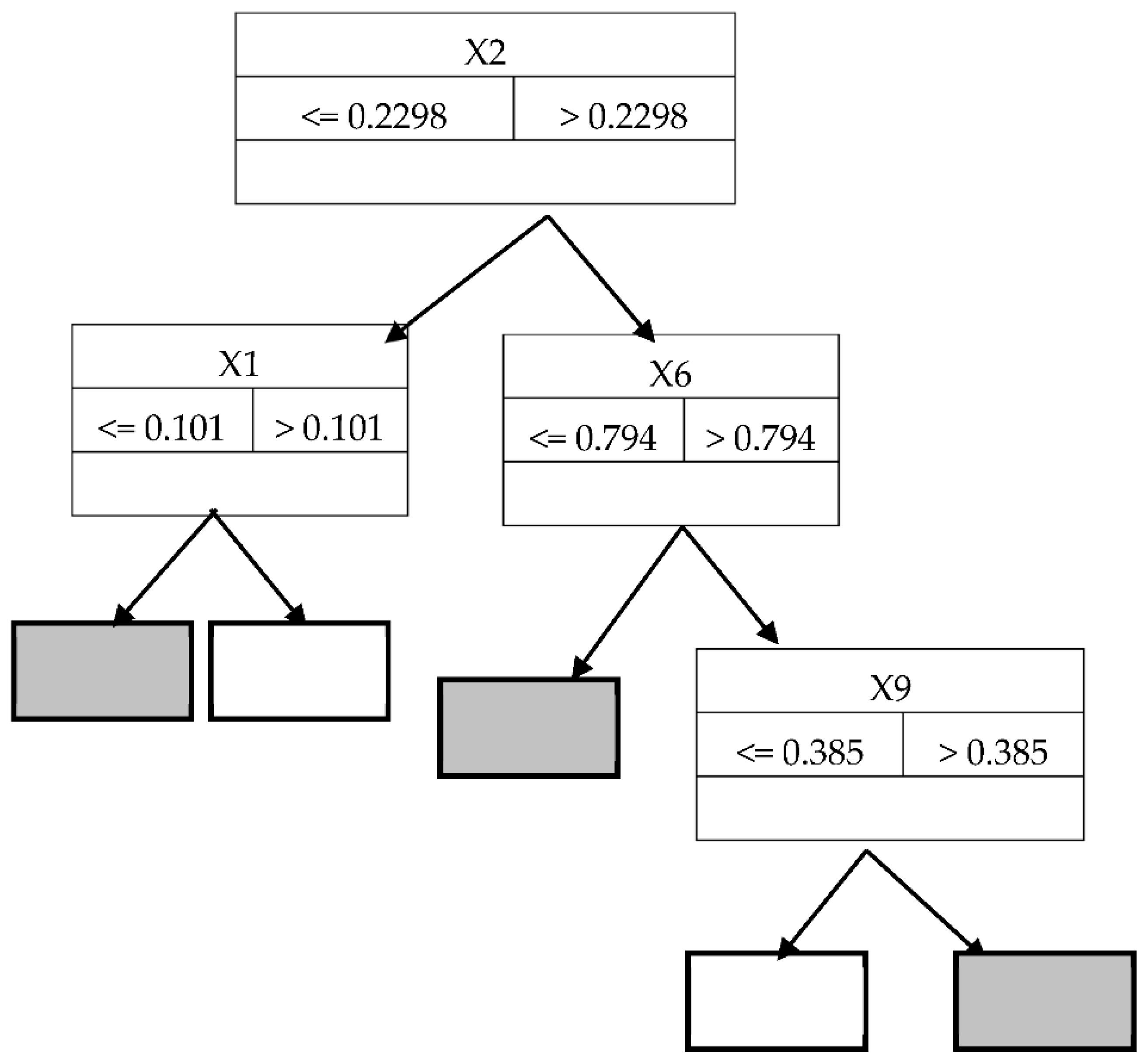
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 <= 0.015 and X6 > 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 <= 85 then 0
- If X1 > 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 > 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 > 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 1
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 <= 0.015 and X6 > 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 > 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 > 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 0
- If X1 > 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 <= 85 then 1
- If X1 > 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 <= 85 then 1
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 > 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 > 85 then 0
- If X1 <= 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 > 70 and DX8 > 85 then 1
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 > 85 then 1
- If X1 <= 0.015 and X6 > 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 > 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 > 0.82 and X8 > 1.05 and DX1 > 70 and DX8 > 85 then 1
- If X1 > 0.015 and X6 <= 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 > 85 then 0
- If X1 > 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 > 85 then 1
- If X1 <= 0.015 and X6 <= 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 > 70 and DX8 > 85 then 1
- If X1 <= 0.015 and X6 > 0.9 and X7 <= 0.82 and X8 > 1.05 and DX1 <= 70 and DX8 > 85 then 1
- If X1 > 0.015 and X6 > 0.9 and X7 > 0.82 and X8 <= 1.05 and DX1 <= 70 and DX8 > 85 then 1
- During the whole analyzed period (all 10 years prior to bankruptcy) the highest effectiveness was achieved using the fuzzy sets model, with 96.2% correct classifications one year before bankruptcy, 95.4% correct classifications two years prior to financial failure, and 93.8% correct classifications three years before bankruptcy;
- The second best forecasting model is the recurrent neural network model with an effectiveness from 91.2% three years before financial crisis to up to 95.2% correct classifications one year prior to bankruptcy;
- An examination of the effectiveness of the dynamic models (fuzzy sets, multilayer and recurrent neural networks) shows that all of them stand out with very good results in the forecasting horizon of up to six years prior to bankruptcy, with an effectiveness above 80%;
- The effectiveness of the static decision tree model is smaller than the effectiveness of the dynamic models for all the analyzed years. Additionally, the model shows significantly bigger decrease of effectiveness while prolonging the period of the forecast than dynamic models;
- The fuzzy sets model as the only dynamic model maintained an effectiveness level above 70% until the eighth year prior to bankruptcy;
- Moreover, all three dynamic models have the fewest Type I errors. Such errors indicate how many bankrupt enterprises are classified as non-bankrupt firms. Type I errors, for obvious financial reasons, are far more dangerous than Type II errors.
5. Conclusions
Funding
Conflicts of Interest
References
- Acosta-González, Eduardo, and Fernando Fernández-Rodríguez. 2014. Forecasting financial failure of firms via genetic algorithms. Computational Economics 43: 133–57. [Google Scholar] [CrossRef]
- Agarwal, Vineet, and Richard Taffler. 2007. Twenty-five years of the Taffler z-score model—Does it really have predictive ability? Accounting and Business Research 37: 285–300. [Google Scholar] [CrossRef]
- Ahn, Byeong, Sung Cho, and Chang Kim. 2000. The integrated methodology of rough set theory and artificial neural networks for business failure prediction. Expert Systems with Applications 18: 65–74. [Google Scholar] [CrossRef]
- Alaka, Hafiz A., Lukumon O. Oyedele, Hakeem A. Owolabi, Vikas Kumar, Saheed O. Ajayi, Olugbenga O. Akinade, and Muhammad Bilal. 2018. Systematic review of bankruptcy prediction models: Towards a framework for tool selection. Expert Systems with Applications 94: 164–84. [Google Scholar] [CrossRef]
- Altman, Edward. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Altman, Edward. 2018. Applications of distress prediction models: What have we learned after 50 years from the Z-score models? International Journal of Financial Studies 6: 70. [Google Scholar] [CrossRef]
- Altman, Edward, and Herbert Rijken. 2006. A point-in-time perspective on through-the-cycle ratings. Financial Analysts Journal 62: 54–70. [Google Scholar] [CrossRef]
- Andres, Javier, Manuel Landajo, and Pedro Lorca. 2005. Forecasting business profitability by using classification techniques: A comparative analysis based on a Spanish case. European Journal of Operational Research 167: 518–42. [Google Scholar] [CrossRef]
- Atiya, Amir. 2001. Bankruptcy prediction for credit risk using neural networks: A survey and new results. IEEE Transactions on Neural Networks 12: 929–35. [Google Scholar] [CrossRef]
- Balcaen, Sofie, and Hubert Ooghe. 2006. 35 years of studies on business failure: An overview of the classic statistical methodologies and their related problems. The British Accounting Review 38: 63–93. [Google Scholar] [CrossRef]
- Bandyopadhyay, Arindam. 2006. Predicting probability of default of Indian corporate bonds: Logistic and Z-score model approaches. The Journal of Risk Finance 7: 255–72. [Google Scholar] [CrossRef]
- Barboza, Flavio, Herbert Kimura, and Edward Altman. 2017. Machine learning models and bankruptcy prediction. Expert Systems with Applications 83: 405–17. [Google Scholar] [CrossRef]
- Beaver, William H. 1966. Financial ratios as predictors of failure. Journal of Accounting Research 4: 71–111. [Google Scholar] [CrossRef]
- Berryman, John. 1992. Small Business Bankruptcy and Failure—A Survey of the Literature. Los Angeles: Small Business Research Institute of Industrial Economics, pp. 1–18. [Google Scholar]
- Brabazon, Anthony, and Michael O’Neil. 2004. Diagnosing corporate stability using grammatical evolution. Journal of Applied Mathematics and Computer Science 1: 293–310. [Google Scholar]
- Bradley, Don, and Michael Rubach. 2002. Trade Credit and Small Business—A Cause of Business Failures? Conway: University of Central Arkansas, pp. 1–7. [Google Scholar]
- Callejon, A.M., A.M. Casado, Martina Fernandez, and J.I. Pelaez. 2013. A system of insolvency prediction for industrial companies using a financial alternative model with neural networks. International Journal of Computational Intelligence Systems 6: 29–37. [Google Scholar] [CrossRef][Green Version]
- Chava, Sudheer, and Robert Jarrow. 2004. Bankruptcy prediction with industry effects. Review of Finance 8: 537–69. [Google Scholar] [CrossRef]
- Cressy, Robert. 2006. Why do most firms die young? Small Business Economics 26: 103–16. [Google Scholar] [CrossRef]
- Crone, Sven, and Steven Finlay. 2012. Instance sampling in credit scoring: An empirical study of sample size and balancing. International Journal of Forecasting 28: 224–38. [Google Scholar] [CrossRef]
- Davies, David. 1997. The Art of Managing Finance. Lincoln: McGraw-Hill Book Co. [Google Scholar]
- Deakin, Edward B. 1972. A discriminant analysis of prediction of business failure. Journal of Accounting Research 3: 167–69. [Google Scholar] [CrossRef]
- Delen, Dursun, Cemil Kuzey, and Ali Uyar. 2013. Measuring firm performance using financial ratios: A decision tree approach. Expert Systems with Applications 40: 3970–83. [Google Scholar] [CrossRef]
- Dong, Manh Cuong, Shaonan Tian, and Cathy W.S. Chen. 2018. Predicting failure risk using financial ratios: Quantile hazard model approach. North American Journal of Economics and Finance 44: 204–20. [Google Scholar] [CrossRef]
- Doumpos, Michalis, and Constantin Zopounidis. 1999. A multinational discrimination method for the prediction of financial distress: the case of Greece. Multinational Finance Journal 3: 71–101. [Google Scholar] [CrossRef]
- Doyle, Jeffrey, Weili Geb, and Sarah McVay. 2007. Determinants of weaknesses in internal control over financial reporting. Journal of Accounting and Economics 44: 193–223. [Google Scholar] [CrossRef]
- Foster, George. 1986. Financial Statement Analysis, 2nd ed. New York: Prentice Hall. [Google Scholar]
- Ganguin, Blaise, and John Bilardello. 2005. Fundamentals of Corporate Credit Analysis, Standard & Poor’s. New York: McGraw-Hill. [Google Scholar]
- Garcia, Vincente, Ana I. Marques, J. Salvador Sanchez, and Humberto Ochoa-Dominguez. 2019. Dissimilarity-Based Linear Models for Corporate Bankruptcy Prediction. Computional Economics 53: 1019–31. [Google Scholar] [CrossRef]
- Giannopoulos, George, and Sindre Sigbjornsen. 2019. Prediction of bankruptcy using financial ratios in the Greek market. Theoretical Economics Letters 9: 1114–28. [Google Scholar] [CrossRef][Green Version]
- Grice, John, and Michael Dugan. 2001. The limitations of bankruptcy prediction models—Some cautions for the researcher. Review of Quantitative Finance and Accounting 17: 151–66. [Google Scholar] [CrossRef]
- Ho, Chun-Yu, Patrick McCarthy, Yi Yang, and Xuan Ye. 2013. Bankruptcy in the pulp and paper industry: Market’s reaction and prediction. Empirical Economics 45: 1205–32. [Google Scholar] [CrossRef]
- Hosaka, Tadaaki. 2019. Bankruptcy prediction using imaged financial ratios and convolutional neural networks. Expert Systems with Applications 117: 287–99. [Google Scholar] [CrossRef]
- Hosmer, David, Stanley Lemeshow, and Rod X. Sturdivant. 2013. Applied Logistic Regression. Hoboken: John Wiley & Sons. [Google Scholar]
- Jackson, Richard H.G., and Anthony Wood. 2013. The performance of insolvency prediction and credit risk models in the UK: A comparative study. The British Accounting Review 45: 183–202. [Google Scholar] [CrossRef]
- Jardin, Philippe. 2015. Bankruptcy prediction using terminal failure processes. European Journal of Operational Research 242: 286–303. [Google Scholar] [CrossRef]
- Jardin, Philippe. 2016. A two-stage classification technique for bankruptcy prediction. European Journal of Operational Research 254: 236–52. [Google Scholar] [CrossRef]
- Jardin, Philippe. 2017. Dynamics of firm financial evolution and bankruptcy prediction. Expert Systems with Applications 75: 25–43. [Google Scholar] [CrossRef]
- Jardin, Philippe. 2018. Failure pattern-based ensembles applied to bankruptcy forecasting. Decision Support Systems 107: 64–77. [Google Scholar] [CrossRef]
- Jardin, Philippe, and Eric Severin. 2011. Predicting corporate bankruptcy using a self-organizing map—An empirical study to improve the forecasting horizon of a financial failure model. Decision Support Systems 51: 701–11. [Google Scholar] [CrossRef]
- Jayasekera, Ranadeva. 2018. Prediction of company failure: Past, present and promising directions for the future. International Review of Financial Analysis 55: 196–208. [Google Scholar] [CrossRef]
- Jovanovic, Boyan. 1982. Selection and the evolution of industry. Econometrica 50: 649–70. [Google Scholar] [CrossRef]
- Kieschnick, Robert, Mark La Plante, and Rabih Moussawi. 2013. Working capital management and shareholders’ wealth. Review of Finance 17: 1827–52. [Google Scholar] [CrossRef]
- Kim, Myoung-Jong, and Dae-Ki Kang. 2010. Ensemble with neural networks for bankruptcy prediction. Expert Systems with Applications 37: 3373–79. [Google Scholar] [CrossRef]
- Kumar, Pramod, and Vadlamani Ravi. 2007. Bankruptcy prediction in banks and firms via statistical and intelligent techniques—A review. European Journal of Operational Research 180: 1–28. [Google Scholar] [CrossRef]
- Laitinen, Erkki K. 2007. Classification accuracy and correlation—LDA in failure prediction. European Journal of Operational Research 183: 210–25. [Google Scholar] [CrossRef]
- Lensberg, Terje, Aasmund Eilifsen, and Thomas E. McKee. 2006. Bankruptcy theory development and classification via genetic programming. European Journal of Operational Research 169: 677–97. [Google Scholar] [CrossRef]
- Li, Leon, and Robert Faff. 2019. Predicting corporate bankruptcy: What matters? International Review of Economics & Finance 62: 1–19. [Google Scholar]
- Liang, Deron, Chia-Chi Lu, Chih-Fong Tsai, and Guan-An Shih. 2016. Financial ratios and corporate governance indicators in bankruptcy prediction: A comprehensive study. European Journal of Operational Research 252: 561–72. [Google Scholar] [CrossRef]
- Lin, Fengyi, Deron Liang, Ching-Chiang Yeh, and Jui-Chieh Huang. 2014. Novel feature selection methods to financial distress prediction. Expert Systems with Applications 41: 2472–83. [Google Scholar] [CrossRef]
- Lukason, Oliver, and Richard C. Hoffman. 2014. Firm Bankruptcy Probability and Causes: An Integrated Study. International Journal of Business and Management 9: 80–91. [Google Scholar] [CrossRef]
- Lyandres, Evgeny, and Alexei Zhdanov. 2013. Investment opportunities and bankruptcy prediction. Journal of Financial Markets 16: 439–76. [Google Scholar] [CrossRef]
- Mcleay, Stuart, and Azmi Omar. 2000. The sensitivity of prediction models to the non-normality of bounded and unbounded financial ratios. British Accounting Review 32: 213–30. [Google Scholar] [CrossRef]
- Mensah, Yaw. 1984. An examination of the stationarity of multivariate bankruptcy prediction models—A methodological study. Journal of Accounting Research 22: 380–95. [Google Scholar] [CrossRef]
- Mihalovic, Matus. 2016. Performance Comparison of Multiple Discriminant Analysis and Logit Models in Bankruptcy Prediction. Economics and Sociology 9: 101–18. [Google Scholar] [CrossRef]
- Min, Jae, and Young-Chan Lee. 2005. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Systems with Applications 28: 603–14. [Google Scholar] [CrossRef]
- Nwogugu, Michael. 2007. Decision-making, risk and corporate governance—A critque of methodological issues in bankruptcy/recovery prediction models. Applied Mathematics and Computation 185: 178–96. [Google Scholar] [CrossRef]
- Orsenigo, Carlotta, and Carlo Vercellis. 2013. Linear versus nonlinear dimensionality reduction for banks credit rating prediction. Knowledge-Based Systems 47: 14–22. [Google Scholar] [CrossRef]
- Pakes, Ariel, and Richard Ericsson. 1998. Empirical implications of alternative models of firm dynamics. Journal of Economic Theory 79: 1–45. [Google Scholar] [CrossRef]
- Psillaki, Maria, Ioannis E. Tsolas, and Dimmitris Margaritis. 2010. Evaluation of credit risk based on firm performance. European Journal of Operational Research 201: 873–81. [Google Scholar] [CrossRef]
- Ptak-Chmielewska, Aneta. 2019. Predicting Micro-Enterprise Failures Using Data Mining Techniques. Journal of Risk and Financial Managament 12: 30. [Google Scholar] [CrossRef]
- Ravisankar, Pediredla, and Vadlamani Ravi. 2010. Financial distress prediction in banks using group method of data handling neural network, counter propagation neural network and fuzzy ARTMAP. Knowledge-Based Systems 23: 823–31. [Google Scholar] [CrossRef]
- Succurro, Marianna, Giuseppe Arcuri, and Giuseppina D. Constanzo. 2019. A combined approach based on robust PCA to improve bankruptcy forecasting. Review of Accounting and Finance 18: 296–320. [Google Scholar] [CrossRef]
- Sun, Jie, Hui Li, Qing-Hua Huang, and Kai-Yu He. 2014. Predicting financial distress and corporate failure—A review from the state-of-the-art definitions, modeling, sampling, and featuring approaches. Knowledge-Based Systems 57: 41–56. [Google Scholar] [CrossRef]
- Tam, Kar Yan. 1991. Neural network models and the prediction of bank bankruptcy. Omega 19: 429–45. [Google Scholar] [CrossRef]
- Tian, Shaonan, and Yan Yu. 2017. Financial ratios and bankruptcy predictions: An international evidence. International Review of Economics and Finance 51: 510–26. [Google Scholar] [CrossRef]
- Tian, Shaonan, Yan Yu, and Hui Guo. 2015. Variable selection and corporate bankruptcy forecasts. Journal of Banking & Finance 52: 89–100. [Google Scholar]
- Tsai, Chih-Fong. 2014. Combining cluster analysis with classifier ensembles to predict financial distress. Information Fusion 16: 46–58. [Google Scholar] [CrossRef]
- Watson, John, and Jim Everett. 1999. Small business failure rates-choice of definition and industry effects. International Small Business Journal 17: 33–49. [Google Scholar] [CrossRef]
- Wu, Desheng Dash, Yidong Zhang, Dexiang Wu, and David L. Olson. 2010. Fuzzy multi-objective programming for supplier selection and risk modeling: A possibility approach. European Journal of Operational Research 200: 774–87. [Google Scholar] [CrossRef]
- Xiao, Zhi, Xianglei Yang, Ying Pang, and Xin Dang. 2012. The prediction for listed companies’ financial distress by using multiple prediction methods with rough set and Dempster-Shafer evidence theory. Knowledge-Based Systems 26: 196–206. [Google Scholar] [CrossRef]
- Zapranis, Achilleas, and Demetrios Ginoglou. 2000. Forecasting corporate failure with neural network approach: The Greek case. Journal of Financial Management & Analysis 13: 11–21. [Google Scholar]
| Indicator Symbol | Critical Value in Fuzzy Sets Model |
|---|---|
| X1 | 0.015 |
| X6 | 0.9 |
| X7 | 0.82 |
| X8 | 1.05 |
| DX1 | 70.0% |
| DX8 | 85.0% |
| Years Prior to Bankruptcy | Multilayer Neural Network | Recurrent Neural Network | Fuzzy Sets | Decision Trees | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | E1 | E2 | S | E1 | E2 | S | E1 | E2 | S | E1 | E2 | |
| 1 year | 93.4% | 6.0% | 7.2% | 95.2% | 4.0% | 5.6% | 96.2% | 3.2% | 4.4% | 93.0% | 8.0% | 6.0% |
| 2 years | 91.8% | 7.6% | 8.8% | 93.6% | 5.6% | 7.2% | 95.4% | 4.4% | 4.8% | 91.2% | 10.0% | 7.6% |
| 3 years | 87.4% | 11.6% | 13.6% | 91.2% | 7.6% | 10.0% | 93.8% | 5.2% | 7.2% | 86.8% | 14.8% | 11.6% |
| 4 years | 82.8% | 16.4% | 18.0% | 87.8% | 10.4% | 14.0% | 90.6% | 7.6% | 11.2% | 81.6% | 19.6% | 17.2% |
| 5 years | 82.4% | 16.8% | 18.4% | 82.4% | 16.8% | 18.4% | 87.8% | 10.8% | 13.6% | 77.2% | 24.0% | 21.6% |
| 6 years | 80.8% | 18.0% | 20.4% | 81.0% | 18.4% | 19.6% | 82.8% | 16.4% | 18.0% | 72.0% | 30.0% | 26.0% |
| 7 years | 74.2% | 25.6% | 26.0% | 77.4% | 21.6% | 23.6% | 80.8% | 18.8% | 19.6% | 65.0% | 35.6% | 34.4% |
| 8 years | 64.4% | 34.4% | 36.8% | 65.0% | 34.4% | 35.6% | 71.4% | 26.0% | 31.2% | 62.8% | 38.0% | 36.4% |
| 9 years | 63.4% | 36.0% | 37.2% | 64.0% | 35.2% | 36.8% | 67.2% | 32.4% | 33.2% | 62.4% | 38.4% | 36.8% |
| 10 years | 63.0% | 36.4% | 37.6% | 63.6% | 35.6% | 37.2% | 65.8% | 32.8% | 35.6% | 61.4% | 39.6% | 37.6% |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korol, T. Dynamic Bankruptcy Prediction Models for European Enterprises. J. Risk Financial Manag. 2019, 12, 185. https://doi.org/10.3390/jrfm12040185
Korol T. Dynamic Bankruptcy Prediction Models for European Enterprises. Journal of Risk and Financial Management. 2019; 12(4):185. https://doi.org/10.3390/jrfm12040185
Chicago/Turabian StyleKorol, Tomasz. 2019. "Dynamic Bankruptcy Prediction Models for European Enterprises" Journal of Risk and Financial Management 12, no. 4: 185. https://doi.org/10.3390/jrfm12040185
APA StyleKorol, T. (2019). Dynamic Bankruptcy Prediction Models for European Enterprises. Journal of Risk and Financial Management, 12(4), 185. https://doi.org/10.3390/jrfm12040185




