An Universal, Simple, Circular Statistics-Based Estimator of α for Symmetric Stable Family
Abstract
:1. Introduction
2. The Trigonometric Moment Estimator
2.1. Special Case 1: ,
2.2. Special Case 2: , Unknown
3. Derivation of the Asymptotic Distribution of the Moment Estimator
4. Improvement Over the Moment Estimator
4.1. Special Case 1: ,
4.2. Special Case 2: , Unknown
5. Derivation of the Asymptotic Distribution of the Modified Truncated Estimators
6. Comparison of the Proposed Estimator With the Hill Estimator and the Characteristic Function Based Estimator
7. Computational Studies
8. Applications
8.1. Inference on the Gold Price Data (In US Dollars) (1980–2013)
8.2. Inference on the Silver Price Data (In US Dollars) (1980–2013)
8.3. Inference on the Silver Price Data (In INR) (1970–2011)
8.4. Inference on the Box and Jenkins Stock Price Data
9. Findings and Concluding Remarks
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C

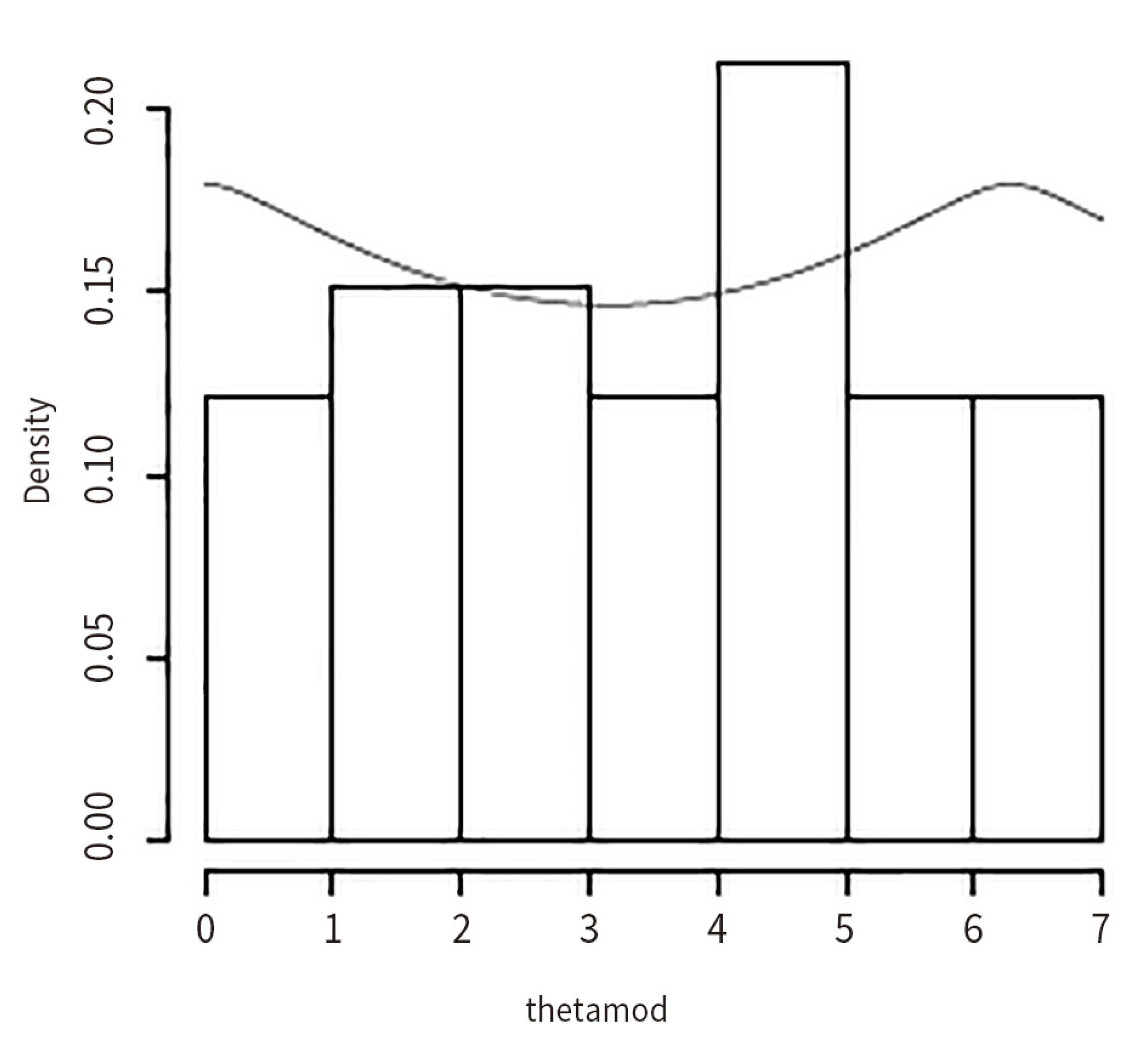
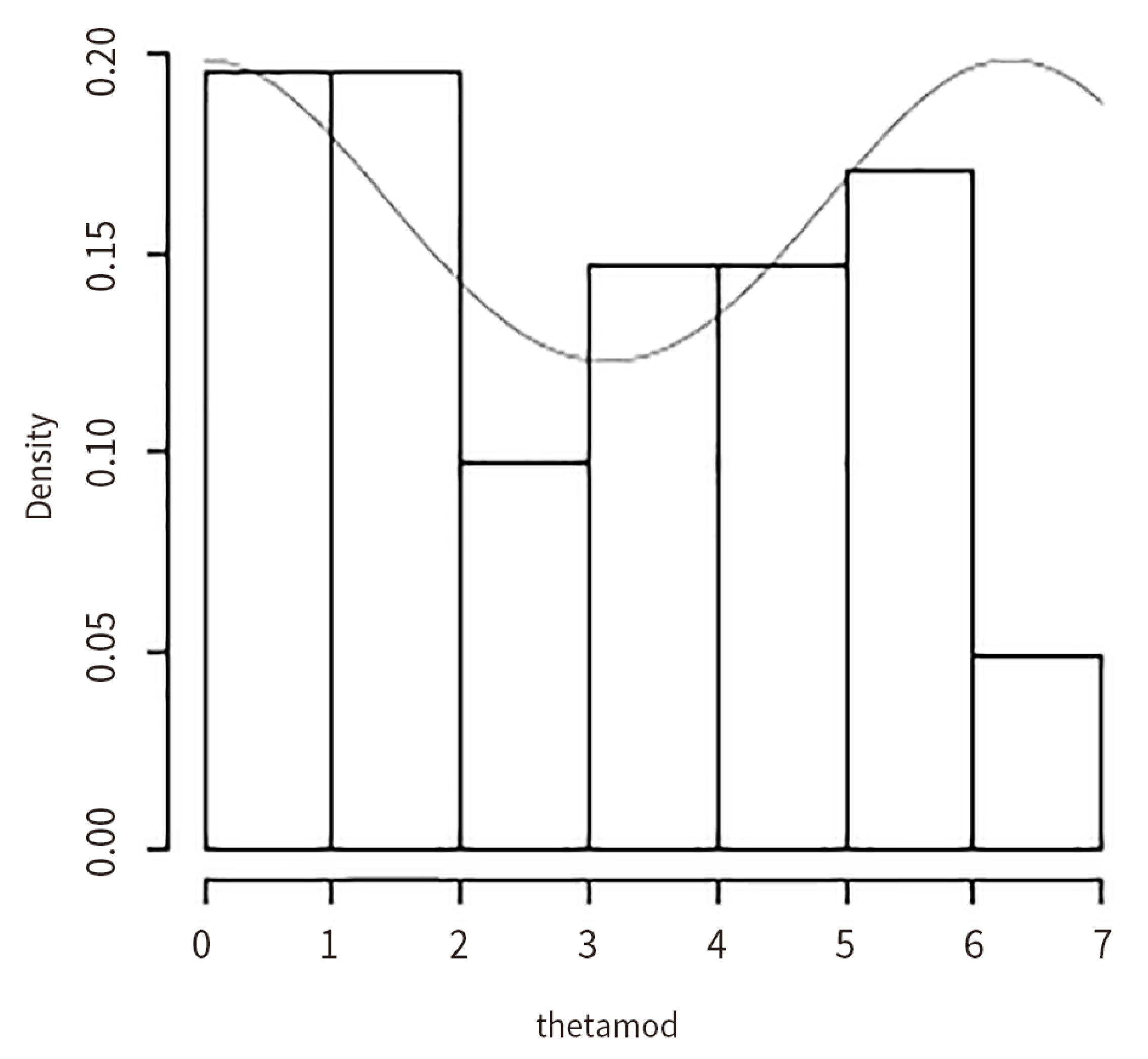
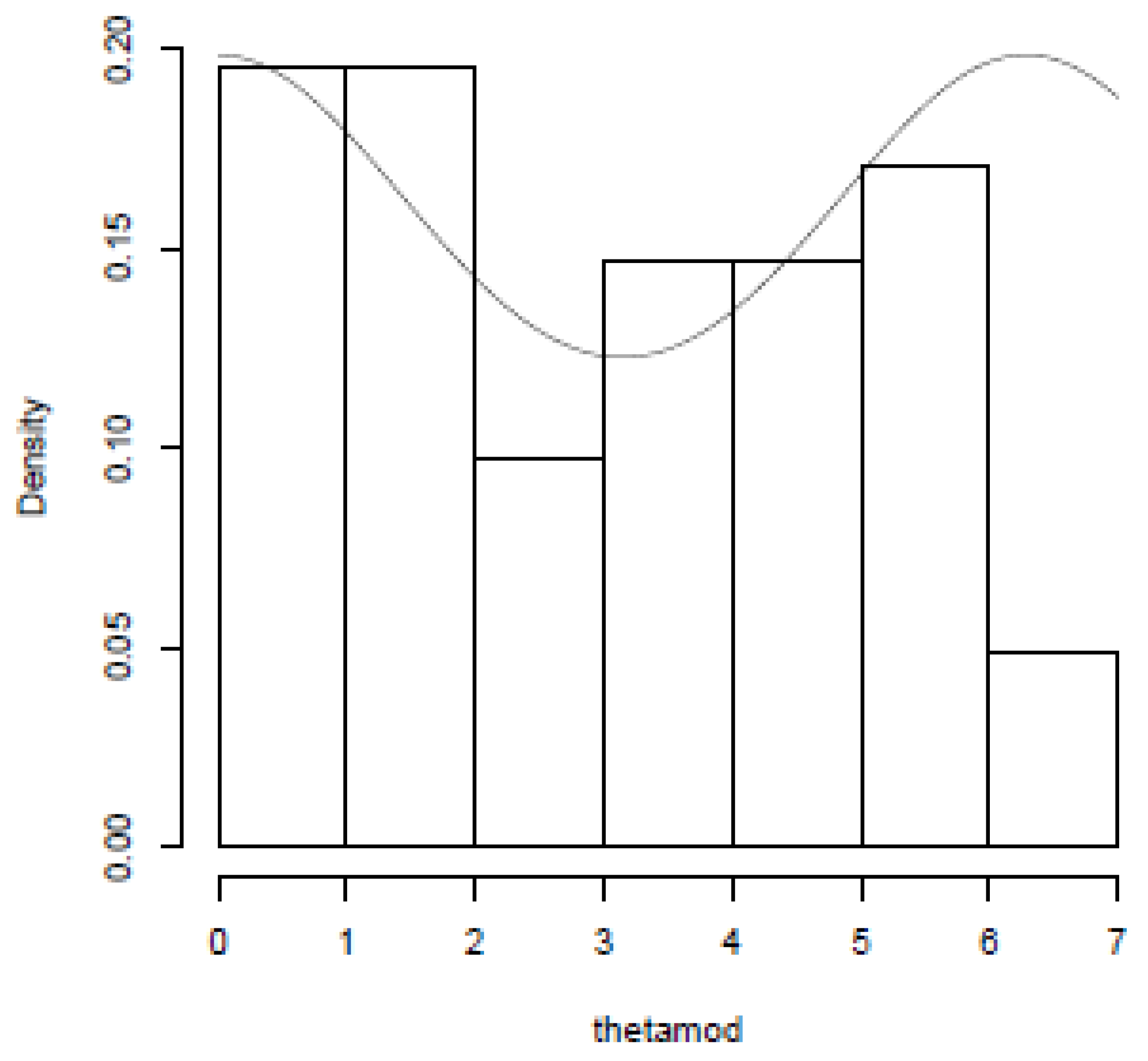
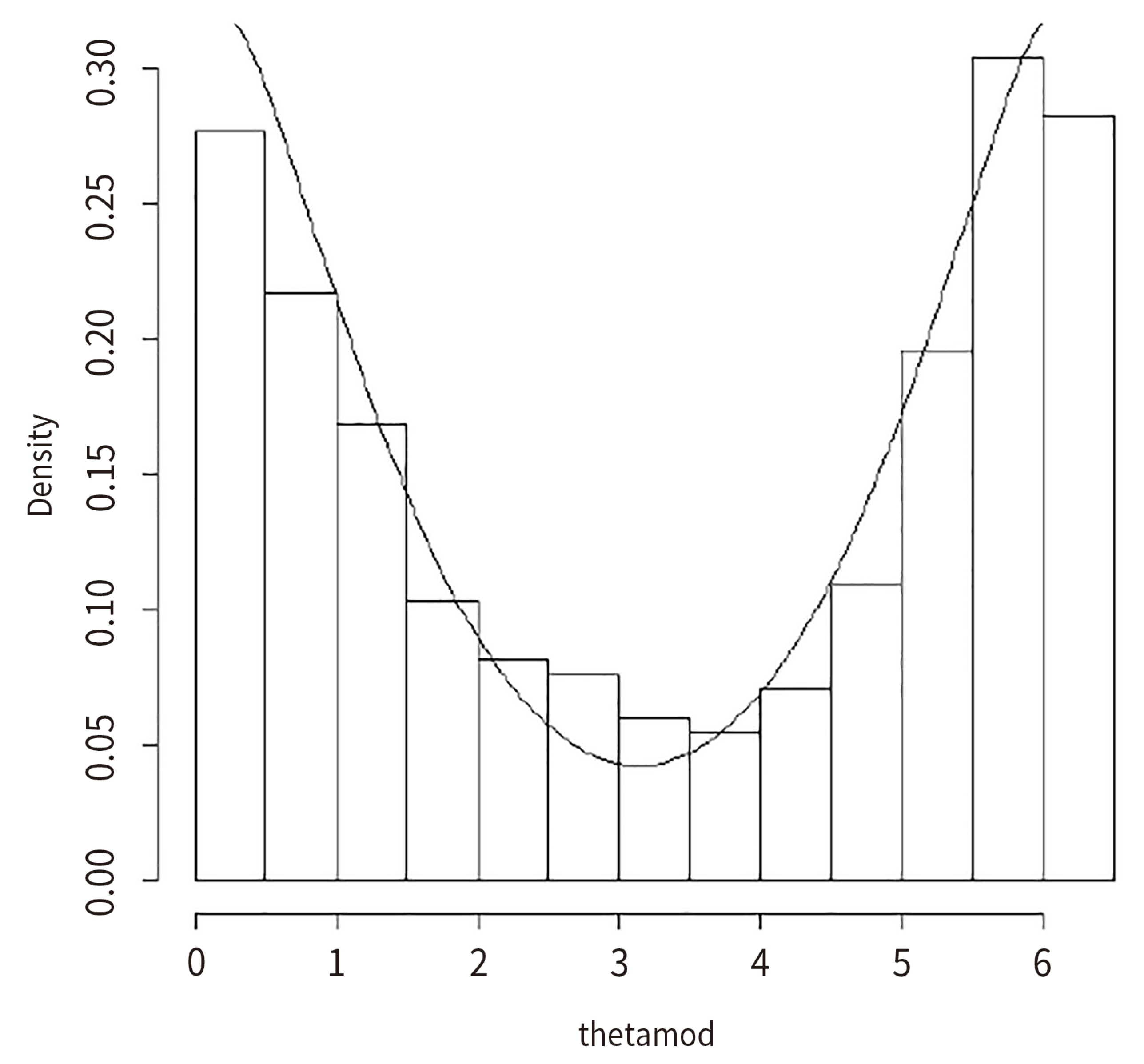
References
- Anderson, Dale N., and Barry C. Arnold. 1993. Linnik Distributions and Processes. Journal of Applied Probability 30: 330–40. [Google Scholar] [CrossRef]
- Box, George Edward Pelham, Gwilym M. Jenkins, Gregory C. Reinsel, and Greta M. Ljung. 2016. Time Series Analysis: Forecasting and Control. Hoboken: John Wiley and Sons. [Google Scholar]
- Casella, George, and Roger L. Berger. 2002. Statistical Inference. Boston: Thomson Learning. [Google Scholar]
- Dufour, Jean-Marie, and Jeong-Ryeol Kurz-Kim. 2010. Exact inference and optimal invariant estimation for the stability parameter of symmetric α-stable distributions. Journal of Empirical Finance 17: 180–94. [Google Scholar] [CrossRef]
- Feller, Williams. 1971. An Introduction to Probability Theory and Its Applications, 3rd ed. New York: Wiley. [Google Scholar]
- Goldie, Charles M., and Richard L. Smith. 1987. Slow variation with remainder: A survey of the theory and its applications. Quarterly Journal of Mathematics, Oxford 38: 45–71. [Google Scholar] [CrossRef]
- Hill, Bruce M. 1975. A simple general approach to inference about the tail of a distribution. The Annals of Statistics 3: 1163–74. [Google Scholar] [CrossRef]
- Jammalamadaka, S. Rao, and Ashis SenGupta. 2001. Topics in Circular Statistics. Hackensack: World Scientific Publishers. [Google Scholar]
- Nolan, John P. 2003. Modeling Financial Data with Stable Distributions. In Handbook of Heavy Tailed Distributions in Finance. Amsterdam: Elsevier, pp. 105–30. [Google Scholar]
- Salimi, Mehdi, NMA Nik Long, Somayeh Sharifi, and Bruno Antonio Pansera. 2018. A multi-point iterative method for solving nonlinear equations with optimal order of convergence. Japan Journal of Industrial and Applied Mathematics 35: 497–509. [Google Scholar] [CrossRef]
- SenGupta, Ashis. 1996. Analysis of Directional Data in Agricultural Research using DDSTAP. Invited paper. Paper presented at Indian Society of Agricultural Statistics Golden Jubilee Conference, New Delhi, India, December 19–21; pp. 43–59. [Google Scholar]
| 0.2 | 0.2 | 0.179 | 0.097 |
| 0.2 | 0.4 | 0.093 | 0.058 |
| 0.2 | 0.6 | 0.084 | 0.053 |
| 0.2 | 0.8 | 0.118 | 0.070 |
| 0.4 | 0.2 | 0.211 | 0.148 |
| 0.4 | 0.4 | 0.094 | 0.079 |
| 0.4 | 0.6 | 0.079 | 0.069 |
| 0.4 | 0.8 | 0.107 | 0.088 |
| 0.6 | 0.2 | 0.270 | 0.209 |
| 0.6 | 0.4 | 0.098 | 0.093 |
| 0.6 | 0.6 | 0.074 | 0.073 |
| 0.6 | 0.8 | 0.096 | 0.092 |
| 0.8 | 0.2 | 0.384 | 0.284 |
| 0.8 | 0.4 | 0.105 | 0.103 |
| 0.8 | 0.6 | 0.071 | 0.070 |
| 0.8 | 0.8 | 0.086 | 0.085 |
| 1.0 | 0.2 | 0.626 | 0.377 |
| 1.0 | 0.4 | 0.118 | 0.117 |
| 1.0 | 0.6 | 0.067 | 0.067 |
| 1.0 | 0.8 | 0.075 | 0.075 |
| Relocation | |||||||
|---|---|---|---|---|---|---|---|
| True Mean = 0 | Sample Mean | Sample Median | |||||
| Sample Size | RMSE1 | k* | RMSE2 | RMSE3 | RMSE4 | ||
| 1.01 | 0.2 | 100 | 0.483 | 12 | 0.486 | 0.529 | 0.514 |
| 1.01 | 0.3 | 100 | 0.468 | 12 | 0.414 | 0.429 | 0.423 |
| 1.01 | 0.4 | 100 | 0.412 | 12 | 0.408 | 0.409 | 0.411 |
| 1.01 | 0.5 | 100 | 0.320 | 12 | 0.428 | 0.415 | 0.432 |
| 1.01 | 0.6 | 100 | 0.277 | 12 | 0.438 | 0.409 | 0.441 |
| 1.01 | 0.7 | 100 | 0.272 | 12 | 0.395 | 0.380 | 0.404 |
| 1.01 | 0.8 | 100 | 0.299 | 12 | 0.418 | 0.414 | 0.427 |
| 1.01 | 0.9 | 100 | 0.403 | 12 | 0.419 | 0.465 | 0.424 |
| 1.01 | 0.2 | 250 | 0.395 | 22 | 0.254 | 0.255 | 0.254 |
| 1.01 | 0.3 | 250 | 0.353 | 22 | 0.258 | 0.261 | 0.258 |
| 1.01 | 0.4 | 250 | 0.242 | 22 | 0.253 | 0.255 | 0.254 |
| 1.01 | 0.5 | 250 | 0.189 | 22 | 0.251 | 0.252 | 0.253 |
| 1.01 | 0.6 | 250 | 0.168 | 22 | 0.255 | 0.250 | 0.256 |
| 1.01 | 0.7 | 250 | 0.165 | 22 | 0.259 | 0.252 | 0.260 |
| 1.01 | 0.8 | 250 | 0.179 | 22 | 0.247 | 0.240 | 0.248 |
| 1.01 | 0.9 | 250 | 0.238 | 22 | 0.256 | 0.256 | 0.257 |
| 1.01 | 0.2 | 500 | 0.360 | 37 | 0.181 | 0.181 | 0.181 |
| 1.01 | 0.3 | 500 | 0.251 | 37 | 0.180 | 0.181 | 0.180 |
| 1.01 | 0.4 | 500 | 0.161 | 37 | 0.178 | 0.179 | 0.179 |
| 1.01 | 0.5 | 500 | 0.131 | 37 | 0.180 | 0.181 | 0.180 |
| 1.01 | 0.6 | 500 | 0.118 | 37 | 0.176 | 0.176 | 0.177 |
| 1.01 | 0.7 | 500 | 0.115 | 37 | 0.181 | 0.179 | 0.181 |
| 1.01 | 0.8 | 500 | 0.125 | 37 | 0.180 | 0.176 | 0.180 |
| 1.01 | 0.9 | 500 | 0.162 | 37 | 0.183 | 0.181 | 0.183 |
| 1.01 | 0.2 | 1000 | 0.295 | 64 | 0.131 | 0.131 | 0.131 |
| 1.01 | 0.3 | 1000 | 0.161 | 64 | 0.132 | 0.132 | 0.132 |
| 1.01 | 0.4 | 1000 | 0.113 | 64 | 0.132 | 0.132 | 0.132 |
| 1.01 | 0.5 | 1000 | 0.092 | 64 | 0.132 | 0.133 | 0.132 |
| 1.01 | 0.6 | 1000 | 0.081 | 64 | 0.131 | 0.131 | 0.131 |
| 1.01 | 0.7 | 1000 | 0.080 | 64 | 0.131 | 0.131 | 0.131 |
| 1.01 | 0.8 | 1000 | 0.086 | 64 | 0.133 | 0.131 | 0.134 |
| 1.01 | 0.9 | 1000 | 0.110 | 64 | 0.131 | 0.129 | 0.131 |
| 1.01 | 0.2 | 2000 | 0.220 | 83 | 0.114 | 0.114 | 0.114 |
| 1.01 | 0.3 | 2000 | 0.110 | 83 | 0.117 | 0.117 | 0.117 |
| 1.01 | 0.4 | 2000 | 0.078 | 83 | 0.116 | 0.116 | 0.116 |
| 1.01 | 0.5 | 2000 | 0.064 | 83 | 0.115 | 0.115 | 0.115 |
| 1.01 | 0.6 | 2000 | 0.058 | 83 | 0.114 | 0.114 | 0.114 |
| 1.01 | 0.7 | 2000 | 0.057 | 83 | 0.115 | 0.115 | 0.115 |
| 1.01 | 0.8 | 2000 | 0.062 | 83 | 0.114 | 0.114 | 0.114 |
| 1.01 | 0.9 | 2000 | 0.078 | 83 | 0.116 | 0.115 | 0.116 |
| 1.01 | 0.2 | 5000 | 0.125 | 193 | 0.074 | 0.074 | 0.074 |
| 1.01 | 0.3 | 5000 | 0.068 | 193 | 0.073 | 0.073 | 0.073 |
| 1.01 | 0.4 | 5000 | 0.049 | 193 | 0.073 | 0.073 | 0.073 |
| 1.01 | 0.5 | 5000 | 0.040 | 193 | 0.073 | 0.073 | 0.073 |
| 1.01 | 0.6 | 5000 | 0.037 | 193 | 0.073 | 0.073 | 0.073 |
| 1.01 | 0.7 | 5000 | 0.036 | 193 | 0.073 | 0.074 | 0.073 |
| 1.01 | 0.8 | 5000 | 0.039 | 193 | 0.074 | 0.074 | 0.074 |
| 1.01 | 0.9 | 5000 | 0.049 | 193 | 0.073 | 0.072 | 0.073 |
| 1.01 | 0.2 | 10000 | 0.083 | 282 | 0.060 | 0.060 | 0.060 |
| 1.01 | 0.3 | 10000 | 0.047 | 282 | 0.061 | 0.061 | 0.061 |
| 1.01 | 0.4 | 10000 | 0.035 | 282 | 0.061 | 0.061 | 0.061 |
| 1.01 | 0.5 | 10000 | 0.029 | 282 | 0.061 | 0.061 | 0.061 |
| 1.01 | 0.6 | 10000 | 0.026 | 282 | 0.061 | 0.061 | 0.061 |
| 1.01 | 0.7 | 10000 | 0.026 | 282 | 0.062 | 0.062 | 0.062 |
| 1.01 | 0.8 | 10000 | 0.027 | 282 | 0.061 | 0.061 | 0.061 |
| 1.01 | 0.9 | 10000 | 0.034 | 282 | 0.061 | 0.061 | 0.061 |
| 1.25 | 0.2 | 100 | 0.549 | 18 | 0.360 | 0.390 | 0.368 |
| 1.25 | 0.3 | 100 | 0.450 | 18 | 0.364 | 0.352 | 0.377 |
| 1.25 | 0.4 | 100 | 0.398 | 18 | 0.357 | 0.321 | 0.364 |
| 1.25 | 0.5 | 100 | 0.333 | 18 | 0.362 | 0.319 | 0.366 |
| 1.25 | 0.6 | 100 | 0.269 | 18 | 0.358 | 0.325 | 0.368 |
| 1.25 | 0.7 | 100 | 0.252 | 18 | 0.362 | 0.342 | 0.370 |
| 1.25 | 0.8 | 100 | 0.264 | 18 | 0.363 | 0.362 | 0.370 |
| 1.25 | 0.9 | 100 | 0.346 | 18 | 0.376 | 0.425 | 0.380 |
| 1.25 | 0.2 | 250 | 0.413 | 42 | 0.202 | 0.213 | 0.206 |
| 1.25 | 0.3 | 250 | 0.355 | 42 | 0.205 | 0.202 | 0.208 |
| 1.25 | 0.4 | 250 | 0.282 | 42 | 0.203 | 0.194 | 0.208 |
| 1.25 | 0.5 | 250 | 0.201 | 42 | 0.199 | 0.189 | 0.205 |
| 1.25 | 0.6 | 250 | 0.163 | 42 | 0.207 | 0.193 | 0.210 |
| 1.25 | 0.7 | 250 | 0.154 | 42 | 0.201 | 0.191 | 0.203 |
| 1.25 | 0.8 | 250 | 0.161 | 42 | 0.203 | 0.201 | 0.207 |
| 1.25 | 0.9 | 250 | 0.207 | 42 | 0.205 | 0.219 | 0.208 |
| 1.25 | 0.2 | 500 | 0.337 | 82 | 0.140 | 0.148 | 0.142 |
| 1.25 | 0.3 | 500 | 0.290 | 82 | 0.140 | 0.139 | 0.142 |
| 1.25 | 0.4 | 500 | 0.192 | 82 | 0.141 | 0.135 | 0.143 |
| 1.25 | 0.5 | 500 | 0.135 | 82 | 0.141 | 0.134 | 0.144 |
| 1.25 | 0.6 | 500 | 0.115 | 82 | 0.141 | 0.134 | 0.143 |
| 1.25 | 0.7 | 500 | 0.106 | 82 | 0.140 | 0.134 | 0.142 |
| 1.25 | 0.8 | 500 | 0.112 | 82 | 0.139 | 0.137 | 0.141 |
| 1.25 | 0.9 | 500 | 0.143 | 82 | 0.140 | 0.147 | 0.143 |
| 1.25 | 0.2 | 1000 | 0.296 | 159 | 0.099 | 0.105 | 0.101 |
| 1.25 | 0.3 | 1000 | 0.222 | 159 | 0.101 | 0.101 | 0.102 |
| 1.25 | 0.4 | 1000 | 0.128 | 159 | 0.099 | 0.097 | 0.101 |
| 1.25 | 0.5 | 1000 | 0.095 | 159 | 0.099 | 0.095 | 0.100 |
| 1.25 | 0.6 | 1000 | 0.079 | 159 | 0.098 | 0.093 | 0.100 |
| 1.25 | 0.7 | 1000 | 0.075 | 159 | 0.100 | 0.096 | 0.101 |
| 1.25 | 0.8 | 1000 | 0.079 | 159 | 0.098 | 0.097 | 0.100 |
| 1.25 | 0.9 | 1000 | 0.100 | 159 | 0.100 | 0.104 | 0.102 |
| 1.25 | 0.2 | 2000 | 0.300 | 314 | 0.314 | 0.316 | 0.313 |
| 1.25 | 0.3 | 2000 | 0.219 | 314 | 0.315 | 0.314 | 0.313 |
| 1.25 | 0.4 | 2000 | 0.088 | 314 | 0.070 | 0.068 | 0.071 |
| 1.25 | 0.5 | 2000 | 0.067 | 314 | 0.071 | 0.068 | 0.072 |
| 1.25 | 0.6 | 2000 | 0.056 | 314 | 0.070 | 0.066 | 0.071 |
| 1.25 | 0.7 | 2000 | 0.053 | 314 | 0.070 | 0.067 | 0.071 |
| 1.25 | 0.8 | 2000 | 0.055 | 314 | 0.069 | 0.068 | 0.071 |
| 1.25 | 0.9 | 2000 | 0.070 | 314 | 0.070 | 0.072 | 0.071 |
| 1.25 | 0.2 | 5000 | 0.206 | 314 | 0.044 | 0.047 | 0.045 |
| 1.25 | 0.3 | 5000 | 0.087 | 776 | 0.045 | 0.045 | 0.045 |
| 1.25 | 0.4 | 5000 | 0.055 | 776 | 0.044 | 0.043 | 0.045 |
| 1.25 | 0.5 | 5000 | 0.042 | 776 | 0.044 | 0.043 | 0.045 |
| 1.25 | 0.6 | 5000 | 0.035 | 776 | 0.045 | 0.043 | 0.045 |
| 1.25 | 0.7 | 5000 | 0.034 | 776 | 0.045 | 0.043 | 0.045 |
| 1.25 | 0.8 | 5000 | 0.036 | 776 | 0.045 | 0.044 | 0.045 |
| 1.25 | 0.9 | 5000 | 0.044 | 776 | 0.045 | 0.046 | 0.045 |
| 1.25 | 0.2 | 10000 | 0.141 | 1547 | 0.032 | 0.034 | 0.032 |
| 1.25 | 0.3 | 10000 | 0.061 | 1547 | 0.032 | 0.032 | 0.032 |
| 1.25 | 0.4 | 10000 | 0.039 | 1547 | 0.031 | 0.030 | 0.031 |
| 1.25 | 0.5 | 10000 | 0.030 | 1547 | 0.031 | 0.030 | 0.032 |
| 1.25 | 0.6 | 10000 | 0.025 | 1547 | 0.031 | 0.030 | 0.032 |
| 1.25 | 0.7 | 10000 | 0.024 | 1547 | 0.031 | 0.030 | 0.032 |
| 1.25 | 0.8 | 10000 | 0.025 | 1547 | 0.031 | 0.031 | 0.032 |
| 1.25 | 0.9 | 10000 | 0.031 | 1547 | 0.031 | 0.032 | 0.032 |
| 1.5 | 0.2 | 100 | 0.702 | 21 | 0.413 | 0.435 | 0.408 |
| 1.5 | 0.3 | 100 | 0.461 | 21 | 0.393 | 0.341 | 0.394 |
| 1.5 | 0.4 | 100 | 0.370 | 21 | 0.404 | 0.332 | 0.396 |
| 1.5 | 0.5 | 100 | 0.311 | 21 | 0.382 | 0.326 | 0.378 |
| 1.5 | 0.6 | 100 | 0.259 | 21 | 0.402 | 0.342 | 0.393 |
| 1.5 | 0.7 | 100 | 0.226 | 21 | 0.386 | 0.350 | 0.385 |
| 1.5 | 0.8 | 100 | 0.227 | 21 | 0.398 | 0.374 | 0.390 |
| 1.5 | 0.9 | 100 | 0.278 | 21 | 0.379 | 0.393 | 0.376 |
| 1.5 | 0.2 | 250 | 0.499 | 51 | 0.222 | 0.228 | 0.221 |
| 1.5 | 0.3 | 250 | 0.343 | 51 | 0.223 | 0.203 | 0.221 |
| 1.5 | 0.4 | 250 | 0.283 | 51 | 0.221 | 0.196 | 0.220 |
| 1.5 | 0.5 | 250 | 0.213 | 51 | 0.221 | 0.196 | 0.220 |
| 1.5 | 0.6 | 250 | 0.161 | 51 | 0.222 | 0.198 | 0.219 |
| 1.5 | 0.7 | 250 | 0.139 | 51 | 0.221 | 0.201 | 0.219 |
| 1.5 | 0.8 | 250 | 0.138 | 51 | 0.219 | 0.208 | 0.219 |
| 1.5 | 0.9 | 250 | 0.171 | 51 | 0.219 | 0.223 | 0.218 |
| 1.5 | 0.2 | 500 | 0.388 | 101 | 0.151 | 0.155 | 0.152 |
| 1.5 | 0.3 | 500 | 0.285 | 101 | 0.152 | 0.140 | 0.151 |
| 1.5 | 0.4 | 500 | 0.226 | 101 | 0.152 | 0.137 | 0.152 |
| 1.5 | 0.5 | 500 | 0.153 | 101 | 0.155 | 0.139 | 0.156 |
| 1.5 | 0.6 | 500 | 0.113 | 101 | 0.150 | 0.136 | 0.151 |
| 1.5 | 0.7 | 500 | 0.098 | 101 | 0.152 | 0.140 | 0.151 |
| 1.5 | 0.8 | 500 | 0.097 | 101 | 0.152 | 0.147 | 0.153 |
| 1.5 | 0.9 | 500 | 0.121 | 101 | 0.153 | 0.156 | 0.152 |
| 1.5 | 0.2 | 1000 | 0.311 | 201 | 0.105 | 0.106 | 0.105 |
| 1.5 | 0.3 | 1000 | 0.245 | 201 | 0.106 | 0.099 | 0.106 |
| 1.5 | 0.4 | 1000 | 0.166 | 201 | 0.105 | 0.096 | 0.105 |
| 1.5 | 0.5 | 1000 | 0.105 | 201 | 0.106 | 0.095 | 0.105 |
| 1.5 | 0.6 | 1000 | 0.079 | 201 | 0.107 | 0.096 | 0.106 |
| 1.5 | 0.7 | 1000 | 0.069 | 201 | 0.106 | 0.099 | 0.106 |
| 1.5 | 0.8 | 1000 | 0.068 | 201 | 0.106 | 0.101 | 0.106 |
| 1.5 | 0.9 | 1000 | 0.084 | 201 | 0.106 | 0.109 | 0.107 |
| 1.5 | 0.2 | 2000 | 0.261 | 400 | 0.075 | 0.076 | 0.075 |
| 1.5 | 0.3 | 2000 | 0.204 | 400 | 0.075 | 0.070 | 0.075 |
| 1.5 | 0.4 | 2000 | 0.113 | 400 | 0.074 | 0.068 | 0.074 |
| 1.5 | 0.5 | 2000 | 0.072 | 400 | 0.075 | 0.068 | 0.075 |
| 1.5 | 0.6 | 2000 | 0.056 | 400 | 0.074 | 0.068 | 0.075 |
| 1.5 | 0.7 | 2000 | 0.048 | 400 | 0.073 | 0.068 | 0.074 |
| 1.5 | 0.8 | 2000 | 0.048 | 400 | 0.074 | 0.071 | 0.075 |
| 1.5 | 0.9 | 2000 | 0.059 | 400 | 0.075 | 0.076 | 0.075 |
| 1.5 | 0.2 | 5000 | 0.222 | 995 | 0.047 | 0.048 | 0.047 |
| 1.5 | 0.3 | 5000 | 0.133 | 995 | 0.047 | 0.044 | 0.047 |
| 1.5 | 0.4 | 5000 | 0.069 | 995 | 0.047 | 0.043 | 0.048 |
| 1.5 | 0.5 | 5000 | 0.046 | 995 | 0.047 | 0.042 | 0.047 |
| 1.5 | 0.6 | 5000 | 0.035 | 995 | 0.047 | 0.043 | 0.047 |
| 1.5 | 0.7 | 5000 | 0.031 | 995 | 0.047 | 0.044 | 0.047 |
| 1.5 | 0.8 | 5000 | 0.030 | 995 | 0.047 | 0.045 | 0.047 |
| 1.5 | 0.9 | 5000 | 0.037 | 995 | 0.047 | 0.048 | 0.047 |
| 1.5 | 0.2 | 10000 | 0.201 | 1991 | 0.033 | 0.034 | 0.034 |
| 1.5 | 0.3 | 10000 | 0.089 | 1991 | 0.033 | 0.031 | 0.033 |
| 1.5 | 0.4 | 10000 | 0.048 | 1991 | 0.033 | 0.030 | 0.033 |
| 1.5 | 0.5 | 10000 | 0.031 | 1991 | 0.033 | 0.030 | 0.033 |
| 1.5 | 0.6 | 10000 | 0.025 | 1991 | 0.033 | 0.030 | 0.033 |
| 1.5 | 0.7 | 10000 | 0.021 | 1991 | 0.033 | 0.031 | 0.033 |
| 1.5 | 0.8 | 10000 | 0.022 | 1991 | 0.033 | 0.032 | 0.033 |
| 1.5 | 0.9 | 10000 | 0.026 | 1991 | 0.033 | 0.033 | 0.033 |
| 1.75 | 0.2 | 100 | 0.890 | 22 | 0.469 | 0.478 | 0.443 |
| 1.75 | 0.3 | 100 | 0.590 | 22 | 0.471 | 0.388 | 0.448 |
| 1.75 | 0.4 | 100 | 0.378 | 22 | 0.489 | 0.378 | 0.457 |
| 1.75 | 0.5 | 100 | 0.276 | 22 | 0.479 | 0.378 | 0.441 |
| 1.75 | 0.6 | 100 | 0.222 | 22 | 0.493 | 0.399 | 0.446 |
| 1.75 | 0.7 | 100 | 0.183 | 22 | 0.470 | 0.408 | 0.449 |
| 1.75 | 0.8 | 100 | 0.169 | 22 | 0.491 | 0.430 | 0.463 |
| 1.75 | 0.9 | 100 | 0.201 | 22 | 0.466 | 0.439 | 0.442 |
| 1.75 | 0.2 | 250 | 0.652 | 54 | 0.264 | 0.253 | 0.252 |
| 1.75 | 0.3 | 250 | 0.400 | 54 | 0.265 | 0.225 | 0.255 |
| 1.75 | 0.4 | 250 | 0.266 | 54 | 0.263 | 0.219 | 0.252 |
| 1.75 | 0.5 | 250 | 0.201 | 54 | 0.260 | 0.219 | 0.249 |
| 1.75 | 0.6 | 250 | 0.153 | 54 | 0.262 | 0.226 | 0.251 |
| 1.75 | 0.7 | 250 | 0.120 | 54 | 0.258 | 0.229 | 0.250 |
| 1.75 | 0.8 | 250 | 0.108 | 54 | 0.264 | 0.239 | 0.251 |
| 1.75 | 0.9 | 250 | 0.125 | 54 | 0.263 | 0.250 | 0.251 |
| 1.75 | 0.2 | 500 | 0.520 | 107 | 0.181 | 0.173 | 0.173 |
| 1.75 | 0.3 | 500 | 0.308 | 107 | 0.181 | 0.154 | 0.173 |
| 1.75 | 0.4 | 500 | 0.213 | 107 | 0.179 | 0.152 | 0.172 |
| 1.75 | 0.5 | 500 | 0.159 | 107 | 0.180 | 0.152 | 0.172 |
| 1.75 | 0.6 | 500 | 0.114 | 107 | 0.180 | 0.156 | 0.174 |
| 1.75 | 0.7 | 500 | 0.084 | 107 | 0.179 | 0.157 | 0.171 |
| 1.75 | 0.8 | 500 | 0.077 | 107 | 0.179 | 0.164 | 0.173 |
| 1.75 | 0.9 | 500 | 0.088 | 107 | 0.180 | 0.171 | 0.171 |
| 1.75 | 0.2 | 1000 | 0.404 | 214 | 0.123 | 0.119 | 0.119 |
| 1.75 | 0.3 | 1000 | 0.242 | 214 | 0.123 | 0.107 | 0.119 |
| 1.75 | 0.4 | 1000 | 0.172 | 214 | 0.122 | 0.104 | 0.118 |
| 1.75 | 0.5 | 1000 | 0.118 | 214 | 0.125 | 0.107 | 0.120 |
| 1.75 | 0.6 | 1000 | 0.080 | 214 | 0.124 | 0.108 | 0.119 |
| 1.75 | 0.7 | 1000 | 0.060 | 214 | 0.122 | 0.109 | 0.118 |
| 1.75 | 0.8 | 1000 | 0.054 | 214 | 0.123 | 0.112 | 0.118 |
| 1.75 | 0.9 | 1000 | 0.062 | 214 | 0.123 | 0.118 | 0.118 |
| 1.75 | 0.2 | 2000 | 0.324 | 428 | 0.088 | 0.083 | 0.084 |
| 1.75 | 0.3 | 2000 | 0.199 | 428 | 0.087 | 0.077 | 0.084 |
| 1.75 | 0.4 | 2000 | 0.141 | 428 | 0.085 | 0.073 | 0.082 |
| 1.75 | 0.5 | 2000 | 0.086 | 428 | 0.086 | 0.074 | 0.082 |
| 1.75 | 0.6 | 2000 | 0.057 | 428 | 0.087 | 0.076 | 0.083 |
| 1.75 | 0.7 | 2000 | 0.043 | 428 | 0.086 | 0.077 | 0.083 |
| 1.75 | 0.8 | 2000 | 0.038 | 428 | 0.087 | 0.079 | 0.083 |
| 1.75 | 0.9 | 2000 | 0.045 | 428 | 0.087 | 0.083 | 0.084 |
| 1.75 | 0.2 | 5000 | 0.244 | 1070 | 0.054 | 0.052 | 0.052 |
| 1.75 | 0.3 | 5000 | 0.159 | 1070 | 0.055 | 0.047 | 0.053 |
| 1.75 | 0.4 | 5000 | 0.094 | 1070 | 0.054 | 0.046 | 0.052 |
| 1.75 | 0.5 | 5000 | 0.054 | 1070 | 0.055 | 0.047 | 0.053 |
| 1.75 | 0.6 | 5000 | 0.035 | 1070 | 0.054 | 0.047 | 0.052 |
| 1.75 | 0.7 | 5000 | 0.027 | 1070 | 0.054 | 0.048 | 0.052 |
| 1.75 | 0.8 | 5000 | 0.024 | 1070 | 0.054 | 0.050 | 0.052 |
| 1.75 | 0.9 | 5000 | 0.028 | 1070 | 0.055 | 0.052 | 0.053 |
| 1.75 | 0.2 | 10000 | 0.199 | 2139 | 0.038 | 0.037 | 0.037 |
| 1.75 | 0.3 | 10000 | 0.133 | 2139 | 0.039 | 0.034 | 0.037 |
| 1.75 | 0.4 | 10000 | 0.067 | 2139 | 0.039 | 0.033 | 0.037 |
| 1.75 | 0.5 | 10000 | 0.038 | 2139 | 0.038 | 0.033 | 0.037 |
| 1.75 | 0.6 | 10000 | 0.025 | 2139 | 0.038 | 0.034 | 0.037 |
| 1.75 | 0.7 | 10000 | 0.019 | 2139 | 0.038 | 0.034 | 0.037 |
| 1.75 | 0.8 | 10000 | 0.017 | 2139 | 0.038 | 0.035 | 0.037 |
| 1.75 | 0.9 | 10000 | 0.020 | 2139 | 0.038 | 0.037 | 0.037 |
| 1.9 | 0.2 | 100 | 1.038 | 22 | 0.568 | 0.542 | 0.504 |
| 1.9 | 0.3 | 100 | 0.672 | 22 | 0.563 | 0.432 | 0.507 |
| 1.9 | 0.4 | 100 | 0.428 | 22 | 0.531 | 0.416 | 0.488 |
| 1.9 | 0.5 | 100 | 0.274 | 22 | 0.549 | 0.430 | 0.498 |
| 1.9 | 0.6 | 100 | 0.189 | 22 | 0.562 | 0.449 | 0.510 |
| 1.9 | 0.7 | 100 | 0.139 | 22 | 0.586 | 0.460 | 0.492 |
| 1.9 | 0.8 | 100 | 0.114 | 22 | 0.585 | 0.493 | 0.512 |
| 1.9 | 0.9 | 100 | 0.125 | 22 | 0.566 | 0.502 | 0.511 |
| 1.9 | 0.2 | 250 | 0.761 | 55 | 0.287 | 0.267 | 0.264 |
| 1.9 | 0.3 | 250 | 0.462 | 55 | 0.287 | 0.232 | 0.264 |
| 1.9 | 0.4 | 250 | 0.280 | 55 | 0.292 | 0.232 | 0.268 |
| 1.9 | 0.5 | 250 | 0.179 | 55 | 0.287 | 0.233 | 0.264 |
| 1.9 | 0.6 | 250 | 0.127 | 55 | 0.288 | 0.238 | 0.264 |
| 1.9 | 0.7 | 250 | 0.092 | 55 | 0.292 | 0.247 | 0.268 |
| 1.9 | 0.8 | 250 | 0.077 | 55 | 0.288 | 0.253 | 0.265 |
| 1.9 | 0.9 | 250 | 0.082 | 55 | 0.288 | 0.262 | 0.268 |
| 1.9 | 0.2 | 500 | 0.601 | 110 | 0.193 | 0.179 | 0.177 |
| 1.9 | 0.3 | 500 | 0.350 | 110 | 0.196 | 0.162 | 0.182 |
| 1.9 | 0.4 | 500 | 0.213 | 110 | 0.197 | 0.162 | 0.184 |
| 1.9 | 0.5 | 500 | 0.137 | 110 | 0.195 | 0.162 | 0.181 |
| 1.9 | 0.6 | 500 | 0.095 | 110 | 0.192 | 0.163 | 0.180 |
| 1.9 | 0.7 | 500 | 0.070 | 110 | 0.193 | 0.168 | 0.181 |
| 1.9 | 0.8 | 500 | 0.056 | 110 | 0.193 | 0.172 | 0.180 |
| 1.9 | 0.9 | 500 | 0.058 | 110 | 0.192 | 0.176 | 0.180 |
| 1.9 | 0.2 | 1000 | 0.487 | 220 | 0.133 | 0.123 | 0.125 |
| 1.9 | 0.3 | 1000 | 0.272 | 220 | 0.134 | 0.113 | 0.126 |
| 1.9 | 0.4 | 1000 | 0.161 | 220 | 0.133 | 0.110 | 0.124 |
| 1.9 | 0.5 | 1000 | 0.105 | 220 | 0.134 | 0.112 | 0.125 |
| 1.9 | 0.6 | 1000 | 0.073 | 220 | 0.136 | 0.115 | 0.126 |
| 1.9 | 0.7 | 1000 | 0.052 | 220 | 0.134 | 0.117 | 0.126 |
| 1.9 | 0.8 | 1000 | 0.041 | 220 | 0.135 | 0.119 | 0.124 |
| 1.9 | 0.9 | 1000 | 0.042 | 220 | 0.136 | 0.124 | 0.128 |
| 1.9 | 0.2 | 2000 | 0.399 | 438 | 0.095 | 0.087 | 0.088 |
| 1.9 | 0.3 | 2000 | 0.212 | 438 | 0.094 | 0.079 | 0.088 |
| 1.9 | 0.4 | 2000 | 0.126 | 438 | 0.095 | 0.078 | 0.088 |
| 1.9 | 0.5 | 2000 | 0.082 | 438 | 0.093 | 0.078 | 0.087 |
| 1.9 | 0.6 | 2000 | 0.055 | 438 | 0.094 | 0.080 | 0.087 |
| 1.9 | 0.7 | 2000 | 0.038 | 438 | 0.094 | 0.081 | 0.087 |
| 1.9 | 0.8 | 2000 | 0.029 | 438 | 0.093 | 0.083 | 0.087 |
| 1.9 | 0.9 | 2000 | 0.030 | 438 | 0.095 | 0.086 | 0.088 |
| 1.9 | 0.2 | 5000 | 0.303 | 1093 | 0.059 | 0.054 | 0.055 |
| 1.9 | 0.3 | 5000 | 0.153 | 1093 | 0.059 | 0.050 | 0.056 |
| 1.9 | 0.4 | 5000 | 0.091 | 1093 | 0.059 | 0.049 | 0.055 |
| 1.9 | 0.5 | 5000 | 0.058 | 1093 | 0.059 | 0.049 | 0.055 |
| 1.9 | 0.6 | 5000 | 0.037 | 1093 | 0.059 | 0.051 | 0.056 |
| 1.9 | 0.7 | 5000 | 0.024 | 1093 | 0.059 | 0.051 | 0.056 |
| 1.9 | 0.8 | 5000 | 0.018 | 1093 | 0.060 | 0.053 | 0.056 |
| 1.9 | 0.9 | 5000 | 0.019 | 1093 | 0.059 | 0.054 | 0.055 |
| 1.9 | 0.2 | 10000 | 0.245 | 2187 | 0.041 | 0.038 | 0.039 |
| 1.9 | 0.3 | 10000 | 0.123 | 2187 | 0.042 | 0.035 | 0.040 |
| 1.9 | 0.4 | 10000 | 0.072 | 2187 | 0.042 | 0.035 | 0.039 |
| 1.9 | 0.5 | 10000 | 0.043 | 2187 | 0.041 | 0.035 | 0.039 |
| 1.9 | 0.6 | 10000 | 0.025 | 2187 | 0.041 | 0.035 | 0.039 |
| 1.9 | 0.7 | 10000 | 0.017 | 2187 | 0.041 | 0.036 | 0.039 |
| 1.9 | 0.8 | 10000 | 0.013 | 2187 | 0.042 | 0.038 | 0.040 |
| 1.9 | 0.9 | 10000 | 0.013 | 2187 | 0.041 | 0.038 | 0.039 |
| Sample Size | RMSE3 | RMSE4 | ||
|---|---|---|---|---|
| 0.2 | 3.0 | 20 | 0.514 | 1.477 |
| 0.4 | 3.0 | 20 | 0.495 | 1.293 |
| 0.6 | 3.0 | 20 | 0.421 | 1.134 |
| 0.8 | 3.0 | 20 | 0.401 | 1.012 |
| 1.0 | 3.0 | 20 | 0.446 | 0.912 |
| 1.2 | 3.0 | 20 | 0.510 | 0.823 |
| 1.4 | 3.0 | 20 | 0.588 | 0.757 |
| 1.6 | 3.0 | 20 | 0.680 | 0.733 |
| 1.8 | 3.0 | 20 | 0.763 | 0.746 |
| 2.0 | 3.0 | 20 | 0.851 | 0.798 |
| 0.2 | 5.0 | 20 | 0.512 | 1.424 |
| 0.4 | 5.0 | 20 | 0.421 | 1.245 |
| 0.6 | 5.0 | 20 | 0.346 | 1.110 |
| 0.8 | 5.0 | 20 | 0.354 | 0.989 |
| 1.0 | 5.0 | 20 | 0.411 | 0.882 |
| 1.2 | 5.0 | 20 | 0.497 | 0.776 |
| 1.4 | 5.0 | 20 | 0.572 | 0.687 |
| 1.6 | 5.0 | 20 | 0.668 | 0.635 |
| 1.8 | 5.0 | 20 | 0.763 | 0.625 |
| 2.0 | 5.0 | 20 | 0.859 | 0.623 |
| 0.2 | 3.0 | 30 | 0.471 | 1.486 |
| 0.4 | 3.0 | 30 | 0.468 | 1.299 |
| 0.6 | 3.0 | 30 | 0.416 | 1.127 |
| 0.8 | 3.0 | 30 | 0.407 | 1.006 |
| 1.0 | 3.0 | 30 | 0.453 | 0.895 |
| 1.2 | 3.0 | 30 | 0.521 | 0.817 |
| 1.4 | 3.0 | 30 | 0.605 | 0.753 |
| 1.6 | 3.0 | 30 | 0.686 | 0.734 |
| 1.8 | 3.0 | 30 | 0.767 | 0.748 |
| 2.0 | 3.0 | 30 | 0.859 | 0.803 |
| 0.2 | 5.0 | 30 | 0.476 | 1.433 |
| 0.4 | 5.0 | 30 | 0.419 | 1.234 |
| 0.6 | 5.0 | 30 | 0.339 | 1.103 |
| 0.8 | 5.0 | 30 | 0.354 | 0.987 |
| 1.0 | 5.0 | 30 | 0.422 | 0.885 |
| 1.2 | 5.0 | 30 | 0.494 | 0.782 |
| 1.4 | 5.0 | 30 | 0.583 | 0.709 |
| 1.6 | 5.0 | 30 | 0.685 | 0.658 |
| 1.8 | 5.0 | 30 | 0.770 | 0.669 |
| 2.0 | 5.0 | 30 | 0.874 | 0.673 |
| 0.2 | 3.0 | 40 | 0.426 | 1.494 |
| 0.4 | 3.0 | 40 | 0.467 | 1.300 |
| 0.6 | 3.0 | 40 | 0.418 | 1.123 |
| 0.8 | 3.0 | 40 | 0.414 | 0.996 |
| 1.0 | 3.0 | 40 | 0.462 | 0.891 |
| 1.2 | 3.0 | 40 | 0.519 | 0.806 |
| 1.4 | 3.0 | 40 | 0.595 | 0.750 |
| 1.6 | 3.0 | 40 | 0.689 | 0.724 |
| 1.8 | 3.0 | 40 | 0.784 | 0.757 |
| 2.0 | 3.0 | 40 | 0.887 | 0.807 |
| 0.2 | 5.0 | 40 | 0.444 | 1.439 |
| 0.4 | 5.0 | 40 | 0.412 | 1.242 |
| 0.6 | 5.0 | 40 | 0.338 | 1.100 |
| 0.8 | 5.0 | 40 | 0.354 | 0.989 |
| 1.0 | 5.0 | 40 | 0.422 | 0.880 |
| 1.2 | 5.0 | 40 | 0.487 | 0.784 |
| 1.4 | 5.0 | 40 | 0.584 | 0.720 |
| 1.6 | 5.0 | 40 | 0.680 | 0.674 |
| 1.8 | 5.0 | 40 | 0.769 | 0.692 |
| 2.0 | 5.0 | 40 | 0.881 | 0.711 |
| 0.2 | 3.0 | 50 | 0.393 | 1.500 |
| 0.4 | 3.0 | 50 | 0.447 | 1.292 |
| 0.6 | 3.0 | 50 | 0.411 | 1.117 |
| 0.8 | 3.0 | 50 | 0.414 | 0.989 |
| 1.0 | 3.0 | 50 | 0.466 | 0.885 |
| 1.2 | 3.0 | 50 | 0.530 | 0.805 |
| 1.4 | 3.0 | 50 | 0.612 | 0.737 |
| 1.6 | 3.0 | 50 | 0.698 | 0.719 |
| 1.8 | 3.0 | 50 | 0.778 | 0.751 |
| 2.0 | 3.0 | 50 | 0.870 | 0.828 |
| 0.2 | 5.0 | 50 | 0.411 | 1.451 |
| 0.4 | 5.0 | 50 | 0.402 | 1.235 |
| 0.6 | 5.0 | 50 | 0.344 | 1.098 |
| 0.8 | 5.0 | 50 | 0.357 | 0.983 |
| 1.0 | 5.0 | 50 | 0.415 | 0.879 |
| 1.2 | 5.0 | 50 | 0.502 | 0.788 |
| 1.4 | 5.0 | 50 | 0.598 | 0.716 |
| 1.6 | 5.0 | 50 | 0.677 | 0.691 |
| 1.8 | 5.0 | 50 | 0.782 | 0.703 |
| 2.0 | 5.0 | 50 | 0.858 | 0.729 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
SenGupta, A.; Roy, M. An Universal, Simple, Circular Statistics-Based Estimator of α for Symmetric Stable Family. J. Risk Financial Manag. 2019, 12, 171. https://doi.org/10.3390/jrfm12040171
SenGupta A, Roy M. An Universal, Simple, Circular Statistics-Based Estimator of α for Symmetric Stable Family. Journal of Risk and Financial Management. 2019; 12(4):171. https://doi.org/10.3390/jrfm12040171
Chicago/Turabian StyleSenGupta, Ashis, and Moumita Roy. 2019. "An Universal, Simple, Circular Statistics-Based Estimator of α for Symmetric Stable Family" Journal of Risk and Financial Management 12, no. 4: 171. https://doi.org/10.3390/jrfm12040171
APA StyleSenGupta, A., & Roy, M. (2019). An Universal, Simple, Circular Statistics-Based Estimator of α for Symmetric Stable Family. Journal of Risk and Financial Management, 12(4), 171. https://doi.org/10.3390/jrfm12040171




