Abstract
Bad decisions have harmful effects on the quality of human life and an increase of their duration expands these undesirable effects. Systematic bad decisions related to dividend policy can affect the investors’ quality of life in the long-term. We propose an agent-based model for the estimation of the duration of systematically making bad decisions, with an application on dividend policy. We propose an algorithm that can be used in modelling the interaction between different classes of shareholders and for predicting this duration. We perform numerical simulations based on this model using NetLogo 6.0.4. We prove that, as a result of agents’ interaction, in some conditions, the duration of systematically making bad decisions can be very long: some numerical simulations suggest that, in some circumstances, this duration can significantly exceed the human lifetime. Additionally, in some conditions, the company can fail before the power is switched. This duration can increase dramatically if the shareholders have a great level of trust in the management’s decisions. As an implication, a greater concern for the quality of financial education, and more performant instruments for controlling the power’s decisions are required.
1. Introduction
At least for some persons, it seems very easy to define a decision as being good or bad. For instance, a religious, racist, or nationalistic individual can have no doubt that all he or she does in the name of his or her faith is a good decision, and what is contrary to the accepted dogma is a bad decision. On the other hand, other persons would consider, without any doubt, that the decisions made in the name of the same values are bad decisions, which affect the life and its quality of many innocent people (e.g., children, victims of different kinds of discrimination), science, education, etc. Finally, all the parties can produce different arguments for supporting their values and can refuse the others’ arguments. In other cases, even the negative effects can be identified by everyone, the parties involved in making decisions support one decision as being the only one acceptable. For instance, for some persons it is difficult to support measures for protecting the environment and reduce emissions, since the GDP/capita is too small and not enough railways and factories are present in the region. For others, sustainable development is a necessity (e.g., Lele 1991; Doyle and Stiglitz 2014; Armeanu et al. 2018). Unfortunately, the incapacity to provide a unanimous final answer for the best decision, and if one decision is definitely bad (at least for some people) it does not mean that the problem is not important. Even more, even if consensus between parties is not achieved, it does not mean that the problem does not exist.
For some reasons, finance can be a safer place for defining a bad decision. One main advantage is that finance has a clear ideology (e.g., the search for maximizing the shareholders’ wealth) (Ross et al. 2010; Belghitar et al. 2019), and also clear instruments for monitoring the deviations from it. If one decision determines a loss (e.g., a decrease in shareholders’ wealth), it is a bad decision. Additionally, if a decision determines a lower return than another, it can be reasonably considered that selecting this one was worse. Probably for this reason the presence of making bad decisions is well documented in economics and finance in different contexts (e.g., De Bondt and Thaler 1995; Rubinstein 2001; Ariely 2009; Campbell et al. 2009; Taleb et al. 2009; Gennaioli et al. 2015, etc.). However, all these conclusions can be formulated only after these decisions produce their outcomes (ex post) (Campbell et al. 2009). Initially, most of them are decisions in a risk-context, which can be better or worse than the others. For instance, making decisions based on the assumed knowledge at one moment, using the classical model, based on Gaussian distribution for modelling return distribution and, thus, neglecting the extreme values, determined losses which were unexpected initially (Taleb 2007; Taleb et al. 2009). It was a bad decision to use the Gaussian distribution but, for the most part, the deciders were convinced that using the Gaussian distribution for modelling returns is a good, normal, one.
In some cases, these decisions can become systematic. Human history provides many examples of making systematically bad decisions, sometimes after a long time of making good decisions (Gilbert 2011; Lucero et al. 2011; Harari 2015). In this paper, we analyze the duration of systematically making bad decisions, defined as the length in time of making erroneous mistakes, based on the same mental algorithm. The end of making bad decisions can be decided by other parties; from this perspective, the end of making bad decisions can be the end of the decider’s position.
In corporate finance theory, based on the principle of maximizing the shareholders’ wealth (Ross et al. 2010; Belghitar et al. 2019), the impact of the existence of one decider that make systematic bad decisions is only marginally considered. However, in some cases, the quality of different decisions can be disputable (Morgan and Hansen 2006). Moreover, this issue becomes more complicated if multi-objective optimization is considered (Lovric et al. 2010). In the same line, different cultural (not financial) values can have an impact on financial decisions (Fidrmuc and Jacob 2010; Ucar 2016). These different values can result in contrary decisions, which can be considered “good” or “bad”, depending on each culture’s perspective.
In certain cases, some agents can make good decisions, but they have to accept the viewpoint imposed by some other agents, which make bad decisions. For instance, at the corporate level, dividend policy is decided by vote, democratically. Some bad decisions made by the dominating group of voters can affect the rational shareholders’ wealth. People are different, thus, different features (e.g., overconfidence, pattern recognition, etc.) of some agents can affect the wealth of other shareholders (Campbell et al. 2009). Bad decisions, but, even more, systematic bad decisions, can affect the investors’ quality of life in the long-term (and sometimes, probably irreversible; for instance, in the case of retired employees, regarding their pension plans).
Shareholders’ wealth can be affected by dividend policy. Dividend policy is discussed in many papers and is approached from different perspectives (Graham and Dodd 1951; Lintner 1964; Miller and Modigliani 1961; Miller and Scholes 1978; Easterbrook 1984; La Porta et al. 2000a, 2000b; Fidrmuc and Jacob 2010; Shao et al. 2010; Ucar 2016; Jiang et al. 2017, etc.). The discussions regarding an optimal dividend policy still continue. Contrary viewpoints can be considered good or bad, depending on each side’s perspective. Thus, the dividend payout decision is a possible fruitful field for analyzing the duration of systematically making bad decisions.
In this paper, we propose a model in which shareholders are not aware instantly about a bad decision made by the shareholders that dominate annual general meetings of shareholders (hereafter, AGM; in Table 1 are provided all the abbreviations and notations). In our paper, we consider a non-homogenous behavior of the shareholders implied in setting a dividend policy at an AGM (and supporting or not the power) through agent-based models (Zambrano and Olaya 2017; Negahban and Smith 2018; McGroarty et al. 2019, etc.). Especially, due to the diversity of the conclusions regarding dividend policy, this is a good field for analysis of the impact of systematically making bad decisions. It is very difficult to state a priori that a decision is bad or not, because each dividend policy can be considered right for some reasons, and wrong for others. For this reason, considering a non-homogenous behavior for the shareholders can be a contribution to the existent literature. Some studies consider, in other contexts, different classes of shareholders, for instance, controlling shareholders versus minority shareholders (La Porta et al. 2000a), each one having specific interests. In our paper, we consider a more general case, in which shareholders can follow the same objective, but having different opinions about the manner of action, or having different perceptions about the company’s perspectives. Moreover, we consider that the option of different shareholders for supporting one of another policy can be reversible in time.

Table 1.
Notations used in the text.
Bad decisions have an impact on the company’s performance. However, their impact is not instant. One issue that complicate even more the problem in some cases is the long period between the moment of making the decision and the moment when the outputs can be checked (see Figure 1). A bad decision is difficult to be identified in earliest stages, but only after a long period. In general, decisions regarding dividend payout (DPRt) are made considering exclusively expected levels for indicators, for example comparing the expected internal rate of return of the proposed investment project (Et(IRRt+1)) with the expected required rate of return (Et(kD,t+1)).
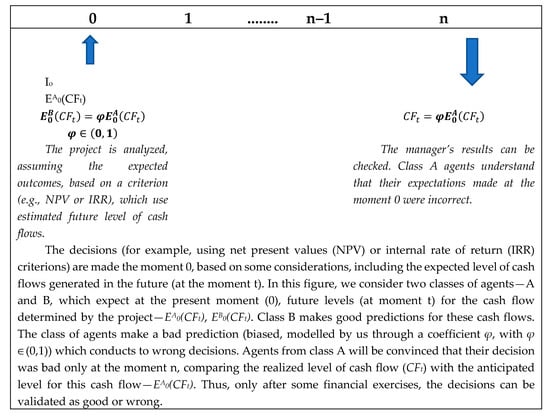
Figure 1.
The long period between the decision-making process and the control of its result.
In this paper, we propose a model, which can be used in simulations, regarding the impact of systematically making bad decisions. We use this model for the estimation of the duration of systematically making bad decisions (hereafter, DSMBD). Some of the issues considered in our study can be found in Dragotă (2016). However, comparative to Dragotă (2016), this study proposes an application for financial management. This application concerns the dividend policy.
We propose an agent-based model for the estimation of DSMBD. We use NetLogo 6.0.4 (https://ccl.northwestern.edu/netlogo/), which offers an easy-to-understand programming language and a graphical interface, where the changes in the simulated environment can be observed in real-time.
In the proposed model, we consider four classes of shareholders, each of them with a specific behavior (as in Dragotă 2016). We propose an algorithm that can be used in modelling their interaction and for predicting DSMBD, considering variables used in the practice of making decisions regarding dividend policy. Thus, the changes in voting structure can be followed in real-time.
We perform some simulations based on the proposed model. We prove that, as a result of agents’ interaction, in some conditions, DSMBD can be very long. Thus, some numerical simulations suggest that, in some circumstances, this duration can significantly exceed the human lifetime. Additionally, in some conditions, the company can fail before the power is switched. DSMBD can increase dramatically if the shareholders have a great level of trust in the management’s decisions. The democratic voting process and the good intentions are not sufficient conditions for making good decisions. As an implication, a greater concern for the quality of financial education, and more performant instruments for controlling the power’s decisions, are required.
Considering its implications, this paper can be useful both for academics and for practitioners. A better understanding of the process of systematically making bad decisions can be beneficial for the academic literature. Highlighting the determining factors that can determine an increase of DSMBD and performing simulations for finding their impact can be a contribution in understanding a less studied process. As far as we know, this approach is new in analyzing dividend policy. For practitioners (e.g., investors in capital markets, other shareholders), it provides a decisional tool for anticipating some possible problems in the decision-making process, for a better control at the corporations’ level. A systematic bad decision can affect the investor’s wealth, with potentially disastrous effects in the long-term. For instance, a person can find that his or her pension funds are negatively affected when it is too late to make adjustments in portfolios.
The remainder of this paper is organized as follows. The next section presents the theoretical background. For our purpose, we have proposed a model for the estimation of DSMBD. Section 3 provides the model design and describes its implementation in NetLogo 6.0.4. Some numerical results are presented and discussed in Section 4. Section 5 concludes this paper.
2. Theoretical Background
Our study is concerned with analyzing the impact of making a systematic bad decision (for the estimation of DSMBD) in AGM, when deciding if the financial resources are directed through dividends or for investments in the company. We propose an agent-based model, which is implemented in NetLogo 6.0.4. Below, the theoretical background related to this issue is presented.
The literature regarding bad decisions made by individuals is vast (e.g., Shefrin and Statman 1985; De Bondt and Thaler 1995; Odean 1998; Rubinstein 2001; Hirshleifer 2001; Campbell et al. 2009; Gennaioli et al. 2015; Morgan and Hansen 2006; Dragotă 2016; Pikulina et al. 2017). In this paper, we consider the impact of making systematically bad decisions in connection to setting a dividend policy. Dividend policy, respectively fixing the portion of the net earnings paid to shareholders, can be an interesting application for analyzing DSMBD. A dividend policy can be considered as optimal from some perspectives, but non-optimal from others. For instance, paying dividends can be a sign of the companies’ interest of protecting the shareholders’ rights (La Porta et al. 2000b), but can also be interpreted as a smaller amount of financial resources for adopting profitable investment projects. For this reason, the discussions in AGM can determine different solutions, which can be optimal, or, to the contrary, wrong, even if they are made with very good intentions and based on rational arguments (sometimes, with sound foundations in financial literature). The harmonization between these contradictory viewpoints can be impossible. For this reason, some agents can be convinced that their decisions are good and can persist in making bad decisions.
At the AGM, shareholders decide the amount that will be paid as dividend. The decision regarding dividend payment consists in fixing a percent p from the net earnings (dividend payout ratio, DPR) to be paid as dividend (a percent equal to (1 − p) is allocated for investments)1. Shareholders are different from many perspectives. A large amount of financial literature analyzes the relations between large (controlling) shareholders and minority shareholders (Shleifer and Vishny 1986; Holderness 2003). Many papers analyze the controlling shareholders’ behavior in connection with dividend policy, mainly related to agency problems (Easterbrook 1984; La Porta et al. 2000b; Fidrmuc and Jacob 2010). Additionally, in their decision, shareholders are (or at least, can be) influenced by the managers proposals regarding the dividend proposed to be paid. Usually, they approve (or not) DPR proposed by management. This can determine also agency costs (Jensen and Meckling 1976). Another segmentation of shareholders in different groups can be made considering some socio-cultural factors. Some papers provide evidence between dividend policies across the world, considering different socio-cultural as determinants of dividend policy (Fidrmuc and Jacob 2010; Shao et al. 2010; Ucar 2016). As an effect, a segmentation in different groups (dominant or not) can be useful in modelling shareholders’ behavior.
Many papers are concerned about dividend policy. Dividend policy is approached from many perspectives (Graham and Dodd 1951; Walter 1956; Miller and Modigliani 1961; Miller and Scholes 1978; Bhattacharya 1979; Kalay 1980; Easterbrook 1984; La Porta et al. 2000a, 2000b; Fidrmuc and Jacob 2010; Shao et al. 2010; Ucar 2016; Jiang et al. 2017, etc.). Some classical papers propose rules in recommending an optimal dividend payout (Graham and Dodd 1951; Walter 1956). Other studies identify the factors that influence the dividend payment (Lintner 1964; La Porta et al. 2000a; Fidrmuc and Jacob 2010; Jiang et al. 2017). Miller and Modigliani (1961) prove, under some restrictive assumptions, the irrelevance of dividend payout on shareholders’ wealth. Different real-life factors challenge the implications of Miller and Modigliani theorem: agency problems (Easterbrook 1984; La Porta et al. 2000a), behavioral and cultural influences (Shao et al. 2010; Ucar 2016), imperfect information and signaling effects (Bhattacharya 1979; Kalay 1980), taxation (Miller and Scholes 1978; Hanlon and Hoopes 2014), etc.
Many papers provide recommendations regarding an optimal dividend policy, contrary to the irrelevance theorem of Miller and Modigliani (1961). For instance, Walter (1956) proposes that dividends should be paid only in the case in which the company can’t offer to its shareholders a rate of return higher than the required rate of capital. Other papers suggest that dividends should be paid if the company is interested by the minority shareholders’ interests (Graham and Dodd 1951; La Porta et al. 2000b). The list of papers providing more or less advices regarding an optimal dividend policy also provide a multitude of divergent advice: pay, do not pay, or it does not matter. Thus, the literature on dividend policy does not produce a consensus for an optimal dividend policy. For this reason, we can reasonably assume that, even if they are convinced that their arguments have sound theoretical foundations, some agents will make, depending by case, a bad decision, and they would not be able to consider their decision is bad. Practically, they will not be able to characterize their decisions as being bad. This situation will conduce to making systematically bad decisions. It is very possible (and reasonably plausible) to appear a segmentation between two classes of agents, respectively the ones that are making good decisions (being convinced that they are making a good decision) and the ones that are making a bad decision (but being also convinced that they are making a good decision).
Over the last years, applications using agent-based modelling have been successfully used in various research fields such as: supply chain management (Walsh and Wellman 2000; Pan and Choi 2016), strategic simulation (Bunn and Oliveira 2003; Wang et al. 2016; Negahban and Smith 2018), operational risk and organizational networks (Frels et al. 2006), decision-making (Rai and Allada 2006; Dougherty et al. 2017; Zambrano and Olaya 2017), customers flows (Tan et al. 2008), algorithmic trading strategies (McGroarty et al. 2019), transport systems (Delcea et al. 2018a, 2018b; Monteiro et al. 2014), etc. The main advantage of agent-based models is their ability to take into account the heterogeneity of agents (McGroarty et al. 2019), meaning that each agent can have his or her own characteristics and can make decisions in accordance with them. Additionally, one agent can observe the environment and the actions/decisions made by other agents and he or she can decide which course of the action will be taken in the following. The adaptability and the responsiveness capacities of the agents make them actively observe and interact with the environment and with other agents. Moreover, the bounded-rationality property that the agents possess make them act as human beings while facing a decision situation, namely, they are just partially and not completely rational (Wilensky and Rand 2015). The abilities and the properties of the agents make the agent-based modelling proper to human-behavior modelling. Strictly related to the AGM situation, the agent-based modelling can be very useful for modelling the shareholders’ behavior if we consider they do not share the same opinion in the context of a democratic vote. In this particular context, the agent-based modelling approach enables us to define several categories (named “classes” in our paper) to which the decision persons might belong to. Depending on one’s class, several properties are enabled, which ensure that the agent is acting according to the assumed behavior of its class. From the interaction among the agents, different emerging behaviors and decisions can be observed and analyzed in depth.
Regarding the usage of the agent based modelling in the research area through the use of NetLogo platform, between 2003–2018, 512 papers using NetLogo have been published in ISI Web-of-Science in areas such as: operations research and management, business economics, finance, computer science, engineering, education and educational research, social sciences, mathematics, environmental sciences and ecology, etc. Thus, we have decided to use NetLogo for conducting the simulations as it offers a friendly user interface and an easy-to-write and understand syntax (Wilensky and Rand 2015). Among the characteristics of NetLogo, which differentiate it from other agent-based modelling software, one can underline that it is a free software, easy to use, and easy to understand even by persons outside the programming area, with a visual interface which allows one to see the changes in agents’ properties in real-time, while the program is running, and which provides an extensive and up-to-date documentation.
The next section presents our model.
3. The Model
This section presents a model for the estimation of DSMBD. We structured this section in six sub-sections. The problem is defined in Section 3.1. We considered four classes of shareholders. Their behavior is described in Section 3.2. In Section 3.3 we discuss the evolution of the company’s performance when making bad decisions persists. The agents’ behavior is strongly influenced by the differences between the realized rate of return and their required rate of return. The manner of the estimation of the required rate of return is discussed in Section 3.4. We discuss the model inputs in Section 3.5. Section 3.6 presents the implementation in NetLogo. The decision-making process can be followed sequentially in Table 2.

Table 2.
The sequence of the decision-making process.
We have chosen the agent-based modelling for representing, analyzing and simulation of this situation as in this type of modelling, each agent, representing a shareholder, can be endowed with a series of properties that makes it unique comparative to the other agents. Even more, as each different groups of shareholders have different expectations and points of view related to the company’s efficient management, the inter-group properties of these agents are easy to model and represent. Even more, the NetLogo software offers a specific tool which enables one to conduct several experiments under different conditions and to observe, in real-time, the agents’ behavior, as individuals and as a part of a particular group.
3.1. The Problem
Shareholders, and also managers, analyze the company’s performance from different viewpoints and use different indicators to measure it. This performance is the result of many different decisions, so the extraction of a single, unique, bad one, for analyzing its impact can be difficult. We have chosen the moment of the AGM for shareholders to simultaneously consider two issues: (1) deciding if the manager is maintained in function; and (2) deciding the amount paid as dividend.
We can present sequentially the series of decisions as:
The decisions made by the management (DECt) are right for the period [−t, 0]:
In the period [1, n], decisions are systematically wrong:
The problem is to find n (the moment in which the manager is switched). In other words, we estimate the duration of making systematically bad decisions (DSMBD) in setting one dividend policy. This duration expresses the length in time of making an inappropriate decision regarding dividend policy. This decision is supported by some agents (some shareholders which sustain this decision) even it is wrong. The supporters of the good decision are in minority (they do not reach more than 50% from the votes even they are right). The switch in sustaining the bad decision can be considered synonymous with a switch in power (as in Dragotă 2016). The manager is switched when the percent of shareholders that support them is lower than 50%. We consider four classes of shareholders, described in Section 3.2.
Dividend policy (respectively, the percent of the net earnings paid as dividend, or, alternatively, the percent invested in the company) is decided in AGM (at the moment t + 1), usually based on the manager’s recommendation, only if NEt > 0. If NEt ≤ 0, we cannot discuss about a dividend policy.
The manager (supported by the controlling shareholders) (Class A agents in our model, see Section 3.2) proposes a dividend policy based on her or his expectations regarding the internal rate of return for the investment projects proposed to be financed from the retained earnings—Et−1(IRRt) and on their expectation regarding the evolution of the market—Et−1(kMt) (this is the market return for projects with a similar risk2):
If E1(IRR2) ≥ E1(kM2), then: DIV1 = 0
If E1(IRR2) < E1(kM2), then: DIV1 = NE1
In other words, the dividend payout ratio (DPR) is:
In our paper, this decision-making process is based on Walter (1956), sometimes defined as the “residual” dividend policy. This policy is widely recognized by practitioners, but also in the financial literature (Aivazian et al. 2006; Kim and Kim 2019).
In practice, the dividend payout ratio follows a Tweedie distribution (Dragotă et al. 2019). This distribution is characterized by a modal value of 0%. This modal value of 0% is confirmed by other studies (Denis and Osobov 2008; Fama and French 2001; von Eije and Megginson 2008; Fatemi and Bildik 2012; Kuo et al. 2013). In our paper, the option between 0% and 100% DPR is considered only for simplifications reasons. It is not the purpose of our paper to justify an optimal dividend policy, but to analyze the impact of a bad decision.
As long as the supporters of the power are dominant (respectively, more than 50% votes), the decision proposed by the management will be adopted.
The decisions made by the management (DECt) are right for the period [−t, 0]. They are determining a stock of wealth for shareholders, which can induce in shareholders a status of safety and also a state of trust for the manager’s performance. A company’s return is, to a large extent, the effect of some decisions made in the past. As an effect, investors can judge one manager’s performance (the return in one year, source for dividend payments) even if this is the effect of the choices made in the past. Moreover, even the results of some projects are not desirable from a financial viewpoint, in real life their effects are combined with the other projects’ effects, finally, the shareholders having access only to some synthetic indicators at the company’s level (like cash flows, net earnings or return on equity). The initial stock of wealth allows the management to make some wrong decisions because their impact is not fatal for the company.
For simplification, in our paper, we assume that no agency problems occur in making the dividend payment decisions, even if they are documented in financial literature (see, for instance, Easterbrook 1984; La Porta et al. 2000a; Kim and Kim 2019) and they can be an interesting field of study. We also assumed that information is symmetrical (as in Dragotă 2016) and we ignored the impact of taxation3.
We assume, as in Dragotă (2016), that the decisions regarding dividend payments are made democratically, in AGM. The decisions are based on the principle one share, one vote4. The ownership structure is assumed to be dispersed. We consider that all the shareholders are exercising their vote. The dividend payout decision requires a simple majority (respectively, more than 50% votes). In our study, we consider that the decisions are made in each financial exercise and we consider in each financial exercise only one round of votes (we consider the final vote for each AGM).
For modelling reasons, we consider that the shareholders do not sell their shares in the considered period and, also, no new shares are issued in this period5. As an effect, the total number of shares and the initial number of shareholders remain constant.
3.2. Shareholders’ Typology and Behavior
We consider four classes of shareholders (agent types) (as in Dragotă 2016) (denoted A, B, C, and D), with xti is the percent in total shares (which correspond to the voting power), with xtA + xtB + xtC + xtD = 1. Each of classes of shareholders (agents) is characterized by some features, described below.
Class A represents the decider (the power). In our study, they are the group of shareholders that make systematically bad decisions, until the power is switched. Agents from this class are overconfident in their decisions (De Bondt and Thaler 1995; Hirshleifer 2001), even if they are wrong. Due to the outputs produced, the behavior of this class of shareholders can be suspected by agency problems, even if they are not real. Additionally, it seems reasonable to anticipate that Class A will suggest that the other shareholders should support their decisions, probably insisting on arguments like trust the expertise of the management which is acting in the benefits of the other shareholders.
Class B represents the opposition, respectively, the group of shareholders that understand that the decisions of the Class A are bad, but are not in power. Their rationality is useless for convincing agents from Class A, and even Class B can be associated with keywords like financial rationality, abilities, or literacy6.
As an observation, each rational agent probably knows that that the expected level of one indicator can be different from its realized level (see Figure 2). As an effect, it can be very difficult to argue that one forecast is, indeed, wrong.
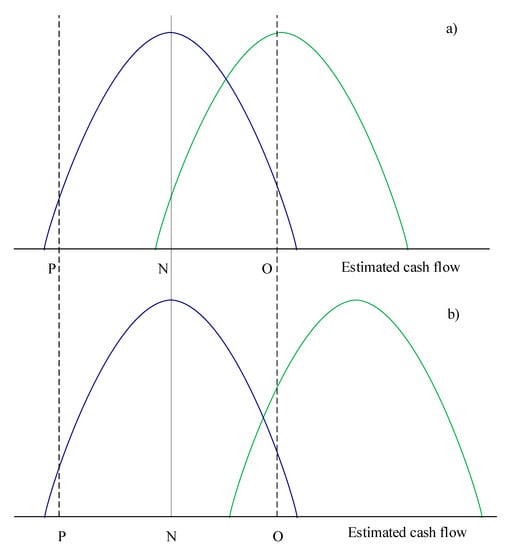
Figure 2.
Two forecasts for future level of cash flows–for each class of agents—A (with green) and B (with blue). The two classes estimate the level of indicator (the estimated cash flow) through its probability distribution. The forecast made by one class of agents (B—in the left, with blue) is better than the second one (A—in the right, with green). In (a), if the realized cash flow is N (from normal, very plausible for the first class of agents’ forecast), it can be interpreted by the second class of agents as an unfavorable scenario of evolution (but still plausible, according to their forecast). A realized cash flow equal to O (from optimistic) should confirm the good forecast made by class A (even it is only a relatively unusual good performance based on the forecast made by class B). (b) depicts an even greater dissonance between the two forecasts. In this case, if the realized cash flow is N, class A can realize that the forecast was indeed wrong, but, also, they can consider that an extreme event occurred.
Class C includes the shareholders that can change their decision. They can learn from past errors (for them, evolution is the keyword). Initially, xtC = 0. Firstly, they support the power (they are in Class D), but they change their vote.
Class D is a residual in this model: xtD = 1 − xA − xB − xtC. Initially, we assume that they support the power, but they can migrate to Class C.
According to these assumptions, xA and xB are fixed (constant in time), with xA ∈ (0, 0.5) and xB ∈ (0, 0.5), and xC and xD are variable. Initially, x0C = 0.
The power is switched democratically when the number of voters against the power is higher than 50% (respectively: xB + xtC > 50%). As in Dragotă (2016), the switch in power in AGM is determined exclusively by the changes in the voting preferences of Class C. Shareholders from Class C analyze the quality of decisions based on the results recorded by the company. As such, they do not evaluate the quality of the decision regarding the dividend payments made at the present moment (t) (see Section 3.1), but the quality of the decisions made in the past moments, as a proxy for the quality of the present decision (see also Table 2). The decision’s quality is quantified comparing the recorded performance with the required one. We considered that the performance is proxied by the realized return of equity (ROEt). Similarly, the required level of performance is quantified through a required rate of return (ROEt*). The evolution of ROE is described in Section 3.3. In Section 3.4 we discuss how they estimate their required rate of return.
At each moment t (the annual shareholders’ meeting), Class C agents: (a) analyze if the realized return of equity ROEt has an acceptable level (is higher or, at least, equal to the required rate of return, ROEt*), deciding if they support the power; and (b) if they support the power, they vote for the recommended dividend policy. Additionally, the AGM is the moment when the agents from Class C can change their voting preference: (i) if ROEt ≥ ROEt*, they are satisfied and keep their voting preference (they will continue to support the power); (ii) if ROEt < ROEt*, they change their voting preferences, voting against the power. As a result, shareholders from Class A are imposing their viewpoint until: xtB + xtC > 0.5.
The changing preferences for Class C agents can be modelled through many different rules (Dragotă 2016). In this paper, we consider two cases. First, we assume that once an agent from Class D pass to Class C, his or her decision is irreversible (situation 1, S1). Secondly (situation 2, S2), we assume that:
We consider that xtC is determined based on the rule defined in Dragotă (2016):
xtC = xt−1C + αt ·Mt ·xt−1D
In this relation, the percent of shareholders which vote against the power (xtC) increase from financial exercise to financial exercise if they are unsatisfied by the level of the rate of return; however, they can change their opinion if the results are satisfying them, becoming more trustful in management’s decision.
As such:
Additionally, by definition, xtC should be at least equal cu 0: xtC ≥ 0.
Mt is a random variable uniformly distributed on [0,1], which can be interpreted as a magnitude of the interest to change the power (as in Dragotă 2016). If Mt = 0, this can be interpreted as a total indifference to the level of return, but also as a conservative attitude (a high level for conservatism, see Hirshleifer 2001). If Mt = 1, the entire population of agents from class D will change their voting preference, joining the class C of agents, immediately after the level of realized return is below the required rate of return. Mt is dependent of different factors that can have an impact on wealth and for this reason is not constant in time7.
xtC can be written as:
xtC = xt−1C + αt ·Mt (1 − xA − xB − xt−1C) = xt−1C (1 − αt ·Mt) + (1 − xA − xB)αt ·Mt
As an observation, shareholders from Class D can migrate to Class C even in the case in which the company records a low performance, even if the dividend policy was correct.
3.3. Evolution of Return on Equity
In our model, shareholders use the return on equity (ROE) recorded by the company in their analyses regarding the quality of the management’s decision (decisions supported by Classes A and D of shareholders) (see Section 3.2). We consider that the company is 100% equity-financed, so assets = equity. Retained earnings are the sole source for financing the investment projects (as in Walter 1956). ROE, as a proxy for the company’s level of performance, is determined by different factors, more or less anticipable. In an over-simplified model (but useful for our application), we can consider ROE as a cumulative effect of: (i) the normal (usual, unaffected by the decider’s bad decision) ROE; (ii) the decrease in ROE determined by making the bad decision; and (iii) the impact of other factors, which are acting independently by the first two components. In other words, ROE is affected by bad decisions, but also by bad forecasts.
The initial level of ROE0 can be considered as a benchmark. It is determined by the ratio between net earnings recorded in the year 0 (NE0) and the level of equity in the previous year:
We consider the period [−t, 0] as being one characterized by making good decisions. As such, in this study, these historical levels of performance are important only for comparing the actual results with them. Moreover, we can assume that all the quantity of information is incorporated in this initial level of ROE, ROE0. The level of total assets at the moment 0, TA0 is considered as an initial stock of shareholders’ wealth and is another input in the model.
However, ROE0 is only a punctual benchmark. Some aleatory factors can influence even this normal ROE. Even if the company maintains constant its level of assets, most probably ROE1 will be different than ROE0. Even if it is considered that no bad decisions are made, it can be assumed that ROEt is a random variable. Each year, NEt is determined by the ROEt (the return at which the capital is invested) and the stock of capital in the previous year, by the accounting identity:
The level of total assets on one moment t (TAt) can be determined as a function by the level of the total assets in the previous year (TAt−1), net earnings (NEt) and dividend payments (DIVt):
In another form:
As an effect, NEt has t components: (1) a component resulted as the return of equity at which initial stock of assets is invested; (2) the result of the investments made in the first financial exercise (t = 1); and (3) the result of the investments made in the second financial exercise (t = 2), …, (t) the result of the investments made in the last financial exercise (t = t − 1). The components (2), (3), … (t) are a function of the internal rates of returns (IRR) corresponding to the invested capital in each financial exercise.
In our model, shareholders decide to invest in the company if the invested capital will determine an increase of their wealth higher than investing on the financial market in projects of similar risk (Walter 1956; Ross et al. 2010)8. In this study, we assume that the decisions at the AGM are made comparing the expected IRR, respectively, Et−1(IRRt), with the expectations regarding the capital market return, Et−1(kMt).
It can be noticed that IRRt ≠ Et−1(IRRt). IRRt = Et−1(IRRt) only in the case of a perfect forecast. Since management is making a bad decision, IRRt can be considered as a random variable, normally distributed, with a mean and a finite standard deviation9,10.
As an observation, in this equation, Et−1(IRRt) is the expectation made by the Class A agents, and it is not optimal (it can be assumed by Class B shareholders make a better prediction).
The bad decision is modelled through a coefficient, bd, which is applied to the estimated rate of internal return of the new projects. For instance, 0.1 means that the expected internal rate of return is over-valuated by 10% by the deciders.
Similarly, market return can be considered as a random variable, normal distributed, with a mean and a finite standard deviation11.
Table 3 presents TA, NE, and ROE in some financial exercises and their rules of evolution12. It can be noted that the bad decisions have impact only if the net earnings are invested in the company. For a numerical simulation of the financial indicators, see Table 4.

Table 3.
Evolution of financial indicators.

Table 4.
Numerical simulation for the financial indicators (example).
3.4. Required Rates of Return
In our paper, we consider in the same model two of the investor’s statuses. On the one hand, investors are making their analysis from a portfolio management’s perspective, being interested about characteristics like return13 and risk of their portfolio, making their judgments in estimating a required rate of return, etc. (Markowitz 1952). On the other hand, they are shareholders and they participate in AGM, being implied in making decisions at the corporate level, like adopting the dividend payout ratio.
In our model, two required rates of return appear as benchmarks, respectively, Et−1(kMt) and ROEt*.
The first indicator is related to the expectations regarding the capital market. We assume that this indicator is estimated by the shareholders. In our study, we consider that, when proposing a dividend policy, the management compares the expected IRR with Et−1(kMt) and decides to pay dividends only if Et−1(kMt) > Et−1(IRRt).
Regarding the second indicator, the required ROE (ROEt*), investors can consider different benchmarks (for a survey, see Dragotă et al. 2013). However, basically, all of these benchmarks can be reduced to two fundamental approaches. On the one hand, they expect a rate of return, related to the characteristic of the project (for instance, in CAPM they require a rate of return higher than risk-free rate and they claim also a risk premium—otherwise they will reject the project) (Ross et al. 2010). On the other hand, investors analyze the alternatives available on the capital market (if they do not invest in the proposed project, what alternatives are available?).
First (but not necessary in this order), they require an acceptable rate of return14. It can be considered that they consider as normal to record (at least) a level for return equal to a benchmark assumed to be normal (this can be considered as an “anchor”). It can be considered that the rate of equity return recorded in the past can be considered as a proxy for future performance. As such, in this study, we assumed, conventionally, that investors consider an average for the past five financial exercises as a first proxy for the required rate of return (noted APROE).
Secondly, shareholders require a rate of return related to IRR (a function of the risk of the investment project). Finally, they accept renouncing dividends in exchange for an acceptable estimated IRR for the projects adopted.
Thirdly, investors analyze the capital market conditions. They compare their return with the returns recorded by other investors, for other investment projects. In our model, we consider that they compare their performance with the capital market return (kMt).
Finally, we can assume that all these benchmarks can be adjusted for some extraordinary events. Shareholders can have a relative tolerance before dismissing their management15. We introduce a coefficient of intolerance for the manager’s performance—τ, with τ ∈ [0, 1]. If this tolerance is maximal, that means that τ = 0. In other words, shareholders do not require a rate of return (however, they require that their wealth to be maintained at the same level, so min (ROEt*) = 0). If shareholders decide to maintain the management in function only if the company records a level of ROE higher than ROEt*, we can state τ = 1 (they are totally intolerant in the case of a lack of performance). This coefficient can be related to some socio-cultural factors (e.g., Schwartz 2006).
Thus:
3.5. Model Inputs
Table 5 presents the model inputs. Many discussions can be made regarding the level of the numerical values included in simulations. The purpose of this article is not to provide levels for these indicators based on empirical data or theoretical literature. The choice of these parameters should be adapted, case by case, function of the analyzed company. For some input variables we have preferred to use round values (e.g., TA0).

Table 5.
Model inputs.
Other variables are intensely studied in different contexts. For instance, if the investors in our simulations should consider the past records of market return as proxies for expected market return, the variability of these expectations should be somehow exaggerated. For instance, the Standard and Poor Composite Index rose 85% (between 1927 and 1929) and 69% (between 1954 and 1957), but fell 56% (between 1973 and 1975) and 52% (between 1929 and 1933) (the standard deviation of the market return was 17%) (Shiller 1987). In our simulations, we have preferred a more prudent approach and we have considered Et−1(kMt) to be normally distributed16, with a mean of 2.5 and a standard deviation of 2.5. Of course, the program allows for considering a larger range.
3.6. Implementation in NetLogo
Four types of agents (see Section 3.2) have been created in NetLogo 6.0.4, belonging to either class A (in red), B (in green), C (in cyan), or D (in orange), as presented in Figure 3. Additionally, four monitors are available for each type of members, where one can easily observe how the number of the members in each category is changing in real-time. Additionally, we have offered the agents the possibility to return to group D, by setting the switch “Group-C-Can-Return-To-Group-D” to “on”. The agents passing from group C to group D will be highlighted by coloring them in yellow, while their number, in real-time, will be counted in the “Group-D-Returned-Members” monitor. The NetLogo code is provided in Appendix A.
Figure 3.
The types of agents created in NetLogo 6.0.4.
A series of variables have been considered in accordance with the model description presented above. The visual interface created in NetLogo 6.0.4. offers the possibility of setting some of these variables’ values at the beginning of the simulation, while the presence of monitors and graphs depicts their evolution in real-time (see Figure 4).
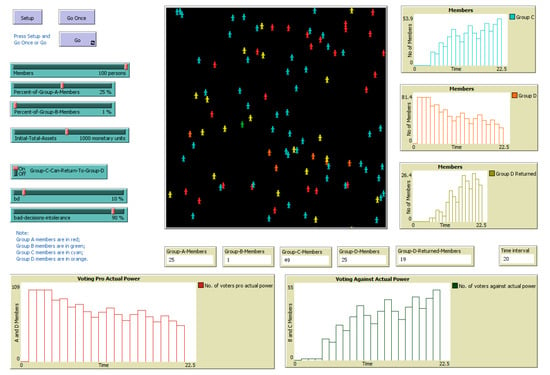
Figure 4.
A snapshot of the NetLogo 6.0.4. model’s interface at t = 20 ticks.
The simulation is stopping when the total number of members in groups A and D is smaller or equal than 50%. The “time interval” monitor depicts the number of ticks needed in order to change the power, where the tick is the time unit in NetLogo.
4. Numerical Results: Discussion
We have considered two main situations, described in Section 3.2, respectively: (i) Situation S1: group D members cannot return to their initial status (once they decide to enter in group C, they remain in this one); (ii) Situation S2: group D members can change their group (becoming member of group C if the performance of the company is changing in worse, but also re-becoming a member of D group if the performance of the company is changing in better). The first situation can be considered more optimistic (as it is easier to be followed), but the second one seems to be more connected to reality. For this reason, the DSMBD estimated in Situation S2 is the indicator which should be taken into account when a prudent approach is required.
For S1, different levels for “the tolerance for the manager’s performance” (τ) and “the impact of making bad decisions” (bd) have been considered (see Table 6 and Table 7). For each situation (S1-1 to S1-13) the model has been run 400 times and the average DSMBD in ticks has been extracted.

Table 6.
Simulation’s results for S1 when bd = 0.1.

Table 7.
Simulation’s results for S1 when τ = 0.5.
For the (S1-1)–(S1-7) situations, we have kept the value of bd constant at the level of 0.1 and we have changed the tolerance for the manager’s performance from 0 to 1. A level of bd = 0.1 can be interpreted as a systematic bad decision, but having a minor impact on financial performance. As a result, it has been observed that the average time (years) needed in order to stop the process of making bad decisions ranges between [12.29, 43.52], depending on the various values of the tolerance for the manager’s decision variable (see Figure 5). Obviously, a systematic bad decision with minor impact can remain unobserved for a longer period.
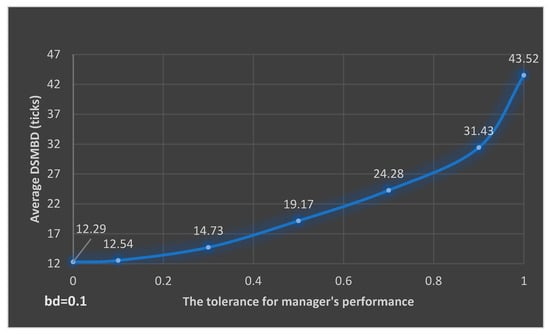
Figure 5.
Average DSMBD versus the tolerance for manager’s performance, when bd = 0.1 and S1 is considered.
As observation, even in the case of τ = 0, DSMBD can reach 10–14 years (iterations). Looking closer to the S1-1 situation in which we encounter zero tolerance for the manager’s performance, an average DSMBD of 12.29 years results. Comparing this to the case in which 10% tolerance is considered, the average DSMBD of 12.54 years is recorded. Considering the individual values obtained from the simulations, it can be observed that the most frequent recorded value is 11 years (in 26% of the cases), the amount of time needed for making bad decisions being in [10, 16] (see Figure 6).
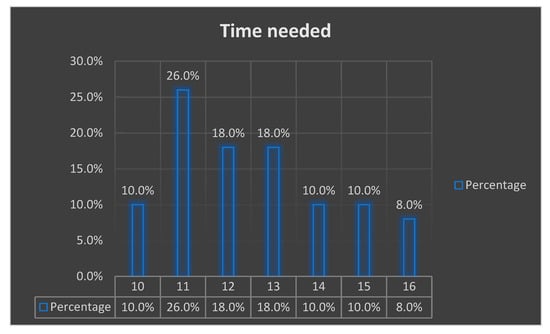
Figure 6.
DSMBD—situation S1-1.
Additionally, from simulations, 32.75% of the cases in S1-2 have reached a DSMBD of 13 units, being also the most frequent value. On the other hand, no particular distribution can be determined for S1-3 average time, as there were a series of most frequent values encountered through simulations, such as: 13, 18, 22, and 26. This situation also occurs for all the other cases starting with S1-4 until S1-7.
Now, considering the two extreme cases: no tolerance (S1-1) and total tolerance for the manager’s performance (S1-7), the average DSMBD difference is of 31.23 years, almost three and a half times more than in the no tolerance case. As expected, for the intermediate situations (S1-2 until S1-6), as the tolerance for manager’s performance is increasing, while the impact of making bad decisions is not changing, the average DSMBD increases.
Considering the S1-4, S1-8 until S1-13 cases, it can be observed that when the deciders have over-confidence in the values of the expected IRR, DSMBD is longer, even though the time difference among the situations with the smallest and the largest average time amount is of only 4.22 time units (see Table 7). All the other average DSMBD values range smoothly among the values recorded for the extreme cases (see Figure 7).
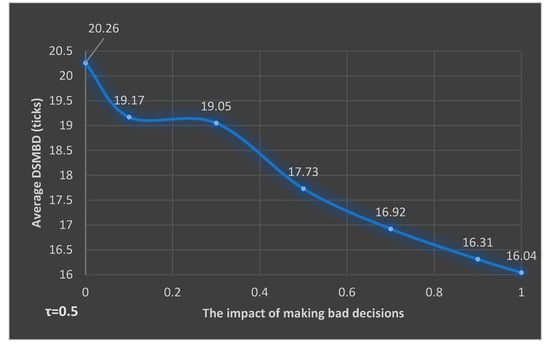
Figure 7.
Average DSMBD versus the impact of making bad decisions, when τ = 0.5 and S1 is considered.
Thus, among the two considered variables (the tolerance for the manager’s performance and the impact of making bad decisions), the tolerance for manager’s decisions has a greater impact, recording an average of 31.23 years (time units) when comparing the extreme cases with zero and total tolerance, while for the impact of making bad decisions considering the extreme cases, a time difference of only 4.22 years (time units) have been recorded. This result can suggest the important role of good monitoring processes, in accordance with Campbell et al. (2009).
We have made the same measurements for the S2 situation, in which the deciders can decide to return to group D. The results are summarized in Table 8 and Table 9 below.

Table 8.
Simulation’s results for S2 when bd = 0.1.

Table 9.
Simulation’s results for S2 when τ = 0.5.
Obviously, the greater the tolerance for the manager’s performance, the longer the average DSMBD is. However, it can be observed that, as the tolerance is higher, DSMBD can take extremely long periods of time until a normal situation is reached (see the S2-7 situation). This length (in years) substantially exceeds the normal life of companies which are in existence at this moment17.
Figure 8 depicts the evolution of the average DSMBD when considering different values for the tolerance for manager’s decision, ranging between zero tolerance (S2-1) and full tolerance (S2-7). It can easily be observed that a tolerance greater than 0.5 can have dramatic results on the DSMBD value.
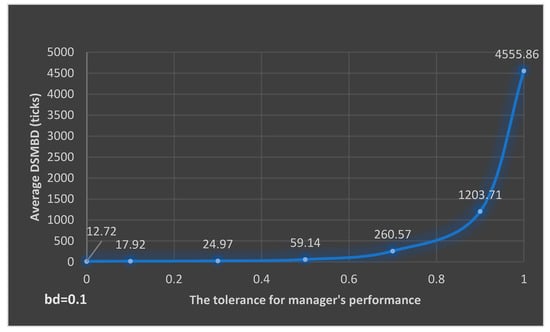
Figure 8.
Average DSMBD versus the tolerance for manager’s performance, when bd = 0.1 and S2 is considered.
In the extreme case of total tolerance (S2-7), the negative effects can perpetuate as much as possible, as people are continually changing their mind and switching groups, making DSMBD very long (supposing that the company can function in these conditions for such a long period).
Considering a low-tolerance situation (case S2-1), which can be plausible in some real-life situations, the average of such bad decisions’ time is 17.92 years, which can be characterized as a double time for not creating major problems within the analyzed economic entity. Moreover, as the tolerance for manager’s performance increases, DSMBD continues to increase, and it can be observed that, after a 0.5 tolerance, it is critically high, reaching, on average, more than 59.14 years (time units).
Comparing (S1-1)–(S1-7) with (S2-1)–(S2-7), it can be observed that for small values of tolerance for the manager’s decisions (τ), DSMBD has comparable values. For example, the time difference between S1-1 and S2-1 is of only 0.43 (practically, 0) years (time units), while for 0.1 tolerance is 5.38 years (cases S1-2 and S2-2), and for 0.3 tolerance is of 10.24 years (cases S1-3 and S2-3). Starting with 0.5 tolerance, differences for DSMBD become notable: 39.97 years for τ = 0.5, 236.29 for τ = 0.7. Higher levels of tolerance make the difference extremely high: 1172.28 years (time units) for 0.9 tolerance and 4512.34 years for total tolerance (τ = 1). Once more, the significant effect the degree of tolerance has on the average DSMBD can be underlined.
As for the impact of making bad decisions, the data in Table 9, shows, as in the previous cases (S2-8 until S2-13), that bd has only a reduced influence over the overall average bad decisions time, making only a 17.49-time units (years) difference.
Figure 9 presents the evolution of DSMBD for various values of the impact of making bad decisions. It can be observed that the decrease of the average DSMBD values is smooth as it was also in Figure 7. The only difference is that in this case the values of DSMBD are higher than in the (S1-8)–(S1-13) situations and the difference among the extreme values is higher in this case.
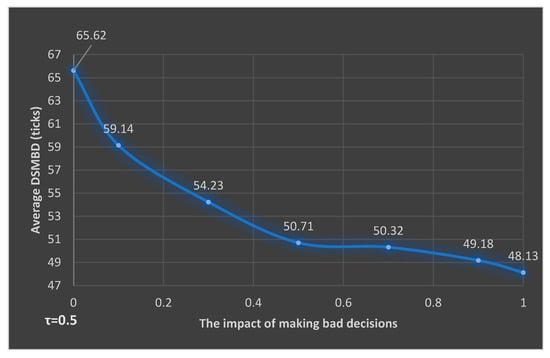
Figure 9.
Average DSMBD versus the impact of making bad decisions, when τ = 0.5 and S2 is considered.
Comparing the two situations (S1 and S2), it can be seen that in both of them, the deciders’ tolerance to manager’s bad decisions can make a difference, having a significant contribution to the overall average decision-making time.
Based on these simulations, we can conclude that the length of the DSMBD can be very long, probably exceeding the lifetime of the company. In some cases, the dominant group (class A in our model) can impose their viewpoint until the end of the company, while the group of rational shareholders (class B in our model) cannot impose theirs. Thus, in the absence of the improving the quality of making judgments and making better decisions, the existence of informed and rational investors is useless.
5. Conclusions
Bad decisions have an impact on the company’s performance. However, their impact is not instant. For this reason, the process of making bad decisions can be very persistent, especially if no agreement about the best solution is existent. In this paper, we propose a model in which shareholders are not instantly aware about a bad decision made by the shareholders that dominate the annual general meeting of shareholders (AGM). This paper analyzes the case in which, for different reasons, the deciders systematically make bad decisions regarding dividend payout. We use this model for the estimation of the DSMBD in setting one dividend policy. We have started from Dragotă (2016), as a general case, and we have made some adjustments in order to adapt this model for the case of financial management, respectively, for dividend policy. We use NetLogo 6.0.4 for modelling, which offers a graphical interface, where the changes in the simulated environment can be observed in real-time.
This paper considers the case in which, in voting one dividend policy or another, individuals are following different objectives based on different values. Unfortunately, the democratic vote and the good intentions are not sufficient for guaranteeing the avoidance of systematically making bad decisions (Dragotă 2016). Since the deciders are convinced that their decisions are right, they have no reason to change them until the results of their actions significantly affect themselves. However, as long as their wealth is determined by other factors, too, they can hardly differentiate between the effect of their decisions and the impact of these other factors. As an effect, they can still be convinced that they are making good decisions. Moreover, even if the outputs are not acceptable, these results can be explained not as the effect of some bad decisions, but as the effect of some nonsystematic, external effects.
Our paper analyzes the conditions in which making bad decisions can become a systematic phenomenon and proposes a model presented both mathematically and numerically on a small example in order to increase its understanding and readability. Using the advantages provided by the agent-based modelling and NetLogo 6.0.4, a model is created and numerically simulated in order to make a proper estimation of DSMBD. In our model, we consider four classes of shareholders, each of them with a specific behavior. We propose an algorithm that can be used in modelling their interaction and for predicting this duration. Thus, the changes in voting structure can be followed in real-time. As far as we know, this approach has not been used in the financial literature concerning dividend policy.
Some cases have been considered, depending on whether hat the deciders can change their groups or not. Additionally, different values for the involved variables have been considered and simulated 400 times each. It has been observed that the deciders’ tolerance to a manager’s bad decisions can make a difference in terms of time.
We prove that, in some circumstances, DSMBD can be very long. Its length can reach a very large number of years, exceeding in some conditions a human lifetime and the maximal age of existing companies on Earth at this moment. Moreover, it can be possible for DSMBD to increase dramatically if the shareholders have a great level of trust in the management’s decisions. Practically, in some conditions, the dominant group (controlling shareholders) can impose their viewpoint until the end of the company, while the group of rational shareholders cannot impose theirs. As a principal implication, an increase of the quality of financial education for top-management and shareholders, and, from here, more performant instruments for controlling the power’s decisions are required. After all, Campbell et al. (2009) warn that “Given the way the brain works, we can’t rely on leaders to spot and safeguard against their own errors in judgment. […] So rather than rely on the wisdom of experienced chairmen, the humility of CEOs, or the standard organizational checks and balances, we urge all involved in important decisions to explicitly consider whether red flags exist and, if they do, to lobby for appropriate safeguards.”
Of course, simulations provide only an artificial environment and our study and their findings can be easily attacked from this perspective. New directions for study can be related to two proposed inputs—the coefficient of impact of bad decisions (bd) and the coefficient of intolerance for the manager’s performance (τ). However, most of the parameters required in our model can be relatively easily imported in real-life, company level context.
Further, one interesting development of the study is to consider the agency problems which occur in dividend payment decision (see, for instance, Dragotă et al. 2009). In this case, multiple objective functions (Lovric et al. 2010), adaptable for different classes of shareholders, could be used. The manner in which the dividend payout is fixed can be a fruitful field of study, especially if the asymmetrical information, the power in negotiation, and the skills required for persuading other individuals to vote somehow are considered. In the same context, valuation the impact of combining financial and non-financial (e.g., ethical objectives) (Ballestero et al. 2012; Mallin 2016) can be another direction for study.
Author Contributions
Conceptualization: V.D.; formal analysis: V.D. and C.D.; investigation: V.D. and C.D.; methodology: V.D. and C.D.; software: C.D.; supervision: V.D.; validation: V.D. and C.D.; visualization: V.D. and C.D.; writing—original draft: V.D. and C.D.; writing—review and editing: V.D. and C.D.
Funding
This research received no external funding.
Acknowledgments
We wish to thank the participants of the 29th European Conference on Operational Research (Valencia, 8–11 July 2018) for their remarks. The remaining errors are ours.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The NetLogo Code
breed [ groupAmembers groupAmember ]
breed [ groupBmembers groupBmember ]
breed [ groupCmembers groupCmember ]
breed [ groupDmembers groupDmember ]
globals [
Previous-DIV
Previous-TA
Previous-NE
Previous-eIRR
All-Previous-ROE
]
to setup
clear-all
reset-ticks
set-default-shape turtles “person”
setup-people
end
to setup-people
create-groupAmembers Percent-of-Group-A-Members * Members/100 [
setxy random-xcor random-ycor
set color red
]
create-groupBmembers Percent-of-Group-B-Members * Members/100 [
setxy random-xcor random-ycor
set color green
]
create-groupCmembers 0 [
setxy random-xcor random-ycor
set color cyan
]
create-groupDmembers Members - count groupAmembers - count groupBmembers - count groupCmembers [
setxy random-xcor random-ycor
set color orange
end
to go
if count groupAmembers + count groupDmembers <= 0.5 * Members [
stop
]
if ticks = 0 [
go-0
]
if ticks = 1 or ticks = 2 [
go-12
]
if ticks > 2 [
go-3n
]
tick
end
to go-0
let TA Initial-Total-Assets
let ROE 0.025
let NE TA * ROE
let DIV 0
ifelse NE <= 0
[
set DIV 0
]
[
let eIRR (random-normal 2.5 0.8)/100
let eKm (random-normal 2.5 2.5)/100
ifelse eIRR >= eKm
[
set DIV 0
]
[
set DIV NE
]
]
set Previous-DIV DIV
set Previous-TA TA
set Previous-NE NE
set All-Previous-ROE (list ROE)
end
to go-12
let TA Previous-TA + Previous-NE - Previous-DIV
let ROE (random-normal 2.5 2.5)/100
let NE TA * ROE
let DIV 0
let eIRR 0
ifelse NE <= 0
[
set DIV 0
]
[
set eIRR (random-normal 2.5 0.8)/100
let eKm (random-normal 2.5 2.5)/100
ifelse eIRR >= eKm
[
set DIV 0
]
[
set DIV NE
]
]
set Previous-DIV DIV
set Previous-TA TA
set Previous-NE NE
set Previous-eIRR eIRR
set All-Previous-ROE fput ROE All-Previous-ROE
end
to go-3n
print word “#” ticks
let TA Previous-TA + Previous-NE - Previous-DIV
let ROE (random-normal 2.5 2.5)/100
let IRR (1.1 - random-float 0.2) * Previous-eIRR * (1 - bd/100)
let NE Previous-TA * ROE + Previous-NE * IRR;
print word “NE:” NE
let DIV 0
let eIRR 0
let eKm 0
ifelse NE <= 0
[
set DIV 0
]
[
set eIRR (random-normal 2.5 0.8)/100
set eKm (random-normal 2.5 2.5)/100
print word “eIRR:” eIRR
print word “eKm:” eKm
ifelse eIRR >= eKm
[
set DIV 0
]
[
set DIV NE
]
]
let CompanyROE NE/TA
print word “CompanyROE:” precision CompanyROE 3
let kM (1.1 - random-float 0.2) * eKm
let aproe compute-aproe
print word “aproe:” aproe
let ROE* bad-decisions-intolerance/100 * max (list kM IRR aproe)
print word “ROE*:” precision ROE* 3
ifelse CompanyROE < ROE*
[
ask n-of (0.2 * count groupDmembers) groupDmembers
[
set breed groupCmembers
set color cyan
]
]
[
print word “Scade C cu “ (0.2 * count groupCmembers)
; scade numarul de agenti din grupul C
if Group-C-Can-Return-To-Group-D
[
ask n-of (0.2 * count groupCmembers) groupCmembers
[
set breed groupDmembers
set color yellow
]
]
]
set Previous-DIV DIV
set Previous-TA TA
set Previous-NE NE
set Previous-eIRR eIRR
set All-Previous-ROE fput ROE All-Previous-ROE
end
to-report compute-aproe
let i 0;
let roe-sum 0
while [i < 5]
[
ifelse i < length All-Previous-ROE
[
set roe-sum roe-sum + item i All-Previous-ROE
]
[
let index length All-Previous-ROE - 1
set roe-sum roe-sum + item index All-Previous-ROE
]
set i i + 1
]
report roe-sum/5
end
References
- Aivazian, Varouj A., Laurence Booth, and Sean Cleary. 2006. Dividend Smoothing and Debt Ratings. Journal Financial and Quantitative Analysis 41: 439–53. [Google Scholar] [CrossRef]
- Ariely, Dan. 2009. The End of Rational Economics. Harvard Business Review 87: 78–84. [Google Scholar]
- Armeanu, Daniel Ştefan, Georgeta Vintilă, and Ștefan Cristian Gherghina. 2018. Empirical Study towards the Drivers of Sustainable Economic Growth in EU-28 Countries. Sustainability 10: 4. [Google Scholar] [CrossRef]
- Ballestero, Enrique, Mila Bravo, Blanca Perez-Gladish, Mar Arenas-Parra, and David Pla-Santamaria. 2012. Socially Responsible Investment: A multicriteria approach to portfolio selection combining ethical and financial objectives. European Journal of Operational Resrearch 216: 487–94. [Google Scholar] [CrossRef]
- Belghitar, Yacine, Ephraim Clark, and Konstantino Kassimatis. 2019. A measure of total firm performance: New insights for the corporate objective. Annals of Operations Research 281: 121–41. [Google Scholar] [CrossRef]
- Bhattacharya, Sudipto. 1979. Imperfect Information, Dividend Policy, and “The Bird in the Hand” Fallacy. Bell Journal of Economics 10: 259–70. [Google Scholar] [CrossRef]
- Bunn, Derek W., and Fernando S. Oliveira. 2003. Evaluating Individual Market Power in Electricity Markets via Agent-Based Simulation. Annals of Operations Research 121: 57–77. [Google Scholar] [CrossRef]
- Campbell, Andrew, Jo Whitehead, and Sydney Finkelstein. 2009. Why Good Leaders Make Bad Decisions. Harvard Business Review 87: 60–66. [Google Scholar]
- De Bondt, Werner F. M., and Richard H. Thaler. 1995. Chapter 13 Financial decision-making in markets and firms: A behavioral perspective. In Handbooks in Operations Research and Management Science. Edited by Robert Alan Jarrow, Vojislav Maksimovic and William T. Ziemba. Amsterdam: Elsevier, pp. 385–410. [Google Scholar] [CrossRef]
- Delcea, Camelia, Liviu-Adrian Cotfas, Nora Chiriță, and Ionuț Nica. 2018a. A Two-Door Airplane Boarding Approach When Using Apron Buses. Sustainability 10: 3619. [Google Scholar] [CrossRef]
- Delcea, Camelia, Liviu-Adrian Cotfas, and Ramona Păun. 2018b. Agent-Based Evaluation of the Airplane Boarding Strategies’ Efficiency and Sustainability. Sustainability 10: 1879. [Google Scholar] [CrossRef]
- Denis, David J., and Igor Osobov. 2008. Why do firms pay dividends? International evidence on the determinants of dividend policy. Journal of Financial Economics 89: 62–82. [Google Scholar] [CrossRef]
- Dougherty, Francis L., Nathaniel P. Ambler, and Konstantinos P. Triantis. 2017. A complex adaptive systems approach for productive efficiency analysis: Building blocks and associative inferences. Annals of Operations Research 250: 45–63. [Google Scholar] [CrossRef]
- Doyle, Michael W., and Joseph E. Stiglitz. 2014. Eliminating Extreme Inequality: A Sustainable Development Goal, 2015–2030. Ethics and International Affairs 28: 5–13. [Google Scholar] [CrossRef]
- Dragotă, Victor. 2016. When Making Bad Decisions Becomes Habit: Modelling the Duration of Making Systematically Bad Decisions. Economic Computation and Economic Cybernetics Studies and Research 50: 123–40. [Google Scholar]
- Dragotă, Mihaela, Victor Dragotă, Lucian Țâțu, and Delia Țâțu. 2009. Income Taxation Regulation and Companies’ Behaviour: Is the Romanian Companies’ Dividend Policy Influenced by the Changes in Income Taxation? Romanian Journal of Economic Forecasting 10: 76–93. [Google Scholar]
- Dragotă, Victor, Nicoleta Vintilă, and Ingrid-Mihaela Dragotă. 2013. Rights and Wrongs in the Estimation of the Cost of Equity: Theoretical and Practical Issues. Paper presented at the 8th International Conference AMIS IAAER 2013, Bucharest, Romania, June 12–13; pp. 484–504. [Google Scholar]
- Dragotă, Victor, Daniel Traian Pele, and Hanaan Yaseen. 2019. Dividend Payout Ratio follows a Tweedie Distribution: International evidence. Economics: The Open-Access, Open-Assessment E-Journal 13: 1–34. Available online: http://www.economics-ejournal.org/economics/journalarticles/2019-45 (accessed on 4 November 2019).
- Easterbrook, Frank H. 1984. Two Agency-Cost Explanations of Dividends. American Economic Review 74: 650–59. [Google Scholar]
- Fama, Eugene F., and Kenneth R. French. 2001. Disappearing Dividends: Changing Firm Characteristics or Lower Propensity to Pay? Journal of Financial Economics 60: 3–43. [Google Scholar] [CrossRef]
- Fatemi, Ali, and Recep Bildik. 2012. Yes, dividends are disappearing: Worldwide evidence. Journal of Banking and Finance 36: 662–77. [Google Scholar] [CrossRef]
- Fidrmuc, Jana P., and Marcus Jacob. 2010. Culture, agency costs and dividends. Journal of Comparative Economics 38: 321–39. [Google Scholar] [CrossRef]
- Frels, Judy, Debra Heisler, James Reggia, and Hans-Joachim Schuetze. 2006. Modeling the Impact of Consumer Interactions in Technology Markets. Journal of Cellular Automata 2: 91–103. [Google Scholar]
- Gennaioli, Nicola, Andrei Shleifer, and Robert Vishny. 2015. Neglected Risks: The Psychology of Financial Crises. American Economic Review 105: 310–14. [Google Scholar] [CrossRef]
- Gilbert, Daniel. 2011. Buried by bad decisions. Nature 474: 275–77. [Google Scholar] [CrossRef] [PubMed]
- Graham, Benjamin, and David L. Dodd. 1951. Security Analysis, 3rd ed. New York: McGraw-Hill, Book Company. [Google Scholar]
- Hanlon, Michelle, and Jeffrey L. Hoopes. 2014. What do firms do when dividend tax rates change? An examination of alternative payout responses. Journal of Financial Economics 114: 105–24. [Google Scholar] [CrossRef]
- Harari, Yuval Noah. 2015. Sapiens: A Brief History of Humankind. London: Vintage Books. [Google Scholar]
- Hirshleifer, David. 2001. Investor Psychology and Asset Pricing. Journal of Finance 56: 1533–97. [Google Scholar] [CrossRef]
- Holderness, Clifford G. 2003. A Survey of Blockholders and Corporate Control. Economic Policy Review 9: 51–64. [Google Scholar] [CrossRef]
- Jensen, Michael C., and William H. Meckling. 1976. Theory of the Firm: Managerial Behavior, Agency Costs and Ownership Structure. Journal of Financial Economics 3: 305–60. [Google Scholar] [CrossRef]
- Jiang, Fuxiu, Yunbiao Ma, and Beibei Shi. 2017. Stock liquidity and dividend payouts. Journal of Corporate Finance 42: 295–314. [Google Scholar] [CrossRef]
- Kalay, Avner. 1980. Signaling, Information Content, and the Reluctance to Cut Dividends. Journal of Financial and Quantitative Analysis 15: 855–69. [Google Scholar] [CrossRef]
- Kim, Hyunseok, and Ju Hyun Kim. 2019. Voluntary zero-dividend paying firms: characteristics and performance. Applied Economics 51: 5420–446. [Google Scholar] [CrossRef]
- Kuo, Jing-Ming, Dennis Philip, and Qingjing Zhang. 2013. What drives the disappearing dividends phenomenon? Journal of Banking and Finance 37: 3499–514. [Google Scholar] [CrossRef]
- La Porta, Robert, Florencio Lopez-de-Silanes, Andrei Shleifer, and Robert W. Vishny. 2000a. Agency Problems and Dividend Policies around the World. Journal of Finance 55: 1–33. [Google Scholar] [CrossRef]
- La Porta, Robert, Florencio Lopez-de-Silanes, Andrei Shleifer, and Robert W. Vishny. 2000b. Investor Protection and Corporate Governance. Journal of Financial Economics 58: 3–27. [Google Scholar] [CrossRef]
- Lele, Sharachchandra M. 1991. Sustainable Development: A Critical Review. World Development 19: 607–21. [Google Scholar] [CrossRef]
- Lintner, John. 1964. Optimal Dividends and Corporate Growth under Uncertainty. Quarterly Journal of Economics 78: 49–95. [Google Scholar] [CrossRef]
- Lovric, Milan, Uzay Kaymak, and Jaap Spronk. 2010. A conceptual model of investor behavior. In Advances in Cognitive Systems (IET Control Engineering Series, 71). Edited by Samia Nefti-Meziani and John O. Grey. London: Institution of Engineering and Technology, pp. 369–94. [Google Scholar]
- Lucero, Lisa J., Joel D. Gunn, and Vernon L. Scarborough. 2011. Climate Change and Classic Maya Water Management. Water 3: 479–94. [Google Scholar] [CrossRef]
- Mallin, Christine A. 2016. Corporate Governance, 5th ed. Oxford: Oxford University Press. [Google Scholar]
- Mare, Codruța, Simona Laura Dragoș, Ingrid-Mihaela Dragotă, and Cristian Dragoș. 2019. Insurance Literacy and Spatial Diffusion in the Life Insurance Market: A Subnational Approach in Romania. Eastern European Economics 57: 375–96. [Google Scholar] [CrossRef]
- Markowitz, Harry. 1952. Portfolio Selection. Journal of Finance 7: 77–91. [Google Scholar] [CrossRef]
- McGroarty, Frank, Ash Booth, Enrico Gerding, and V.L. Raju Chinthalapati. 2019. High frequency trading strategies, market fragility and price spikes: An agent based model perspective. Annals of Operations Research 282: 217–44. [Google Scholar] [CrossRef]
- Miller, Merton H., and Franco Modigliani. 1961. Dividend Policy, Growth, and the Valuation of Shares. Journal of Business 34: 411–33. [Google Scholar] [CrossRef]
- Miller, Merton H., and Myron S. Scholes. 1978. Dividends and taxes. Journal of Financial Economics 6: 333–64. [Google Scholar] [CrossRef]
- Monteiro, Nuno, Rosaldo Rossetti, Pedro Campos, and Zafeiris Kokkinogenis. 2014. A Framework for a Multimodal Transportation Network: An Agent-based Model Approach. Transportation Research Procedia 4: 213–27. [Google Scholar] [CrossRef]
- Morgan, John, and James Hansen. 2006. Escalating Commitment to Failing Financial Decisions: Why Does It Occur? Journal of Business & Leadership: Research, Practice, and Teaching (2005–2012) 2: 37–45. Available online: http://scholars.fhsu.edu/jbl/vol2/iss1/6 (accessed on 4 November 2019).
- Negahban, Ashkan, and Jefrey S. Smith. 2018. A joint analysis of production and seeding strategies for new products: An agent-based simulation approach. Annals of Operations Research 268: 41–62. [Google Scholar] [CrossRef]
- Nenova, Tatiana. 2003. The value of corporate voting rights and control: A cross-country analysis. Journal of Financial Economics 68: 325–51. [Google Scholar] [CrossRef]
- Odean, Terrance. 1998. Are Investors Reluctant to Realize Their Losses? Journal of Finance 53: 1775–98. [Google Scholar] [CrossRef]
- Pan, An, and Tsan-Min Choi. 2016. An agent-based negotiation model on price and delivery date in a fashion supply chain. Annals of Operations Research 242: 529–57. [Google Scholar] [CrossRef]
- Pikulina, Elena, Luc Renneboog, and Philippe Tobler. 2017. Overconfidence and investment: An experimental approach. Journal of Corporate Finance 43: 175–92. [Google Scholar] [CrossRef]
- Rai, Rahul, and Venkat Allada. 2006. Agent-based optimization for product family design. Annals of Operations Research 143: 147–56. [Google Scholar] [CrossRef]
- Ross, Stephen A., Randolph W. Westerfield, and Jeffrey Jaffe. 2010. Corporate Finance, 9th ed. New York: McGraw-Hill/Irwin. [Google Scholar]
- Rubinstein, Mark. 2001. Rational Markets: Yes or No? The Affirmative Case. Financial Analysts Journal 57: 15–29. [Google Scholar] [CrossRef]
- Samuelson, W., and R. J. Zeckhauser. 1988. Status Quo Bias in Decision Making. Journal of Risk & Uncertainty 1: 7–59. [Google Scholar]
- Schwartz, Shalom H. 2006. A Theory of Cultural Value Orientations: Explication and Applications. Comparative Sociology 5: 137–82. [Google Scholar] [CrossRef]
- Shao, Liang, Chuck C.Y. Kwok, and Omrane Guedhami. 2010. National culture and dividend policy. Journal of International Business Studies 41: 1391–414. [Google Scholar] [CrossRef]
- Shefrin, Hersh, and Meir Statman. 1985. The Disposition to Sell Winners Too Early and Ride Losers Too Long: Theory and Evidence. Journal of Finance 40: 777–90. [Google Scholar] [CrossRef]
- Shiller, Robert J. 1987. The Volatility of Stock Market Prices. Science 235: 33–37. [Google Scholar] [CrossRef] [PubMed]
- Shleifer, Andrei, and Robert W. Vishny. 1986. Large Shareholders and Corporate Control. Journal of Political Economy 94: 461–88. [Google Scholar] [CrossRef]
- Taleb, Nassim N. 2007. The Black Swan: The Impact of Highly Improbable. New York: Random House. [Google Scholar]
- Taleb, Nassim N., Daniel G. Goldstein, and Mark W. Spitznagel. 2009. The Six Mistakes Executives Make in Risk Management. Harvard Business Review 87: 78–81. [Google Scholar]
- Tan, WenAn, Weiming Shen, Lida Xu, Bosheng Zhou, and Li Ling. 2008. A Business Process Intelligence System for Enterprise Process Performance Management. IEEE Transactions on Systems Man and Cybernetics Part C—Applications and Reviews 38: 745–56. [Google Scholar] [CrossRef]
- Ucar, Erdem. 2016. Local Culture and Dividends: Local Culture and Dividends. Financial Management 45: 105–40. [Google Scholar] [CrossRef]
- von Eije, Henk, and William L. Megginson. 2008. Dividends and share repurchases in the European Union. Journal of Financial Economics 89: 347–74. [Google Scholar] [CrossRef]
- Walsh, William E., and Michael P. Wellman. 2000. Modeling Supply Chain Formation in Multiagent Systems. In Agent Mediated Electronic Commerce II. Edited by Moukas Alexandros, Ygge Fredrik and Sierra Carles. Berlin/Heidelberg: Springer, pp. 94–101. [Google Scholar] [CrossRef]
- Walter, James E. 1956. Dividend Policies and Common Stock Prices. Journal of Finance 11: 29–41. [Google Scholar] [CrossRef]
- Wang, Haizhong, Alireza Mostafizi, Lori A. Cramer, Dan Cox, and Hyoungsu Park. 2016. An agent-based model of a multimodal near-field tsunami evacuation: Decision-making and life safety. Transportation Research Part C—Emerging Technology 64: 86–100. [Google Scholar] [CrossRef]
- Wilensky, Uri, and William Rand. 2015. An Introduction to Agent-Based Modeling: Modeling Natural, Social, and Engineered Complex Systems with NetLogo. Cambridge: The MIT Press. [Google Scholar]
- Zambrano, Cristian, and Yris Olaya. 2017. An agent-based simulation approach to congestion management for the Colombian electricity market. Annals of Operations Research 258: 217–36. [Google Scholar] [CrossRef]
| 1 | De facto, a dividend is defined as apart from net income, and the dividend payout decision is conditioned by the available cash flows, and not by net earnings. If one company records net earnings, but do not record a higher (or equal) amount of cash flows, as long as both dividends and financing investment projects require cash payments, the dividend policy is only a matter of (theoretical) accounting (Dragotă et al. 2019). In this study, we will consider a simplified case, respectively, profit ≡ cash flow. Signaling theories on dividends (e.g., Bhattacharya 1979; Kalay 1980) state that companies that pay dividends signal that they have sufficient cash for paying them, while non-payers can be suspected as not having it. |
| 2 | It can be noted that this rate of return is not a realized one. Investors expect to record this promised rate of return, so an adequate notation is still Et−1(kMt). |
| 3 | Taxation can have an impact on dividend payments (see, among others, Dragotă et al. 2009). Walter (1956) analyzes the impact of taxation, too. |
| 4 | The model can be easily generalized for the case of multiple classes of shares, with different voting power, according to the company’s statute (see, for instance, (Nenova 2003), for the case of dual classes of shares). |
| 5 | A similar result occurs if the new shareholders (the buyers) replicate the behavior of the former shareholders (the sellers). |
| 6 | As observation, when the impact of factors like financial literacy or education is discussed, it has to be interpreted cautiously. For instance, Mare et al. (2019) found that insurance literacy has an impact on financial decisions, but education (in general) does not. |
| 7 | Individuals prefer in many situations the status quo (the “anchoring” effect) (Samuelson and Zeckhauser 1988). As an effect, in this paper, we considered that Class C agents do no change their voting preference instantly. In a different context, Harari (2015, pp. 264–67) provides historical evidence regarding this “anchoring” effect and explains it by a necessity of human beings to make sense of their decisions. If they should accept the fact that their past decision was wrong, they should accept that their past “sacrifices” were unuseful. |
| 8 | This statement is formalized in the corporate finance literature through classical selection criteria, like the net present value (NPV) > 0 and IRR > the required rate of return (Ross et al. 2010; Dragotă et al. 2013). |
| 9 | Theoretically, the realized IRR can take values in the (−∞, ∞) interval. |
| 10 | Some readers can have objections to this manner of formulation, considering that the expected rate of return is a function of the realized rate of return, and not vice versa. In our simple formulation, if we consider Et−1(IRRt) as function of IRRt, IRRt should be generated randomly. |
| 11 | Similar to the formulation of IRRt, if we consider Et−1(kMt) as function of kMt, kMt should be generated randomly. |
| 12 | Shareholders’ wealth at moment t (Wt) is structured in two components: the initial capital invested in company and the capitalized dividends. |
| 13 | In the entire paper we consider the real rates of returns, even it is not specified expressly. In a more general context, we can assume that it is not important if we prefer real or nominal rates of returns as long as all the comparisons and considerations regarding these rates are consider the coherence between rates (e.g., compare real rates of returns with real rates of return, and nominal rates of returns with nominal rates of returns). |
| 14 | Most of the papers in finance stipulate that this required rate of return is related to the assumed risk. |
| 15 | This variable can be also connected to the aversion to loss (Shefrin and Statman 1985; Odean 1998). |
| 16 | We have considered a normal distribution, and not a fat-tail one (e.g., McGroarty et al. 2019) for this variable due to the NetLogo limitations. |
| 17 | According to Wikipedia (https://en.wikipedia.org/wiki/List_of_oldest_companies, accessed on 23 July 2019), the oldest company still in function is Nishiyama Onsen Keiunkan (founded in 705 AD, so with an age less than 1400 years). Of course, such a long period of existence can be explained by making good decisions. From this perspective, it is implausible that, for a company to function for so many years, making systematically bad decisions, large levels of DSMBD can be interpreted as a failure before the change of the decider. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).