Generalized Mean-Reverting 4/2 Factor Model
Abstract
1. Introduction
2. Model Description
3. Results
3.1. Change of Measure
3.2. Characteristic Function
4. Discussion: One Common Factor in Two Dimensions
4.1. Pricing Option
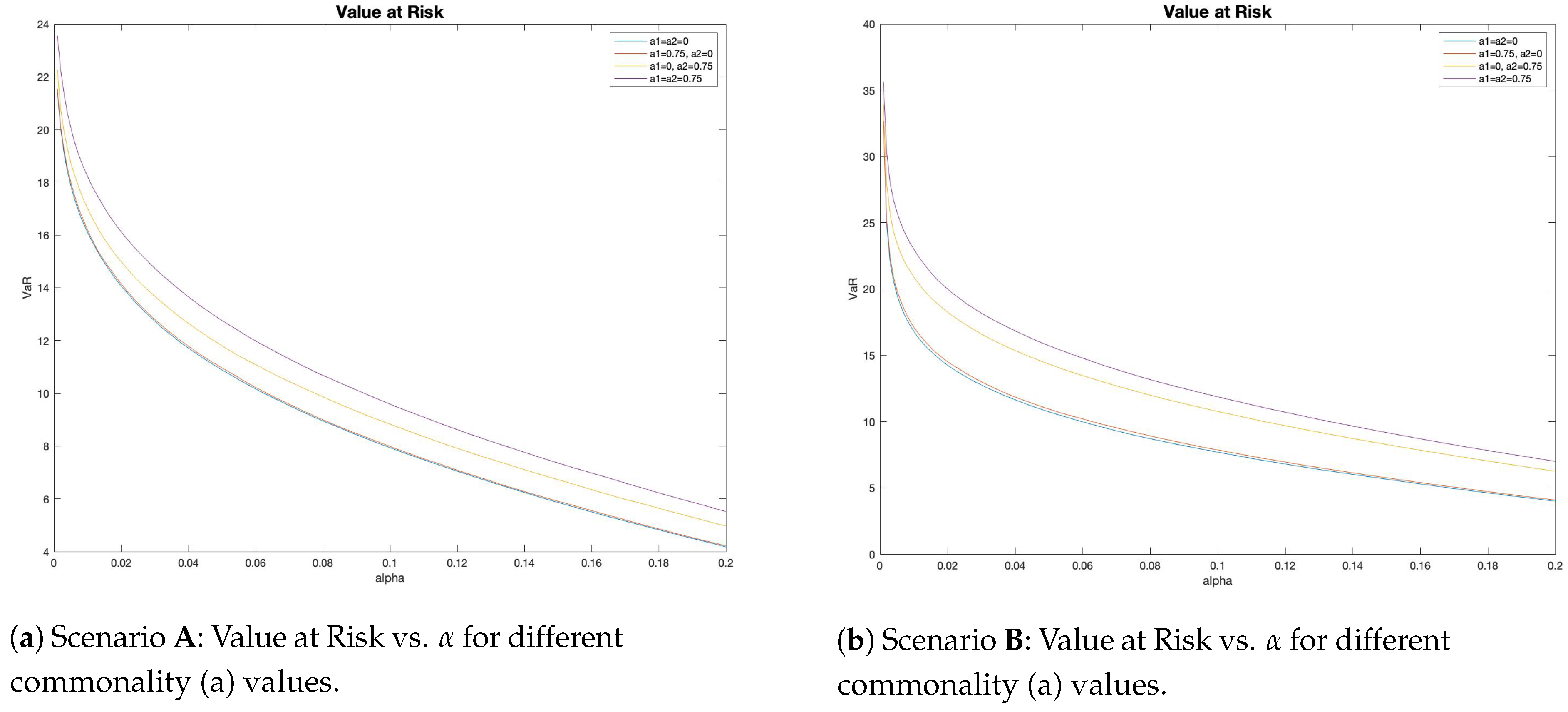
4.2. Risk Measures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proofs
Appendix B. Helpful Results
- with
- with
References
- Baldeaux Jan, Martino Grasselli, and Eckhard Platen. 2015. Pricing Currency Derivatives Under the Benchmark Approach. Journal of Banking & Finance 53: 34–48. [Google Scholar]
- Carr, Peter, and Dilip B. Madan. 1999. Option Valuation using the FFT. Journal of Computational Finance 2: 61–73. [Google Scholar] [CrossRef]
- Caldana, Ruggero, and Gianluca Fusai. 2013. A general closed-form spread option pricing formula. Journal of Banking and Finance 37: 4893–906. [Google Scholar] [CrossRef]
- Cheng, Peng, and Olivier Scaillet. 2007. Linear-quadratic jump-diffusion modelling. Mathematical Finance 17: 575–98. [Google Scholar] [CrossRef]
- Chiarella, Carl, Boda Kang, Christina Sklibosios Nikitopoulos, and Thuy Tô. 2013. Humps in the volatility structure of the crude oil futures market: New evidence. Energy Economics 40: 989–1000. [Google Scholar] [CrossRef]
- Christoffersen, Peter, Steven Heston, and Kris Jacobs. 2009. The shape and term structure of the index option smirk: Why multifactor stochastic volatility models work so well. Management Science 55: 1914–32. [Google Scholar] [CrossRef]
- De Col, Alvise, Alessandro Gnoatto, and Martino Grasselli. 2013. Smiles all around: FX joint calibration in a multi-Heston model. Journal of Banking & Finance 37: 3799–818. [Google Scholar]
- Da Fonseca, José, Martino Grasselli, and Claudio Tebaldi. 2007. Option Pricing when Correlations are Stochastic: An Analytical Framework. Review of Derivatives Research 10: 151–80. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, and Raman Uppal. 2007. Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? The Review of Financial Studies 22: 1915–53. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Marc Nerlove. 1989. The dynamics of exchange rate volatility: A multivariate latent factor ARCH model. Journal of Applied Econometrics 4: 1–21. [Google Scholar] [CrossRef]
- Escobar, Marcos. 2018. A Stochastic Volatility Factor Model of Heston type. Statistical Properties and Estimation. Stochastics 90: 172–99. [Google Scholar] [CrossRef]
- Escobar, Marcos, and Christoph Gschnaidtner. 2016. Parameters recovery via calibration in the Heston model: A comprehensive review. Wilmott 2016: 60–81. [Google Scholar] [CrossRef]
- Escobar, Marcos, and Zhenxian Gong. 2019. The mean-reverting 4/2 stochastic volatility model: Properties and Financial Applications. submitted. [Google Scholar]
- Engle, Robert. 2002. Dynamic Conditional Correlation: A Simple Class of Multivariate Generalized Autoregressive Conditional Heteroskedasticity Models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar]
- Fusai, Gianluca, Marina Marena, and Andrea Roncoroni. 2018. Analytical pricing of discretely monitored Asian-style options: Theory and application to commodity markets. Journal of Banking and Finance 32: 2033–45. [Google Scholar] [CrossRef]
- Gourieroux, Christian. 2006. Continuous Time Wishart Process for Stochastic Risk. Econometric Reviews 25: 1–41. [Google Scholar] [CrossRef]
- Grasselli, Martino. 2017. The 4/2 stochastic volatility model: A unified approach for the Heston and the 3/2 model. Mathematical Finance 27: 1013–34. [Google Scholar] [CrossRef]
- Gnoatto, Alessandro, Martino Grasselli, and Eckhard Platenn. 2018. A penny saved is a penny earned: Less expensive zero coupon bonds. In arXiv. [Google Scholar]
- Heston, Steven L. 1993. A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bonds and Currency Options. Review of Financial Studies 6: 327–43. [Google Scholar] [CrossRef]
- Medvedev Alexey, Olivier Scaillet. 2007. Approximation and calibration of short-term implied volatilities under jump-diffusion stochastic volatility. Review of Financial Studies 20: 427–59. [Google Scholar] [CrossRef]
- Muhle-Karbe, Johannes, Oliver Pfaffel, and Robert Stelzer. 2012. Option pricing in multivariate stochastic volatility models of OU type. SIAM Journal on Financial Mathematics 3: 66–94. [Google Scholar] [CrossRef][Green Version]
- Platen, Eckhard. 1997. A Non-Linear Stochastic Volatility Model. Financial Mathematics Research Report No. FMRR 005-97. Canberra: Center for Financial Mathematics, Australian National University. [Google Scholar]
- Platen, Eckhard, and David Cochran Heath. 2010. A Benchmark Approach to Quantitative Finance. Berlin and Heidelberg: Springer. [Google Scholar]
- Schneider Lorenz, Bertrand Tavin. 2018. From the Samuelson volatility effect to a Samuelson correlation effect: An analysis of crude oil calendar spread options. Journal of Banking and Finance 95: 185–202. [Google Scholar] [CrossRef]
- Schwartz, Eduardo S. 1997. The stochastic behavior of commodity prices: Implications for valuation and hedging. The Journal of Finance 52: 923–73. [Google Scholar] [CrossRef]
| 1 | This can also be applied to volatility indexes, such as those reported by the Chicago Board Options Exchange (CBOE), which are clearly a mean-reverting asset class with stochastic volatility. |
| 2 | Variations on c will be studied in future research as part of a calibration exercise (see Medvedev and Scaillet 2007 for viable approaches and Escobar and Gschnaidtner 2016 for some pitfalls). |

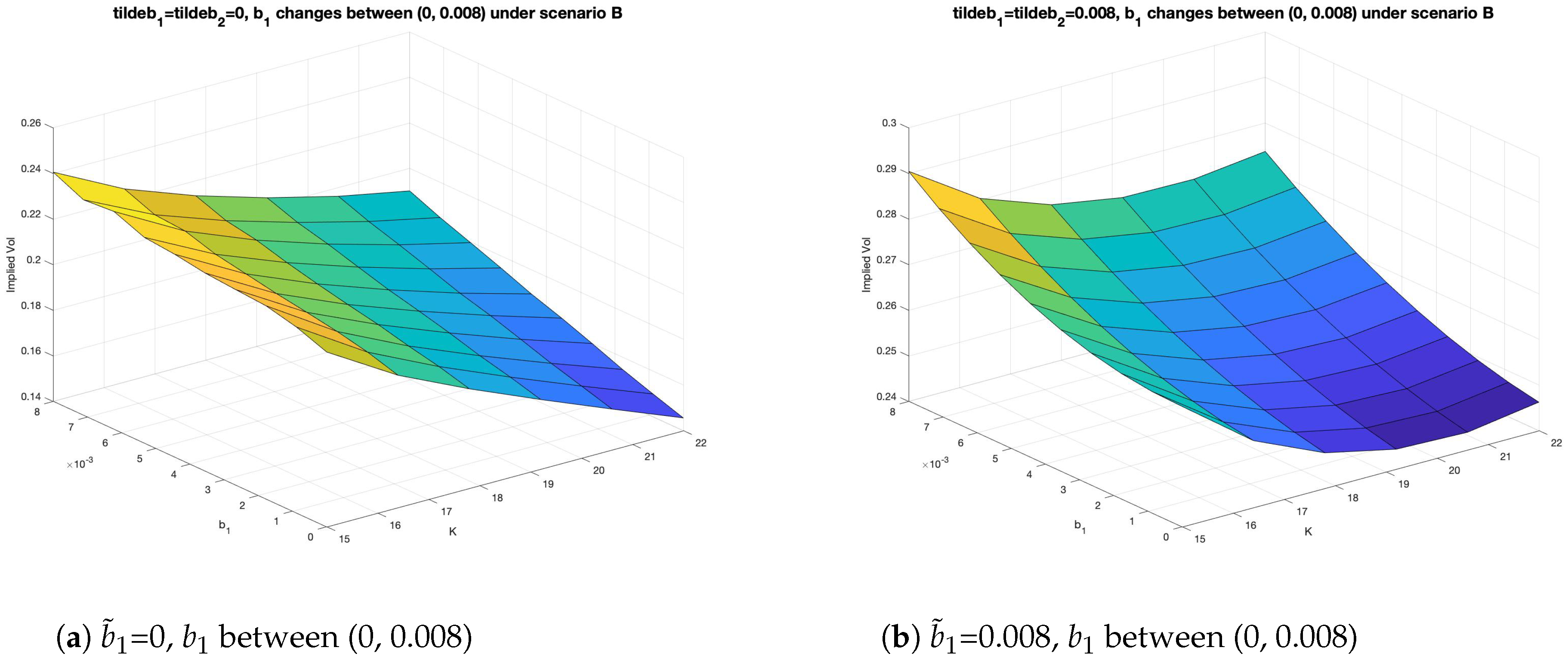
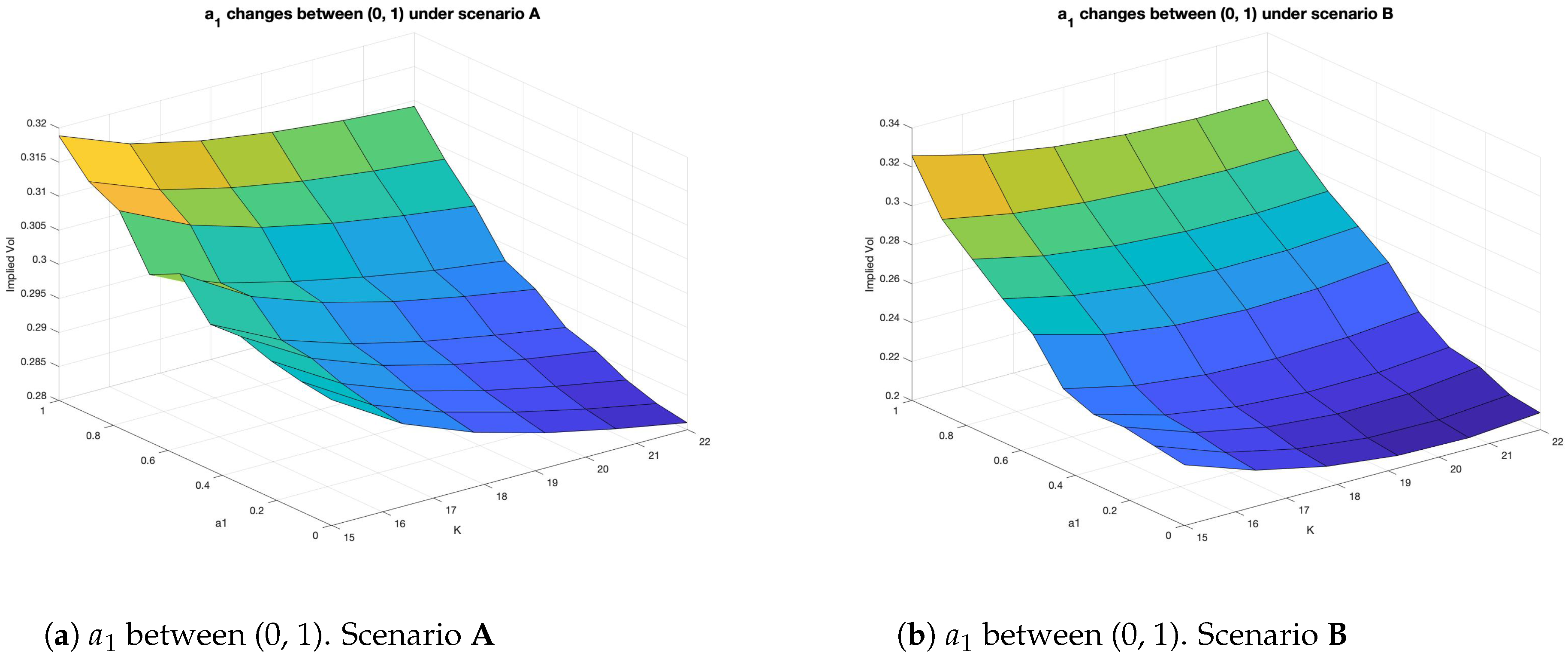
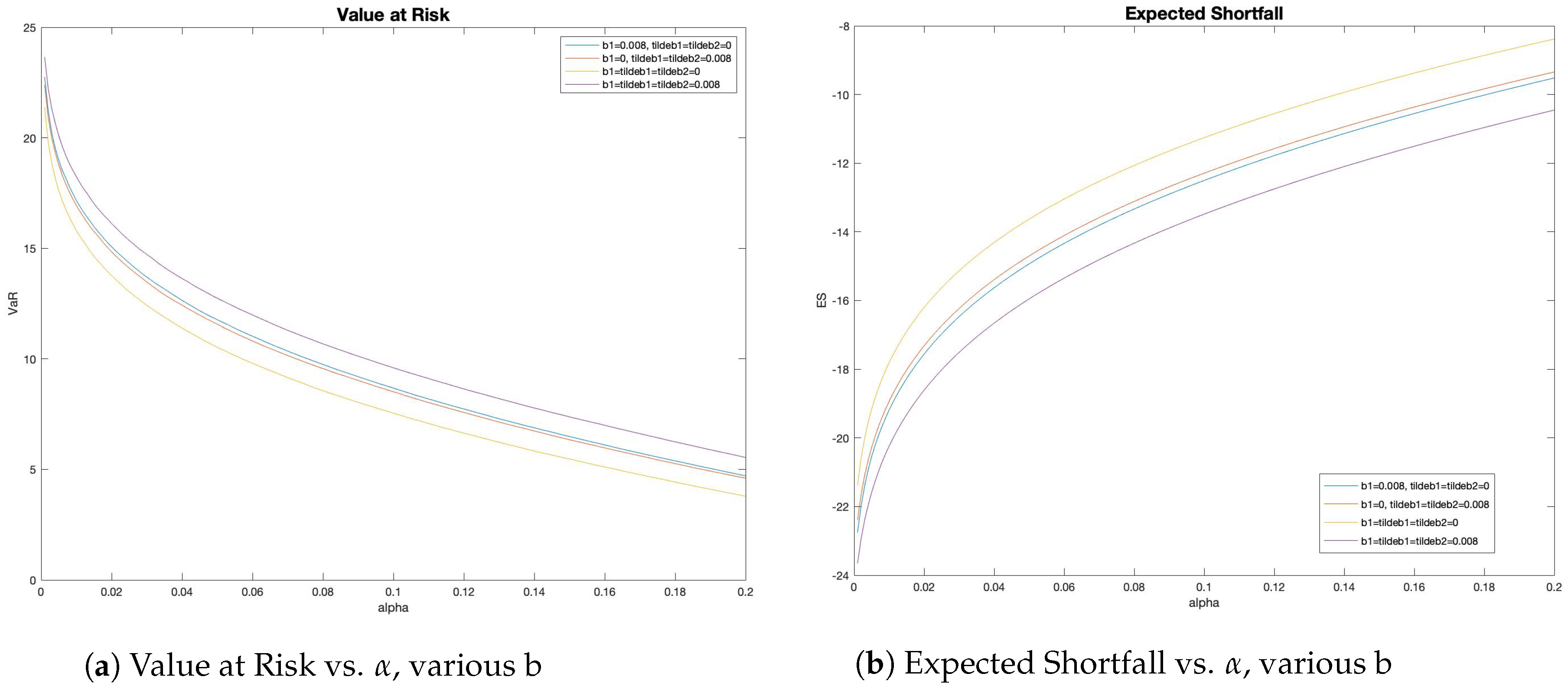
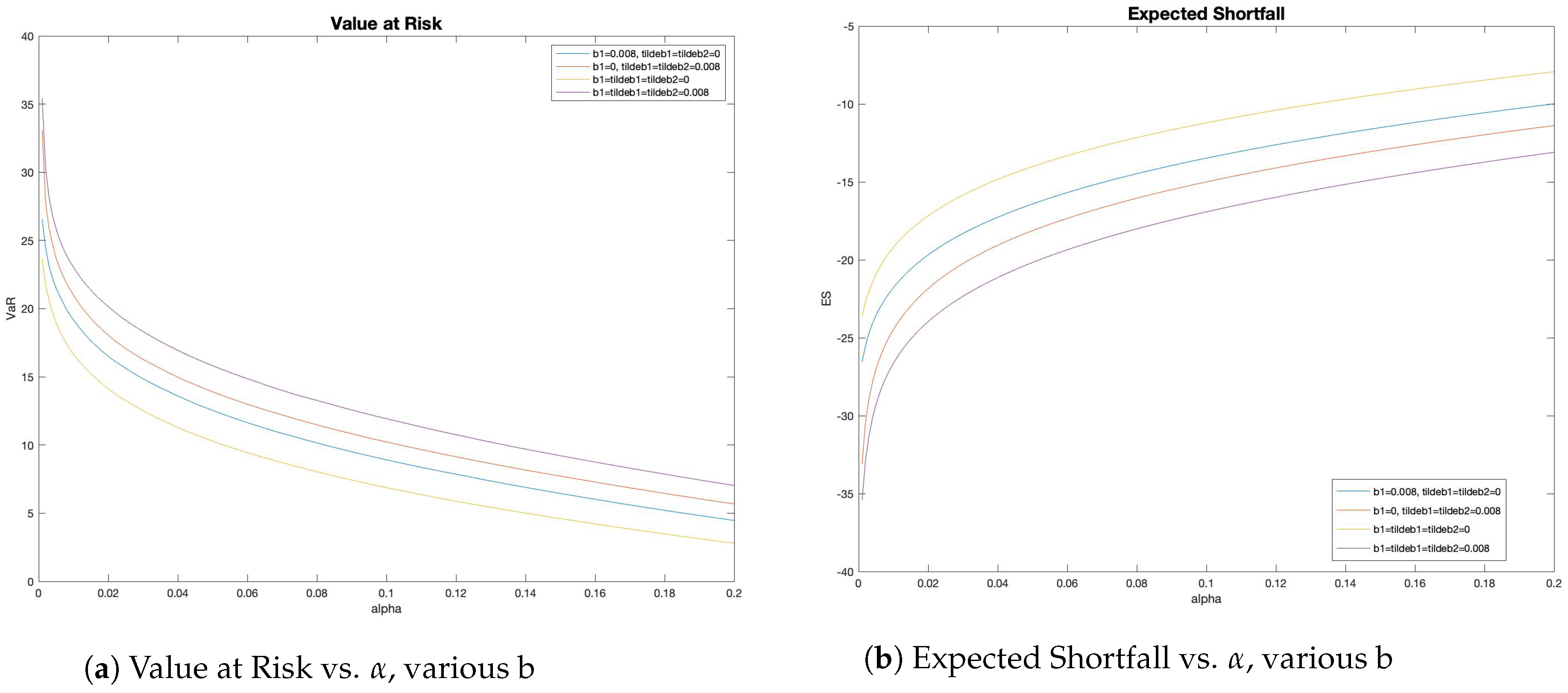
| Initial Values |
|---|
| Commodity Drift, Schwartz (1997) |
| Commodity St. Volatility, Heston (1993); Schwartz (1997). Scenario A |
| Commodity St. Volatility, Heston et al. (2009); Schwartz (1997). Scenario B |
| New parameters. |
| 0.008, = = 0 | , = = 0.008 | = = = 0 | = = 0.008 | |
|---|---|---|---|---|
| 0.0494 | 0.0489 | 0.0503 | 0.0480 | |
| 0.0760 | 0.0754 | 0.0764 | 0.0750 | |
| 0.0663 | 0.0680 | 0.0618 | 0.0729 | |
| 0.0367 | 0.0390 | 0.0323 | 0.0445 | |
| 0.3194 | 0.0896 | 0.1060 | 0.2799 | |
| −0.4287 | −0.4520 | −0.4443 | −0.4406 | |
| -0.4148 | −0.4511 | −0.4420 | −0.4280 |
| 0.008, = = 0 | , = = 0.008 | = = = 0 | = = 0.008 | |
|---|---|---|---|---|
| 0.0514 | 0.0504 | 0.0527 | 0.0499 | |
| 0.0774 | 0.0775 | 0.0787 | 0.0754 | |
| 0.0360 | 0.0606 | 0.0247 | 0.1022 | |
| 0.0359 | 0.1508 | 0.0248 | 0.0723 | |
| 0.7533 | 0.0099 | 0.4698 | 0.0156 | |
| −0.4509 | −0.2031 | −0.5560 | −0.0273 | |
| −0.4496 | −0.0398 | −0.5517 | −0.2444 |
| , | , | |||
|---|---|---|---|---|
| 0.0491 | 0.0492 | 0.0493 | 0.0492 | |
| 0.0761 | 0.0757 | 0.0746 | 0.0759 | |
| 0.0658 | 0.0727 | 0.0660 | 0.0732 | |
| 0.0371 | 0.0370 | 0.0444 | 0.0447 | |
| 0.0000 | −0.0011 | 0.0004 | 0.2841 | |
| −0.4523 | −0.4400 | −0.4529 | −0.4430 | |
| −0.4507 | −0.4521 | −0.4285 | −0.4279 |
| , | , | |||
|---|---|---|---|---|
| 0.0514 | 0.0496 | 0.0512 | 0.0500 | |
| 0.0768 | 0.0772 | 0.0756 | 0.0752 | |
| 0.0420 | 0.0733 | 0.0420 | 0.0857 | |
| 0.0507 | 0.0564 | 0.0746 | 0.0719 | |
| 0.0004 | −0.0000 | −0.0005 | 0.0039 | |
| −0.1126 | −0.0047 | −0.3203 | −0.2634 | |
| −0.1600 | −0.2544 | −0.0164 | −0.0111 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Escobar-Anel, M.; Gong, Z. Generalized Mean-Reverting 4/2 Factor Model. J. Risk Financial Manag. 2019, 12, 159. https://doi.org/10.3390/jrfm12040159
Cheng Y, Escobar-Anel M, Gong Z. Generalized Mean-Reverting 4/2 Factor Model. Journal of Risk and Financial Management. 2019; 12(4):159. https://doi.org/10.3390/jrfm12040159
Chicago/Turabian StyleCheng, Yuyang, Marcos Escobar-Anel, and Zhenxian Gong. 2019. "Generalized Mean-Reverting 4/2 Factor Model" Journal of Risk and Financial Management 12, no. 4: 159. https://doi.org/10.3390/jrfm12040159
APA StyleCheng, Y., Escobar-Anel, M., & Gong, Z. (2019). Generalized Mean-Reverting 4/2 Factor Model. Journal of Risk and Financial Management, 12(4), 159. https://doi.org/10.3390/jrfm12040159





