Correcting the Bias in the Practitioner Black-Scholes Method
Abstract
1. Introduction
2. The PBS Method
3. The Smearing Method in Prediction
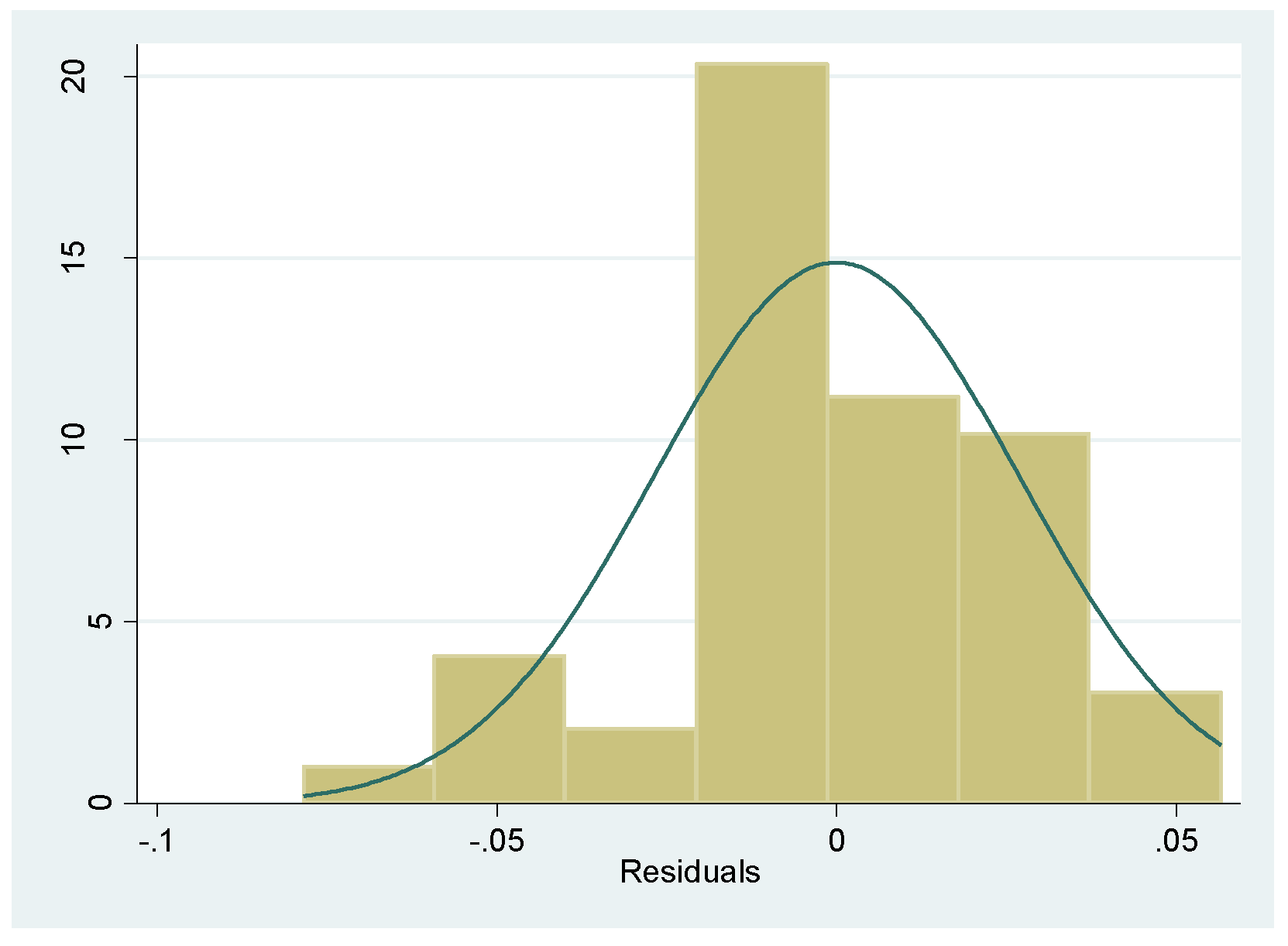
4. Estimation of the IV Equation by NLLS on Option Price Data
5. Estimation of IV Equations Using Real Data
6. A Monte Carlo Analysis of PBS with Smearing
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Data Availability Statement
Appendix A. Data Used for Single Day Estimation in Section 5
| t | Date | Expirydate | C | S | K | rf | tau | iv |
|---|---|---|---|---|---|---|---|---|
| 1 | 27 July 2000 | 16 December 2000 | 40.5 | 1449.62 | 1550 | 0.0598 | 0.3890411 | 0.18459306 |
| 2 | 27 July 2000 | 16 September 2000 | 2.875 | 1449.62 | 1600 | 0.0598 | 0.139726 | 0.16379156 |
| 3 | 27 July 2000 | 19 August 2000 | 8.125 | 1449.62 | 1500 | 0.0598 | 0.0630137 | 0.16414911 |
| 4 | 27 July 2000 | 16 December 2000 | 7 | 1449.62 | 1700 | 0.0598 | 0.3890411 | 0.16543757 |
| 5 | 27 July 2000 | 19 August 2000 | 12.625 | 1449.62 | 1485 | 0.0598 | 0.0630137 | 0.16855563 |
| 6 | 27 July 2000 | 19 August 2000 | 157.125 | 1449.62 | 1300 | 0.0598 | 0.0630137 | 0.29000379 |
| 7 | 27 July 2000 | 19 August 2000 | 133 | 1449.62 | 1325 | 0.0598 | 0.0630137 | 0.26658718 |
| 8 | 27 July 2000 | 19 August 2000 | 26.375 | 1449.62 | 1455 | 0.0598 | 0.0630137 | 0.18138442 |
| 9 | 27 July 2000 | 16 September 2000 | 14.75 | 1449.62 | 1525 | 0.0598 | 0.139726 | 0.17296152 |
| 10 | 27 July 2000 | 16 September 2000 | 47.25 | 1449.62 | 1450 | 0.0598 | 0.139726 | 0.19113849 |
| 11 | 27 July 2000 | 19 August 2000 | 18.625 | 1449.62 | 1470 | 0.0598 | 0.0630137 | 0.1738262 |
| 12 | 27 July 2000 | 16 September 2000 | 36.125 | 1449.62 | 1470 | 0.0598 | 0.139726 | 0.18486601 |
| 13 | 27 July 2000 | 21 October 2000 | 6.25 | 1449.62 | 1625 | 0.0598 | 0.2356164 | 0.16558332 |
| 14 | 27 July 2000 | 19 August 2000 | 109.125 | 1449.62 | 1350 | 0.0598 | 0.0630137 | 0.24189121 |
| 15 | 27 July 2000 | 19 August 2000 | 1.625 | 1449.62 | 1545 | 0.0598 | 0.0630137 | 0.15661302 |
| 16 | 27 July 2000 | 19 August 2000 | 11.125 | 1449.62 | 1490 | 0.0598 | 0.0630137 | 0.16827447 |
| 17 | 27 July 2000 | 16 December 2000 | 31.75 | 1449.62 | 1575 | 0.0598 | 0.3890411 | 0.18067305 |
| 18 | 27 July 2000 | 19 August 2000 | 14.5 | 1449.62 | 1480 | 0.0598 | 0.0630137 | 0.17055967 |
| 19 | 27 July 2000 | 19 August 2000 | 3.6875 | 1449.62 | 1525 | 0.0598 | 0.0630137 | 0.1615991 |
| 20 | 27 July 2000 | 17 March 2001 | 61.375 | 1449.62 | 1575 | 0.0598 | 0.6383561 | 0.19218853 |
| 21 | 27 July 2000 | 16 December 2000 | 13.5 | 1449.62 | 1650 | 0.0598 | 0.3890411 | 0.17021512 |
| 22 | 27 July 2000 | 19 August 2000 | 1.3125 | 1449.62 | 1550 | 0.0598 | 0.0630137 | 0.15584699 |
| 23 | 27 July 2000 | 16 September 2000 | 63.625 | 1449.62 | 1425 | 0.0598 | 0.139726 | 0.20124521 |
| 24 | 27 July 2000 | 16 September 2000 | 38.875 | 1449.62 | 1465 | 0.0598 | 0.139726 | 0.18695045 |
| 25 | 27 July 2000 | 19 August 2000 | 16.5 | 1449.62 | 1475 | 0.0598 | 0.0630137 | 0.17231101 |
| 26 | 27 July 2000 | 17 March 2001 | 5.125 | 1449.62 | 1850 | 0.0598 | 0.6383561 | 0.16320811 |
| 27 | 27 July 2000 | 16 December 2000 | 62.625 | 1449.62 | 1500 | 0.0598 | 0.3890411 | 0.19390107 |
| 28 | 27 July 2000 | 16 September 2000 | 23 | 1449.62 | 1500 | 0.0598 | 0.139726 | 0.17839537 |
| 29 | 27 July 2000 | 19 August 2000 | 31.875 | 1449.62 | 1445 | 0.0598 | 0.0630137 | 0.18350645 |
| 30 | 27 July 2000 | 16 September 2000 | 1.5 | 1449.62 | 1625 | 0.0598 | 0.139726 | 0.1619217 |
| 31 | 27 July 2000 | 19 August 2000 | 35 | 1449.62 | 1440 | 0.0598 | 0.0630137 | 0.18568564 |
| 32 | 27 July 2000 | 16 December 2000 | 4.75 | 1449.62 | 1725 | 0.0598 | 0.3890411 | 0.16223686 |
| 33 | 27 July 2000 | 16 December 2000 | 3.125 | 1449.62 | 1750 | 0.0598 | 0.3890411 | 0.15914554 |
| 34 | 27 July 2000 | 16 December 2000 | 9.5 | 1449.62 | 1675 | 0.0598 | 0.3890411 | 0.16608682 |
| 35 | 27 July 2000 | 16 September 2000 | 19.375 | 1449.62 | 1510 | 0.0598 | 0.139726 | 0.17603378 |
| 36 | 27 July 2000 | 19 August 2000 | 2.0625 | 1449.62 | 1540 | 0.0598 | 0.0630137 | 0.15860899 |
| 37 | 27 July 2000 | 16 December 2000 | 18.125 | 1449.62 | 1625 | 0.0598 | 0.3890411 | 0.17263715 |
| 38 | 27 July 2000 | 19 August 2000 | 29.125 | 1449.62 | 1450 | 0.0598 | 0.0630137 | 0.18295443 |
| 39 | 27 July 2000 | 16 September 2000 | 81.125 | 1449.62 | 1400 | 0.0598 | 0.139726 | 0.20730415 |
| 40 | 27 July 2000 | 21 October 2000 | 20.625 | 1449.62 | 1550 | 0.0598 | 0.2356164 | 0.17530438 |
| 41 | 27 July 2000 | 16 September 2000 | 33.875 | 1449.62 | 1475 | 0.0598 | 0.139726 | 0.1846462 |
| 42 | 27 July 2000 | 16 September 2000 | 100.625 | 1449.62 | 1375 | 0.0598 | 0.139726 | 0.21527798 |
| 43 | 27 July 2000 | 16 December 2000 | 24.25 | 1449.62 | 1600 | 0.0598 | 0.3890411 | 0.1764836 |
| 44 | 27 July 2000 | 19 August 2000 | 64.75 | 1449.62 | 1400 | 0.0598 | 0.0630137 | 0.2074976 |
| 45 | 27 July 2000 | 19 August 2000 | 3 | 1449.62 | 1530 | 0.0598 | 0.0630137 | 0.15969375 |
| 46 | 27 July 2000 | 21 October 2000 | 65.625 | 1449.62 | 1450 | 0.0598 | 0.2356164 | 0.19772039 |
| 47 | 27 July 2000 | 16 September 2000 | 5.125 | 1449.62 | 1575 | 0.0598 | 0.139726 | 0.16519108 |
| 48 | 27 July 2000 | 16 September 2000 | 8.875 | 1449.62 | 1550 | 0.0598 | 0.139726 | 0.16814606 |
| 49 | 27 July 2000 | 19 August 2000 | 45.25 | 1449.62 | 1425 | 0.0598 | 0.0630137 | 0.19296223 |
| 50 | 27 July 2000 | 17 March 2001 | 35.625 | 1449.62 | 1650 | 0.0598 | 0.6383561 | 0.18229888 |
| 51 | 27 July 2000 | 16 September 2000 | 41.5 | 1449.62 | 1460 | 0.0598 | 0.139726 | 0.18801008 |
Appendix B
References
- Andreou, Panayiotis C., Chris Charalambous, and Spiros H. Martzoukos. 2014. Assessing the performance of symmetric and asymmetric implied volatility functions. Review of Quantitative Finance and Accounting 42: 373–97. [Google Scholar] [CrossRef]
- Bakshi, Gurdip, Charles Cao, and Zhiwu Chen. 1997. Empirical performance of alternative option pricing models. The Journal of Finance 52: 2003–49. [Google Scholar] [CrossRef]
- Christoffersen, Peter, and Kris Jacobs. 2004. The importance of the loss function in option valuation. Journal of Financial Economics 72: 291–318. [Google Scholar] [CrossRef]
- Duan, Naihua. 1983. Smearing estimate: A nonparametric retransformation method. Journal of the American Statistical Association 78: 605–10. [Google Scholar] [CrossRef]
- Duan, J., Genevieve Gauthier, J. Simonato, and Caroline Sasseville. 2006. Approximating the GJR-GARCH and EGARCH option pricing models analytically. Journal of Computational Finance 9: 41. [Google Scholar] [CrossRef]
- Dumas, Bernard, Jeff Fleming, and Robert E. Whaley. 1998. Implied volatility functions: Empirical tests. The Journal of Finance 53: 2059–106. [Google Scholar] [CrossRef]
- Hausman, Jerry A. 1978. Specification tests in econometrics. Econometrica 46: 1251–71. [Google Scholar] [CrossRef]
- Heston, Steven L., and Saikat Nandi. 2000. A closed form GARCH option pricing model. The Review of Financial Studies 13: 585–625. [Google Scholar] [CrossRef]
- Hull, John. 2011. Fundamentals of Futures and Options Markets, 7th ed. London: Pearson. [Google Scholar]
- Yin, Y. 2018. Flexible Option Valuation Methods. Unpublished M.Phil. thesis, University of East Anglia, Norwich, UK. [Google Scholar]
| 1 | Examples of option pricing models for which a comparison against the benchmark of PBS is likely to be very useful are: Bakshi et al.’s (1997) SVSI-J model which allows volatility, interest rates, and jumps all to be stochastic; Heston and Nandi’s (2000) model built on the assumption of a GARCH process in the underlying index; and Duan et al.’s (2006) models built on even more general assumptions such as GJR-GARCH (TGARCH) and EGARCH. |
| 2 | The Black-Scholes formula (Hull 2011) also contains as arguments: current price of the underlying; strike price; time-to-expiry, risk-free rate. Since the focus here is on volatility, we suppress these arguments and express the option value as a function of only the volatility of the underlying, σ. |
| 3 | The log-linear form (5) is clearly a new and untested class of implied volatility function. However, since ln(·) is a monotonically increasing function, any non-monotonic pattern in the original IV function (such as the well-known “volatility smile”) is obviously reproduced (albeit with a different shape) when the log of IV is used. Other authors (e.g., Andreou et al. 2014) address the negativity problem by applying a lower bound on predicted IV, using for example in place of in (4). On Monte Carlo evidence, we find that this approach tends to exacerbate biases in option values. For this reason, and also because the lower-bound correction is ad-hoc, we prefer the log-linear approach. |
| 4 | The data is extracted from OptionMetrics http://www.optionmetrics.com/. |
| 5 | For the positively skewed error, we simulate . For the negatively skewed error, we apply the same formula with the sign reversed. Note that these skewed distributions have the same mean and variance as the normal error N(0, 0.02822) used for the symmetric case. |
| 6 | The Wald test can be applied following estimation of a NLLS model in STATA by using the test command immediately after the nl command. |

| Variable | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| IV Mean Only | IV (Standard PBS) | Log(IV) (Log-Linear PBS) | NLLS (Log IV) | |
| K | −0.00414 *** | −0.0168 *** | −0.00626 *** | |
| (−8.91) | (−8.85) | (−4.55) | ||
| K2 | 0.00000131 *** | 0.00000517 *** | 0.00000159 ** | |
| (7.98) | (7.72) | (3.27) | ||
| τ | 1.104 *** | 3.978 *** | −0.256 | |
| (4.34) | (3.83) | (−0.38) | ||
| τ2 | 0.0262 | −0.136 | −0.421 ** | |
| (0.49) | (−0.62) | (−3.48) | ||
| K * τ | −0.000668 *** | −0.00222 ** | 0.000594 | |
| (−3.76) | (−3.06) | (1.24) | ||
| constant | 0.182 *** | 3.426 *** | 11.72 *** | 4.003 *** |
| (50.33) | (10.42) | (8.73) | (4.10) | |
| σ | 0.0259 | 0.00692 | 0.0282 | |
| n | 51 | 51 | 51 | 51 |
| R2 | 0 | 0.936 | 0.954 | |
| Hausman χ2(5) (p-value) | 516.0 | |||
| (0.0000) | ||||
| (1) PBS MEAN | (2) PBS IV (Standard PBS) | (3) PBS LogIV SMEARING | (4) NLLS | |
|---|---|---|---|---|
| Symmetric error: | ||||
| In sample: | ||||
| BIAS | 0.0972 | 0.0127 | 0.0005 | −0.0031 |
| MAE | 2.4102 | 0.6714 | 0.6428 | 0.6324 |
| MSE | 9.5759 | 0.9086 | 0.8262 | 0.7435 |
| Out of sample: | ||||
| BIAS | 0.0937 | 0.0092 | −0.0033 | −0.0067 |
| MAE | 2.4147 | 0.7640 | 0.7413 | 0.7681 |
| MSE | 9.6238 | 1.2787 | 1.1951 | 1.2787 |
| Negatively skewed error: | ||||
| In sample: | ||||
| BIAS | 0.0965 | 0.0129 | 0.0007 | −0.0028 |
| MAE | 2.4081 | 0.6269 | 0.5983 | 0.5891 |
| MSE | 9.5111 | 0.8620 | 0.7798 | 0.7017 |
| Out of sample: | ||||
| BIAS | 0.0979 | 0.0143 | 0.0018 | −0.0015 |
| MAE | 2.4132 | 0.7096 | 0.6891 | 0.7118 |
| MSE | 9.5551 | 1.2064 | 1.1290 | 1.1948 |
| Positively skewed error: | ||||
| In sample: | ||||
| BIAS | 0.0974 | 0.0127 | 0.0005 | −0.0033 |
| MAE | 2.4137 | 0.6510 | 0.6188 | 0.6113 |
| MSE | 9.6282 | 0.9629 | 0.8786 | 0.7908 |
| Out of sample: | ||||
| BIAS | 0.0959 | 0.0112 | −0.0013 | −0.0049 |
| MAE | 2.4176 | 0.7385 | 0.7119 | 0.7120 |
| MSE | 9.6708 | 1.3516 | 1.2623 | 1.3573 |
| Distributional Assumption | P(Reject H0) with Log-Linear Regression | P(Reject H0) with NLLS |
|---|---|---|
| Symmetric error | 0.052 | 0.473 |
| Negatively skewed error | 0.053 | 0.396 |
| Positively skewed error | 0.054 | 0.399 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, Y.; Moffatt, P.G. Correcting the Bias in the Practitioner Black-Scholes Method. J. Risk Financial Manag. 2019, 12, 157. https://doi.org/10.3390/jrfm12040157
Yin Y, Moffatt PG. Correcting the Bias in the Practitioner Black-Scholes Method. Journal of Risk and Financial Management. 2019; 12(4):157. https://doi.org/10.3390/jrfm12040157
Chicago/Turabian StyleYin, Yun, and Peter G. Moffatt. 2019. "Correcting the Bias in the Practitioner Black-Scholes Method" Journal of Risk and Financial Management 12, no. 4: 157. https://doi.org/10.3390/jrfm12040157
APA StyleYin, Y., & Moffatt, P. G. (2019). Correcting the Bias in the Practitioner Black-Scholes Method. Journal of Risk and Financial Management, 12(4), 157. https://doi.org/10.3390/jrfm12040157






