Dynamic Responses of Major Equity Markets to the US Fear Index
Abstract
:1. Introduction
2. Review of the Relevant Literature
2.1. Time Series Properties
2.2. Information Content of the VIX
2.3. Cross Market Association between the VIX and Equities
2.4. The Predictive Power of the VIX
3. Data
4. Methodology
Structural Vector Autoregressive Formulation
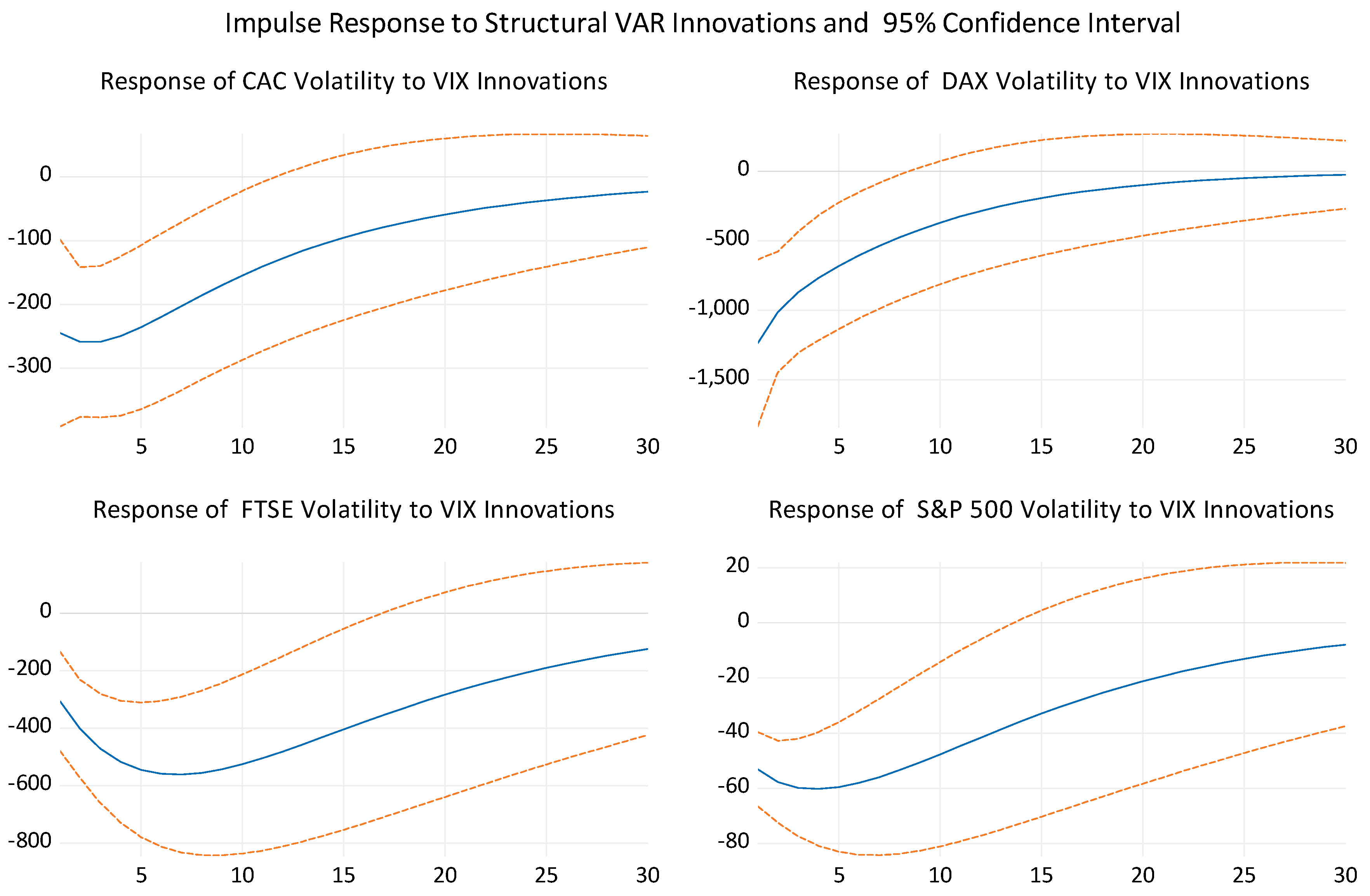
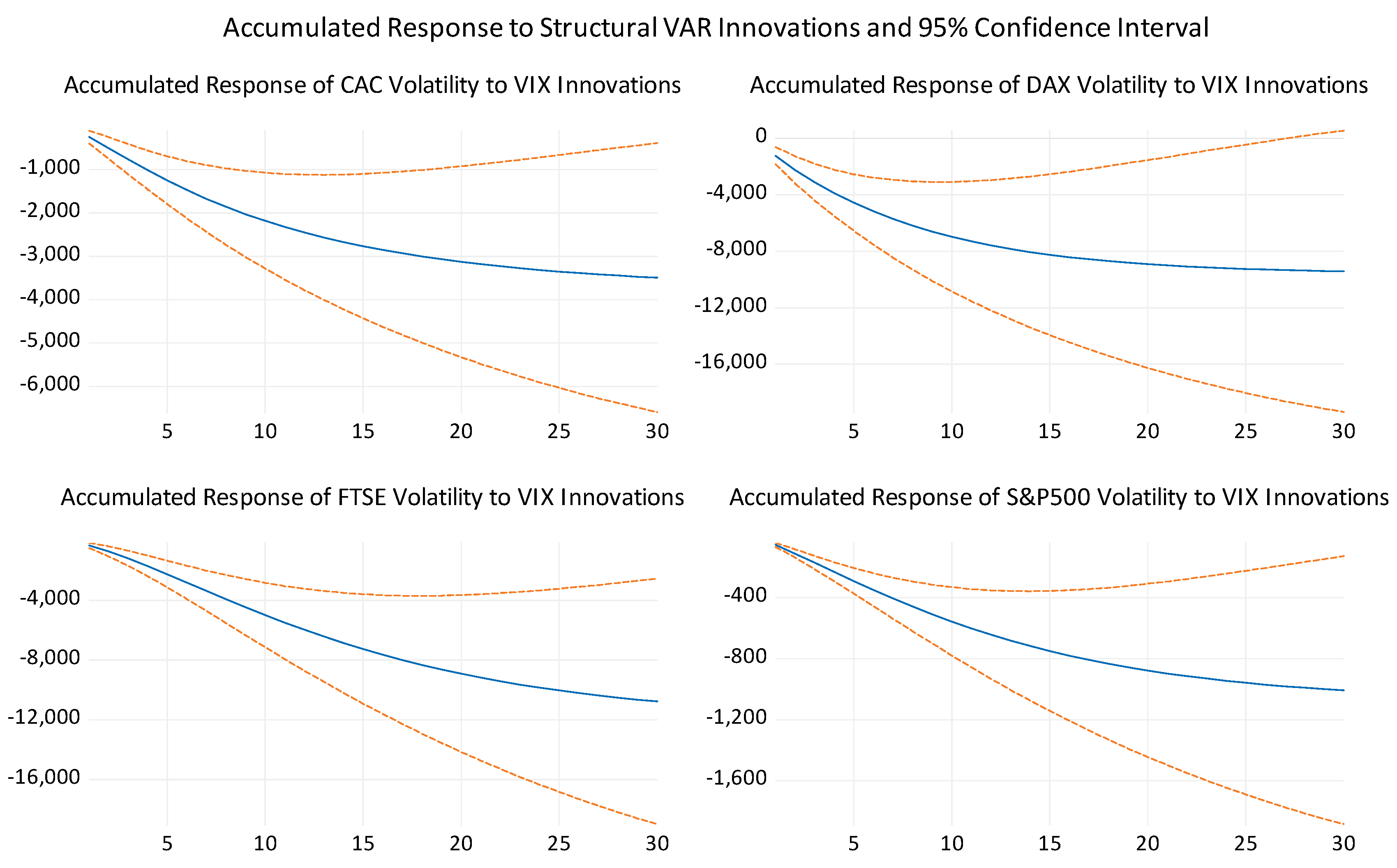
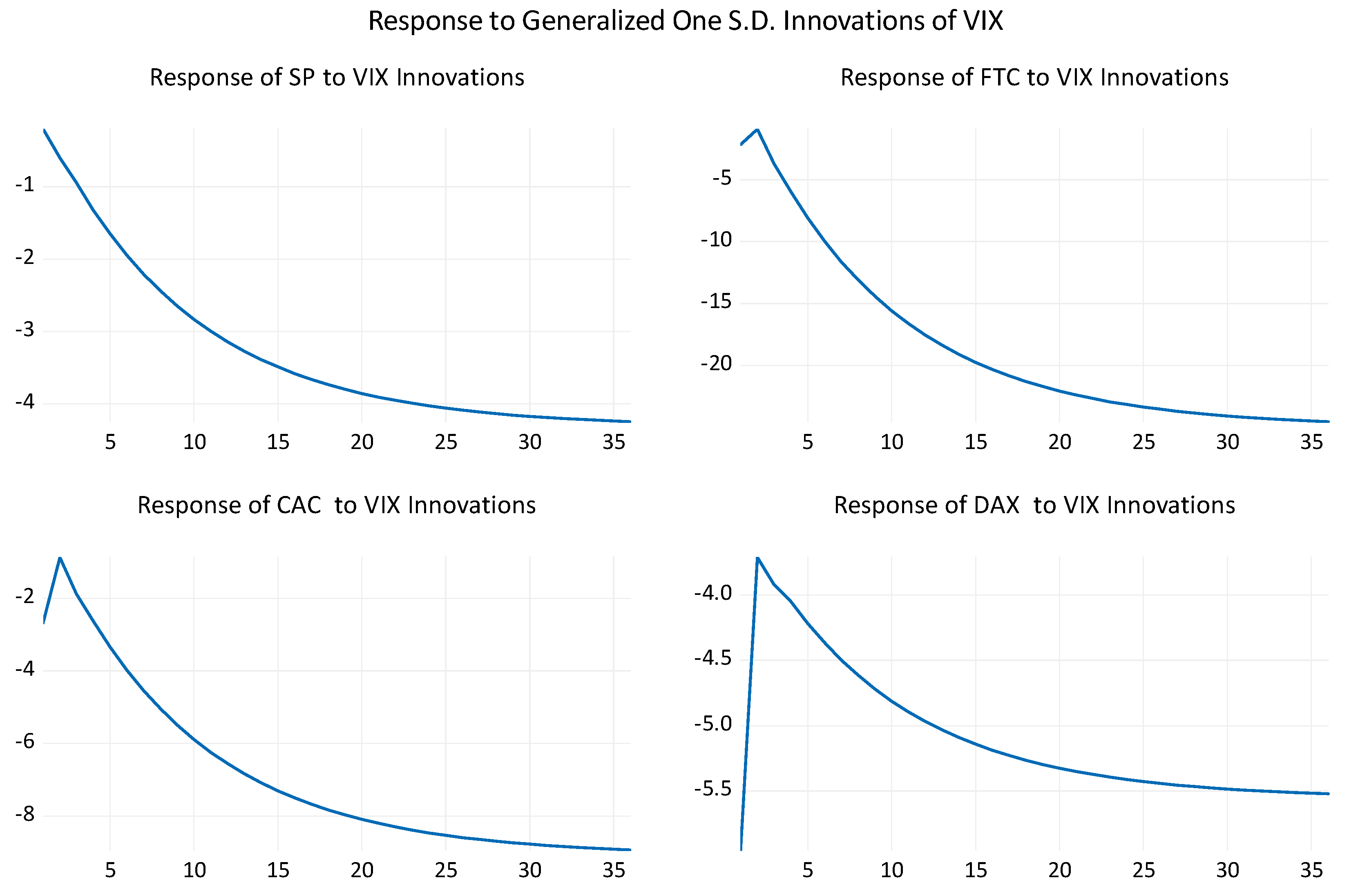
5. Empirical Results
Nonlinear Causality Test Results
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adrangi, Bahram, Hannah Baade, and Kambiz Raffiee. 2019. Dynamic Responses of the Economy to Monetary Shocks in the United Kingdom. Review of Economics & Finance 15: 31–45. [Google Scholar]
- Adrangi, Bahram, Arjun Chatrath, Joseph Macri, and Kambiz Raffiee. 2015. Crude oil price volatility spillovers into major equity markets. Journal of Energy Markets 8: 77–95. [Google Scholar]
- Adrangi, Bahram, Arjun Chatrath, Joseph Macri, and Kambiz Raffiee. 2018. U.S. Diesel Fuel Price Responses to the Global Crude Oil Supply and Demand. Annals of Financial Economics 13: 181–25. [Google Scholar]
- Akaike, Hirotugu. 1974. A new look at the statistical model identification. In Selected Papers of Hirotugu Akaike. New York: Springer, pp. 215–22. [Google Scholar]
- Ang, Andrew, Robert J. Hodrick, Yuhang Xing, and Xiaoyan Zhang. 2006. The cross-section of volatility and expected returns. The Journal of Finance 61: 259–99. [Google Scholar]
- Badshah, Ihsan Ullah, Bart Frijns, and Alireza Tourani-Rad. 2013. Contemporaneous spill-over among equity, gold, and exchange rate Implied Volatility Indices. Journal of Futures Markets 33: 555–72. [Google Scholar]
- Bai, Jushan, and Pierre Perron. 2003. Computation and analysis of multiple structural change models. Journal of Applied Econometrics 18: 1–22. [Google Scholar]
- Bakshi, Gurdip, Nengjiu Ju, and Hui Ou-Yang. 2006. Estimation of continuous-time models with an application to equity volatility dynamics. Journal of Financial Economics 82: 227–49. [Google Scholar]
- Becker, Ralph, Adam Clements, and Andrew McClelland. 2009. The jump component of S&P 500 volatility and the VIX index. Journal of Banking & Finance 33: 1033–38. [Google Scholar]
- Bekaert, Geert, and Marie Hoerova. 2014. The VIX, the variance premium and stock market volatility. Journal of Econometrics 183: 181–92. [Google Scholar]
- Blair, Bevan J., Ser-Huang Poon, and Stephen J. Taylor. 2010. Forecasting S&P 100 volatility: the incremental information content of implied volatilities and high-frequency index returns. In Handbook of Quantitative Finance and Risk Management. Boston: Springer, pp. 1333–44. [Google Scholar]
- Blair, Bevan J., Ser-Huang Poon, and Stephen Taylor. 2001. Forecasting S&P 100 volatility: The incremental information content of implied volatilities and high frequency index returns. Journal of Econometrics 105: 5–26. [Google Scholar]
- Blanchard, Olivier Jean, and Danny Quah. 1989. The dynamic Effects of aggregate Demand and Supply Disturbances. American Economic Review 79: 655–73. [Google Scholar]
- Boscaljan, Brian L., and John M. Clark. 2013. Do large shocks in VIX signal a flight-to-safety in the gold market? Journal of Applied Finance 2: 120–31. [Google Scholar]
- Carr, Peter, and Liuren Wu. 2006. A Tale of Two Indices. The Journal of Derivatives 13: 13–29. [Google Scholar]
- Connolly, Robert, Chris Stivers, and Licheng Sun. 2005. Stock market uncertainty and the stock-bond return relation. Journal of Financial and Quantitative Analysis 40: 161–94. [Google Scholar] [CrossRef]
- Corrado, Charles J., and Thomas W. Miller Jr. 2005. The forecast quality of CBOE implied volatility indexes. Journal of Futures Markets: Futures, Options, and Other Derivative Products 25: 339–73. [Google Scholar]
- Dotsis, George, Dimitris Psychoyios, and George Skiadopoulos. 2007. An empirical comparison of continuous-time models of implied volatility indices. Journal of Banking & Finance 31: 3584–603. [Google Scholar]
- Durand, Robert B., Dominic Lim, and Kenton Zumwalt. 2011. Fear and the FAMA-French factors. Financial Management 40: 409–26. [Google Scholar]
- Fama, Eugene, and Kenneth R. French. 1993. Common risk factors in the returns on stocks and bonds. Journal of Financial Economics 33: 3–56. [Google Scholar]
- Fernandes, Marcelo, Marcelo C. Medeiros, and Marcel Scharth. 2014. Modeling and predicting the CBOE market volatility index. Journal of Banking & Finance 40: 1–10. [Google Scholar]
- Fleming, Jeff, Barbara Ostdiek, and Robert E. Whaley. 1995. Predicting stock market volatility: A new measure. Journal of Futures Markets 15: 265–302. [Google Scholar] [CrossRef]
- Frijns, Bart, Christian Tallau, and Alireza Tourani-Rad. 2010. The information content of implied volatility: Evidence from Australia. Journal of Futures Markets: Futures, Options, and Other Derivative Products 30: 134–55. [Google Scholar]
- Geweke, John. 1984. Inference and causality in economic time series models. In Handbook of Econometrics. Edited by Zvi Griliches and Michael D. Intriligator. Amsterdam: Elsevier, vol. 2, pp. 1101–44. [Google Scholar]
- Giot, Pierre. 2005. Relationships between implied volatility indices and stock index returns. Journal of Portfolio Management 31: 92–100. [Google Scholar]
- Granger, Clive W. 1969. Investigating causal relations by econometric models and cross-spectral methods. Econometrica: Journal of the Econometric Society 37: 424–38. [Google Scholar]
- Jiang, George J., and Yisong S. Tian. 2007. Extracting model-free volatility from option prices: An examination of the VIX index. The Journal of Derivatives 14: 35–60. [Google Scholar]
- Johansen, Søren, and Katarina Juselius. 1990. Maximum likelihood estimation and inference on cointegration—With applications to the demand for money. Oxford Bulletin of Economics and statistics 52: 169–210. [Google Scholar]
- Jubinski, Daniel, and Amy F. Lipton. 2013. VIX, gold, silver, and oil: How do commodities react to financial market volatility? Journal of Accounting and Finance 13: 70–88. [Google Scholar]
- Kilian, Lutz, and Cheolbeom Park. 2009. The impact of oil price shocks on the US stock market. International Economic Review 50: 1267–87. [Google Scholar]
- Lütkepohl, Helmut. 2005. New Introduction to Multiple Time Series Analysis. Berlin: Springer. [Google Scholar]
- MacKinnon, James G., Alfred A. Haug, and Leo Michelis. 1999. Numerical distribution functions of likelihood ratio tests for cointegration. Journal of Applied Econometrics 14: 563–77. [Google Scholar]
- Mills, Terence C., and Raphael N. Markellos. 2008. The Econometric Modelling of Financial Time Series. Cambridge: Cambridge University Press. [Google Scholar]
- Moraux, Franck, Patrick Navatte, and Christophe Villa. 1999. The predictive power of the French market volatility index: a multi horizons study. Review of Finance 2: 303–20. [Google Scholar]
- Neffelli, Marco, and Marina R. Resta. 2018. Is VIX Still the Investor Fear Gauge? Evidence for the US and BRIC Markets. SSRN. [Google Scholar] [CrossRef] [Green Version]
- Psychoyios, Dimitris, George Dotsis, and Raphael N. Markellos. 2010. A jump diffusion model for VIX volatility options and futures. Review of Quantitative Finance and Accounting 35: 245–69. [Google Scholar]
- Rapach, David E., Jack K. Strauss, and Guofu Zhou. 2013. lnternational stock return predictability: What is the role of the United States? Journal of Finance 68: 1633–62. [Google Scholar]
- Sari, Ramazan, Ugur Soytas, and Erk Hacihasanoglu. 2011. Do global risk perceptions influence world oil prices? Energy Economics 33: 515–24. [Google Scholar]
- Sarwar, Ghulam. 2012a. Intertemporal relations between the market volatility index and stock index returns. Applied Financial Economics 22: 899–909. [Google Scholar]
- Sarwar, Ghulam. 2012b. Is VIX an investor fear gauge in BRIC equity markets? Journal of Multinational Financial Management 22: 55–65. [Google Scholar]
- Sarwar, Ghulam. 2014. US stock market uncertainty and cross-market European stock returns. Journal of Multinational Financial Management 28: 1–14. [Google Scholar]
- Sarwar, Ghulam, and Walayet Khan. 2017. The effect of US stock market uncertainty on emerging market returns. Emerging Markets Finance and Trade 53: 1796–811. [Google Scholar]
- Simon, David P. 2003. The Nasdaq volatility index during and after the bubble. The Journal of Derivatives 11: 9–24. [Google Scholar]
- Sims, Christopher A. 1989. Models and their uses. American Journal of Agricultural Economics 71: 489–94. [Google Scholar]
- Sims, Christopher A., James H. Stock, and Mark W. Watson. 1990. Inference in linear time series models with some unit roots. Econometrica: Journal of the Econometric Society 58: 113–44. [Google Scholar]
- Skalin, Joakim, and Timo Teräsvirta. 1999. Another Look at Swedish Business Cycles. Journal of Applied Econometrics 14: 359–78. [Google Scholar]
- Skiadopoulos, George. 2004. The Greek implied volatility index: construction and properties. Applied Financial Economics 14: 1187–96. [Google Scholar]
- Smales, Lee A. 2016. Risk-on/Risk-off: Financial market response to investor fear. Finance Research Letters 17: 125–34. [Google Scholar]
- Stock, James H. 1987. Asymptotic properties of least squares estimators of cointegrating vectors. Econometrica: Journal of the Econometric Society, 1035–56. [Google Scholar] [CrossRef]
- Wagner, Niklas, and Alexander Szimayer. 2004. Local and spillover shocks in implied market volatility: Evidence for the US and Germany. Research in International Business and Finance 18: 237–51. [Google Scholar]
- West, Kenneth D. 1988. Asymptotic normality, when regressors have a unit root. Econometrica: Journal of the Econometric Society 56: 1397–1417. [Google Scholar]
- Whaley, Robert E. 1993. Derivatives on market volatility: Hedging tools long overdue. The Journal of Derivatives 1: 71–84. [Google Scholar]
- Whaley, Robert E. 2000. The investor fear gauge. Journal of Portfolio Management 26: 12. [Google Scholar]
- Whaley, Robert E. 2008. Understanding the VIX. Journal of Portfolio Management 35: 98–105. [Google Scholar]
- Yunus, Nafeesa. 2013. Contagion in international financial markets: A recursive cointegration approach. Journal of Multinational Financial Management 23: 327–37. [Google Scholar]
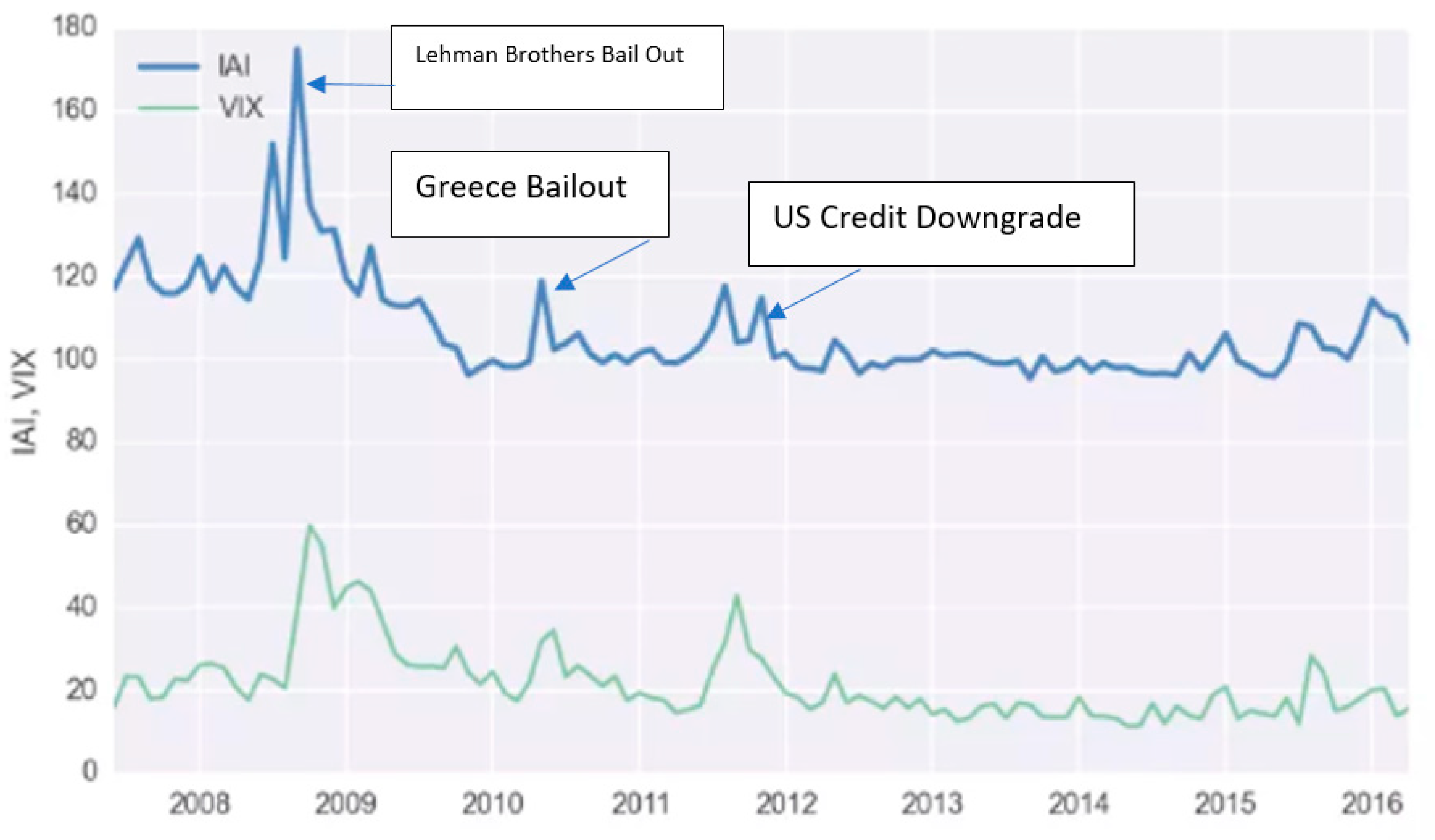
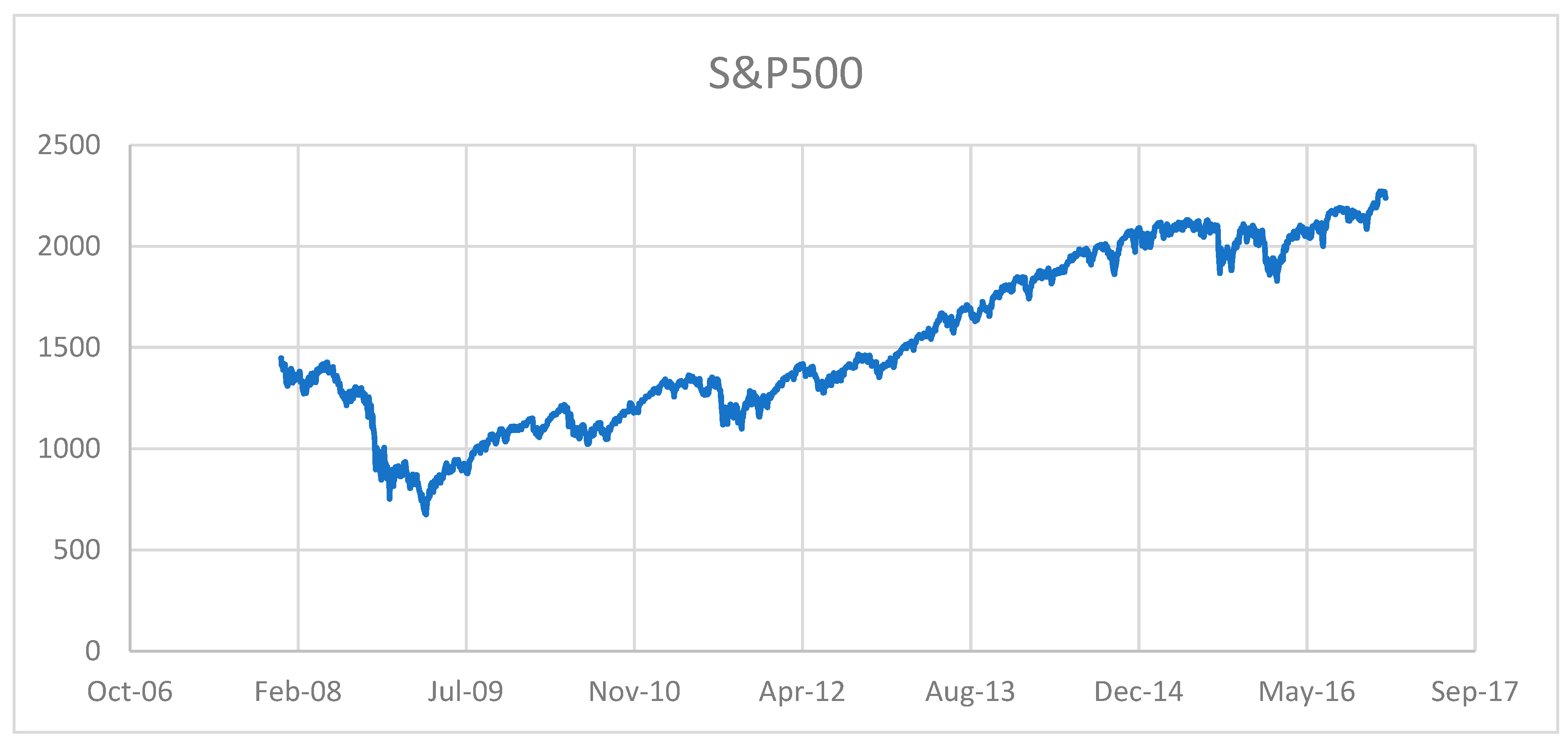
| 1 | Academic and the popular sources have argued that the VIX may suffer from computational flaws and perhaps even manipulated. For instance, there has been periods that VIX predictions and market movements have diverged during some time periods. As an example, for four months between 8 August 2017 and 8 November 2017, the VIX was up 19%, signaling rising fear among market participants. This would imply a downward trend in S&P 500. However, the S&P 500 was rising in an upward trajectory. Other periods of strong divergences between VIX and S&P 500 are April 2007 to October 2007 and December 2014 to February 2015. |
| 2 | Other implied volatility indices have been devised following the CBOE VIX, including: the VXN and VXD in the CBOE, the VDAX-NEW in Germany, the VX1 and VX6 in France, and the VSTOXX in the Eurex, among others. |
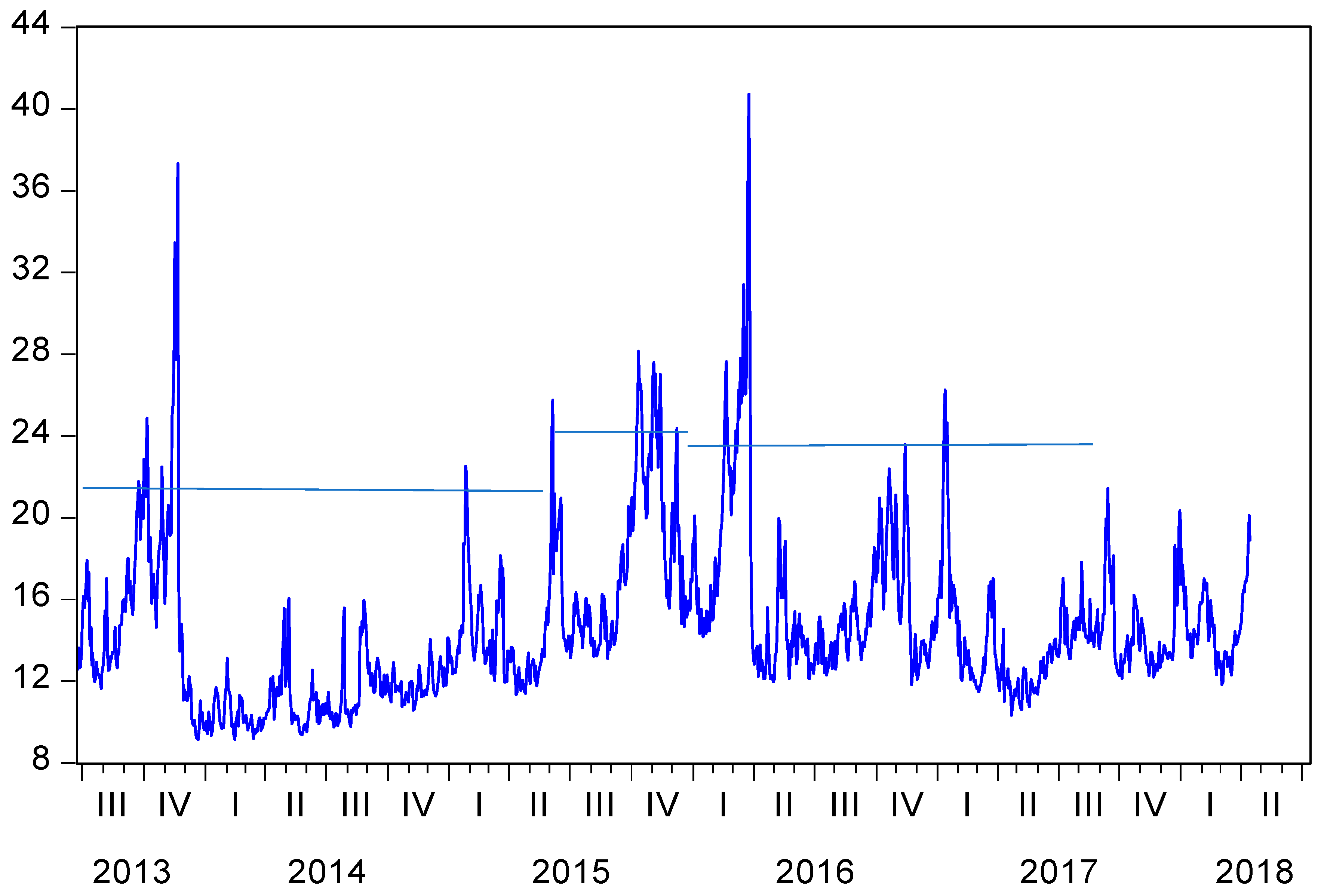



| Panel A: Bai Perron Test of Structural Breaks | |||||
| Break Test | Scaled F-Statistic | Critical Value * | Dates | ||
| 0 vs. 1 b | 43.310 | 11.47 | 8/12/2015 | ||
| 1 vs. 2 b | 20.905 | 12.95 | 5/17/2016 | ||
| 2 vs. 3 b | 19.799 | 14.03 | 2/13/2017 | ||
| 3 vs. 4 | 1.427 | 14.85 | |||
| ADF Unit Root Test with Structural Break | |||||
| Based on Minimizing the Dickey-Fuller t-statistic 1st | −7.110 a | ||||
| Based on Minimizing the Dickey-Fuller t-statistic 1st | −6.774 a | ||||
| Based on Minimizing the Dickey-Fuller t-statistic 1st | −6.770 a | ||||
| Panel B: Levels 6/24/2013–8/12/2015 | |||||
| Tests | CAC | DAX | FTSE | S&P | VIX |
| ADF | −2.826 | −2.409 | −4.216 a | −4.141 a | −5.058 a |
| PP | −2.847 | −2.409 | −4.392 a | −4.137 a | −4.753 a |
| KPPS | 0.284 a | 0.256 a | 0.109 | 0.390 a | 0.328 a |
| ARCH-LM | 6.934 a | 8.788 a | 7.848 a | 13.345 a | |
| Panel C: Levels 8/13/2015–5/17/2016 | |||||
| Tests | CAC | DAX | FTSE | S&P | VIX |
| ADF | −2.538 | −2.286 | −3.301 c | −2.394 | −3.052 |
| PP | −2.600 | 2.354 | −3.282 c | −2.442 | −2.911 |
| KPPS | 0.145 b | 0.152 b | 0.177 b | 0.165 b | 0.165 b |
| ARCH-LM | 6.934 a | 8.788 a | 7.848 a | 13.345 a | |
| Panel D: Levels 5/18/2016–2/13/2017 | |||||
| Tests | CAC | DAX | FTSE | S&P | VIX |
| ADF | −3.065 | −2.539 | −2.599 | −3.179 c | −4.024 a |
| PP | −3.192c | −2.616 | −2.581 | −3.166 c | −4.137 a |
| KPPS | 0.103 | 0.208 b | 0.081 | 0.200 b | 0.114 |
| ARCH-LM | 2.191 | 2.693c | 13.955 a | 29.097 a | |
| Panel E: Summary descriptive statistics for model variables. All variables are in level | |||||
| Statistics | CAC | DAX | FTSE | S&P | VIX |
| Mean | 64.730 | 79733.720 | 107.271 | 72.388 | |
| Stand Dev | 8.231 | 27324.000 | 102.228 | 34.522 | |
| Skewness | 0.281 | 0.977 | 0.992 | 0.899 | |
| Kurtosis | 1.912 | 2.563 | 3.858 | 3.013 | |
| J-B | 33.149 a | 87.081 a | 103.658 | 71.473 a | |
| Panel F: Johansen-Juselius Cointegration Test, unrestricted VAR lag order = 6 | |||||
| r = The number of cointegrating vectors among the four variables | |||||
| vector | λm | p-Value | λt | p-Value | |
| r = 0 | 40.271 a | 0.001 | 70.191 a | 0.000 | |
| r ≤ 1 | 26.011 a | 0.009 | 29.919 b | 0.048 | |
| r ≤ 2 | 3.860 | 0.873 | 3.908 | 0.910 | |
| r ≤ 3 | 0.047 | 0.827 | 0.047 | 0.827 | |
| CAC | ||||||
| Period | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 1.523907 | 23.06727 | 53.16470 | 17.57172 | 6.186519 | 0.009798 |
| 10 | 3.325619 | 19.33011 | 62.15958 | 15.28370 | 3.158607 | 0.068011 |
| 20 | 3.553793 | 16.78376 | 68.39097 | 12.85680 | 1.914194 | 0.054273 |
| 30 | 3.596813 | 15.23153 | 72.33904 | 10.97169 | 1.416521 | 0.041231 |
| DAX | ||||||
| Period | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 222.0597 | 15.51648 | 74.49980 | 0.168141 | 9.667806 | 0.147774 |
| 10 | 688.4700 | 12.91648 | 82.06945 | 0.217239 | 4.644559 | 0.152269 |
| 20 | 935.9210 | 10.97281 | 85.79171 | 0.446709 | 2.689165 | 0.099600 |
| 30 | 1090.002 | 9.727636 | 87.40137 | 0.853079 | 1.945311 | 0.072604 |
| FTSE | ||||||
| Period | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 1308.442 | 11.12727 | 40.32318 | 7.713062 | 33.81403 | 7.022454 |
| 10 | 4132.530 | 9.762820 | 47.22903 | 8.129161 | 32.40228 | 2.476710 |
| 20 | 5707.291 | 9.125213 | 49.48482 | 8.540962 | 30.72729 | 2.121724 |
| 30 | 6718.869 | 8.916086 | 50.41408 | 8.771329 | 29.85478 | 2.043726 |
| SP | ||||||
| Period | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 438.4022 | 0.698788 | 20.86801 | 0.167246 | 8.772745 | 69.49321 |
| 10 | 993.6533 | 2.033265 | 32.29965 | 2.183065 | 16.41988 | 47.06415 |
| 20 | 1107.649 | 2.374618 | 35.12433 | 3.529921 | 17.92936 | 41.04177 |
| 30 | 1141.226 | 2.445579 | 35.85994 | 4.117280 | 18.04220 | 39.53501 |
| Factorization: Structural | ||||||
| CAC | ||||||
| Period | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 1.847290 | 5.629366 | 42.89547 | 8.235468 | 1.730171 | 41.50953 |
| 10 | 4.213181 | 20.57815 | 46.04785 | 5.384713 | 1.144778 | 26.84451 |
| 20 | 4.803299 | 22.96667 | 44.30306 | 5.285415 | 1.125518 | 26.31934 |
| 30 | 5.022063 | 23.30053 | 44.05778 | 5.270821 | 1.125361 | 26.24551 |
| DAX | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 1031.178 | 8.503843 | 40.11901 | 3.069205 | 0.485771 | 47.82217 |
| 10 | 1540.439 | 17.22094 | 45.11183 | 3.074743 | 0.384313 | 34.20818 |
| 20 | 1595.023 | 17.90871 | 44.26796 | 3.222857 | 0.390217 | 34.21025 |
| 30 | 1602.747 | 17.95395 | 44.20409 | 3.234434 | 0.390874 | 34.21664 |
| FTSE | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 4240.179 | 6.352564 | 17.10188 | 17.15250 | 9.062495 | 50.33057 |
| 10 | 5679.630 | 31.55825 | 32.41167 | 7.387517 | 7.149734 | 21.49282 |
| 20 | 5779.511 | 38.40037 | 32.18627 | 5.762504 | 6.048016 | 17.60284 |
| 30 | 5786.676 | 39.48003 | 31.75040 | 5.582793 | 5.804940 | 17.38184 |
| S&P 500 | S.E. | VIX | CAC | DAX | FTSE | S&P 500 |
| 1 | 1212.531 | 27.93073 | 44.85573 | 5.416856 | 20.34589 | 1.450803 |
| 10 | 2840.446 | 38.13473 | 48.99117 | 1.206103 | 9.250807 | 2.417189 |
| 20 | 3281.835 | 39.88873 | 45.88734 | 1.480075 | 7.741952 | 5.001906 |
| 30 | 3377.665 | 40.11354 | 45.20379 | 1.576134 | 7.521768 | 5.584767 |
| Factorization: Structural | ||||||
| Panel A: 24 June 2013–12 August 2015 | |||||
| Causing Variable | Caused Variables | ||||
| Lags | VIX | CAC | DAX | FTSE | S&P 500 |
| 5 | 0.307 | 0.178 | 0.880 | 0.998 | |
| 6 | 0.002 | 0.012 | 0.361 | 0.086 | |
| 7 | 0.016 | 0.062 | 0.260 | 0.097 | |
| 8 | 0.027 | 0.083 | 0.124 | 0.958 | |
| 9 | 0.039 | 0.037 | 0.001 | 0.797 | |
| 10 | 0.033 | 0.016 | 0.004 | 0.901 | |
| Panel B: 13 August 2015–17 May 2016 | |||||
| CAC | DAX | FTSE | S&P 500 | ||
| 5 | 0.754 | 0.968 | 0.749 | 0.662 | |
| 6 | 0.618 | 0.882 | 0.007 | 0.048 | |
| 7 | 0.041 | 0.028 | 0.077 | 0.065 | |
| 8 | 0.074 | 0.094 | 0.073 | 0.003 | |
| 9 | 0.073 | 0.857 | 0.690 | 0.004 | |
| 10 | 0.706 | 0.707 | 0.474 | 0.536 | |
| Panel C: 18 May–13 February 2017 | |||||
| CAC | DAX | FTSE | S&P 500 | ||
| 5 | 0.996 | 0.999 | 0.701 | 0.101 | |
| 6 | 0.974 | 0.868 | 0.838 | 0.169 | |
| 7 | 0.984 | 0.943 | 0.806 | 0.317 | |
| 8 | 0.838 | 0.822 | 0.772 | 0.634 | |
| 9 | 0.561 | 0.647 | 0.608 | 0.499 | |
| 10 | 0.194 | 0.512 | 0.385 | 0.536 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adrangi, B.; Chatrath, A.; Macri, J.; Raffiee, K. Dynamic Responses of Major Equity Markets to the US Fear Index. J. Risk Financial Manag. 2019, 12, 156. https://doi.org/10.3390/jrfm12040156
Adrangi B, Chatrath A, Macri J, Raffiee K. Dynamic Responses of Major Equity Markets to the US Fear Index. Journal of Risk and Financial Management. 2019; 12(4):156. https://doi.org/10.3390/jrfm12040156
Chicago/Turabian StyleAdrangi, Bahram, Arjun Chatrath, Joseph Macri, and Kambiz Raffiee. 2019. "Dynamic Responses of Major Equity Markets to the US Fear Index" Journal of Risk and Financial Management 12, no. 4: 156. https://doi.org/10.3390/jrfm12040156
APA StyleAdrangi, B., Chatrath, A., Macri, J., & Raffiee, K. (2019). Dynamic Responses of Major Equity Markets to the US Fear Index. Journal of Risk and Financial Management, 12(4), 156. https://doi.org/10.3390/jrfm12040156





