Forecasting Realized Volatility Using a Nonnegative Semiparametric Model
Abstract
1. Introduction
2. A Nonnegative Semiparametric Model
2.1. Related Volatility Models
2.2. Realized Volatility
2.3. The Model
3. Robust Estimation and Forecasting
3.1. Robust Estimation of
3.2. Estimation of and
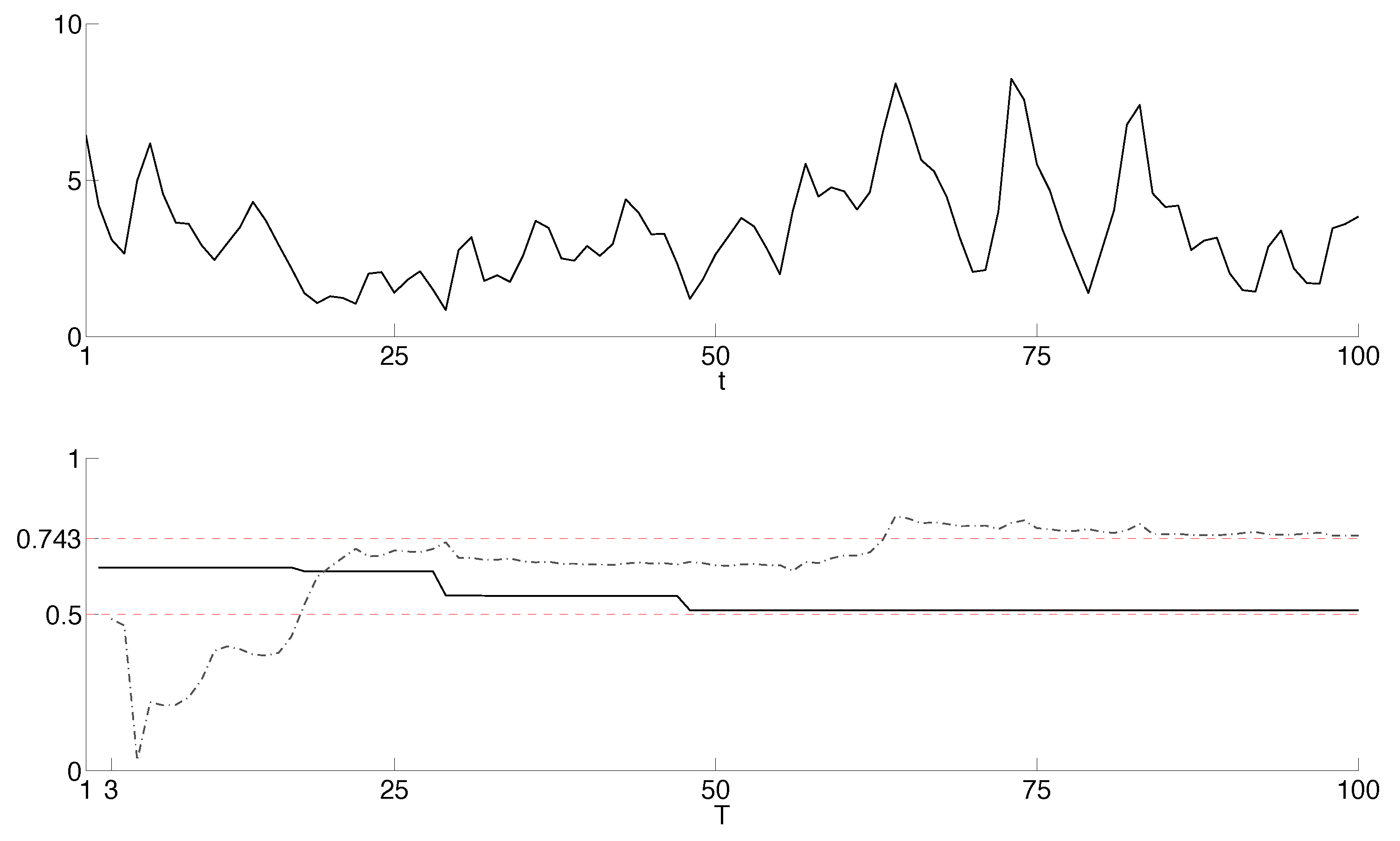
4. Monte Carlo Studies
5. An Empirical Study
5.1. Alternative Models
5.1.1. Exponential Smoothing
5.1.2. ARFIMA()
5.1.3. HAR
5.2. Forecast Accuracy Measures
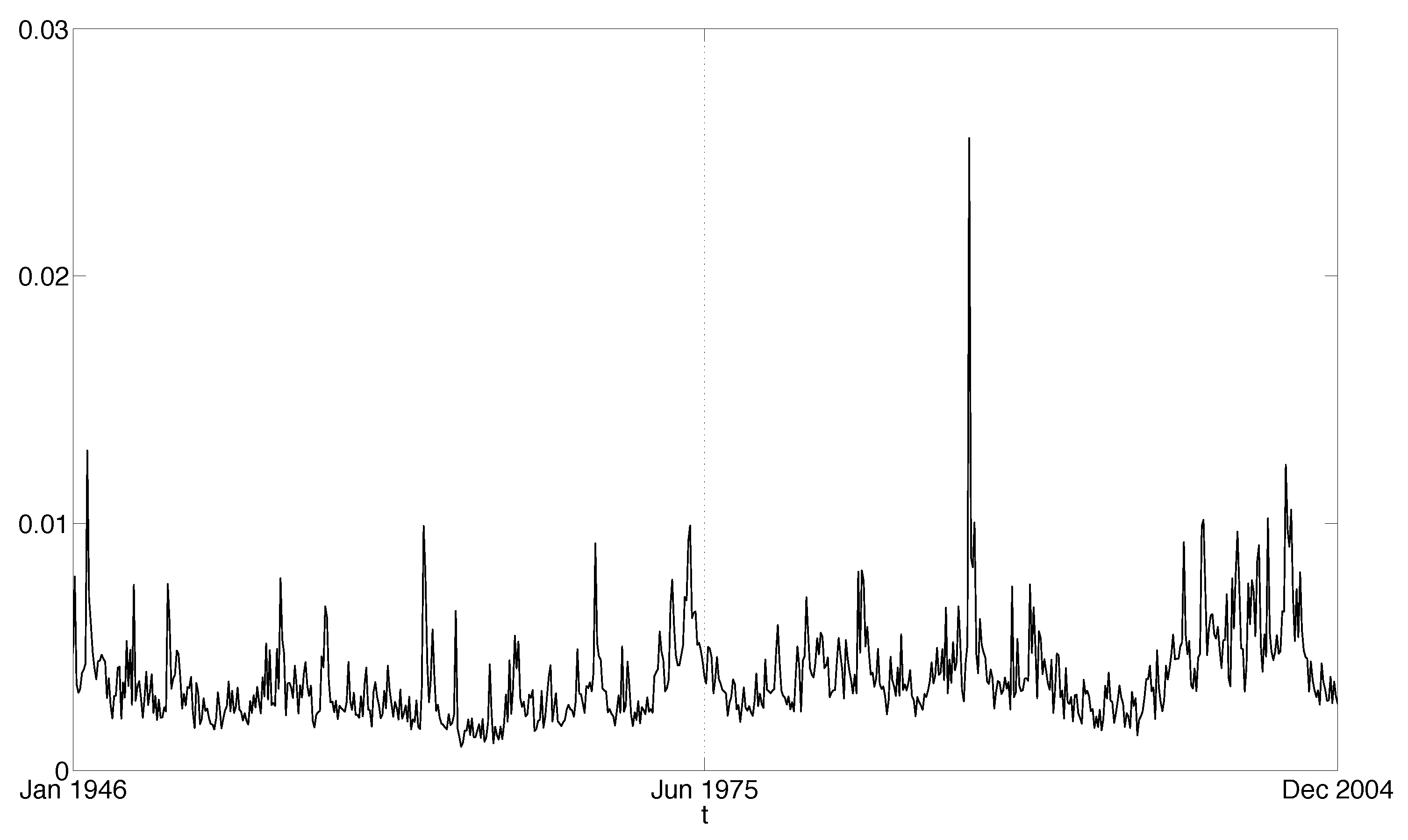
5.3. Data
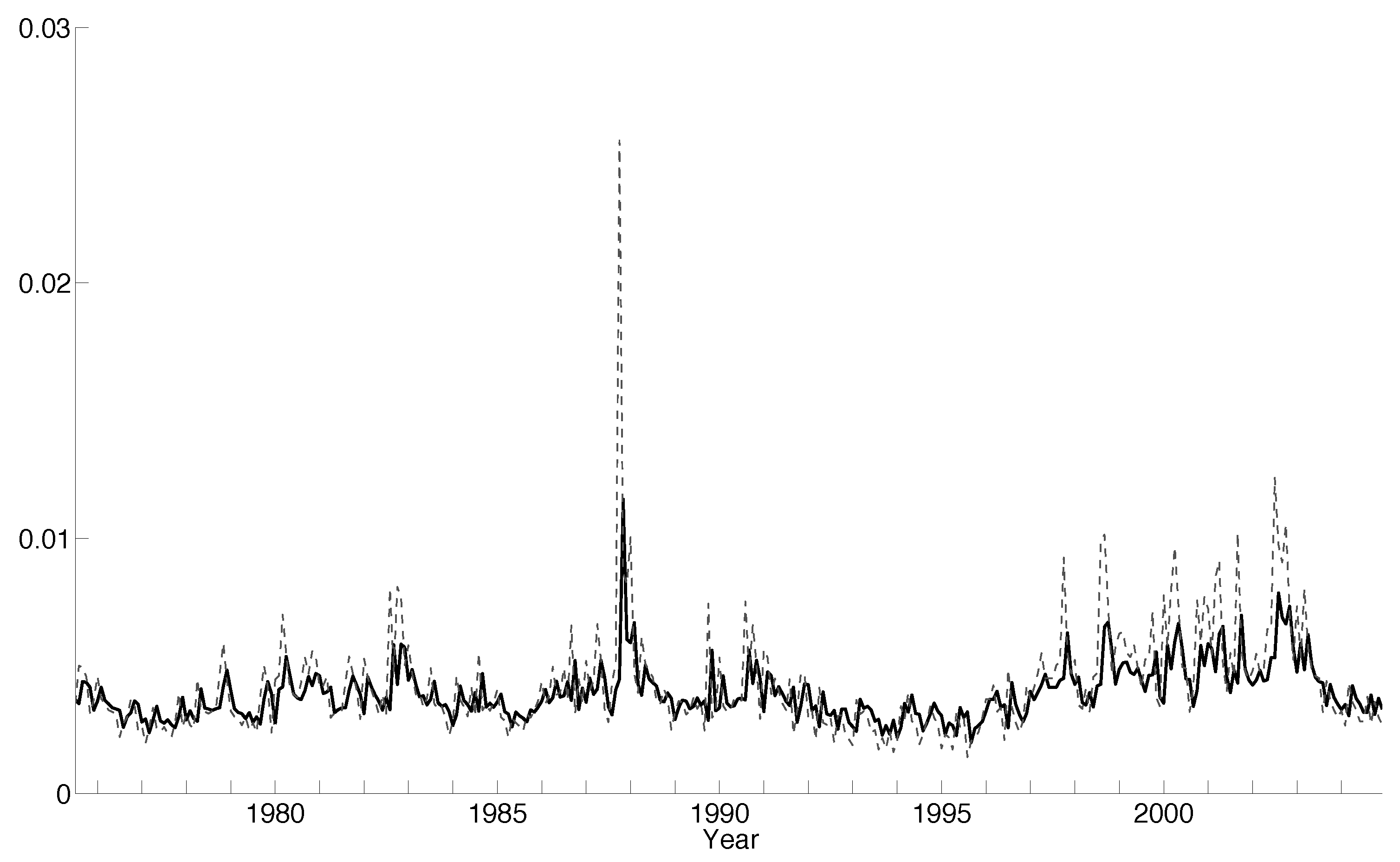
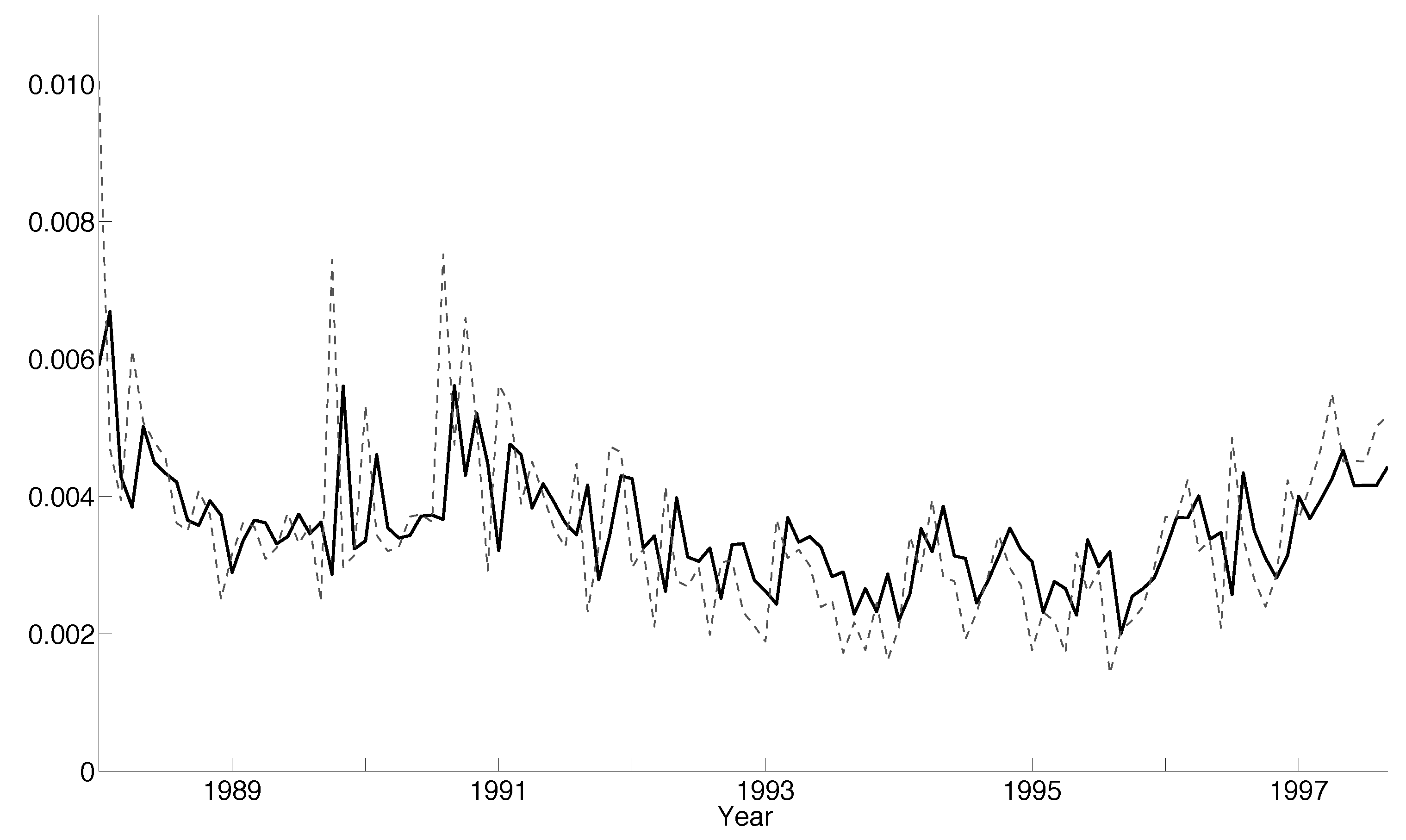
5.4. Empirical Results
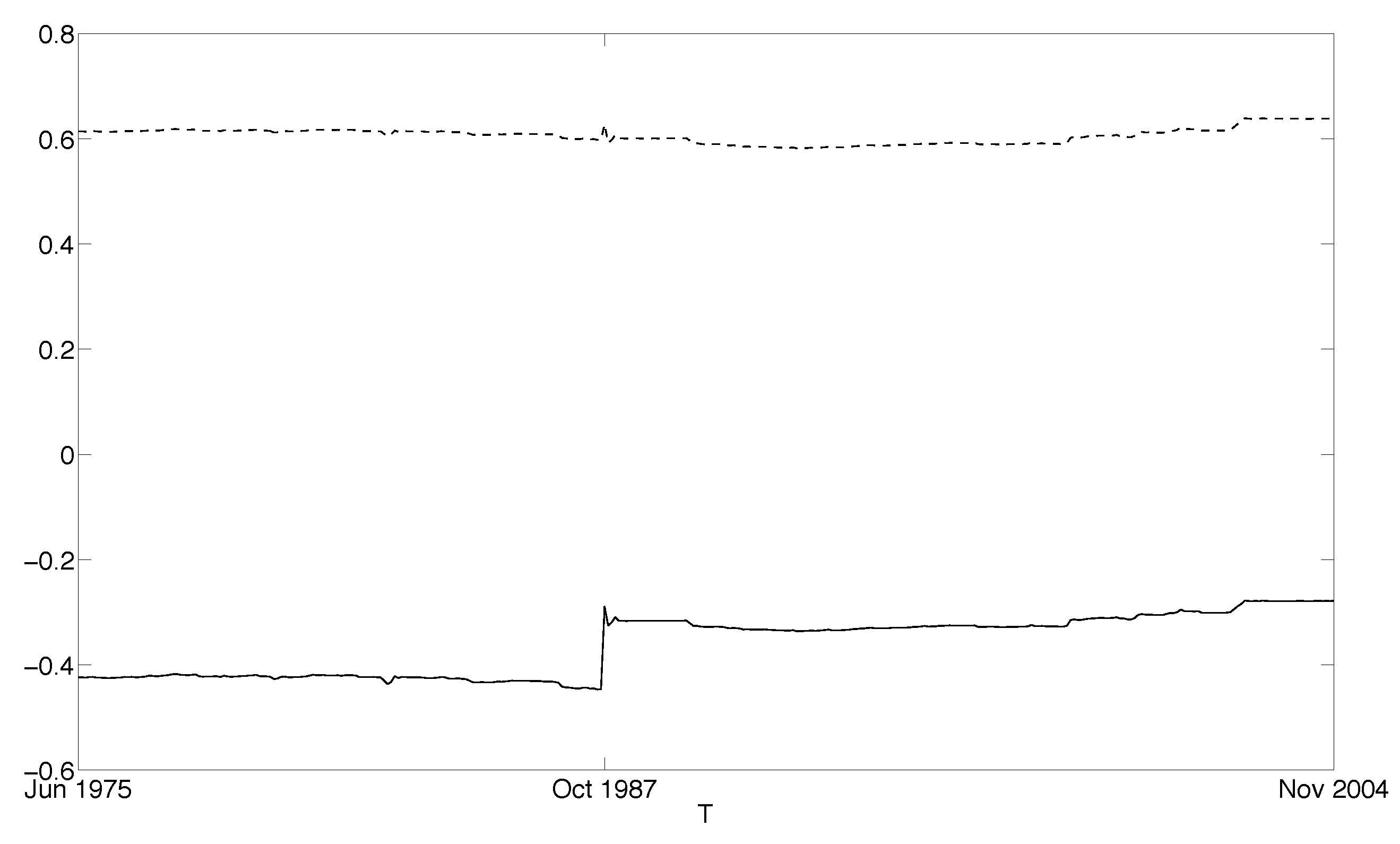
5.4.1. Sample including the 1987 Crash
5.4.2. Sample Post the 1987 Crash
6. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Andersen, Torben G., and Tim Bollerslev. 1998. Answering the skeptics: Yes, standard volatility models do provide accurate forecasts. International Economic Review 39: 885–905. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2001. The distribution of realized exchange rate volatility. Journal of the American Statistical Association 96: 42–55. [Google Scholar] [CrossRef]
- Andersen, Torben G., Tim Bollerslev, Francis X. Diebold, and Paul Labys. 2003. Modeling and forecasting realized volatility. Econometrica 71: 579–625. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2001. Non-Gaussian Ornstein-Uhlenbeck-based models and some of their uses in financial economics. Journal of the Royal Statistical Society. Series B (Statistical Methodology) 63: 167–241. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, Ole E., and Neil Shephard. 2002. Econometric analysis of realized volatility and its use in estimating stochastic volatility models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 64: 253–80. [Google Scholar] [CrossRef]
- Beran, Jan. 1995. Maximum likelihood estimation of the differencing parameter for invertible short and long memory autoregressive integrated moving average models. Journal of the Royal Statistical Society. Series B (Methodological) 57: 659–72. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Ray Y. Chou, and Kenneth F. Kroner. 1992. ARCH modeling in finance: A review of the theory and empirical evidence. Journal of Econometrics 52: 5–59. [Google Scholar] [CrossRef]
- Bollerslev, Tim, Robert F. Engle, and Daniel B. Nelson. 1994. Chapter 49 ARCH models. Handbook of Econometrics 4: 2959–3038. [Google Scholar]
- Box, George E. P., and David R. Cox. 1964. An analysis of transformations. Journal of the Royal Statistical Society: Series B (Methodological) 26: 211–43. [Google Scholar] [CrossRef]
- Chen, Willa W., and Rohit S. Deo. 2004. Power transformations to induce normality and their applications. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 66: 117–30. [Google Scholar] [CrossRef]
- Chung, Ching-Fan, and Richard T. Baillie. 1993. Small sample bias in conditional sum-of-squares estimators of fractionally integrated ARMA models. Empirical Economics 18: 791–806. [Google Scholar] [CrossRef]
- Cipollini, Fabrizio, Robert F. Engle, and Giampiero M. Gallo. 2006. Vector Multiplicative Error Models: Representation and Inference. Working Paper 12690. Cambridge, UK: National Bureau of Economic Research. [Google Scholar]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- Datta, Somnath, and William P. McCormick. 1995. Bootstrap inference for a first-order autoregression with positive innovations. Journal of the American Statistical Association 90: 1289–300. [Google Scholar] [CrossRef]
- Davis, Richard A., and William P. McCormick. 1989. Estimation for first-order autoregressive processes with positive or bounded innovations. Stochastic Processes and their Applications 31: 237–50. [Google Scholar] [CrossRef]
- Deo, Rohit, Clifford Hurvich, and Yi Lu. 2006. Forecasting realized volatility using a long-memory stochastic volatility model: Estimation, prediction and seasonal adjustment. Journal of Econometrics 131: 29–58. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Roberto S. Mariano. 1995. Comparing predictive accuracy. Journal of Business & Economic Statistics 13: 253–63. [Google Scholar]
- Doornik, Jurgen A. 2009. An Object-Oriented Matrix Programming Language Ox 6. London: Timberlake Consultants Press. [Google Scholar]
- Doornik, Jurgen A., and Marius Ooms. 2004. Inference and forecasting for ARFIMA models with an application to US and UK inflation. Studies in Nonlinear Dynamics & Econometrics 8. [Google Scholar] [CrossRef]
- Duan, Jin-Chuan. 1997. Augmented GARCH(p,q) process and its diffusion limit. Journal of Econometrics 79: 97–127. [Google Scholar] [CrossRef]
- Feigin, Paul D., and Sidney I. Resnick. 1992. Estimation for autoregressive processes with positive innovations. Communications in Statistics. Stochastic Models 8: 685–717. [Google Scholar] [CrossRef]
- Fernandes, Marcelo, and Joachim Grammig. 2006. A family of autoregressive conditional duration models. Journal of Econometrics 130: 1–23. [Google Scholar] [CrossRef]
- Ghalanos, Alexios. 2019. Rugarch: Univariate GARCH Models. R Package Version 1.4-1. Available online: https://cran.r-project.org/web/packages/rugarch/index.html (accessed on 4 August 2019).
- Ghysels, Eric, Andrew C. Harvey, and Eric Renault. 1996. Stochastic volatility. In Statistical Methods in Finance. Handbook of Statistics. Amsterdam: Elsevier, vol. 14, pp. 119–91. [Google Scholar]
- Gonçalves, Sílvia, and Nour Meddahi. 2011. Box-Cox transforms for realized volatility. Journal of Econometrics 160: 129–44. [Google Scholar] [CrossRef]
- Granger, Clive W. J., and Paul Newbold. 1976. Forecasting transformed series. Journal of the Royal Statistical Society. Series B (Methodological) 38: 189–203. [Google Scholar] [CrossRef]
- Hansen, Peter Reinhard, and Asger Lunde. 2006. Consistent ranking of volatility models. Journal of Econometrics 131: 97–121. [Google Scholar] [CrossRef]
- Hansen, Peter Reinhard, Zhuo Huang, and Howard Howan Shek. 2012. Realized GARCH: A joint model for returns and realized measures of volatility. Journal of Applied Econometrics 27: 877–906. [Google Scholar] [CrossRef]
- Hentschel, Ludger. 1995. All in the family: Nesting symmetric and asymmetric GARCH models. Journal of Financial Economics 39: 71–104. [Google Scholar] [CrossRef]
- Higgins, Matthew L., and Anil K. Bera. 1992. A class of nonlinear ARCH models. International Economic Review 33: 137–58. [Google Scholar] [CrossRef]
- Hyndman, Rob J., and Anne B. Koehler. 2006. Another look at measures of forecast accuracy. International Journal of Forecasting 22: 679–88. [Google Scholar] [CrossRef]
- Jacod, Jean. 2017. Limit of random measures associated with the increments of a Brownian semimartingale. Journal of Financial Econometrics 16: 526–69. [Google Scholar] [CrossRef]
- Jennrich, Robert I. 1969. Asymptotic properties of non-linear least squares estimators. The Annals of Mathematical Statistics 40: 633–43. [Google Scholar] [CrossRef]
- J.P. Morgan. 1996. RiskMetricsTM–Technical Document. London: J.P. Morgan. [Google Scholar]
- Lopez, Jose A. 2001. Evaluating the predictive accuracy of volatility models. Journal of Forecasting 20: 87–109. [Google Scholar] [CrossRef]
- Nielsen, Bent, and Neil Shephard. 2003. Likelihood analysis of a first-order autoregressive model with exponential innovations. Journal of Time Series Analysis 24: 337–44. [Google Scholar] [CrossRef]
- Patton, Andrew J. 2011. Volatility forecast comparison using imperfect volatility proxies. Journal of Econometrics 160: 246–56. [Google Scholar] [CrossRef]
- Phillips, Peter C.B. 1987. Time series regression with a unit root. Econometrica 55: 277–301. [Google Scholar] [CrossRef]
- Poon, Ser-Huang, and Clive W. J. Granger. 2003. Forecasting volatility in financial markets: A review. Journal of Economic Literature 41: 478–539. [Google Scholar] [CrossRef]
- Preve, Daniel P. A. 2015. Linear programming-based estimators in nonnegative autoregression. Journal of Banking & Finance 61: 225–34. [Google Scholar]
- Shephard, Neil. 2005. Stochastic Volatility: Selected Readings. Oxford: Oxford University Press. [Google Scholar]
- Shimotsu, Katsumi, and Peter C. B. Phillips. 2005. Exact local Whittle estimation of fractional integration. The Annals of Statistics 33: 1890–933. [Google Scholar] [CrossRef]
- Sowell, Fallaw. 1992. Maximum likelihood estimation of stationary univariate fractionally integrated time series models. Journal of Econometrics 53: 165–88. [Google Scholar] [CrossRef]
- Taylor, Stephen J. 2007. Modelling Financial Time Series, 2nd ed. Singapore: World Scientific. [Google Scholar]
- Tukey, John W. 1977. Exploratory Data Analysis. Boston: Addison-Wesley. [Google Scholar]
- Yu, Jun, Zhenlin Yang, and Xibin Zhang. 2006. A class of nonlinear stochastic volatility models and its implications for pricing currency options. Computational Statistics & Data Analysis 51: 2218–231. [Google Scholar]
| 1 | Generally, the distribution of a Box-Cox transformed random variable cannot be normal as its support is bounded either above or below. |
| 2 | See Section 3 for a detailed discussion on the linear programming estimator. |
| 3 | In ABDL (2003) RV is referred to as the realized variance, . Although the authors build time series models for the realized variance, they forecast the realized volatility. In contrast, the present paper builds time series models for and forecasts, the realized volatility, which seems more appropriate. Consequently, the bias correction, as described in ABDL (2003), is not required. |
| 4 | |
| 5 | Some common m-dependent specifications include () and (), where is an i.i.d. sequence of random variables. |
| 6 | More generally, suppose that for some natural number n, then . |
| 7 | Whenever necessary we use the subscript T to emphasize on the sample size. |
| 8 | For instance, if and then . |
| 9 | We also applied the exact ML method of Sowell (1992) and the exact local Whittle estimator of Shimotsu and Phillips (2005) in our empirical study and found that the forecasts remained essentially unchanged. |
| 10 | The Ox language of Doornik (2009) was used to estimate the two ARFIMA models. Matlab code and data used in this paper can be downloaded from http://www.mysmu.edu/faculty/yujun/research.html. |
| 11 | |
| 12 | While we consider the recursive forecasting scheme one could, of course, also consider the rolling or fixed scheme. |
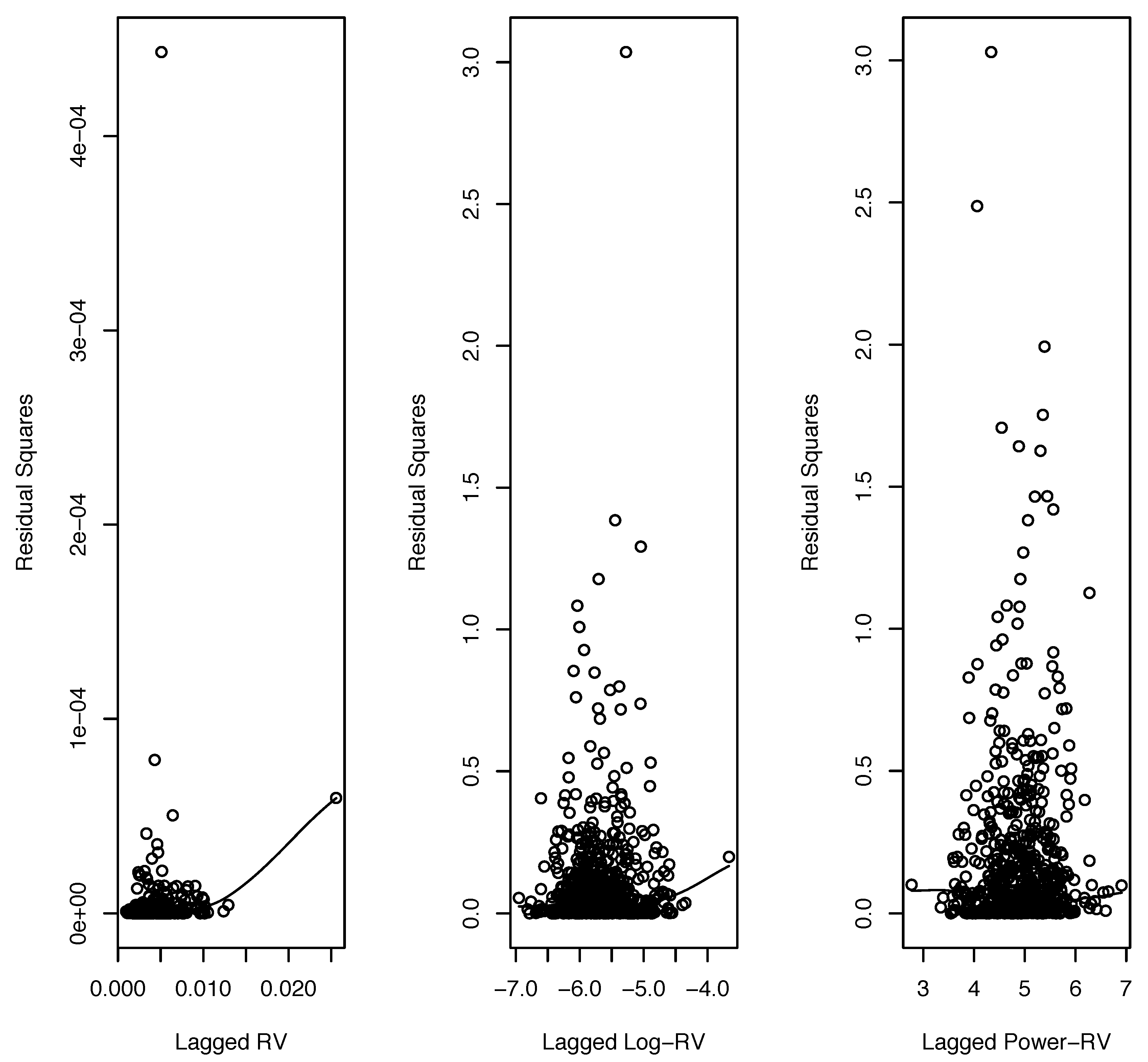
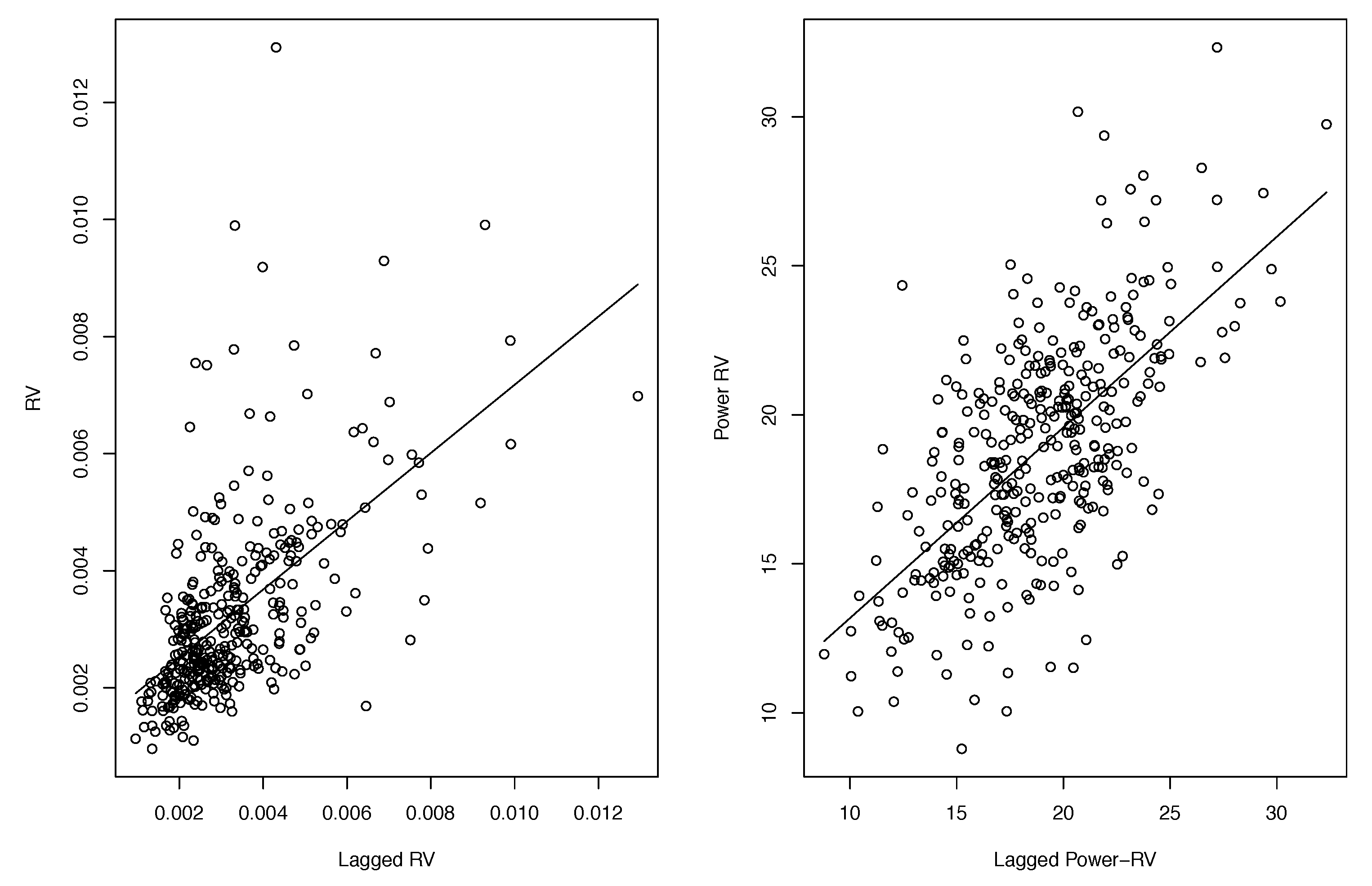
| 13 | We explored all non-zero -values on Tukey’s ladder of power transformations in (13) and found that produced the strongest linear relationship (an increase in from 0.341 to 0.410). |
| Mean | Median | Maximum | Skewness | Kurtosis | JB | |
|---|---|---|---|---|---|---|
| RV | ||||||
| log-RV | ||||||
| power-RV |
| Parameter | Estimator | Bias | MSE | Bias | MSE | Bias | MSE | ||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Estimator | Bias | MSE | Bias | MSE | Bias | MSE | ||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Maximum | Skewness | Kurtosis | JB | ||||
|---|---|---|---|---|---|---|---|---|
| RV | ||||||||
| log-RV |
| MAE | MAPE | MSE | MSPE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Rank | Value | Rank | Value | Rank | Value | Rank | ||||
| ES | 1.268 | 9 | 31.04 | 11 | 3.862 | 11 | 15.30 | 9 | |||
| AR | 0.975 | 6 | 20.93 | 6 | 3.312 | 9 | 7.80 | 5 | |||
| HAR | 0.945 | 2 | 20.75 | 3 | 3.018 | 5 | 7.29 | 2 | |||
| log-AR | 0.954 | 4 | 20.74 | 2 | 3.076 | 8 | 7.56 | 4 | |||
| log-HAR | 0.937 | 1 | 20.90 | 5 | 2.866 | 3 | 7.33 | 3 | |||
| sGARCH | 1.101 | 8 | 27.23 | 9 | 3.344 | 10 | 12.43 | 7 | |||
| realGARCH | 1.089 | 7 | 28.05 | 10 | 3.026 | 6 | 12.93 | 8 | |||
| log-ARFIMA() | 0.961 | 5 | 22.09 | 8 | 2.847 | 1 | 8.04 | 6 | |||
| log-ARFIMA() | 0.961 | 5 | 22.08 | 7 | 2.851 | 2 | 8.04 | 6 | |||
| TNTAR | 0.954 | 4 | 20.78 | 4 | 3.075 | 7 | 7.56 | 4 | |||
| TNTAR | 0.948 | 3 | 20.47 | 1 | 2.911 | 4 | 6.96 | 1 | |||
| MAE | MAPE | MSE | MSPE | |
|---|---|---|---|---|
| ES | 0.000 | 0.000 | 0.001 | 0.001 |
| AR | 0.275 | 0.680 | 0.208 | 0.431 |
| HAR | 0.660 | 0.961 | 0.607 | 0.480 |
| log-AR | 0.898 | 0.754 | 0.973 | 0.968 |
| log-HAR | 0.418 | 0.824 | 0.003 | 0.482 |
| sGARCH | 0.001 | 0.000 | 0.057 | 0.000 |
| realGARCH | 0.001 | 0.000 | 0.709 | 0.000 |
| log-ARFIMA() | 0.728 | 0.034 | 0.008 | 0.188 |
| log-ARFIMA() | 0.725 | 0.035 | 0.008 | 0.184 |
| MAE | MAPE | MSE | MSPE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Value | Rank | Value | Rank | Value | Rank | Value | Rank | ||||
| ES | 1.077 | 10 | 35.38 | 11 | 1.707 | 11 | 20.18 | 11 | |||
| AR | 0.783 | 7 | 23.88 | 8 | 1.258 | 6 | 10.73 | 8 | |||
| HAR | 0.749 | 2 | 22.68 | 3 | 1.079 | 1 | 9.28 | 2 | |||
| log-AR | 0.779 | 6 | 23.38 | 4 | 1.272 | 8 | 10.53 | 6 | |||
| log-HAR | 0.750 | 3 | 22.45 | 2 | 1.123 | 2 | 9.37 | 3 | |||
| sGARCH | 0.963 | 8 | 32.90 | 9 | 1.387 | 9 | 18.77 | 9 | |||
| realGARCH | 0.991 | 9 | 33.73 | 10 | 1.480 | 10 | 19.51 | 10 | |||
| log-ARFIMA() | 0.779 | 6 | 23.65 | 7 | 1.160 | 3 | 10.24 | 5 | |||
| log-ARFIMA() | 0.778 | 5 | 23.61 | 6 | 1.162 | 4 | 10.22 | 4 | |||
| TNTAR | 0.777 | 4 | 23.45 | 5 | 1.260 | 7 | 10.58 | 7 | |||
| TNTAR | 0.744 | 1 | 21.27 | 1 | 1.163 | 5 | 8.18 | 1 | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Eriksson, A.; Preve, D.P.A.; Yu, J. Forecasting Realized Volatility Using a Nonnegative Semiparametric Model. J. Risk Financial Manag. 2019, 12, 139. https://doi.org/10.3390/jrfm12030139
Eriksson A, Preve DPA, Yu J. Forecasting Realized Volatility Using a Nonnegative Semiparametric Model. Journal of Risk and Financial Management. 2019; 12(3):139. https://doi.org/10.3390/jrfm12030139
Chicago/Turabian StyleEriksson, Anders, Daniel P. A. Preve, and Jun Yu. 2019. "Forecasting Realized Volatility Using a Nonnegative Semiparametric Model" Journal of Risk and Financial Management 12, no. 3: 139. https://doi.org/10.3390/jrfm12030139
APA StyleEriksson, A., Preve, D. P. A., & Yu, J. (2019). Forecasting Realized Volatility Using a Nonnegative Semiparametric Model. Journal of Risk and Financial Management, 12(3), 139. https://doi.org/10.3390/jrfm12030139




