Can Higher Capital Discipline Bank Risk: Evidence from a Meta-Analysis
Abstract
1. Introduction
2. Data and Methodology
2.1. Data
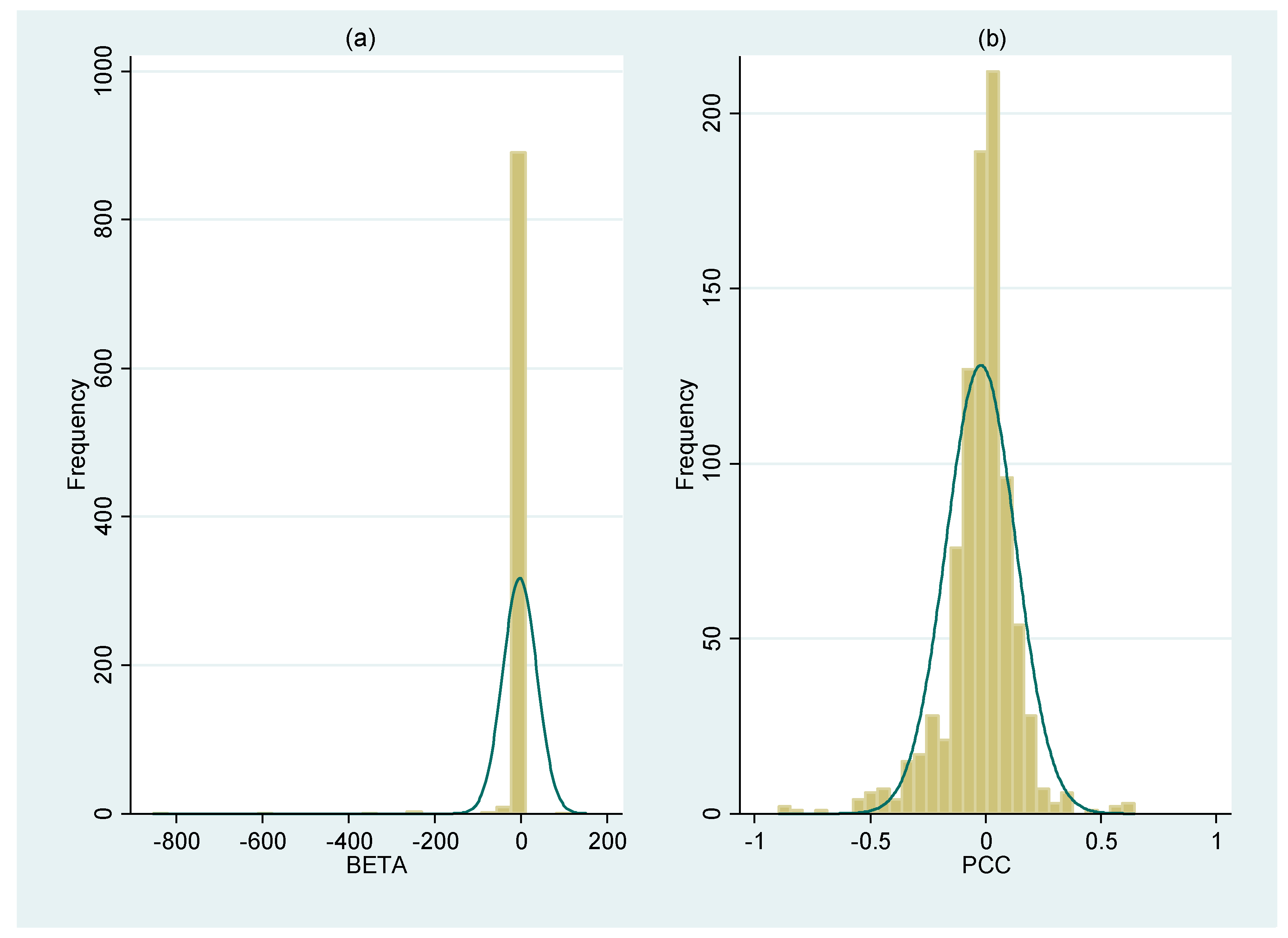
2.2. Standardized Effect Sizes
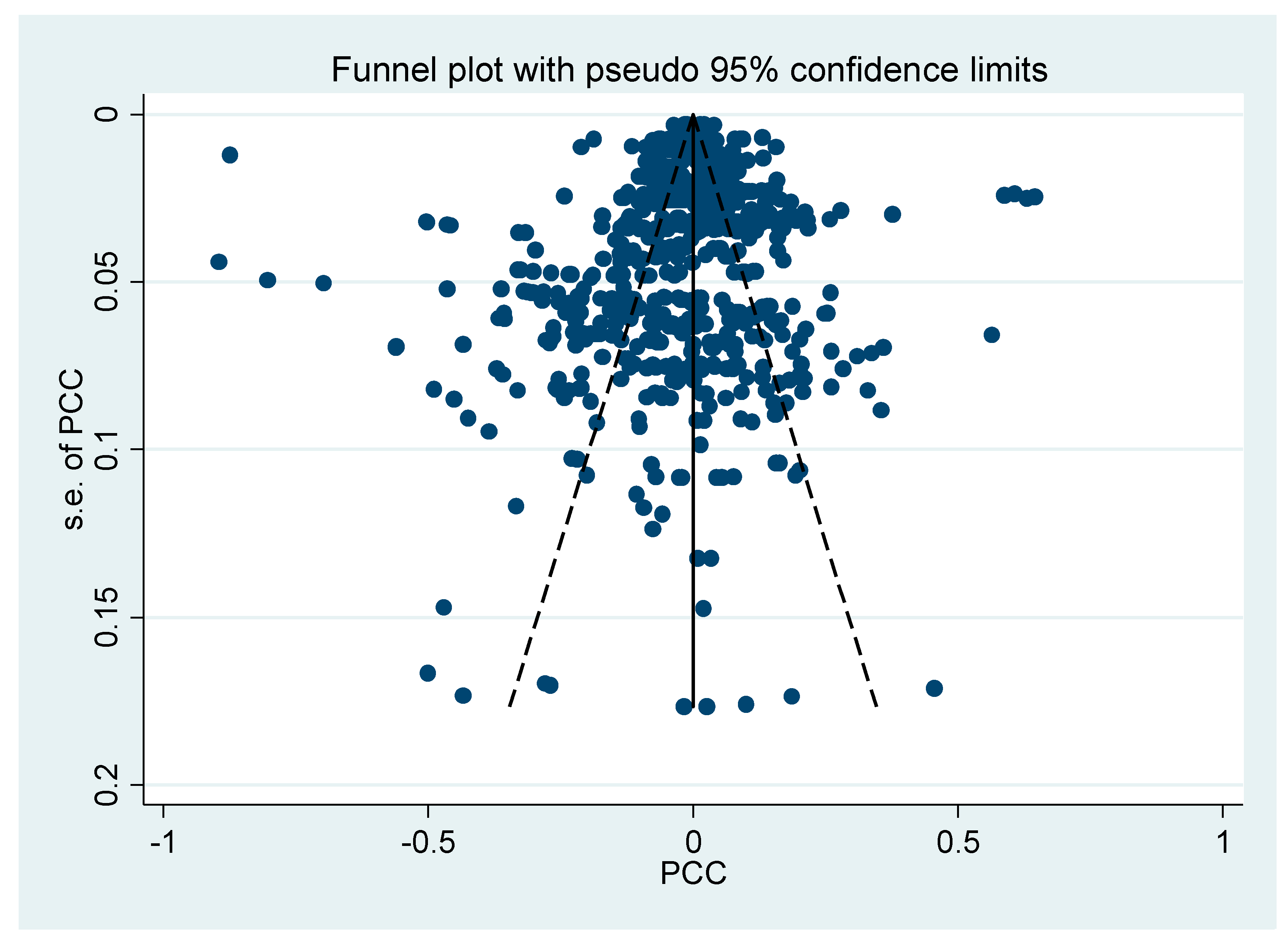
2.3. Publication Bias
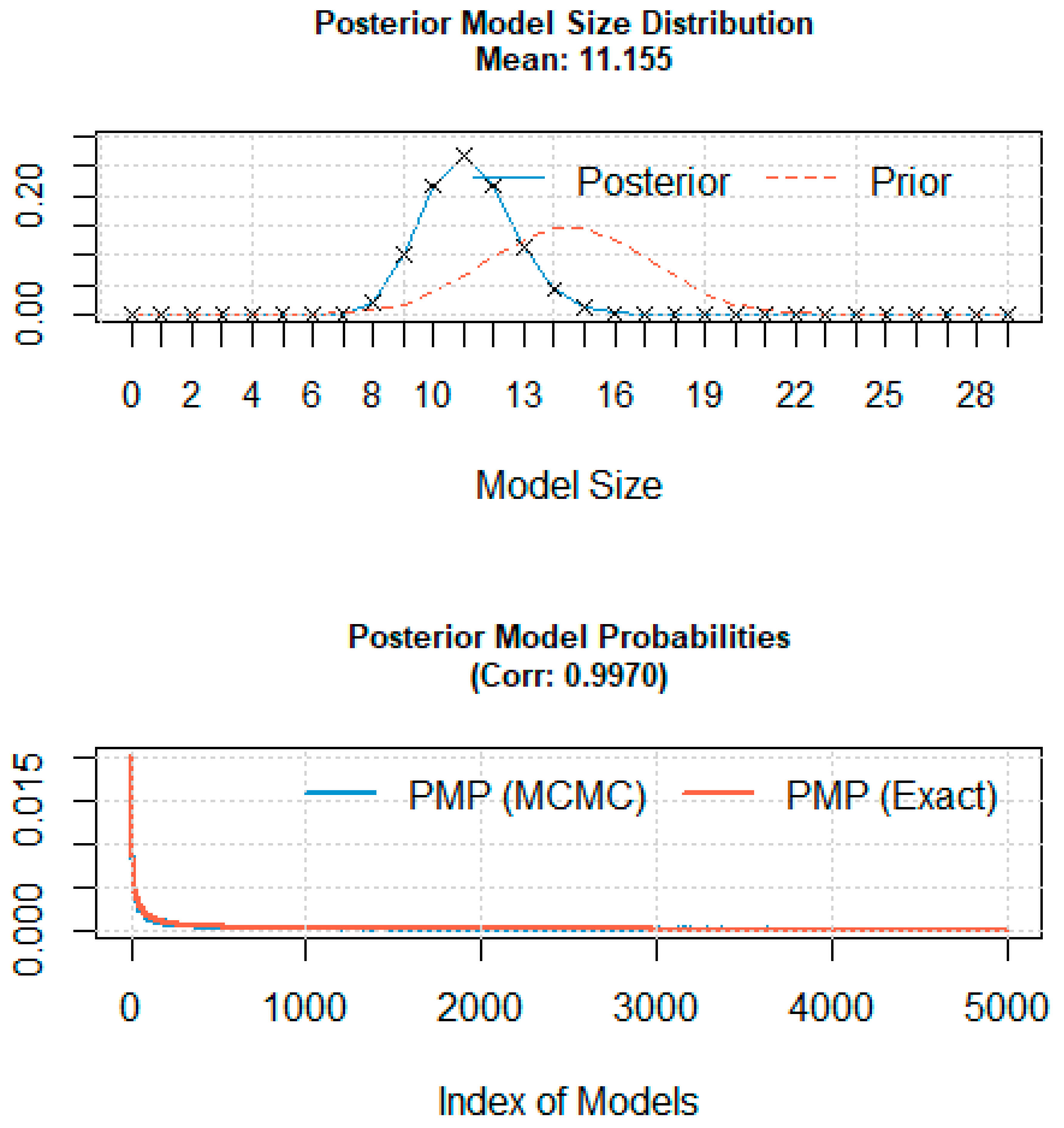
2.4. Meta-Regression Analysis
3. Results
4. Further Analysis
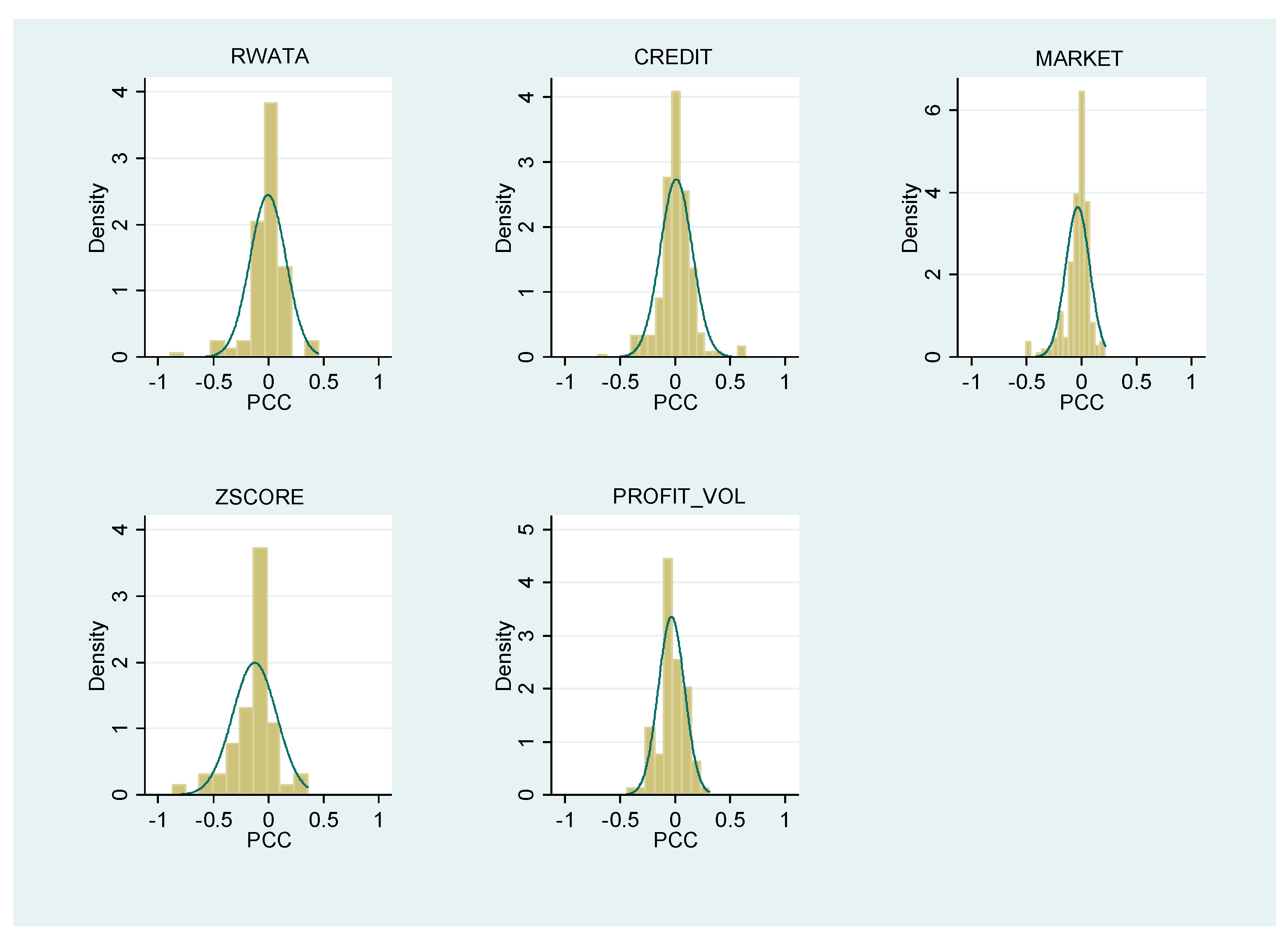
4.1. Different Risk Measurements
4.2. Benchmark and Best-Practice Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. List of Surveyed Studies
- Abou-El-Sood, Heba. 2017. Corporate governance structure and capital adequacy: implications to bank risk taking. International Journal of Managerial Finance 13: 165–85.
- Aggarwal, Raj, and Kevin T. Jacques. 2001. The impact of FDICIA and prompt corrective action on bank capital and risk: Estimates using a simultaneous equations model. Journal of Banking & Finance 25: 1139–60.
- Akinsoyinu, Clements Adeyinka. 2015. The Impact of Capital Regulation on Bank Capital and Risk Decision. Evidence for European Global Systemically Important Banks.
- Alkadamani, Khaled. 2015. Capital adequacy, bank behavior and crisis: evidence from emergent economies. European Journal of Sustainable Development 4: 329–38.
- Altunbas, Yener, Santiago Carbo, P. M. Gardener Edward, and Philip Molyneux. 2007. Examining the Relationships between Capital, Risk and Efficiency in European Banking. European Financial Management 13: 49–70. doi:10.1111/j.1468-036X.2006.00285.x.
- Al-Zubi, Khaled, Mohammad Al-Abadi, and Hanadi Afaneh. 2008. Capital adequacy, risk profiles and bank behaviour: Empirical evidence from Jordan. Jordan Journal of Business Administration 4: 89–106.
- Angkinand, Apanard Penny, James R. Barth, John S. Jahera, Jr., Triphon Phumiwasana, and Clas Wihlborg. 2013. Regulatory and market forces in controlling bank risk-taking: a cross-country analysis. Journal of Current Issues in Finance, Business and Economics 6: 271–86.
- Ashraf, Badar, Sidra Arshad, and Yuancheng Hu. 2016. Capital Regulation and Bank Risk-Taking Behavior: Evidence from Pakistan. International Journal of Financial Studies 4: 16.
- Athanasoglou, Panayiotis. 2011. “Bank capital and risk in the South Eastern European region.” Working paper No.137. Bank of Greece.
- Awdeh, Ali, C El-Moussawi, and Fouad Machrouh. 2011. The effect of capital requirements on banking risk. International Research Journal of Finance and Economics 66: 133–46.
- Banerjee, Gaurango, Abhiman Das, Kalidas Jana, and Shekar Shetty. 2017. Effects of derivatives usage and financial statement items on capital market risk measures of Bank stocks: evidence from India. Journal of Economics and Finance 41: 487–504. doi:10.1007/s12197-016-9366-6.
- Barrell, Ray, E Philip Davis, Tatiana Fic, and Dilruba Karim. 2011. Bank capital composition, regulation and risk taking. Working paper. NIESR and Brunel University, London.
- Basher, Syed Abul, Lawrence M. Kessler, and Murat K. Munkin. 2017. Bank capital and portfolio risk among Islamic banks. Review of Financial Economics 34: 1–9. doi:10.1016/j.rfe.2017.03.004.
- Beatty, Anne, and Anne Gron. 2001. Capital, portfolio, and growth: Bank behavior under risk-based capital guidelines. Journal of Financial Services Research 20: 5–31. doi:10.1023/A:1011146725028.
- Berger, Allen N. 1995. The relationship between capital and earnings in banking. Journal of Money, Credit and Banking 27: 432–56.
- Bichsel, Robert, and Jürg Blum. 2004. The relationship between risk and capital in Swiss commercial banks: a panel study. Applied Financial Economics 14: 591–97. doi:10.1080/0960310042000233881.
- Bitar, Mohammad, Wadad Saad, and Mohammed Benlemlih. 2016. Bank risk and performance in the MENA region: The importance of capital requirements. Economic Systems 40: 398–421. doi:10.1016/j.ecosys.2015.12.001.
- Blundell-Wignall, Adrian, and Caroline Roulet. 2013. Macro-prudential policy, bank systemic risk and capital controls. OECD Journal. Financial Market Trends 2013: 7–28. doi:10.1787/19952872.
- Bougatef, Khemaies, and Nidhal Mgadmi. 2016. The impact of prudential regulation on bank capital and risk-taking: The case of MENA countries. The Spanish Review of Financial Economics 14: 51–56. doi:10.1016/j.srfe.2015.11.001.
- Bouheni, Faten Ben, Hachmi Ben Ameur, Abdoulkarim Idi Cheffou, and Fredj Jawadi. 2014. The Effects of Regulation and Supervision on European Banking Profitability and Risk: A Panel Data Investigation. Journal of Applied Business Research 30: 16–65.
- Bouheni, Faten Ben, and Houssem Rachdi. 2015. Bank Capital Adequacy Requirements And Risk-Taking Behavior In Tunisia: A Simultaneous Equations Framework. Journal of Applied Business Research 31: 231.
- Camara, Boubacar, Laetitia Lepetit, and Amine Tarazi. 2013. Ex ante capital position, changes in the different components of regulatory capital and bank risk. Applied Economics 45: 4831–56.
- Cannata, Francesco, and Mario Quagliariello. 2006. Capital and risk in Italian banks: A simultaneous equation approach. Journal of Banking Regulation 7: 283–97.
- Carey, Mark. 1995. Partial market value accounting, bank capital volatility, and bank risk. Journal of Banking & Finance 19: 607–22. doi:10.1016/0378-4266(94)00142-P.
- Cebenoyan, A. Sinan, and Philip E. Strahan. 2004. Risk management, capital structure and lending at banks. Journal of Banking & Finance 28: 19–43. doi:10.1016/S0378-4266(02)00391-6.
- Coote, Howard. 2004. Bank Default Risk and Capital Regulation: Evidence from Jamaica. Paper presented at the XXXVI Annual Monetary Studies Conference, Bank of Jamaica.
- Nachane, D. M., and Ghosh Saibal. 2001. Risk-Based Standards, Portfolio Risk and Bank Capital: An Econometric Study. Economic and Political Weekly 36: 871–76.
- Das, Nupur Moni, and Joyeeta Deb. 2017. Regulatory Capital and Its Impact on Credit Risk: The Case of Indian Commercial Banks. IUP Journal of Bank Management 16: 7–22.
- Deelchand, Tara, and Carol Padgett. 2009. The relationship between risk, capital and efficiency: Evidence from Japanese cooperative banks. Working paper
- Delis, Manthos D., Kien C. Tran, and Efthymios G. Tsionas. 2012. Quantifying and explaining parameter heterogeneity in the capital regulation-bank risk nexus. Journal of Financial Stability 8: 57–68. doi:10.1016/j.jfs.2011.04.002.
- Demsetz, Rebecca S., and Philip E. Strahan. 1997. Diversification, Size, and Risk at Bank Holding Companies. Journal of Money, Credit and Banking 29: 300–13. doi:10.2307/2953695.
- Deng, Saiying, and Elyas Elyasiani. 2008. Geographic Diversification, Bank Holding Company Value, and Risk. Journal of Money, Credit and Banking 40: 1217–38.
- Dionne, Georges, and Tarek M. Harchaoui. 2008. Bank Capital, Securitization and Credit Risk: an Empirical Evidence. Assurances et Gestion des Risques 75: 459–84.
- Dong, Xianlei, Jia Liu, and Beibei Hu. 2012. Research on the relationship of commercial bank’s loan loss provision and earning management and capital management. Journal of Service Science and Management 5: 171.
- ElBannan, Mona A. 2015. Do consolidation and foreign ownership affect bank risk taking in an emerging economy? An empirical investigation. Managerial Finance 41: 874–907.
- Gaston, Giordana, and Ingmar Schumacher. 2012. An Empirical Study on the Impact of Basel III Standards on Banks? Default Risk: The Case of Luxembourg. Working paper No. 37. St. Louis: Federal Reserve Bank of St Louis.
- Gatev, Evan, Til Schuermann, and Philip E. Strahan. 2009. Managing Bank Liquidity Risk: How Deposit-Loan Synergies Vary with Market Conditions. The Review of Financial Studies 22: 995–1020.
- Godlewski, Christophe J. 2005. Bank capital and credit risk taking in emerging market economies. Journal of Banking Regulation 6: 128–45.
- Gregory, Katina, and Gerhard Hambusch. 2015. Factors driving risk in the US banking industry. International Journal of Managerial Finance 11: 388–410.
- Grossman, Richard S., and Masami Imai. 2013. Contingent capital and bank risk-taking among British banks before the First World War. The Economic History Review 66: 132.
- Hao, Jia, and Kuncheng KC Zheng. 2016. Bank Equity Capital and Risk-Taking Behavior: The Effect of Competition. Working paper.
- Haq, Mamiza, Robert Faff, Rama Seth, and Sunil Mohanty. 2014. Disciplinary tools and bank risk exposure. Pacific-Basin Finance Journal 26: 37–64. doi:10.1016/j.pacfin.2013.10.005.
- Hogan, Thomas L. 2015. Capital and risk in commercial banking: A comparison of capital and risk-based capital ratios. The Quarterly Review of Economics and Finance 57: 32–45. doi:10.1016/j.qref.2014.11.003.
- Hogan, Thomas L., and Neil R. Meredith. 2016. Risk and risk-based capital of U.S. bank holding companies. Journal of Regulatory Economics 49: 86–112. doi:10.1007/s11149-015-9289-8.
- Holod, Dmytro, Yuriy Kitsul, and Gökhan Torna. 2017. Market risk-based capital requirements, trading activity, and bank risk. Journal of Banking and Finance. doi:10.1016/j.jbankfin.2017.08.019.
- Hoque, Hafiz, Dimitris Andriosopoulos, Kostas Andriosopoulos, and Raphael Douady. 2015. Bank regulation, risk and return: Evidence from the credit and sovereign debt crises. Journal of Banking & Finance 50: 455–74. doi:10.1016/j.jbankfin.2014.06.003.
- How, Janice C. Y., Karim Melina Abdul, and Peter Verhoeven. 2005. Islamic financing and bank risks: The case of Malaysia. Thunderbird International Business Review 47: 75–94.
- Hussain, M Ershad, and M Kabir Hassan. 2005. Basel capital requirements and bank credit risk taking in developing countries. Working paper.
- Jabra, Wiem Ben, Zouheir Mighri, and Faysal Mansouri. 2017. Bank capital, profitability and risk in BRICS banking industry. Global Business and Economics Review 19: 89–119
- Jacques, Kevin, and Peter Nigro. 1997. Risk-based capital, portfolio risk, and bank capital: A simultaneous equations approach. Journal of Economics and Business 49: 533–47. doi:10.1016/s0148-6195(97)00038-6.
- Kalluru, Siva Reddy. 2009. Ownership Structure, Performance and Risk in Indian Commercial Banks. IUP Journal of Applied Finance 15: 31–45.
- Kasman, Adnan, and Oscar Carvallo. 2013. Efficiency and Risk in Latin American Banking: Explaining Resilience. Emerging Markets Finance and Trade 49: 105–30. doi:10.2753/REE1540-496X490207.
- Kouretas, Georgios, Chris Tsoumas, and Anastasios A. Drakos. 2013. Ownership, institutions and bank risk-taking in Central and Eastern European countries. Working paper. St. Louis: Federal Reserve Bank of St Louis.
- Kumar, Vijay, Abdur Rahman Aleemi, and Akhtiar Ali. 2015. The Determinants of Systematic Risk: Empirical Evidence from Pakistan’s Banking Sector. Global Management Journal for Academic & Corporate Studies 5: 146–54.
- Laeven, Luc, Lev Ratnovski, and Hui Tong. 2016. Bank size, capital, and systemic risk: Some international evidence. Journal of Banking & Finance 69: S25–S34. doi:10.1016/j.jbankfin.2015.06.022.
- Lee, Chien-Chiang, and Meng-Fen Hsieh. 2013. The impact of bank capital on profitability and risk in Asian banking. Journal of International Money and Finance 32: 251–81. doi:10.1016/j.jimonfin.2012.04.013.
- Lee, Chien-Chiang, Shao-Lin Ning, and Chi-Chuan Lee. 2015. How does Bank Capital Affect Bank Profitability and Risk? Evidence from China’s WTO Accession. China & World Economy 23: 19–39, doi:10.1111/cwe.12119.
- Lee, Tung-Hao, and Shu-Hwa Chih. 2013. Does financial regulation affect the profit efficiency and risk of banks? Evidence from China’s commercial banks. North American Journal of Economics and Finance 26: 705.
- Lin, Shu Ling, Dar-Yeh Hwang, Keh Luh Wang, and Zhe Wen Xie. 2013. Banking Capital and Risk-taking Adjustment under Capital Regulation: The Role of Financial Freedom, Concentration and Governance Control. International Journal of Management, Economics and Social Sciences 2: 99–128.
- Lin, Shu Ling. 2011. Do supervisory mechanisms or market discipline relate to bank capital requirements and risk-taking adjustment? International evidence. African Journal of Business Management 5: 2766–85. doi:10.5897/AJBM10.1108.
- Lucia Dalla, Pellegrina. 2012. Does capitalization enhance efficient risk undertaking? Accounting Research Journal 25: 185–207. doi:10.1108/10309611211290167.
- Maji, Santi Gopal, and Utpal Kumar De. 2015. Regulatory capital and risk of Indian banks: a simultaneous equation approach. Journal of Financial Economic Policy 7: 140–56.
- Makri, Vasiliki. 2016. Towards an investigation of credit risk determinants in Eurozone countries. Accounting and Management Information Systems 15: 27–57.
- Maraghni, Hichem. 2016. Bank Regulation, Capital Ratio Behaviour and Risk Taking in a Simultanious Approach. International Journal of Financial Research 8: 43.
- Michalak, Tobias C., and André Uhde. 2012. Credit risk securitization and bank soundness in Europe. Quarterly Review of Economics and Finance 52: 272.
- Mohammad, M. Rahman, Zheng Changjun, and N. Ashraf Badar. 2015. Bank Size, Risk-taking and Capital Regulation in Bangladesh. Eurasian Journal of Business and Economics 8: 95–114. doi:10.17015/ejbe.2015.015.05.
- Moussa, Mohamed. 2015. The Relationship between Capital and Bank Risk: Evidence from Tunisia. International Journal of Economics and Finance 7: 223–32.
- Pereira, João André Marques, and Richard Saito. 2015. Coordination of capital buffer and risk profile under supervision of Central Bank (Coordenação entre capital buffer e perfil de risco sob supervisão do Banco Central). Revista Brasileira de Finanças 13: 73–101.
- Pham Thien Nguyen, Thanh, and Son Hong Nghiem. 2015. The interrelationships among default risk, capital ratio and efficiency. Managerial Finance 41: 507–25.
- Rachdi, Houssem, Mohamed Ali Trabelsi, and Naama Trad. 2013. Banking Governance and Risk: The Case of Tunisian Conventional Banks. Working paper. St. Louis: Federal Reserve Bank of St Louis.
- Rahman, Mohammed Mizanur, Changjun Zheng, Badar Nadeem Ashraf, and Mohammad Morshedur Rahman. 2018. Capital requirements, the cost of financial intermediation and bank risk-taking: Empirical evidence from Bangladesh. Research in International Business and Finance 44: 488–503. doi:10.1016/j.ribaf.2017.07.119.
- Rahman, Nora Azureen Abdul, Nor Hayati Ahmad, and Nur Adiana Hiau Abdullah. 2012. Ownership structure, capital regulation and bank risk taking. Journal of Business and Economics 176.
- Raj, Aggarwal, and T. Jacques Kevin. 1998. Assessing the impact of prompt corrective action on bank capital and risk. Economic Policy Review—Federal Reserve Bank of New York 4: 23–32.
- Rajhi, Mohamed, and Wiem Hmadi. 2011. Examining the determinants of risk-taking in European banks. Journal of Business Studies Quarterly 3: 98–111
- Rajhi, Mohamed Tahar, and Wiem Hmadi. 2011. Governance and bank risk-taking: a comparison analysis between commercial and cooperative French banks. Journal of Business Studies Quarterly 3: 260–73.
- Rime, Bertrand. 2001. Capital requirements and bank behaviour: Empirical evidence for Switzerland. Journal of Banking & Finance 25: 789–805. doi:1016/S0378-4266(00)00105-9.
- Saadaoui, Zied. 2011. Risk-based capital standards and bank behaviour in emerging and developed countries. Journal of Banking Regulation 12: 180–91. doi:10.1057/jbr.2010.26.
- Sakawa, Hideaki, and Naoki Watanabel. 2016. Bank risk-taking and the board of directors’ role: evidence from Japan. Current Politics and Economics of Northern and Western Asia 25: 585–600
- Saunders, Anthony, Elizabeth Strock, and Nickolaos G. Travlos. 1990. Ownership Structure, Deregulation, and Bank Risk Taking. The Journal of Finance 45: 643–54. doi:10.2307/2328676
- Shrieves, Ronald E., and Drew Dahl. 1992. The relationship between risk and capital in commercial banks. Journal of Banking & Finance 16: 439–57. doi:10.1016/0378-4266(92)90024-T.
- Soedarmono, Wahyoe, Philippe Rous, and Amine Tarazi. 2010. Bank capital requirement, managerial self-interest and risk-taking: Evidence from Indonesian banks. Working paper.
- Sok-Gee, Chan, Eric H. Y. Koh, and Karim Mohd Zaini Abd. 2016. The Chinese banks’ directors and their risk-taking behavior. Chinese Management Studies 10: 291–311. doi:10.1108/CMS-10-2015-0226.
- Tan, Yong, and Christos Floros. 2013. Risk, capital and efficiency in Chinese banking. Journal of International Financial Markets, Institutions and Money 26: 378–93. doi:10.1016/j.intfin.2013.07.009
- Trabelsi, Mohamed Ali, and Naama Trad. 2017. Profitability and risk in interest-free banking industries: a dynamic panel data analysis. International Journal of Islamic and Middle Eastern Finance and Management 10: 454–69.
- Van Roy, Patrick. 2008. Capital requirements and bank behavior in the early 1990s: Cross country evidence. International Journal of Central Banking 4: 29–60
- Vinh, Nguyen Thi Hong. 2016. Effects of bank capital on profitability and credit risk: the case of Vietnam’s commercial banks. Journal of Economic Development: 117–37.
- Zhang, Zong-yi, Jun Wu, and Qiong-fang Liu. 2008. Impacts of Capital Adequacy Regulation on Risk-taking Behaviors of Banking. Systems Engineering—Theory & Practice 28: 183–89. doi:10.1016/S1874-8651(09)60035-1.
- Zheng, Changjun, Niluthpaul Sarker, and Shamsun Nahar. 2018. Factors affecting bank credit risk: An empirical insight. Journal of Applied Finance and Banking 8: 45–67
- Zribi, Nabila, and Younes Boujelbegrave. 2011. The factors influencing bank credit risk: The case of Tunisia. Journal of accounting and taxation 3: 70–78.
Appendix B
References
- Admati, Anat R., Peter M. DeMarzo, Martin F. Hellwig, and Paul Pfleiderer. 2013. Fallacies, Irrelevant Facts, and Myths in the Discussion of Capital Regulation: Why Bank Equity Is Not Socially Expensive. St. Louis: Federal Reserve Bank of St Louis. [Google Scholar]
- Aiello, Francesco, and Graziella Bonanno. 2016. Efficiency in banking: A meta-regression analysis. International Review of Applied Economics 30: 112–49. [Google Scholar] [CrossRef]
- Aiello, Francesco, and Graziella Bonanno. 2018. On the sources of heterogeneity in banking efficiency literature. Journal of Economic Surveys 32: 194–225. [Google Scholar] [CrossRef]
- Altunbas, Yener, Santiago Carbo, P. M. Gardener Edward, and Philip Molyneux. 2007. Examining the Relationships between Capital, Risk and Efficiency in European Banking. European Financial Management 13: 49–70. [Google Scholar] [CrossRef]
- BIS. 2018. History of the Basel Committee. Available online: https://www.bis.org/bcbs/history.htm?m=3%7C14%7C573%7C76 (accessed on 31 December 2018).
- De Luca, Giuseppe, Jan R. Magnus, and Franco Peracchi. 2018. Weighted-average least squares estimation of generalized linear models. Journal of Econometrics 204: 1–17. [Google Scholar] [CrossRef]
- DouCouliagos, Chris. 2016. Meta-regression analysis: Producing credible estimates from diverse evidence. IZA World of Labor 2016: 320. [Google Scholar] [CrossRef]
- Doucouliagos, Chris, and Tom D. Stanley. 2013. Are all economic facts greatly exaggerated? Theory competition and selectivity. Journal of Economic Surveys 27: 316–39. [Google Scholar] [CrossRef]
- Egger, Matthias, George Davey Smith, Martin Schneider, and Christoph Minder. 1997. Bias in meta-analysis detected by a simple, graphical test. BMJ 315: 629–34. [Google Scholar] [CrossRef] [PubMed]
- Einmahl, John H. J., Kamlesh Kumar, and Jan R. Magnus. 2011. On the choice of prior in Bayesian model averaging. Discussion Paper 2011-003, Center for Economic Research, Tilburg University, Tilburg, The Netherlands. [Google Scholar]
- Feld, Lars P., Jost H. Heckemeyer, and Michael Overesch. 2013. Capital structure choice and company taxation: A meta-study. Journal of Banking & Finance 37: 2850–66. [Google Scholar]
- Fidrmuc, Jarko, and Ronja Lind. 2018. Macroeconomic Impact of Basel III: Evidence from a Meta-Analysis. Journal of Banking & Finance. [Google Scholar] [CrossRef]
- Field, Andy P., and Raphael Gillett. 2010. How to do a meta-analysis. British Journal of Mathematical and Statistical Psychology 63: 665–94. [Google Scholar] [CrossRef]
- Gale, Douglas. 2010. Capital regulation and risk sharing. International Journal of Central Banking 6: 187–204. [Google Scholar]
- Gechert, Sebastian. 2015. What fiscal policy is most effective? A meta-regression analysis. Oxford Economic Papers 67: 553–80. [Google Scholar] [CrossRef]
- Glass, Gene V. 1976. Primary, secondary, and meta-analysis of research. Educational Researcher 5: 3–8. [Google Scholar] [CrossRef]
- King, William R, and Jun He. 2005. Understanding the role and methods of meta-analysis in IS research. Communications of the Association for Information Systems 16: 32. [Google Scholar] [CrossRef]
- Leamer, Edward E. 1978. Specification Searches: Ad Hoc Inference with Nonexperimental Data. Hoboken: John Wiley & Sons Incorporated, vol. 53. [Google Scholar]
- Light, Richard J., and David B. Pillemer. 1984. Summing up; The Science of Reviewing Research. Cambridge: Harvard University Press. [Google Scholar]
- Luca, Giuseppe De, and Jan R Magnus. 2011. Bayesian model averaging and weighted-average least squares: Equivariance, stability, and numerical issues. The Stata Journal 11: 518–44. [Google Scholar] [CrossRef]
- Magnus, Jan R., Owen Powell, and Patricia Prüfer. 2010. A comparison of two model averaging techniques with an application to growth empirics. Journal of Econometrics 154: 139–53. [Google Scholar] [CrossRef]
- Peters, Jaime L., Alex J. Sutton, David R. Jones, Keith R. Abrams, and Lesley Rushton. 2008. Contour-enhanced meta-analysis funnel plots help distinguish publication bias from other causes of asymmetry. Journal of Clinical Epidemiology 61: 991–96. [Google Scholar] [CrossRef]
- Raftery, Adrian E. 1995. Bayesian model selection in social research. Sociological Methodology 25: 111–63. [Google Scholar] [CrossRef]
- Rosenthal, Robert. 1979. The file drawer problem and tolerance for null results. Psychological Bulletin 86: 638. [Google Scholar] [CrossRef]
- Shrieves, Ronald E., and Drew Dahl. 1992. The relationship between risk and capital in commercial banks. Journal of Banking & Finance 16: 439–57. [Google Scholar] [CrossRef]
- Stanley, Tom D., and Stephen B. Jarrell. 1989. Meta-regression analysis: A quantitative method of literature surveys. Journal of Economic Surveys 3: 161–70. [Google Scholar] [CrossRef]
- Sterne, Jonathan A. C., David Gavaghan, and Matthias Egger. 2000. Publication and related bias in meta-analysis: Power of statistical tests and prevalence in the literature. Journal of Clinical Epidemiology 53: 1119–29. [Google Scholar] [CrossRef]
- Valickova, Petra, Tomas Havranek, and Roman Horvath. 2015. Financial development and economic growth: A meta-analysis. Journal of Economic Surveys 29: 506–26. [Google Scholar] [CrossRef]
- World Bank. 2018. Global Financial Development Database. Washington: World Bank. [Google Scholar]
- Zigraiova, Diana, and Tomas Havranek. 2016. Bank competition and financial stability: Much ado about nothing? Journal of Economic Surveys 30: 944–81. [Google Scholar] [CrossRef]

| Country | Observations | Studies | Mean | S.D | Min | Max | Median |
|---|---|---|---|---|---|---|---|
| Bangladesh | 20 | 3 | −0.252 | 0.087 | −0.370 | −0.071 | −0.284 |
| Brazil | 3 | 1 | 0.084 | 0 | 0.084 | 0.084 | 0.084 |
| Canada | 7 | 1 | 0.100 | 0.014 | 0.078 | 0.120 | 0.099 |
| China | 36 | 6 | −0.122 | 0.245 | −0.803 | 0.164 | −0.073 |
| Egypt | 7 | 1 | 0.186 | 0.064 | 0.112 | 0.255 | 0.159 |
| France | 4 | 1 | 0.066 | 0.241 | −0.181 | 0.284 | 0.081 |
| India | 35 | 6 | −0.125 | 0.191 | −0.500 | 0.457 | −0.146 |
| Indonesia | 4 | 1 | −0.218 | 0.081 | −0.285 | −0.100 | −0.243 |
| Italy | 5 | 1 | −0.010 | 0.034 | −0.054 | 0.017 | 0.013 |
| Jamaica | 4 | 1 | −0.009 | 0.071 | −0.11. | 0.051 | 0.012 |
| Japan | 8 | 3 | 0.068 | 0.121 | −0.171 | 0.218 | 0.105 |
| Jordan | 6 | 1 | 0.010 | 0.144 | −0.210 | 0.203 | −0.013 |
| Lebanon | 2 | 1 | −0.109 | 0.019 | −0.122 | −0.095 | −0.109 |
| Luxembourg | 4 | 1 | −0.345 | 0.356 | −0.873 | −0.130 | −0.189 |
| Malaysia | 3 | 2 | 0.079 | 0.423 | −0.212 | 0.565 | −0.116 |
| Pakistan | 12 | 2 | −0.063 | 0.266 | −0.331 | 0.355 | −0.092 |
| Russian Federation | 6 | 1 | 0.023 | 0.026 | −0.001 | 0.065 | 0.016 |
| Switzerland | 12 | 2 | 0.104 | 0.05 | 0.007 | 0.166 | 0.128 |
| Tunisia | 13 | 5 | −0.075 | 0.270 | −0.488 | 0.210 | 0.015 |
| UK | 10 | 1 | −0.053 | 0.025 | −0.072 | −0.007 | −0.066 |
| US | 241 | 20 | −0.018 | 0.106 | −0.503 | 0.213 | 0 |
| Vietnam | 2 | 1 | −0.487 | 0.296 | −0.697 | −0.278 | −0.487 |
| Cross-country | 466 | 32 | 0.003 | 0.127 | −0.895 | 0.646 | 0.008 |
| Total | 910 | 89 | −0.021 | 0.154 | −1.000 | 0.646 | −0.001 |
| Begg Test | Egger Test | |||
|---|---|---|---|---|
| z | p-Value | p-Value | ||
| Bias | −3.48 | <0.0001 | −0.454 | 0.039 |
| Observation | 910 | 910 | ||
| Variable | Label | Description | N | Mean PCC | S.D |
|---|---|---|---|---|---|
| Dependent variable | PCC | Standardized effect of bank capital on risk | 910 | −0.019 | 0.151 |
| Measurement of RISK variable | RWATA | Dummy variable, equal 1 if risk is measured as Risk-weighted assets over Total assets | 132 | −0.003 | 0.163 |
| CREDIT | Dummy variable, equal 1 if risk is measured as Non-performing loan ratio, loan loss reserve/provision ratio, Risk-weighted loans over assets, Distance to Default | 325 | 0.012 | 0.146 | |
| MARKET | Dummy variable, equal 1 if risk is measured as total market risk, idiosyncratic risk, specific risk, systematic risk, market risk | 226 | −0.034 | 0.110 | |
| ZSCORE | Dummy variable, equal 1 if risk is measured as Z-score | 105 | 0.125 | 0.200 | |
| PROFIT_VOL | Dummy variable, equal 1 if risk is measured as standard deviation of bank profitability (ROA, ROE) | 95 | −0.031 | 0.119 | |
| RISK_OTHER | Dummy variable, equal 1 if less frequent measurements of risk are used (Reference Group) | 43 | 0.066 | 0.126 | |
| RISK_DIF | Dummy variable, equal 1 if RISK is measured in first differences | 202 | 0.007 | 0.127 | |
| Measurement of CAPITAL variable | CAP | Dummy variable, equal 1 if the numerator in capital measurement is Total Regulatory Capital | 324 | −0.022 | 0.153 |
| TIER1 | Dummy variable, equal 1 if the numerator in capital measurement is Tier 1 Regulatory Capital | 190 | 0.006 | 0.129 | |
| EQUITY | Dummy variable, equal 1 if the numerator in capital measurement is Equity | 341 | −0.029 | 0.156 | |
| CAP_TA | Dummy variable, equal 1 if the denominator in capital measurement is Total Assets | 507 | −0.003 | 0.157 | |
| CAP_RWA | Dummy variable, equal 1 if the numerator in capital measurement is Risk-weighted Assets (Reference group) | 383 | −0.037 | 0.137 | |
| CAP_OTHER | Dummy variable, equal 1 if less frequent measurements of capital are used (Reference Group) | 64 | −0.014 | 0.159 | |
| Model | NONLN | Dummy variable, equal 1 if capital is quadratic or interacted with other variables | 133 | 0.008 | 0.105 |
| DYN | Dummy variable, equal 1 if the dynamic of risk is considered | 301 | −0.033 | 0.154 | |
| ENDO | Dummy variable, equal 1 if the endogeneity of capital is considered | 410 | −0.019 | 0.143 | |
| TIME_EFFECT | Dummy variable, equal 1 if Time effect is considered | 449 | −0.024 | 0.121 | |
| VAR_NO a | Number of explanatory variables in the model | 910 | 9.841 | 4.413 | |
| Estimation Method | EST_OLS | Dummy variable, equal 1 if estimation method is pooled OLS | 218 | −0.017 | 0.156 |
| EST_PANEL | Dummy variable, equal 1 if estimation method is Fixed Effects, Random Effects, Least Square Dummy Variables | 230 | −0.013 | 0.156 | |
| EST_IV | Dummy variable, equal 1 if estimation method is Instrumental Variables estimation | 214 | −0.004 | 0.155 | |
| EST_DYN | Dummy variable, equal 1 if estimation method is Dynamic Panel Data estimation | 201 | −0.049 | 0.139 | |
| EST_OTHER | Dummy variable, equal 1 if less frequently method is used (Reference Group) | 81 | 0.0004 | 0.113 | |
| Sample Characteristics | SAMPLE a | The logarithm of the total number of observations used | 910 | 6.981 | 1.639 |
| DATA_ANNUAL | Dummy variable, equal 1 if annual data is used, 0 if higher frequency data is used | 780 | −0.021 | 0.157 | |
| BHC | Dummy variable, equal 1 if only bank holding companies are examined | 204 | −0.032 | 0.104 | |
| COM | Dummy variable, equal 1 if only commercial banks are examined | 246 | −0.042 | 0.16 | |
| TYPE_OTHER | Dummy variable, equal 1 if other bank types or a mix of banks are examined (Reference Group) | 664 | −0.011 | 0.146 | |
| HIGH | Dummy variable, equal 1 if the study is conducted in high income countries | 445 | −0.014 | 0.121 | |
| UPPER | Dummy variable, equal 1 if the study is conducted in upper income countries | 59 | −0.072 | 0.225 | |
| LOW | Dummy variable, equal 1 if the study is conducted in lower and low-income countries | 102 | −0.117 | 0.217 | |
| Publication Characteristics | JNAL | Dummy variable, equal 1 if the study was published as a journal article, 0 if the study is a working paper | 815 | −0.016 | 0.154 |
| PUB_QUAL | Dummy variable, equal 1 if the study was published in a journal indexed in ISI, SSCI, or ranked in ABDC list, 0 otherwise | 629 | −0.01 | 0.152 | |
| CITE a | The logarithm of the number of Google Scholar citations normalized by the difference between 2018 and the year the study first appeared in Google Scholar | 910 | 0.573 | 0.484 |
| Variables | BMA | WALS | OLS | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Coef. | SE | PIP | Coef. | SE | |t| | Coef. | SE | P > t | |
| RWATA | −0.0228 | 0.0267 | 0.4798 | −0.0673 | 0.0218 | 0.22 | −0.0213 | 0.0337 | 0.5280 |
| CREDIT | 0.0034 | 0.0105 | 0.1275 | −0.0274 | 0.0187 | 0.46 | −0.0082 | 0.0261 | 0.7530 |
| MARKET | −0.0427 a | 0.0234 | 0.8428 | −0.0590 b | 0.0187 | 1.29 | −0.0376 | 0.0262 | 0.1510 |
| ZSCORE | 0.1362 a | 0.0185 | 1.0000 | 0.0954 b | 0.0209 | 4.55 | −0.1287 *** | 0.0349 | 0.0000 |
| PROFIT_VOL | −0.0012 | 0.0067 | 0.0539 | −0.0556 b | 0.0214 | 1.61 | −0.0404 | 0.0273 | 0.1390 |
| RISK_DIF | 0.0605 a | 0.0241 | 0.9344 | 0.0692 b | 0.0184 | 2.62 | 0.0653*** | 0.0196 | 0.0010 |
| CAP | −0.0070 | 0.0140 | 0.2427 | −0.0117 b | 0.0201 | 1.16 | 0.0315 | 0.0203 | 0.1200 |
| TIER1 | 0.0020 | 0.0079 | 0.0883 | 0.0098 b | 0.0213 | 1.19 | 0.0336 * | 0.0200 | 0.0940 |
| EQUITY | −0.0656 a | 0.0165 | 0.9970 | −0.0587 b | 0.0221 | 1.55 | −0.0428 ** | 0.0204 | 0.0360 |
| CAP_TA | 0.0991 a | 0.0149 | 1.0000 | 0.0760 b | 0.0138 | 5.28 | 0.1018 *** | 0.0180 | 0.0000 |
| NONLN | −0.0008 | 0.0048 | 0.0443 | −0.0325 | 0.0145 | 0.78 | −0.0122 | 0.0153 | 0.4250 |
| DYN | −0.0769 a | 0.0135 | 1.0000 | −0.0664 b | 0.0134 | 3.31 | −0.0535 *** | 0.0156 | 0.0010 |
| ENDO | −0.0002 | 0.0025 | 0.0266 | −0.0058 b | 0.0133 | 1.15 | −0.0260 * | 0.0153 | 0.0890 |
| TIME_EFFECT | −0.0391 a | 0.0147 | 0.9543 | −0.0400 | 0.0113 | 0.34 | −0.0102 | 0.0157 | 0.5170 |
| EST_OLS | −0.0004 | 0.0032 | 0.0308 | 0.0207 | 0.0198 | 0.68 | 0.0158 | 0.0212 | 0.4560 |
| EST_PANEL | 0.0005 | 0.0035 | 0.0401 | 0.0379 b | 0.0169 | 2.09 | 0.0450 ** | 0.0177 | 0.0110 |
| EST_IV | 0.0078 | 0.0157 | 0.2430 | 0.0433 | 0.0214 | 0.76 | 0.0245 | 0.0207 | 0.2380 |
| EST_DYN | 0.0001 | 0.0025 | 0.0226 | 0.0406 | 0.0220 | 0.13 | 0.0168 | 0.0256 | 0.5120 |
| VAR_NO | 0.0000 | 0.0002 | 0.0230 | 0.0019 b | 0.0011 | 1.11 | 0.0016 | 0.0013 | 0.2200 |
| SAMPLE | 0.0057 a | 0.0052 | 0.6172 | 0.0119 b | 0.0036 | 3.05 | 0.0129 *** | 0.0049 | 0.0080 |
| DATA_ANNUAL | −0.0001 | 0.0030 | 0.0247 | −0.0052 | 0.0161 | 0.42 | 0.0025 | 0.0172 | 0.8840 |
| BHC | −0.0085 | 0.0158 | 0.2699 | −0.0316 b | 0.0173 | 1.99 | −0.0319 | 0.0211 | 0.1300 |
| COM | −0.0015 | 0.0064 | 0.0756 | −0.0178 | 0.0117 | 0.65 | −0.0044 | 0.0164 | 0.7890 |
| HIGH | −0.0005 | 0.0036 | 0.0417 | 0.0057 b | 0.0118 | 2.28 | 0.0287 ** | 0.0133 | 0.0310 |
| UPPER | 0.0157 | 0.0251 | 0.3312 | 0.0587 | 0.0180 | 0.11 | 0.0080 | 0.0296 | 0.7870 |
| LOW | 0.0007 | 0.0122 | 0.0199 | 0.0866 | 0.0753 | 0.49 | 0.0391 | 0.0954 | 0.6820 |
| JNAL | −0.0001 | 0.0033 | 0.0230 | 0.0042 b | 0.0162 | 1.95 | 0.0360 * | 0.0209 | 0.0850 |
| PUB_QUAL | 0.0310 a | 0.0193 | 0.7940 | 0.0349 | 0.0108 | 0.89 | −0.0188 | 0.0172 | 0.2740 |
| CITE | 0.0191 a | 0.0199 | 0.5489 | 0.0245 b | 0.0119 | 6.00 | 0.0838 *** | 0.0159 | 0.0000 |
| RWATA | CREDIT | MARKET | ZSCORE | PROFIT_VOL | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | |t| | Coef. | |t| | Coef. | |t| | Coef. | |t| | Coef. | |t| | |
| RISK_DIF | −0.0440 | 0.57 | 0.1090 * | 3.89 | −0.1180 * | 1.09 | 0.1270 * | 1.63 | 0.0730 | 0.60 |
| CAP | −0.0410 | 0.67 | 0.0210 | 0.84 | 0.1430 * | 4.57 | −0.0900 * | 1.20 | −0.1200 * | 1.38 |
| TIER1 | −0.0300 | 0.45 | 0.0370 * | 1.34 | 0.1300 * | 4.27 | −0.0270 | 0.34 | −0.1890 | 0.79 |
| EQUITY | −0.0500 * | 1.93 | 0.0390 | 0.65 | −0.1500 * | 1.83 | −0.1890 * | 2.00 | ||
| CAP_TA | 0.1130 * | 2.51 | 0.0940 * | 4.40 | −0.0230 | 0.35 | 0.0730 * | 1.22 | 0.0750 * | 1.49 |
| NONLN | 0.0400 * | 1.03 | −0.0110 | 0.45 | −0.1120 * | 3.57 | −0.1130 * | 1.89 | 0.1670 * | 1.65 |
| DYN | −0.1630 * | 2.79 | −0.0740 * | 4.20 | 0.0440 | 0.58 | −0.0820 * | 1.31 | −0.0910 * | 1.06 |
| ENDO | 0.1300 * | 1.47 | −0.0440 * | 1.99 | −0.0280 * | 1.05 | 0.1910 * | 2.91 | −0.1570 * | 1.97 |
| TIME_EFFECT | 0.0470 * | 1.00 | −0.0470 * | 2.81 | 0.0040 | 0.19 | 0.0100 | 0.25 | −0.1160 * | 1.03 |
| EST_OLS | 0.1020 | 0.98 | −0.0150 | 0.55 | −0.0270 | 0.53 | −0.0430 | 0.50 | −0.0640 | 0.34 |
| EST_PANEL | 0.0440 | 0.47 | 0.0420 * | 1.84 | −0.0650 * | 1.28 | 0.0310 | 0.41 | 0.0790 | 0.41 |
| EST_IV | −0.0540 | 0.62 | 0.0220 | 0.79 | 0.0580 * | 1.16 | −0.1080 * | 1.36 | 0.1540 * | 1.04 |
| EST_DYN | −0.0140 | 0.17 | 0.0160 | 0.51 | −0.0210 | 0.37 | −0.1980 * | 2.20 | 0.1440 * | 1.05 |
| VAR_NO | −0.0030 | 0.54 | 0.0050* | 2.66 | −0.0030 * | 1.79 | 0.0220 * | 3.26 | 0.0110 * | 1.76 |
| SAMPLE | 0.0010 | 0.08 | 0.0290* | 4.87 | −0.0040 | 0.64 | −0.0190 * | 1.22 | 0.0080 | 0.63 |
| DATA_ANNUAL | −0.2740 * | 3.06 | 0.0370 | 0.81 | −0.1430 * | 3.66 | −0.0030 | 0.05 | 0.0300 | 0.19 |
| BHC | −0.2450 * | 2.50 | −0.0010 | 0.03 | −0.1180 * | 4.06 | −0.0510 | 0.73 | 0.1700 | 0.71 |
| COM | 0.1320 * | 2.35 | −0.0590 * | 3.25 | 0.1440 * | 3.00 | −0.0970 * | 1.85 | 0.0110 | 0.23 |
| HIGH | 0.0190 | 0.39 | −0.0330 * | 1.74 | 0.0500 * | 1.44 | −0.1050 * | 1.86 | 0.0020 | 0.04 |
| UPPER | −0.1170 * | 1.04 | 0.0390 * | 1.42 | −0.0380 | 0.54 | 0.0880 * | 1.80 | 0.0030 | 0.06 |
| LOW | 0.1990 * | 1.69 | 0.0420 | 0.74 | ||||||
| JNAL | 0.0550 | 0.47 | 0.0030 | 0.13 | 0.2310 * | 2.06 | −0.0870 | 0.29 | ||
| PUB_QUAL | 0.1910 * | 2.25 | −0.0280 * | 1.36 | −0.1530 * | 5.17 | 0.2390 * | 4.83 | −0.0420 | 0.61 |
| CITE | −0.1550 * | 1.40 | 0.0670 * | 3.77 | 0.0240 | 0.49 | −0.3370 * | 5.56 | 0.1920 | 0.61 |
| Constant | 0.0700 | 0.40 | −0.2990 * | 3.52 | −0.0020 | 0.02 | 0.1910 * | 1.28 | −0.1540 | 0.84 |
| N | 132 | 325 | 226 | 105 | 95 | |||||
| Benchmark Results | Best Practice | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | BHC | COM | HIGH | UPPER | Total | BHC | COM | HIGH | UPPER | |
| RWATA | 0.095145 | 0.12521 | 0.062582 | 0.089907 | 0.057983 | −0.05177 | 0.141112 | −0.09247 | −0.04699 | 0.031717 |
| CREDIT | −0.25384 | −0.26528 | −0.24567 | −0.25831 | −0.24554 | −0.04857 | −0.04393 | −0.03629 | −0.02123 | −0.09672 |
| MARKET | −0.01142 | −0.02494 | −0.01238 | −0.01647 | 0.001743 | 0.004052 | 0.088588 | −0.03307 | −0.04116 | 0.034949 |
| ZSCORE | 0.173826 | 0.191152 | 0.188451 | 0.162209 | 0.190169 | 0.129122 | 0.295267 | 0.171561 | 0.275456 | 0.167132 |
| PROFIT_VOL | −0.04567 | −0.12419 | −0.09766 | −0.02968 | −0.0726 | −0.18316 | −0.24249 | −0.17905 | −0.20342 | −0.16056 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, Q.T.T.; Nguyen, S.T.B.; Nguyen, Q.V. Can Higher Capital Discipline Bank Risk: Evidence from a Meta-Analysis. J. Risk Financial Manag. 2019, 12, 134. https://doi.org/10.3390/jrfm12030134
Nguyen QTT, Nguyen STB, Nguyen QV. Can Higher Capital Discipline Bank Risk: Evidence from a Meta-Analysis. Journal of Risk and Financial Management. 2019; 12(3):134. https://doi.org/10.3390/jrfm12030134
Chicago/Turabian StyleNguyen, Quang T. T., Son T. B. Nguyen, and Quang V. Nguyen. 2019. "Can Higher Capital Discipline Bank Risk: Evidence from a Meta-Analysis" Journal of Risk and Financial Management 12, no. 3: 134. https://doi.org/10.3390/jrfm12030134
APA StyleNguyen, Q. T. T., Nguyen, S. T. B., & Nguyen, Q. V. (2019). Can Higher Capital Discipline Bank Risk: Evidence from a Meta-Analysis. Journal of Risk and Financial Management, 12(3), 134. https://doi.org/10.3390/jrfm12030134





