Abstract
Monetary policy is forward looking and, in its pursuit of transparency, it communicates its economic projections to the public at large. As a result, there is interest in whether these projections are credible. We argue that central to that credibility is the public’s ability to replicate the FOMC’s projections using publicly available data only. In other words, is it possible to anticipate, reliably and independently, what the FOMC will anticipate for the federal funds rate? To address this question, we assemble FOMC projections from 1992 to 2017; examine their statistical properties; postulate models to predict FOMC projections; and estimate the parameters of these models. We are not arguing that the FOMC determines their projections using these models. Rather, these equations are the ones that the public could use to forecast FOMC forecasts and to anticipate interest-rate decisions.
1. The Question
Starting in late 2007, US monetary authorities began releasing their Summary of Economic Projections (SEP) with the goal of enhancing the public’s understanding of their policies. Importantly, these projections are not mere extrapolations of existing trends but the result of an FOMC directive to participants to craft appropriate monetary policies:1
“Appropriate monetary policy is defined as the future policy most likely to foster outcomes for economic activity and inflation that best satisfy the participant’s interpretation of the Federal Reserve’s dual objectives of maximum employment and price stability.”2
That FOMC participants disagree on the appropriate federal funds rate is clear from Figure 1:
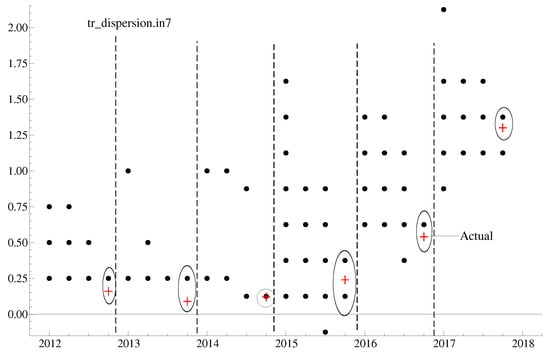
Figure 1.
Appropriate Federal Funds Rates for the Current Year.
What is not clear is how these disagreements enhance the public’s understanding of monetary policy: if FOMC participants disagree to this extent about what is appropriate, why would they expect the public to understand their decisions?
We are not the first to note the tension between the intended transparency of the SEP and the dispersion of appropriate policies. Faust (2016) notes that
The SEP, in my view, deserves a special place in the annals of obfuscation in the service of transparency. The SEP is the paradigm case of the second type of communication: it is purely a depiction of the policymakers’ different views on the outlook and appropriate policy, with no hints about how any differences may be resolved.(Faust 2016, p. 17)
Furthermore, Faust’s critique applies to the history of FOMC forecasts and not just to the SEP. Indeed, following Romer (2010), we report in Figure 2 and Figure 3 participant-specific projections of inflation and unemployment from 1992 to 2012, along with recent FOMC’s SEP.3 This record shows that disagreements about the outlook among FOMC members are the norm: the 2008 financial crisis only exacerbated them. Furthermore, the record also shows that FOMC projections are notoriously inaccurate and thus the public cannot rely on the accuracy of these projections as a substitute for understanding monetary policy or its credibility.4
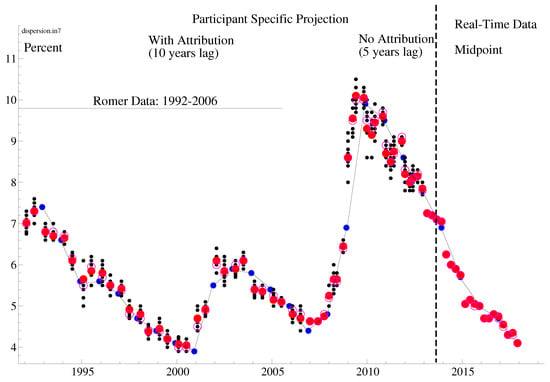
Figure 2.
Current-Year Projections for Unemployment.
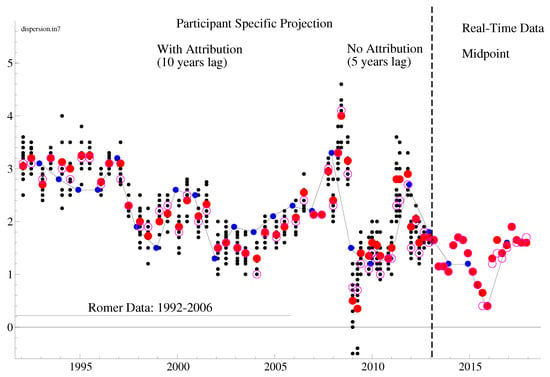
Figure 3.
Current-year Projections for Inflation.
Thus, if taken at face value, these observations suggest that the public’s effort to scrutinize the SEP is misplaced and that the FOMC’s effort in assembling them is wasteful, which is the essence of Faust’s critique. The question we address here is whether there is a suitable approach to bypass his critique.
Addressing this question involves modeling a process that by design, is secretive. To this end, we argue that FOMC projections can enhance the public’s understanding if they are, at a minimum, replicable by the public.5 Indeed, asking if FOMC projections are replicable amounts to asking whether it is possible to extract a narrative of the FOMC’s views of the economy’s functioning. However, we want a narrative that is consistent with the FOMC record, that can be rejected by the data, that uses publicly available data, that is statistically reliable, and that helps in mapping FOMC projections into FOMC interest-rate decisions.
2. FOMC Reaction Function
Critics of the SEP argue that reconciling differences in the FOMC’s appropriate policies involves the FOMC making its reaction function available to the public.6 Faust states
As noted above, the most important function to convey regards the reaction function of the policymakers. However, the SEP approach of providing separate variable-by-variable summaries of the 19 forecasts obscures any link between the paths of the federal funds rate as depicted in the dot-plot and the forecasts of the other variables.(Faust 2016, p. 18)
Bernanke (2016) reinforces Faust’s observations by noting that
Wouldn’t it be easier if the FOMC just provided its reaction function, together with collective projections of key macroeconomic variables? In principle, yes; and in fact, in the course of expanding the SEP, the FOMC under my chairmanship experimented with developing a consensus committee forecast, together with alternative scenarios, that could be released to the public.(Bernanke 2016, p. 7)
A fair question to ask, then, is how would knowledge of a single reaction function help the public?7 Indeed, a reaction function that depends on variables that the public cannot observe directly—the FOMC’s own forecasts—is not a reaction function helpful to the public. Thus, the provision of the reaction function would need to be accompanied by the FOMC forecasts. For example, suppose that both the reaction function and the forecasts are known:8
where is the median of the distribution of the FOMC projections for the current-year federal funds rate made at time and are the median of the current-year projections for inflation and unemployment made at time t.9 Please note that in addition to this information, the FOMC would need to provide the values for the natural rate of unemployment and the neutral interest rate. Assuming that and yields remarkably close interest-rate predictions for meetings since 2016 but not before then (Figure 4):
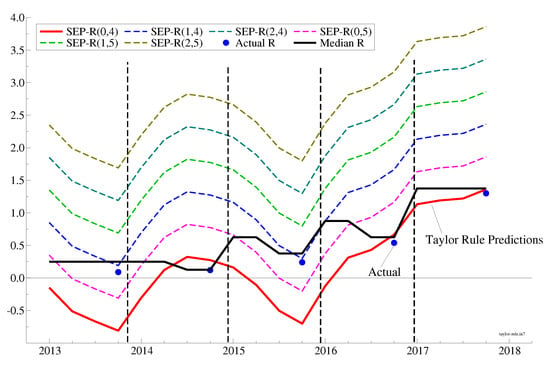
Figure 4.
Interest-Rate Predictions—Sensitivity to Values of the Natural Rate.
Thus, this hypothetical reaction function helps us to detect ex-post inconsistencies between the rule and FOMC decisions. However, what is needed is to anticipate decisions and then, react to the gap between decisions and expectations. However, if one wants an ex-ante prediction of the interest rate that can then be compared to the FOMC decisions, then one needs to forecast FOMC forecasts; we do that below.
However, even if all these considerations were, somehow, addressed, an important obstacle in implementing Bernanke’s “consensus forecasts” is, at the risk of stating the obvious, the lack of consensus among FOMC participants. Indeed, Figure 5 shows three measures of the dispersion of the appropriate federal funds rate for the current year and one year ahead. How would this heterogeneity of interest-rate forecasts be incorporated in the FOMC reaction function?
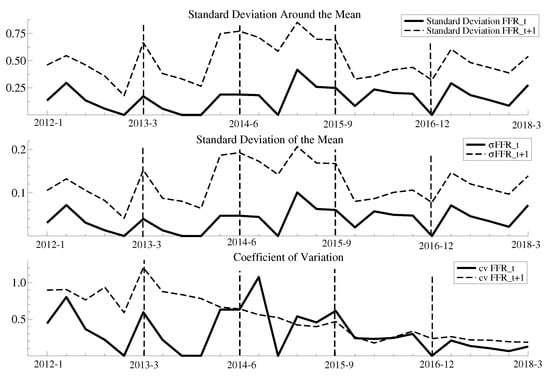
Figure 5.
Dispersion of Appropriate Interest Rates.
To be sure, we are not the first to note this heterogeneity. Indeed, Rülke and Tillman (2011) examine whether FOMC participants exhibit herd behavior. Furthermore, Figure 1 shows instances of seemingly extreme values. For example, forecasts for unemployment in 2010 made during the April 2009 meeting might be construed as extreme. Tillman (2011) and Nakazono (2013) have noted such instances and they attribute them to the differential behavior of FOMC participants who are not voting during the meeting. Indeed, they argue that these participants might submit “extreme” forecasts as a way of registering their disagreements.10 There is, however, an important question: If heterogeneity is so prevalent and damning, why are dissents in FOMC decisions so rare an occurrence?
To answer this question, we introduce the hypothesis of "Constrained Heterogeneity" in which the different views of FOMC participants are reconciled by the persuasiveness of the FOMC Chair:
And the question is, are we ever going to converge? I would feel my job is to get everybody to see that off-white is not a bad alternative. (Laughter) As brilliant as your choice was, maybe you could live with off-white, and it’s not so bad. And we can converge on that and it’s going to function just fine and maybe we can agree.Yellen (2018)
To be sure, we are not the first to note the relevancy of Chair effects. Bernanke (2016) and Powell (2018) argue that the Chair of the FOMC may exert idiosyncratic influence on the target federal funds rate or capture declines in the neutral rate. This possibility has testable implications that are examined below. Specifically, we consider models that are very different by design: we want to extract results that are robust to fundamentally different formulations. To be sure, we are not arguing that the FOMC determines their projections using these models. Rather, we argue that these models are the ones that the public could use to replicate projections of the FOMC.
3. Empirical Taylor Rules
3.1. Single Equation
One approach to examine the relevancy of the Constrained Heterogeneity hypothesis is to reformulate the Taylor rule as a General Unrestricted Model (GUM)
where
- is the median federal funds rate for the tth year made during the tth FOMC meeting
- is the median inflation projection for the tth year made during the tth FOMC meeting
- is the median unemployment projection for the tth year made during the tth FOMC meeting
- dummy variable equal to one for Bernanke’s tenure as Chair of the FOMC
- dummy variable equal to one for Yellen’s tenure as Chair of the FOMC
- dummy variable equal to one for Powell’s tenure as Chair of the FOMC
- and are projections from the Survey of Professional Forecasters for inflation and unemployment, respectively, available in real time prior to the FOMC meeting
- and are the actual values for inflation and unemployment prior to the FOMC meetings.11
- and are coefficients of variation of the distribution of FOMC participants’ appropriate federal funds rate (Figure 5). Please note that we allow current and one-year-ahead uncertainty
- is a polynomial of degree one in the lag operator.
This formulation has several useful features. First, it can assess the relevancy of Faust’s critique. Specifically, if then information about the FOMC’s inflation and unemployment forecasts is not needed for predicting Second, if then measured heterogeneity in interest-rate forecasts is not relevant for predicting the interest rate. Third, if the role of the FOMC Chair is not important for interest rates, then .
For estimation we combine projections for FOMC meetings held from 2012 to December 2017 with Autometrics, a computer-automated algorithm, developed by Doornik and Hendry (2013).12 Their algorithm combines least squares with selection criteria that excludes insignificant coefficients and tests for both parameter constancy and white-noise residuals. The critical values for rejection are applied to the model as such and not specific coefficients. Selecting a critical value for rejecting a model involves a tradeoff between a conservative and a liberal strategy. A conservative strategy views the cost of including irrelevant variables as greater than the cost of excluding relevant variables; the liberal strategy views the cost of including irrelevant variables as lower than the cost of excluding relevant variables. We use a 1% significance level for the liberal strategy and a 0.01% for our conservative strategy (Table 1).

Table 1.
Estimation Results for Single Equation for the Federal Funds Rate—Sensitivity to Target Size.
The estimation results reveal several features of interest:
- Sole reliance on the GUM suggests that the previous value of the federal funds rate is the most important factor in explaining movements in that interest rate; neither FOMC Chair effects nor participants’ difference, nor economic data (FOMC’s or public) are statistically important.
- The implementation of Autometrics reveals that Chair effects are relevant and that their long-run values are robust to the choice of strategy.
- FOMC’s current-year forecasts of inflation and unemployment are not relevant for forecasting FOMC rate decisions. In other words, one cannot reject the null hypothesis that This confirms the relevancy of Faust’s critique.
- Estimates using a 0.01% significance level show that persistence is not relevant and that information about both inflation and unemployment play statistically important roles. The exclusion of persistence, odd at first, is reasonable once one realizes that persistence is already embodied in the FOMC Chair. However, the Chair embodies more than history: It embodies the power to persuade participants around the Chair’s view. Given this persuasive power, it is not surprising to find that one cannot reject the null hypothesis that In other words, heterogeneity among FOMC participants is not relevant for explaining the federal funds rate so long as the Chair is persuasive in reconciling differences among FOMC participants.
3.2. Sensitivity Analysis
The simplicity of this formulation comes with a price: it ignores that FOMC projections are jointly determined and that the forecast horizon extends the current year.13 Thus, a fair question to ask is how sensitive are the results to relaxing two key assumptions that we have maintained so far.
Removing these limitations, though feasible, involves tradeoffs among computational feasibility, interaction detail, and econometric sophistication. Specifically, we now develop empirical models that explain the median of FOMC projections for inflation, unemployment, and the federal funds rate; we focus on current and one-year-ahead projections for FOMC meetings held from 2012 to 2017 (Figure 6).
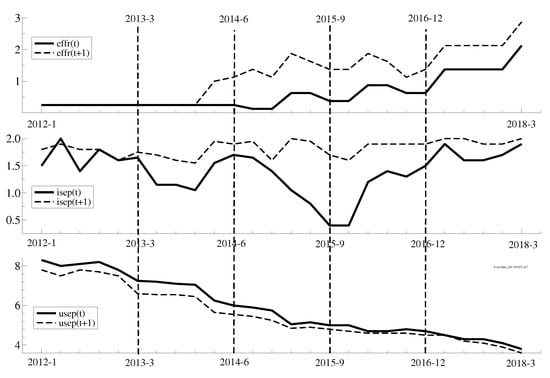
Figure 6.
FOMC Forecasts—Current and One Year Ahead.
The data show two properties of interest. First, differences between current and one-year-ahead projections have been, over this period, one-sided. For example, the median projection for the appropriate federal funds rate for one year ahead is effectively equal to the current year plus a fairly constant "term" premium. For inflation, the one-year-ahead projections are well anchored around two percent, even though projections for the current year depart from their target. For unemployment, the projections reveal sustained optimism that next year will have a lower unemployment rate. Second, the projections reveal an FOMC that expects to meet its dual mandate next year despite evidence to the contrary in the current year.14
3.2.1. Design
General Structure
An ideal formulation to model FOMC forecasts is
where
- and are the inflation projections for the current year and one year ahead, respectively, made during the tth FOMC meeting
- and are the unemployment projections for the current year and one year ahead, respectively, made during the tth FOMC meeting
- and are the federal funds rate in the current and one-year-ahead projections, respectively, made during the tth FOMC meeting
This formulation emphasizes FOMC projections as jointly determined for a given period and across periods; recognizes that the current-year target for the federal funds rate is influenced by previous FOMC projections and from data generated outside the FOMC that is publicly available; allows for forecast persistence from the six endogenous variables to influence the forecast for the interest rate; assumes linearity in the parameters, the same degree of stationarity, and allows for Chair-specific effects. As exogenous variables we use available data from the Survey of Professional Forecasters for inflation and unemployment and actual values of inflation and unemployment.
The richness of this formulation comes with a price: it has 141 parameters to estimate (including those of but only 144 observations (6 Thus, there is a need to reduce the number of parameters. Doing so involves tradeoffs among computational feasibility, details about transmission channels, and econometric reliability, and the number of observations. To this end, we consider models that differ in design and estimation approaches.
Vector Autoregresive Approach
We begin with a VAR to explain current and one-year-ahead projections for inflation, unemployment, and the federal funds rate for a total of six endogenous variables:
where, owing to the large number of coefficients, we constrain the coefficient for to be the same as the coefficient for .
Based on the estimation results, the model offers a fair replication of the FOMC projections (Figure 7). In terms of the adequacy for statistical inference, the residuals do not exhibit serial correlation or departures from normality (Figure 8).
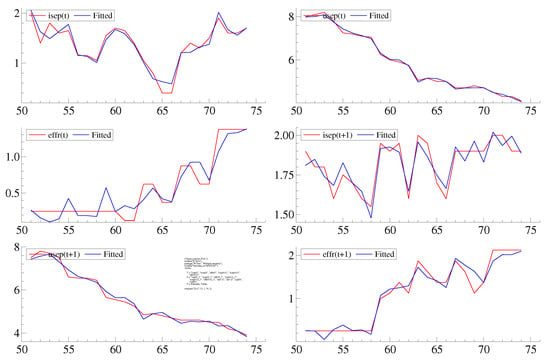
Figure 7.
Actual versus Fitted FOMC Forecasts—VAR.
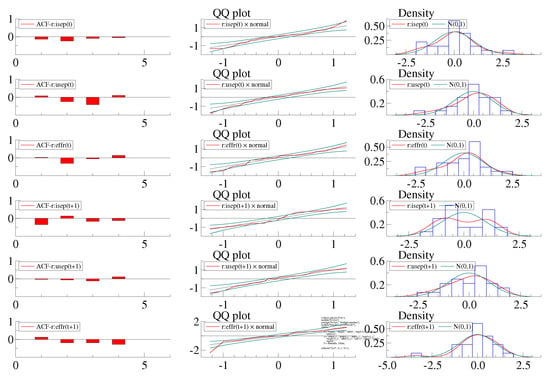
Figure 8.
Tests of Serial Independence and Normality of Disturbances for VAR.
To examine whether the model is dynamically stable, we use impulse responses. A one-percentage- point upward revision to the current-year inflation rate leads to a transitory upward revision in the federal funds rate projection for the current year and a downward revision for the one-year-ahead projections for the federal funds rate (Figure 9). A one-percentage-point upward revision in the current-year projection for unemployment is accompanied by an upward revision in the federal funds rate projection for the current year (Figure 10).
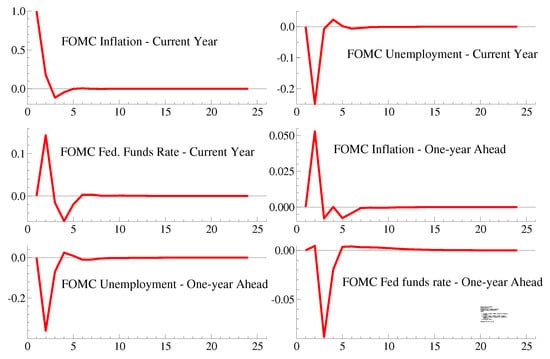
Figure 9.
Impulse Responses to a one-percent inflation revision—VAR.
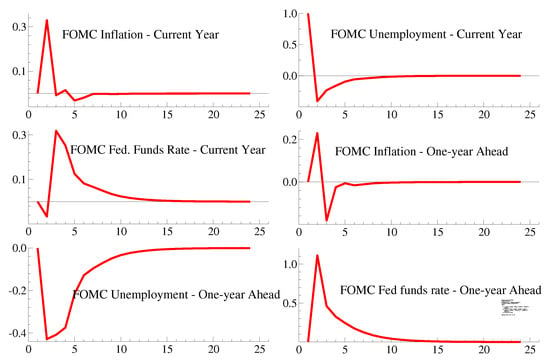
Figure 10.
Impulse Responses to a one-percent unemployment revision—VAR.
Thus, though the model is dynamically stable, the associated impulse responses are not consistent with the dual mandate and hence not suitable as a replication of the FOMC process.
“Incredible Restrictions” Formulation
As an alternative to the VAR, we introduce incredible (but hopefully useful) parameter restrictions. Specifically, the model has six endogenous variables that are grouped into a recursive structure in which projections for the current year determine the one-year-ahead projections but not the other way around. The structure for the current-year projections is
The structure for one-year-ahead projections is
where Arguing that these restrictions are ad-hoc is elaborating on the obvious. The relevant question is whether they are helpful in addressing Faust’s critique.
For estimation we apply FIML to data on the median of FOMC participant projections for FOMC meetings held from 2012 to December 2017; the results are shown in Table 2 below. For the current-year predictions, the results suggest that simultaneity is weak at best: increases in barely lower and (cols. 1 and 2). In addition, increases in raise whereas increases in lower (col. 3). The results also indicate that movements in current-year predictions for unemployment are transmitted to one-year-ahead predictions for unemployment almost one for one (col. 5). For one-year-ahead inflation, the pass-through is considerably smaller and barely significant. The results also indicate that FOMC Chair effects are both positive and significant for the current-year interest rate (col. 3). These effects are also positive, significant for the one-year-ahead inflation rate, and with a value very close to the FOMC target for the inflation rate (col. 4).

Table 2.
FIML Estimation Results of Parameters of Structural Model: 2012–2017.
Except for one-year-ahead projection for inflation, the model offers a fair replication of the FOMC projections (Figure 11). In terms of the adequacy for statistical inference, the residuals do not exhibit serial correlation or departures from normality (Figure 12).
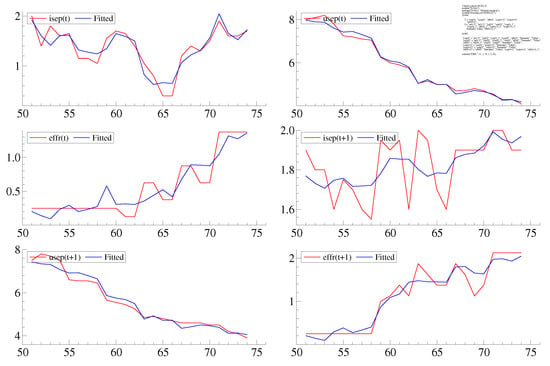
Figure 11.
Actual versus Fitted FOMC Forecasts—FIML.
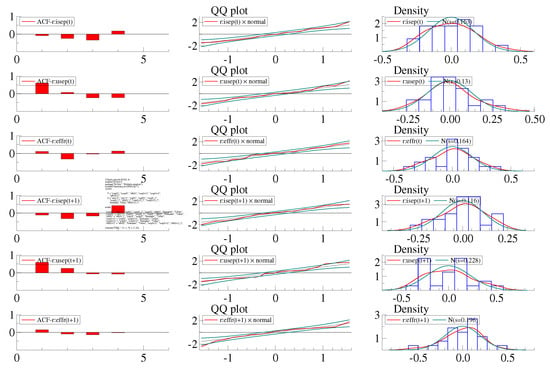
Figure 12.
Tests of Serial Independence and Normality of Disturbances for FIML.
In terms of dynamic stability, a one-percentage-point upward revision of the forecast inflation rate raises both the current- and one-year-ahead interest rate (Figure 13). A one-percentage-point upward revision in the unemployment projections for the current year lowers the federal funds rate projection for both the current and the one-year-ahead projections (Figure 14).
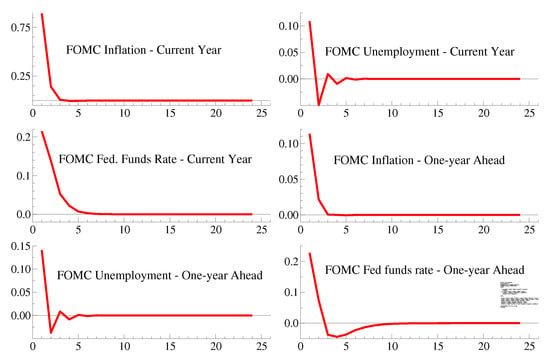
Figure 13.
Impulse Responses to a one-percent inflation revision FIML.
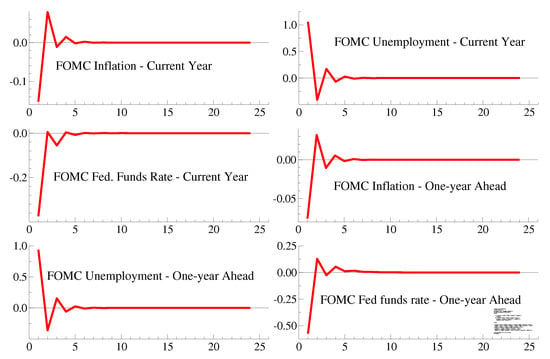
Figure 14.
Impulse Responses to a one-percent unemployment revision FIML.
Thus, apart from suggesting dynamic stability, this model’s results are consistent with the dual mandate.
3.2.2. Sensitivity Assessment
From the standpoint of predicting the rate decision, the models developed can be used to obtain the reduced-form coefficients for these coefficients are akin to rules of thumb and they are reported in Table 3.15

Table 3.
Static Long-Run Solutions for the current-year projections for the federal funds rate by about 25 basis points.
The results reveal three features of interest:
- Increases in the actual inflation rate raises the federal funds
- An increase of one percentage point in the SPF unemployment rate reduces the federal funds rate from 30 to 50 basis points.
- Chair-specific effects are significant and positive across models; the point estimates are somewhat sensitive to the estimation method. These effects reflect the power of persuasion of the FOMC Chair.
Again, we are not arguing that the FOMC determines their projections using these equations. Rather, these equations are the ones that the public could use to forecast FOMC forecasts and to anticipate interest-rate decisions.
4. Conclusions
This paper is not about invalidating Faust’s critique: The SEP offers no way to reconcile the dispersion of appropriate interest-rate policies and, hence, it appears as useless. To Faust and Bernanke, the way to reconcile these differences is for the FOMC to provide its reaction function. We argue that providing a reaction function that relies on variables the public does not observe is not helpful. This paper is about the feasibility of bypassing the absence of the FOMC reaction function.
Though the FOMC provides the SEP in real time, it is released along with the interest-rate decision. Furthermore, even a casual reading of FOMC transcripts reveals that the FOMC considers many variables in their decision-making process: term structures (foreign and domestic), exchange rates, and interest rates (foreign and domestic), among others. Therefore, if what we want is to anticipate that decision, then we need to forecast the FOMC’s own forecasts. The models developed show that it is feasible to build models to forecast FOMC forecasts based on publicly available data. To be sure, we are not arguing that the FOMC participants determine their projections using econometric formulations only. Rather, that these models are the ones that the public could use to anticipate FOMC’s forecasts and decisions.16 The results show that it is possible to replicate accurately the FOMC projections, to obtain results that are consistent with expectations, and to extract simple rules of thumb to predict interest-rate decisions. In other words, we find the SEP to be useful for understanding monetary policy in the United States.
There are many objections to our findings. First, there is no guarantee that a replicable, but unknown, model even exists. Indeed, our work is subject to the criticism that we are testing a joint hypothesis: that the mapping exists and that our approach offers a characterization of it. Second, from a modeling standpoint, our mapping treats SPF forecasts as given. Third, the sample period is brief and the number of observations is small and correspond to an unusual circumstances in U.S. history. Finally, we have not undertaken an exhaustive sensitivity analysis of our econometric results. Thus, taken as whole, these limitations underscore the undeniably tentative character of our results.
Author Contributions
Conceptualization and writing, J.M. Date development and estimation, S.Y.K.
Funding
This research received no external funding.
Acknowledgments
The calculations in this paper are carried out with OxMetrics (8). We are grateful to two anonymous referees for their insights. We also received comments from Gordon Bodnar, Neil Ericsson, David Hendry, Fred Joutz, Simon Sheng, and Tara Sinclair. Earlier versions of this paper were presented at George Washington’s Research Program on Forecasting (February 2018), joint with the Federal Forecasters Consortium (FFC), at the meetings of the Society of Government Economists (March 2018), and at the George Washington University’s 21st Dynamic Econometrics Conference (March 2019). All the Internet links were accessed on 13 November 2018.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Arai, Natsuki. 2015. Evaluating the Efficiency of FOMC’s New Economic Projections. Journal of Money, Credit and Banking 48: 1019–49. [Google Scholar] [CrossRef]
- Bernanke, Ben. 2016. Federal Reserve Economic Projections: What Are They Good for? Available online: https://www.brookings.edu/blog/ben-bernanke/2016/11/28/federal-reserve-economic-projections/ (accessed on 13 November 2018).
- Doornik, Jurgen A., and David F. Hendry. 2013. PcGive 14. 3 vols, London: Timberlake Consultants Press. [Google Scholar]
- Faust, Jon. 2016. Available online: https://www.brookings.edu/wp-content/uploads/2016/11/wp25_faust_monetarypolicytransparency_final1.pdf (accessed on 13 November 2018).
- Fendel, Ralf, and Jan-Christoph Rülke. 2012. Are Heterogenous FOMC Forecasts Consistent with the Fed’s Monetary Policy? Economic Letters 116: 5–7. [Google Scholar] [CrossRef]
- Granger, Clive, and David F. Hendry. 2004. A Dialogue Concerning a New Instrument for Econometric Modeling. Econometric Theory 21: 278–97. [Google Scholar] [CrossRef]
- Hendry, David F., and Hans-Martin Krolzig. 2003. New Developments in Automatic General-to-Specific Modeling. In Econometrics and the Philosophy of Economics. Edited by Bernt Stigum. Princeton: Princeton University Press. [Google Scholar]
- Nakazono, Yoshiyuki. 2013. Strategic Behavior of Federal Open Market Committee Board Members: Evidence from Member’s Forecasts. Journal of Economic Behavior & Organization 93: 62–70. [Google Scholar]
- Phillips, Peter. 2004. Automated Discovery in Econometrics. Cowles Foundation Discussion Paper No. 1469. New Haven: Yale University. [Google Scholar]
- Powell, Jerome. 2018. Monetary Policy in a Changing Economy. Available online: https://www.federalreserve.gov/newsevents/speech/files/powell20180824a.pdf (accessed on 13 November 2018).
- Romer, David. 2010. A New Data Set on Monetary Policy: The Economic Forecasts of Individual Members of the FOMC. Journal of Money, Credit, and Banking 42: 951–57. [Google Scholar] [CrossRef]
- Rülke, Jan-Christoph, and Peter Tillman. 2011. Do FOMC Members Herd? Economic Letters 11: 176–79. [Google Scholar] [CrossRef]
- Sheng, Simon. 2015. Evaluating the Economic Forecasts of FOMC Members. International of Forecasting 31: 165–75. [Google Scholar] [CrossRef]
- Tillman, Peter. 2011. Strategic Forecasting of the FOMC. European Journal of Political Economy 27: 547–53. [Google Scholar] [CrossRef][Green Version]
- Yellen, Janet. 2018. Interview. Available online: https://www.brookings.edu/wp-content/uploads/2018/03/es_20180227_yellen_bernanke_transcript.pdf (accessed on 13 November 2018).
| 1 | See also Page 3 of http://www.federalreserve.gov/mediacenter/files/FOMCpresconf20151216.pdf. Please note that FOMC participants are not picking just any value of the federal funds rate they deem appropriate. Rather, their values vary in steps of 0.125 percentage points; the steps might vary from meeting to meeting. Thus, their interpretation of the appropriate monetary policy is not unconstrained. |
| 2 | |
| 3 | The data assembled by Romer (2010) contains participant-specific projections for 1992 to 2006 with attribution. We replicated his data, added the observations for 2007 with attribution, and extended the data to include FOMC participants through 2012 but without attribution because they are not available. Please note that there are no comparable data for the interest rates. |
| 4 | Note, further, that forecast accuracy is not an FOMC mandate. Intuitively, FOMC participants are not impartial observers of their own forecasts but rather must influence the economy to meet their dual mandate. As a result, a narrow interpretation of forecast accuracy is not useful if that accuracy means high inflation and high unemployment. Furthermore, forecast revisions cannot be unambiguously interpreted as reactions to news. As indicated earlier, FOMC participants’ projections depend on their assessments of the appropriate monetary policy. Thus, even if FOMC participants had and released a shared knowledge of the economy, its usefulness to the public would be transitory because the makeup of the FOMC participants changes over time. New participants would bring their own interpretation of appropriate monetary policy which would translate into different interest-rate projections, even in the absence of economic news. |
| 5 | Previous work includes Arai (2015); Fendel and Rülke (2012); Nakazono (2013); Rülke and Tillman (2011), and Sheng (2015). |
| 6 | Please note that adherence to a single reaction function contradicts the FOMC directive embodied in the SEP. |
| 7 | The above remarks raise several questions. First, why do Faust and Bernanke use the singular when referring to the reaction function? Indeed, the FOMC directive associated with the SEP allows for the possibility of 19 reaction functions. Heuristically, the FOMC participant determines the appropriate interest rate that minimizes the welfare loss of deviations of inflation and unemployment from the dual mandate. Subject to the behavior of the economy, the FOMC participant would solve
|
| 8 | We focus on these two variables because the record of press releases of FOMC decisions and Bluebooks, documenting the alternative options over which FOMC members vote, indicates that the outlook for economic activity (i.e., unemployment) and inflation are the most important considerations for determining the outlook for interest rates. See page 52 of https://www.federalreserve.gov/monetarypolicy/files/FOMC20090128bluebook20090122.pdf. |
| 9 | Please note that the median of R need not correspond to a participant with the median of or Mismatch of medians can be solved if the FOMC released the participant-specific projections with attribution. |
| 10 | One way to detect extreme values is to see if the distributions of forecasts are asymmetric. Because normal distributions are symmetric, finding evidence of normality would reject the presence of fat-tails or extreme forecasts. |
| 11 | Please note that we do not include Greenbook/Teal book forecasts as an alternative to publicly available data in real time because they are released with a five-year delay. |
| 12 | For a discussion of the issues raised by automated specification, see Hendry and Krolzig (2003); Granger and Hendry (2004); and Phillips (2004). |
| 13 | The FOMC also provides projections for two and three years ahead but modeling those is beyond the scope of this paper. |
| 14 | Data sources and the associated time series properties are available on request. |
| 15 | The reduced form coefficients for Equation (1) above is
|
| 16 | Nevertheless, the Board of Governors posts the Eviews files needed to run the staff’s model FRB/US; see https://www.federalreserve.gov/econres/us-models-package.htm. This posting requires of the public an intimate familiarity with computer software. Even if that familiarity is present, one should not associate the views of the Board with the views of the FOMC as the dispersion of forecasts for the last 15 years demonstrates. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).