The Outperformance Probability of Mutual Funds
Abstract
:1. Motivation
- The OP compares some strategy with a specified benchmark, which need not necessarily be the money-market account.
- It is a probability. Thus, it is easy to understand also for a nonacademic audience, more precisely, for people who are not educated in statistics or probability theory.
- The holding period of the investor is considered random. This enables us to compute the performance of an investment opportunity for arbitrary liquidity preferences.
- The first one is conceptual:
- (a)
- A simple thought experiment reveals that comparing two performance measures with one another, where each one compares an investment opportunity with the money-market account, can lead to completely different conclusions than evaluating only one performance measure that compares the given investment opportunities without taking the money-market account into consideration at all. The former comparison refers to the question of which of the two investment opportunities is better able to outperform the money-market account, whereas the latter comparison refers to the question of whether the first investment opportunity is able to outperform the second. In general, performance measures are not linear and so the former comparison does not imply the latter, i.e., an investment opportunity that is better able to produce excess returns than another investment opportunity need not be better than the other.
- (b)
- Most performance measures presume that the holding period of the investor is fixed. This assumption is clearly violated in real-life because investors usually do not know, in advance, when they will liquidate all their assets. We solve this problem by incorporating any holding-time distribution, which specifies the individual liquidity preference of the investor. It can be either discrete or continuous and it can have a finite or infinite right endpoint. Any fixed holding period can be considered a special case, which means that we can treat one-period models, too.
- The second one is empirical:
- (a)
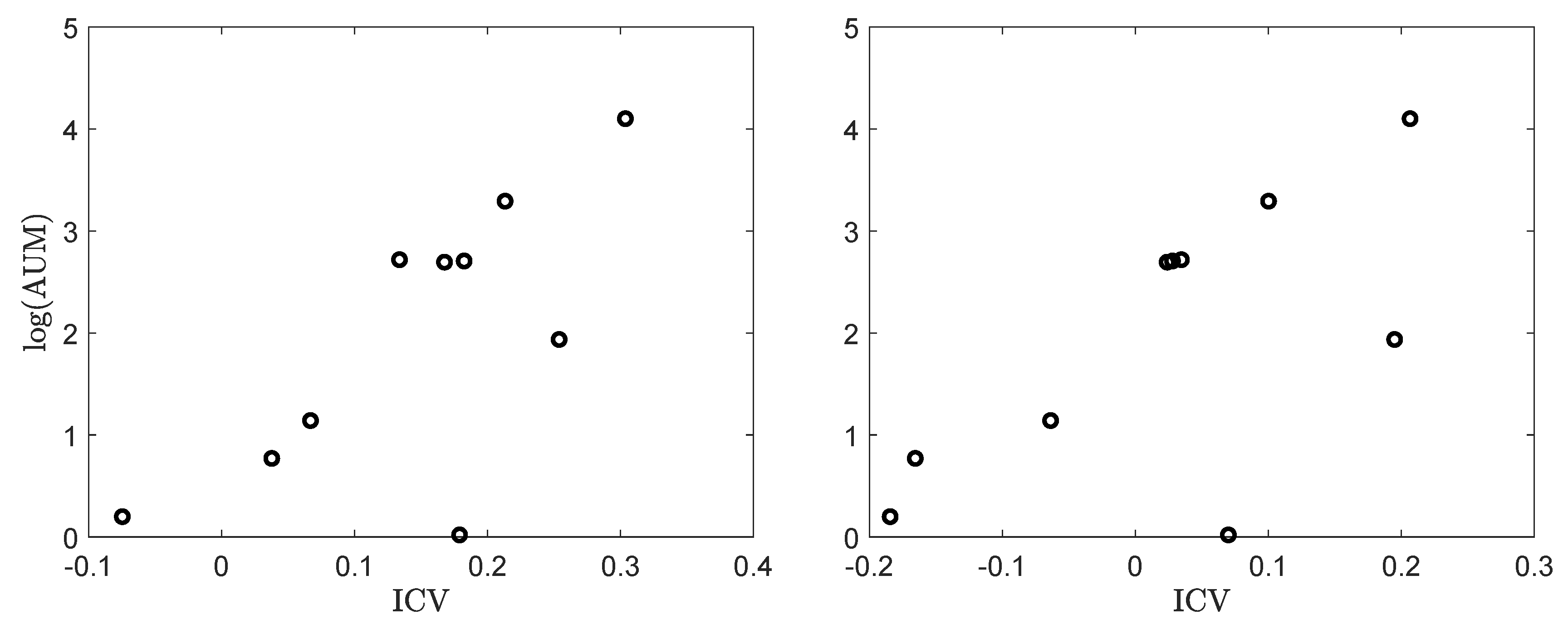
- The natural logarithm of the assets under management of the mutual funds that are taken into consideration are highly correlated with their inverse coefficient of variation (ICV). The ICV is a return-to-risk measure, which is based on differential log-returns but not (necessarily) on excess log-returns, and in the Brownian-motion framework it is the main ingredient of the OP. This means that capital allocation and relative performance are strongly connected to one another, which suggests that market participants take differential (log-)returns implicitly into account when making their investment decisions.
- (b)
- We emphasize our results by comparing the p-values of the differences between the Sharpe ratios of all mutual funds and the Sharpe ratios of the given benchmarks. The p-values indicate that it is hard to distinguish between the former and the latter Sharpe ratios. For this reason, we cannot say that any fund is better than the benchmark by comparing two Sharpe ratios with one another. A completely different picture evolves when considering the p-values of the ICVs of all funds with respect to their benchmarks. Those p-values are much lower and economically significant, i.e., it turns out that most funds are able to beat their benchmarks.
2. The Outperformance Probability
2.1. Basic Assumptions and Definition
2.2. Theoretical Properties
2.3. Statistical Inference
2.4. Discussion
- It is based on a parametric model, namely the geometric Brownian motion. While this model is standard in financial mathematics, we may doubt that value processes follow a geometric Brownian motion in real life. The assumption that log-returns are independent and identically normally distributed contradicts the stylized facts of empirical finance.
- We assume that the time of liquidation does not depend on whether or not the strategy outperforms the benchmark. This assumption might be violated, for example, if investors suffer from the disposition effect, i.e., if they tend to sell winners too early and ride losers too long (Shefrin and Statman 1985).
- Also the holding-time distribution follows a parametric model, which can either be true or false, too. Indeed, we have to choose some model for T but need not necessarily know its parameters. However, in order to estimate the parameters of F, we would need appropriate data and then the statistical properties of the ML-estimator might change essentially.
3. Empirical Investigation
3.1. General Observations
“The recent increase in the number and types of index funds that are available to individual investors makes this a matter of practical as well as theoretical significance. Numerous index funds, which track the Standard and Poor’s (S&P) 500 Index or various small-stock, bond, value, growth, or international indexes, are now widely available to individual investors. […] Given that there are sufficient index funds to span most investors’ risk choices, that the index funds are available at low cost, and that the low cost of index funds means that a combination of index funds is likely to outperform an active fund of similar risk, the question is, why select an actively managed fund?”
3.2. Empirical Results
3.2.1. Fixed Holding Period
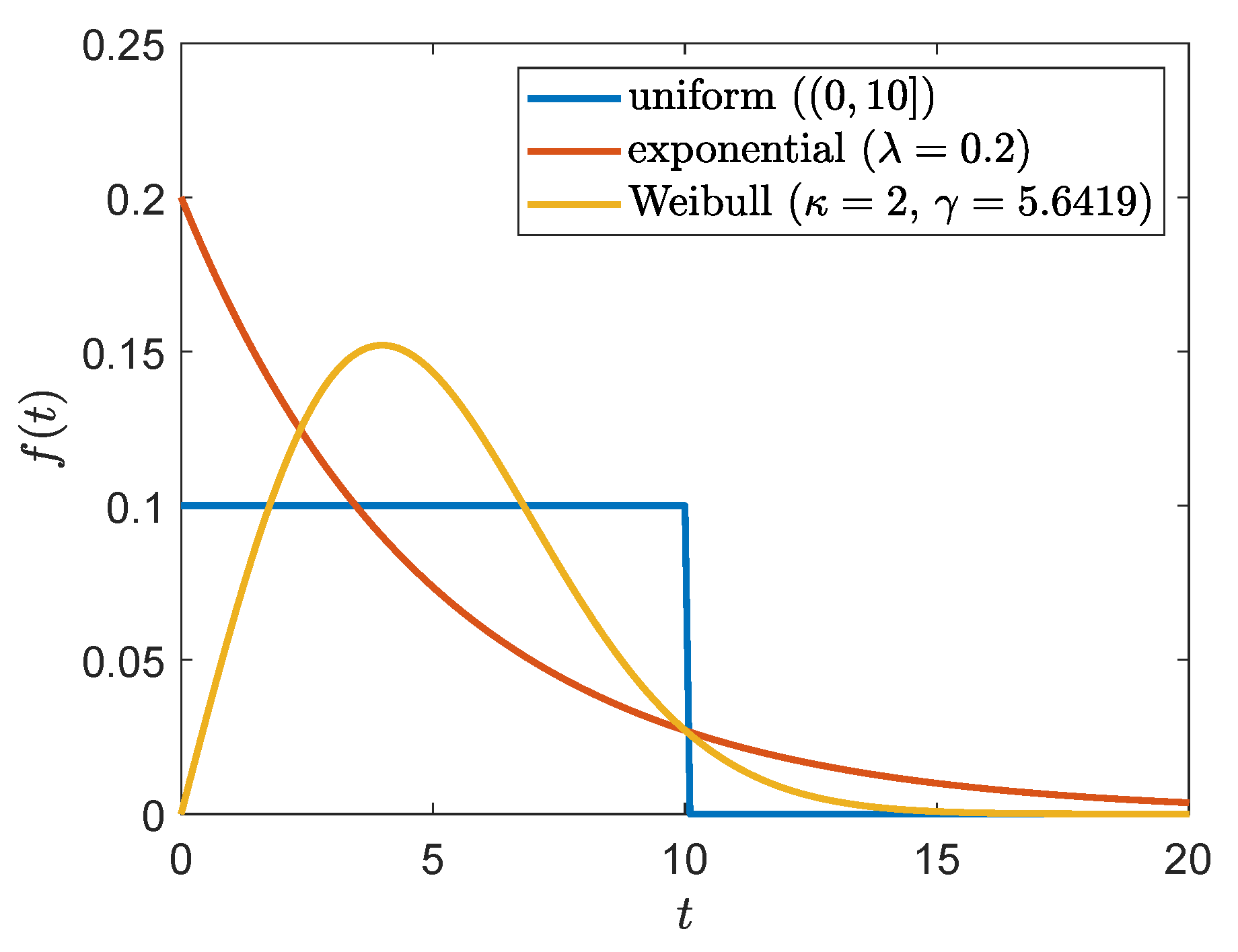
3.2.2. Uniformly Distributed Holding Period
3.2.3. Exponentially Distributed Holding Period
3.2.4. Weibull Distributed Holding Period
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alexander, Gordon J., and Alexandre M. Baptista. 2003. Portfolio performance evaluation using value at risk. Journal of Portfolio Management 29: 93–102. [Google Scholar] [CrossRef]
- Baweja, Meena, Ratnesh R. Saxena, and Deepak Sehgal. 2015. Portfolio optimization using conditional Sharpe ratio. International Letters of Chemistry, Physics and Astronomy 53: 130–36. [Google Scholar] [CrossRef]
- Burke, Gibbons. 1994. A sharper Sharpe ratio. Futures 23: 56. [Google Scholar]
- Chow, Victor, and Christine W. Lai. 2015. Conditional Sharpe ratios. Finance Research Letters 12: 117–33. [Google Scholar] [CrossRef]
- Dowd, Kevin. 2000. Adjusting for risk: An improved Sharpe ratio. International Review of Economics and Finance 9: 209–22. [Google Scholar] [CrossRef]
- Eling, Martin, and Frank Schuhmacher. 2006. Hat die Wahl des Performancemaßes einen Einfluss auf die Beurteilung von Hedgefonds-Indizes? Kredit und Kapital 39: 419–54. [Google Scholar]
- Elton, Edwin J., Martin J. Gruber, and Christopher R. Blake. 1996. The persistence of risk-adjusted mutual fund performance. Journal of Business 69: 133–57. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 2010. Luck versus skill in the cross-section of mutual fund returns. Journal of Finance 65: 1915–47. [Google Scholar] [CrossRef]
- Frahm, Gabriel. 2016. Pricing and valuation under the real-world measure. International Journal of Theoretical and Applied Finance 19. [Google Scholar] [CrossRef]
- Frahm, Gabriel. 2018. An intersection-union test for the Sharpe ratio. Risks 6. [Google Scholar] [CrossRef]
- Grinblatt, Mark, and Sheridan Titman. 1989. Mutual fund performance: An analysis of quarterly portfolio holdings. Journal of Business 62: 393–416. [Google Scholar] [CrossRef]
- ICI. 2019. Worldwide Regulated Open-End Fund Assets and Flows, Fourth Quarter 2018. Available online: https://www.iciglobal.org/iciglobal/research/stats/ww/ci.ww_q4_18.global (accessed on 6 April 2019).
- Ippolito, Richard A. 1989. Efficiency with costly information: A study of mutual fund performance, 1965–1984. Quarterly Journal of Economics 104: 1–23. [Google Scholar] [CrossRef]
- Jensen, Michael C. 1968. The performance of mutual funds in the period 1945–1964. Journal of Finance 23: 389–416. [Google Scholar] [CrossRef]
- Keating, Con, and William F. Shadwick. 2002. A universal performance measure. Journal of Performance Measurement 6: 59–84. [Google Scholar]
- Kestner, Lars N. 1996. Getting a handle on true performance. Futures 25: 44–46. [Google Scholar]
- Lin, Mei-Chen, and Pin-Huang Chou. 2003. The pitfall of using Sharpe ratio. Finance Letters 1: 84–89. [Google Scholar]
- Lintner, John. 1965. The valuation of risky assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics 47: 13–37. [Google Scholar] [CrossRef]
- Lo, Andrew W. 2002. The statistics of Sharpe ratios. Financial Analysts Journal 58: 36–52. [Google Scholar] [CrossRef]
- Lusardi, Annamaria, and Olivia S. Mitchell. 2013. The Economic Importance of Financial Literacy: Theory and Evidence. Technical Report. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Merton, Robert C. 1973. Theory of rational option pricing. Bell Journal of Economics and Management Science 4: 141–83. [Google Scholar] [CrossRef]
- Mossin, Jan. 1966. Equilibrium in a capital asset market. Econometrica 34: 768–83. [Google Scholar] [CrossRef]
- OECD. 2016. OECD/INFE International Survey of Adult Financial Literacy Competencies. Technical Report. Paris: OECD. [Google Scholar]
- Sharpe, William F. 1964. 1964 Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance 19: 425–42. [Google Scholar]
- Sharpe, William F. 1966. Mutual fund performance. Journal of Business 39: 119–38. [Google Scholar] [CrossRef]
- Sharpe, William F. 1994. The Sharpe ratio. Journal of Portfolio Management 21: 49–58. [Google Scholar] [CrossRef]
- Shefrin, Hersh, and Meir Statman. 1985. The disposition to sell winners too early and ride losers too long: Theory and evidence. Journal of Finance 40: 777–90. [Google Scholar] [CrossRef]
- Sortino, Frank, Robert Van Der Meer, and Auke Plantinga. 1999. The Dutch triangle. Journal of Portfolio Management 26: 50–58. [Google Scholar] [CrossRef]
- Treynor, Jack L. 1961. Market value, time, and risk. Available online: https://dx.doi.org/10.2139/ssrn.2600356 (accessed on 25 June 2019).
- Young, Terry W. 1991. Calmar ratio: A smoother tool. Futures 20: 1. [Google Scholar]
| 1 | Each excess return is a differential return but not vice versa. |
| 2 | It is a matter of fact that some students do not understand even the distinction between parameter and estimator after attending a statistics course. |
| 3 | According to Lusardi and Mitchell (2013, pp. 15–16), we can expect that a large number of people cannot understand the question at all because they are unfamiliar with stocks, bonds, and mutual funds. |
| 4 | From now on, we will omit the subscript “” for notational convenience. |
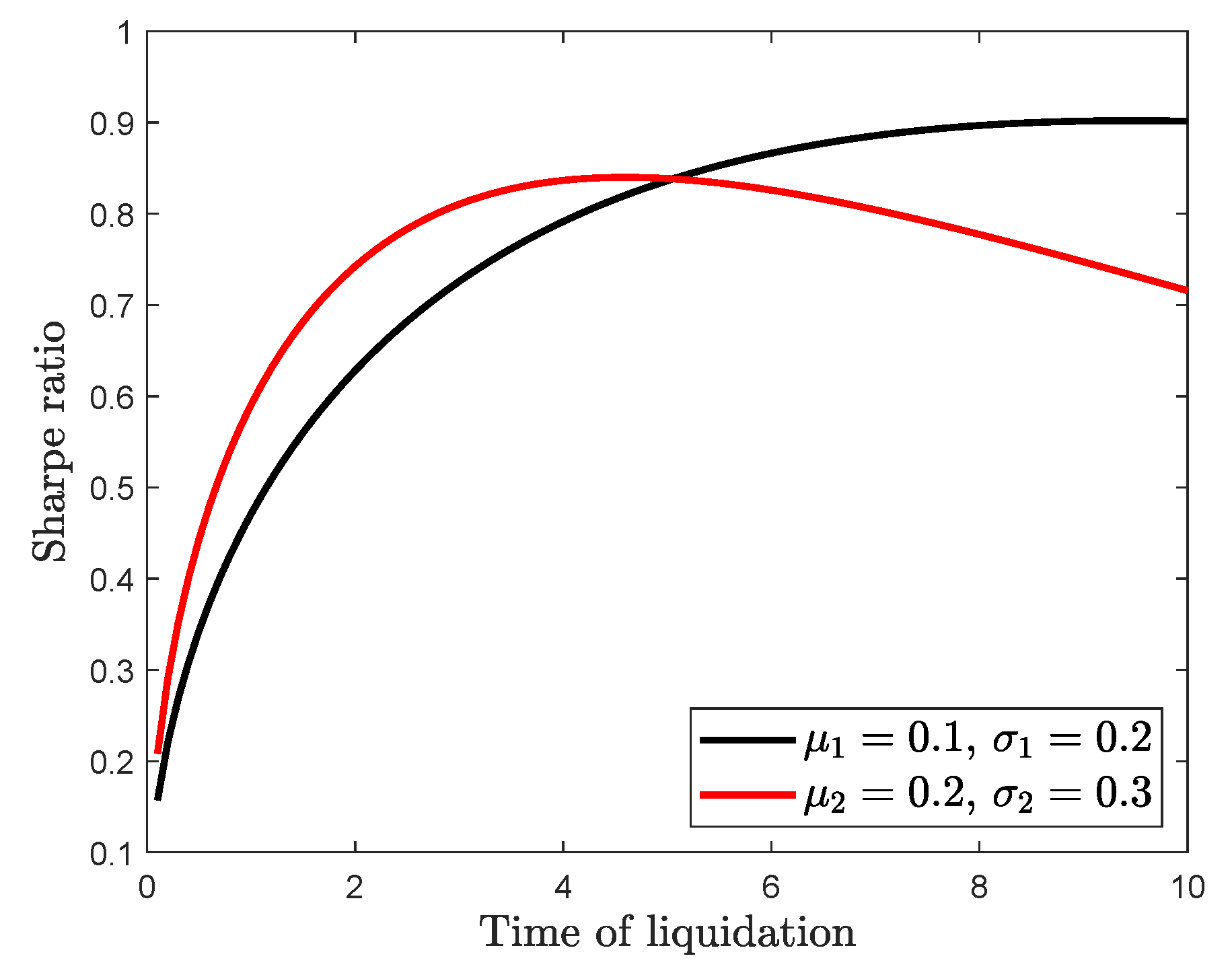
| 5 | In the given example, the critical time point is, approximately, years. |
| 6 | The reason why we focus on ETFs is discussed in Section 3.1. |
| 7 | |
| 8 | does not imply that but . |
| 9 | Thus, if a strategy has a higher OP than another strategy, given some holding-time distribution, the same holds true for any other holding-time distribution. |
| 10 | This term can be attributed to the estimation error regarding the standard deviation of X (Frahm 2018). |
| 11 | This is true whenever for any . |
| 12 | This is not a linear regression equation because . |
| 13 | This kind of situation cannot happen in our Brownian-motion framework. |
| 14 | It holds that and so the drift coefficient can be considered the internal rate of return on the fund. |
| 15 | |
| 16 | Note that this is precisely the case in which we have that . |

| Benchmark/Fund | Symbol | ER (%) | AUM (bn $) | |||
|---|---|---|---|---|---|---|
| SPDR S&P 500 ETF | SPY | 0.0995 | 0.1815 | 0.0830 | 0.09 | 264.06 |
| iShares Russell 1000 Growth ETF | IWF | 0.1064 | 0.1774 | 0.0906 | 0.20 | 44.44 |
| iShares 7–10 Year Treasury Bond ETF | IEF | 0.0465 | 0.0656 | 0.0444 | 0.15 | 13.31 |
| Money market | – | 0.0100 | 0.0007 | 0.0100 | – | – |
| Cash | – | 0 | 0 | 0 | – | – |
| Fidelity Blue Chip Growth | FBGRX | 0.1135 | 0.1919 | 0.0951 | 0.72 | 26.89 |
| T. Rowe Price Blue Chip Growth | TRBCX | 0.1200 | 0.1974 | 0.1005 | 0.70 | 60.37 |
| Franklin Growth A | FKGRX | 0.1064 | 0.1708 | 0.0918 | 0.84 | 14.96 |
| JPMorgan Large Cap Growth A | OLGAX | 0.1105 | 0.1900 | 0.0924 | 0.94 | 15.15 |
| Vanguard Morgan Growth | VMRGX | 0.1094 | 0.1889 | 0.0915 | 0.37 | 14.79 |
| Morgan Stanley Institutional Growth A | MSEGX | 0.1299 | 0.2164 | 0.1064 | 0.89 | 6.93 |
| BlackRock Capital Appreciation | MAFGX | 0.1060 | 0.1931 | 0.0873 | 0.76 | 3.13 |
| AllianzGI Focused Growth Fund Admin | PGFAX | 0.1129 | 0.1942 | 0.0940 | 0.99 | 1.02 |
| Goldman Sachs Large Cap Growth Insights | GCGIX | 0.1015 | 0.1829 | 0.0848 | 0.53 | 2.16 |
| Pioneer Disciplined Growth A | PINDX | 0.0993 | 0.2077 | 0.0777 | 0.87 | 1.22 |
| ⌀ | 0.1110 | 0.1933 | 0.0922 | 0.76 | 14.66 |
| Symbol | Ordinary | Generalized | ||
|---|---|---|---|---|
| SPY | IWF | IEF | ||
| SPY | 0.4933 | – | – | – |
| IWF | 0.5433 | – | – | – |
| IEF | 0.5579 | – | – | – |
| FBGRX | 0.5396 | 0.2480 | 0.1608 | 0.2970 |
| TRBCX | 0.5576 | 0.3570 | 0.2854 | 0.3187 |
| FKGRX | 0.5649 | 0.1433 | 0.0020 | 0.2914 |
| OLGAX | 0.5292 | 0.1568 | 0.0788 | 0.2874 |
| VMRGX | 0.5264 | 0.1954 | 0.0801 | 0.2824 |
| MSEGX | 0.5544 | 0.3304 | 0.2903 | 0.3366 |
| MAFGX | 0.4973 | 0.1014 | −0.0074 | 0.2628 |
| PGFAX | 0.5304 | 0.2185 | 0.1338 | 0.2921 |
| GCGIX | 0.5007 | 0.0436 | −0.1372 | 0.2541 |
| PINDX | 0.4302 | −0.0028 | −0.1008 | 0.2198 |
| ⌀ | 0.5231 | 0.1792 | 0.0786 | 0.2842 |
| Symbol | Benchmark | ||||
|---|---|---|---|---|---|
| SPY | IWF | IEF | LIBOR | Cash | |
| FBGRX | 0.2133 | 0.1002 | 0.2245 | 0.4429 | 0.4947 |
| TRBCX | 0.3038 | 0.2066 | 0.2432 | 0.4584 | 0.5088 |
| FKGRX | 0.1825 | 0.0279 | 0.2307 | 0.4790 | 0.5373 |
| OLGAX | 0.1339 | 0.0346 | 0.2156 | 0.4335 | 0.4858 |
| VMRGX | 0.1677 | 0.0239 | 0.2115 | 0.4312 | 0.4839 |
| MSEGX | 0.2539 | 0.1950 | 0.2503 | 0.4454 | 0.4913 |
| MAFGX | 0.0669 | −0.0638 | 0.1896 | 0.4001 | 0.4516 |
| PGFAX | 0.1790 | 0.0699 | 0.2182 | 0.4326 | 0.4838 |
| GCGIX | 0.0378 | −0.1656 | 0.1865 | 0.4088 | 0.4632 |
| PINDX | −0.0747 | −0.1845 | 0.1387 | 0.3259 | 0.3738 |
| ⌀ | 0.1464 | 0.0244 | 0.2109 | 0.4258 | 0.4774 |
| Symbol | ||||||
|---|---|---|---|---|---|---|
| SPY | IWF | IEF | SPY | IWF | IEF | |
| FBGRX | 0.2133 | 0.1002 | 0.2245 | 0.0463 | −0.0183 | −0.0038 |
| (0.1970) | (0.3444) | (0.1848) | (0.2908) | (0.5168) | (0.5233) | |
| TRBCX | 0.3038 | 0.2066 | 0.2432 | 0.0643 | −0.0003 | 0.0142 |
| (0.1123) | (0.2044) | (0.1654) | (0.2193) | (0.5003) | (0.4149) | |
| FKGRX | 0.1825 | 0.0279 | 0.2307 | 0.0717 | 0.0071 | 0.0216 |
| (0.2329) | (0.4556) | (0.1782) | (0.1756) | (0.4935) | (0.3822) | |
| OLGAX | 0.1339 | 0.0346 | 0.2156 | 0.0360 | −0.0286 | −0.0141 |
| (0.2963) | (0.4450) | (0.1944) | (0.3664) | (0.5264) | (0.5706) | |
| VMRGX | 0.1677 | 0.0239 | 0.2115 | 0.0331 | −0.0315 | −0.0170 |
| (0.2513) | (0.4619) | (0.1989) | (0.3315) | (0.5289) | (0.6200) | |
| MSEGX | 0.2539 | 0.1950 | 0.2503 | 0.0611 | −0.0035 | 0.0110 |
| (0.1550) | (0.2178) | (0.1585) | (0.3071) | (0.5032) | (0.4575) | |
| MAFGX | 0.0669 | −0.0638 | 0.1896 | 0.0040 | −0.0606 | −0.0460 |
| (0.3946) | (0.6006) | (0.2243) | (0.4829) | (0.5556) | (0.7294) | |
| PGFAX | 0.1790 | 0.0699 | 0.2182 | 0.0371 | −0.0275 | −0.0130 |
| (0.2371) | (0.3899) | (0.1915) | (0.3403) | (0.5252) | (0.5728) | |
| GCGIX | 0.0378 | −0.1656 | 0.1865 | 0.0074 | −0.0571 | −0.0426 |
| (0.4400) | (0.7460) | (0.2280) | (0.4587) | (0.5524) | (0.7818) | |
| PINDX | −0.0747 | −0.1845 | 0.1387 | −0.0631 | −0.1277 | −0.1131 |
| (0.6173) | (0.7696) | (0.2897) | (0.7481) | (0.6165) | (0.8875) | |
| Fund | SPY | IWF | IEF | LIBOR | Cash | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | |
| FBGRX | 0.6833 | 0.1992 | 0.1788 | 0.5886 | 0.2176 | 0.3419 | 0.6921 | 0.1967 | 0.1644 | 0.8390 | 0.1367 | 0.0066 | 0.8657 | 0.1210 | 0.0013 |
| TRBCX | 0.7515 | 0.1772 | 0.0779 | 0.6780 | 0.2006 | 0.1874 | 0.7068 | 0.1925 | 0.1414 | 0.8473 | 0.1320 | 0.0042 | 0.8724 | 0.1168 | 0.0007 |
| FKGRX | 0.6584 | 0.2053 | 0.2203 | 0.5249 | 0.2227 | 0.4555 | 0.6970 | 0.1954 | 0.1566 | 0.8580 | 0.1257 | 0.0022 | 0.8852 | 0.1084 | 0.0002 |
| OLGAX | 0.6176 | 0.2134 | 0.2907 | 0.5308 | 0.2225 | 0.4449 | 0.6851 | 0.1987 | 0.1758 | 0.8338 | 0.1395 | 0.0084 | 0.8613 | 0.1237 | 0.0017 |
| VMRGX | 0.6462 | 0.2080 | 0.2411 | 0.5213 | 0.2228 | 0.4619 | 0.6819 | 0.1995 | 0.1810 | 0.8325 | 0.1402 | 0.0088 | 0.8604 | 0.1243 | 0.0019 |
| MSEGX | 0.7149 | 0.1899 | 0.1289 | 0.6686 | 0.2029 | 0.2030 | 0.7122 | 0.1908 | 0.1331 | 0.8403 | 0.1359 | 0.0061 | 0.8640 | 0.1220 | 0.0014 |
| MAFGX | 0.5595 | 0.2207 | 0.3938 | 0.4433 | 0.2209 | 0.6013 | 0.6642 | 0.2040 | 0.2105 | 0.8145 | 0.1496 | 0.0177 | 0.8437 | 0.1340 | 0.0052 |
| PGFAX | 0.6556 | 0.2060 | 0.2251 | 0.5621 | 0.2204 | 0.3890 | 0.6872 | 0.1981 | 0.1723 | 0.8333 | 0.1398 | 0.0085 | 0.8603 | 0.1243 | 0.0019 |
| GCGIX | 0.5336 | 0.2224 | 0.4399 | 0.3556 | 0.2084 | 0.7558 | 0.6617 | 0.2046 | 0.2147 | 0.8196 | 0.1470 | 0.0148 | 0.8498 | 0.1305 | 0.0037 |
| PINDX | 0.4337 | 0.2201 | 0.6184 | 0.3400 | 0.2050 | 0.7825 | 0.6217 | 0.2127 | 0.2835 | 0.7669 | 0.1711 | 0.0594 | 0.7984 | 0.1574 | 0.0290 |
| ⌀ | 0.6254 | 0.2062 | 0.2815 | 0.5213 | 0.2144 | 0.4623 | 0.6810 | 0.1993 | 0.1833 | 0.8285 | 0.1417 | 0.0137 | 0.8561 | 0.1263 | 0.0047 |
| Fund | SPY | IWF | IEF | LIBOR | Cash | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | |
| FBGRX | 0.6716 | 0.1839 | 0.1754 | 0.5834 | 0.2042 | 0.3414 | 0.6798 | 0.1813 | 0.1607 | 0.8124 | 0.1208 | 0.0049 | 0.8359 | 0.1064 | 0.0008 |
| TRBCX | 0.7341 | 0.1607 | 0.0726 | 0.6667 | 0.1854 | 0.1843 | 0.6932 | 0.1767 | 0.1371 | 0.8197 | 0.1164 | 0.0030 | 0.8418 | 0.1027 | 0.0004 |
| FKGRX | 0.6485 | 0.1906 | 0.2179 | 0.5235 | 0.2099 | 0.4555 | 0.6842 | 0.1798 | 0.1528 | 0.8291 | 0.1107 | 0.0015 | 0.8531 | 0.0952 | 0.0001 |
| OLGAX | 0.6106 | 0.1994 | 0.2896 | 0.5291 | 0.2096 | 0.4449 | 0.6733 | 0.1834 | 0.1723 | 0.8078 | 0.1235 | 0.0063 | 0.8321 | 0.1088 | 0.0011 |
| VMRGX | 0.6372 | 0.1935 | 0.2392 | 0.5201 | 0.2100 | 0.4619 | 0.6703 | 0.1843 | 0.1777 | 0.8067 | 0.1241 | 0.0067 | 0.8312 | 0.1094 | 0.0012 |
| MSEGX | 0.7007 | 0.1740 | 0.1244 | 0.6580 | 0.1879 | 0.2002 | 0.6982 | 0.1749 | 0.1286 | 0.8136 | 0.1201 | 0.0045 | 0.8345 | 0.1073 | 0.0009 |
| MAFGX | 0.5560 | 0.2076 | 0.3937 | 0.4466 | 0.2078 | 0.6014 | 0.6539 | 0.1891 | 0.2078 | 0.7906 | 0.1331 | 0.0145 | 0.8165 | 0.1184 | 0.0037 |
| PGFAX | 0.6459 | 0.1913 | 0.2228 | 0.5585 | 0.2073 | 0.3888 | 0.6752 | 0.1827 | 0.1688 | 0.8073 | 0.1237 | 0.0065 | 0.8312 | 0.1094 | 0.0012 |
| GCGIX | 0.5317 | 0.2095 | 0.4399 | 0.3645 | 0.1939 | 0.7577 | 0.6516 | 0.1897 | 0.2122 | 0.7952 | 0.1306 | 0.0119 | 0.8219 | 0.1151 | 0.0026 |
| PINDX | 0.4376 | 0.2069 | 0.6186 | 0.3499 | 0.1902 | 0.7850 | 0.6144 | 0.1987 | 0.2823 | 0.7480 | 0.1545 | 0.0542 | 0.7763 | 0.1407 | 0.0248 |
| ⌀ | 0.6174 | 0.1917 | 0.2794 | 0.5200 | 0.2006 | 0.4621 | 0.6694 | 0.1841 | 0.1800 | 0.8030 | 0.1258 | 0.0114 | 0.8274 | 0.1113 | 0.0037 |
| Fund | SPY | IWF | IEF | LIBOR | Cash | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | |
| FBGRX | 0.6598 | 0.1683 | 0.1712 | 0.5782 | 0.1905 | 0.3407 | 0.6672 | 0.1655 | 0.1562 | 0.7868 | 0.1087 | 0.0042 | 0.8081 | 0.0966 | 0.0007 |
| TRBCX | 0.7165 | 0.1449 | 0.0675 | 0.6553 | 0.1699 | 0.1803 | 0.6795 | 0.1608 | 0.1322 | 0.7934 | 0.1050 | 0.0026 | 0.8134 | 0.0936 | 0.0004 |
| FKGRX | 0.6386 | 0.1754 | 0.2147 | 0.5221 | 0.1972 | 0.4555 | 0.6713 | 0.1640 | 0.1481 | 0.8019 | 0.1002 | 0.0013 | 0.8237 | 0.0875 | 0.0001 |
| OLGAX | 0.6035 | 0.1852 | 0.2881 | 0.5273 | 0.1969 | 0.4448 | 0.6613 | 0.1677 | 0.1681 | 0.7827 | 0.1110 | 0.0054 | 0.8046 | 0.0986 | 0.0010 |
| VMRGX | 0.6281 | 0.1786 | 0.2365 | 0.5189 | 0.1973 | 0.4619 | 0.6586 | 0.1687 | 0.1735 | 0.7817 | 0.1115 | 0.0058 | 0.8038 | 0.0991 | 0.0011 |
| MSEGX | 0.6863 | 0.1580 | 0.1193 | 0.6473 | 0.1726 | 0.1966 | 0.6840 | 0.1590 | 0.1236 | 0.7879 | 0.1081 | 0.0039 | 0.8067 | 0.0974 | 0.0008 |
| MAFGX | 0.5526 | 0.1945 | 0.3934 | 0.4498 | 0.1948 | 0.6016 | 0.6436 | 0.1738 | 0.2044 | 0.7673 | 0.1194 | 0.0126 | 0.7905 | 0.1066 | 0.0032 |
| PGFAX | 0.6362 | 0.1762 | 0.2197 | 0.5550 | 0.1942 | 0.3886 | 0.6631 | 0.1671 | 0.1645 | 0.7823 | 0.1112 | 0.0056 | 0.8038 | 0.0991 | 0.0011 |
| GCGIX | 0.5298 | 0.1967 | 0.4398 | 0.3734 | 0.1790 | 0.7603 | 0.6414 | 0.1745 | 0.2089 | 0.7714 | 0.1172 | 0.0103 | 0.7954 | 0.1039 | 0.0022 |
| PINDX | 0.4414 | 0.1937 | 0.6189 | 0.3600 | 0.1750 | 0.7882 | 0.6071 | 0.1843 | 0.2806 | 0.7290 | 0.1389 | 0.0496 | 0.7544 | 0.1262 | 0.0219 |
| ⌀ | 0.6093 | 0.1771 | 0.2769 | 0.5187 | 0.1867 | 0.4618 | 0.6577 | 0.1685 | 0.1760 | 0.7784 | 0.1131 | 0.0101 | 0.8004 | 0.1009 | 0.0033 |
| Fund | SPY | IWF | IEF | LIBOR | Cash | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | OP | Std | p | |
| FBGRX | 0.6756 | 0.1890 | 0.1764 | 0.5852 | 0.2088 | 0.3415 | 0.6840 | 0.1864 | 0.1619 | 0.8215 | 0.1266 | 0.0056 | 0.8462 | 0.1121 | 0.0010 |
| TRBCX | 0.7400 | 0.1662 | 0.0744 | 0.6706 | 0.1905 | 0.1853 | 0.6978 | 0.1820 | 0.1385 | 0.8292 | 0.1222 | 0.0035 | 0.8524 | 0.1083 | 0.0006 |
| FKGRX | 0.6519 | 0.1955 | 0.2186 | 0.5240 | 0.2144 | 0.4555 | 0.6886 | 0.1850 | 0.1540 | 0.8391 | 0.1165 | 0.0018 | 0.8643 | 0.1008 | 0.0001 |
| OLGAX | 0.6130 | 0.2042 | 0.2899 | 0.5297 | 0.2141 | 0.4449 | 0.6773 | 0.1885 | 0.1734 | 0.8167 | 0.1293 | 0.0072 | 0.8422 | 0.1146 | 0.0014 |
| VMRGX | 0.6403 | 0.1984 | 0.2398 | 0.5205 | 0.2145 | 0.4619 | 0.6743 | 0.1894 | 0.1787 | 0.8155 | 0.1300 | 0.0076 | 0.8413 | 0.1151 | 0.0015 |
| MSEGX | 0.7055 | 0.1793 | 0.1259 | 0.6617 | 0.1930 | 0.2011 | 0.7029 | 0.1802 | 0.1301 | 0.8227 | 0.1259 | 0.0052 | 0.8447 | 0.1131 | 0.0012 |
| MAFGX | 0.5572 | 0.2121 | 0.3937 | 0.4454 | 0.2124 | 0.6014 | 0.6574 | 0.1941 | 0.2086 | 0.7988 | 0.1389 | 0.0158 | 0.8258 | 0.1242 | 0.0043 |
| PGFAX | 0.6492 | 0.1962 | 0.2235 | 0.5598 | 0.2119 | 0.3889 | 0.6793 | 0.1879 | 0.1699 | 0.8162 | 0.1296 | 0.0073 | 0.8413 | 0.1151 | 0.0015 |
| GCGIX | 0.5324 | 0.2140 | 0.4399 | 0.3614 | 0.1988 | 0.7571 | 0.6551 | 0.1947 | 0.2129 | 0.8035 | 0.1364 | 0.0130 | 0.8315 | 0.1209 | 0.0031 |
| PINDX | 0.4362 | 0.2115 | 0.6185 | 0.3465 | 0.1951 | 0.7842 | 0.6170 | 0.2034 | 0.2827 | 0.7544 | 0.1601 | 0.0560 | 0.7838 | 0.1465 | 0.0264 |
| ⌀ | 0.6201 | 0.1966 | 0.2801 | 0.5205 | 0.2053 | 0.4622 | 0.6734 | 0.1892 | 0.1811 | 0.8118 | 0.1316 | 0.0123 | 0.8374 | 0.1171 | 0.0041 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frahm, G.; Huber, F. The Outperformance Probability of Mutual Funds. J. Risk Financial Manag. 2019, 12, 108. https://doi.org/10.3390/jrfm12030108
Frahm G, Huber F. The Outperformance Probability of Mutual Funds. Journal of Risk and Financial Management. 2019; 12(3):108. https://doi.org/10.3390/jrfm12030108
Chicago/Turabian StyleFrahm, Gabriel, and Ferdinand Huber. 2019. "The Outperformance Probability of Mutual Funds" Journal of Risk and Financial Management 12, no. 3: 108. https://doi.org/10.3390/jrfm12030108
APA StyleFrahm, G., & Huber, F. (2019). The Outperformance Probability of Mutual Funds. Journal of Risk and Financial Management, 12(3), 108. https://doi.org/10.3390/jrfm12030108




