Credit Scoring in SME Asset-Backed Securities: An Italian Case Study
Abstract
1. Introduction
2. Literature Review
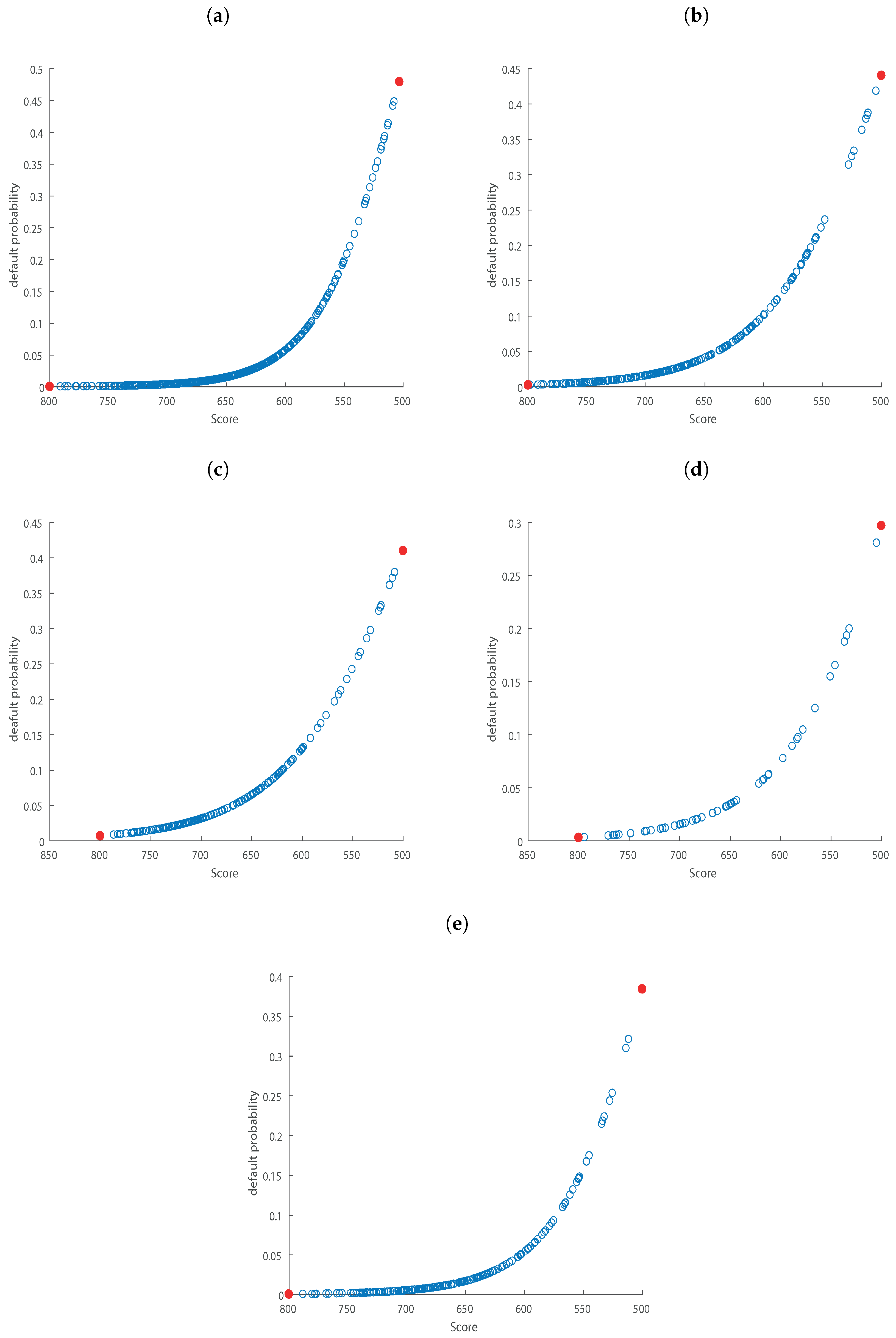
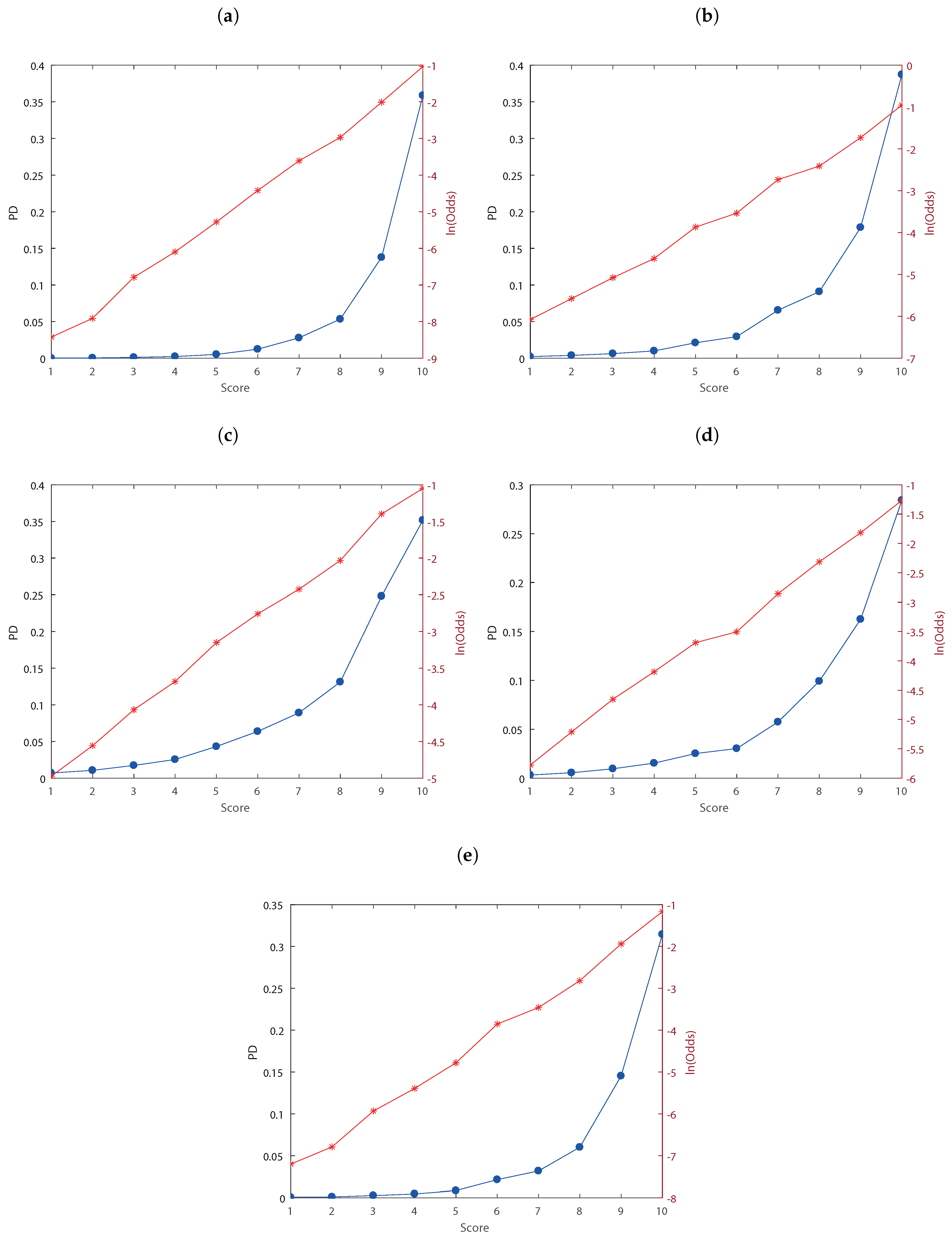
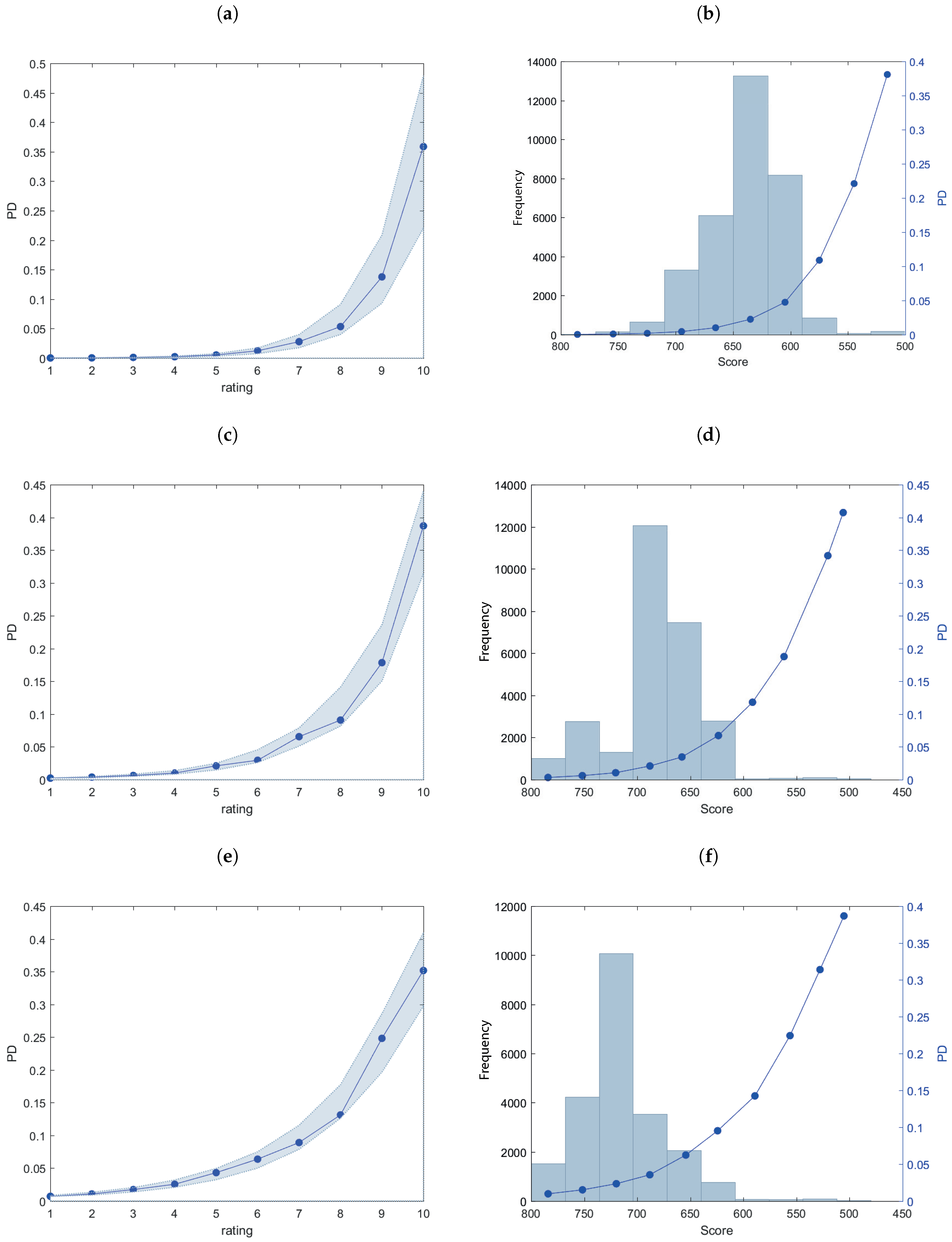
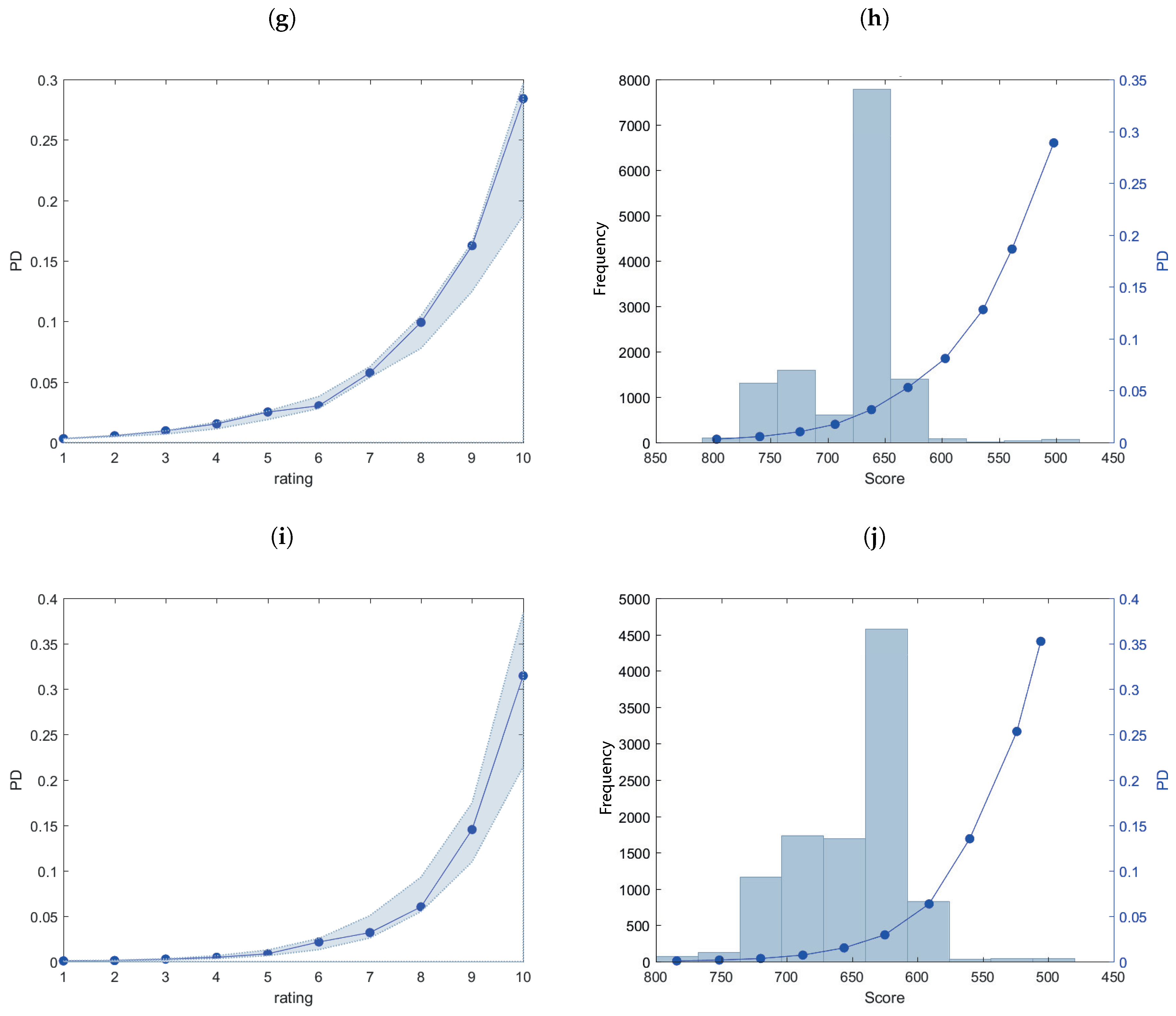
3. Empirical Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Rating | Freq. | Perc. | Cum. | Rating | Freq. | Perc. | Cum. | Rating | Freq. | Perc. | Cum. | Rating | Freq. | Perc. | Cum. | Rating | Freq. | Perc. | Cum. |
| A | 4 | 0.01 | 0.01 | A | 31 | 0.11 | 0.11 | A | 57 | 0.25 | 0.25 | A | 106 | 0.81 | 0.81 | A | 42 | 0.41 | 0.41 |
| B | 30 | 0.09 | 0.10 | B | 1250 | 4.52 | 4.63 | B | 1919 | 8.57 | 8.82 | B | 1306 | 10.03 | 10.84 | B | 95 | 0.92 | 1.33 |
| C | 301 | 0.92 | 1.02 | C | 2519 | 9.11 | 13.74 | C | 8002 | 35.72 | 44.54 | C | 1506 | 11.56 | 22.41 | C | 523 | 5.06 | 6.39 |
| D | 716 | 2.18 | 3.20 | D | 1288 | 4.66 | 18.39 | D | 7610 | 33.97 | 78.51 | D | 502 | 3.85 | 26.26 | D | 1562 | 15.12 | 21.50 |
| E | 3498 | 10.65 | 13.85 | E | 7355 | 26.59 | 44.98 | E | 1775 | 7.92 | 86.43 | E | 1413 | 10.85 | 37.11 | E | 1149 | 11.12 | 32.62 |
| F | 7272 | 22.15 | 36.00 | F | 12165 | 43.97 | 88.95 | F | 2060 | 9.20 | 95.63 | F | 6877 | 52.81 | 89.92 | F | 2988 | 28.92 | 61.54 |
| G | 15679 | 47.75 | 83.75 | G | 2660 | 9.62 | 98.57 | G | 751 | 3.35 | 98.98 | G | 1163 | 8.93 | 98.85 | G | 3148 | 30.47 | 92.01 |
| H | 4984 | 15.18 | 98.93 | H | 150 | 0.54 | 99.11 | H | 72 | 0.32 | 99.30 | H | 30 | 0.23 | 99.08 | H | 711 | 6.88 | 98.89 |
| I | 153 | 0.47 | 99.40 | I | 82 | 0.30 | 99.41 | I | 115 | 0.51 | 99.81 | I | 39 | 0.30 | 99.38 | I | 32 | 0.31 | 99.20 |
| L | 197 | 0.60 | 100.00 | L | 164 | 0.59 | 100.00 | L | 42 | 0.19 | 100.00 | L | 81 | 0.62 | 100.00 | L | 83 | 0.80 | 100.00 |
| 2014H1 | Non-Defaulted | Defaulted | pd_actual (%) | Total | 2014H2 | Non-Defaulted | Defaulted | pd_actual (%) | Total | |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 4 | 0 | 0.00 | 4 | 31 | 0 | 0.00 | 31 | ||
| B | 30 | 0 | 0.00 | 30 | 1229 | 21 | 1.68 | 1250 | ||
| C | 298 | 3 | 1.00 | 301 | 2482 | 37 | 1.47 | 2519 | ||
| D | 707 | 9 | 1.26 | 716 | 1267 | 21 | 1.63 | 1288 | ||
| E | 3452 | 46 | 1.32 | 3498 | 7186 | 169 | 2.30 | 7355 | ||
| F | 7169 | 103 | 1.42 | 7272 | 11819 | 346 | 2.84 | 12165 | ||
| G | 15264 | 415 | 2.65 | 15679 | 2587 | 73 | 2.74 | 2660 | ||
| H | 4810 | 174 | 3.49 | 4984 | 146 | 4 | 2.67 | 150 | ||
| I | 134 | 19 | 12.42 | 153 | 58 | 24 | 29.27 | 82 | ||
| L | 62 | 135 | 68.53 | 197 | 46 | 118 | 71.95 | 164 | ||
| 2015H1 | Non-Defaulted | Defaulted | pd_actual (%) | Total | 2015H2 | Non-Defaulted | Defaulted | pd_actual (%) | Total | |
| A | 57 | 0 | 0.00 | 57 | 105 | 1 | 0.94 | 106 | ||
| B | 1890 | 29 | 1.51 | 1919 | 1286 | 20 | 1.53 | 1306 | ||
| C | 7825 | 177 | 2.21 | 8002 | 1478 | 28 | 1.86 | 1506 | ||
| D | 7366 | 244 | 3.21 | 7610 | 491 | 11 | 2.19 | 502 | ||
| E | 1742 | 33 | 1.86 | 1775 | 1377 | 36 | 2.55 | 1413 | ||
| F | 2015 | 45 | 2.18 | 2060 | 6681 | 196 | 2.85 | 6877 | ||
| G | 715 | 36 | 4.79 | 751 | 1142 | 21 | 1.81 | 1163 | ||
| H | 69 | 3 | 4.17 | 72 | 30 | 0 | 0.00 | 30 | ||
| I | 37 | 78 | 67.83 | 115 | 36 | 3 | 7.69 | 39 | ||
| L | 8 | 34 | 80.95 | 42 | 25 | 56 | 69.14 | 81 | ||
| 2016H1 | Non-Defaulted | Defaulted | pd_actual % | Total | ||||||
| A | 42 | 0 | 0.00 | 42 | ||||||
| B | 95 | 0 | 0.00 | 95 | ||||||
| C | 517 | 6 | 1.15 | 523 | ||||||
| D | 1547 | 15 | 0.96 | 1562 | ||||||
| E | 1136 | 13 | 1.13 | 1149 | ||||||
| F | 2929 | 59 | 1.97 | 2988 | ||||||
| G | 3050 | 98 | 3.11 | 3148 | ||||||
| H | 695 | 16 | 2.25 | 711 | ||||||
| I | 27 | 5 | 15.63 | 32 | ||||||
| L | 38 | 45 | 54.22 | 83 |
| 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| pd_model | pd_actual | pd_model | pd_actual | pd_model | pd_actual | pd_model | pd_actual | pd_model | pd_actual | |||||
| A | 0.02 | 0.00 | 0.23 | 0.00 | 0.69 | 0.00 | 0.31 | 0.94 | 0.08 | 0.00 | ||||
| B | 0.04 | 0.00 | 0.38 | 1.68 | 1.05 | 1.51 | 0.55 | 1.53 | 0.11 | 0.00 | ||||
| C | 0.11 | 1.00 | 0.63 | 1.47 | 1.72 | 2.21 | 0.95 | 1.86 | 0.27 | 1.15 | ||||
| D | 0.23 | 1.26 | 1.00 | 1.63 | 2.54 | 3.21 | 1.53 | 2.19 | 0.46 | 0.96 | ||||
| E | 0.52 | 1.32 | 2.11 | 2.30 | 4.31 | 1.86 | 2.51 | 2.55 | 0.86 | 1.13 | ||||
| F | 1.23 | 1.42 | 2.95 | 2.84 | 6.37 | 2.18 | 3.02 | 2.85 | 2.15 | 1.97 | ||||
| G | 2.78 | 2.65 | 6.55 | 2.74 | 8.90 | 4.79 | 5.74 | 1.81 | 3.19 | 3.11 | ||||
| H | 5.34 | 3.49 | 9.09 | 2.67 | 13.12 | 4.17 | 9.92 | 0.00 | 6.02 | 2.25 | ||||
| I | 13.77 | 12.42 | 17.85 | 29.27 | 24.81 | 67.83 | 16.26 | 7.69 | 14.54 | 15.63 | ||||
| L | 35.87 | 68.53 | 38.72 | 71.95 | 35.17 | 80.95 | 28.42 | 69.14 | 31.45 | 54.22 | ||||
References
- Altman, Edward I. 1968. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. The Journal of Finance 23: 589–609. [Google Scholar] [CrossRef]
- Altman, Edward I. 1977. Predicting performance in the savings and loan association industry. Journal of Monetary Economics 3: 443–66. [Google Scholar] [CrossRef]
- Anderson, Raymond. 2007. The Credit Scoring Toolkit: Theory and Practice for Retail Credit Risk Management and Decision Automation. Oxford: Oxford University Press. [Google Scholar]
- Barnes, Paul. 1982. Methodological implications of non-normally distributed financial ratios. Journal of Business Finance & Accounting 9: 51–62. [Google Scholar]
- Beaver, William H. 1968. Alternative accounting measures as predictors of failure. The Accounting Review 43: 113–22. [Google Scholar]
- Blum, Marc. 1974. Failing company discriminant analysis. Journal of Accounting Research 12: 1–25. [Google Scholar] [CrossRef]
- Bryant, Stephanie M. 1997. A case-based reasoning approach to bankruptcy prediction modeling. Intelligent Systems in Accounting, Finance & Management 6: 195–214. [Google Scholar]
- Buta, Paul. 1994. Mining for financial knowledge with cbr. Ai Expert 9: 34–41. [Google Scholar]
- Caprara, Cristina, Davide Tommaso, and Roberta Mantovani. 2015. Corporate Credit Risk Research. Technical Report. Bologna: CRIF Rating. [Google Scholar]
- Chesser, Delton L. 1974. Predicting loan noncompliance. The Journal of Commercial Bank Lending 56: 28–38. [Google Scholar]
- Cortes, Corinna, and Vladimir Vapnik. 1995. Support-vector networks. Machine Learning 20: 273–97. [Google Scholar] [CrossRef]
- CSFB. 1997. Credit Risk+. Technical Document. New York: Credit Suisse First Boston. [Google Scholar]
- Deakin, Edward B. 1972. A discriminant analysis of predictors of business failure. Journal of Accounting Research 10: 167–79. [Google Scholar] [CrossRef]
- Dietsch, Michel, Klaus Düllmann, Henri Fraisse, Philipp Koziol, and Christine Ott. 2016. Support for the Sme Supporting Factor: Multi-Country Empirical Evidence on Systematic Risk Factor for Sme Loans. Frankfurt am Main: Deutsche Bundesbank Discussion Paper Series. [Google Scholar]
- Edmister, Robert O. 1972. An empirical test of financial ratio analysis for small business failure prediction. Journal of Financial and Quantitative Analysis 7: 1477–93. [Google Scholar] [CrossRef]
- European Parliament, Council of the European Union. 2013. Regulation (EU) No 575/2013 on Prudential Requirements for Credit Institutions and Investment Firms and Amending Regulation (EU) No 648/2012. Brussels: Official Journal of the European Union. [Google Scholar]
- Hamer, Michelle M. 1983. Failure prediction: Sensitivity of classification accuracy to alternative statistical methods and variable sets. Journal of Accounting and Public Policy 2: 289–307. [Google Scholar] [CrossRef]
- Hand, David J., and William E. Henley. 1997. Statistical classification methods in consumer credit scoring: A review. Journal of the Royal Statistical Society: Series A (Statistics in Society) 160: 523–41. [Google Scholar] [CrossRef]
- Hopkin, Richard, Anna Bak, and Sidika Ulker. 2014. High-Quality Securitization for Europe—The Market at a Crossroads. London: Association for Financial Markets in Europe. [Google Scholar]
- Jo, Hongkyu, Ingoo Han, and Hoonyoung Lee. 1997. Bankruptcy prediction using case-based reasoning, neural networks, and discriminant analysis. Expert Systems with Applications 13: 97–108. [Google Scholar] [CrossRef]
- Karels, Gordon V., and Arun J. Prakash. 1987. Multivariate normality and forecasting of business bankruptcy. Journal of Business Finance & Accounting 14: 573–93. [Google Scholar]
- Kim, Hong Sik, and So Young Sohn. 2010. Support vector machines for default prediction of smes based on technology credit. European Journal of Operational Research 201: 838–46. [Google Scholar] [CrossRef]
- Martin, Daniel. 1977. Early warning of bank failure: A logit regression approach. Journal of Banking & Finance 1: 249–76. [Google Scholar]
- Mays, Elizabeth, and Niall Lynas. 2004. Credit Scoring for Risk Managers: The Handbook for Lenders. Mason: Thomson/South-Western Ohio. [Google Scholar]
- Min, Jae H., and Young-Chan Lee. 2005. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Systems With Applications 28: 603–14. [Google Scholar] [CrossRef]
- Mironchyk, Pavel, and Viktor Tchistiakov. 2017. Monotone Optimal Binning Algorithm for Credit Risk Modeling. Utrecht: Working Paper. [Google Scholar]
- Müller, Marlene, and Bernd Rönz. 2000. Credit scoring using semiparametric methods. In Measuring Risk in Complex Stochastic Systems. Berlin and Heidelberg: Springer, pp. 83–97. [Google Scholar]
- Odom, Marcus D., and Ramesh Sharda. 1990. A neural network model for bankruptcy prediction. Paper Presented at 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, June 17–21; pp. 163–68. [Google Scholar]
- Ohlson, James A. 1980. Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research 18: 109–31. [Google Scholar] [CrossRef]
- Park, Cheol-Soo, and Ingoo Han. 2002. A case-based reasoning with the feature weights derived by analytic hierarchy process for bankruptcy prediction. Expert Systems with Applications 23: 255–64. [Google Scholar] [CrossRef]
- Refaat, Mamdouh. 2011. Credit Risk Scorecard: Development and Implementation Using SAS. Available online: Lulu.com (accessed on 15 October 2018).
- Řezáč, Martin, and František Řezáč. 2011. How to measure the quality of credit scoring models. Finance a úvěr: Czech Journal of Economics and Finance 61: 486–507. [Google Scholar]
- Satchel, Stephen, and Wei Xia. 2008. Analytic models of the roc curve: Applications to credit rating model validation. In The Analytics of Risk Model Validation. Amsterdam: Elsevier, pp. 113–33. [Google Scholar]
- Siddiqi, Naeem. 2017. Intelligent Credit Scoring: Building and Implementing Better Credit Risk Scorecards. Hoboken: John Wiley & Sons. [Google Scholar]
- Sinkey, Jr., and Joseph F. 1975. A multivariate statistical analysis of the characteristics of problem banks. The Journal of Finance 30: 21–36. [Google Scholar] [CrossRef]
- Stuhr, David P., and Robert Van Wicklen. 1974. Rating the financial condition of banks: A statistical approach to aid bank supervision. Monthly Review 56: 233–38. [Google Scholar]
- Tam, Kar Yan, and Melody Y. Kiang. 1992. Managerial applications of neural networks: The case of bank failure predictions. Management Science 38: 926–47. [Google Scholar] [CrossRef]
- Thomas, Lyn C., Dabid B. Edelman, and Jonathan N. Crook. 2002. Credit Scoring and Its Applications: Siam Monographs on Mathematical Modeling and Computation. Philadelphia: University City Science Center, SIAM. [Google Scholar]
- Van Gestel, Tony, Bart Baesens, Johan Suykens, Marcelo Espinoza, Dirk-Emma Baestaens, Jan Vanthienen, and Bart De Moor. 2003. Bankruptcy prediction with least squares support vector machine classifiers. Paper presented at 2003 IEEE International Conference on Computational Intelligence for Financial Engineering, Hong Kong, March 20–23; pp. 1–8. [Google Scholar]
- Wilson, Rick L., and Ramesh Sharda. 1994. Bankruptcy prediction using neural networks. Decision Support Systems 11: 545–57. [Google Scholar] [CrossRef]
- Zeng, Guoping. 2013. Metric divergence measures and information value in credit scoring. Journal of Mathematics 2013: 848271. [Google Scholar] [CrossRef]
- Zhang, Guoqiang, Michael Y. Hu, B. Eddy Patuwo, and Daniel C. Indro. 1999. Artificial neural networks in bankruptcy prediction: General framework and cross-validation analysis. European Journal of Operational Research 116: 16–32. [Google Scholar] [CrossRef]
| 1. | The list of the ECB templates is available at https://www.ecb.europa.eu/paym/coll/loanlevel/transmission/html/index.en.html. |
| 2. | The ECB and the national central banks of the Eurosystem have been lending unlimited amounts of capital to the bank system as a response to the financial crisis. For more information see: https://www.ecb.europa.eu/explainers/tell-me-more/html/excess_liquidity.en.html. |
| 3. | A default shall be considered to have occurred with regard to a particular obligor when either or both of the following have taken place: (a) the institution considers that the obligor is unlikely to pay its credit obligations to the institution, the parent undertaking or any of its subsidiaries in full, without recourse by the institution to actions such as realising security; (b) the obligor is past due more than 90 days on any material credit obligation to the institution, the parent undertaking or any of its subsidiaries. Relevant authorities may replace the 90 days with 180 days for exposures secured by residential or SME commercial real estate in the retail exposure class (as well as exposures to public sector entities). |
| 4. | CRIF Ratings is an Italian credit rating agency authorized to assign ratings to non-financial companies based in the European Union. The agency is subject to supervision by the ESMA (European Securities and Markets Authority) and has been recognized as an ECAI (External Credit Assessment Institution). |
| 5. | The complete list of fields definitions and criteria can be found at https://www.ecb.europa.eu/paym/coll/loanlevel/shared/files/RMBS_Taxonomy.zip?bc2bf6081ec990e724c34c634cf36f20. |
| 6. | The Credit Risk Plus model assumes independence between default events. Therefore, the probability generating function for the whole portfolio corresponds to the product of the individual probability generating functions. |
| 7. | The approximation ignores terms of degree 2 and higher in the default probabilities. The expression derived from this approximation is exact in the limit as the PD tends to zero, and five good approximations in practice. |
| 8. |
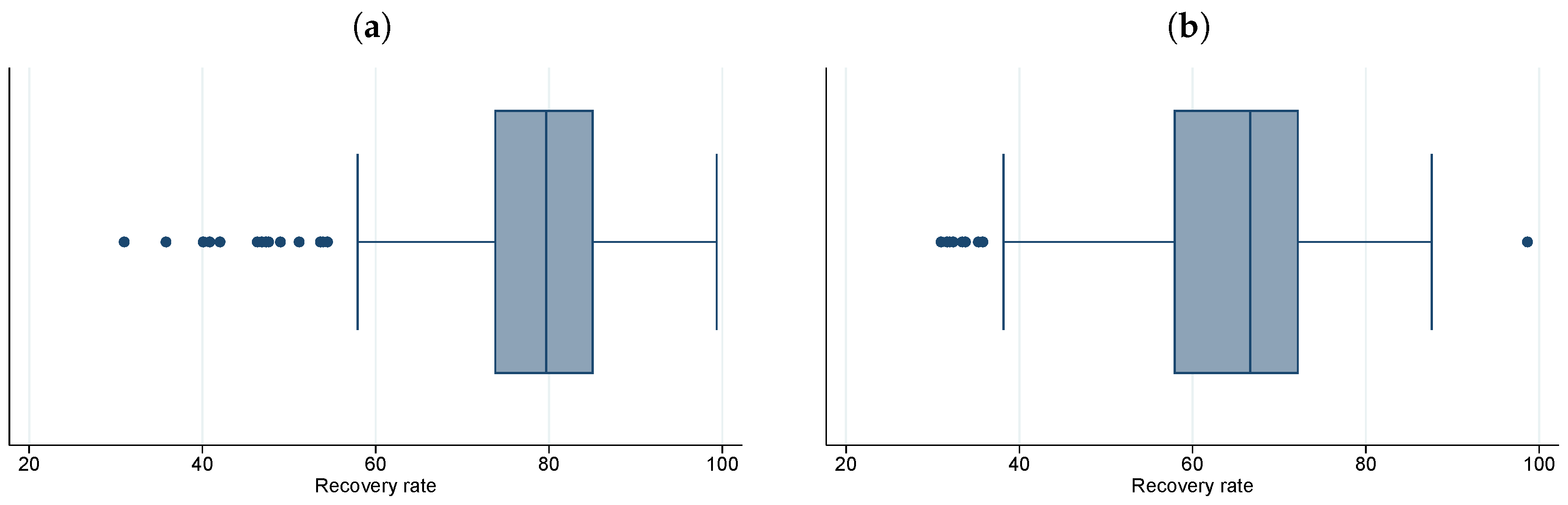
| Pool Cut-Off Date | Non-Defaulted | Defaulted | % Default | Tot. |
|---|---|---|---|---|
| 2014H1 | 31930 | 904 | 2.75 | 32834 |
| 2014H2 | 26851 | 813 | 2.94 | 27664 |
| 2015H1 | 21724 | 679 | 3.03 | 22403 |
| 2015H2 | 12651 | 372 | 2.86 | 13023 |
| 2016H1 | 10076 | 257 | 2.49 | 10333 |
| Tot. | 103232 | 3025 | 2.84 | 106257 |
| Pool Cut-Off Date | Collateral Database | Loan Database | Borrower Database |
|---|---|---|---|
| 2014H1 | 53,418 | 36,812 | 32,834 |
| 2014H2 | 45,694 | 30,774 | 27,664 |
| 2015H1 | 34,583 | 24,640 | 22,403 |
| 2015H2 | 14,472 | 14,000 | 13,023 |
| 2016H1 | 11,474 | 11,100 | 10,333 |
| Tot. | 159,641 | 117,326 | 106,257 |
| Variable | 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 |
|---|---|---|---|---|---|
| Interest Rate Index | 0.04 | 0.08 | 0.01 | 0.00 | 0.00 |
| Business Type | 0.02 | 0.05 | 0.02 | 0.03 | 0.02 |
| Basel Segment | 0.00 | 0.01 | 0.00 | 0.00 | 0.01 |
| Seniority | 0.09 | 0.08 | 0.02 | 0.12 | 0.29 |
| Interest Rate Type | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Nace Code | 0.05 | 0.01 | 0.01 | 0.01 | 0.07 |
| Number of Collateral | 0.00 | 0.00 | 0.03 | 0.00 | 0.00 |
| Weighted Average Life | 0.26 | 0.27 | 0.22 | 0.16 | 0.37 |
| Maturity | 0.00 | 0.08 | 0.00 | 0.08 | 0.00 |
| Payment ratio | 0.11 | 0.08 | 0.14 | 0.09 | 0.10 |
| Loan To Value | 0.10 | 0.08 | 0.07 | 0.06 | 0.11 |
| Geographic Region | 0.01 | 0.00 | 0.02 | 0.01 | 0.03 |
| LoanToValue 2015H1 | Non-Defaulted | Defaulted | Probability | WOE |
|---|---|---|---|---|
| 0–0.285 | 3383 | 67 | 50.49 | 0.35 |
| 0.285–0.333 | 1523 | 31 | 49.12 | 0.33 |
| 0.333–0.608 | 3531 | 89 | 39.67 | 0.11 |
| 0.608–0.769 | 3357 | 95 | 35.33 | 0.002 |
| 0.769–1 | 2074 | 77 | 26.93 | −0.26 |
| 1–inf | 2904 | 117 | 24.82 | −0.35 |
| Tot. | 16772 | 476 | 35.23 |
| Variable | 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 |
|---|---|---|---|---|---|
| Coefficient | Coefficient | Coefficient | Coefficient | Coefficient | |
| (int.) | 3.550 *** | 3.481 *** | 3.456 *** | 3.523 *** | 3.652 *** |
| InterestRateIndex | 0.698 *** | ||||
| Seniority | 1.489 *** | 1.493 *** | 0.598 | 1.325 *** | 0.944 *** |
| Code_Nace | 1.048 *** | 0.952 *** | 0.798 ** | 0.927 ** | 0.947 *** |
| WeightedAverageLife | 1.007 *** | 0.953 *** | 1.168 *** | 0.912 *** | 0.798 *** |
| Payment_Ratio | 2.456 *** | 2.296 *** | 1.482 *** | 2.300 *** | 2.253 *** |
| Geographic_Region | 1.675 *** | 1.405 *** | 1.432 *** | 0.903 *** | |
| Observations | 32834 | 27664 | 22403 | 13023 | 10333 |
| Chi2-statistic vs. constant model | 670 | 541 | 373 | 190 | 222 |
| p-value | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| Statistics | 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 |
|---|---|---|---|---|---|
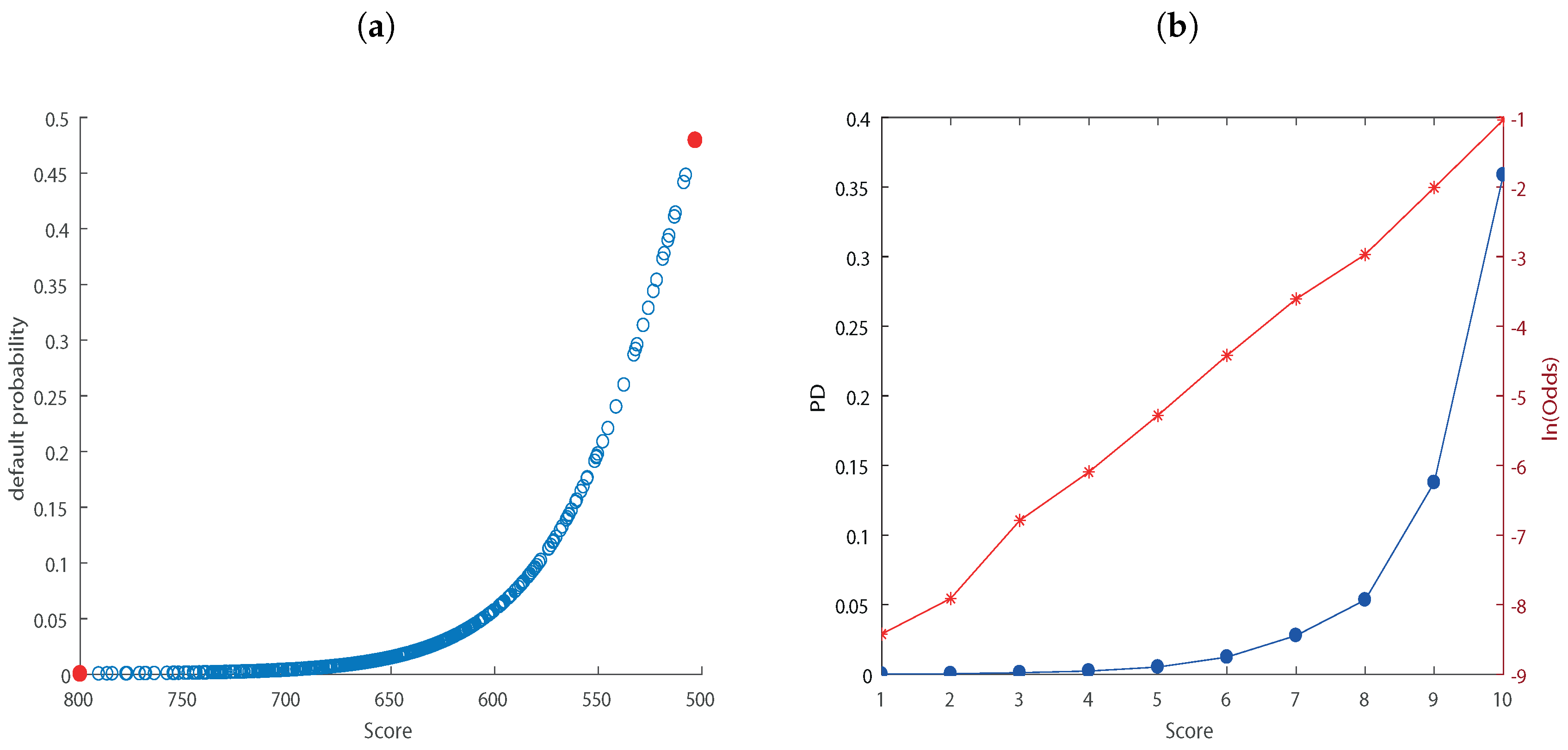
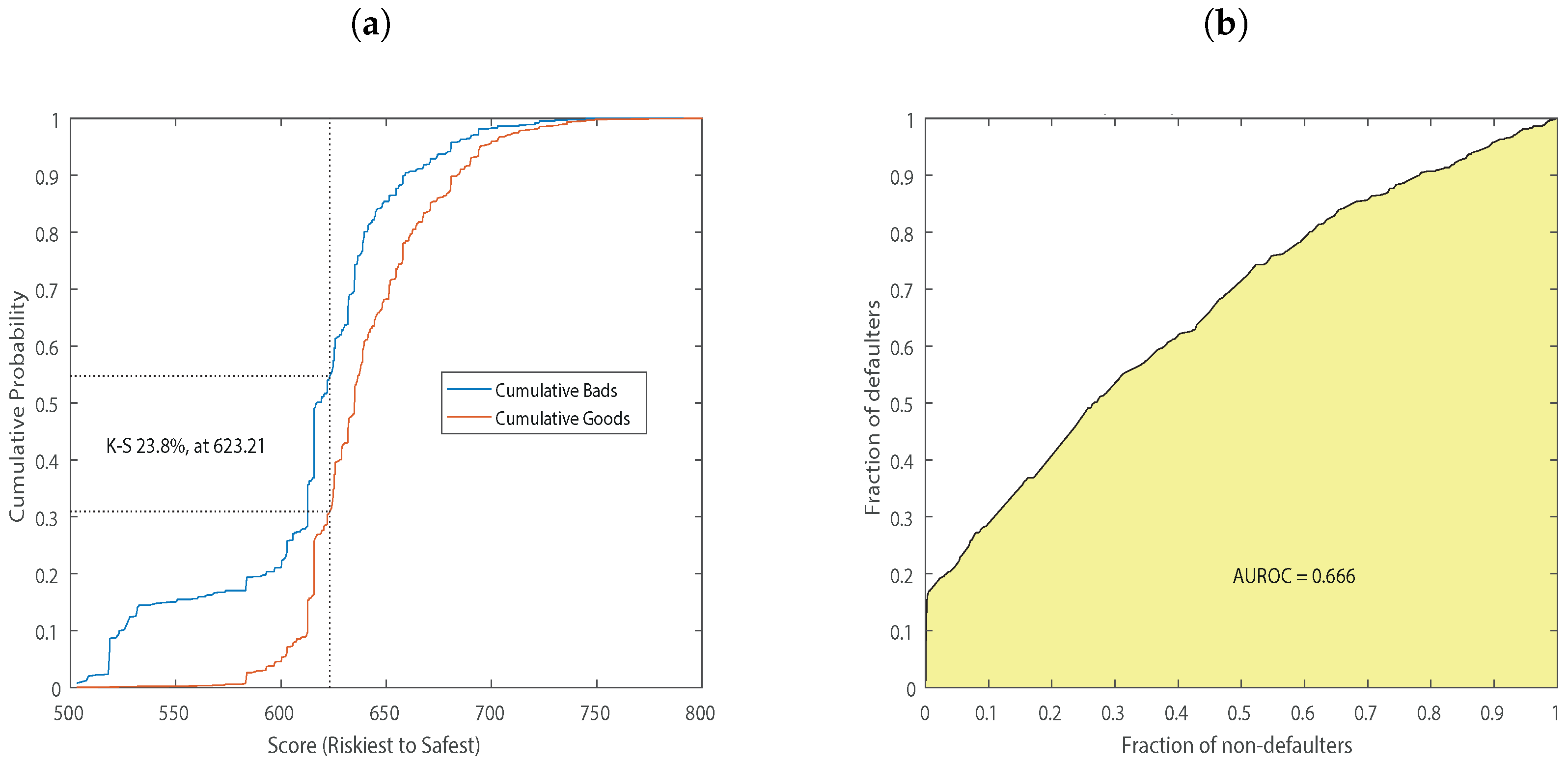
| Area under ROC curve | 0.66 | 0.62 | 0.62 | 0.60 | 0.68 |
| KS statistic | 0.23 | 0.18 | 0.18 | 0.15 | 0.27 |
| KS score | 623.21 | 621.4 | 636.43 | 545.84 | 632.18 |
| Statistics | 2014H1 | 2014H2 | 2015H1 | 2015H2 | 2016H1 |
|---|---|---|---|---|---|
| Area under ROC curve | 0.68 | 0.62 | 0.62 | 0.63 | 0.68 |
| KS statistic | 0.27 | 0.17 | 0.17 | 0.18 | 0.27 |
| KS score | 610.76 | 654.45 | 662.80 | 673.09 | 628.56 |
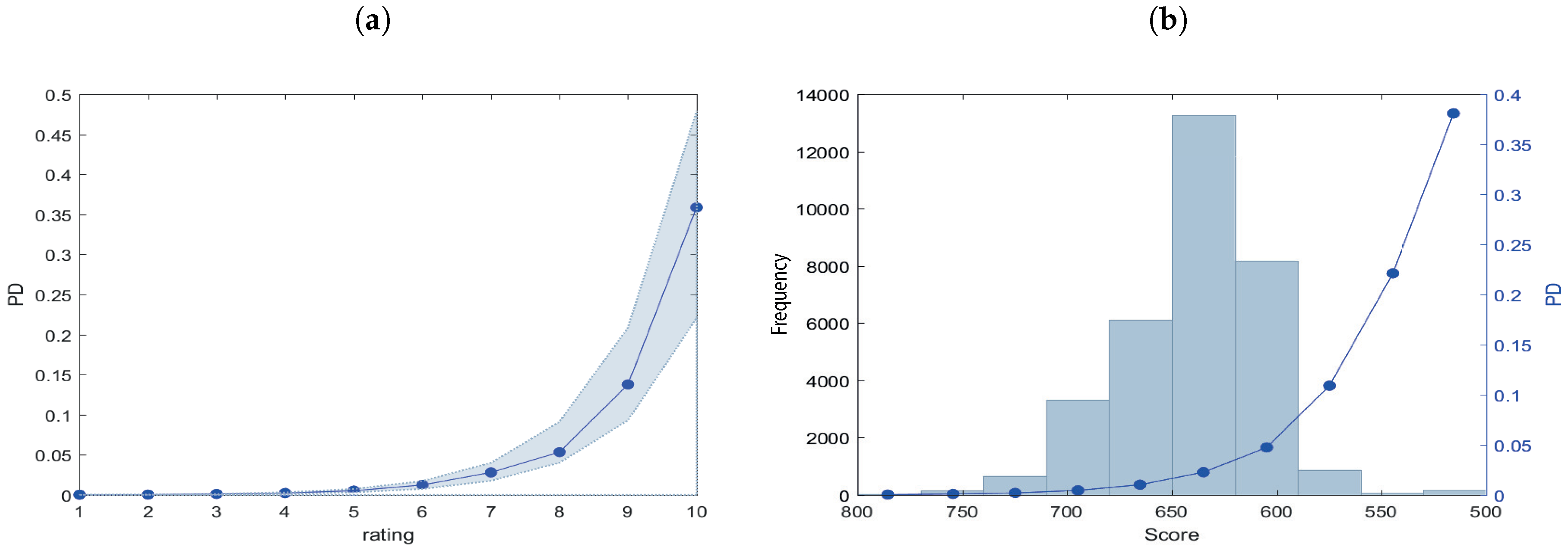
| Rating 2014H1 | Non-Defaulted | Defaulted | pd_actual (%) | Total | pd_estimate | pd_actual | |
|---|---|---|---|---|---|---|---|
| A | 4 | 0 | 0.00 | 4 | A | 0.02 | 0.00 |
| B | 30 | 0 | 0.00 | 30 | B | 0.04 | 0.00 |
| C | 298 | 3 | 1.00 | 301 | C | 0.11 | 1.00 |
| D | 707 | 9 | 1.26 | 716 | D | 0.23 | 1.26 |
| E | 3452 | 46 | 1.32 | 3498 | E | 0.52 | 1.32 |
| F | 7169 | 103 | 1.42 | 7272 | F | 1.23 | 1.42 |
| G | 15264 | 415 | 2.65 | 15679 | G | 2.78 | 2.65 |
| H | 4810 | 174 | 3.49 | 4984 | H | 5.34 | 3.49 |
| I | 134 | 19 | 12.42 | 153 | I | 13.77 | 12.42 |
| L | 62 | 135 | 68.53 | 197 | L | 35.87 | 68.53 |
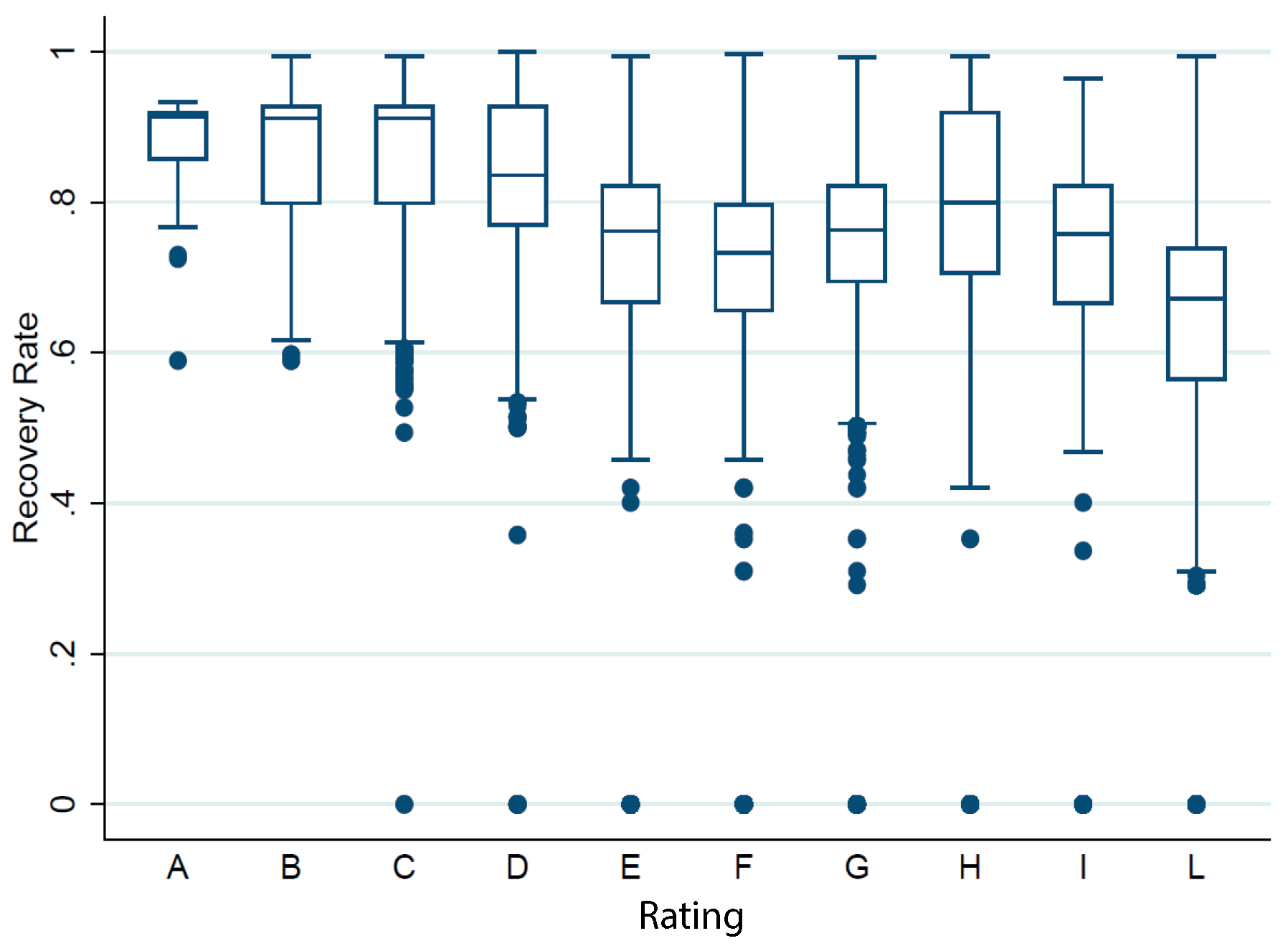
| Rating | Average Recovery Rate (%) |
|---|---|
| A | 87.5 |
| B | 86.6 |
| C | 86.7 |
| D | 83.8 |
| E | 75.6 |
| F | 72.5 |
| G | 75.7 |
| H | 77.4 |
| I | 70.3 |
| L | 62.5 |
| Rating | Estimate | Frequency | ||
|---|---|---|---|---|
| Mean (%) | st.dev (%) | Mean (%) | st.dev (%) | |
| A | 0.27 | 0.26 | 0.19 | 0.38 |
| B | 0.43 | 0.41 | 0.94 | 0.77 |
| C | 0.74 | 0.64 | 1.54 | 0.45 |
| D | 1.15 | 0.92 | 1.85 | 0.79 |
| E | 2.06 | 1.51 | 1.83 | 0.55 |
| F | 3.15 | 1.94 | 2.25 | 0.55 |
| G | 5.43 | 2.52 | 3.02 | 0.98 |
| H | 8.70 | 3.15 | 2.51 | 1.42 |
| I | 17.45 | 4.41 | 26.57 | 21.84 |
| L | 33.93 | 4.02 | 68.96 | 8.61 |
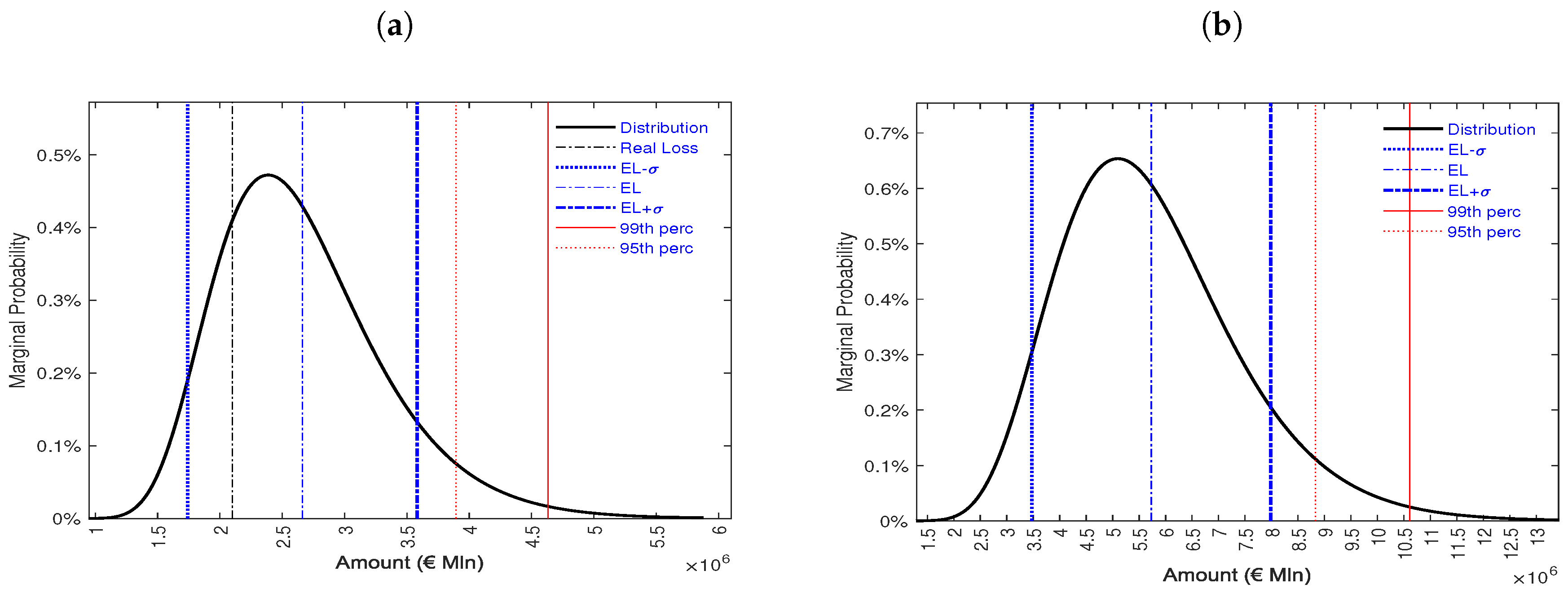
| Threshold | Amount (€) | Percentage (%) |
|---|---|---|
| Capital exposed to risk | 48922828 | 100.00 |
| EL − | 1991170 | 4.07 |
| EL | 2661592 | 5.44 |
| EL + | 3332014 | 6.81 |
| 95th percentile | 3894574 | 7.96 |
| 99th percentile | 4630839 | 9.46 |
| Threshold | Amount (€) | Percentage (%) |
|---|---|---|
| Capital exposed to risk | 247841024 | 100.00 |
| EL − | 4026790 | 1.62 |
| EL | 5729076 | 2.31 |
| EL + | 7431362 | 2.99 |
| 95th percentile | 8828005 | 3.56 |
| 99th percentile | 10608768 | 4.28 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bedin, A.; Billio, M.; Costola, M.; Pelizzon, L. Credit Scoring in SME Asset-Backed Securities: An Italian Case Study. J. Risk Financial Manag. 2019, 12, 89. https://doi.org/10.3390/jrfm12020089
Bedin A, Billio M, Costola M, Pelizzon L. Credit Scoring in SME Asset-Backed Securities: An Italian Case Study. Journal of Risk and Financial Management. 2019; 12(2):89. https://doi.org/10.3390/jrfm12020089
Chicago/Turabian StyleBedin, Andrea, Monica Billio, Michele Costola, and Loriana Pelizzon. 2019. "Credit Scoring in SME Asset-Backed Securities: An Italian Case Study" Journal of Risk and Financial Management 12, no. 2: 89. https://doi.org/10.3390/jrfm12020089
APA StyleBedin, A., Billio, M., Costola, M., & Pelizzon, L. (2019). Credit Scoring in SME Asset-Backed Securities: An Italian Case Study. Journal of Risk and Financial Management, 12(2), 89. https://doi.org/10.3390/jrfm12020089






