Multi-Period Investment Strategies under Cumulative Prospect Theory
Abstract
1. Introduction
2. The Model
2.1. The Benchmarked Wealth
Examples of the Benchmark
2.2. Portfolio Constraints
2.3. The CPT Risk Criterion
- (i)
- (ii)
- (iii)
- with and
- (iv)
- with and
3. Methodology
3.1. Single Period Objective
3.2. Multiple Period Objective
3.3. Time Inconsistency
3.4. Results
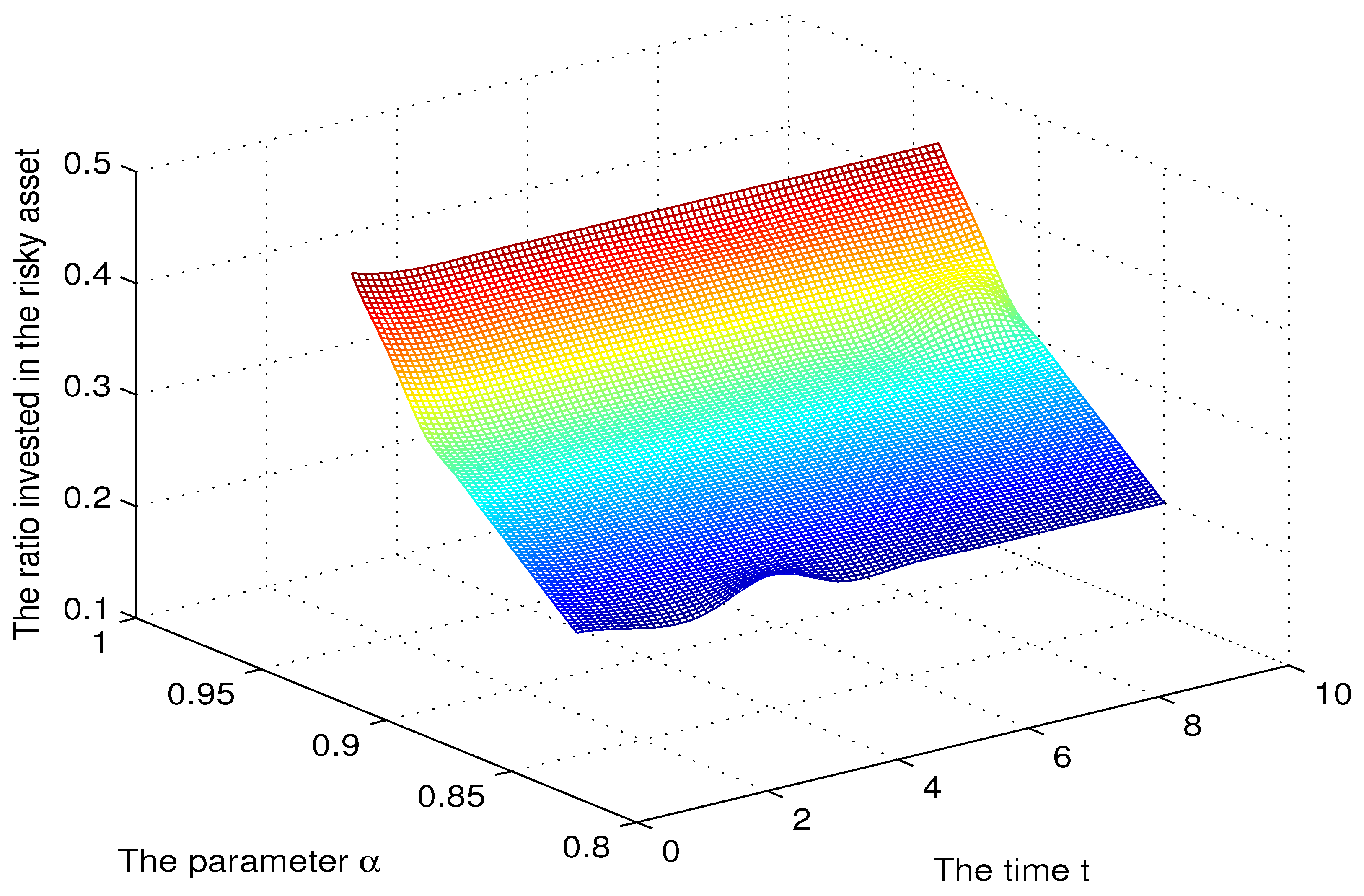
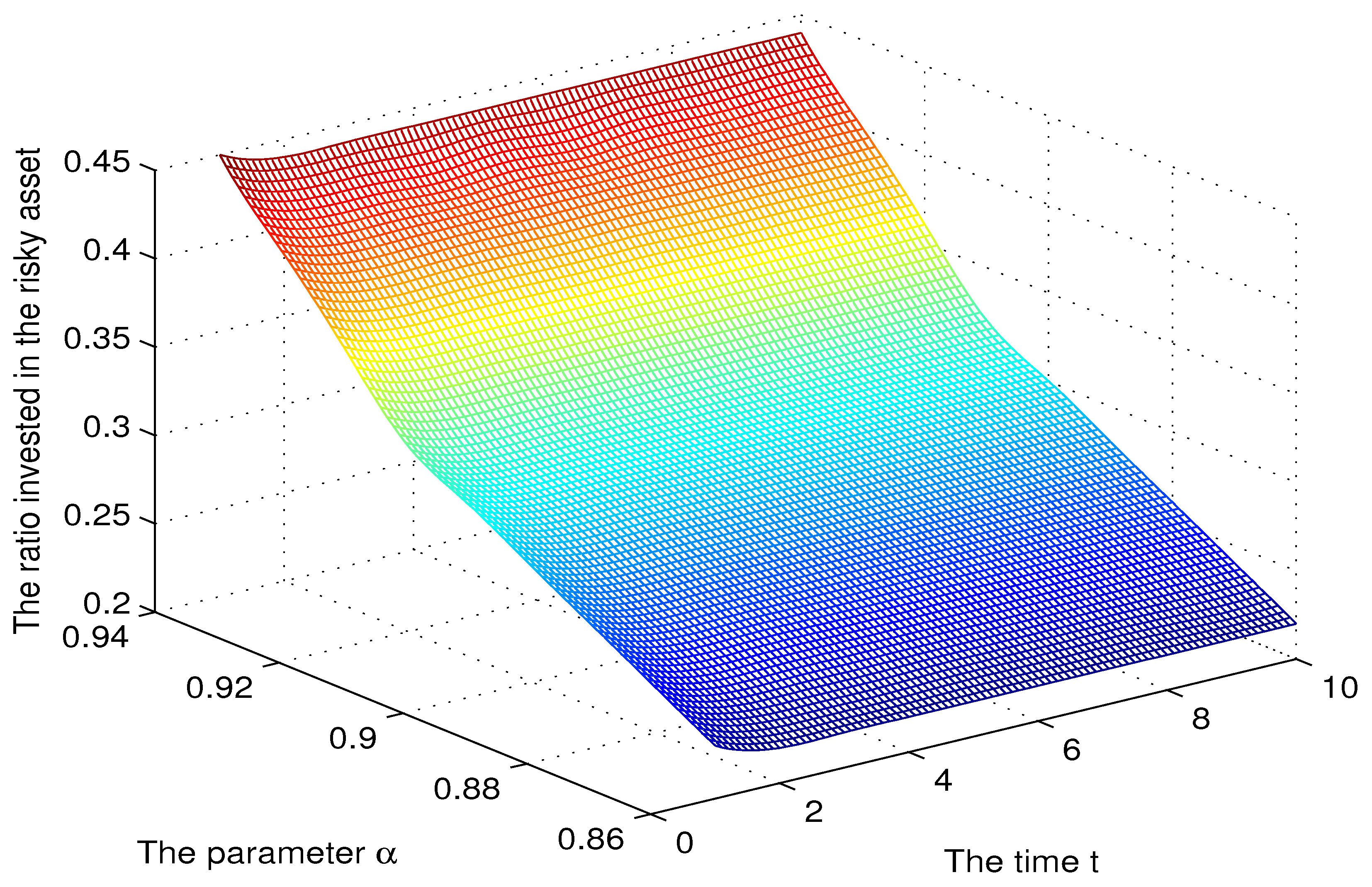
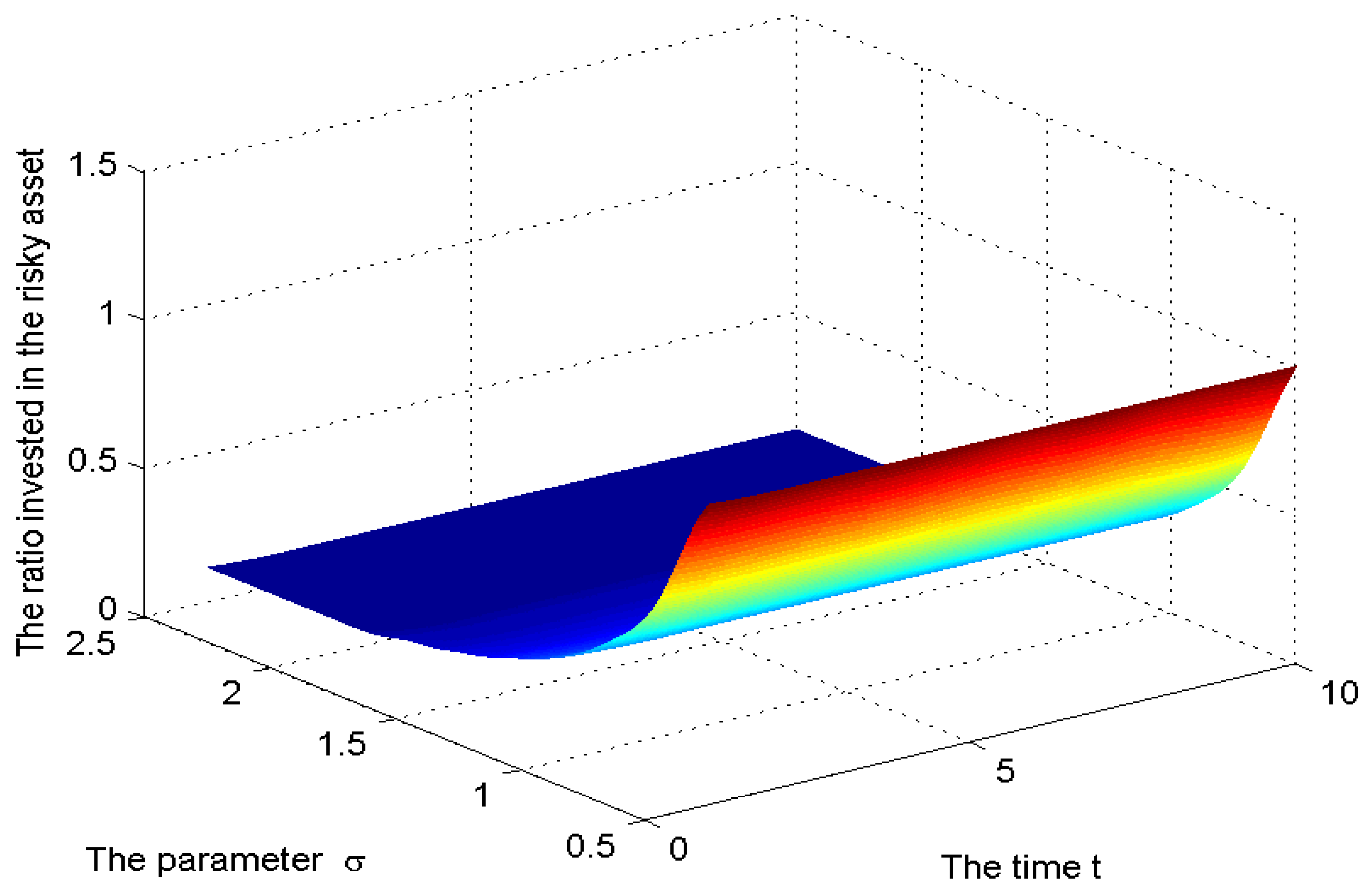
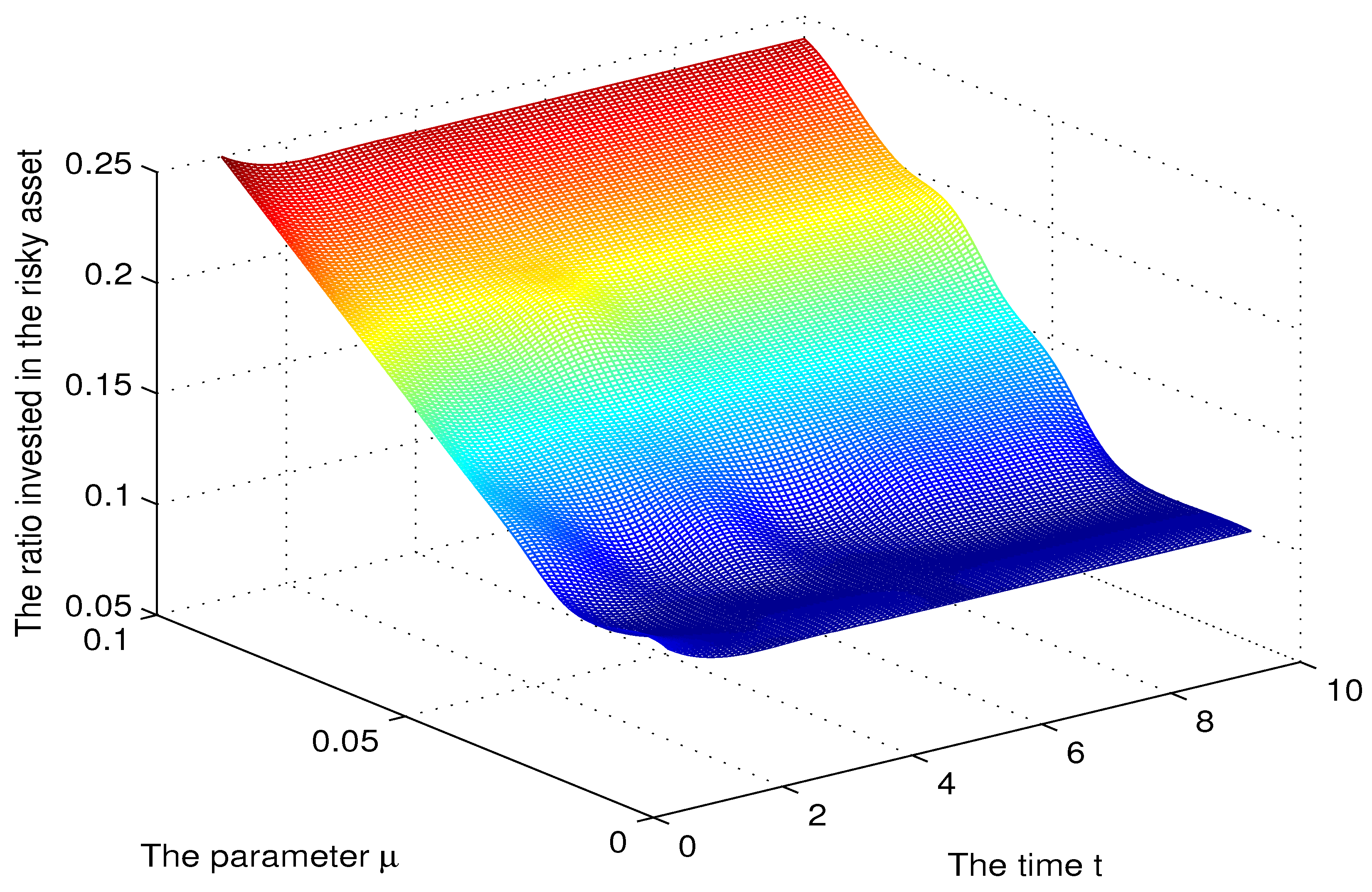
3.5. Numerical Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Proof of Proposition 2
Appendix C. Proof of Proposition 3
References
- Bernard, Carole, and Mario Ghossoub. 2010. Static Portfolio Choice under Cumulative Prospect Theory. Mathematics and Financial Economics 2: 277–306. [Google Scholar] [CrossRef]
- Carassus, Laurence, and Miklos Rasonyi. 2015. On optimal investment for a behavioural investor in multi-period incomplete market models. Math. Finance 25: 115–53. [Google Scholar] [CrossRef]
- Chateauneuf, Alain, Rose-Anne Dana, and Jean-Marc Tallon. 2000. Optimal risk-sharing rules and equilibria with Choquet-expected-utility. Journal of Mathematical Economics 34: 191–214. [Google Scholar] [CrossRef]
- Choquet, Gustave. 1953. Theory of capacities. Annales de l’Institut Fourier 5: 131–295. [Google Scholar] [CrossRef]
- Da, Zhi, and Pengjie Gao. 2009. Clientele Change, Persistent Liquidity Shock, and Bond Return Reversals after Rating Downgrades. SSRN. [Google Scholar] [CrossRef]
- Garcia, Fernando, Francisco Guijarro, Javier Oliver, and Rima Tamosiuniene. 2018. Hybrid fuzzy neural network to predict price direction in the German DAX-30 index. Technological and Economic Development of Economy 24: 2161–78. [Google Scholar] [CrossRef]
- Gregoriou, Greg N. 2011. Handbook of Short Selling, 1st ed.Waltham: Academic Press, eBook ISBN 9780123877253, Hardcover ISBN 9780123877246. [Google Scholar]
- Guijarro, Francisco. 2018. A similarity measure for the cardinality constrained frontier in the mean–variance optimization model. Journal of the Operational Research Society 69: 928–45. [Google Scholar] [CrossRef]
- He, Xue Dong, and Xun Yu Zhou. 2011a. Portfolio Choice under Cumulative Prospect Theory: An Analytical Treatment. Management Science 57: 315–31. [Google Scholar] [CrossRef]
- He, Xue Dong, and Xun Yu Zhou. 2011b. Portfolio Choice via Quantiles. Mathematical Finance 21: 203–31. [Google Scholar] [CrossRef]
- Ingersoll, Jonathan. 2008. Non-monotonicity of the Tversky Kahneman probability-weighting function: A cautionary note. European Financial Management 14: 385–90. [Google Scholar] [CrossRef]
- Ishimura, Naoyuki, Bold Javkhlan, MasaAki Nakamura, and Zheng Wei. 2013. Models of the Short Interest Rate in Discrete Processes. Open Journal of Applied Sciences 3: 12–14. [Google Scholar] [CrossRef]
- Jin, Hanqing, and Xun Yu Zhou. 2008. Behavioral portfolio selection in continuous time. Mathematical Finance 18: 385–426. [Google Scholar] [CrossRef]
- Kwak, Minsuk, and Traian A. Pirvu. 2018. Cumulative Prospect Theory with Skewed Return Distribution. SIAM Journal on Financial Mathematics 9: 54–89. [Google Scholar] [CrossRef]
- Kwak, Minsuk, Traian A. Pirvu, and Huayue Zhang. 2014. A multi-period equilibrium pricing model. Journal of Applied Mathematics 2014: 408685. [Google Scholar] [CrossRef]
- Li, Duan, and Wan-Lung Ng. 2000. Optimal dynamic portfolio selection: Multiperiod mean-variance formulation. Mathematical Finance 3: 387–406. [Google Scholar] [CrossRef]
- Pirvu, Traian A., and Klaas Schulze. 2012. Multi-stock portfolio optimization under prospect theory. Mathematics and Financial Economics 6: 337–62. [Google Scholar] [CrossRef]
- Pirvu, Traian A., and Huayue Zhang. 2013. Utility indifference pricing: A time consistent approach. Applied Mathematical Finance 20: 304–26. [Google Scholar] [CrossRef]
- Shi, Yun, Xiangyu Cui, and Duan Li. 2015. Discrete-time behavioural portfolio selection under prospect theory. Journal of Economic Dynamics and Control 61: 283–302. [Google Scholar] [CrossRef]
- Strub, Moris, and Duan Li. 2017. Does Reference Point Updating Lead to Time-Inconsistent Investment? SSRN. [Google Scholar] [CrossRef]
- Tversky, Amos, and Daniel Kahneman. 1979. Prospect theory: An analysis of decision under rick. Econometrica 47: 262–91. [Google Scholar]
- Tversky, Amos, and Daniel Kahneman. 1992. Advances in prospect theory: Cumulative representation of uncertainty. Journal of Risk and Uncertainty 5: 297–323. [Google Scholar] [CrossRef]
| 1 | This assumption is made to render the portfolio problem tractable. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, L.; Pirvu, T.A. Multi-Period Investment Strategies under Cumulative Prospect Theory. J. Risk Financial Manag. 2019, 12, 83. https://doi.org/10.3390/jrfm12020083
Deng L, Pirvu TA. Multi-Period Investment Strategies under Cumulative Prospect Theory. Journal of Risk and Financial Management. 2019; 12(2):83. https://doi.org/10.3390/jrfm12020083
Chicago/Turabian StyleDeng, Liurui, and Traian A. Pirvu. 2019. "Multi-Period Investment Strategies under Cumulative Prospect Theory" Journal of Risk and Financial Management 12, no. 2: 83. https://doi.org/10.3390/jrfm12020083
APA StyleDeng, L., & Pirvu, T. A. (2019). Multi-Period Investment Strategies under Cumulative Prospect Theory. Journal of Risk and Financial Management, 12(2), 83. https://doi.org/10.3390/jrfm12020083





