Equalizing Seasonal Time Series Using Artificial Neural Networks in Predicting the Euro–Yuan Exchange Rate
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
- An independent variable was time (it is a time trend). A dependent variable was the Euro and Chinese Yuan exchange rate.
- A continuous independent variable was time. Seasonal fluctuation was represented by a categorical variable in the form of the year, month, day in the month, and day in the week in which the value was measured. Each variable were examined separately. We thus worked with the possible daily, monthly, and annual seasonal fluctuations of the time series. A dependent variable was the Euro and Chinese Yuan exchange rate.
- Linear,
- Logistic,
- Atanh,
- Exponential,
- Sinus.
4. Results
4.1. Neural Structures A
4.2. Neural Structures B
4.3. Comparising Results of A and B
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baptista, Dario, Sandy Abreu, Fillipe Freitas, Rita Vasconcelos, and Fernando Morgado-Dias. 2013. A survey of software and hardware use in artificial neural networks. Neural Computing and Applications 23: 591–99. [Google Scholar] [CrossRef]
- Cai, Zongwu, Linna Chen, and Ying Fang. 2012. A New Forecasting Model for USD/CNY Exchange Rate. Studies in Nonlinear Dynamics & Econometrics 16: 1–18. [Google Scholar] [CrossRef]
- Chen, An-Sing, and Mark T. Leung. 2005. Performance evaluation of neural network architectures: the case of predicting foreign exchange correlations. Journal of Forecasting 24: 403–20. [Google Scholar] [CrossRef]
- Chen, Pin-Chang, Chih-Yao Lo, and Hung-Teng Chang. 2009. An Empirical Study of the Artificial Neural Network for Currency Exchange Rate Time Series Prediction. Paper presented at Sixth International Symposium on Neural Networks, Wuhan, China, May 26–29; pp. 543–49. [Google Scholar]
- Clements, Kenneth, Yihui Lan, and Jiawei Si. 2018. Uncertainty in currency mispricing. Applied Economics 50: 2297–312. [Google Scholar] [CrossRef]
- Falát, Lukas, Zuzana Staníková, Mária Ďurišová, Beata Holková, and Tatiana Potkanová. 2015. Application of Neural Network Models in Modelling Economic Time Series with Non-constant Volatility. Paper presented at International Scientific Conference: Business Economics and Management, Izmir, Turkey, April 28–30; pp. 600–7. [Google Scholar] [CrossRef]
- Galeshchuk, Svitlana, and Sumitra Mukherjee. 2017. Deep networks for predicting direction of change in foreign exchange rates. Intelligent Systems in Accounting Finance & Management 24: 100–10. [Google Scholar] [CrossRef]
- Jebran, Khalil, and Amjad Iqbal. 2016. Dynamics of volatility spillover between stock market and foreign Exchange market: Evidence from Asian Countries. Financial Innovation 2. [Google Scholar] [CrossRef]
- Kearney, Fearghal, Mark Cummins, and Finbarr Murphy. 2016. Forecasting implied volatility in foreign exchange markets: A functional time series approach. The European Journal of Finance 24: 1–18. [Google Scholar] [CrossRef]
- Klieštik, Tomáš. 2013. Models of autoregression conditional heteroskedasticity garch and arch as a tool for modeling the volatility of financial time series. Ekonomicko-manažerské spektrum 7: 2–10. [Google Scholar]
- Liu, Zhaocheng, Ziran Zheng, Xiyu Liu, and Gongxi Wang. 2009. Modelling and Prediction of the CNY Exchange Rate Using RBF Neural Network. Paper presented at 2009 International Conference on Business Intelligence and Financial Engineering, Beijing, China, July 24–26; pp. 38–41. [Google Scholar] [CrossRef]
- Mai, Yong, Huan Chen, Jun-Zhong Zou, and Sai-Ping Li. 2018. Currency co-movement and network correlation structure of foreign Exchange market. Physica A-Statistical Mechanics and its Applications 492: 65–74. [Google Scholar] [CrossRef]
- Martinovic, Marko, Zeljko Pozega, and Boris Crnkovic. 2017. Analysis of Time Series for the Currency Pair Croatian Kuna/Euro. Ekonomski Vjesnik 30: 37–49. [Google Scholar]
- Milovanovic, Miroslav, Dragan Antic, Marko Milojkovic, Sasa S. Nikolic, Miodrag Spasic, and Stanisa Peric. 2017. Time Series Forecasting with Orthogonal Endocrine Neural Network Based on Postsynaptic Potentials. Journal of Dynamic Systems, Measurement, and Control 139. [Google Scholar] [CrossRef]
- Nag, Ashok, and Amit Mitra. 2002. Forecasting daily foreign exchange rates using genetically optimized neural networks. Journal of Forecasting 21: 501–11. [Google Scholar] [CrossRef]
- Pradeepkumar, Dadabada, and Vadlamani Ravi. 2018. Soft computing hybrids for FOREX rate prediction: A comprehensive review. Computers & Operations Research 99: 262–84. [Google Scholar] [CrossRef]
- Rodrigues, Fillipe, Ioulia Markou, and Francisco C. Pereira. 2019. Combining time-series and textual data for taxi demand prediction in event areas: A deep learning approach. Information Fusion 49: 120–29. [Google Scholar] [CrossRef]
- Rostan, Pierre, and Alexandra Rostan. 2018. The versatility of spectrum analysis for forecasting financial time series. Journal of Forecasting 37: 327–39. [Google Scholar] [CrossRef]
- Rowland, Zuzana, and Jaromír Vrbka. 2016. Using artificial neural networks for prediction of key indicators of a company in global world. Paper presented at 16th International Scientific Conference on Globalization and its Socio-Economic Consequences, Rajecke Teplice, Slovakia, October 5–6; pp. 1896–1903. [Google Scholar]
- Shen, Furao, Jing Chao, and Jinxi Zhao. 2015. Forecasting exchange rate using deep belief networks and conjugate gradient method. Neurocomputing 167: 243–53. [Google Scholar] [CrossRef]
- Veselý, Arnost. 2011. Economic classification and regression problems and neural networks. Agricultural Economics - Zemedelska Ekonomika 57: 150–57. [Google Scholar] [CrossRef]
- Vochozka, Marek, and Jaromír Vrbka. 2019. Estimation of the development of the Euro to Chinese Yuan exchange rate using artificial neural networks. Paper presented at Innovative Economic Symposium 2018—SHS Web of Conferences, Beijing, China, November 8–9. [Google Scholar] [CrossRef]
- Vrbka, Jaromír, and Zuzana Rowland. 2017. Stock price development forecasting using neural networks. Paper presented at Innovative Economic Symposium 2017—SHS Web of Conferences, Ceske Budejovice, Czech Republic, October 19; p. 39. [Google Scholar] [CrossRef]
- Wang, Yimo, and Yonghua Yang. 2016. Analysis on the Impact of RMB Exchange Rates on Manufacturing Trade between China and EU Zone. Paper presented at 2016 2nd International konference on humanities and social Science Research, Singapore, July 29–31; pp. 42–45. [Google Scholar] [CrossRef]
- World Bank. 2018. Available online: https://www.worldbank.org/ (accessed on 9 February 2019).
- Zhang, Yan-Qing, and Xuhui Wan. 2007. Statistical fuzzy interval neural networks for currency exchange rate time series prediction. Applied Soft Computing 7: 1149–56. [Google Scholar] [CrossRef]
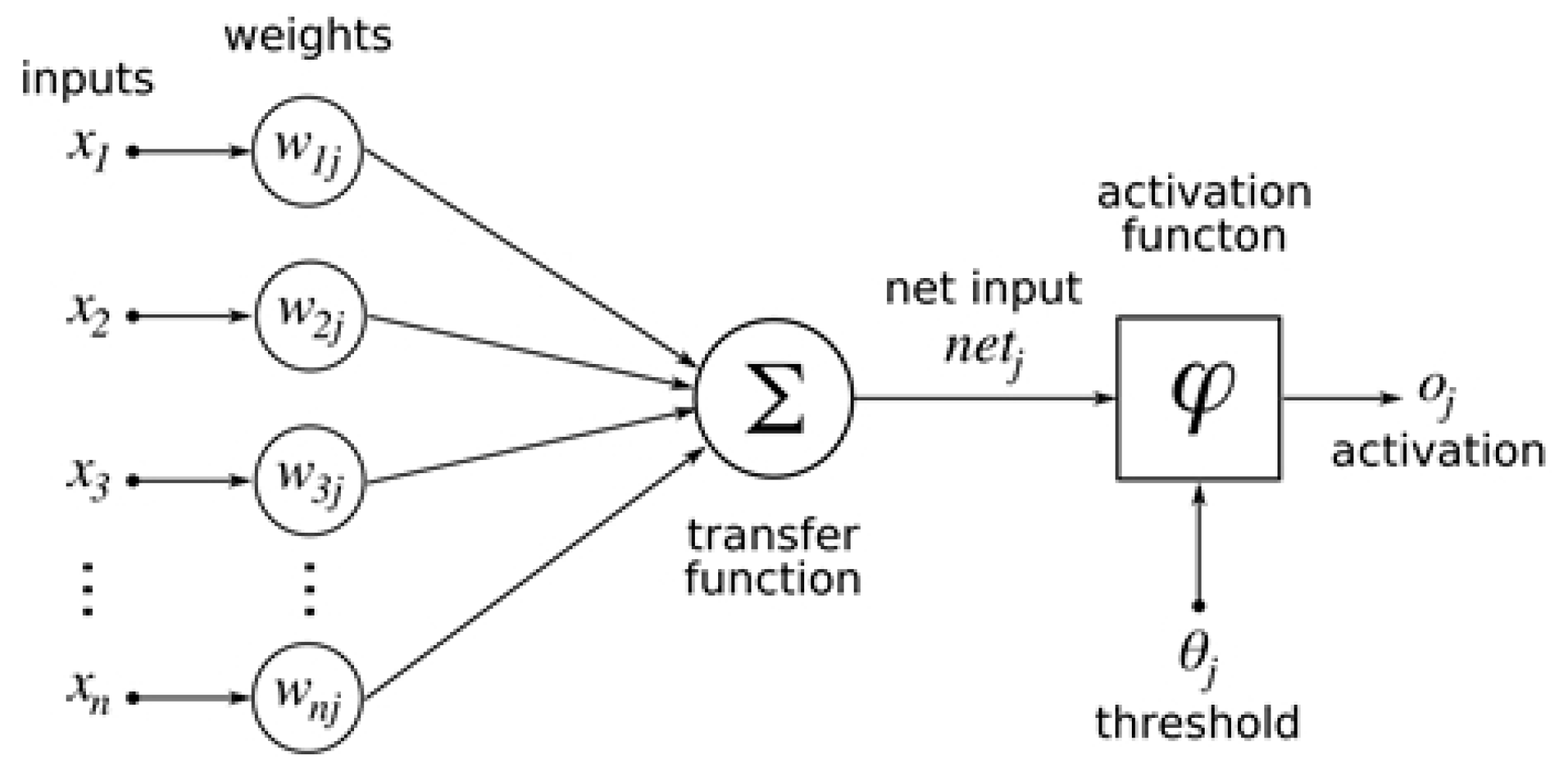
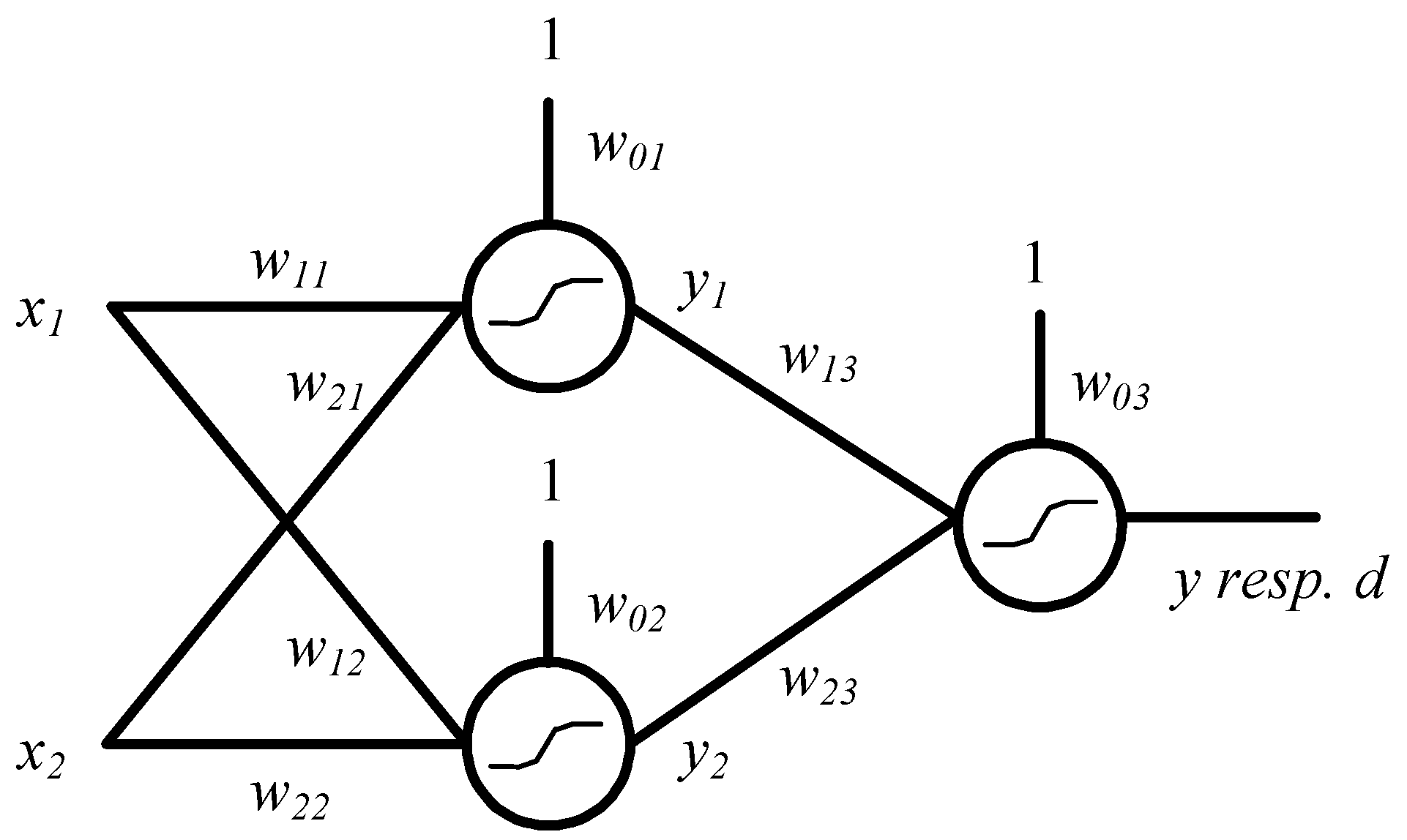
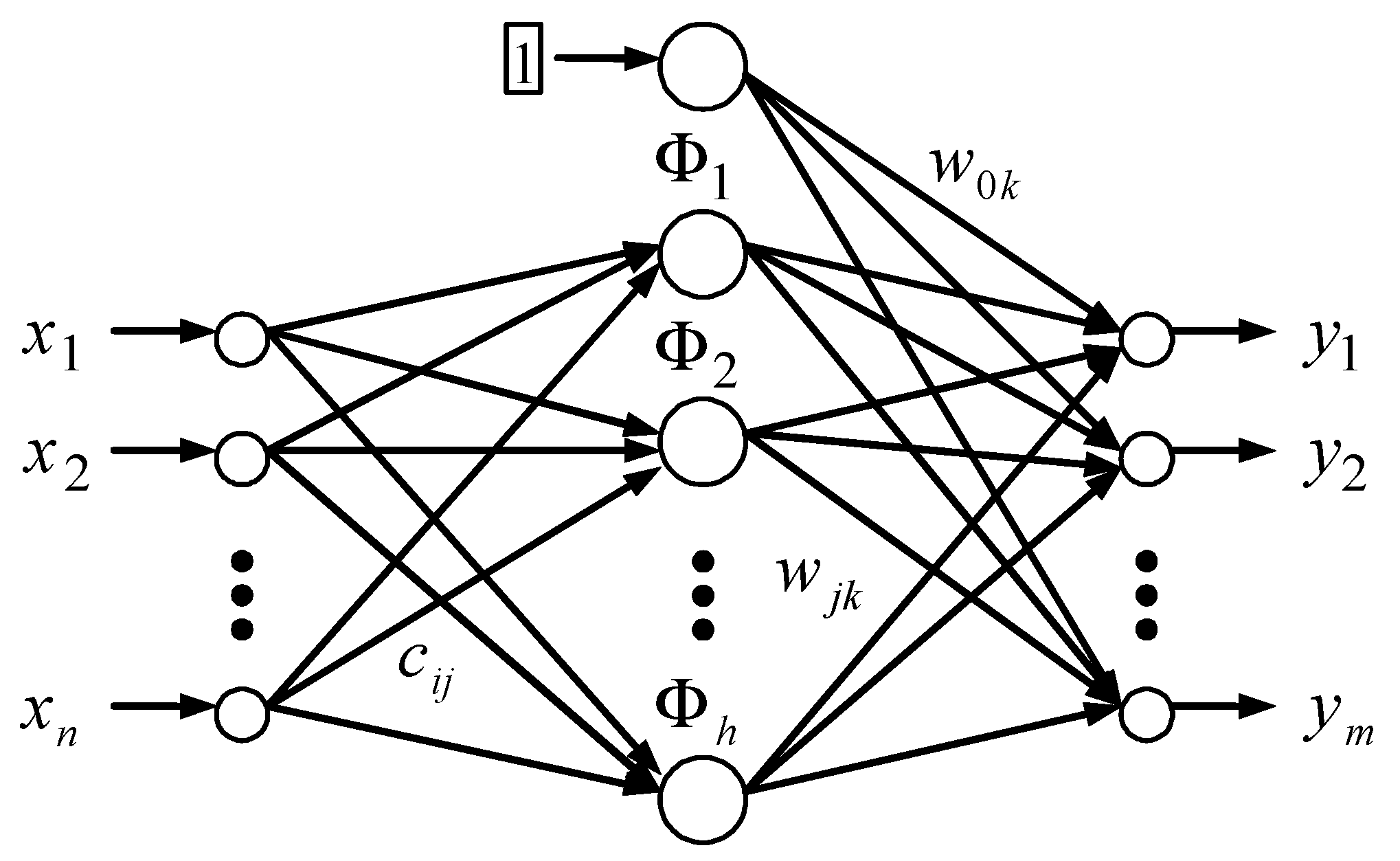
| 1 | The least squares method was used. Generating networks was finished if there was no improvement, i.e., the sum of the square was not lower. We thus retained the neural structures whose sum of residuals squares to development of Euro and Chinese Yuan was as low as possible (zero in the ideal case). |
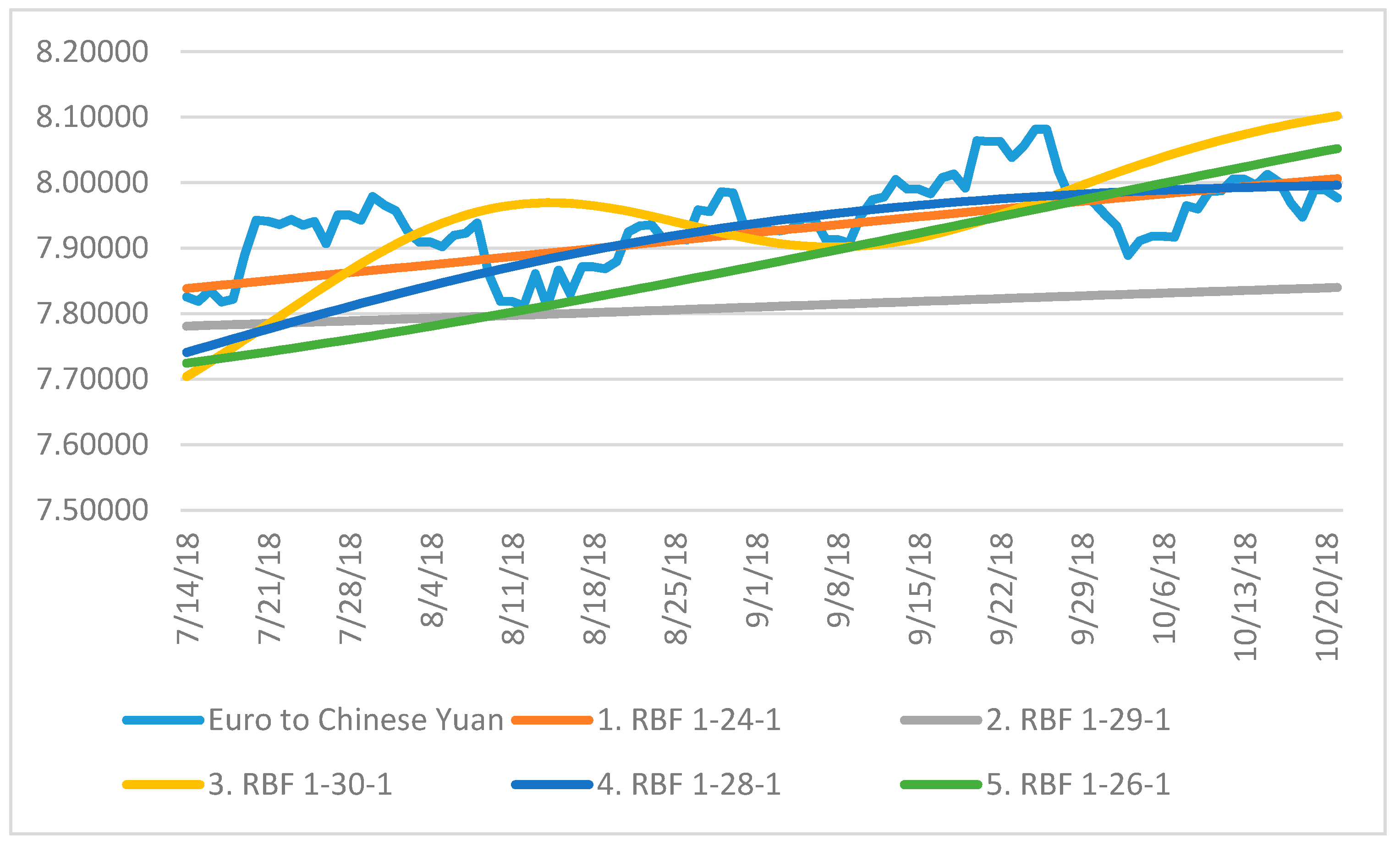
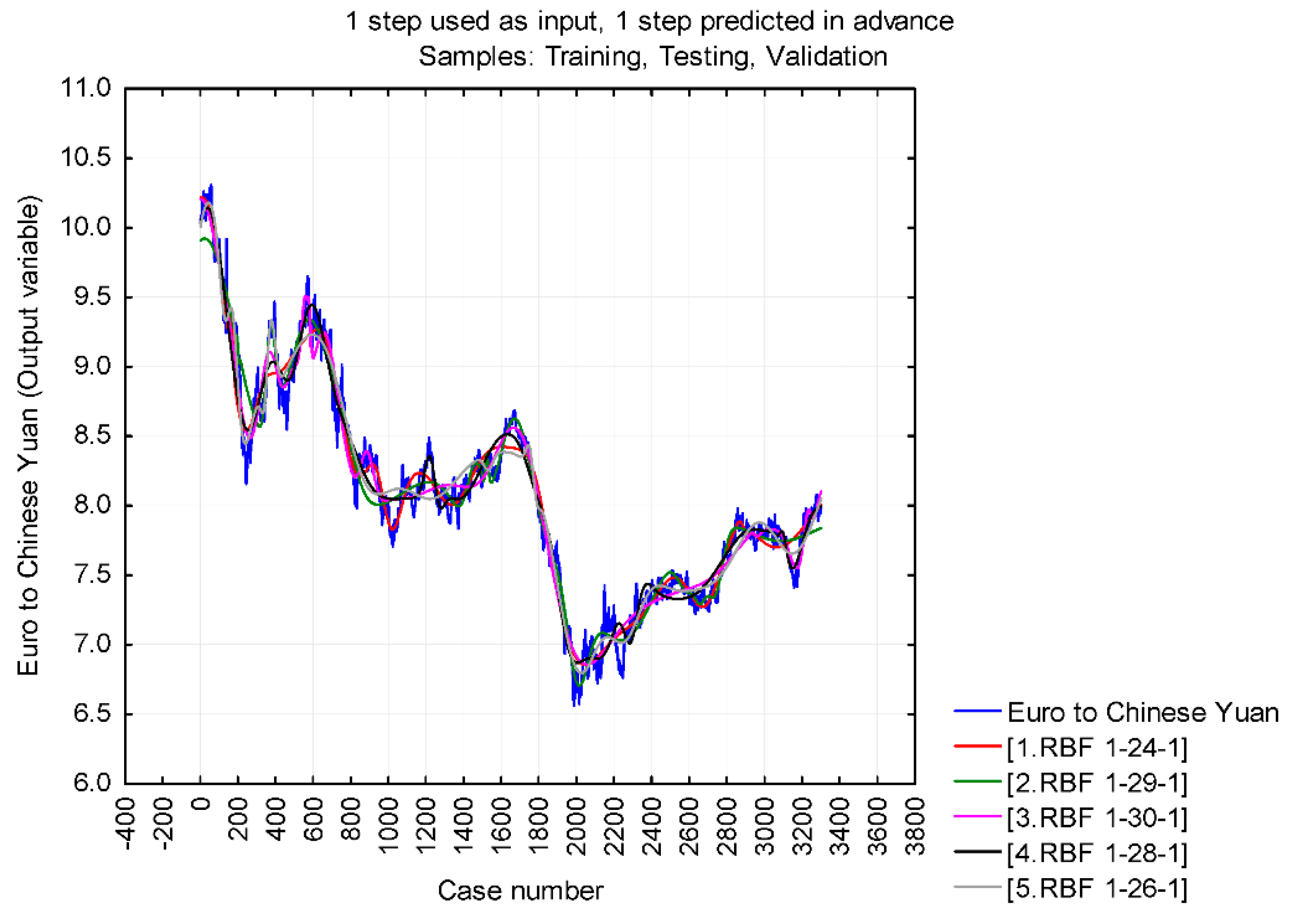
| Samples | Case (Input Variable) | Euro to Chinese Yuan (Output Target) |
|---|---|---|
| Minimum (training) | 1.000 | 6.56070 |
| Maximum (training) | 3303.000 | 10.29420 |
| Mean (training) | 1643.786 | 8.08101 |
| Standard deviation (training) | 939.260 | 0.75919 |
| Minimum (testing) | 11.000 | 6.56980 |
| Maximum (testing) | 3302.000 | 10.25190 |
| Mean (testing) | 1664.707 | 8.06546 |
| Standard deviation (testing) | 957.966 | 0.76986 |
| Minimum (validation) | 20.000 | 6.58290 |
| Maximum (validation) | 3297.000 | 10.30830 |
| Mean (validation) | 1677.677 | 8.09958 |
| Standard deviation (validation) | 1438.254 | 1.20789 |
| Minimum (overall) | 1.000 | 6.56070 |
| Maximum (overall) | 3303.000 | 10.30830 |
| Mean (overall) | 1652.000 | 8.08147 |
| Standard deviation (overall) | 953.638 | 0.76206 |
| Index | Network | Training Perform. | Testing Perform. | Validation Perform. | Training Error | Testing Error | Validation Error | Training Algorithm | Error Function | Activation of Hidden Layer | Output Activation Function |
|---|---|---|---|---|---|---|---|---|---|---|---|
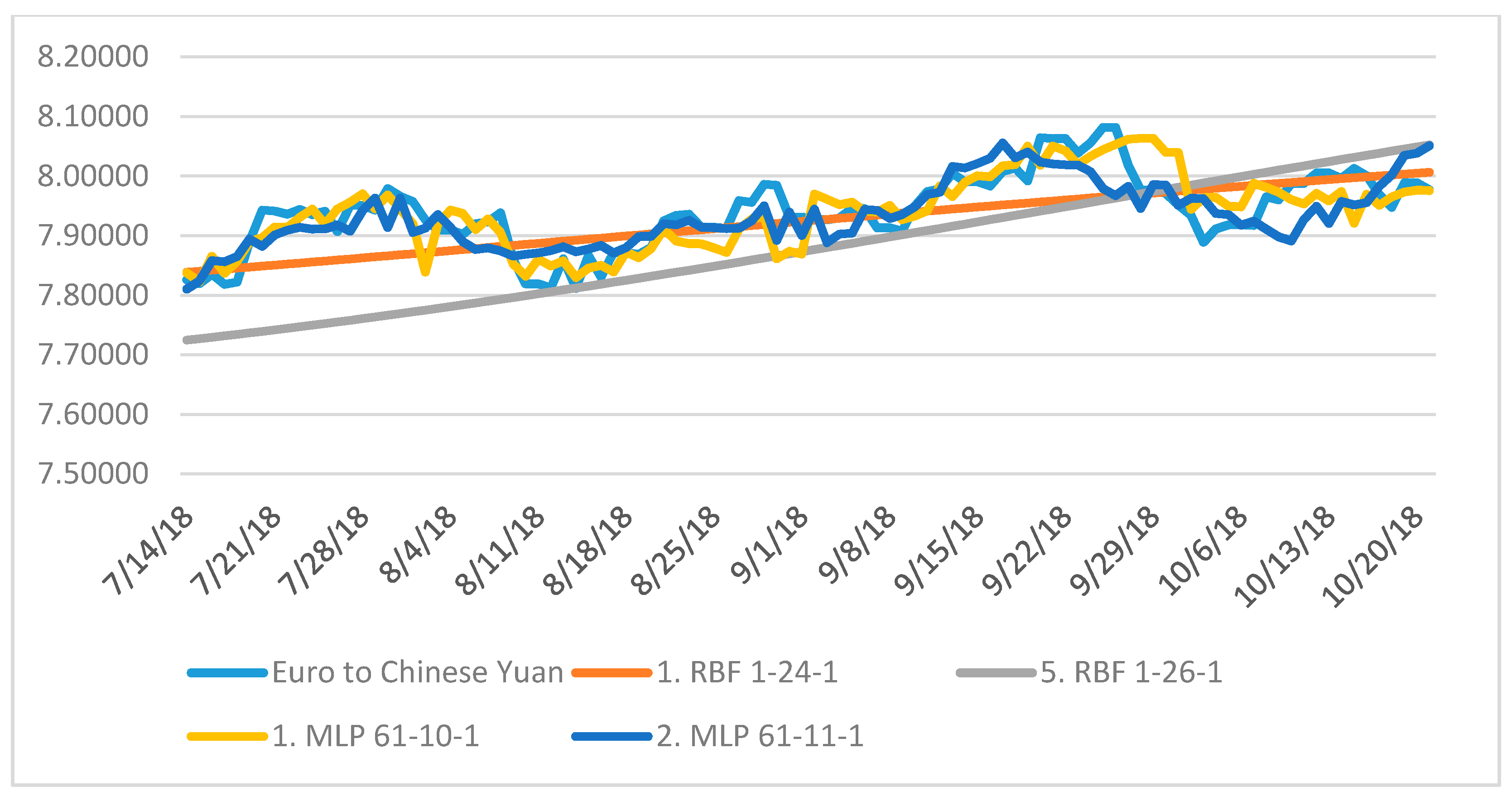
| 1 | RBF 1-24-1 | 0.983554 | 0.984770 | 0.984081 | 0.009370 | 0.009020 | 0.009390 | RBFT | Sum.sq. | Gaussian | Identity |
| 2 | RBF 1-29-1 | 0.981894 | 0.981738 | 0.983707 | 0.010306 | 0.010730 | 0.009532 | RBFT | Sum.sq.. | Gaussian | Identity |
| 3 | RBF 1-30-1 | 0.984826 | 0.985312 | 0.984546 | 0.008650 | 0.008742 | 0.009129 | RBFT | Sum.sq. | Gaussian | Identity |
| 4 | RBF 1-28-1 | 0.984362 | 0.984673 | 0.983238 | 0.008913 | 0.009007 | 0.009832 | RBFT | Sum.sq.. | Gaussian | Identity |
| 5 | RBF 1-26-1 | 0.983486 | 0.984695 | 0.984107 | 0.009407 | 0.009014 | 0.009311 | RBFT | Sum.sq. | Gaussian | Identity |
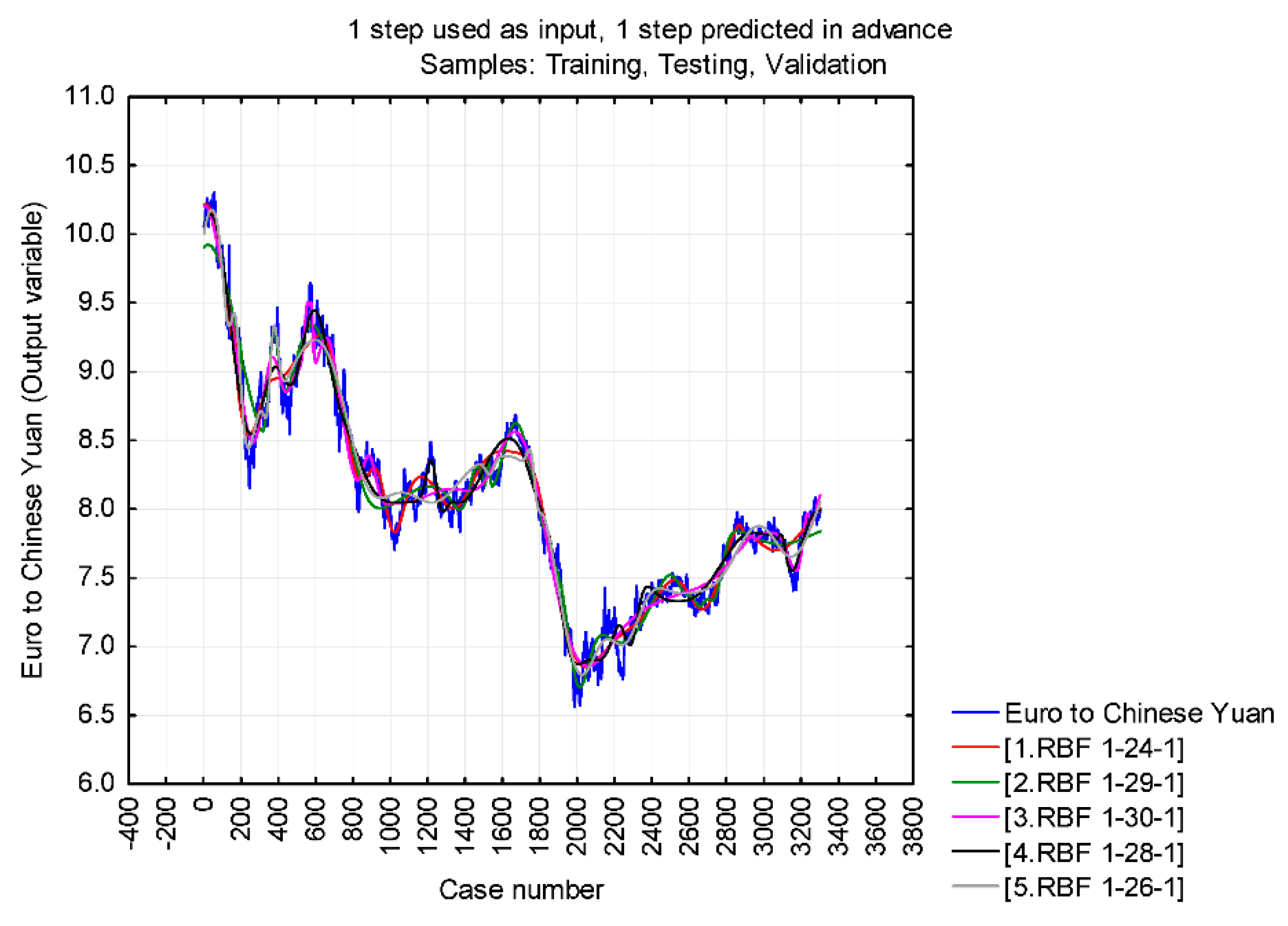
| Network | Euro to Chinese Yuan (Training) | Euro to Chinese Yuan (Testing) | Euro to Chinese Yuan (Validation) |
|---|---|---|---|
| 1. RBF 1-24-1 | 0.983554 | 0.984770 | 0.984081 |
| 2. RBF 1-29-1 | 0.981894 | 0.981738 | 0.983707 |
| 3. RBF 1-30-1 | 0.984826 | 0.985312 | 0.984546 |
| 4. RBF 1-28-1 | 0.984362 | 0.984673 | 0.983238 |
| 5. RBF 1-26-1 | 0.983486 | 0.984695 | 0.984107 |
| Statistics | 1. RBF 1-24-1 | 2. RBF 1-29-1 | 3. RBF 1-30-1 | 4. RBF 1-28-1 | 5. RBF 1-26-1 |
|---|---|---|---|---|---|
| Minimal prediction (training) | 6.85480 | 6.70498 | 6.85756 | 6.86930 | 6.79547 |
| Maximal prediction (training) | 10.21765 | 9.92194 | 10.20493 | 10.14413 | 10.17991 |
| Minimal prediction (testing) | 6.85511 | 6.70617 | 6.85749 | 6.86959 | 6.79648 |
| Maximal prediction (testing) | 10.21718 | 9.92191 | 10.20358 | 10.14384 | 10.17832 |
| Minimal prediction (validation) | 6.85528 | 6.70502 | 6.85825 | 6.87002 | 6.79581 |
| Maximal prediction (validation) | 10.21006 | 9.92164 | 10.19128 | 10.14073 | 10.18000 |
| Minimal residuals (training) | −0.45897 | −0.70049 | −0.40403 | −0.39654 | −0.45631 |
| Maximal residuals (training) | 0.56285 | 0.41491 | 0.47297 | 0.49684 | 0.58830 |
| Minimal residuals (testing) | −0.47026 | −0.69190 | −0.38432 | −0.38399 | −0.43711 |
| Maximal residua (testing) | 0.47346 | 0.40493 | 0.43641 | 0.45880 | 0.41700 |
| Minimal residuals (validation) | −0.45710 | −0.56530 | −0.35886 | −0.38681 | −0.42207 |
| Maximal residuals (validation) | 0.57571 | 0.42783 | 0.46780 | 0.50829 | 0.58714 |
| Minimal standard residua (training) | −4.74158 | −6.90008 | −4.34425 | −4.20036 | −4.70472 |
| Maximal standard residuals (training) | 5.81469 | 4.08702 | 5.08551 | 5.26279 | 6.06549 |
| Minimal standard residuals (testing) | −4.95139 | −6.67959 | −4.11032 | −4.04606 | −4.60389 |
| Maximal standard residuals (testing) | 4.98511 | 3.90916 | 4.66740 | 4.83434 | 4.39212 |
| Minimal standard residuals (validation) | −4.71717 | −5.79008 | −3.75590 | −3.90102 | −4.37405 |
| Maximal standard residuals (validation) | 5.94113 | 4.38203 | 4.89604 | 5.12617 | 6.08474 |
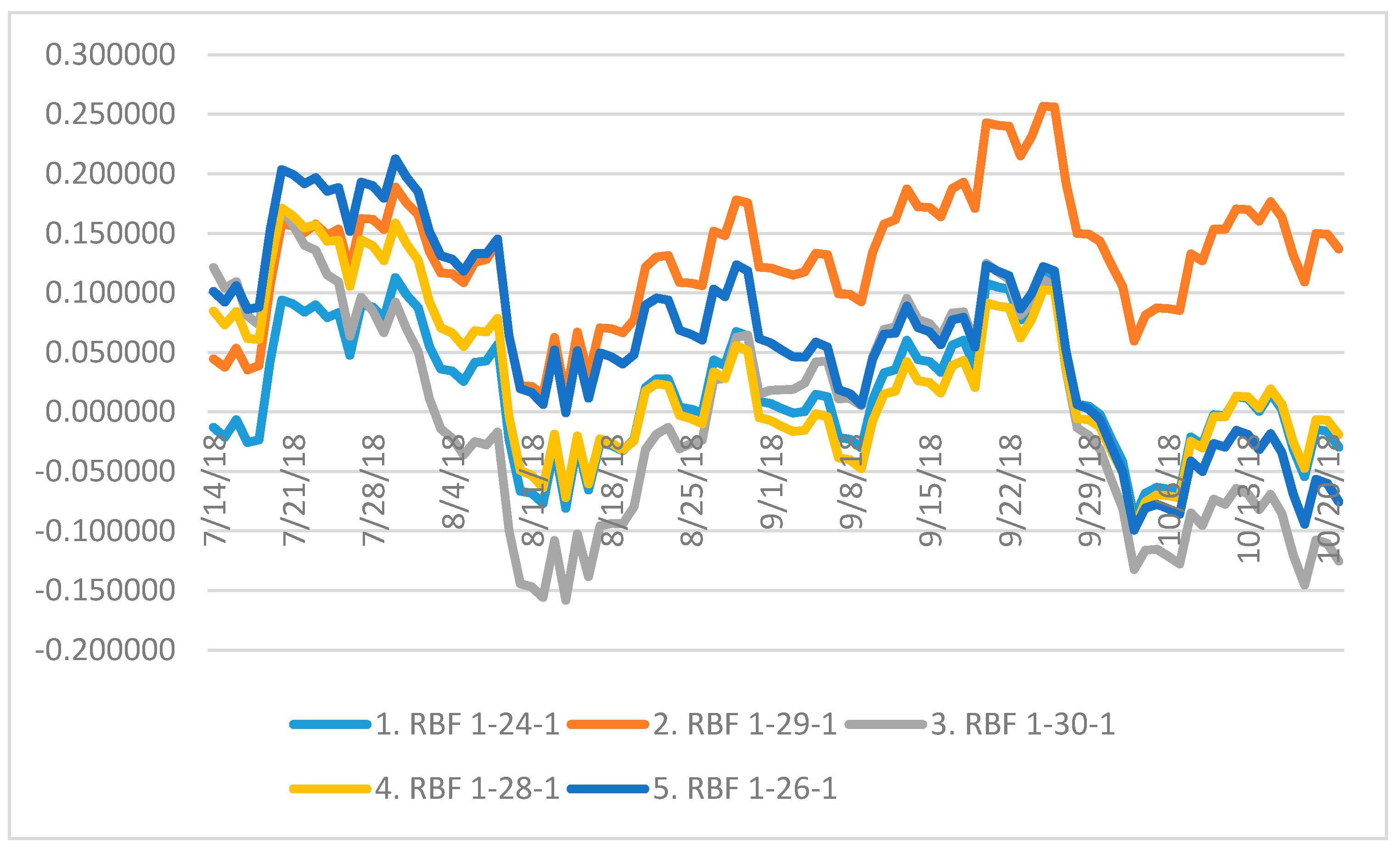
| Statistics | 1. RBF 1-24-1 | 2. RBF 1-29-1 | 3. RBF 1-30-1 | 4. RBF 1-28-1 | 5. RBF 1-26-1 |
|---|---|---|---|---|---|
| Sum of residuals | 10.753689 | 1.369654 | 10.598169 | 4.290912 | 0.676559 |
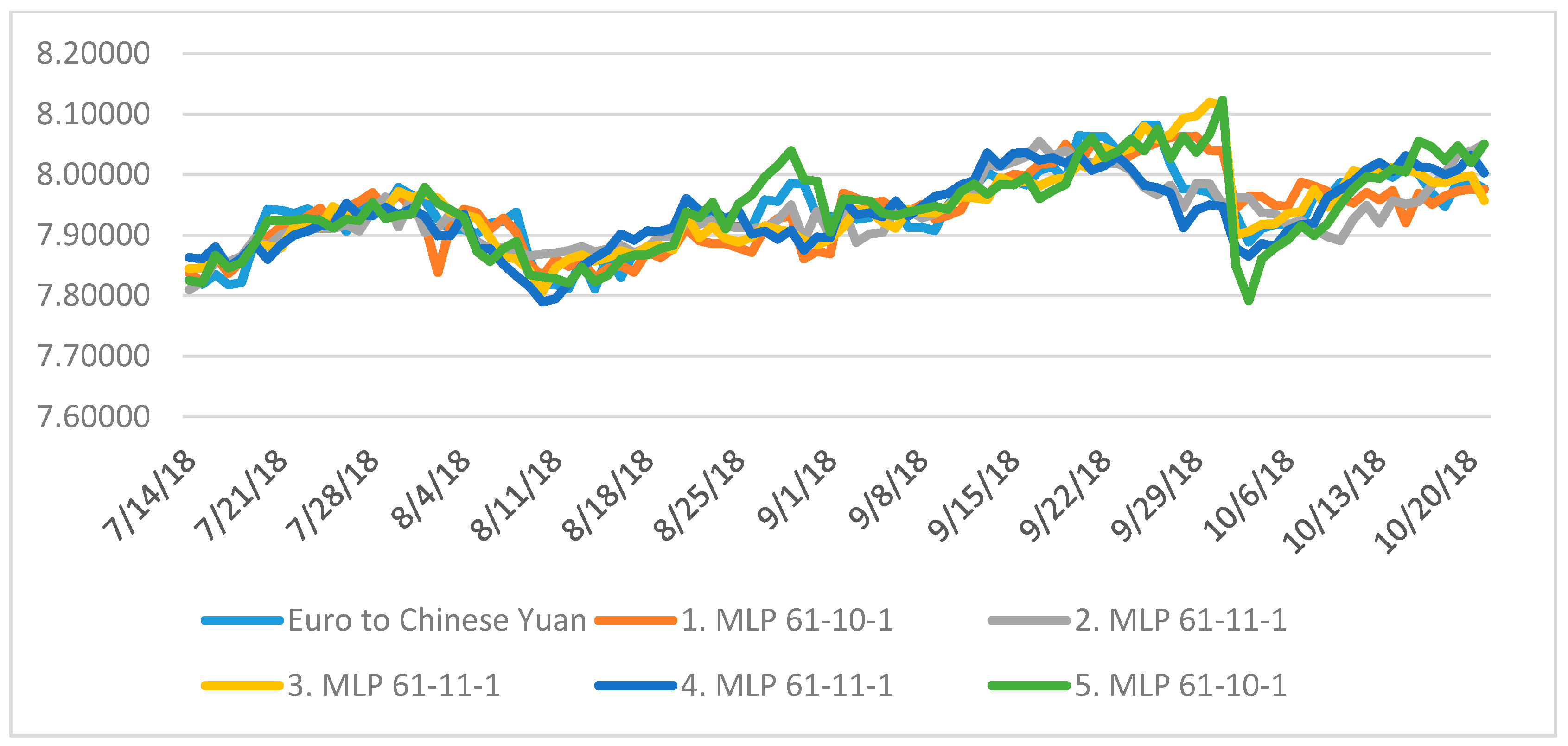
| Index | Network | Training Perform. | Testing Perform. | Validation Perform. | Training Error | Testing Error | Validation Error | Training Algorithm | Error Function | Activation of Hidden Layer | Output Activation Function |
|---|---|---|---|---|---|---|---|---|---|---|---|
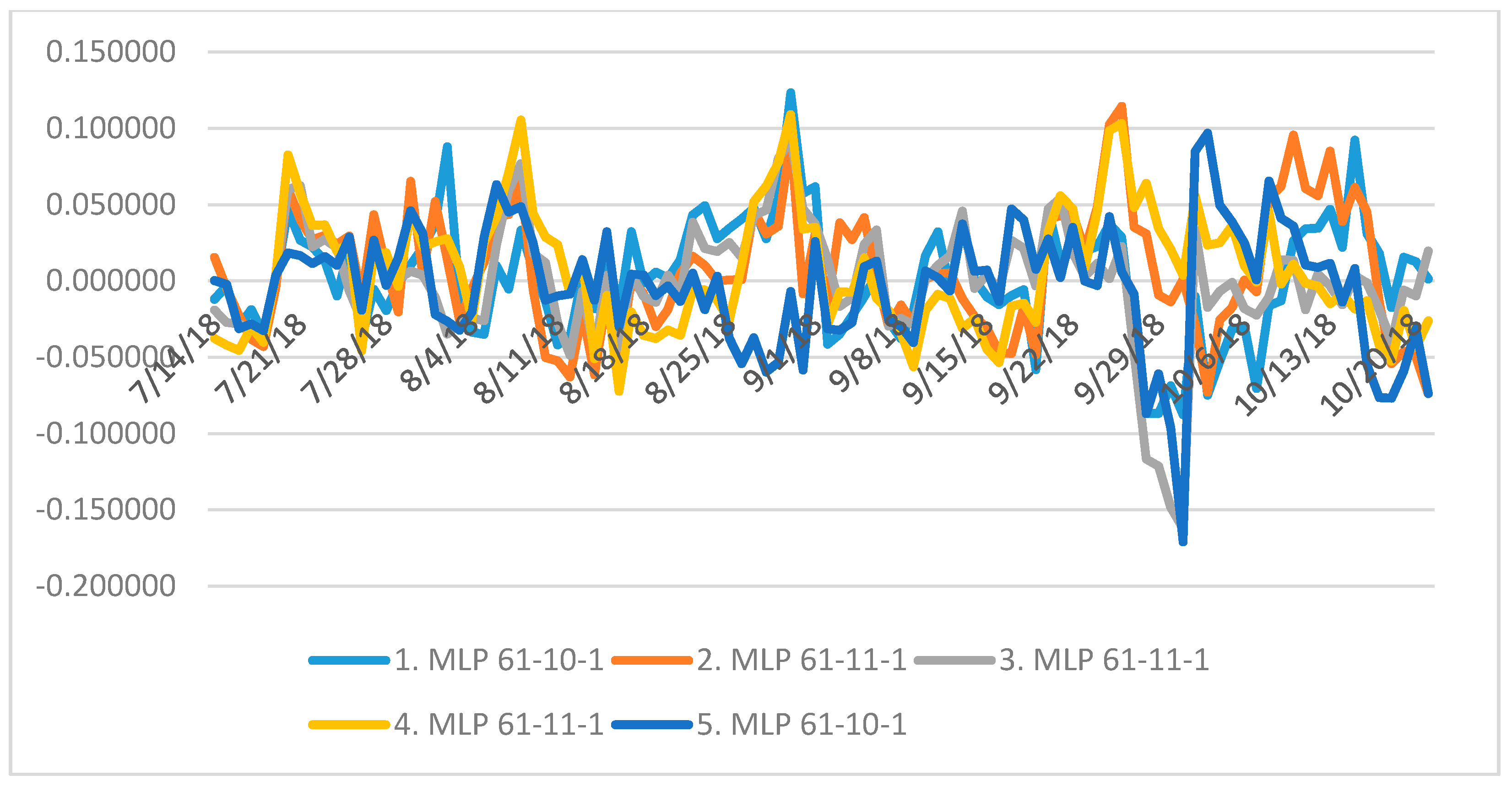
| 1 | MLP 61-10-1 | 0.998390 | 0.997106 | 0.996723 | 0.000924 | 0.001732 | 0.001931 | BFGS (Quasi-Newton) 419 | Sum.sq. | Tanh | Identity |
| 2 | MLP 61-11-1 | 0.998491 | 0.996916 | 0.996710 | 0.000866 | 0.001831 | 0.001958 | BFGS (Quasi-Newton) 468 | Sum.sq. | Tanh | Tanh |
| 3 | MLP 61-11-1 | 0.998505 | 0.997400 | 0.996715 | 0.000858 | 0.001549 | 0.001944 | BFGS (Quasi-Newton) 475 | Sum.sq. | Tanh | Sinus |
| 4 | MLP 61-11-1 | 0.998490 | 0.997074 | 0.996715 | 0.000866 | 0.001744 | 0.001939 | BFGS (Quasi-Newton) 394 | Sum.sq. | Tanh | Identity |
| 5 | MLP 61-10-1 | 0.998250 | 0.996974 | 0.996990 | 0.001004 | 0.001799 | 0.001801 | BFGS (Quasi-Newton) 398 | Sum.sq. | Tanh | Logistic |
| Network | Euro to Chinese Yuan (Training) | Euro to Chinese Yuan (Testing) | Euro to Chinese Yuan (Validation) |
|---|---|---|---|
| 1. MLP 61-10-1 | 0.998390 | 0.997106 | 0.996723 |
| 2. MLP 61-11-1 | 0.998491 | 0.996916 | 0.996710 |
| 3. MLP 61-11-1 | 0.998505 | 0.997400 | 0.996715 |
| 4. MLP 61-11-1 | 0.998490 | 0.997074 | 0.996715 |
| 5. MLP 61-10-1 | 0.998250 | 0.996974 | 0.996990 |
| Statistics | 1. MLP 61-10-1 | 2. MLP 61-11-1 | 3. MLP 61-11-1 | 4. MLP 61-11-1 | 5. MLP 61-10-1 |
|---|---|---|---|---|---|
| Minimal prediction (training) | 6.59204 | 6.60787 | 6.61005 | 6.59059 | 6.65057 |
| Maximal prediction (training) | 10.25774 | 10.20064 | 10.25455 | 10.28336 | 10.22089 |
| Minimal prediction (testing) | 6.62588 | 6.63547 | 6.63945 | 6.64194 | 6.64934 |
| Maximal prediction (testing) | 10.32071 | 10.19929 | 10.23666 | 10.24191 | 10.21010 |
| Minimal prediction (validation) | 6.57746 | 6.68662 | 6.67522 | 6.62117 | 6.66080 |
| Maximal prediction (validation) | 10.23630 | 10.19925 | 10.23854 | 10.28137 | 10.20854 |
| Minimal residuals (training) | −0.16067 | −0.18343 | −0.15628 | −0.16430 | −0.19135 |
| Maximal residuals (training) | 0.39922 | 0.49966 | 0.49448 | 0.45441 | 0.46364 |
| Minimal residuals (testing) | −0.25721 | −0.22189 | −0.18788 | −0.23063 | −0.18800 |
| Maximal residua (testing) | 0.19605 | 0.22268 | 0.21866 | 0.18687 | 0.29676 |
| Minimal residuals (validation) | −0.22231 | −0.16419 | −0.16207 | −0.20030 | −0.17103 |
| Maximal residuals (validation) | 0.55087 | 0.53214 | 0.56542 | 0.53715 | 0.48879 |
| Minimal standard residuals (training) | −5.28571 | −6.23421 | −5.33626 | −5.58204 | −6.03872 |
| Maximal standard residuals (training) | 13.13338 | 16.98175 | 16.88430 | 15.43838 | 14.63152 |
| Minimal standard residuals (testing) | −6.18008 | −5.18477 | −4.77384 | −5.52315 | −4.43254 |
| Maximal standard residuals (testing) | 4.71053 | 5.20318 | 5.55595 | 4.47499 | 6.99679 |
| Minimal standard residuals (validation) | −5.05836 | −3.71056 | −3.67572 | −4.54863 | −4.03019 |
| Maximal standard residuals (validation) | 12.53453 | 12.02629 | 12.82361 | 12.19844 | 11.51780 |
| Statistics | 1. MLP 61-10-1 | 2. MLP 61-11-1 | 3. MLP 61-11-1 | 4. MLP 61-11-1 | 5. MLP 61-10-1 |
|---|---|---|---|---|---|
| Sum of residuals | −0.677755 | 0.636444 | −0.584423 | 0.844007 | 0.000112 |
| Identification | 1. MLP 61-10-1 | 2. MLP 61-11-1 | 3. MLP 61-11-1 | 4. MLP 61-11-1 | 5. MLP 61-10-1 |
|---|---|---|---|---|---|
| January | 11.049 | 10.823 | 10.760 | 9.576 | 10.583 |
| February | 10.208 | 10.706 | 10.649 | 10.921 | 10.558 |
| March | 9.355 | 8.753 | 9.338 | 10.224 | 10.468 |
| April | 9.499 | 9.986 | 9.890 | 8.145 | 10.492 |
| May | 11.698 | 11.565 | 10.245 | 9.952 | 10.897 |
| June | 11.160 | 10.691 | 9.916 | 10.696 | 10.429 |
| July | 10.346 | 9.732 | 9.475 | 9.349 | 9.144 |
| August | 10.046 | 9.895 | 9.921 | 10.141 | 10.288 |
| September | 9.110 | 8.090 | 8.765 | 10.172 | 8.540 |
| October | 10.895 | 9.889 | 9.385 | 11.000 | 11.284 |
| November | 9.608 | 9.249 | 8.992 | 9.866 | 9.779 |
| December | 8.495 | 9.717 | 9.073 | 9.373 | 10.747 |
| Minimum | 8.495 | 8.090 | 8.765 | 8.145 | 8.540 |
| Maximum | 11.698 | 11.565 | 10.760 | 11.000 | 11.284 |
| Identification | 1. MLP 61-10-1 | 2. MLP 61-11-1 | 3. MLP 61-11-1 | 4. MLP 61-11-1 | 5. MLP 61-10-1 |
|---|---|---|---|---|---|
| 1 | 5.927 | 5.566 | 4.828 | 5.766 | 5.784 |
| 2 | 5.199 | 5.490 | 5.185 | 5.099 | 5.149 |
| 3 | 4.806 | 4.281 | 4.438 | 4.469 | 4.152 |
| 4 | 3.970 | 3.610 | 4.044 | 3.686 | 3.654 |
| 5 | 3.746 | 3.189 | 3.515 | 4.268 | 3.457 |
| 6 | 3.402 | 3.321 | 3.412 | 3.828 | 3.342 |
| 7 | 3.606 | 3.758 | 3.603 | 4.113 | 3.950 |
| 8 | 3.611 | 3.770 | 3.596 | 3.731 | 3.511 |
| 9 | 3.740 | 4.015 | 3.782 | 3.447 | 4.004 |
| 10 | 4.066 | 3.742 | 4.040 | 3.495 | 4.225 |
| 11 | 4.102 | 3.579 | 4.245 | 3.702 | 4.096 |
| 12 | 3.638 | 3.511 | 3.583 | 4.091 | 3.923 |
| 13 | 3.890 | 3.806 | 3.702 | 3.743 | 4.264 |
| 14 | 4.071 | 4.305 | 3.853 | 4.373 | 4.403 |
| 15 | 4.327 | 4.281 | 3.050 | 4.186 | 4.111 |
| 16 | 3.915 | 3.924 | 3.119 | 3.792 | 3.957 |
| 17 | 3.749 | 3.760 | 3.268 | 3.489 | 3.924 |
| 18 | 3.812 | 3.883 | 3.710 | 3.841 | 3.747 |
| 19 | 3.925 | 3.974 | 3.923 | 3.840 | 3.937 |
| 20 | 4.502 | 3.790 | 4.516 | 4.120 | 4.211 |
| 21 | 4.178 | 3.781 | 4.432 | 4.134 | 4.089 |
| 22 | 3.519 | 3.460 | 3.663 | 3.393 | 3.720 |
| 23 | 3.127 | 3.339 | 3.330 | 3.400 | 3.390 |
| 24 | 3.246 | 3.500 | 3.323 | 3.213 | 3.525 |
| 25 | 3.142 | 3.765 | 3.603 | 3.611 | 3.665 |
| 26 | 3.228 | 3.366 | 3.337 | 3.570 | 3.673 |
| 27 | 3.365 | 3.252 | 3.376 | 3.106 | 3.817 |
| 28 | 3.796 | 3.823 | 3.667 | 3.685 | 4.272 |
| 29 | 3.855 | 3.893 | 3.586 | 3.253 | 4.068 |
| 30 | 4.729 | 4.690 | 4.167 | 4.148 | 4.377 |
| 31 | 3.278 | 2.671 | 2.514 | 2.821 | 2.814 |
| Minimum | 3.127 | 2.671 | 2.514 | 2.821 | 2.814 |
| Maximum | 5.927 | 5.566 | 5.185 | 5.766 | 5.784 |
| Identification | 1. MLP 61-10-1 | 2. MLP 61-11-1 | 3. MLP 61-11-1 | 4. MLP 61-11-1 | 5. MLP 61-10-1 |
|---|---|---|---|---|---|
| Monday | 15.837 | 15.551 | 16.293 | 16.503 | 16.774 |
| Tuesday | 16.647 | 17.015 | 16.715 | 17.139 | 17.460 |
| Wednesday | 18.542 | 17.779 | 16.550 | 17.462 | 18.049 |
| Thursday | 17.204 | 17.463 | 16.446 | 17.196 | 18.050 |
| Friday | 18.093 | 17.418 | 16.697 | 17.139 | 17.271 |
| Saturday | 17.244 | 16.603 | 16.491 | 17.022 | 17.487 |
| Sunday | 17.903 | 17.266 | 17.218 | 16.953 | 18.119 |
| Minimum | 15.837 | 15.551 | 16.293 | 16.503 | 16.774 |
| Maximum | 18.542 | 17.779 | 17.218 | 17.462 | 18.119 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vochozka, M.; Horák, J.; Šuleř, P. Equalizing Seasonal Time Series Using Artificial Neural Networks in Predicting the Euro–Yuan Exchange Rate. J. Risk Financial Manag. 2019, 12, 76. https://doi.org/10.3390/jrfm12020076
Vochozka M, Horák J, Šuleř P. Equalizing Seasonal Time Series Using Artificial Neural Networks in Predicting the Euro–Yuan Exchange Rate. Journal of Risk and Financial Management. 2019; 12(2):76. https://doi.org/10.3390/jrfm12020076
Chicago/Turabian StyleVochozka, Marek, Jakub Horák, and Petr Šuleř. 2019. "Equalizing Seasonal Time Series Using Artificial Neural Networks in Predicting the Euro–Yuan Exchange Rate" Journal of Risk and Financial Management 12, no. 2: 76. https://doi.org/10.3390/jrfm12020076
APA StyleVochozka, M., Horák, J., & Šuleř, P. (2019). Equalizing Seasonal Time Series Using Artificial Neural Networks in Predicting the Euro–Yuan Exchange Rate. Journal of Risk and Financial Management, 12(2), 76. https://doi.org/10.3390/jrfm12020076






