Does Managerial Power Increase Selective Hedging? Evidence from the Oil and Gas Industry
Abstract
:1. Introduction
2. Hypothesis Development
3. Data and Methodology
3.1. Sample
3.2. Model Specification
3.3. Variables
3.3.1. Selective Hedging
3.3.2. Corporate Governance Variables
3.3.3. Other Variables
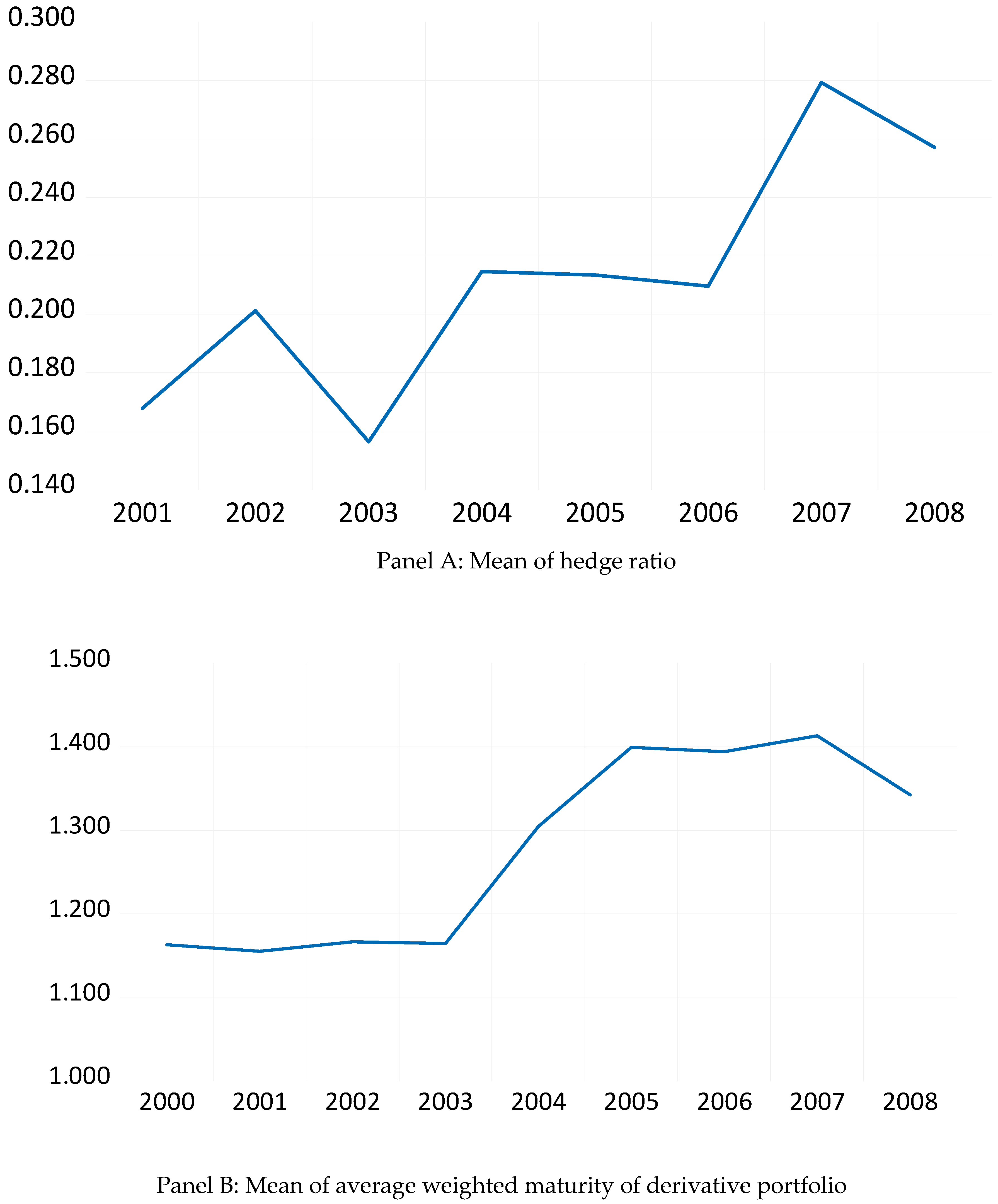
3.4. Descriptive Statistics
4. Empirical Results
4.1. Determinants of Selective Hedging
4.2. Robustness Tests and Reconciliation with Previous Literature
5. Selective Hedging and Performance
Selective Hedging and Derivative Cash Flows
6. Conclusions
Funding
Conflicts of Interest
Appendix A. Stylized Example of Calculation of SELHEDGE
References
- Adam, Tim. 2009. Capital expenditures, financial constraints, and the use of options. Journal of Financial Economics 92: 238–51. [Google Scholar] [CrossRef]
- Adam, Tim R., and Chitru S. Fernando. 2006. Hedging, speculation, and shareholder value. Journal of Financial Economics 81: 283–309. [Google Scholar] [CrossRef]
- Adam, Tim R., Chitru S. Fernando, and Evgenia Golubeva. 2015. Managerial Overconfidence and Corporate Risk Management. Journal of Banking and Finance 60: 195–208. [Google Scholar] [CrossRef]
- Adam, Tim R., Chitru S. Fernando, and Jesus M. Salas. 2017. Why do firms engage in selective hedging? Evidence from the gold mining industry. Journal of Banking and Finance 77: 269–82. [Google Scholar] [CrossRef]
- Andrén, Niclas, and Håkan Jankensgård. 2015. Wall of cash: The investment-cash flow sensitivity when capital becomes abundant. Journal of Banking and Finance 50: 204–13. [Google Scholar] [CrossRef]
- Bebchuk, Lucian Arye, John C. Coates IV, and Guhan Subramanian. 2002. The powerful antitakeover force of staggered boards: Theory, evidence, and policy. Stanford Law Review 54: 887–951. [Google Scholar] [CrossRef]
- Beber, Alessandro, and Daniela Fabbri. 2012. Who times the foreign exchange market? Corporate speculation and CEO characteristics. Journal of Corporate Finance 18: 1065–87. [Google Scholar] [CrossRef]
- Bodnar, Gordon M., Gregory S. Hayt, and Richard C. Marston. 1998. 1998 Wharton survey of financial risk management by US non-financial firms. Financial Management 27: 70–91. [Google Scholar] [CrossRef]
- Brickley, James A., Jeffrey L. Coles, and Gregg Jarrell. 1997. Leadership structure: Separating the CEO and Chairman of the Board. Journal of Corporate Finance 3: 189–220. [Google Scholar] [CrossRef]
- Brown, Gregory W., Peter R. Crabb, and David Haushalter. 2006. Are firms successful at selective hedging? The Journal of Business 79: 2925–49. [Google Scholar] [CrossRef]
- Chung, Kee H., and Hao Zhang. 2011. Corporate governance and institutional ownership. Journal of Financial and Quantitative Analysis 46: 247–73. [Google Scholar] [CrossRef]
- Clayton Williams. 2006. 10-K Filing. Available online: https://www.sec.gov/edgar.shtml (accessed on 5 March 2019).
- Croci, Ettore, Alfonso Del Giudice, and Håkan Jankensgård. 2017. CEO age, risk incentives, and hedging strategy. Financial Management 46: 687–716. [Google Scholar] [CrossRef]
- Fabling, Richard, and Arthur Grimes. 2015. Over the Hedge: Do Exporters Practice Selective Hedging? Journal of Futures Markets 35: 321–38. [Google Scholar] [CrossRef]
- Froot, Kenneth A., David S. Scharfstein, and Jeremy C. Stein. 1993. Risk management: Coordinating corporate investment and financing policies. Journal of Finance 485: 1629–58. [Google Scholar] [CrossRef]
- Géczy, Christopher C., Bernadette A. Minton, and Catherine M. Schrand. 2007. Taking a view: Corporate speculation, governance, and compensation. The Journal of Finance 62: 2405–43. [Google Scholar] [CrossRef]
- Haushalter, G. David. 2000. Financing policy, basis risk, and corporate hedging: Evidence from oil and gas producers. The Journal of Finance 55: 107–52. [Google Scholar] [CrossRef]
- Heckman, James J. 1979. Sample selection bias as a specification error. Econometrica 47: 1251–71. [Google Scholar] [CrossRef]
- Hermalin, Benjamin E., and Michael S. Weisbach. 2003. Boards of directors as an endogenously determined institution: A survey of the economic literature. Federal Reserve Bank of New York Economic Policy Review 9: 7–26. [Google Scholar]
- Jensen, Michael C. 1986. Agency Costs of Free Cash Flow, Corporate Finance, and Takeovers. American Economic Review 76: 323–29. [Google Scholar]
- Jin, Yanbo, and Philippe Jorion. 2006. Firm value and hedging: Evidence from U.S. oil and gas producers. The Journal of Finance 61: 893–919. [Google Scholar] [CrossRef]
- Kalcheva, Ivalina, and Karl V. Lins. 2007. International evidence on cash holdings and expected managerial agency problems. Review of Financial Studies 20: 1087–112. [Google Scholar] [CrossRef]
- Kumar, Praveen, and Ramon Rabinovitch. 2013. CEO entrenchment and corporate hedging: Evidence from the oil and gas industry. Journal of Financial and Quantitative Analysis 48: 887–917. [Google Scholar] [CrossRef]
- Petroquest. 2006. 10-K Filing. Available online: https://www.sec.gov/edgar.shtml (accessed on 5 March 2019).
- Shleifer, Andrei, and Robert W. Vishny. 1986. Large shareholders and corporate control. The Journal of Political Economy 3: 461–88. [Google Scholar] [CrossRef]
- Shleifer, Andrei, and Robert W. Vishny. 1997. A survey of corporate governance. Journal of Finance 52: 737–83. [Google Scholar] [CrossRef]
- Smith, Clifford W., and Rene M. Stulz. 1985. The determinants of firms’ hedging policies. Journal of Financial & Quantitative Analysis 20: 391–405. [Google Scholar]
- Stulz, René M. 1984. Optimal hedging policies. The Journal of Financial and Quantitative Analysis 19: 127–40. [Google Scholar] [CrossRef]
- Stulz, René M. 1996. Rethinking risk management. Journal of Applied Corporate Finance 9: 8–25. [Google Scholar] [CrossRef]
- Treanora, Stephen D., Daniel A. Rogersb, David A. Carterc, and Betty J. Simkinsc. 2014. Exposure, hedging, and value: New evidence from the U.S. airline industry. International Review of Financial Analysis 34: 200–11. [Google Scholar] [CrossRef]
- Tufano, Peter. 1996. Who manages risk? An empirical examination of risk management practices in the gold mining industry. The Journal of Finance 51: 1097–137. [Google Scholar] [CrossRef]
| 1 | Firms with SIC 1311 are engaged in exploration and production, whereas SIC 2611 are petroleum refinement firms. While 2611 firms have downstream assets, they tend also to have significant upstream assets. No firm included is net short in oil and gas assets. |
| 2 | The shock was not anticipated. Prior to 2004, the forward curve gave little or no indication about the increase that was about to take place, suggesting that it was largely unexpected by industry participants. Futures prices did not start their rise until spot prices started rising. |
| 3 | Examples of search words are: item 7a, hedge, derivative, market risk, swap, collar, forward, and floor. |
| 4 | Disclosure of market risks for US companies is regulated by Financial Reporting Release No. 48 (“FRR 48”), issued by SEC in 1997. |
| 5 | The annual report of Clayton Williams is informative in this regard (Clayton Williams 2006). They state that: “The decision to initiate or terminate commodity hedges is made by management based on its expectation of future market price movements. We have no set goals for the percentage of our production we hedge […]” |
| 6 | The hedge ratio is defined as the fraction of annual production hedged. First the sum of hedged contracts is calculated as the number of linear hedging instruments (forwards, futures, and swaps) plus put options bought. This amount is then divided by expected production. Both magnitudes are expressed in terms of barrels of oil equivalents. For simplicity, it is assumed that expected production is equal to realized production (i.e., perfect foresight). Natural gas is converted into barrels of oil equivalents using the standard assumption that 6 Mcf of gas has the same energy content as 1 bbl of oil. |
| 7 | An insurance strategy involves the purchase of put options that provide a payoff if the firm’s output price falls below a pre-defined level (the strike price). |
| 8 | Linear strategies refer to hedging strategies for which the payoff is a linear function of the underlying price risk. This category includes forwards, futures, and price swaps. |
| 9 | Purchases of put options are generally financed with cash-on-hand or by selling call options. The latter is typically referred to as a “collar” strategy and is a very common strategy in the oil and gas industry. |
| 10 | The winsorization at the 2.5 and 97.5th percentiles is required to deal with outlier issues that remain if the 1st and 99th percentiles are used. Negative equity occurs in a non-trivial fraction of firm years in the oil and gas industry, which creates many extreme values for financial ratios. |
| 11 | Unfortunately, the three giant firms do not report their derivative portfolios in tabular form and are hence excluded from the hedging-subsample. |
| 12 | To account for this, in the multivariate estimations I use an alternative definition of INSIDEOWN, which adds 1 and then takes the natural log. The results from using this variable are reported in Section 4. |
| 13 | Correlation tables are available from the author on request. |
| 14 | The following statement by Petroquest is entirely typical (Petroquest 2006): “We periodically seek to reduce our exposure to commodity price volatility by hedging a portion of production through commodity derivative instruments”. These disclaimer-like statements provide little or no guidance as to what logic guides the firm’s hedging decisions, leaving investors largely in the dark about future derivative positions. |
| 15 | This number is lower than the 367 firm-years classified as derivative usage reported in Section 3. SELHEDGE is calculated in terms of year-on-year changes, so that the first year (2000) drops out. On the other hand, adding to the number of observations on SELHEDGE, is the fact that a firm that has previously hedged, but does not do so in a given year, automatically is coded as a 1 for D_AMOUNT because it indicates a major shift in portfolio composition (from positive values to zero). |
| 16 | Data to compute PRODUCTION is obtained from Capital IQ. The number is expressed in barrels of oil equivalents (thousand). |
| 17 | In untabulated regressions, board size is found to also reduce the probability of being classified as a hedger. Firms with large boards therefore seem to hedge less, and, conditional on hedging, also hedge less selectively. |
| 18 | Leverage is not included in the empirical model of Adam et al. (2015), who instead choose to include the Z-score and its quadratic term. |
| 19 | For example, a firm may state that “in 200X revenues were decreased by Y million due to hedging activities”. An unrealized component may be included in this number to the extent that the firm sees a change in the fair value of its hedging assets and liabilities and does not apply hedge accounting. However, the prevailing practice among oil and gas firms is to include only realized effects in revenue. Unrealized gains and losses are typically placed in operating expenses, or in other expenses (not included in operating income). |
| 20 | If the outlier observation is included the p-value increases to 0.06. |
| Firm-Years | Mean | Median | 25th | 75th | St.dev. | |
|---|---|---|---|---|---|---|
| ASSETS ($/thousand) | 842 | 7,019,932 | 151,993 | 12,263 | 1,231,053 | 25,960,495 |
| CAPEX | 842 | 0.182 | 0.162 | 0.062 | 0.258 | 0.144 |
| CASH | 842 | 0.136 | 0.044 | 0.012 | 0.171 | 0.189 |
| LEVERAGE | 842 | 0.266 | 0.215 | 0.049 | 0.359 | 0.288 |
| STAGGER | 842 | 0.375 | 0.000 | 0.000 | 1.000 | 0.484 |
| INSIDEOWN | 842 | 21.303 | 12.800 | 4.000 | 32.500 | 21.870 |
| INSTITUTION | 842 | 12.232 | 6.600 | 0.000 | 21.400 | 15.419 |
| BLOCK | 842 | 16.809 | 12.600 | 0.000 | 26.750 | 17.723 |
| BOARDSIZE | 842 | 7.334 | 7.000 | 5.000 | 9.000 | 2.866 |
| EXECSSHARE | 842 | 0.265 | 0.200 | 0.125 | 0.333 | 0.188 |
| CHAIRCEO | 842 | 0.671 | 1.000 | 0.000 | 1.000 | 0.470 |
| DERIVATIVE | 842 | 0.513 | 1.000 | 0.000 | 1.000 | 0.500 |
| Hedgers | Non-Hedgers | Difference | |
|---|---|---|---|
| ASSETS (th.) | 12,994,632 | 808,697 | 12,185,935 *** |
| CAPEX | 0.209 | 0.152 | 0.056 |
| CASH | 0.049 | 0.220 | (0.170) *** |
| LEVERAGE | 0.282 | 0.252 | 0.030 * |
| STAGGER | 0.474 | 0.239 | 0.235 |
| INSIDEOWN | 11.450 | 30.711 | (19.261) *** |
| INSTITUTION | 18.096 | 5.909 | (12.186) *** |
| BLOCK | 21.418 | 11.996 | 9.422 |
| BOARDSIZE | 8.598 | 6.061 | 2.536 *** |
| EXECSSHARE | 0.179 | 0.352 | (0.172) *** |
| CHAIRCEO | 0.672 | 0.655 | 0.017 |
| Model 1 | Model 2 | Model 3 | |
|---|---|---|---|
| CONSTANT | −0.726 | 1.423 | −0.499 |
| (−0.44) | (0.73) | (−0.30) | |
| LOG(ASSETS) | 0.208 ** | −0.386 | 0.188 * |
| (2.04) | (−1.18) | (1.83) | |
| CAPEX | 0.609 | 0.876 | 0.722 |
| (0.52) | (0.70) | (0.60) | |
| CASH | 0.181 | −0.357 | −1.002 |
| (0.08) | (−0.15) | (−0.45) | |
| LEVERAGE | −1.506 ** | −1.241 * | −1.549 ** |
| (−2.11) | (−1.65) | (−2.14) | |
| STAGGER | 0.535 ** | 0.478 * | 0.526 * |
| (1.96) | (1.66) | (1.86) | |
| INSIDEOWN | 0.059 *** | 0.043 *** | 0.044 *** |
| (3.46) | (3.06) | (3.14) | |
| INSTITUTION | 0.008 | 0.010 | 0.005 |
| (0.98) | (1.17) | (0.67) | |
| BOARDSIZE | −0.162 * | −0.128 | −0.130 |
| (−1.94) | (−1.49) | (−1.55) | |
| EXECSSHARE | −0.527 | −0.254 | −0.479 |
| (−0.32) | (−0.16) | (−0.30) | |
| CHAIRCEO | −0.160 | −0.280 | −0.168 |
| (−0.57) | (−0.96) | (−0.58) | |
| POST2003 | −0.567 * | −0.363 | −0.679 ** |
| (−1.80) | (−0.97) | (−2.14) | |
| LOG(PRODUCTION) | 0.419 | ||
| (0.74) | |||
| LOG(PRODUCTION(−1)) | 0.205 | ||
| (0.38) | |||
| CHANGE(PRODUCTION) | 17.38 | ||
| (0.66) | |||
| Observations | 352 | 315 | 315 |
| Observations = 1 | 256 | 228 | 228 |
| McFadden R−SQR | 0.072 | 0.054 | 0.068 |
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | Model 7 | |
|---|---|---|---|---|---|---|---|
| CONSTANT | −0.189 | −1.742 | −0.693 | 0.472 | −4.036 | −0.629 | 0.196 |
| (−0.13) | (−1.14) | (−0.43) | (0.32) | (−1.32) | (−0.28) | (0.11) | |
| LOG(ASSETS) | 0.208 ** | 0.265 *** | 0.205 ** | 0.141 | 0.340 * | 0.203 | 0.142 |
| (2.29) | (2.77) | (2.02) | (1.48) | (1.80) | (1.60) | (1.36) | |
| CAPEX | 0.794 | 0.860 | 0.924 | 0.607 | 5.511 ** | −0.616 | 0.563 |
| (0.75) | (0.78) | (0.78) | (0.54) | (2.19) | (−0.36) | (0.51) | |
| CASH | 0.905 | 1.001 | −0.311 | −0.434 | 1.275 | 0.696 | 0.329 |
| (0.46) | (0.50) | (−0.14) | (−0.21) | (0.36) | (0.24) | (0.15) | |
| LEVERAGE | −1.231 * | −1.169 * | −1.552 ** | −1.686 ** | 0.068 | −1.854 * | −1.325 * |
| (−1.81) | (−1.67) | (−2.18) | (−2.42) | (0.06) | (−1.81) | (−1.95) | |
| STAGGER | 0.153 | 0.160 | 0.526 * | 0.527** | −0.208 | 0.918 ** | 0.469 * |
| (0.62) | (0.63) | (1.93) | (2.03) | (−0.44) | (2.57) | (1.80) | |
| INSIDEOWN | 0.033 *** | 0.049 *** | 0.054 *** | 0.038 *** | 0.079 *** | 0.055 ** | |
| (2.99) | (3.54) | (3.45) | (3.08) | (2.62) | (2.48) | ||
| LOG(INSIDEOWN) | 0.326 ** | ||||||
| (2.04) | |||||||
| INSTITUTION | 0.005 | 0.007 | 0.005 | 0.008 | 0.008 | 0.011 | 0.006 |
| (0.66) | (0.92) | (0.62) | (0.99) | (0.55) | (0.99) | (0.78) | |
| BOARDSIZE | −0.209 *** | −0.186 ** | −0.141 * | −0.133 | −0.165 | −0.182 | −0.141 * |
| (−2.68) | (−2.33) | (−1.67) | (−1.64) | (−1.16) | (−1.58) | (−1.72) | |
| EXECSSHARE | −1.054 | 0.271 | −0.743 | −1.474 | 0.242 | −2.416 | −0.373 |
| (−0.76) | (0.17) | (−0.47) | (−1.00) | (0.11) | (−0.79) | (−0.24) | |
| CHAIRCEO | −0.209 | −0.151 | −0.146 | −0.058 | −0.078 | −0.202 | −0.276 |
| (−0.81) | (−0.58) | (−0.52) | (−0.21) | (−0.17) | (−0.53) | (−1.00) | |
| POST2003 | −0.677 ** | −0.564 * | −0.484 | −0.855 *** | 0.705 ** | ||
| (−2.37) | (−1.93) | (−1.54) | (−2.77) | (2.45) | |||
| Observations | 352 | 352 | 352 | 352 | 166 | 176 | 352 |
| Observations = 1 | 230 | 224 | 264 | 251 | 136 | 120 | 256 |
| Period fixed effects | No | No | No | No | No | No | No |
| McFadden R−SQR | 0.059 | 0.073 | 0.071 | 0.066 | 0.116 | 0.086 | 0.049 |
| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| CONSTANT | −0.023 *** | −0.140 *** | −0.049 | −0.183 *** |
| (−3.61) | (−3.50) | (−0.94) | (−5.53) | |
| SELHEDGE | −0.018 * | −0.162 *** | 0.003 | |
| (−1.91) | (−2.82) | (0.36) | ||
| LOG(ASSETS) | 0.006 *** | 0.001 | 0.009 *** | |
| (2.92) | (0.52) | (4.58) | ||
| INSIDEOWN | 0.000 | 0.000 | 0.003 *** | |
| (0.86) | (0.83) | (5.66) | ||
| SELHEDGE*LOG(ASSETS) | 0.010 *** | |||
| (2.66) | ||||
| SELHEDGE*INSIDEOWN | −0.002 *** | |||
| (−2.84) | ||||
| Period fixed effects | Yes | Yes | Yes | Yes |
| Observations | 260 | 300 | 260 | 260 |
| Adj. R−SQR | 0.189 | 0.158 | 0.206 | 0.209 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jankensgård, H. Does Managerial Power Increase Selective Hedging? Evidence from the Oil and Gas Industry. J. Risk Financial Manag. 2019, 12, 71. https://doi.org/10.3390/jrfm12020071
Jankensgård H. Does Managerial Power Increase Selective Hedging? Evidence from the Oil and Gas Industry. Journal of Risk and Financial Management. 2019; 12(2):71. https://doi.org/10.3390/jrfm12020071
Chicago/Turabian StyleJankensgård, Håkan. 2019. "Does Managerial Power Increase Selective Hedging? Evidence from the Oil and Gas Industry" Journal of Risk and Financial Management 12, no. 2: 71. https://doi.org/10.3390/jrfm12020071
APA StyleJankensgård, H. (2019). Does Managerial Power Increase Selective Hedging? Evidence from the Oil and Gas Industry. Journal of Risk and Financial Management, 12(2), 71. https://doi.org/10.3390/jrfm12020071




