1. Introduction
A variety of arbitrage free models for approximating quoted option prices have been available for some time. The quotations are typically in terms of (
Black and Scholes 1973;
Merton 1973) implied volatilities for the traded strikes and maturities. Consequently, the set of such quotations is now popularly referred to as the volatility surface. Some of the models are nonparametric with the
Dupire (
1994) local volatility model being a popular example. The local volatility model is specified in terms of a deterministic function
that expresses the local volatility for the stock if the stock were to be at level
K at time
Though the options quoted are many in number, ranging from a few hundred to thousands on a single underlying asset, the arbitrage free conditions thereon are considerably restrictive. As a result it is believed that the volatility surface has far fewer degrees of freedom than the number of traded options. Attempts are then made at parametric descriptions of implied volatilities directly, often with five to ten parameters for each of the traded maturities. For examples one may refer to
Gatheral (
2006). These parametric models can be open to arbitrage possibilities. On occasion conditions are developed on the parameters to ensure that the resulting model for the surface is arbitrage free (
Fengler (
2009),
Gatheral and Jacquier (
2014), and
Guo et al. (
2016)). Alternatively, numerous parametric models are written for the underlying stock price process resulting in option prices that are arbitrage free by construction. Well known examples include
Merton (
1976),
Madan and Seneta (
1990),
Heston (
1993),
Eberlein and Keller (
1995),
Barndorff-Nielsen (
1998),
Madan et al. (
1998),
Kou (
2002),
Eberlein and Prause (
2002),
Carr et al. (
2002),
Niccolato and Vernados (
2003),
Carr and Wu (
2003),
Carr et al. (
2007) and
Carr and Nadtochiy (
2017) to mention a few.
It is known that the arbitrage free property is equivalent to the existence of a one dimensional Markov martingale model for the suitably discounted asset price with option prices then given as expectations of suitably discounted option payoffs under the specified martingale probability (
Kellerer 1972;
Carr and Madan 2005;
Davis and Hobson 2007). Among the martingale models there are numerous examples of higher dimensional stochastic evolutions, as evidenced by the
Heston (
1993),
Carr et al. (
2003) and
Niccolato and Vernados (
2003) stochastic volatility models, with the martingale property holding for just the discounted asset price and not for the auxiliary variables like the volatility. Since these models produce initial option prices free of static arbitrage there therefore then also exists a one dimensional Markov martingale consistent with the option prices being discounted expectations under this one dimensional Markov process that is often not exhibited. An example of such a Markov martingale could be the local volatility model derived from the stochastic volatility option prices at the initial time. The focus of this paper however, will be on parsimonious parametric one dimensional Markov martingale models for the suitably discounted asset price.
Many of the examples of such models in the literature are given by processes of independent increments that may or may not be time homogeneous. The time homogeneous processes are examples of Lévy processes that do not fit well across maturities (
Konikov and Madan 2002). Lévy processes provably have the skewness and excess kurtosis of the return distribution decreasing like the reciprocal of the square root of the horizon and the horizon respectively. Observed market implied distributions do not posses such sharp rates of decline in these higher moments. Additive or processes with a specific time inhomogeneity based on scaling self decomposable laws at unit time were introduced in
Carr et al. (
2007). They were termed Sato processes following their development by
Sato (
1991). It was shown that they provide an adequate fit to the option prices across both the strike and maturity domains with a few (or four to five) parameters.
Most of these models, via independence across time, formulate analytical characteristic functions for the return density at arbitrary horizons. The technology of fast Fourier transforms introduced in
Carr and Madan (
1999) then yields call option prices directly on a Fourier inversion of analytical transforms for the suitably exponentially dampened call option prices. The method works well for relatively near-the-money option strikes with log forward strike ratios within 20 to 40 percent in absolute value. However, post the financial crisis of 2008 the market depth in downside strikes has expanded considerably as documented later in this paper. For extremal strikes in the two tails we observe that model prices obtained by Fourier inversion have difficulties in calibrating to their quoted counterparts. After numerous attempts with a variety approaches at calibrations using Fourier inversion, not reported here, we concluded that for the wide range of option strikes now being actively quoted one may need to change the pricing technology away from Fourier inversion of characteristic functions. The reliance on independence built into some characteristic functions is also a further restriction that it may be advantageous to avoid.
Before moving on in an alternate direction it is worth noting that there have been extensions of Fourier methods with respect to dealing with deep out of the money options. One such approach is the use of saddle point approximations developed in
Rogers and Zane (
1999),
Xiong et al. (
2005), and
Carr and Madan (
2009) for example. However the approximations are particular to each strike and maturity and it is not clear what underlying process will tie all the approximations together in a single process approximation for all strikes and maturities. Yet another approach is to invert for the density adopted in
Fang and Oosterlee (
2008) and
Kirkby (
2015) and then integrate the payoff against the density. The option prices themselves are smoother objects than distribution functions that are smoother than densities and we anticipate that inversions for second derivatives in tails should generally be more problematic than the inversion for the option price. In any case our interest is also to enhance the use of models not amenable to the presence of analytical characteristic functions.
We therefore turn our attention to calibrating one dimensional Markov processes that permit the transition densities to be both time inhomogeneous and depend nonlinearly on the level of the underlying asset price. A possible solution is to employ finite state continuous time Markov chain approximations to describe state transition rate matrices as introduced in
Mijatovič and Pistorius (
2011). The matrix exponentials of these matrices deliver probability elements that on multiplication across time steps permit time inhomogeneity in the formation of risk neutral density approximations at arbitrary horizons. These probability elements may be used to compute the model option prices. The state spaces used may employ the use of non-uniform grids, concentrated near the forward. The objective here is to report on the use of such an approach for the volatility surface on
as at 8 February 2018 as a test case. This option surface had 2695 option prices across 28 maturities between a few days to two years.
The outline for the rest of the paper is as follows.
Section 2 documents the growth in the traded options, their moneyness spreads, and the number of maturities being traded across time. The need to cope with this expansion using one dimensional Markov models is then set by the requirements induced by the absence of static arbitrage. These conditions are briefly reviewed in
Section 3.
Section 4 reports on the difficulties faced by Fourier inversion methodologies on our test data set.
Section 5 presents arguments for the selection of parametric models describing the local motion of the underlying asset price.
Section 6 develops the mechanics for finite state continuous time Markov chain approximation methodologies. Results based on spatial homogeneity and time inhomogeneity for our test case data set are presented in
Section 7.
Section 8 reports results for stylized models permitting spatial inhomogeneity coupled with time homogeneity.
Section 9 reports results for both time and spatial inhomogeneity for our test case.
Section 10 concludes.
2. Option Trading Over Time
The number of options traded, their moneyness and the number of maturities quoted have been developing over time. Back in the late 1990s, when Fourier transform technology was developed, the concern was over a few hundred options across some ten maturities for the index options and a smaller set for single names. The range of moneyness measured as the log strike to forward ratio was within typically plus or minus The Fourier methodology served this purpose well for the decade 1998–2008. The year 2008 was hit by a financial crisis demonstrating substantial downward moves in asset prices occurring over a short period that was well within existing option maturities. The result has been a growth in the number of options being traded, their moneyness spread and the number of maturities being traded.
Here we first present graphs for the number of option quotes, their moneyness levels and the number of maturities quoted below the maturity of two and a half years over the period 2001 to 2018 for the S&P 500 Index (
) as the underlying asset. Also presented are graphs for options on
the exchange traded fund tracking the
over the period 2013–2018.
Figure 1 presents kernel smoothed data on these magnitudes.
The number of options traded has grown to a few thousand while the number of maturities has more than doubled to over The moneyness on the down side has moved substantially. The shifts have occurred since the crisis of Since 2014 we have weekly options trading and initially the expiries were on Friday but now also include Mondays and Wednesdays. The time to maturity can then be as low as a few days with a substantial strike range. At some intermediate and longer maturities we also have a large number of strikes trading that are quite far from the forward and pose particular problems for Fourier inversion technology. The data sets call for new pricing technologies and after reviewing the associated no arbitrage requirements we go on to develop one such technology.
3. No Arbitrage Considerations
Suppose we have out of the money European option prices
for strike
K and maturity
on an underlying asset with current spot price
and forward price
for maturity
T. For
the price is that for a put options while for
the price is that of a call option. The respective payoffs are
and
where
denotes the unobserved price of the asset at time
Let
denote the current discount curve or the price of a risk free dollar promised at time
A static arbitrage is a trade initiated today with all positions being held to the longest maturity accessed at zero initial cost that unwinds at a nonnegative, nonzero, final (at longest maturity held) outcome. In the absence of static arbitrage nonnegative, nonzero final outcomes must have a positive current cost. Furthermore, under the law of one price the value of a linear combination of positions must be the value of the same linear combination of their payoffs. As a consequence (
Ross 1978) for each fixed
T there exists a state pricing kernel
such that for a portfolio of positions delivering
its value
is
In particular
From the absence of static arbitrage the value of nonnegative, nonzero
are positive and hence
h is nonnegative. Defining a probability density
by
we observe that
or that valuations are given by discounted expected values taken with respect to the market implied densities
In particular
Differentiaton with respect to
K (
Breeden and Litzenberger 1978) yields that the absolute value of the derivative is a tail probability under the density
q
where
Thus the static arbitrage free option prices contain valuable information on the implied pricing densities.
Since the forward contract delivering
at time
T has a zero initial cost it follows that
It follows that
has densities
that all have a unit expectation. Explicitly we have that
It is shown in
Appendix A that these densities are increasing in the convex order. As a consequence there exists a one dimensional Markov martingale
(
Kellerer 1972,
Carr and Madan 2005,
Davis and Hobson 2007) starting at unity with probability law
such that for all
T
Numerous papers focus attention on conditions to be placed on implied volatilities consistent with positive values for butterfly and calendar spread arbitrages and thereby the absence of arbitrage with no explicit construction of the implied one dimensional Markov martingale. The focus here will be on such explicit constructions.
The supposition of this section so far of assuming that one has access to option prices free of static arbitrage is generally false. What one may have is access to best bid and offer prices that are not necessarily simultaneously updated but with some level of synchronicity for end of day prices. Mid quotes for volatilities may be constructed using some weighting structures or least squares approximations delivered by models to such. It is not at all clear that the resulting prices are arbitrage free. Nonetheless, for various marking and valuation purposes there is an interest in constructing arbitrage free approximations to such potentially arbitrageable mid quote constructions. Hence the fitting of option quotes exactly, using arbitrage free frameworks, is not even to be attempted. The observed prices are to be treated as perhaps close to some arbitrage free collection and only approximations to these candidate quotes are being sought.
4. Fourier Transform Issues
Fourier transform-based pricing especially when it is conducted using the fast Fourier transform is very efficient and fast. The construction exploits the fact that the large step characteristic function is based on multiplying the characteristic functions relevant for various subintervals. In this regard it is well suited to regime switching models as developed for example in
Elliott and Osakwe (
2006). More generally they are applicable when infinitesimal generators are linear in state variables (
Duffie et al. 2000,
2003). However, there is a deficiency in the approach that arises for extreme strikes far out in the tails where the calculations can be unstable. The instability arises as trigonometric approximations get oscillatory with unreliable sums as one gets further out in the tails.
We recognize that the Fourier transform approach has significant advantages, not least among which is its speed. It is more than adequate for numerous applications and the objective is not to diminish these features that we continue to employ in a variety of contexts. The intention is to develop and advance the Markov chain approximation as an alternate that has its own advantages and possible applications. The particular Fourier pricing approach being reported on here is that of
Carr and Madan (
1999) with
points delivering prices at strikes determined by the strike spacing. The prices for actual traded strikes are interpolated from these values. The method has been widely implemented for some twenty years now and we were motivated to consider the Markov chain method on observing problems in this traditional method in the extreme tail strikes now being traded. Additionally, the Markov chain method has its own advantages when infinitesimal generators are no longer linear in state variables as is the case for affine processes by construction.
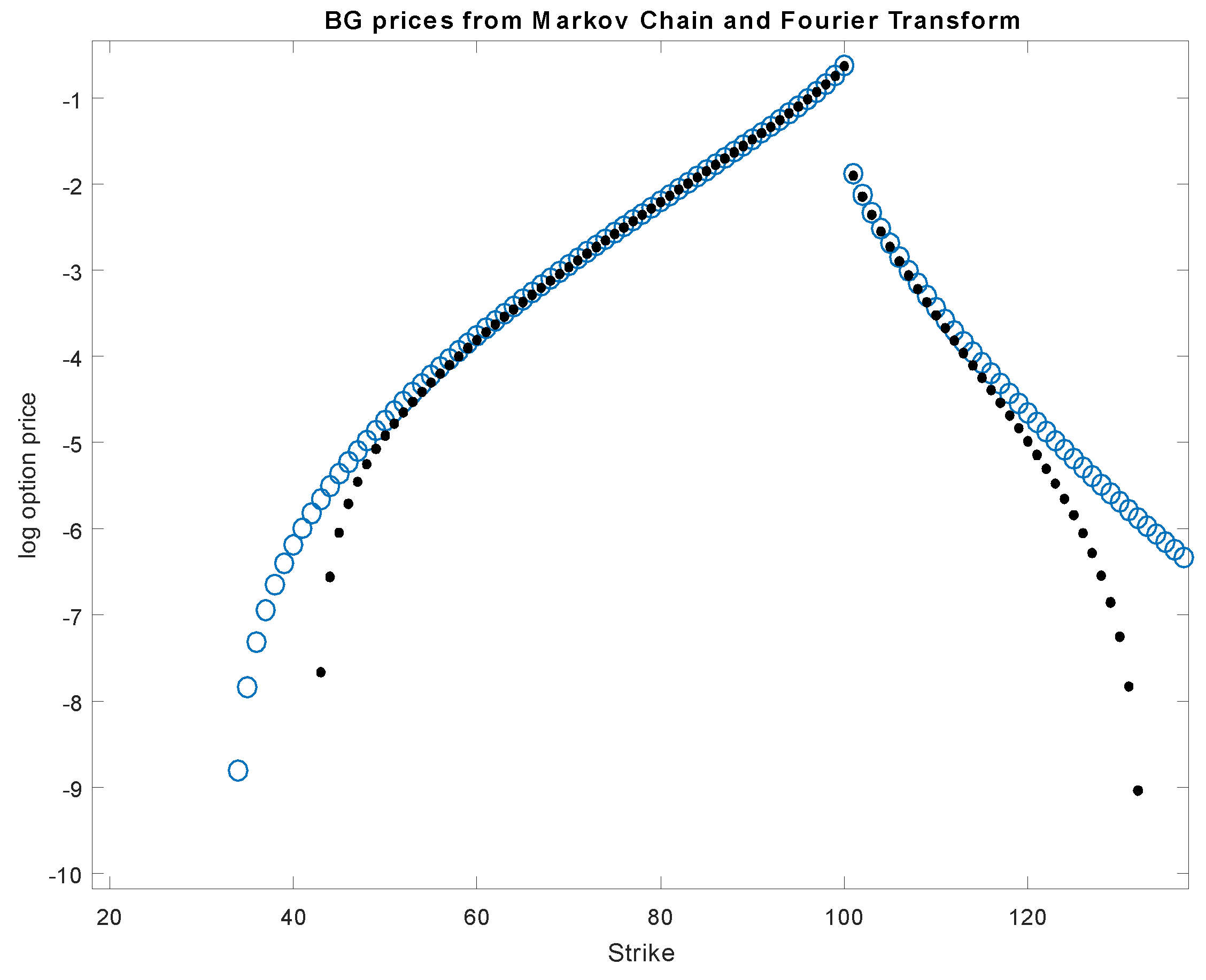
To highlight this issue we take the logarithm of the stock to be driven by a bilateral gamma Lévy process introduced in detail later in the paper and construct the option prices in two ways for a stylized parameter set. The first way is to employ an 800 point finite state continuous time Markov chain approximation building transition rate matrices whose matrix exponential raised to power of the time horizon delivers the probability element that may be used to evaluate option prices. The second uses the classical Fourier inversion methodology. For the bilateral gamma parameter set
with a maturity of
and strikes ranging from 30 to 130 for a spot of 100 and zero rates and dividend yields
Figure 2 presents both calculations.
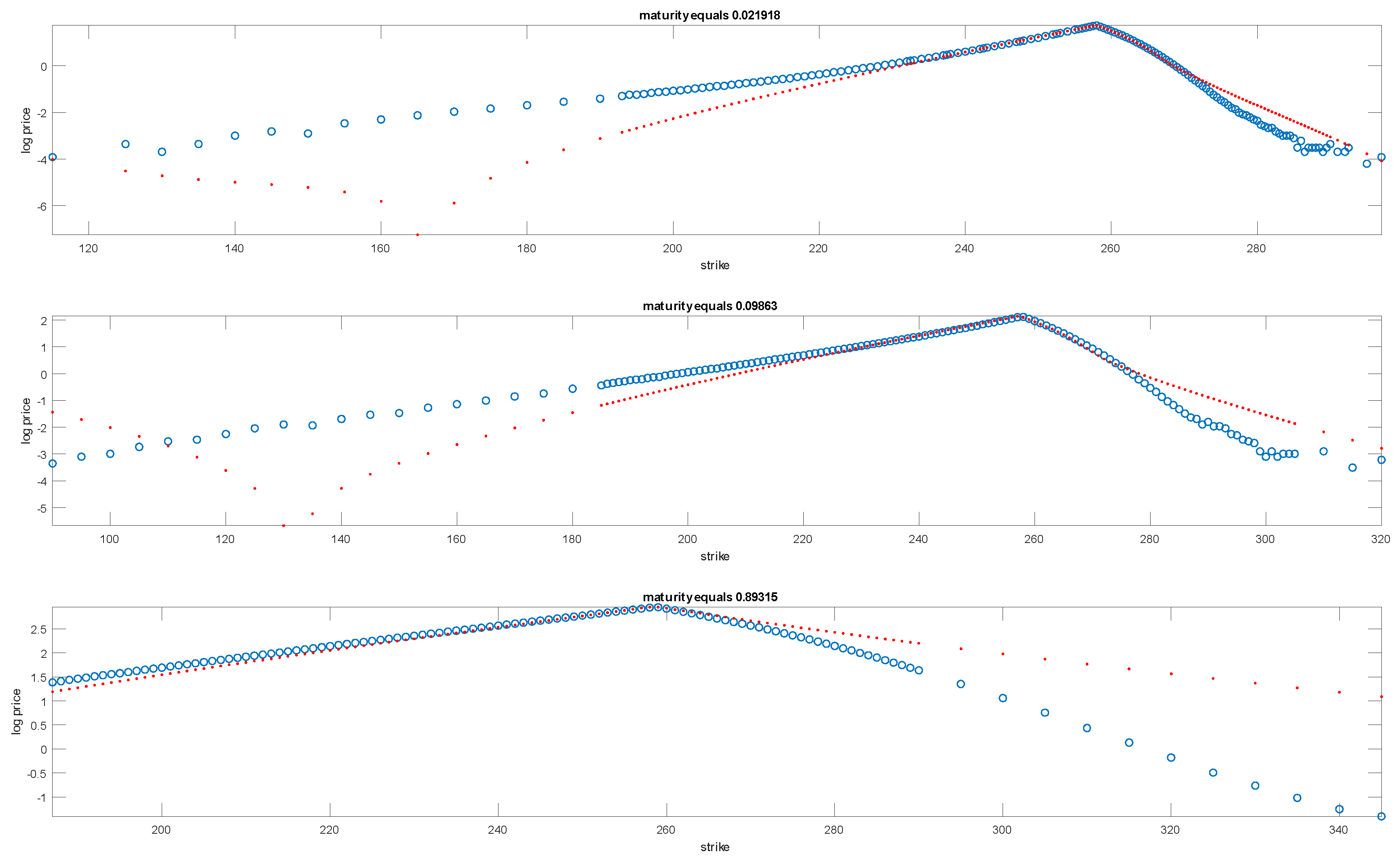
On actual data we estimated the bilateral gamma model separately for each of 28 maturities for
options as at 20180208 by the Fourier transform methodology and present a sample of model log prices as functions of strike along with log quoted price at a handful of nine sample maturities in
Figure 3. The regions where put prices decline and call prices increase are when model prices have gone negative. We observe an inability in model performance especially at the shorter maturities.
For three maturities where the results were not good the graphs are presented in
Figure 4.
One observes that here the strike range is very wide indeed and this has impacted the ability of the optimizer to cope with the required calibration when constrained to Fourier inversion. Given the ability of Markov chain approximations to be more stable over a wider range and their ability to cope with the absence of independence in evolution we turn our attention to developing this methodology as an alternative particularly relevant to current market conditions where strike ranges of interest have grown considerably.
Table 1 presents a sample of fitted and quoted out-of-the-money put option prices for
as at 27 December 2017 for the maturity of 23 days.
5. Modeling Transition Rates
For a one dimensional Markov process for the asset price
or more exactly its logarithm
one has to specify the law of motion as a function of the level of the process
X and the current time
t. A classical example is the risk neutral Dupire local volatility model where the local motion is a Brownian motion with some volatility
and drift equal to the interest rate
r for the asset price and
for the logarithm. This is a very restrictive single parameter local motion. It is a maximal entropy law conditional on the drift and variance level. The literature has however questioned the relevance of the use of a normal distribution with respect to calendar time.
Clark (
1973) and
Ané and Geman (
2002) have argued for the use of the normal distribution with respect to a random time change related to economic activity. Specific models incorporating such random time changes include the variance gamma model of
Madan and Seneta (
1990) and
Madan et al. (
1998) among others. Some other examples are presented in
Barndorff-Nielsen (
1998), and
Eberlein and Keller (
1995). More recently,
Madan et al. (
2018) argue that for a maximal entropy time change the time change should follow a gamma distribution and this delivers the variance gamma model of
Madan and Seneta (
1990). It was already observed in
Madan and Seneta (
1990) that the variance gamma model is a difference of two independent gamma processes each separately modeling the upward and downward motion of markets. Differentiating the drift on the two sides delivers the three parameter variance gamma model of
Madan et al. (
1998) that may also be cast as Brownian motion with drift time changed by a gamma process with unit and a positive variance rate. When written as the difference of two gamma processes the two processes have the same speed or variance rates but different scaling coefficients. More recently
Madan and Wang (
2017),
Madan et al. (
2017) have argued for differentiating the speeds for the upward and downward processes on noting that data support smaller and more frequent up moves as compared to the downward moves. These observations are consistent with the remark that markets take the escalator up and the elevator down. This kind of asymmetry is also reflected in the widening downside moneyness reported earlier relative to the stable up side moneyness levels. The difference of two gamma processes with differing scale and speed on both sides is referred to as the bilateral gamma model as first introduced in
Küchler and Tappe (
2008).
Madan et al. (
2018) also note that maximal entropy considerations for upward and downward motions suggest gamma process models for the two sides. These considerations suggest the use of a four parameter bilateral gamma model for the local motion of the logarithm of the asset price. There is uncertainty in both directions and this uncertainty has separate directional drifts and volatility rates suggestive of a minimal four parameter model for the local motion. A classical exponential correction is employed to lock in the right forward price, thereby formulating martingale models for the asset price relative to the forward as is required by the no arbitrage conditions.
The standard gamma process
has time
t density
given by
The characteristic function is
The process is an infinitely divisible increasing pure jump process with Lévy density
The general gamma process has scale and speed coefficients
with the process being
with density
given by
The characteristic function is
and Lévy density
The bilateral gamma process is the difference of two independent gamma processes with parameters for the positive and negative components of
and
respectively with
where
are two independent gamma processes. The characteristic function for
X is
We take the local motion to be bilateral gamma where all the four parameters may depend nonlinearly on
using deterministic functions
and
The bilateral gamma process has a complicated probability density identified in
Küchler and Tappe (
2008). However, in building transition rates the Lévy measures suffice and they are analytical and fairly simple.
6. Continuous Time Markov Chain Approximations
The first step in building continuous time Markov chain approximations to Markov processes is to define the state space. Here we follow
Mijatovič and Pistorius (
2011) to employ a non-uniform grid for the state space. The total number of points
M is taken to even, while
are the lowest and highest values for the logarithm of the spot price. The current value is
There are two density parameters
and
and on setting
and
the grid is defined by
We employed a low volatility of
and set
Note that
and
The next step is the construction of the transition rate matrix from state i to state j at time For all rows The current state is and we seek the transition rates to states The first and last rows of A are identically zero to kill the process at these boundaries. For rows 3 to we proceed as follows. One first looks up the deterministic functions however specified to obtain and and set
For
and
, thereby ignoring for now the immediately upper and lower diagonals, one defines the jump size distance
The transition rates are defined in terms of tail measure functions
Specifically
For the upper and lower diagonal we need to determine the two value and For this purpose if the local quadratic variation is high enough or above a threshold, we employ a diffusion approximation. Otherwise we just organize getting drift correct for the move in the stock price.
Let
and
The total quadratic variation is
while the local quadratic variation is the integral of
against the Lévy measure in the interval
where
and
that we denote by
We employed the diffusion approximation if
For this approximation the vector
satisfies
where
and defining
set
When
is below one percent of the aggregate quadratic variation
we just monitor the drift and define
If
we set
and set
while for
we set
and
For the second row we take the third from the second element onwards followed by a trailing zero with diagonal reset as the negative of the off diagonal. Similarly for last but one we take the first elements of the last but two starting with an initial zero and reset the diagonal. This completes the definition of a transition rate matrix at a particular
Transition rate matrices
are defined at a finite set of time points
for
using the space dependence for this maturity that applies for all times
and greater than
To access the probability element at an arbitrary time
t let
k be the largest
j below
The probability element at time
t is given by the central row of
This probability element is then used to price options at time
t by discounting expected payouts using the probability element.
Though attention is restricted here to one dimensional Markov process approximations the general method of Markov chain approximations has been extended to multifactor models in
Cui et al. (
2017) and
Kirkby et al. (
2017). Stochastic local volatility extansions may be found in
Cui et al. (
2018) along with a rigorous error analysis in
Li and Zhang (
2017). The time dependence is however accommodated in a piecewise fashion as opposed to employing smooth functions for the time dependence as appear in local volatility models of
Dupire (
1994) and
Carr et al. (
2003).
7. Bilateral Gamma Extensions
As already noted the data set for the results reported in this paper are options on as at 8 February 2018 comprising 2695 options over 28 maturities. Two sets of results are presented, one for the Fourier transform approach applied to the Sato process based on the bilateral gamma model at unit time across all 28 maturities. The second employs bilateral gamma evolution in each of seven time intervals using a continuous time Markov chain approximation with no space inhomogeneity as the parameters are kept invariant to the current stock price. There is only a time dependence in the transition rate matrices for These results are reported in separate subsections.
7.1. Fourier Transform Applied to the Sato Process Based on The Bilateral Gamma
The Sato process based on the variance gamma model was introduced in
Carr et al. (
2007) on recognizing that Lévy processes were structurally incapable of fitting option prices across maturities. It was observed in
Konikov and Madan (
2002) that all Lévy processes by virtue of the linearity of the characteristic exponent in time, had skewness and excess kurtosis of term return distributions that fell like the reciprocal of the square of the term or the term respectively. However, these entities may be estimated model free from option prices using the results of
Breeden and Litzenberger (
1978) to determine that they may be constant or slightly increasing or decreasing with the term, but definitely not decreasing at rates embedded in Lévy processes. These observations led
Carr et al. (
2007) to consider time scaling and make links to the works of
Sato (
1991). Sato showed that for a subclass of infinitely divisible laws and hence laws of Lévy processes at unit time termed self-decomposable laws one may also associate with them an additive process that reproduces as its marginal distributions the distribution at unit time scaled by a function of time. Furthermore if one invokes the hypothesis of self similarity the scaling function reduces to a power function of the time to maturity.
Carr et al. (
2007) observed that he variance gamma model had a unit time distribution that was self decomposable and hence the additive process identified by Sato was available as a candidate process possibly consistent with return distributions embedded in option prices across maturities. Empirical work reported in their paper confirmed the adequacy of such processes now called Sato processes as adequate models for option data across strike and maturity. They reported on the performance of a variety of self decomposable laws with the variance gamma being among the simplest and empirically adequate ones. One easily observes that the bilateral gamma extension of the variance gamma is also self decomposable and hence there is a Sato process associated with the bilateral gamma model at unit time.
It is also worth noting that self decomposable laws were characterized by
Lévy (
1937) and
Khintchine (
1938) as limit laws much like the Gaussian law itself on allowing more general scaling functions than the square root of the number of independent of shocks being averaged in taking the limit. Given the large number of potential news events and shocks being responded to in markets over a short period like day or so, it seems reasonable to restrict modeling attention to such limit laws at unit time. We therefore proceed here with the Sato process associated with the bilateral gamma model at unit time. Let
X be a bilateral gamma law at unit time with parameters
and
. The marginal laws at other maturities
t for the Sato process are given by
for a scaling coefficient
The characteristic function for
is then derived as
Hence the Sato process model termed
after scaled self decomposable associated with the bilateral gamma, is five parameter model including the scaling parameter
along with the four bilateral gamma parameters.
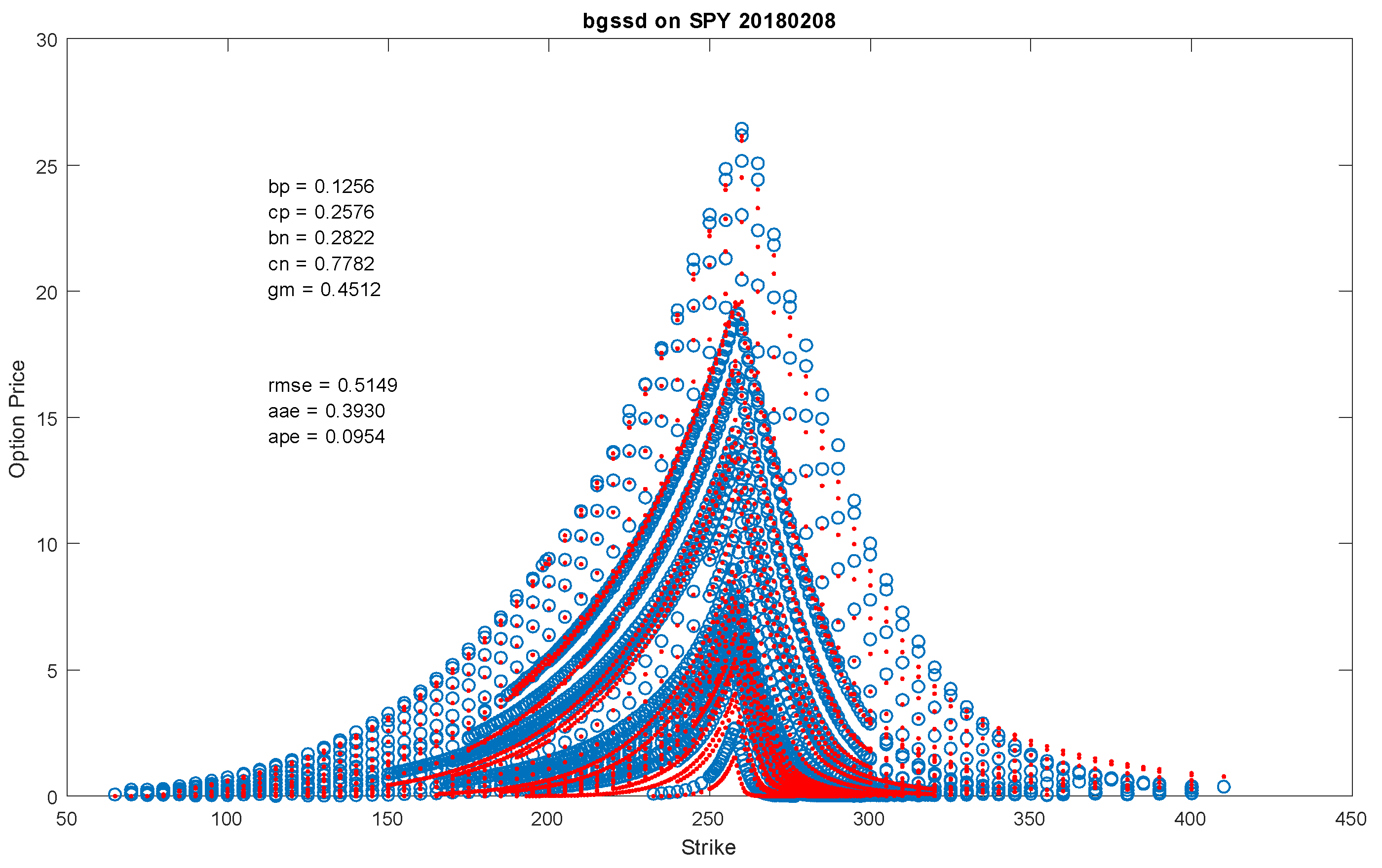
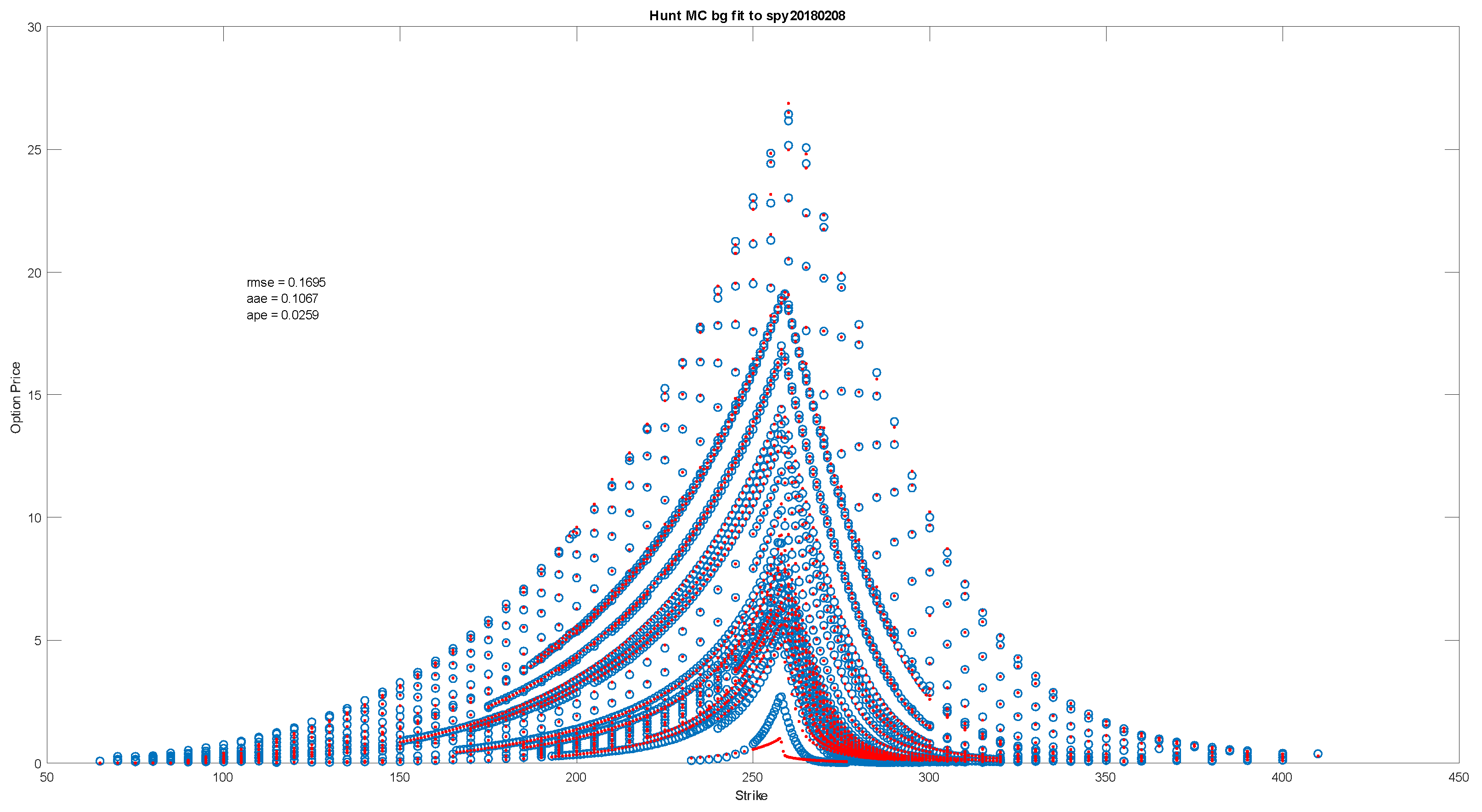
This model was fit to all 2695 options on
as at 8 February 2018 using the Fourier inversion methods of
Carr and Madan (
1999). The result of the fit is presented in
Figure 5 that also reports the parameter values and fit statistics. An average percentage error of near nine percent is a bit too high to consider the model as an acceptable one for many applications. One may observe some of the poorer fits in the tails on a log price plot, a feature characteristic of Fourier methods for strikes this far out.
7.2. Forward Bilateral Gamma via Markov Chain Approximation
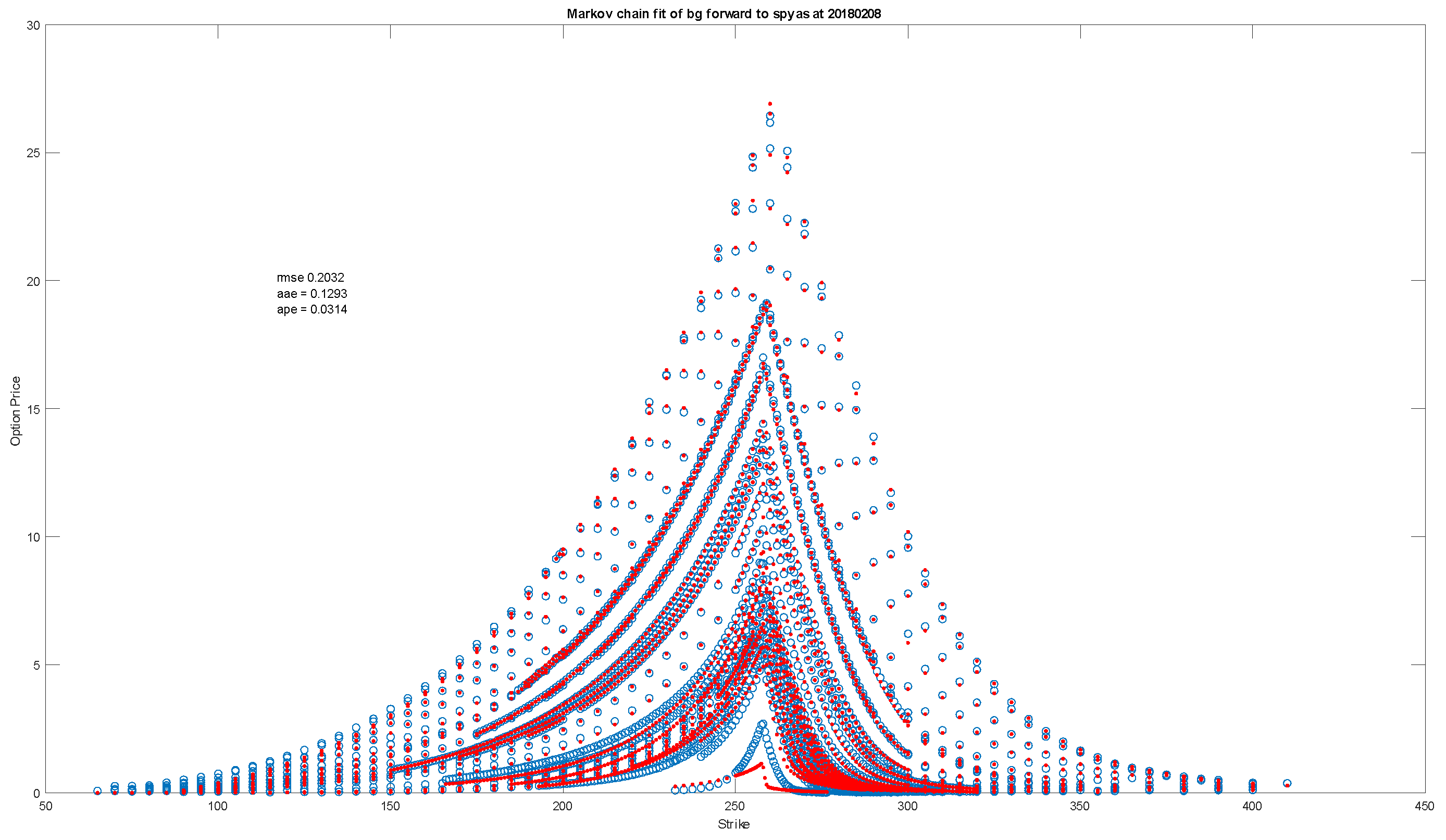
The forward bilateral gamma construction supposes that the bilateral gamma parameters for the local motion of the logarithm of the asset price depend just on calendar time and are independent of the level of the asset price. Here we also take the dependence on time to be piecewise constant with a pre-specified set of time points at which the parameters change. For our test case of the as at 8 February 2018 we have all maturities below 2 years. The pre-specified time points for parameter shifts were set at a week, a month, a quarter, a half year, a year, a year and a half and two years. The parameters relevant for an arbitrary time point t are those for the smallest pre-specified point above The total number of pre-specified time points is seven and with four bilateral gamma parameters to be estimated at each of these time points we have parameters in the forward bilateral gamma model. The parameters are used to build seven transition rate matrices for the time points The Markov chain approximation then delivers the probability elements for arbitrary t that is used to evaluate expected payouts discounted to time zero for the option prices.
Figure 6 presents a graph of the fit along with fit statistics. The calibrated parameter values are presented in a matrix displaying seven rows for the four bilateral gamma at each pre-specified time point.
The calibrated parameter matrix was as follows
Table 2. The four columns present the values for
and
8. Stylized Bilateral Gamma Spatially Inhomogeneous and Temporally Homogeneous Model Results
Before attempting a calibration of a spatially inhomogeneous model on our test data set we first report on an investigation of a calibration on a stylized data set where the exact dependence of parameters on the underlying asset price is known by construction. The dependence of parameters on the logarithm of underlying asset price was modeled using logistic functions of the form
whereby
is the left limit for the parameter value while
is the right limit and
controls the speed of transition. The stylized data was generated using
with the left and right limits for the four parameters as presented in
Table 3.
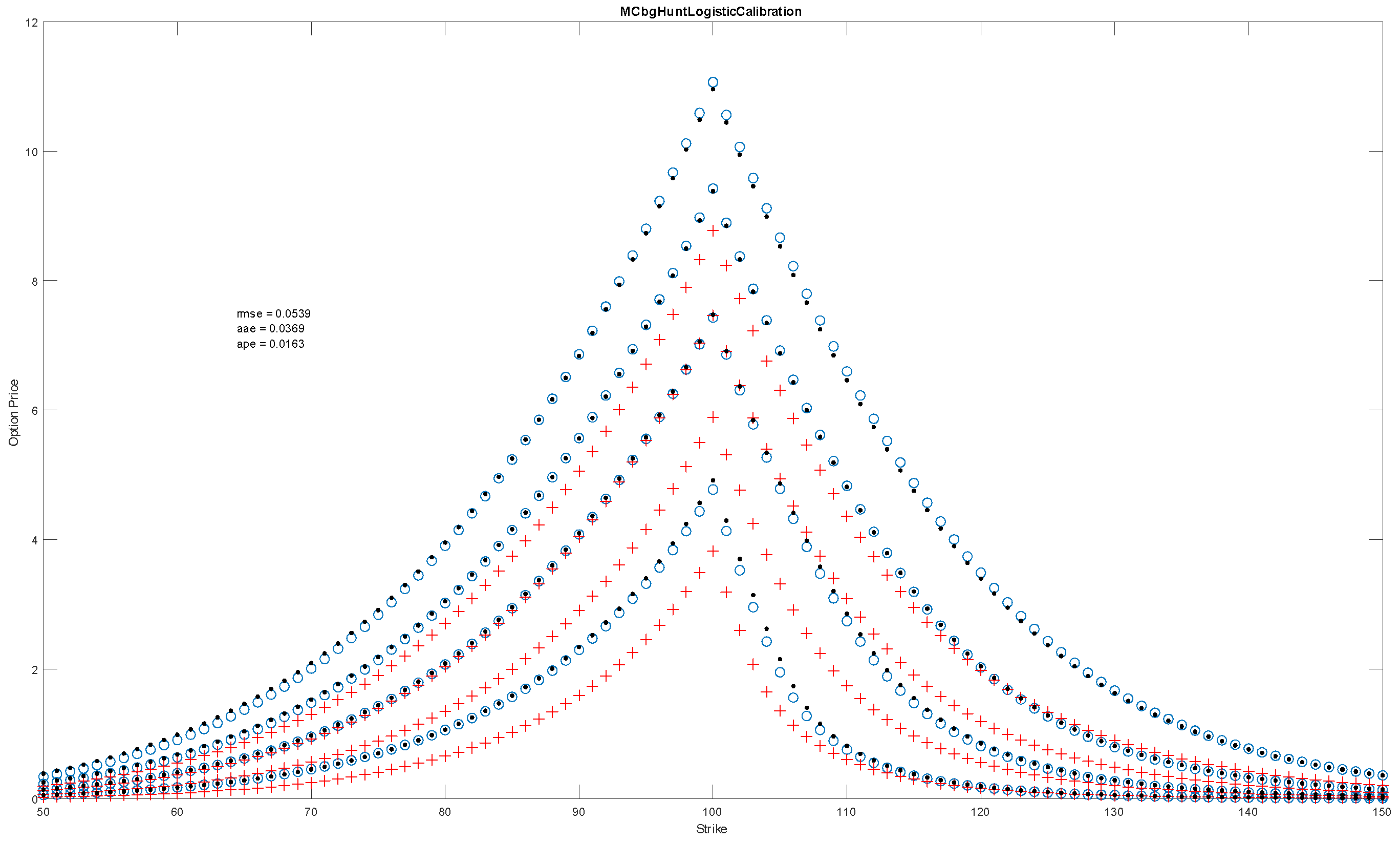
This parametric dependence was used to generate stylized true option values at four maturities of and 12 months for 101 strikes ranging from 50 to 150 in steps of a dollar with the spot at 100 and zero rates and dividends. A graph of these prices against their strikes for all four maturities is presented when the calibration fit is later displayed.
For the space dependence to be calibrated we do not suppose any knowledge of the functional form of this dependence. Hence we cannot estimate the parameters of the logistic function. Instead we fix a grid of seven points for the log price relative to the forward. These values were taken at and For a starting value for the parameters we take the value of the parameter specific logistic function evaluated at these points. The calibration employs a nonlinear Gaussian process regression as an interpolator and extrapolator to infer the intermediate values at arbitrary levels of moneyness for which parameter values may be sought. Hyper parameters in the Gaussian process regression were frozen upfront.
Figure 7 presents the stylized true values, the prices at the initial starting point, and the model calibrated values using a single transition matrix as there is no time dependence.
The calibrated parameters are presented
Table 4.
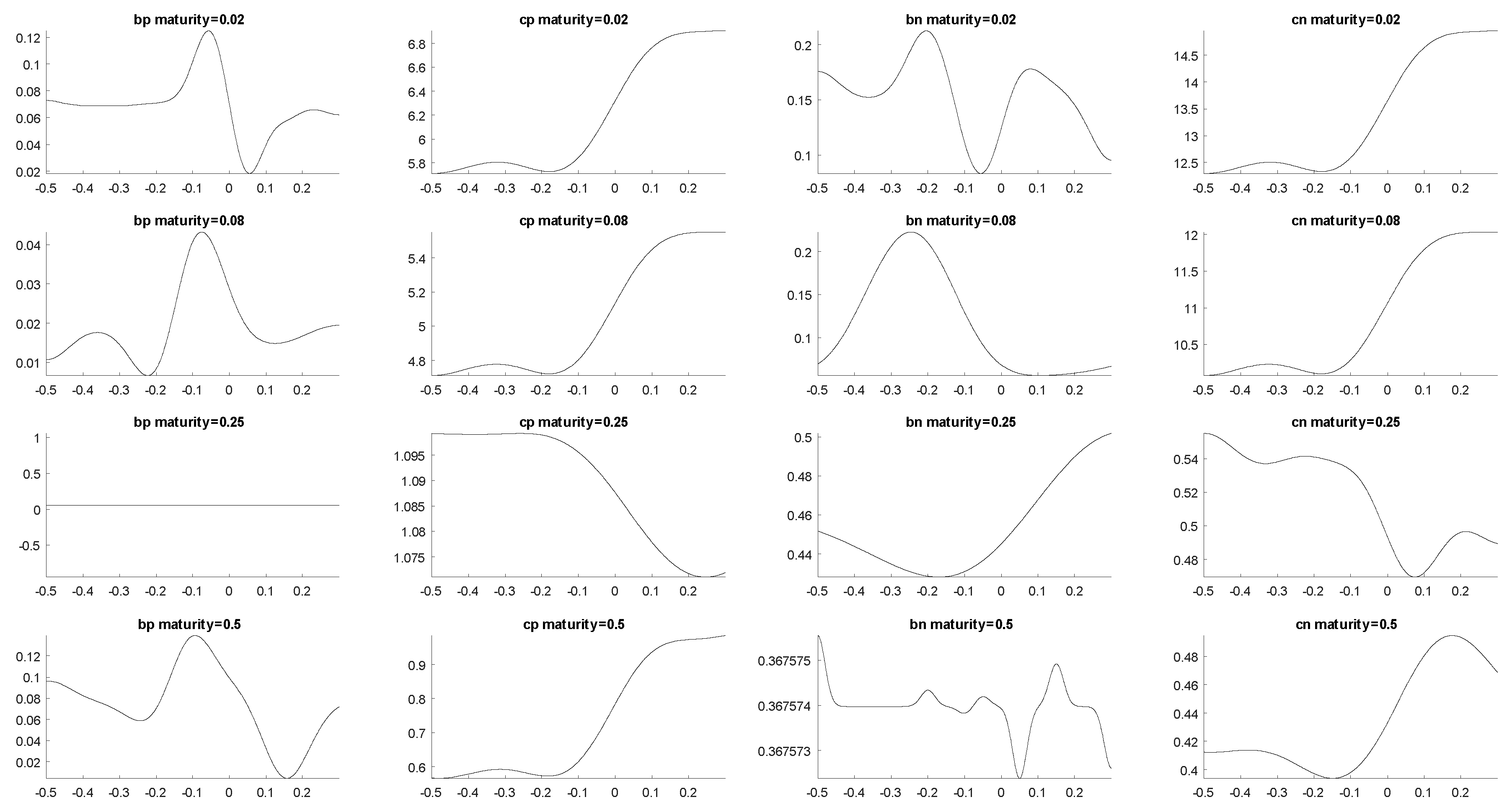
Additionally, we present in
Figure 8 a graph of the true functional dependence between each of the four parameters and the calibrated dependence as constructed from the values reported in
Table 2 using Gaussian process regression with the frozen hyper parameters. We observe that the first four parameters were reasonably well calibrated but the behavior of
was not captured in this exercise.
9. Time and Space Inhomogeneity for Local Bilateral Gamma as Applied to on 8 February 2018
We finally present the results for both a space and time dependence of all four parameters. With a seven point space and time grid each of the four parameters requires a specification of values for the space time dependence. The result is a model with parameters. As a starting value we used the result from the model for the time dependence. For the space dependence we take the parameter values in the forward model at an intermediate value and a final value and set these as left and right limits for a logistic interpolation using the value for the rate at which the logistic function moves from left to right.
Figure 9 presents a graph of the fit along with the fit statistics.
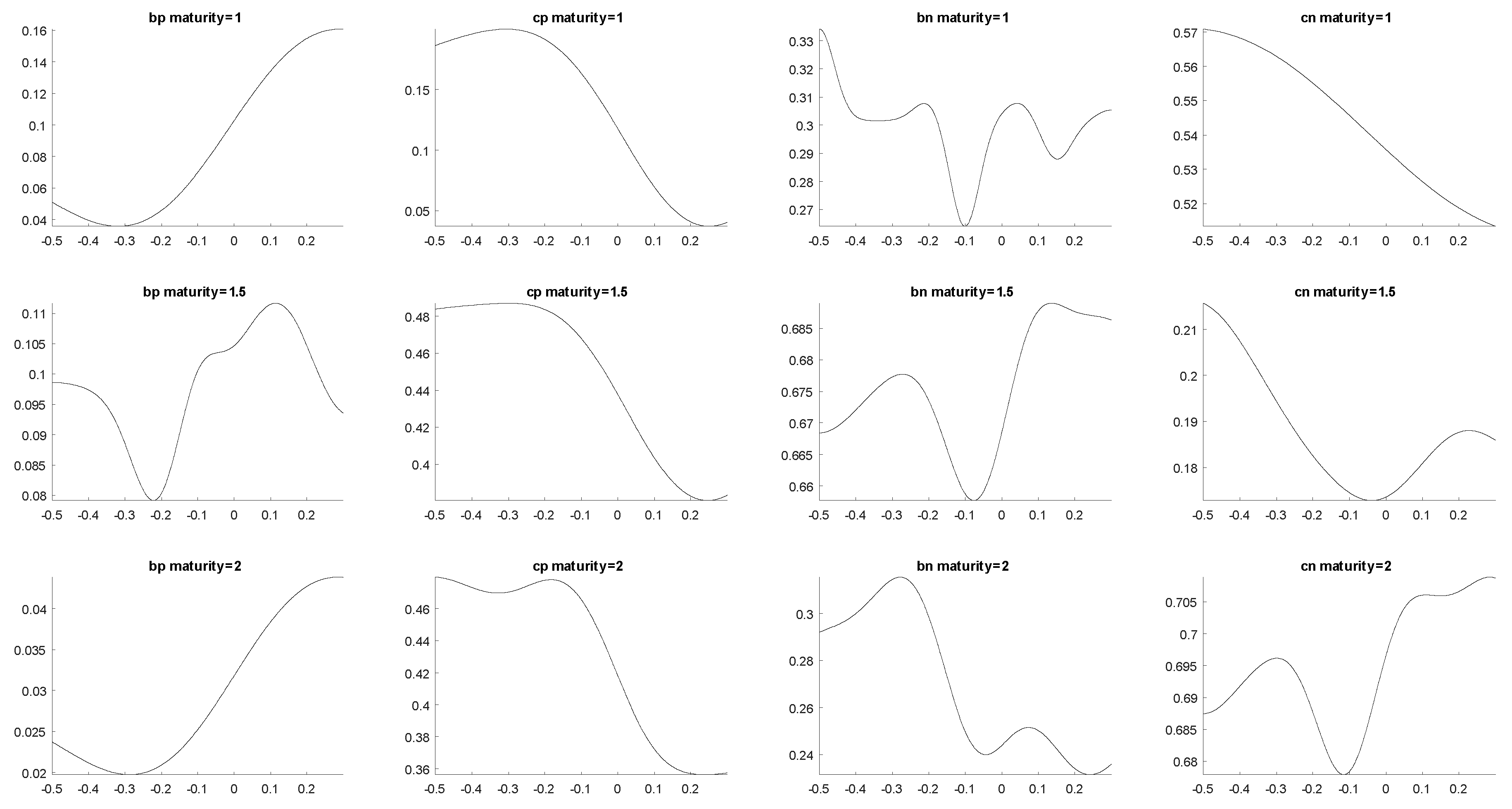
Additionally, we present in
Figure 10 and
Figure 11 the estimated functional dependence of the four parameters on moneyness for the first four and last three maturities respectively.
10. Conclusions
It is argued that the expansion in the number of maturities being currently quoted and the growth in the associated breadth of strikes involved, renders the use of Fourier inversion methodologies for volatility surface calibration relatively problematic. An alternative of continuous time Markov chain approximation is proposed and shown to be adequate, competitive and it is anticipated that the method is also quite stable. It is at the moment slow to implement but this can be addressed in further research devoted to enhancing its speed.
The Markov chain approximation is also more general and not constrained to working with processes with independent increments. It can accommodate a wide variety of local evolution models though the illustrations of the current paper are restricted to the bilateral gamma process. One may easily incorporate subcases with only time or space inhomogeneity but not both. One may also restrict spatial dependence to a subset of parameters as opposed to allowing them all to change.
Calibrations are illustrated for data on 2695 options across 28 maturities for as at 8 February 2018. The Sato process based on the bilateral gamma attains a root mean square error of Just time inhomogeneity with a finite (800) state continuous time Markov chain reduces this to . Allowing spatial dependence takes it down further to