Time-Varying Price–Volume Relationship and Adaptive Market Efficiency: A Survey of the Empirical Literature
Abstract
1. Introduction
- To classify the literature based on the approach to the weak-form of the efficiency
- To categorize the studies in each approach based on the relationships studied
- To compare each relationship studied based on the methodology adopted
- To discover the scope for future research
2. The Random Nature of Price Fluctuations and Efficient Market Hypothesis
“a market with great number of rational profit maximizers actively competing, with each trying to predict future market values of individual securities, and where current important information is almost freely available to all participants.”
3. Adaptive Market Hypothesis
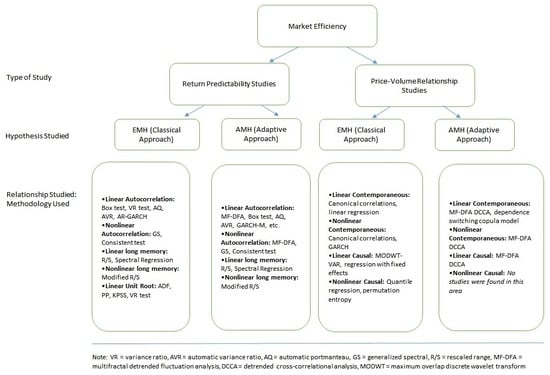
4. Return Predictability Studies
4.1. Return Predictability and EMH
4.2. Return Predictability and AMH
4.2.1. Testing Efficiency with Hurst Exponent
4.2.2. Testing Adaptive Efficiency with Modified Standard Tests
4.2.3. Testing Efficiency Using Both Modified-Standard and MF-DFA Methods
5. Price–Volume Relationship Studies
5.1. Price–Volume Relationship and EMH
5.2. Price–Volume Relationship and AMH
6. Research Gap
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahmed, Amira Akl. 2014. Evolving and relative efficiency of mena stock markets: Evidence from rolling joint variance ratio tests. Ensayos Revista de Economía (Ensayos Journal of Economics) 33: 91–126. [Google Scholar]
- Al-Khazali, Osamah, and Ali Mirzaei. 2017. Stock market anomalies, market efficiency and the adaptive market hypothesis: Evidence from islamic stock indices. Journal of International Financial Markets Institutions and Money 51: 190–208. [Google Scholar] [CrossRef]
- Anagnostidis, Panagiotis, Christos Varsakelis, and Christos J. Emmanouilides. 2016. Has the 2008 financial crisis affected stock market efficiency? the case of eurozone. Physica A: Statistical Mechanics and Its Applications 447: 116–28. [Google Scholar] [CrossRef]
- Andreou, Elena, Nikitas Pittis, and Aris Spanos. 2001. On modelling speculative prices: The empirical literature. Journal of Economic Surveys 15: 187–220. [Google Scholar] [CrossRef]
- Azad, A. S. M. Sohel, Saad Azmat, Victor Fang, and Piyadasa Edirisuriya. 2014. Unchecked manipulations, price-volume relationship and market efficiency: Evidence from emerging markets. Research in International Business and Finance 30: 51–71. [Google Scholar] [CrossRef]
- Bachelier, Louis. 1900. Théorie de la spéculation. In Annales Scientifiques de l’École Normale Supérieure. Paris: Gauthier-Villars, vol. 17, pp. 21–86. [Google Scholar]
- Bacry, Emmanuel, Jean Delour, and Jean-François Muzy. 2001. Modelling financial time series using multifractal random walks. Physica A: Statistical Mechanics and Its Applications 299: 84–92. [Google Scholar] [CrossRef]
- Balcilar, Mehmet, Elie Bouri, Rangan Gupta, and David Roubaud. 2017. Can volume predict bitcoin returns and volatility? A quantiles-based approach. Economic Modelling 64: 74–81. [Google Scholar] [CrossRef]
- Ball, Ray. 1978. Anomalies in relationships between securities’ yields and yield-surrogates. Journal of Financial Economics 6: 103–26. [Google Scholar] [CrossRef]
- Banz, Rolf W. 1981. The relationship between return and market value of common stocks. Journal of Financial Economics 9: 3–18. [Google Scholar] [CrossRef]
- Barkoulas, John T., Christopher F. Baum, and Nickolaos Travlos. 2000. Long memory in the greek stock market. Applied Financial Economics 10: 177–84. [Google Scholar] [CrossRef]
- Basu, Sanjoy. 1977. Investment performance of common stocks in relation to their price-earnings ratios: A test of the efficient market hypothesis. The Journal of Finance 32: 663–82. [Google Scholar] [CrossRef]
- Beaver, William H. 1981. Market efficiency. The Accounting Review 56: 23. [Google Scholar]
- Blume, Lawrence, David Easley, and Maureen O’hara. 1994. Market statistics and technical analysis: The role of volume. The Journal of Finance 49: 153–81. [Google Scholar] [CrossRef]
- Brealey, Richard A., Stewart C. Myers, Franklin Allen, and Pitabas Mohanty. 2011. Principles of Corporate Finance, 10th ed. New York: McGraw-Hill/Irwin. [Google Scholar]
- Caginalp, Gunduz, and Mark DeSantis. 2017. Does price efficiency increase with trading volume? evidence of nonlinearity and power laws in etfs. Physica A: Statistical Mechanics and Its Applications 467: 436–52. [Google Scholar] [CrossRef]
- Cajueiro, Daniel O., and Benjamin M. Tabak. 2004. The hurst exponent over time: Testing the assertion that emerging markets are becoming more efficient. Physica A: Statistical Mechanics and Its Applications 336: 521–37. [Google Scholar] [CrossRef]
- Campbell, John Y., John J. Champbell, John W. Campbell, Andrew W. Lo, Andrew Wen-Chuan Lo, and Archie Craig MacKinlay. 1997. The Econometrics of Financial Markets. Princeton: Princeton University Press. [Google Scholar]
- Campbell, John Y., Sanford J. Grossman, and Jiang Wang. 1993. Trading volume and serial correlation in stock returns. The Quarterly Journal of Economics 108: 905–39. [Google Scholar] [CrossRef]
- Charfeddine, Lanouar, and Karim Ben Khediri. 2016. Time varying market efficiency of the gcc stock markets. Physica A: Statistical Mechanics and Its Applications 444: 487–504. [Google Scholar] [CrossRef]
- Charles, Amélie, and Olivier Darné. 2009. Variance-ratio tests of random walk: An overview. Journal of Economic Surveys 23: 503–27. [Google Scholar] [CrossRef]
- Charles, Amélie, Olivier Darné, and Jae H. Kim. 2017. Adaptive markets hypothesis for islamic stock indices: Evidence from dow jones size and sector-indices. International Economics 151: 100–12. [Google Scholar] [CrossRef]
- Chen, Gong-Meng, Michael Firth, and Oliver M. Rui. 2001. The dynamic relation between stock returns, trading volume, and volatility. Financial Review 36: 153–74. [Google Scholar] [CrossRef]
- Chen, Shiu-Sheng. 2012. Revisiting the empirical linkages between stock returns and trading volume. Journal of Banking and Finance 36: 1781–88. [Google Scholar] [CrossRef]
- Cheung, Yin-Wong, and Kon S. Lai. 1995. Practitioners corner: Lag order and critical values of a modified dickey-fuller test. Oxford Bulletin of Economics and Statistics 57: 411–19. [Google Scholar] [CrossRef]
- Chordia, Tarun, and Bhaskaran Swaminathan. 2000. Trading volume and cross-autocorrelations in stock returns. The Journal of Finance 55: 913–35. [Google Scholar] [CrossRef]
- Chuang, Chia-Chang, Chung-Ming Kuan, and Hsin-Yi Lin. 2009. Causality in quantiles and dynamic stock return–volume relations. Journal of Banking & Finance 33: 1351–60. [Google Scholar]
- Ciner, Cetin. 2015. Time variation in systematic risk, returns and trading volume: Evidence from precious metals mining stocks. International Review of Financial Analysis 41: 277–83. [Google Scholar] [CrossRef]
- Clark, Peter K. 1973. A subordinated stochastic process model with finite variance for speculative prices. Econometrica 41: 135–55. [Google Scholar] [CrossRef]
- Conrad, Jennifer, and Gautam Kaul. 1988. Time-variation in expected returns. Journal of Business 61: 409–25. [Google Scholar] [CrossRef]
- Cont, Rama. 2001. Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance 1: 223–36. [Google Scholar] [CrossRef]
- Cootner, Paul H. 1962. Stock prices: Ramdom vs. systematic changes. Industrial Management Review (pre-1986) 3: 24. [Google Scholar]
- Copeland, Thomas E. 1976. A model of asset trading under the assumption of sequential information arrival. The Journal of Finance 31: 1149–68. [Google Scholar] [CrossRef]
- Cornelius, Peter K. 1993. A note on the informational efficiency of emerging stock markets. Review of World Economics 129: 820–28. [Google Scholar] [CrossRef]
- Cowles, Alfred. 1933. Can stock market forecasters forecast? Econometrica 1: 309–24. [Google Scholar] [CrossRef]
- Crouch, Robert L. 1970. The volume of transactions and price changes on the new york stock exchange. Financial Analysts Journal 26: 104–9. [Google Scholar] [CrossRef]
- Daniel, Kent D., David Hirshleifer, and Avanidhar Subrahmanyam. 2001. Overconfidence, arbitrage, and equilibrium asset pricing. The Journal of Finance 56: 921–65. [Google Scholar] [CrossRef]
- De Bondt, Werner F. M., and Richard Thaler. 1985. Does the stock market overreact? The Journal of Finance 40: 793–805. [Google Scholar] [CrossRef]
- De Bondt, Werner P. M. 1993. Betting on trends: Intuitive forecasts of financial risk and return. International Journal of Forecasting 9: 355–71. [Google Scholar] [CrossRef]
- De Long, J. Bradford, Andrei Shleifer, Lawrence H. Summers, and Robert J. Waldmann. 1990. Noise trader risk in financial markets. Journal of Political Economy 98: 703–38. [Google Scholar] [CrossRef]
- Degutis, Augustas, and Lina Novickytė. 2014. The efficient market hypothesis: A critical review of literature and methodology. Ekonomika 93: 7–23. [Google Scholar] [CrossRef]
- Delcey, Thomas. 2018. Efficient Market Hypothesis, Eugene Fama and Paul Samuelson: A Reevaluation. Discussion Paper hal-01618347. Copenhagen: HAL. [Google Scholar]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Domínguez, Manuel A., and Ignacio N. Lobato. 2003. Testing the martingale difference hypothesis. Econometric Reviews 22: 351–77. [Google Scholar] [CrossRef]
- El Alaoui, Marwane. 2017. Price–volume multifractal analysis of the moroccan stock market. Physica A: Statistical Mechanics and Its Applications 486: 473–85. [Google Scholar] [CrossRef]
- Elliott, Graham, Thomas J. Rothenberg, and James H. Stock. 1996. Efficient tests for an autoregressive unit root. Econometrica 64: 813–36. [Google Scholar] [CrossRef]
- Emerson, Rebecca, Stephen G. Hall, and Anna Zalewska-Mitura. 1997. Evolving market efficiency with an application to some bulgarian shares. Economics of Planning 30: 75–90. [Google Scholar] [CrossRef]
- Epps, Thomas W. 1975. Security price changes and transaction volumes: Theory and evidence. The American Economic Review 65: 586–97. [Google Scholar]
- Epps, Thomas W., and Mary Lee Epps. 1976. The stochastic dependence of security price changes and transaction volumes: Implications for the mixture-of-distributions hypothesis. Econometrica 44: 305–21. [Google Scholar] [CrossRef]
- Escanciano, J. Carlos, and Ignacio N. Lobato. 2009. An automatic portmanteau test for serial correlation. Journal of Econometrics 151: 140–49. [Google Scholar] [CrossRef]
- Escanciano, J. Carlos, and Carlos Velasco. 2006. Generalized spectral tests for the martingale difference hypothesis. Journal of Econometrics 134: 151–85. [Google Scholar] [CrossRef]
- Fakhry, Bachar. 2016. A literature review of the efficient market hypothesis. Turkish Economic Review 3: 431–42. [Google Scholar]
- Fama, Eugene F. 1965. The behavior of stock market prices. Journal of Business 38: 34–105. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1970. Efficient capital markets: A review of theory and empirical work. The Journal of Finance 25: 383–417. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1991. Efficient capital markets: Ii. The Journal of Finance 46: 1575–617. [Google Scholar] [CrossRef]
- Fama, Eugene F. 1998. Market efficiency, long-term returns, and behavioral finance. Journal of Financial Economics 49: 283–306. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1988. Dividend yields and expected stock returns. Journal of Financial Economics 22: 3–25. [Google Scholar] [CrossRef]
- Fama, Eugene F., and Kenneth R. French. 1995. Size and book-to-market factors in earnings and returns. The Journal of Finance 50: 131–55. [Google Scholar] [CrossRef]
- Ferreira, Paulo. 2019. Assessing the relationship between dependence and volume in stock markets: A dynamic analysis. Physica A: Statistical Mechanics and Its Applications 516: 90–97. [Google Scholar] [CrossRef]
- Ferson, Wayne E., and Campbell R. Harvey. 1993. The risk and predictability of international equity returns. Review of Financial Studies 6: 527–66. [Google Scholar] [CrossRef]
- Gagnon, Louis, and G. Andrew Karolyi. 2009. Information, trading volume, and international stock return comovements: Evidence from cross-listed stocks. Journal of Financial and Quantitative Analysis 44: 953–86. [Google Scholar] [CrossRef]
- Gârleanu, Nicolae, and Lasse Heje Pedersen. 2018. Efficiently inefficient markets for assets and asset management. The Journal of Finance 73: 1663–712. [Google Scholar] [CrossRef]
- Gebka, Bartosz, and Mark E. Wohar. 2013. Causality between trading volume and returns: Evidence from quantile regressions. International Review of Economics & Finance 27: 144–59. [Google Scholar]
- Ghazani, Majid Mirzaee, and Seyed Babak Ebrahimi. 2019. Testing the adaptive market hypothesis as an evolutionary perspective on market efficiency: Evidence from the crude oil prices. Finance Research Letters 30: 60–68. [Google Scholar] [CrossRef]
- Gilson, Ronald J., and Reinier H. Kraakman. 1984. The mechanisms of market efficiency. Virginia Law Review 70: 549–644. [Google Scholar] [CrossRef]
- Godfrey, Michael D., Clive W. J. Granger, and Oskar Morgenstern. 1964. The random-walk hypothesis of stock market behavior. Kyklos 17: 1–30. [Google Scholar] [CrossRef]
- Gozbasi, Onur, Ilhan Kucukkaplan, and Saban Nazlioglu. 2014. Re-examining the turkish stock market efficiency: Evidence from nonlinear unit root tests. Economic Modelling 38: 381–84. [Google Scholar] [CrossRef]
- Grossman, Sanford J., and Joseph E. Stiglitz. 1980. On the impossibility of informationally efficient markets. The American Economic Review 70: 393–408. [Google Scholar]
- Gündüz, Lokman, and Abdulnasser Hatemi-J. 2005. Stock price and volume relation in emerging markets. Emerging Markets Finance and Trade 41: 29–44. [Google Scholar] [CrossRef]
- Gupta, Rakesh, and Junhao Yang. 2011. Testing weak form efficiency in the indian capital market. International Research Journal of Finance and Economics 75: 108–19. [Google Scholar]
- Gupta, Suman, Debojyoti Das, Haslifah Hasim, and Aviral Kumar Tiwari. 2018. The dynamic relationship between stock returns and trading volume revisited: A modwt-var approach. Finance Research Letters 27: 91–98. [Google Scholar] [CrossRef]
- Harris, Lawrence. 1987. Transaction data tests of the mixture of distributions hypothesis. Journal of Financial and Quantitative Analysis 22: 127–41. [Google Scholar] [CrossRef]
- Harris, Milton, and Artur Raviv. 1993. Differences of opinion make a horse race. Review of Financial Studies 6: 473–506. [Google Scholar] [CrossRef]
- Hasan, Rashid, and M. Mohammed Salim. 2017. Power law cross-correlations between price change and volume change of indian stocks. Physica A: Statistical Mechanics and Its Applications 473: 620–31. [Google Scholar] [CrossRef]
- He, Ling-Yun, and Shu-Peng Chen. 2011. Nonlinear bivariate dependency of price–volume relationships in agricultural commodity futures markets: A perspective from multifractal detrended cross-correlation analysis. Physica A: Statistical Mechanics and Its Applications 390: 297–308. [Google Scholar] [CrossRef]
- He, Ling-Yun, and Xing-Chun Wen. 2015. Predictability and market efficiency in agricultural futures markets: A perspective from price–volume correlation based on wavelet coherency analysis. Fractals 23: 1550003. [Google Scholar] [CrossRef]
- He, Ling-Yun, Sheng Yang, Wen-Si Xie, and Zhi-Hong Han. 2014. Contemporaneous and asymmetric properties in the price-volume relationships in china’s agricultural futures markets. Emerging Markets Finance and Trade 50: 148–66. [Google Scholar] [CrossRef]
- Hiemstra, Craig, and Jonathan D. Jones. 1994. Testing for linear and nonlinear granger causality in the stock price-volume relation. The Journal of Finance 49: 1639–64. [Google Scholar]
- Hiremath, Gourishankar S., and Seema Narayann. 2016. Testing the adaptive market hypothesis and its determinants for the indian stock markets. Finance Research Letters 19: 173–80. [Google Scholar] [CrossRef]
- Hiremath, Gourishankar S., and Jyoti Kumari. 2014. Stock returns predictability and the adaptive market hypothesis in emerging markets: Evidence from india. SpringerPlus 3: 428. [Google Scholar] [CrossRef]
- Horta, Paulo, Sérgio Lagoa, and Luis Martins. 2014. The impact of the 2008 and 2010 financial crises on the hurst exponents of international stock markets: Implications for efficiency and contagion. International Review of Financial Analysis 35: 140–53. [Google Scholar] [CrossRef]
- Hull, Matthew, and Frank McGroarty. 2014. Do emerging markets become more efficient as they develop? Long memory persistence in equity indices. Emerging Markets Review 18: 45–61. [Google Scholar] [CrossRef]
- Ito, Mikio, Akihiko Noda, and Tatsuma Wada. 2016. The evolution of stock market efficiency in the us: A non-bayesian time-varying model approach. Applied Economics 48: 621–35. [Google Scholar] [CrossRef]
- Jarrow, Robert A., and Martin Larsson. 2012. The meaning of market efficiency. Mathematical Finance: An International Journal of Mathematics, Statistics and Financial Economics 22: 1–30. [Google Scholar] [CrossRef]
- Jennings, Robert H., and Christopher B. Barry. 1983. Information dissemination and portfolio choice. Journal of Financial and Quantitative Analysis 18: 1–19. [Google Scholar] [CrossRef]
- Jensen, Michael C. 1978. Some anomalous evidence regarding market efficiency. Journal of Financial Economics 6: 95–101. [Google Scholar] [CrossRef]
- Karpoff, Jonathan M. 1986. A theory of trading volume. The Journal of Finance 41: 1069–87. [Google Scholar] [CrossRef]
- Karpoff, Jonathan M. 1987. The relation between price changes and trading volume: A survey. Journal of Financial and Quantitative Analysis 22: 109–26. [Google Scholar] [CrossRef]
- Kendall, Maurice George, and A. Bradford Hill. 1953. The analysis of economic time-series-part i: Prices. Journal of the Royal Statistical Society. Series A (General) 116: 11–34. [Google Scholar] [CrossRef]
- Khediri, Karim Ben, and Lanouar Charfeddine. 2015. Evolving efficiency of spot and futures energy markets: A rolling sample approach. Journal of Behavioral and Experimental Finance 6: 67–79. [Google Scholar] [CrossRef]
- Khuntia, Sashikanta, and J. K. Pattanayak. 2018. Adaptive market hypothesis and evolving predictability of bitcoin. Economics Letters 167: 26–28. [Google Scholar] [CrossRef]
- Kiem, Donald B. 1983. Size-related anomalies and stock return seasonality: Further empirical evidence. Journal of Financial Economics 12: 13–32. [Google Scholar] [CrossRef]
- Kim, Jae H., Abul Shamsuddin, and Kian-Ping Lim. 2011. Stock return predictability and the adaptive markets hypothesis: Evidence from century-long u.s. data. Journal of Empirical Finance 18: 868–79. [Google Scholar] [CrossRef]
- Kim, Jae H. 2009. Automatic variance ratio test under conditional heteroskedasticity. Finance Research Letters 6: 179–85. [Google Scholar] [CrossRef]
- Konak, Fatih, and Yasin Şeker. 2014. The efficiency of developed markets: Empirical evidence from ftse 100. Journal of Advanced Management Science 2: 29–32. [Google Scholar] [CrossRef]
- Kruse, Robinson. 2011. A new unit root test against estar based on a class of modified statistics. Statistical Papers 52: 71–85. [Google Scholar] [CrossRef]
- Kwiatkowski, Denis, Peter C. B. Phillips, Peter Schmidt, and Yongcheol Shin. 1992. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? Journal of Econometrics 54: 159–78. [Google Scholar] [CrossRef]
- Lamoureux, Christopher G., and William D. Lastrapes. 1990. Heteroskedasticity in stock return data: Volume versus garch effects. The Journal of Finance 45: 221–29. [Google Scholar] [CrossRef]
- Lee, Bong-Soo, and Oliver M. Rui. 2002. The dynamic relationship between stock returns and trading volume: Domestic and cross-country evidence. Journal of Banking and Finance 26: 51–78. [Google Scholar] [CrossRef]
- Lee, Charles, and Bhaskaran Swaminathan. 2000. Price momentum and trading volume. The Journal of Finance 55: 2017–69. [Google Scholar] [CrossRef]
- LeRoy, Stephen F. 1973. Risk aversion and the martingale property of stock prices. International Economic Review 14: 436–46. [Google Scholar] [CrossRef]
- LeRoy, Stephen F. 1976. Efficient capital markets: Comment. The Journal of Finance 31: 139–41. [Google Scholar] [CrossRef]
- LeRoy, Stephen F. 1989. Efficient capital markets and martingales. Journal of Economic Literature 27: 1583–621. [Google Scholar]
- LeRoy, Stephen F., and Richard D. Porter. 1981. The present-value relation: Tests based on implied variance bounds. Econometrica 49: 555–74. [Google Scholar] [CrossRef]
- Lim, Kian-Ping, and Robert Brooks. 2011. The evolution of stock market efficiency over time: A survey of the empirical literature. Journal of Economic Surveys 25: 69–108. [Google Scholar] [CrossRef]
- Lim, Kian-Ping, Weiwei Luo, and Jae H. Kim. 2013. Are us stock index returns predictable? Evidence from automatic autocorrelation-based tests. Applied Economics 45: 953–62. [Google Scholar] [CrossRef]
- Lin, Hsin-Yi. 2013. Dynamic stock return-volume relation: Evidence from emerging asian markets. Bulletin of Economic Research 65: 178–93. [Google Scholar] [CrossRef]
- Ljung, Greta M., and George E. P. Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Llorente, Guillermo, Roni Michaely, Gideon Saar, and Jiang Wang. 2002. Dynamic volume-return relation of individual stocks. The Review of Financial Studies 15: 1005–47. [Google Scholar] [CrossRef]
- Lo, Andrew W. 1989. Long-Term Memory in Stock Market Prices. Technical Report. Cambridge: National Bureau of Economic Research. [Google Scholar]
- Lo, Andrew W. 1991. Long-term memory in stock market prices. Econometrica 59: 1279–313. [Google Scholar] [CrossRef]
- Lo, Andrew W. 2004. The adaptive markets hypothesis. Journal of Portfolio Management 30: 15–29. [Google Scholar] [CrossRef]
- Lo, Andrew W. 2005. Reconciling efficient markets with behavioral finance: The adaptive markets hypothesis. Journal of Investment Consulting 7: 21–44. [Google Scholar]
- Lo, Andrew W. 2012. Adaptive markets and the new world order (corrected may 2012). Financial Analysts Journal 68: 18–29. [Google Scholar] [CrossRef]
- Lo, Andrew W., and A. Craig MacKinlay. 1988. Stock market prices do not follow random walks: Evidence from a simple specification test. The Review of Financial Studies 1: 41–66. [Google Scholar] [CrossRef]
- Lucas, Robert E., Jr. 1978. Asset prices in an exchange economy. Econometrica: Journal of the Econometric Society 46: 1429–45. [Google Scholar] [CrossRef]
- Mahajan, Sarika, and Balwinder Singh. 2008. An empirical analysis of stock price-volume relationship in indian stock market. Vision 12: 1–13. [Google Scholar] [CrossRef]
- Malkiel, Burton G. 1989. Efficient market hypothesis. In Finance. Edited by John Eatwell, Murray Milgate and Peter Newman. London: The New Palgrave. Palgrave Macmillan, pp. 127–34. [Google Scholar]
- Malkiel, Burton G. 2003. The efficient market hypothesis and its critics. Journal of Economic Perspectives 17: 59–82. [Google Scholar] [CrossRef]
- Malkiel, Burton G. 2005. Reflections on the efficient market hypothesis: 30 years later. Financial Review 40: 1–9. [Google Scholar] [CrossRef]
- Mandelbrot, Benoit B., Adlai J. Fisher, and Laurent E. Calvet. 1997. A Multifractal Model of Asset Returns. Cowles Foundation Discussion Paper 1164, Sauder School of Business Working Paper. Amsterdam: Elsevier, November. [Google Scholar]
- Matilla-García, Mariano, Manuel Ruiz Marín, and Mohammed I. Dore. 2014. A permutation entropy based test for causality: The volume-stock price relation. Physica A: Statistical Mechanics and Its Applications 398: 280–88. [Google Scholar] [CrossRef]
- Milionis, Alexandros E. 2007. Efficient capital markets: A statistical definition and comments. Statistics & Probability Letters 77: 607–13. [Google Scholar]
- Milionis, Alexandros E., and Demetrios Moschos. 2000. On the validity of the weak–form efficient markets hypothesis applied to the london stock exchange: comment. Applied Economics Letters 7: 419–21. [Google Scholar] [CrossRef]
- Moosa, Imad A., and Param Silvapulle. 2000. The price-volume relationship in the crude oil futures market some results based on linear and nonlinear causality testing. International Review of Economics and Finance 9: 11–30. [Google Scholar] [CrossRef]
- Nasiri, Sina, Eralp Bektas, and G. Reza Jafari. 2018. The impact of trading volume on the stock market credibility: Bohmian quantum potential approach. Physica A: Statistical Mechanics and Its Applications 512: 1104–12. [Google Scholar] [CrossRef]
- Neely, Christopher J., Paul A. Weller, and Joshua M. Ulrich. 2009. The adaptive markets hypothesis: Evidence from the foreign exchange market. Journal of Financial and Quantitative Analysis 44: 467–88. [Google Scholar] [CrossRef]
- Ng, Serena, and Pierre Perron. 2001. Lag length selection and the construction of unit root tests with good size and power. Econometrica 69: 1519–54. [Google Scholar] [CrossRef]
- Noda, Akihiko. 2016. A test of the adaptive market hypothesis using a time-varying ar model in japan. Finance Research Letters 17: 66–71. [Google Scholar] [CrossRef]
- O’Hara, Maureen. 2003. Presidential address: Liquidity and price discovery. The Journal of Finance 58: 1335–54. [Google Scholar] [CrossRef]
- Osborne, Maury F. M. 1959. Brownian motion in the stock market. Operations Research 7: 145–73. [Google Scholar] [CrossRef]
- Pesaran, M. Hashem, and Allan Timmermann. 1995. Predictability of stock returns: Robustness and economic significance. The Journal of Finance 50: 1201–28. [Google Scholar] [CrossRef]
- Phillips, Peter C. B., and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Podobnik, Boris, Davor Horvatic, Alexander M. Petersen, and H. Eugene Stanley. 2009. Cross-correlations between volume change and price change. Proceedings of the National Academy of Sciences of the United States of America 106: 22079–84. [Google Scholar] [CrossRef] [PubMed]
- Poterba, James M., and Lawrence H. Summers. 1988. Mean reversion in stock prices: Evidence and implications. Journal of Financial Economics 22: 27–59. [Google Scholar] [CrossRef]
- Rizvi, Syed Aun R., and Shaista Arshad. 2017. Analysis of the efficiency–integration nexus of japanese stock market. Physica A: Statistical Mechanics and Its Applications 470: 296–308. [Google Scholar] [CrossRef]
- Roberts, Harry V. 1967. Statistical versus Clinical Prediction of the Stock Market. Chicago: Centre for Research in Security Prices, University of Chicago, unpublished manuscript. [Google Scholar]
- Rockinger, Michael, and Giovanni Urga. 2000. The evolution of stock markets in transition economies. Journal of Comparative Economics 28: 456–72. [Google Scholar] [CrossRef]
- Rodriguez, Elsa, Manuel Aguilar-Cornejo, Ricardo Femat, and Jose Alvarez-Ramirez. 2014. Us stock market efficiency over weekly, monthly, quarterly and yearly time scales. Physica A: Statistical Mechanics and Its Applications 413: 554–64. [Google Scholar] [CrossRef]
- Ruan, Qingsong, Wei Jiang, and Guofeng Ma. 2016. Cross-correlations between price and volume in Chinese gold markets. Physica A: Statistical Mechanics and Its Applications 451: 10–22. [Google Scholar] [CrossRef]
- Rubinstein, Mark. 1975. Securities market efficiency in an arrow-debreu economy. The American Economic Review 65: 812–24. [Google Scholar]
- Saatcioglu, Kemal, and Laura T. Starks. 1998. The stock price-volume relationship in emerging stock markets: The case of Latin America. International Journal of Forecasting 14: 215–25. [Google Scholar] [CrossRef]
- Samuelson, Paul A. 1965. Proof that properly anticipated prices fluctuate randomly. Industrial Management Review 6: 41–49. [Google Scholar]
- Schwert, G. William. 2003. Anomalies and market efficiency. Handbook of the Economics of Finance 1: 939–74. [Google Scholar]
- Sensoy, Ahmet, and Benjamin M. Tabak. 2015. Time-varying long term memory in the european union stock markets. Physica A: Statistical Mechanics and Its Applications 436: 147–58. [Google Scholar] [CrossRef]
- Sewell, Martin. 2012. The efficient market hypothesis: Empirical evidence. International Journal of Statistics and Probability 1: 164. [Google Scholar] [CrossRef][Green Version]
- Shiller, Robert J. 1981. Do stock prices move too much to be justified by subsequent changes in dividends? American Economic Review 17: 83–104. [Google Scholar]
- Shiller, Robert J. 2003. From efficient markets theory to behavioral finance. Journal of Economic Perspectives 71: 421–36. [Google Scholar] [CrossRef]
- Silvapulle, Param, and Jong-Seo Choi. 1999. Testing for linear and nonlinear granger causality in the stock price-volume relation: Korean evidence. Quarterly Review of Economics and Finance 39: 59–76. [Google Scholar] [CrossRef]
- Simon, Herbert A. 1955. A behavioral model of rational choice. The Quarterly Journal of Economics 69: 99–118. [Google Scholar] [CrossRef]
- Smirlock, Michael, and Laura Starks. 1988. An empirical analysis of the stock price-volume relationship. Journal of Banking and Finance 12: 31–41. [Google Scholar] [CrossRef]
- Steiger, William. 1964. A Test of Nonrandomness in Stock Price Changes. Cambridge: MIT Press. [Google Scholar]
- Stošić, Dusan, Darko Stošić, Tatijana Stošić, and H. Eugene Stanley. 2015. Multifractal properties of price change and volume change of stock market indices. Physica A: Statistical Mechanics and Its Applications 428: 46–51. [Google Scholar]
- Sukpitak, Jessada, and Varagorn Hengpunya. 2016. The influence of trading volume on market efficiency: The dcca approach. Physica A: Statistical Mechanics and Its Applications 458: 259–65. [Google Scholar] [CrossRef]
- Suominen, Matti. 2001. Trading volume and information revelation in stock market. Journal of Financial and Quantitative Analysis 36: 545–65. [Google Scholar] [CrossRef]
- Tauchen, George E., and Mark Pitts. 1983. The price variability-volume relationship on speculative markets. Econometrica: Journal of the Econometric Society 51: 485–505. [Google Scholar] [CrossRef]
- Timmermann, Allan, and Clive W. J. Granger. 2004. Efficient market hypothesis and forecasting. International Journal of Forecasting 20: 15–27. [Google Scholar] [CrossRef]
- Ţiţan, Alexandra Gabriela. 2015. The efficient market hypothesis: Review of specialized literature and empirical research. Procedia Economics and Finance 32: 442–49. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Goodness C. Aye, and Rangan Gupta. 2019. Stock market efficiency analysis using long spans of data: A multifractal detrended fluctuation approach. Finance Research Letters 28: 398–411. [Google Scholar] [CrossRef]
- Todea, Alexandru, Adrian Zoicas-Ienciu, and Angela-Maria Filip. 2009. Profitability of the moving average strategy and the episodic dependencies: Empirical evidence from european stock markets. European Research Studies Journal 12: 63–72. [Google Scholar]
- Tranfield, David, David Denyer, and Palminder Smart. 2003. Towards a methodology for developing evidence-informed management knowledge by means of systematic review. British Journal of Management 14: 207–22. [Google Scholar] [CrossRef]
- Tripathy, Naliniprava. 2011. The relation between price changes and trading volume: A study in indian stock market. Interdisciplinary Journal of Research in Business 1: 81–95. [Google Scholar]
- Tuyon, Jasman, and Zamri Ahmad. 2016. Behavioural finance perspectives on malaysian stock market efficiency. Borsa Istanbul Review 16: 43–61. [Google Scholar] [CrossRef]
- Urquhart, Andrew, and Robert Hudson. 2013. Efficient or adaptive markets? evidence from major stock markets using very long run historic data. International Review of Financial Analysis 28: 130–42. [Google Scholar] [CrossRef]
- Urquhart, Andrew, and Frank McGroarty. 2016. Are stock markets really efficient? evidence of the adaptive market hypothesis. International Review of Financial Analysis 47: 39–49. [Google Scholar] [CrossRef]
- Wang, Dong-Hua, Yuan-Yuan Suo, Xiao-Wen Yu, and Man Lei. 2013. Price–volume cross-correlation analysis of csi300 index futures. Physica A: Statistical Mechanics and Its Applications 392: 1172–79. [Google Scholar] [CrossRef]
- Wang, Yudong, Li Liu, and Rongbao Gu. 2009. Analysis of efficiency for shenzhen stock market based on multifractal detrended fluctuation analysis. International Review of Financial Analysis 18: 271–76. [Google Scholar] [CrossRef]
- Wang, Yi-Chiuan, Jyh-Lin Wu, and Yi-Hao Lai. 2018. New evidence on asymmetric return–volume dependence and extreme movements. Journal of Empirical Finance 45: 212–27. [Google Scholar] [CrossRef]
- Wood, Robert A., Thomas H. McInish, and J. Keith Ord. 1985. An investigation of transactions data for nyse stocks. The Journal of Finance 40: 723–39. [Google Scholar] [CrossRef]
- Working, Holbrook. 1934. A random-difference series for use in the analysis of time series. Journal of the American Statistical Association 29: 11–24. [Google Scholar] [CrossRef]
- Worthington, Andrew C., and Helen Higgs. 2004. Random walks and market efficiency in european equity markets. Global Journal of Finance and Economics 1: 59–78. [Google Scholar]
- Yen, Gili, and Cheng-Few Lee. 2008. Efficient market hypothesis (emh): Past, present and future. Review of Pacific Basin Financial Markets and Policies 11: 305–29. [Google Scholar] [CrossRef]
- Zalewska-Mitura, Anna, and Stephen G. Hall. 1999. Examining the first stages of market performance: A test for evolving market efficiency. Economics Letters 64: 1–12. [Google Scholar] [CrossRef]
| 1. | Delcey (2018) classifies the definition of EMH as ‘Fama’s EMH’ and ‘Samuelson’s EMH’. Fama’s EMH is based on the claim that prices reflect economic fundamentals and the prices fluctuate randomly as they converge to fundamental values, while ‘Samuelson’s EMH’ based on the pure random nature of price changes with no regard to fundamental value. |
| 2. | Readers may refer to Emerson et al. (1997); Zalewska-Mitura and Hall (1999); Lo (2004, 2005) to see the development of literature in time-varying market efficiency. |
| 3. | The price–volume relationship is important for four reasons: (a) to get insights into the structure of financial markets (b) combination of price and volume data is useful in understanding the consequences of event studies (c) to understand speculative prices and (d) it has high impact on future contracts |
| EMH (Classical) | AMH (Adaptive) | |
|---|---|---|
| Linear autocorrelation | Box test—Q, VR test, AQ, AVR, Wild bootstrap AVR and AR-GARCH (Kim 2009; Rockinger and Urga 2000) | MF-DFA (rolling subsample), Box test, autocorrelation tests, AQ, VR, AVR, wild bootstrap AVR, time-varying AR model, GARCH-M (Sensoy and Tabak 2015; Tiwari et al. 2019) |
| Nonlinear autocorrelation | GS, Consistent test, Wild bootstrap GS (Gozbasi et al. 2014) | MF-DFA, GS test, Consistent test (Khuntia and Pattanayak 2018; Kim et al. 2011) |
| Linear long memory | R/S, Spectral Regression (Barkoulas et al. 2000) | MF-DFA, R/S (Hull and McGroarty 2014) |
| Nonlinear long memory | modified R/S, ESTAR unit root test (Gozbasi et al. 2014) | MF-DFA, Modified R/S analysis (Todea et al. 2009) |
| Linear unit root | ADF, PP, DF-GLS, NP, KPSS or VR test (Konak and Şeker 2014), (Gupta and Yang 2011) | — |
| EMH (Classical) | AMH (Adaptive) | |
|---|---|---|
| Linear Contemporaneous | Canonical correlations, linear regression (Chen 2012; He et al. 2014; Lee and Swaminathan 2000) | MF-DFA DCCA (rolling subsample), dependence switching copula model, MF-DFA and MF-DXA (Ferreira 2019; Hasan and Salim 2017) |
| Nonlinear Contemporaneous | Canonical correlations, nonlinear regression, GARCH (Chordia and Swaminathan 2000; He et al. 2014) | MF-DFA DCCA (rolling subsample), dependence switching copula model, MF-DFA and MF-DXA (Khuntia and Pattanayak 2018) |
| Linear Causal | MODWT-VAR, causality tests based on quantiles, Granger causality, regression with fixed effects (Balcilar et al. 2017; Chordia and Swaminathan 2000; Gupta et al. 2018; Lin 2013) | MF-DFA DCCA (rolling subsample), dependence switching copula model, MF-DFA and MF-DXA (Stošić et al. 2015) |
| Nonlinear Causal | Regression with fixed effects, quantile regression, permutation entropy (Caginalp and DeSantis 2017; Hiemstra and Jones 1994; Matilla-García et al. 2014) | —— |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patil, A.C.; Rastogi, S. Time-Varying Price–Volume Relationship and Adaptive Market Efficiency: A Survey of the Empirical Literature. J. Risk Financial Manag. 2019, 12, 105. https://doi.org/10.3390/jrfm12020105
Patil AC, Rastogi S. Time-Varying Price–Volume Relationship and Adaptive Market Efficiency: A Survey of the Empirical Literature. Journal of Risk and Financial Management. 2019; 12(2):105. https://doi.org/10.3390/jrfm12020105
Chicago/Turabian StylePatil, Ashok Chanabasangouda, and Shailesh Rastogi. 2019. "Time-Varying Price–Volume Relationship and Adaptive Market Efficiency: A Survey of the Empirical Literature" Journal of Risk and Financial Management 12, no. 2: 105. https://doi.org/10.3390/jrfm12020105
APA StylePatil, A. C., & Rastogi, S. (2019). Time-Varying Price–Volume Relationship and Adaptive Market Efficiency: A Survey of the Empirical Literature. Journal of Risk and Financial Management, 12(2), 105. https://doi.org/10.3390/jrfm12020105