Abstract
This study analyzes forecasts of Bitcoin price using the autoregressive integrated moving average (ARIMA) and neural network autoregression (NNAR) models. Employing the static forecast approach, we forecast next-day Bitcoin price both with and without re-estimation of the forecast model for each step. For cross-validation of forecast results, we consider two different training and test samples. In the first training-sample, NNAR performs better than ARIMA, while ARIMA outperforms NNAR in the second training-sample. Additionally, ARIMA with model re-estimation at each step outperforms NNAR in the two test-sample forecast periods. The Diebold Mariano test confirms the superiority of forecast results of ARIMA model over NNAR in the test-sample periods. Forecast performance of ARIMA models with and without re-estimation are identical for the estimated test-sample periods. Despite the sophistication of NNAR, this paper demonstrates ARIMA enduring power of volatile Bitcoin price prediction.
1. Introduction
Bitcoin, the world’s first decentralised and currently biggest digital currency, is similar to synthetic commodity money, which shares the attributes of both commodity (e.g., gold) and fiat money (e.g., US dollar) (Selgin 2015). Bitcoin was introduced in 2008 by a group of programmers using the pseudonym ‘Satoshi Nakamoto’ (Cheah and Fry 2015). Some argue that it has the same finite economic attributes of gold and labelled as digital gold (Popper 2015). Meanwhile, the acceptance of the Bitcoin is still debatable due to its frictionless nature, lack of intrinsic value, and unclear issuing authority (Ciaian et al. 2016). The price volatility of Bitcoin makes it one of the most speculative digital currency, and a poor form of “holder of value”. Investors can lose their capital due to high volatility and uncertainty of Bitcoin price.
Media coverage about Bitcoin drew in amateur investors leading to a gambling mentality (Roberts 2017). However, Bitcoin is coming into the mainstream with large institutional investors eyeing its potential. Despite its limitations, Bitcoin is the most valuable and popular cryptocurrency to date (Corbet et al. 2019).
Bitcoin price has been extremely volatile since the inception of the cryptocurrency (Dwyer 2015). Due to concerns with speculative trading, in January 2018, Facebook banned all ads for Bitcoin and other cryptocurrencies (Robertson 2018). Additionally, experts foresee another financial crisis in the near future caused by the cryptocurrency boom (Lam et al. 2018). A major crash of the Bitcoin price can be triggered by a cyber hack and a government crackdown, and can take weeks or months to bounce back (Roberts 2017). Typically, investors predict future Bitcoin price based on past trends. But it is not easy to predict future Bitcoin price with a high level of accuracy. The price of Bitcoin follows a boom-bust pattern due to its speculative nature (Cheah and Fry 2015). Additionally, Bitcoin investors are speculative and short term oriented (Salisu et al. 2019).
Due to the progressive price change and increase in the market cap, the popularity of investment in Bitcoin has been increasing dramatically. Meanwhile, Urquhart (2016) found that Bitcoin is an inefficient market. Caporale et al. (2018) also observe inefficiency in the cryptocurrency market. In the same vein, due to high price volatility, speculators have a generic question of whether the price of Bitcoin can be forecasted in advance.
Thus far, there have been limited attempts in the literature to forecast the price of Bitcoin. Katsiampa (2017) scrutinised the in-sample goodness-of-fit of GARCH models for Bitcoin price but did not perform out-sample forecast. Kristjanpoller and Minutolo (2018) proposed a hybrid-forecasting model to predict Bitcoin price volatility, integrating artificial neural network (ANN), generalised autoregressive conditional heteroscedasticity (GARCH) and principal components analysis (PCA). They found that the accuracy of the hybrid model increases after incorporation of PCA pre-processing. Similar to Katsiampa (2017), Kristjanpoller and Minutolo (2018) also only examined in-sample forecast performance. Meanwhile, Aalborg et al. (2018) found that Bitcoin returns cannot be predicted (R2 ≤ 0.01) using explanatory variables (i.e., google trend, trading volume, transaction volume, VIX index, and unique user addresses).
Given that Bitcoin is becoming more popular, yet still volatile and not well explained, a need exists to study methods to better understand its price fluctuations. Accurately forecasting the daily movements can increase the returns of day traders and consequently make the market more efficient. The choice of forecasting models can have a significant effect on performance (Chen et al. 2019). We contribute to the Bitcoin forecasting literature by testing autoregressive integrated moving average (ARIMA) and neural network autoregression (NNAR). ARIMA is one of the traditional forecasting methods, and NNAR is a rather sophisticated and more modern approach to forecasting (Hyndman and Athanasopoulos 2018). To ensure validation and implementation, as suggested by Adya and Collopy (1998), we use ex-ante Bitcoin forecast performance using a relatively large sample, and multiple training and testing samples to demonstrate the stability of the forecast results. By following this procedure, we differentiate the results of this study with the ones mentioned earlier.
In the next section, we discuss existing literature on Bitcoin price modelling. Section 3 presents daily Bitcoin price data used in this study. Section 4 presents the adopted forecast methodologies and performance measures. The analysis and findings are presented in Section 5, and final remarks are made in Section 6.
2. Literature Review
Bitcoin is the most popular among the cryptocurrencies (Kyriazis 2019). Recent fluctuations in Bitcoin price has captured the attention of academic researchers (Beneki et al. 2019). Given the nescancy of this research stream, previous studies on Bitcoin and other digital currencies (for instance, Ethereum, Litecoin, Ripple) mainly explain the concepts, principles and economics of cryptocurrencies (Segendorf 2014; Dwyer 2015; Becker et al. 2011). Among the authors, Dwyer (2015) addressed the principles of Bitcoin and other relevant digital currencies. The author explains the supply and demand of digital currencies, equilibria of Bitcoin, uses of Bitcoin in exchange for goods and services with a rivalry to other currencies (Dwyer 2015). Likewise, Brière et al. (2015) investigated the connection of Bitcoin with other cryptocurrencies.
The total market cap of Bitcoin is approximately USD237 billion (as of 30 March 2018), which is nearly 42.69% of the entire cryptocurrency market capitalizations (coinmarketcap.com). As such, some studies consider the price dynamics of Bitcoin (Brandvold et al. 2015; Ciaian et al. 2016). Brandvold et al. (2015) investigated the price discovery of Bitcoin exchanges and find that two exchanges—Mt.Gox and BTC-e, are leading the market with the maximum information share. Besides, Ciaian et al. (2016) studied the underlying economics of Bitcoin price by taking into account the traditional determinants of the currency price. Moreover, Shubik (2014) and Rogojanu and Badea (2014) studied Bitcoin in the setting of alternative monetary systems by considering the challenges of the economic environment. Meanwhile, Bouoiyour and Selmi (2014); Bouoiyour et al. (2014) and Yermack (2013) described Bitcoin as a speculative investment or speculative bubble. Similarly, according to Yermack (2013), Bitcoin behaves more like a speculative investment rather than currency. It fails to satisfy the features of currency as a medium of exchange, a store of value, and a unit of account. In the same vein, Molnár et al. (2015) studied the exchange rate risk of Bitcoin by comparing with other variables, for instance, gold and Euro and find that Bitcoin is more volatile and riskier than gold and Euro, which restrict the applicability of Bitcoin as a medium of transaction. Furthermore, Bouri et al. (2017) investigated the Bitcoin price and its volatility and found persistence in the Bitcoin price and volatility.
As Bitcoin price volatility is exceptionally high, speculators have a general quest whether future Bitcoin price can be forecasted. Bitcoin price or return forecasting is getting more attention due to its boom-bust nature. Speculators are looking for tools and techniques that can forecast Bitcoin price with higher accuracy, at least better than the naïve forecast to set their investment portfolios in a profit margin. The majority of the studies on Bitcoin either focus on price returns and volatility or consider Bitcoin as a speculative investment or bubble (Bouoiyour and Selmi 2014; Bouoiyour et al. 2014; Yermack 2013). Some studies consider risk, hedge and safe haven attributes of Bitcoin and Ethereum (Beneki et al. 2019, Bouri et al. 2017). However, to the best of the authors’ knowledge, there are no studies on the forecasting of test-sample (out-sample) Bitcoin price (also see Corbet et al. 2019). Thus, this study presents a novel approach to forecasting daily Bitcoin price using both with and without model re-estimation at each step while comparing ARIMA and NNAR models.
3. Data
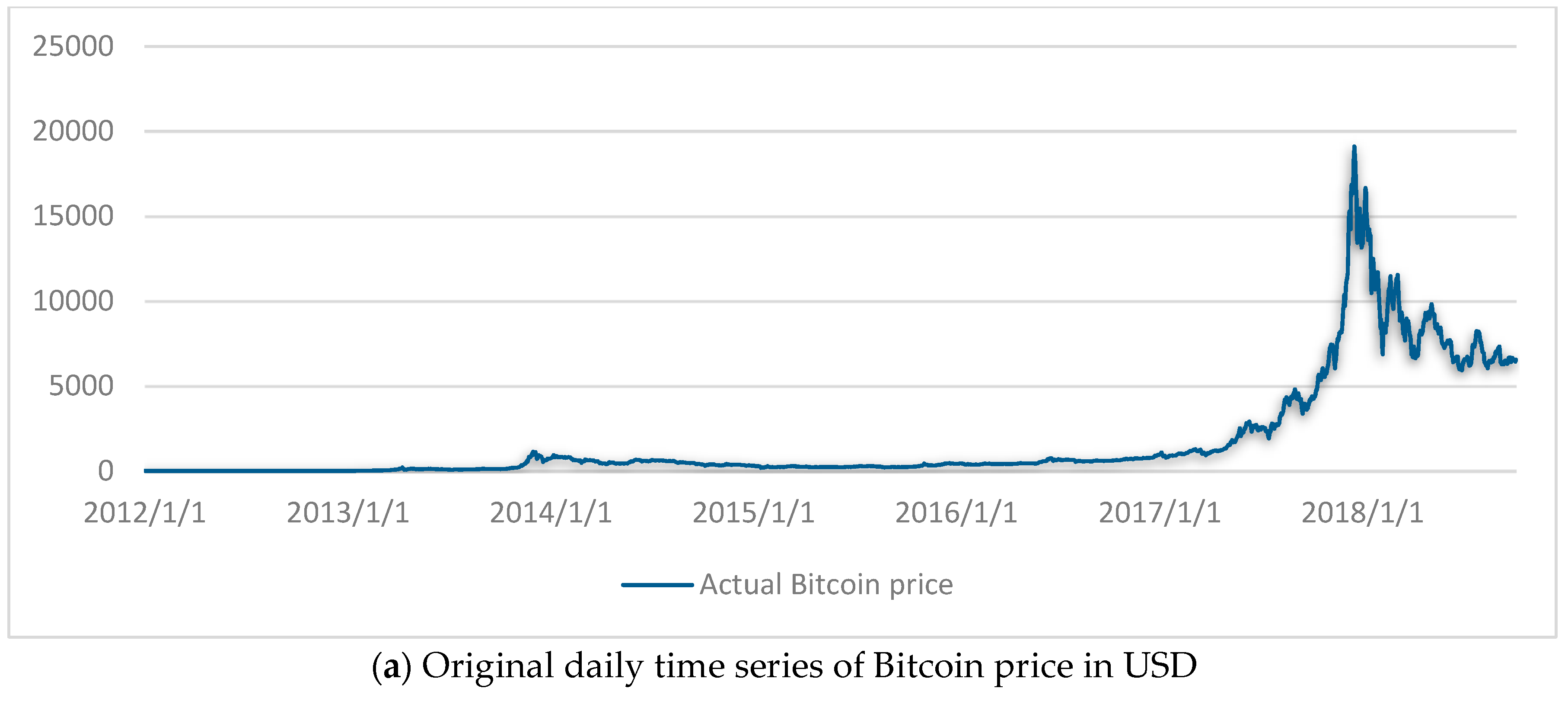
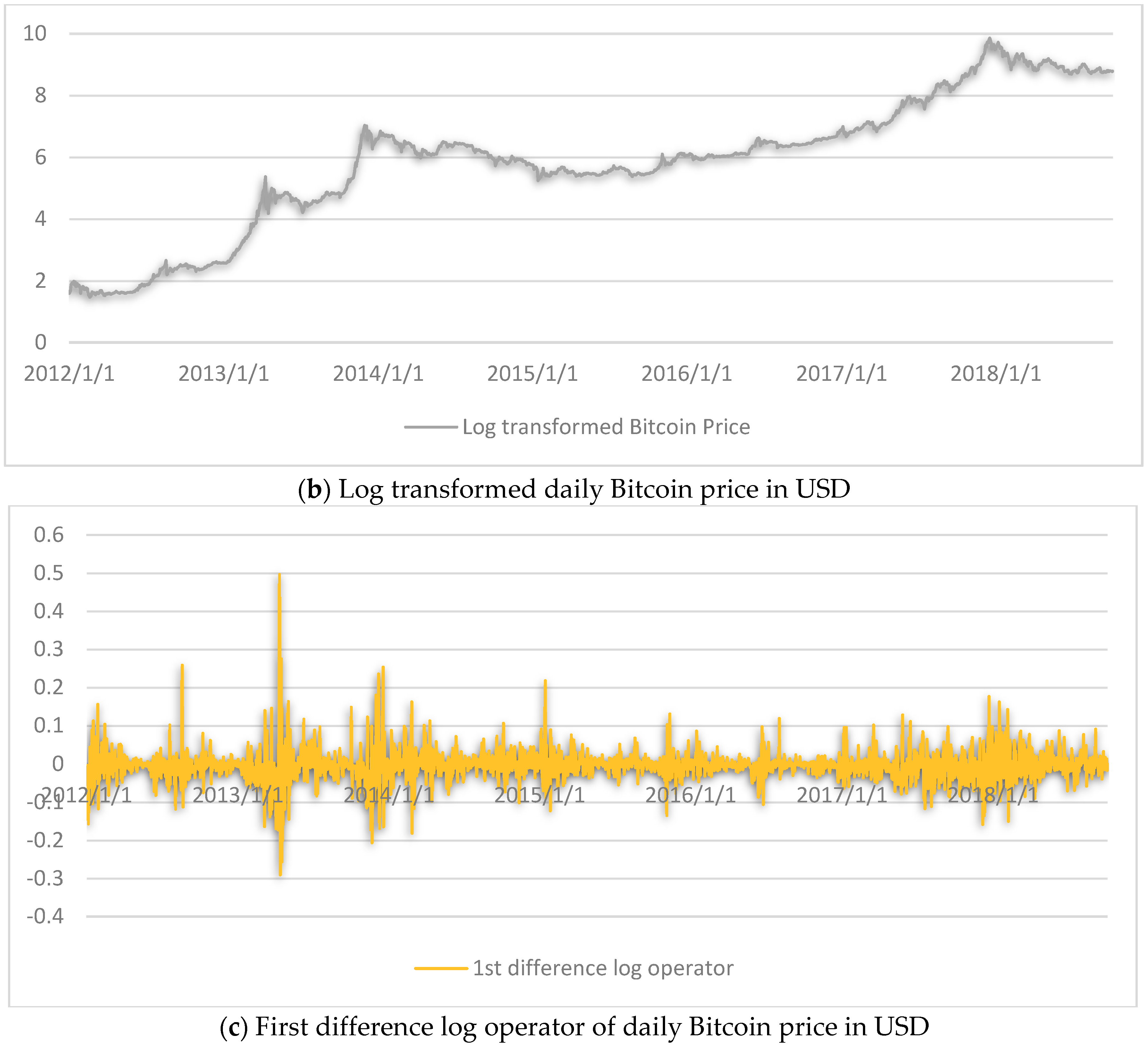
Daily Bitcoin exchange rate data (USD per Bitcoin) is collected from the Quandl1 database. Data from the same source has been used by others, too (Chu et al. 2015). We use daily Bitcoin price data from 1 January 2012 to 4 October 20182, daily Bitcoin price of 2466 days. Figure 1 presents the (a) original time series along with (b) log-transformed and (c) first differenced log operator series. For the effectiveness of forecast validation (Adya and Collopy 1998), we divide the dataset into a training-sample (in-sample) and test-sample (out-sample). We consider two training-samples and subsequently two-test samples for cross-validation purposes. The first training sample is from 1 January 2012 until 14 May 2013 (500 days), and the second from 1 January 2012 until 25 June 2017 (2000 days). As a consequence, the first test-sample is from 15 May 2013 to 4 October 2018 (1966 days), and the second from 16 June 2017 to 4 October 2018 (466 days).
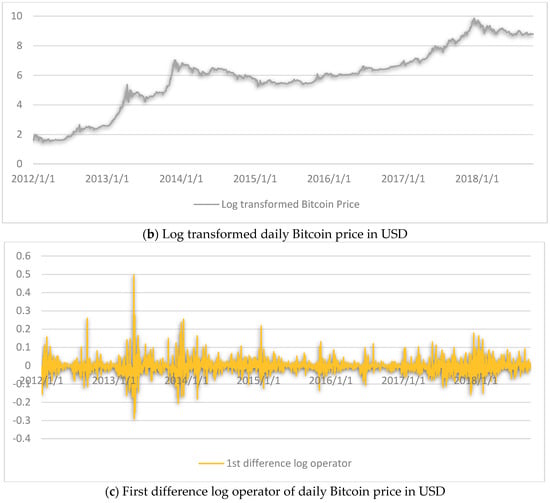
Figure 1.
(a) Original, (b) log-transformed and (c) first difference log operator bitcoin price in USD.
At the end of 2014, the price of Bitcoin dropped significantly to USD 302 (www.coindesk.com). The cause of the price decline was the suspension of trading of Bitcoin by Mt. Gox, one of the leading Bitcoin exchanges, which handled 70% of the Bitcoin exchange worldwide at that time. They reported that around 850,000 Bitcoins were hacked, which belongs to customers and are worth around USD 3.5 billion (Roberts 2017). The incident resulted in a lack of confidence in the security system of Bitcoin; thus, the price decline continued until 2016. At the beginning of 2017, the Bitcoin price increased dramatically, and at the end of 2017 the price of Bitcoin surged at USD 19,661.63, but again after five days from 17 December 2017 it dropped to USD 12,616.64 (www.coindesk.com).
Stationarity of data is a prerequisite for predictive modelling, particularly when using autoregressive time series models such as ARIMA. Table 1 shows results of the stationary test of the training-data samples using the Augmented Dicky-Fuller test (ADF) (Dickey and Fuller 1979) and Phillips-Perron test (PP) (Phillips and Perron 1988). Data, both in levels and log-transformed series, are not stationary but become stationary at first difference log operator; thus, the ARIMA modelling approach is feasible. It might be noted that the stationarity of data is not essential for neural network models (Hyndman and Athanasopoulos 2018).

Table 1.
Stationary test of data.
4. Methodology
4.1. Forecast Methods
Association of Bitcoin prices with other micro and macro-economic indicators, such as oil price and gold price, are still not clear (Aalborg et al. 2018). Thus, the univariate modelling approach, where data speaks for itself (Gujarati and Porter 2003), becomes an appropriate forecasting tool. Additionally, a positive association between past and future values of Bitcoin price is evident in the literature (Caporale et al. 2018). However, the degree of association varies over time (Caporale et al. 2018); thus, re-estimating the forecast model every time for the one-step forecast with each additional daily Bitcoin price becomes relevant. Additionally, this signifies the essence for investigating non-linear approach. Thus, we employ two univariate time series models—ARIMA and NNAR. Application of ARIMA can be found in many fields of studies such as in finance (Ariyo et al. 2014), shipping (Munim and Schramm 2017), logistics (Miller 2018), and electric power (Contreras et al. 2003). Meanwhile, NNAR models are also used to forecast global solar radiation (Benmouiza and Cheknane 2013), river flow (Abrahart and See 2000), tourism demand (Álvarez-Díaz et al. 2018). For both ARIMA and NNAR models, we scrutinize forecasting next-day Bitcoin price with and without re-estimating the forecast model for each step. For the computational purpose, we used the Forecast package (Hyndman and Khandakar 2007) in the R software.
4.1.1. ARIMA
ARIMA is probably the most popular method when it comes to time series forecasting, initially developed by Box and Jenkins (1976). Typically, an ARIMA model has two components: an autoregressive (AR) component and a moving average (MA) component. The AR component models association between the value of a variable at a specified time with its value in previous time(s), and the MA component models association between values of error term of a variable at a specified time with its error term value in previous time(s). The integrated (I) component comes into consideration when the time series becomes stationary after the first (or second) difference. An ARIMA (p,d,q) model can be represented by Equation (1).
Here, ; is the Bitcoin price in USD at time t, is the Bitcoin price in USD of all previous periods until lag , is the parameter for , is the error term in time t, is the error term of all previous periods until lag and is the parameter for .
4.1.2. Neural Network Autoregression (NNAR)
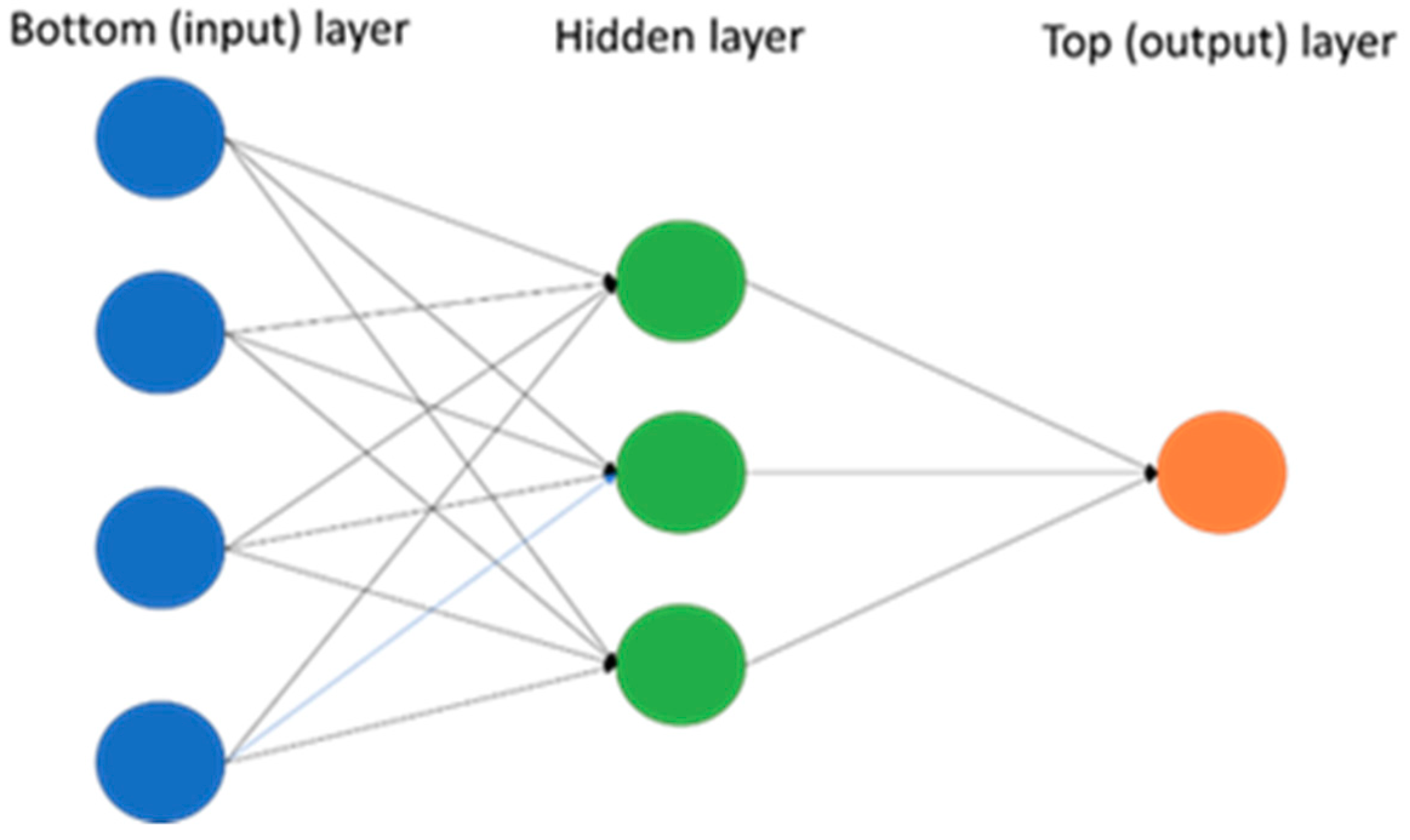
Artificial neural network (ANN) methods rely on mathematical models in a similar pattern as ‘neurons’ in the brain. ANN models help design complex non-linear associations between the dependent variable and its predictors (Adya and Collopy 1998; Hyndman and Athanasopoulos 2018). The simplest ANN models would only have predictors (independent variables or inputs) in the bottom layer and the dependent variable (output) in the top layer, which would be equivalent to a linear regression model. After adding the hidden layer(s) in-between bottom and top layers, the ANN structure becomes non-linear. A sample ANN model is depicted in Figure 2. This type of ANN is called multi-layered feed-forward network, where each layer of neurons (nodes) receive inputs from the previous layer. The inputs to each node are estimated using a weighted linear combination, as in Equation (2):
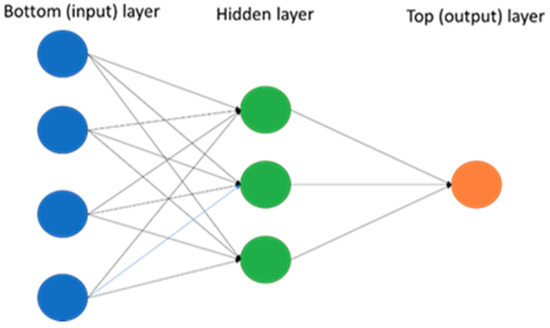
Figure 2.
An ANN model with four inputs and one hidden layer with three neurons.
Here, is the value of output node , is the constant for node , is the weight from the input node to output node , represents the inputs, and is number of input variables. In the hidden layer, Equation (2) is transformed into non-linear function using sigmoid, as shown in Equation (3).
The parameters are “learned” from the training data. To prevent the weights from becoming too large, usually, the values of the weights are restricted. Decay parameter—the parameter that restricts the weights is typically set to be equal to 0.1 (Hyndman and Athanasopoulos 2018). With time series data such as daily Bitcoin price, lagged values of the time series can be used as inputs in an ANN structure, which is known as neural network autoregression (NNAR). A non-seasonal feed-forward network model with one hidden layer is usually denoted as NNAR (p,k), where p represents the number of lags and k represents the number of nodes in the hidden layer.
4.2. Forecast Accuracy Measures
Forecasting models are evaluated based on their accuracy of the forecast. Typical forecast accuracy measures such as RMSE (root mean square error) and MAPE (mean absolute percent error) are criticised for their instability with varying number of test-sample forecast periods. Thus, we adopt three indices to measure the accuracy of forecast results: RMSE, MAPE, and MASE (mean absolute scaled error). MASE was proposed by Hyndman and Koehler (2006) as a remedy to overcome the drawbacks of RMSE and MAPE when dealing with a varying number of test-sample periods. The three adopted accuracy measures can be expressed as follows:
Here, is the forecast error calculated as , is the actual Bitcoin price at time , is the forecasted price at time , is the total number of observations and is the forecast error of the naïve forecast.
5. Empirical Results
First, the appropriate ARIMA and NNAR models are to be selected to forecast next-day Bitcoin price for the test-sample. ARIMA models are chosen based on the lowest AIC, while considering the PP test for stationarity using the auto.arima function provided by the Forecast package in R. However, it is challenging to select the appropriate NNAR model. For the first training-sample period (500 days), 14 different NNAR(p,k) specifications are estimated and evaluated for the forecast (without re-estimation) performance of the first test-sample period (1966 days). The results are presented in Figure A1 in Appendix A. Interestingly, training-sample forecast performance gets better with increasing the numbers of lags and hidden layers (see Figure A1a) but NNAR (2,1) performs best for test-sample forecast (see Figure A1b). Therefore, NNAR (2,1) is selected for the estimation of the first training and test samples. The same 14 models are estimated and compared for the second training and test samples (see Figure A2), and NNAR (1,2) is selected based on test-sample forecast performance. In the employed NNAR framework, it is noteworthy that test-sample forecast performance is always better with a lower number of lags and nodes in contrast to the training-sample forecast performance.
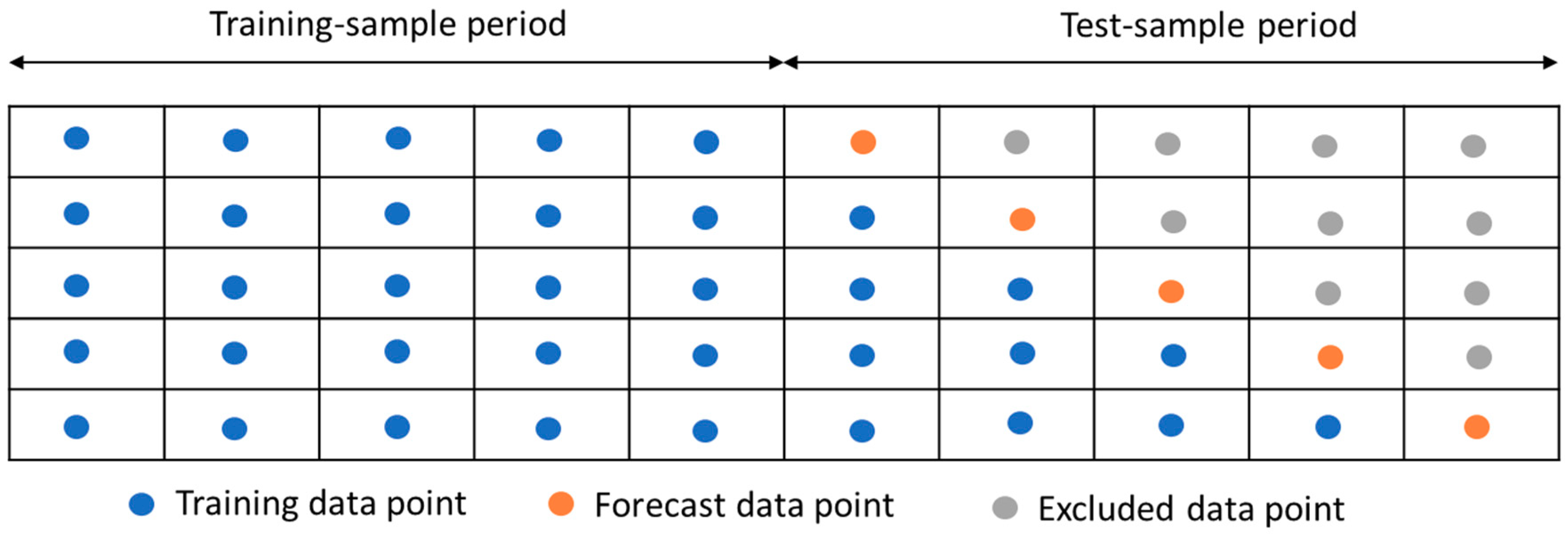
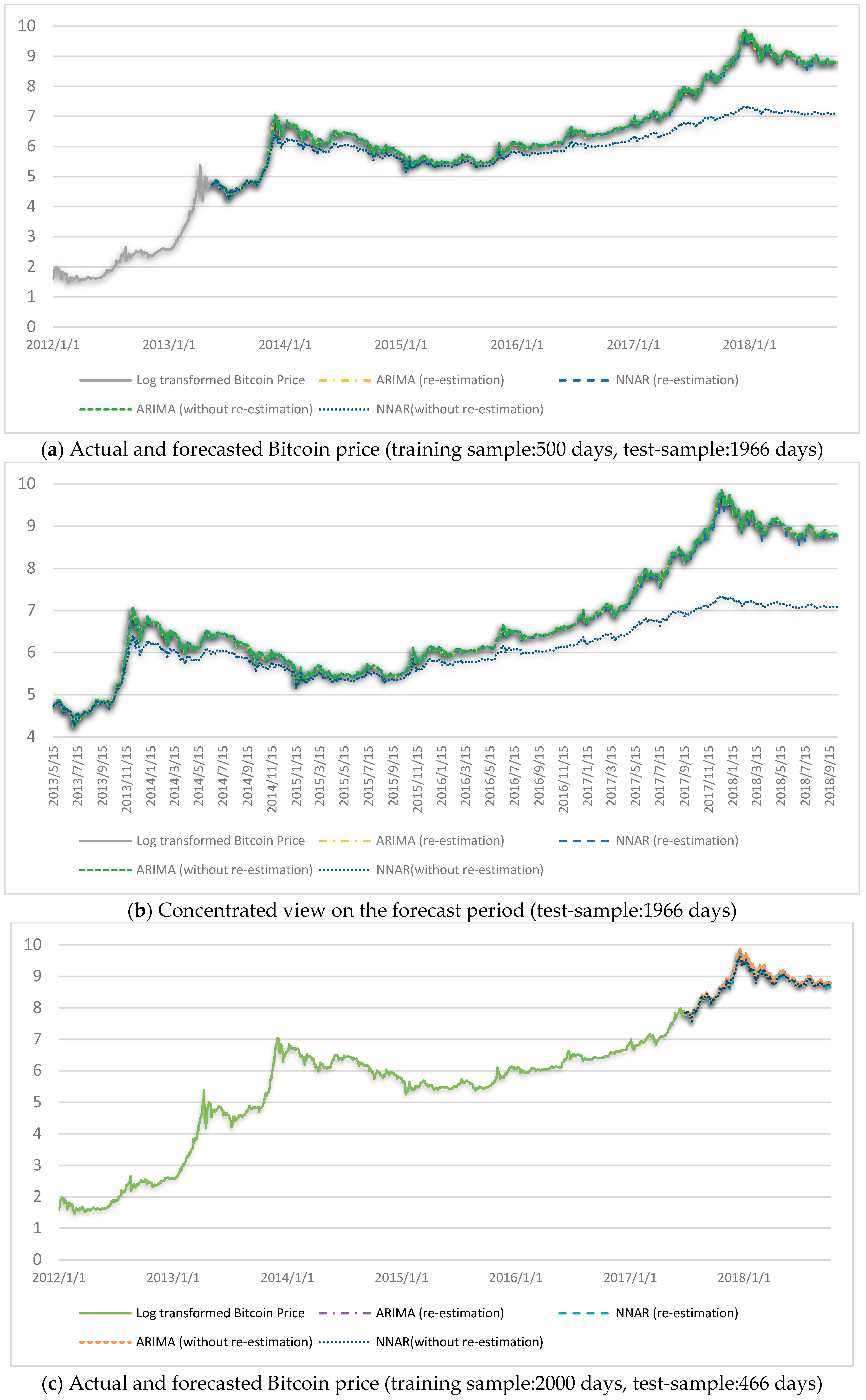
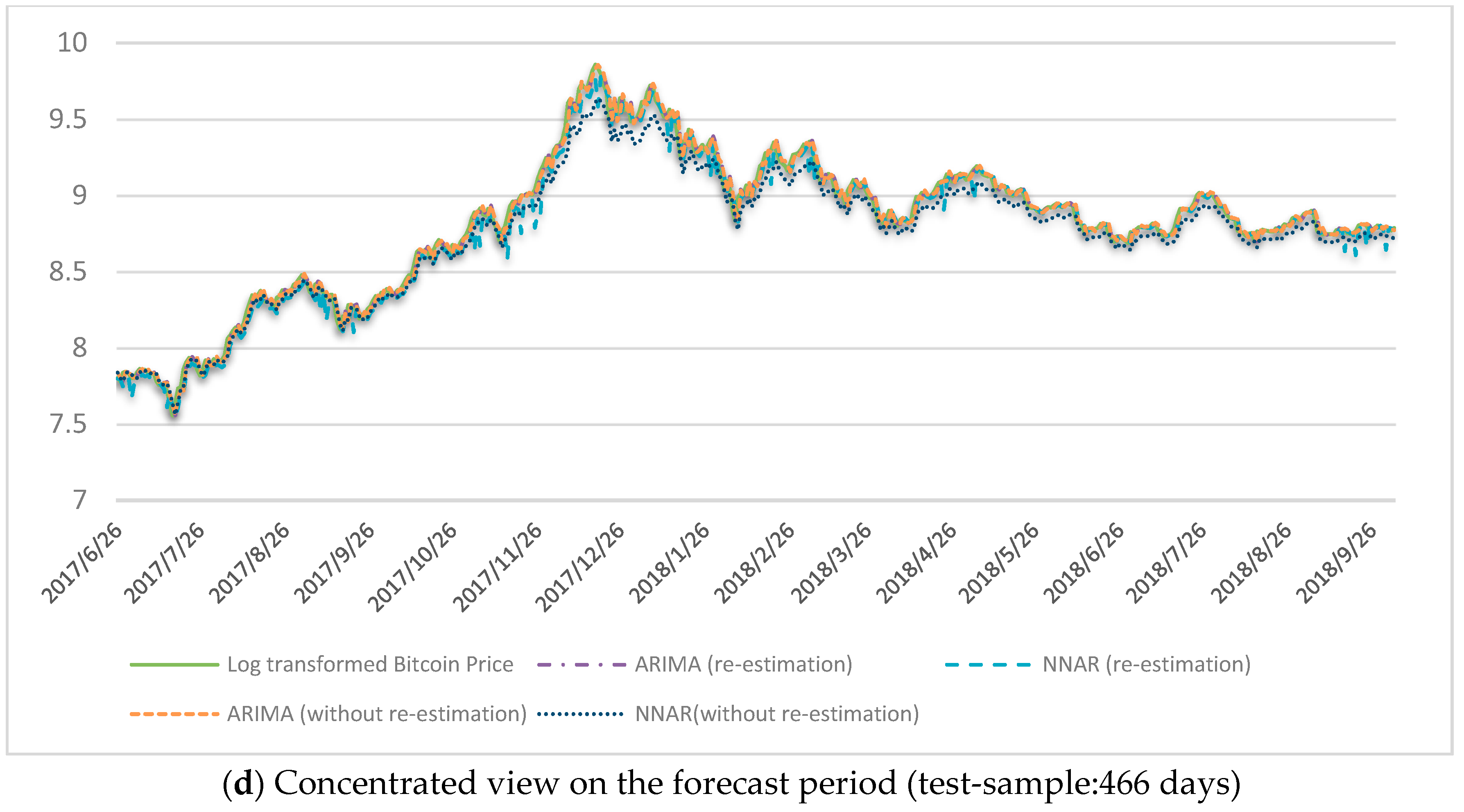
For next-day Bitcoin price forecast without re-estimation of the model for next step, the two selected models for first training and test samples are ARIMA (4,1,0) and NNAR (2,1), and for the second training and test samples are ARIMA (4,1,1) and NNAR (1,2). We adopt the static forecast approach, as depicted in Figure 3. When using an autoregressive model in the static forecast approach, the actual value of the dependent variable in previous periods is used to estimate each step forecast for the training sample. On the contrary, when forecasting multiple periods, dynamic forecast approach uses the previously forecasted value (out-sample period) of the dependent variable to compute a forecast. In Table 2, first, we present the training-sample forecast performance of ARIMA and NNAR models by means of RMSE, MAPE and MASE. Then, in Table 3, we present the test-sample forecast performance of the employed models. According to Table 2, NNAR models perform better than ARIMA in the first training-sample period, but ARIMA is better in the second training-sample. According to Table 3, for both cases, without and with re-estimation of forecast models for next-day Bitcoin price forecasting, ARIMA models outperform NNAR in the test-sample forecast. Log-transformed Bitcoin price series and its forecasted values using ARIMA and NNAR under different estimation approaches are presented in Figure 4.
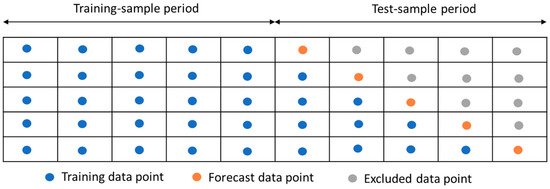
Figure 3.
Illustration of static forecast approach.

Table 2.
Training-sample forecast performance.

Table 3.
Test-sample static forecast performance.
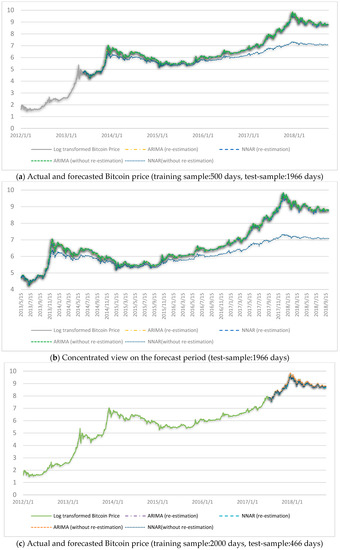
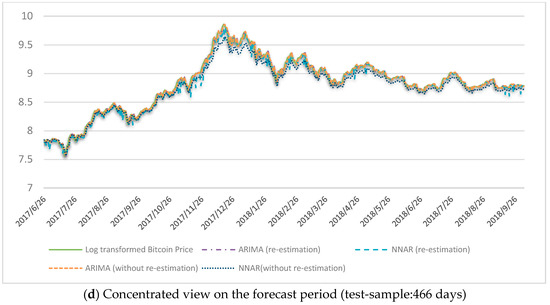
Figure 4.
Bitcoin price forecast. (a,b) refer to the first training and test samples forecast in comprehensive and concentrated view, respectively, and (c,d) refer to the second training and test samples forecast in comprehensive and concentrated view, respectively.
To confirm the validity of forecast models, diagnostic checks are conducted. p-values of the Box-Ljung (BL) test (Ljung and Box 1978) suggest that residuals of all employed models are free from autocorrelation (p-values > 0.05 considering eight lags). The BL test result of squared residuals of ARIMA models indicates the presence of conditional heteroscedasticity (p-values < 0.05); thus, future research on Bitcoin price forecast should consider nested ARIMA models combining ARCH and GARCH. The Jarque-Bera test (Jarque and Bera 1980) results suggest that residuals are not normally distributed (p-values < 0.05). Normality of residuals should not be an issue for the NNAR model as the error series in such models are assumed to be homoscedastic (and normally distributed) when training the model based on the training-sample (Hyndman and Athanasopoulos 2018).
Further, we perform the Diebold Mariano (DM) test (Diebold and Mariano 1995) to compare test-sample forecast results obtained from the two models used, ARIMA and NNAR. DM test results are presented in Table 4. In this case, the alternative hypothesis is that the forecast results of the second method are less accurate than the first method. Thus, a p-value of less than 0.05 indicates better accuracy of the first method. Result of the DM test is similar to as revealed in Table 3—the ARIMA model is more accurate than NNAR in forecasting the test-sample Bitcoin price. It is noteworthy that, forecast of ARIMA models, with or without model re-estimation in each step, are identical. Meanwhile, the NNAR model with re-estimation in each step performs considerably better than the without re-estimation approach.

Table 4.
DM test of forecast results.
6. Discussion and Conclusions
This study forecasts the next-day Bitcoin price using two univariate models—ARIMA and NNAR. Based on the employed forecast accuracy measures (RMSE, MAPE and MASE), while NNAR models perform better than ARIMA in the first training-sample (500 days) Bitcoin price forecasts, ARIMA models outperform NNAR models in both the test-samples. In line with this, from Figure 4, one could argue than NNAR models perform better than ARIMA (see Table 2) in times of less volatility, but not during extremely volatile test-sample periods of Bitcoin price, particularly in the year 2018. Furthermore, the DM test suggests the same, that is, ARIMA forecast results are more accurate than the NNAR forecasts in the test-sample forecasts.
Meanwhile, existing studies offer interesting insights. In a review of neural network models in forecasting, Adya and Collopy (1998) find that neural networks are not necessarily the best modelling approach for all types of data. Abrahart and See (2000) and Álvarez-Díaz et al. (2018) find that ARIMA and NNAR perform similarly. On the other hand, similar to this study, Alon et al. (2001) and Munim and Schramm (2018) also find that neural networks outperform ARIMA in some training-sample, but the opposite holds for test-sample. The reason for better accuracy of ARIMA models could be that we employ the feed-forward NNAR model, which is found to be inferior by Ho et al. (2002) as well when comparing with ARIMA and recurrent neural network (RNN) models. Thus, future study should attempt the RNN approach to Bitcoin price forecast. Furthermore, according to the DM test results, the forecast of ARIMA models are similar for with or without model re-estimation in each step. However, the NNAR model with re-estimation in each step performs better than without re-estimation. Thus, this unique approach of model re-estimation at each step can be adopted in inter-day forecasts, such as in next-hour and next-minute Bitcoin price (also stock price) forecasts. However, the model re-estimation approach to forecast next-day price increases computational duration slightly. To this end, with the growing market-cap of cryptocurrencies and extreme volatility of cryptocurrency prices, further attention should be paid to modelling their returns.
Author Contributions
Conceptualization Z.H.M. and I.A., Data curation Z.H.M., Methodology Z.H.M., Visualization Z.H.M., Introduction M.H.S., Literature review M.H.S. and I.A., Writing–review & editing Z.H.M., M.H.S. and I.A.
Funding
The APC was funded by the University of Agder.
Acknowledgments
The authors would like to thank the two anonymous reviewers and Qazi Haque for useful suggestions on an earlier draft of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The 14 Estimated NNAR(p,k) Models
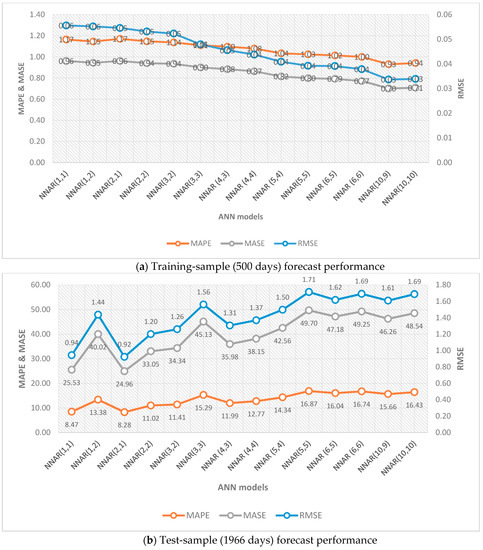
Figure A1.
Examined NNAR model performance. (a,b) The first training and test-sample forecast performance, respectively.
Figure A1.
Examined NNAR model performance. (a,b) The first training and test-sample forecast performance, respectively.
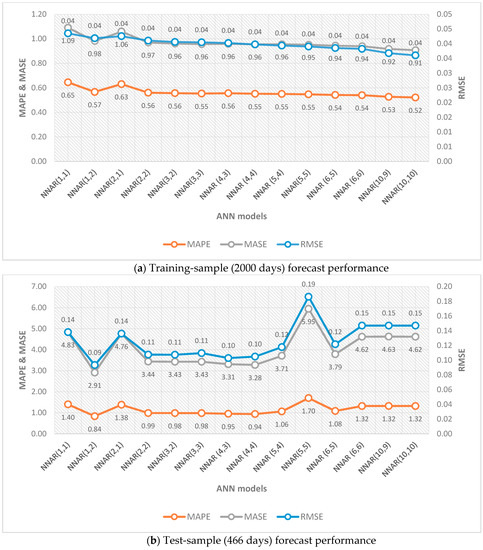
Figure A2.
Examined NNAR model performance. (a,b) The second training and test-sample forecast performance, respectively.
Figure A2.
Examined NNAR model performance. (a,b) The second training and test-sample forecast performance, respectively.
References
- Aalborg, Halvor Aarhus, Peter Molnár, and Jon Erik de Vries. 2018. What can explain the price, volatility and trading volume of Bitcoin? Finance Research Letters. [Google Scholar] [CrossRef]
- Abrahart, Robert J., and Linda See. 2000. Comparing neural network and autoregressive moving average techniques for the provision of continuous river flow forecasts in two contrasting catchments. Hydrological Processes 14: 2157–72. [Google Scholar] [CrossRef]
- Adya, Monica, and Fred Collopy. 1998. How effective are neural networks at forecasting and prediction? A review and evaluation. Journal of Forecasting 17: 481–95. [Google Scholar] [CrossRef]
- Alon, Ilan, Min Qi, and Robert J. Sadowski. 2001. Forecasting aggregate retail sales: A comparison of artificial neural networks and traditional methods. Journal of Retailing and Consumer Services 8: 147–56. [Google Scholar] [CrossRef]
- Álvarez-Díaz, Marcos, Manuel González-Gómez, and María Otero-Giráldez. 2018. Forecasting international tourism demand using a non-linear autoregressive neural network and genetic programming. Forecasting 1: 90–106. [Google Scholar] [CrossRef]
- Ariyo, Adebiyi Ayodele Adewumi, Ayo Oluyinka Adewumi, and Korede Charles. 2014. Stock price prediction using the ARIMA model. Paper presented at the 2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation, Cambridge, UK, March 26–28. [Google Scholar]
- Becker, Jörg, Dominic Breuker, Tobias Heide, Justus Holler, Hans Rauer, and Rainer Böhme. 2011. The Bitcoin System. Münster. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2041492 (accessed on 5 June 2019).
- Beneki, Christina, Alexandros Koulis, Nikolaos A Kyriazis, and Stephanos Papadamou. 2019. Investigating volatility transmission and hedging properties between Bitcoin and Ethereum. Research in International Business and Finance 48: 219–27. [Google Scholar] [CrossRef]
- Benmouiza, Khalil, and Ali Cheknane. 2013. Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models. Energy Conversion and Management 75: 561–69. [Google Scholar] [CrossRef]
- Bouoiyour, Jamal, and Refk Selmi. 2014. What Bitcoin Looks Like? Technical Report. Munich: University Library of Munich. [Google Scholar]
- Bouoiyour, Jamal, Refk Selmi, and Aviral Tiwari. 2014. Is Bitcoin Business Income or Speculative Bubble? Unconditional vs. Conditional Frequency Domain Analysis. Munich: University Library of Munich. [Google Scholar]
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017. On the hedge and safe haven properties of Bitcoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Box, George Edward Pelham, and Gwilym Meirion Jenkins. 1976. Time Series Analysis: Forecasting and Control. revised ed. San Francisco: Holden-Day. [Google Scholar]
- Brandvold, Morten, Peter Molnár, Kristian Vagstad, and Ole Christian Andreas Valstad. 2015. Price discovery on Bitcoin exchanges. Journal of International Financial Markets, Institutions and Money 36: 18–35. [Google Scholar] [CrossRef]
- Brière, Marie, Kim Oosterlinck, and Ariane Szafarz. 2015. Virtual currency, tangible return: Portfolio diversification with bitcoin. Journal of Asset Management 16: 365–73. [Google Scholar] [CrossRef]
- Caporale, Guglielmo Maria, Luis Gil-Alana, and Alex Plastun. 2018. Persistence in the Cryptocurrency Market. Research in International Business and Finance 46: 141–48. [Google Scholar] [CrossRef]
- Cheah, Eng-Tuck, and John Fry. 2015. Speculative bubbles in Bitcoin markets? An empirical investigation into the fundamental value of Bitcoin. Economics Letters 130: 32–36. [Google Scholar] [CrossRef]
- Chen, An-Sing, Hung-Chou Chang, and Lee-Young Cheng. 2019. Time-varying Variance Scaling: Application of the Fractionally Integrated ARMA Model. The North American Journal of Economics and Finance 47: 1–12. [Google Scholar] [CrossRef]
- Chu, Jeffrey, Saralees Nadarajah, and Stephen Chan. 2015. Statistical analysis of the exchange rate of bitcoin. PLoS ONE 10: e0133678. [Google Scholar] [CrossRef] [PubMed]
- Ciaian, Pavel, Miroslava Rajcaniova, and d’Artis Kancs. 2016. The economics of BitCoin price formation. Applied Economics 48: 1799–815. [Google Scholar] [CrossRef]
- Contreras, Javier, Rosario Espinola, Francisco J. Nogales, and Antonio J. Conejo. 2003. ARIMA models to predict next-day electricity prices. IEEE Transactions on Power Systems 18: 1014–20. [Google Scholar] [CrossRef]
- Corbet, Shaen, Brian Lucey, Andrew Urquhart, and Larisa Yarovaya. 2019. Cryptocurrencies as a financial asset: A systematic analysis. International Review of Financial Analysis 62: 182–99. [Google Scholar] [CrossRef]
- Dickey, David A., and Wayne A. Fuller. 1979. Distribution of the estimators for autoregressive time series with a unit root. Journal of the American Statistical Association 74: 427–31. [Google Scholar]
- Diebold, Francis X., and Robert S Mariano. 1995. Comparing predictive accuracy. Journal of Business & Economic Statistics 13: 253–63. [Google Scholar]
- Dwyer, Gerald P. 2015. The economics of Bitcoin and similar private digital currencies. Journal of Financial Stability 17: 81–91. [Google Scholar] [CrossRef]
- Gujarati, Damodar N., and Dawn C. Porter. 2003. Basic Econometrics, 4th ed.New York: McGraw-Hill. [Google Scholar]
- Ho, Sui-Lau, Min Xie, and Thong Ngee Goh. 2002. A comparative study of neural network and Box-Jenkins ARIMA modeling in time series prediction. Computers & Industrial Engineering 42: 371–75. [Google Scholar]
- Hyndman, Rob J., and George Athanasopoulos. 2018. Forecasting: Principles and Practice. Melbourne: OTexts. Available online: https://otexts.com/fpp2/ (accessed on 10 March 2019).
- Hyndman, Rob John, and Yeasmin Khandakar. 2007. Automatic Time Series for Forecasting: The Forecast Package for R. Melbourne: Department of Econometrics and Business Statistics, Monash University. [Google Scholar]
- Hyndman, Rob John, and Anne B. Koehler. 2006. Another look at measures of forecast accuracy. International Journal of Forecasting 22: 679–88. [Google Scholar] [CrossRef]
- Jarque, Carlos Manuel, and Anil Kumar Bera. 1980. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Economics Letters 6: 255–59. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Kristjanpoller, Werner, and Marcel C. Minutolo. 2018. A hybrid volatility forecasting framework integrating GARCH, artificial neural network, technical analysis and principal components analysis. Expert Systems with Applications 109: 1–11. [Google Scholar] [CrossRef]
- Kyriazis, Nikolaos A. 2019. A Survey on Efficiency and Profitable Trading Opportunities in Cryptocurrency Markets. Journal of Risk and Financial Management 12: 67. [Google Scholar] [CrossRef]
- Lam, Eric, Mathieu Benhamou, and Adrian Leung. 2018. Did Bitcoin Just Burst? How It Compares to History’s Big Bubbles. Available online: https://www.bloomberg.com/news/articles/2018-01-17/did-bitcoin-just-burst-how-it-compares-to-history-s-big-bubbles (accessed on 17 January 2018).
- Ljung, Greta Marianne, and George George Edward Pelham Box. 1978. On a measure of lack of fit in time series models. Biometrika 65: 297–303. [Google Scholar] [CrossRef]
- Miller, Jason. 2018. ARIMA Time Series Models for Full Truckload Transportation Prices. Forecasting 1: 121–34. [Google Scholar] [CrossRef]
- Molnár, Peter, Kristian Vagstad, and Ole Christian Andreas Valstad. 2015. A Bit Risky? A Comparison between Bitcoin and Other Assets using an Intraday Value at Risk Approach Working Paper. Available online: http://www.diva-portal.org/smash/get/diva2:742882/fulltext01.pdf (accessed on 5 June 2019).
- Munim, Ziaul Haque, and Hans-Joachim Schramm. 2017. Forecasting container shipping freight rates for the Far East–Northern Europe trade lane. Maritime Economics & Logistics 19: 106–25. [Google Scholar]
- Munim, Ziaul Haque, and Hans-Joachim Schramm. 2018. Forecasting container freight rates: A comparison of artificial neural network and conventional methods. Paper presented at the Annual conference of the International Association of Maritime Economists (IAME), Mombasa, Kenya, September 11–14. [Google Scholar]
- Phillips, Peter Charles Bonest, and Pierre Perron. 1988. Testing for a unit root in time series regression. Biometrika 75: 335–46. [Google Scholar] [CrossRef]
- Popper, Nathaniel. 2015. Digital Gold: Bitcoin and the Inside Story of the Misfits and Millionaires Trying to Reinvent Money. New York: Harper. [Google Scholar]
- Roberts, Jeff John. 2017. 5 Big Bitcoin Crashes: What We Learned. Fortune. Available online: https://finance.yahoo.com/news/5-big-bitcoin-crashes-learned-174604444.html (accessed on 5 June 2019).
- Robertson, Adi. 2018. Facebook Bans All Ads for Bitcoin, ICOs, and Other Cryptocurrency. Available online: https://www.theverge.com/2018/1/30/16951670/facebook-cryptocurrency-bitcoin-ico-deceptive-marketing-ban (accessed on 31 January 2018).
- Rogojanu, Angela, and Liana Badea. 2014. The issue of competing currencies: Case study–Bitcoin. Theoretical and Applied Economics 11: 103–14. [Google Scholar]
- Salisu, Afees A., Kazeem Isah, and Lateef O. Akanni. 2019. Improving the predictability of stock returns with Bitcoin prices. The North American Journal of Economics and Finance 48: 857–67. [Google Scholar] [CrossRef]
- Segendorf, Björn. 2014. What is Bitcoin? Sveriges Riksbank Economic Review 7: 71–87. Available online: http://www.riksbank.se/Documents/Rapporter/POV/2014/2014_2/rap_pov_artikel_4_1400918_eng.pdf (accessed on 5 June 2019).
- Selgin, George. 2015. Synthetic commodity money. Journal of Financial Stability 17: 92–99. [Google Scholar] [CrossRef]
- Shubik, Martin. 2014. Simecs, Ithaca Hours, Berkshares, Bitcoins and Walmarts. Cowles Foundation Discussion Paper No. 1947. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2435902 (accessed on 5 June 2019).
- Urquhart, Andrew. 2016. The inefficiency of Bitcoin. Economics Letters 148: 80–82. [Google Scholar] [CrossRef]
- Yermack, David. 2013. Is Bitcoin a Real Currency? An Economic Appraisal. Technical Report. National Bureau of Economic Research Working Paper No. 19747. Cambridge: National Bureau of Economic Research. Available online: https://www.nber.org/papers/w19747 (accessed on 5 June 2019).
| 1 | |
| 2 | Bitcoin price data for three days, that is, 6–8 January 2015 was not available. |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).