Inflation Propensity of Collatz Orbits: A New Proof-of-Work for Blockchain Applications
Abstract
1. Introduction
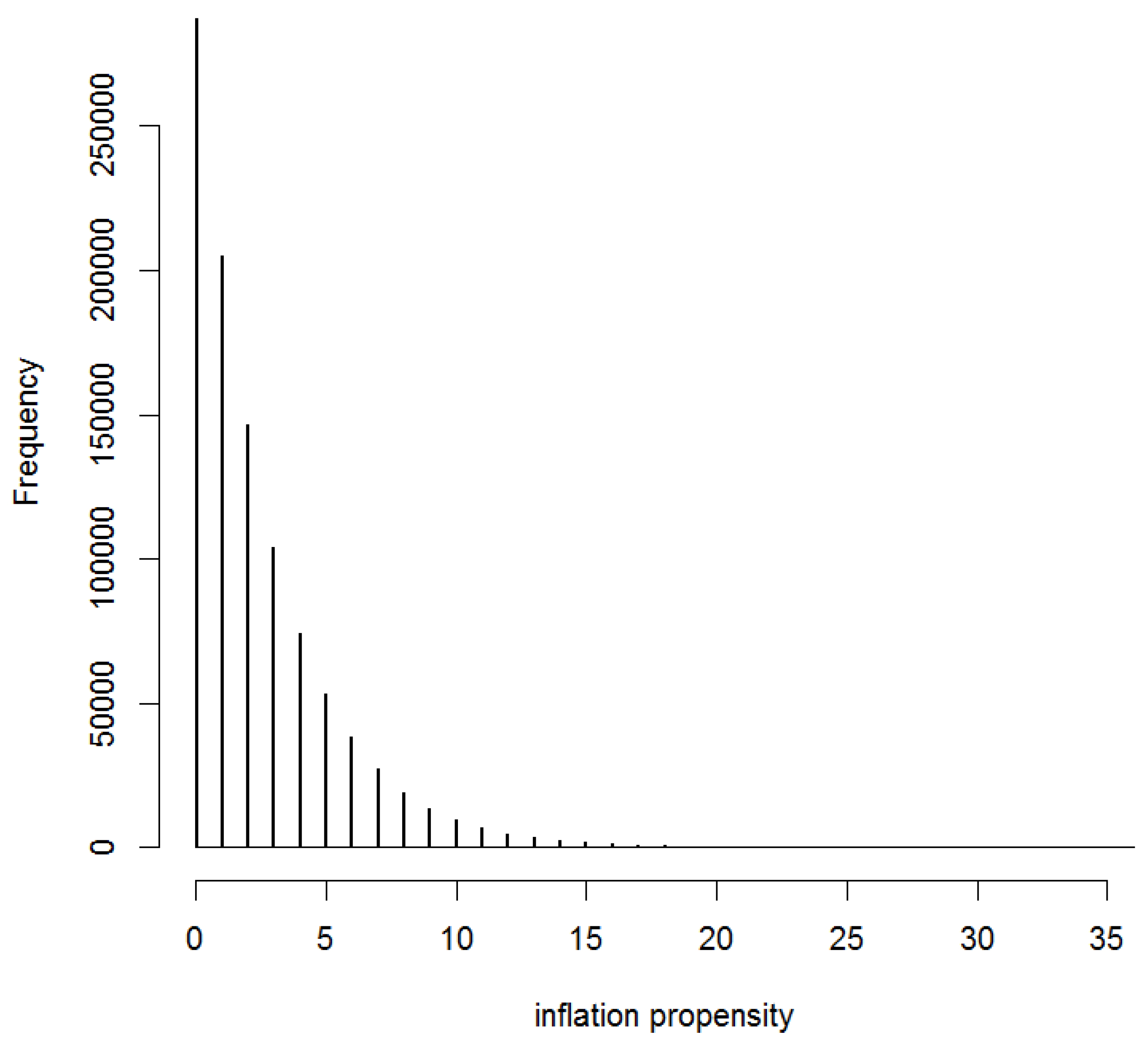
2. Inflation Propensity
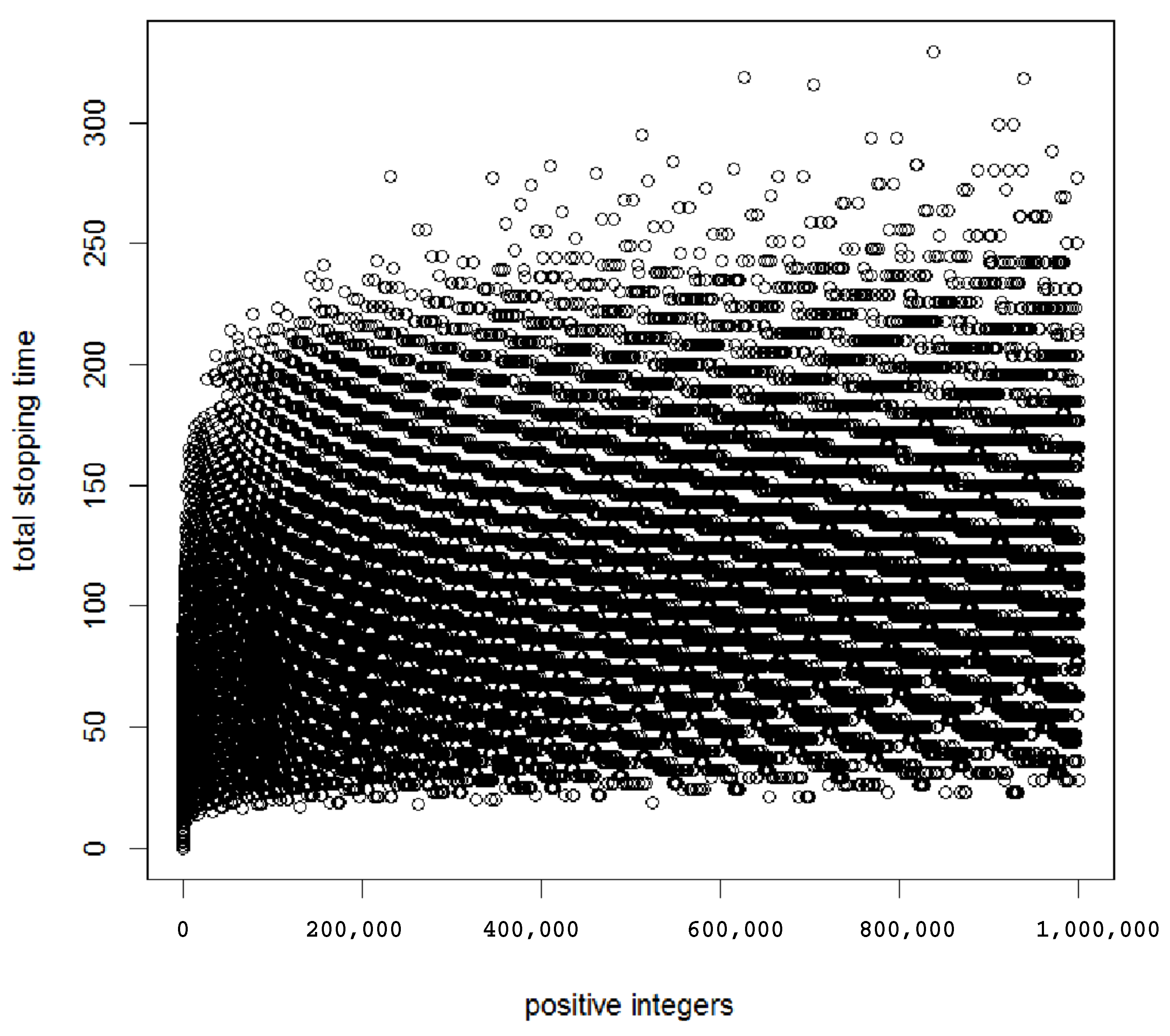
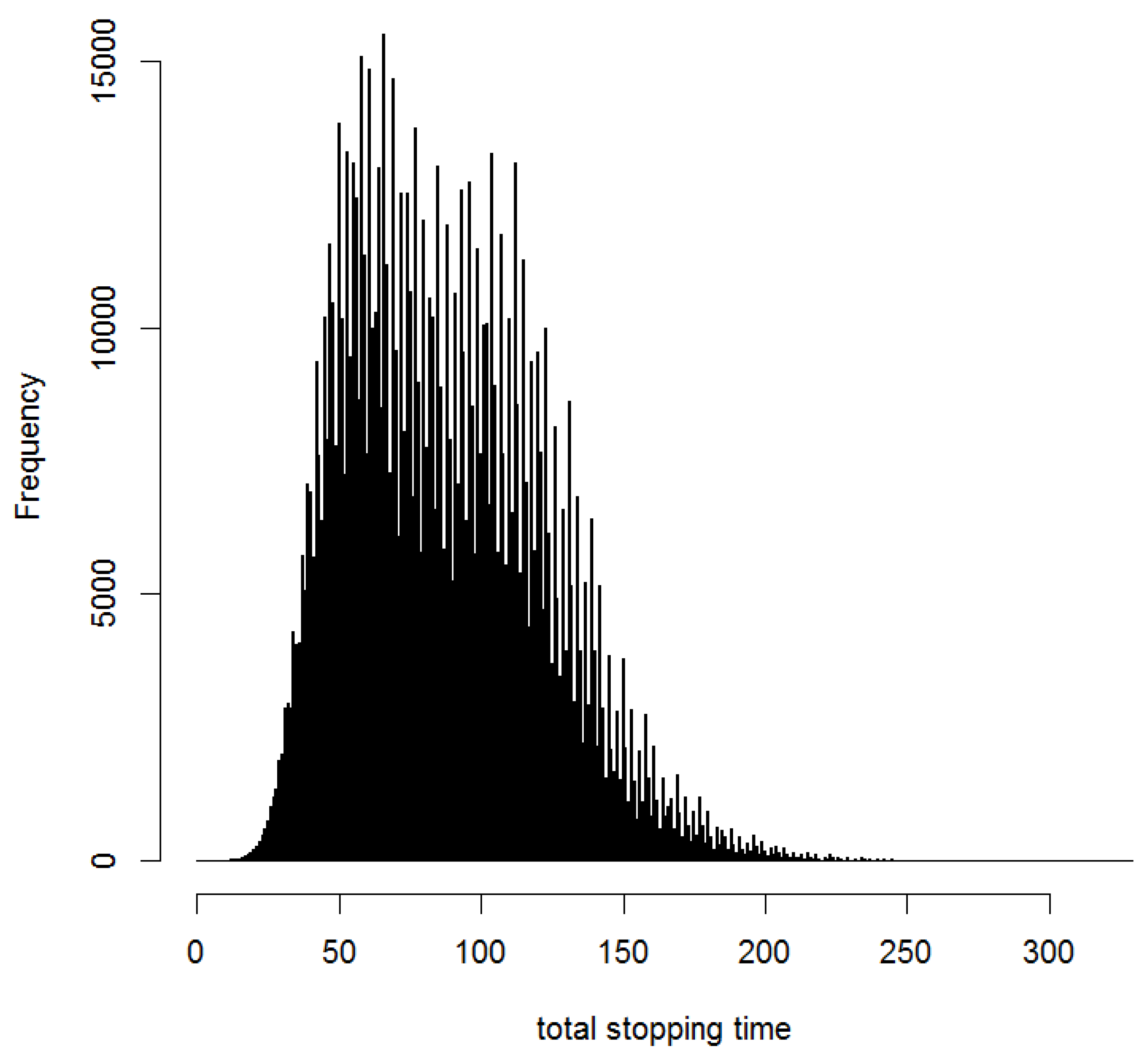
3. Empirical Results
4. Application
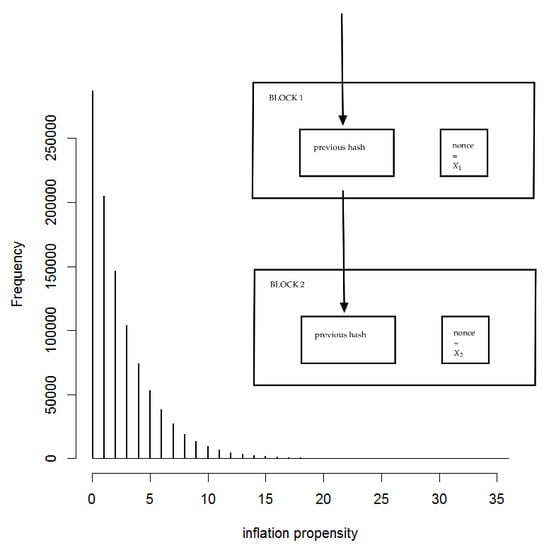
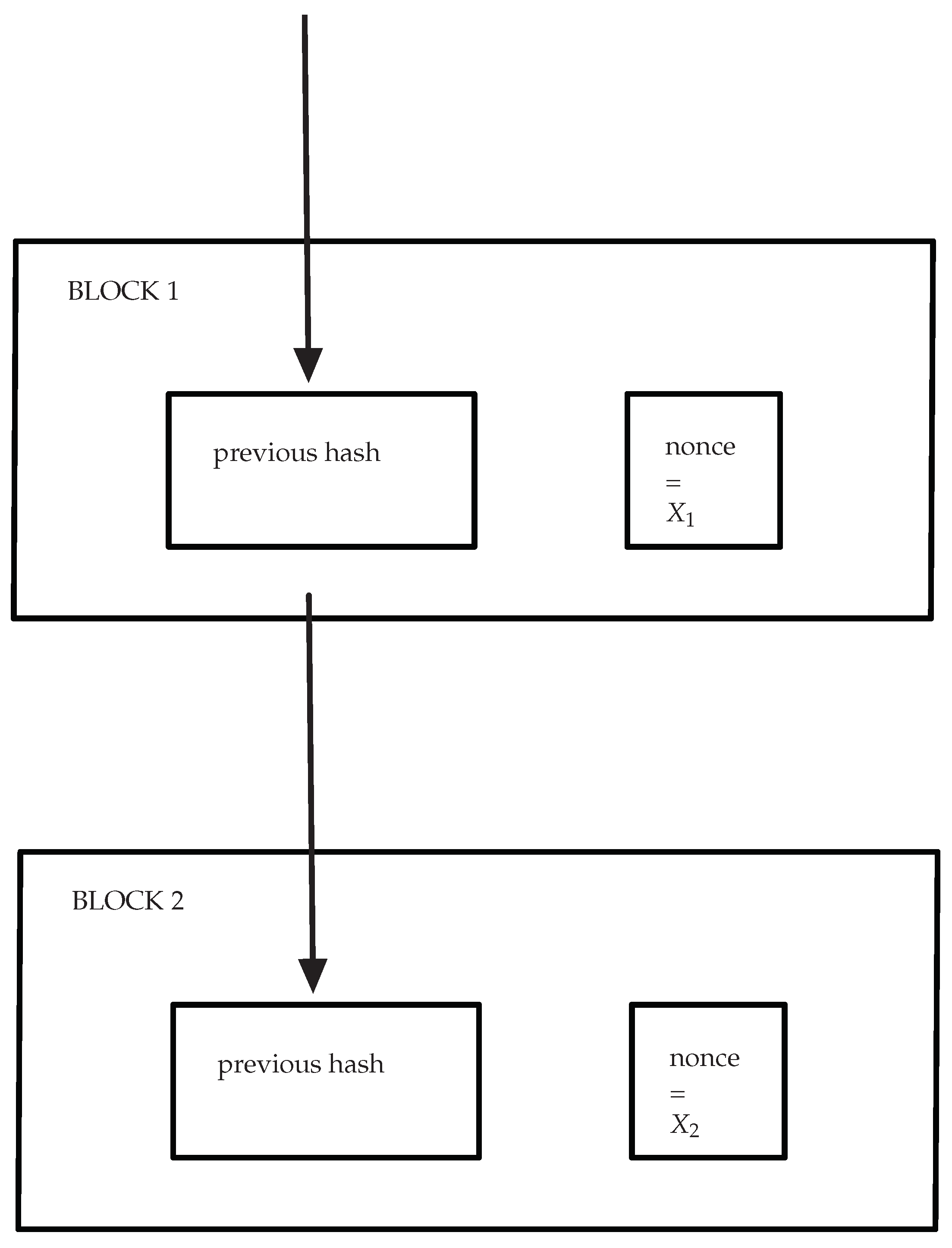
4.1. Collatz-Based Proof-of-Work
4.2. Example: Bitcoin Genesis Hash
4.3. Advantages of the Collatz-Based Proof-of-Work
5. Conclusions
Funding
Conflicts of Interest
Appendix A. Distribution of Inflation Propensity for the First 1 × 1011 Integers
| Observations | |
|---|---|
| 0 | 28,631,964,381 |
| 1 | 20,434,254,718 |
| 2 | 14,583,348,496 |
| 3 | 10,407,804,534 |
| 4 | 7,427,954,284 |
| 5 | 5,301,161,512 |
| 6 | 3,783,166,989 |
| 7 | 2,699,976,430 |
| 8 | 1,927,052,441 |
| 9 | 1,375,229,862 |
| 10 | 981,424,318 |
| 11 | 700,353,911 |
| 12 | 499,868,474 |
| 13 | 356,795,944 |
| 14 | 254,706,290 |
| 15 | 181,761,315 |
| 16 | 129,757,032 |
| 17 | 92,628,127 |
| 18 | 66,127,176 |
| 19 | 47,199,172 |
| 20 | 33,676,458 |
| 21 | 24,024,158 |
| 22 | 17,138,021 |
| 23 | 12,231,945 |
| 24 | 8,727,118 |
| 25 | 6,225,787 |
| 26 | 4,432,544 |
| 27 | 3,162,432 |
| 28 | 2,251,004 |
| 29 | 1,599,248 |
| 30 | 1,139,341 |
| 31 | 814,975 |
| 32 | 583,455 |
| 33 | 416,994 |
| 34 | 298,683 |
| 35 | 212,914 |
| 36 | 150,443 |
| 37 | 106,613 |
| 38 | 76,749 |
| 39 | 55,452 |
| 40 | 39,947 |
| 41 | 28,495 |
| 42 | 20,259 |
| 43 | 14,253 |
| 44 | 10,396 |
| 45 | 7791 |
| 46 | 5431 |
| 47 | 3690 |
| 48 | 2640 |
| 49 | 1984 |
| 50 | 1448 |
| 51 | 1041 |
| 52 | 745 |
| 53 | 595 |
| 54 | 467 |
| 55 | 347 |
| 56 | 234 |
| 57 | 170 |
| 58 | 127 |
| 59 | 72 |
| 60 | 41 |
| 61 | 21 |
| 62 | 20 |
| 63 | 17 |
| 64 | 17 |
| 65 | 9 |
| 66 | 2 |
| 67 | 0 |
| 68 | 1 |
| 69 | 0 |
Appendix B. Python Code for Genesis Block
import hashlib, struct, binascii, time, sys, optparse
from construct import *
def main(): options = get_args() input_script = create_input_script(options.timestamp) output_script = create_output_script(options.pubkey) tx = create_transaction(input_script, output_script,options) hash_merkle_root = hashlib.sha256(hashlib.sha256(tx).digest()).digest() print_block_info(options, hash_merkle_root) block_header = create_block_header(hash_merkle_root, options.time, options.bits, options.nonce) genesis_hash, nonce = generate_hash(block_header, options.nonce, options.bits) announce_found_genesis(genesis_hash, nonce) def get_args(): parser = optparse.OptionParser() parser.add_option("-t", "--time", dest="time", default=int(1231006505), type="int", help="the (unix) time
when the genesisblock is created")
parser.add_option("-z", "--timestamp", dest="timestamp", default= "The Times 03/Jan/2009 Chancellor on brink of second bailout for banks",
type="string", help="the pszTimestamp found in the coinbase of the genesisblock") parser.add_option("-n", "--nonce", dest="nonce", default=0, type="int", help="the first value of the nonce that will be incremented when searching the genesis hash")
parser.add_option("-p", "--pubkey", dest="pubkey", default="04678afdb0fe5548271967f1a67130b7105cd6a828e03909 a67962e0ea1f61deb649f6bc3f4cef38c4f35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f",
type="string", help="the pubkey found in the output script") parser.add_option("-v", "--value", dest="value", default=5000000000, type="int", help="the value in coins for the output, full value (exp. in bitcoin 5000000000 - To get other coins value: Block Value * 100000000)")
parser.add_option("-b", "--bits", dest="bits", type="int", help="the target in compact representation, associated to a difficulty of 1") (options, args) = parser.parse_args() if not options.bits:
options.bits = 40 return options
def create_input_script(psz_timestamp): psz_prefix = ""
if len(psz_timestamp) > 76: psz_prefix = ’4c’ script_prefix = ’04ffff001d0104’ + psz_prefix + chr(len(psz_timestamp)).encode(""’hex’) print (script_prefix + psz_timestamp.encode(’hex’))
return (script_prefix + psz_timestamp.encode(’hex’)).decode(’hex’) def create_output_script(pubkey): script_len = ’41’
OP_CHECKSIG = ’ac’
return (script_len + pubkey + OP_CHECKSIG).decode(’hex’) def create_transaction(input_script, output_script,options): transaction = Struct("transaction",
Bytes("version", 4),
Byte("num_inputs"),
StaticField("prev_output", 32),
UBInt32(’prev_out_idx’),
Byte(’input_script_len’),
Bytes(’input_script’, len(input_script)),
UBInt32(’sequence’),
Byte(’num_outputs’),
Bytes(’out_value’, 8),
Byte(’output_script_len’),
Bytes(’output_script’, 0x43),
UBInt32(’locktime’))
tx = transaction.parse(’\x00’*(127 + len(input_script)))
tx.version = struct.pack(’<I’, 1)
tx.num_inputs = 1 tx.prev_output = struct.pack(’<qqqq’, 0,0,0,0)
tx.prev_out_idx = 0xFFFFFFFF tx.input_script_len = len(input_script) tx.input_script = input_script tx.sequence = 0xFFFFFFFF tx.num_outputs = 1 tx.out_value = struct.pack(’<q’ ,options.value)
tx.output_script_len = 0x43 tx.output_script = output_script tx.locktime = 0 return transaction.build(tx)
def create_block_header(hash_merkle_root, time, bits, nonce): block_header = Struct(’<q’"block_header",
Bytes("version",4),
Bytes("hash_prev_block", 32),
Bytes("hash_merkle_root", 32),
Bytes("time", 4),
Bytes("bits", 4),
Bytes("nonce", 4))
genesisblock = block_header.parse(’\x00’*80)
genesisblock.version = struct.pack(’<I’, 1)
genesisblock.hash_prev_block = struct.pack(’<qqqq’, 0,0,0,0)
genesisblock.hash_merkle_root = hash_merkle_root genesisblock.time = struct.pack(’<I’, time)
genesisblock.bits = struct.pack(’<I’, bits)
genesisblock.nonce = struct.pack(’<I’, nonce)
return block_header.build(genesisblock)
#Collatz inflation propensity def inflation_propensity(x): xMax=x stepToMaximum=0 while x > 1:
if x % 2 == 0:
x = x / 2 else:
x = (3 * x + 1) / 2 if x > xMax:
xMax=x stepToMaximum+= 1 return stepToMaximum
def generate_hash(data_block, start_nonce, bits): print ’Searching for genesis hash..’
nonce = start_nonce last_updated = time.time() header_hash = generate_hashes_from_block(data_block) print(binascii.hexlify(header_hash)) orbitTrajectory=int(header_hash.encode(’hex_codec’), 16) print(orbitTrajectory) timeInit=time.time() while True:
xi=inflation_propensity(orbitTrajectory) last_updated = calculate_hashrate(nonce, last_updated, orbitTrajectory,timeInit) if xi==bits:
return (generate_hashes_from_block(data_block), nonce)
else:
nonce = nonce + 1 orbitTrajectory += 1 data_block = data_block[0:len(data_block) - 4] + struct.pack(’<I’, nonce) def generate_hashes_from_block(data_block): header_hash = hashlib.sha256(hashlib.sha256(data_block).digest()).digest()[::-1] return header_hash
def calculate_hashrate(nonce, last_updated, orbitTrajectory, timeinit): if nonce % 10000 == 0:
now = time.time() hashrate = round(10000/(now - last_updated)) sys.stdout.write("\r%s Xis/s, Orbit: %s, Total time: %s minutes "
%(str(hashrate), str(orbitTrajectory), str((now-timeinit)/60))) sys.stdout.flush() return now
else:
return last_updated
def print_block_info(options, hash_merkle_root): print "merkle hash: " + hash_merkle_root[::-1].encode(’hex_codec’) print "pszTimestamp: " + options.timestamp
print "pubkey: " + options.pubkey
print "time: " + str(options.time)
print "bits: " + str(hex(options.bits))
def announce_found_genesis(genesis_hash, nonce): print "genesis hash found!"
print "nonce: " + str(nonce)
print "genesis hash: " + genesis_hash.encode(’hex_codec’) main() |
References
- Back, Adam. 2002. Hashcash-A Denial of Service Counter-Measure. Available online: http://hashcash.org/papers/hashcash.pdf (accessed on 25 November 2018).
- Bae, Minyoung, Ju-Sung Kang, and Yongjin Yeom. 2017. A Study on the One-to-Many Authentication Scheme for Cryptosystem Based on Quantum Key Distribution. Paper presented at IEEE Conference on Platform Technology and Service (PlatCon), Busan, Korea, February 13–15; pp. 1–4. [Google Scholar]
- Biryukov, Alex, and Dmitry Khovratovich. 2017. Equihash: Asymmetric proof-of-work based on the generalized birthday problem. Ledger 2: 1–30. [Google Scholar] [CrossRef]
- Conway, John H. 1972. Unpredictable iterations. Paper presented at 1972 Number Theory Conference, Boulder, CO, USA, August 14–18; pp. 49–52. [Google Scholar]
- Crandall, Richard E. 1978. On the 3x + 1 problem. Mathematics of Computation 32: 1281–92. [Google Scholar]
- Dwork, Cynthia, and Moni Naor. 1992. Pricing via processing or combatting junk mail. Paper presented at Annual International Cryptology Conference, Santa Barbara, CA, USA, August 16–20; Berlin and Heidelberg: Springer, pp. 139–47. [Google Scholar]
- e Silva, T. Oliveira. 2010. Empirical verification of the 3x+ 1 and related conjectures. In The Ultimate Challenge: The 3x+ 1 Problem. Edited by Jeffrey C. Lagarias. Providence: American Mathematical Society, pp. 189–207. ISBN 978-0821849408. [Google Scholar]
- Hartikka, Lauri. 2017. GenesisH0. Available online: https://github.com/lhartikk/GenesisH0 (accessed on 1 September 2018).
- Honda, Takumi, Yasuaki Ito, and Koji Nakano. 2017. GPU-accelerated Exhaustive Verification of the Collatz Conjecture. International Journal of Networking and Computing 7: 69–85. [Google Scholar] [CrossRef]
- King, Sunny. 2013. Primecoin: Cryptocurrency with Prime Number Proof-of-Work. Bitcoin Magazine, July 7. [Google Scholar]
- Kiktenko, Evgeniy O., Nikolay O. Pozhar, Maxim N. Anufriev, Anton S. Trushechkin, Ruslan R. Yunusov, Yuri V. Kurochkin, and Aleksey K. Fedorov. 2018. Quantum-secured blockchain. Quantum Science and Technology 3: 035004. [Google Scholar] [CrossRef]
- Kontorovich, Alex V., and Jeffrey C. Lagarias. 2010. Stochastic models for the 3x+ 1 and 5x+ 1 problems and related problems. In The Ultimate Challenge: The 3x+ 1 Problem. Edited by Jeffrey C. Lagarias. Providence: American Mathematical Society, pp. 131–88. ISBN 978-0821849408. [Google Scholar]
- Kurtz, Stuart A., and Janos Simon. 2007. The undecidability of the generalized Collatz problem. Paper presented at International Conference on Theory and Applications of Models of Computation, Shanghai, China, May 22–25; Berlin and Heidelberg: Springer, pp. 542–53. [Google Scholar]
- Lagarias, Jeffrey C. 1985. The 3x+ 1 problem and its generalizations. The American Mathematical Monthly 92: 3–23. [Google Scholar] [CrossRef]
- Lagarias, Jeffrey C., ed. 2010. The 3x+1 problem: An overview. In The Ultimate Challenge: The 3x+ 1 Problem. Providence: American Mathematical Society, pp. 3–30. ISBN 978-0821849408. [Google Scholar]
- Minsky, Marvin L. 1961. Recursive unsolvability of Post’s problem of “tag” and other topics in the theory of Turing machines. Annals of Mathematics 74: 437–55. [Google Scholar] [CrossRef]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System, Self-published.
- Nichols, Daniel. 2018. Analogues of the 3x + 1 Problem in Polynomial Rings of Characteristic 2. Experimental Mathematics 27: 100–10. [Google Scholar] [CrossRef]
- Percival, Colin. 2009. Stronger Key Derivation via Sequential Memory-Hard Functions, Self-published.
- Rubin, Jeremy. 2017. The Problem with ASICBOOST, Self-published.
- Terras, Riho. 1976. A stopping time problem on the positive integers. Acta Arithmetica 30: 241–52. [Google Scholar] [CrossRef]
- Tromp, John. 2015. Cuckoo cycle: A memory bound graph-theoretic proof-of-work. Paper presented at International Conference on Financial Cryptography and Data Security, San Juan, PR, USA, January 26–30; Berlin and Heidelberg: Springer, pp. 49–62. [Google Scholar]
- Urvoy, Tanguy. 2001. Regularity of congruential graphs. Paper presented at Mathematical Foundations of Computer Science 2000, MFCS 2000, Bratislava, Slovakia, August 28–September 1; Edited by Mogens Nielsen and Branislav Rovan. Lecture Notes in Computer Science. Berlin and Heidelberg: Springer, vol. 1893. [Google Scholar]
- Wood, Gavin. 2014. Ethereum: A secure decentralised generalised transaction ledger. Ethereum Project Yellow Paper 151: 1–32. [Google Scholar]
| 1. | also called “trajectory” or “forward orbit”. |
| Name | ∼Fully Diluted (Y2050) Marketcap/15 October 2018 | Underlying Algorithm |
|---|---|---|
| Bitcoin (BTC) | $134,308,812,450 | SHA-256 |
| Ethereum (ETH) | $29,787,293,584 | SHA-3 |
| Bitcoin Cash (BCH) | $9,225,442,784 | SHA-256 |
| Litecoin (LTC) | $4,430,985,913 | Scrypt |
| Dash (DASH) | $2,956,683,098 | X11 |
| Monero (XMR) | $2,300,499,210 | CryptoNight |
| ZCash (ZEC) | $2,262,517,311 | Equihash |
| Ethereum Classic (ETC) | $2,161,731,159 | SHA-3 |
| Dogecoin (DOGE) | $1,402,169,807 | Scrypt |
| Siacoin (SC) | $564,862,312 | Blake-2b |
| Bitcoin Gold (BTG) | $526,927,423 | Equihash |
| Digibyte (DGB) | $483,402,492 | SHA-256 and others |
| ReddCoin (RDD) | $447,635,857 | Scrypt |
| Bitcoin Diamond (BCD) | $343,664,370 | X13 |
| ZenCash (ZEN) | $275,245,426 | SHA-3 |
| Verge (XVG) | $229,929,732 | Scrypt |
| Zcoin (XZC) | $194,506,940 | Equihash |
| Monacoin (MONA) | $124,690,762 | Scrypt |
| Syscoin (SYS) | $81,207,881 | Scrypt |
| Zclassic (ZCL) | $67,149,925 | Equihash |
| Vertcoin (VTC) | $53,917,212 | Lyra2REv2 |
| Bitcoin Private (BTCP) | $51,124,537 | Equihash |
| LBRY Credits (LBC) | $41,220,511 | LBRY |
| Einsteinium (EMC2) | $25,808,910 | Scrypt |
| GameCredits (GAME) | $13,734,781 | Scrypt |
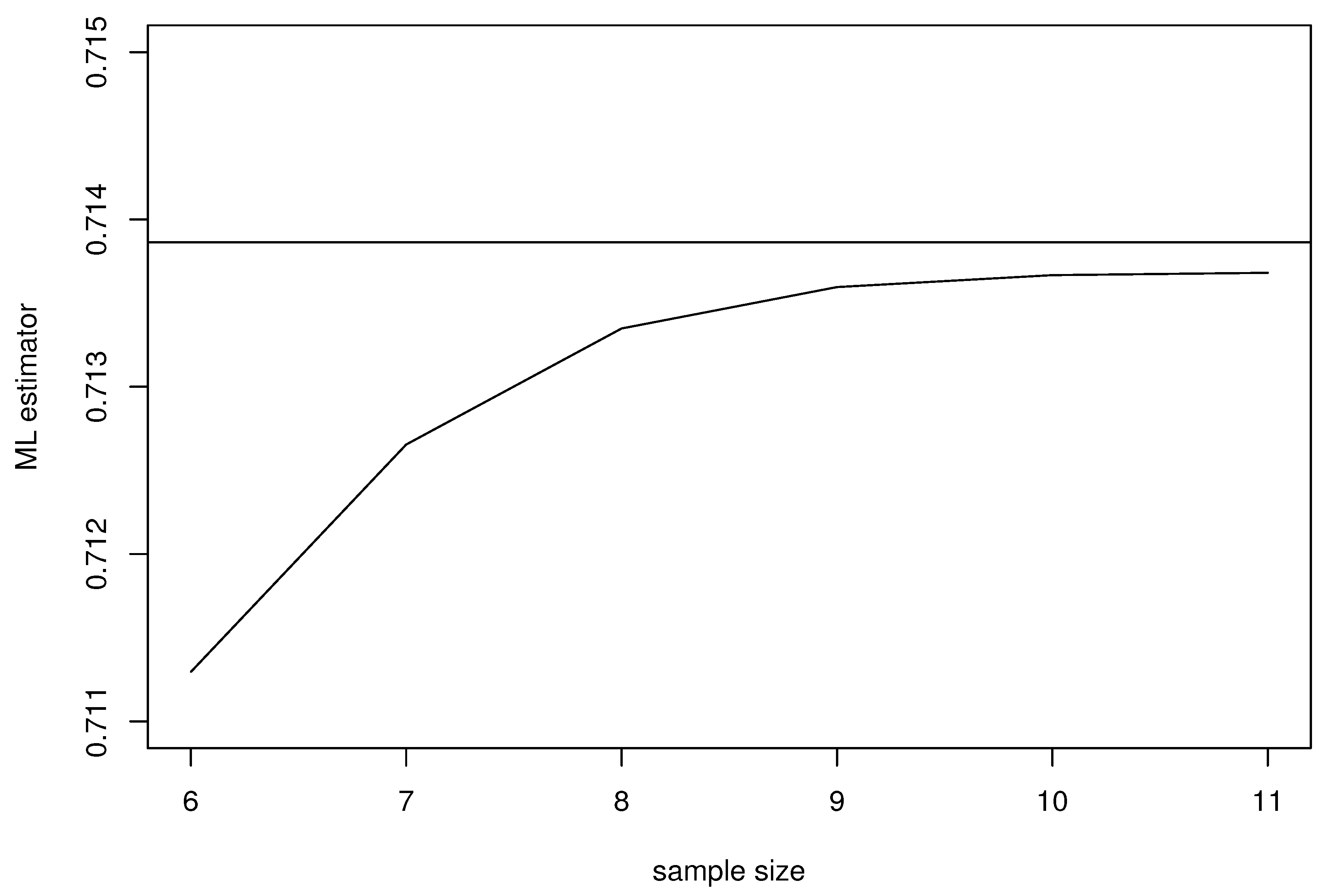
| Sample 1 | Sample 1 | Sample 1 | Sample 1 | ||
|---|---|---|---|---|---|
| 0.7133482 | 0.7135956 | 0.713667 | 0.713681 | ||
| Percentile | p-Value | p-Value | p-Value | p-Value | |
| 0 | 29 | 0.01 | 0.15 | 0.70 | 0.64 |
| 1 | 49 | 0.04 | 0.19 | 0.70 | 0.14 |
| 2 | 64 | 0.09 | 0.00 | 0.23 | 0.25 |
| 3 | 74 | 0.15 | 0.00 | 0.36 | 0.39 |
| 4 | 82 | 0.08 | 0.00 | 0.11 | 0.35 |
| 5 | 87 | 0.05 | 0.00 | 0.01 | 0.37 |
| 6 | 91 | 0.07 | 0.00 | 0.00 | 0.13 |
| 7 | 93 | 0.11 | 0.00 | 0.00 | 0.03 |
| 8 | 95 | 0.00 | 0.00 | 0.00 | 0.04 |
| 9 | 97 | 0.00 | 0.00 | 0.00 | 0.03 |
| 10 | 98 | 0.00 | 0.00 | 0.00 | 0.00 |
| block header hash | 37d25f7f472fde7bb5b84f4bb319097c580383911b45eff10e68afa06073d6c0 |
| corresponding integer | 25248903652996148805237565338196318809513309980842754974279018460154571249344 |
| merkle hash | 4a5e1e4baab89f3a32518a88c31bc87f618f76673e2cc77ab2127b7afdeda33b |
| pszTimestamp | The Times 3 January 2009 Chancellor on brink of second bailout for banks |
| pubkey | 04678afdb0fe5548271967f1a67130b7105cd6a828e03909a67962e0ea1f61deb649f6bc3f4cef38c4f |
| 35504e51ec112de5c384df7ba0b8d578a4c702b6bf11d5f | |
| time | 1231006505 |
| inflation propensity target | 40 (0 × 28) |
| nounce | 3420991 |
| genesis hash | 9ed4d59e375c60e568524ac7fdfcce2c36dd8d449a20b0be8c9f6f9dbd2f8709 |
| computational time | 28 min |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bocart, F. Inflation Propensity of Collatz Orbits: A New Proof-of-Work for Blockchain Applications. J. Risk Financial Manag. 2018, 11, 83. https://doi.org/10.3390/jrfm11040083
Bocart F. Inflation Propensity of Collatz Orbits: A New Proof-of-Work for Blockchain Applications. Journal of Risk and Financial Management. 2018; 11(4):83. https://doi.org/10.3390/jrfm11040083
Chicago/Turabian StyleBocart, Fabian. 2018. "Inflation Propensity of Collatz Orbits: A New Proof-of-Work for Blockchain Applications" Journal of Risk and Financial Management 11, no. 4: 83. https://doi.org/10.3390/jrfm11040083
APA StyleBocart, F. (2018). Inflation Propensity of Collatz Orbits: A New Proof-of-Work for Blockchain Applications. Journal of Risk and Financial Management, 11(4), 83. https://doi.org/10.3390/jrfm11040083