Abstract
In the present paper, we investigate connectedness within cryptocurrency markets as well as across the Bitcoin index (hereafter, BPI) and widely traded asset classes such as traditional currencies, stock market indices and commodities, such as gold and Brent oil. A spill over index approach with the spectral representation of variance decomposition networks, is employed to measure connectedness. Results show no significant spillover effects between the nascent market of cryptocurrencies and other financial markets. We suggest that cryptocurrencies are real independent financial instruments that pose no danger to financial system stability. Concerning the connectedness within the cryptocurrency markets, we report a time–frequency–dynamics connectedness nature. Moreover, the decomposition of the total spill over index is mostly dominated by a short frequency component (2–4 days) leading to the conclusion that this nascent market is highly speculative at present. These findings provide insights for regulators and potential international investors.
1. Introduction
Since the systemic failure of the global equity markets during the recent financial crisis in 2008, the public at large has lost confidence in the traditional monetary system. This situation has made non-traditional currency exchange (i.e., digital currency or cryptocurrency) encroach on our daily lives and has become part of the new world economy in this century.1 Bitcoin2 is a digital currency that has triggered the interest of many users (e.g., companies, merchants, investors, etc.) due to its decentralization, anonymity and freedom, combined with lower fees than those exacted by incumbent payment systems (Joshi 2017). The cryptocurrency markets (popularized by Bitcoin) have arguably been a panacea for the global economic system (Kerner 2014).
Despite that, many economies have been less welcoming of cryptocurrencies, with regulators issuing some of the strongest warnings. It is no secret that the cryptocurrency nature provides a high level of anonymity from the gazing eyes of states, which can therefore facilitate money laundering, tax evasion and terrorist financing.3 The controversial opinions about this nascent market have drawn significant attention from the mainstream press and various financial blogs, as well as a wide range of people, which indicates the vital importance of this phenomenon.
Despite its sharp popularity and its huge volatility that occurred from time to time, there are still fewer academic works assessing cryptocurrencies from the economic–finance perspectives4. Prior studies are concentrated on understanding their moneyless properties, according to gold and traditional currency or compared to a well-known asset such as stocks, bonds, etc. (Barber et al. 2012; Bell 2013; Glaser et al. 2014). As most findings show, Bitcoin is neither a convertible tangible asset (such as gold) nor a fiat currency (such as dollar). There exist other studies focusing on the determinants of bitcoin prices (Buchholz et al. 2012; Kristoufek 2013; van Wijk 2013; Dyhrberg 2015a). Their research results suggest multiple factors that may play important roles in explaining its evolution (e.g., supply–demand fundamentals, the attractiveness for investors, popularity in the media, transaction volume, etc.). The past few years have witnessed considerable research concerning the importance of adding cryptocurrency to a portfolio with equity and with other assets classes (Briere et al. 2013; Eisel et al. 2015; Bouri et al. 2017a). A comparative analysis of different results (see Section 3) shows that no definitive conclusions can be reached in regard to key functions of the Bitcoins for the global economic system. This paper does not lead to any of these research areas. The aim here is to provide empirical insights on the direction and intensity of information transmission within Bitcoins, and between Bitcoins and the global economic system.
A substantial body of literature has investigated the volatility spillover between the same type of asset classes, e.g., stock, bond, commodity and FX markets, between oil and stock markets, between FX and stock market, among other Aftab et al. (2015) and Aviral et al. (2018). The absence of empirical works addressing spillover effects within the Bitcoin markets, and across Bitcoins and other asset classes, is the motive for this study.
In a recent show of the acceptance of cryptocurrencies by the financial world, several Bitcoin derivatives exchanges opened5. In 2016, Chicago Mercantile Exchange (CME) group and Crypto Facilities Ltd. have launched two Bitcoin pricing products: BRR (Bitcoin Reference Rate) and BRTI (a real-time index of the US dollars of one Bitcoin). Therefore, the growing range of acceptance on the various fronts of cryptocurrencies and their started integration with more traditional financial markets may make them develop more relationships, create information flows and induce shocks. This study attempts to explore these features, by evaluating their connectedness with each other, and with other markets such as traditional currencies, stocks and commodities, using the spill over index approach and extensions. These markets are selected for two major reasons. The major reason is the great interest of these asset classes for financial analysts and investors, who use them for risk hedging alternatives or as investment opportunities. The second one is that the number and intensity of crises in these markets in recent decades have sharpened. This seeks to provide a valuable insight for investors about the influences they have on one another and on the stability of Bitcoin markets.
The spill over index approach has been proposed by Diebold et al. (2009). The basic spill over index idea is simple but often effective in ranking assets by their systemic importance. Following the original method of Diebold et al. (2009), the Forecast Error Variance Decomposition (hereafter, FEVD) networks associated with an n-variable vector auto-regressive model (VAR) is used to define weighted and directed networks from market data. In Diebold et al. (2012), authors proposed the generalized variance decompositions of Pesaran and Shin (1998) (GFEVD hereafter), which are invariant to variable ordering, to identify uncorrelated structural shocks from correlated reduced form shocks. More recently, Barunik et al. (2017) have been interested in frequency origins of connectedness variables. Using the spectral technique, Barunik et al. (2017) document that such frequency domains are important for a deep understanding of the different sources of risk spill over, that remain hidden when time domain measures are used (i.e., the effects are simply aggregated through frequencies). In this paper, we follow these extensions to assess volatility spill overs within cryptocurrencies and from BPI to several currencies and stock market indices, as well as commodities, and vice versa.
Our underlying data are daily and cover the period 7 October 2010 to 8 February 2018. The data includes the return of BPI made by Coindesk. Moreover, our data covers the daily return of five popular stock indexes (i.e., SP500, NASDAQ, FTSE100, HangSeng and Nikkei225) and currencies (i.e., EUR/USD, GBP/USD, USD/JPY, USD/CHF and USD/CAD). For commodity markets, we limit our attention to the daily return of gold and Brent futures contracts. We calculate return as the change in the log closed prices. Then, the volatility is expressed as the absolute value of these changes. This approach dates back at least to Davidian and Carroll (1987), who argue that absolute return volatility is more robust against symmetric and non-normality variables.
Our results exhibit a time-varying pattern of connectedness within cryptocurrencies. The decomposition of the total spill over index (TSI) is dominated by a short frequency component (2–4 days). This shows that the market is mostly controlled by speculative behavior. We have shown also that volatility shocks in the cryptocurrency market may not propagate to other financial markets and vice versa.
The remainder of this paper proceeds as follows: we begin by presenting a background and a literature review on cryptocurrencies. Then, we describe our methodology on how we calculate the average (i.e., total) spill overs and to identify connectedness frequency. Afterwards, we present our data and substantive results in Section 5 and Section 6, respectively. To finish, we conclude in Section 7.
2. Brief Background on Cryptocurrencies
The most popular virtual currency is Bitcoin, with a market capitalization of about 40% of the entire cryptocurrency market.6 In its purest form, a digital coin is a peer-to-peer payment cash system and an unregulated currency introduced in 2008 without legal tender status.7 The proposed protocol is related to a decentralized system to confirm transactions and to assure that the supply of Bitcoins is, and remains, limited. This system functions without the backing of a central bank or any other monitoring authority. It allows any two willing parties to transact directly with each other without the need for a trusted third party.8 The record in the system is secured through cryptography by allowing the protection of data from theft or alteration. The cryptography can be also used for user authentication.
Once confirmed, every transaction is recorded in a “block chain” which is a tamper-proof public ledger technology. Every payment is validated by each network node. While this ecosystem provides an effective protection against “counterfeiting” and ownership disputes, it is still vulnerable to theft. Owners require a cryptographic key pair (i.e., private and public keys). Each owner [trader] transfers coin [bitcoin] to the next [owner] by digitally signing a hash of the previous transaction and the public key of the next owner and adding these to the end of the block chain9. A payee can verify the signatures to verify the chain of ownership. Thereby, Bitcoin can be defined as a chain of digital signatures.
On 2 October 2013, the U.S. government followed by China regulators shut down websites involved in that activity, thus creating a bigger shock in this market. Despite this action, Bitcoin price has continued to climb with the undetermined rate. For instance, Bitcoin started in 2017 at less than $US1000 then in December it went up to around $US20,000, which meant that it notched up a gain of 1318% for the year 2017. This certainly looked like speculative hysteria. In February 2018, cryptocurrencies also reached a record $600 billion in market value after the recovery; with the inevitable $700 billion marks right around the corner (i.e., will happen very soon).10 Even though it has soared in market capitalization this year, the cryptocurrency market remains small compared to other traditional financial markets.
To date, there are 1400 digital currencies in the world and many countries (at least 32 countries) authorize the use of them. It is possible also to convert Bitcoin into all major currencies, but 90% of the daily trading volume is processed in Chinese Yuan and 6% in US dollars.11
Due to this mysterious rise of trading volume, the Bitcoin phenomenon demands a deeper investigation, which is the main objective of this study.
3. Literature Review
Although Bitcoins have been of interest in law and computer science for a long time, it has not significantly attracted the focus of economic and financial researchers. First of all, we mention the study of Nakamoto (2008), as the elusive creator of bitcoin. Following its proposal, Bitcoin was originally presented as a purely peer-to-peer version of electronic cash that allows online payments directly from one party to another without going through any monitoring institution. After that, the sharp spike in bitcoin price, and its huge volatility from time to time, has steered debate amongst economists.
Some papers have concentrated on the characteristics of cryptocurrencies following different forms of money and other well-known assets; among others Grinberg (2011), Wu and Pandey (2014), Barber et al. (2012), Whelan (2013) and Glaser et al. (2014). For example, Grinberg (2011) shows that bitcoin has a competitive advantage to make micropayments. However, Wu and Pandey (2014) finds that bitcoin does not have the key attributes of a currency and it should be regarded as a very illiquid financial asset. Whelan (2013) argues that bitcoin might look like the dollar. The main difference is that the dollar is backed by a government entity, while bitcoin is created and managed by non-government entities. Moreover, users’ intentions to participate in the Bitcoin ecosystems are described by Glaser et al. (2014), finding that new users tend to trade Bitcoin on a speculative investment intention basis rather than as a means of paying for goods or services. Likewise, Yermack (2015) claims that Bitcoins closely resemble speculative investments, and their trading style demonstrates characteristics similar to stock trading.
Other papers have concentrated on the price formation of cryptocurrencies; among others Buchholz et al. (2012), Kristoufek (2013), van Wijk (2013), Dyhrberg (2015a). As for the case of any other assets, these authors argued that the price of Bitcoin is determined by several factors such as demand–supply fundamentals, investor’s speculative behavior and global financial indicators related to equity markets, foreign exchange rate or crude oil and gold. Ali et al. (2014) also include other factors that influence the value of virtual currencies, such as risk-return trade-offs, transaction costs or relative benefits, and habit formation.
Briere et al. (2013) provide a tentative first look at how Bitcoin might be a suitable instrument for diversification. The researchers concluded that Bitcoin delivers high diversification benefits as it correlates negatively with most of the analyzed stock market indices. More recently, Gangwal (2016) wrote about the effect of including Bitcoin to the portfolio of an international investor. Using mean-variance analysis, the author argued that adding Bitcoin to portfolios always yields a diversification benefit (i.e., a higher Sharpe ratio). This means that Bitcoin return offsets its volatility risk. Due to the non-normal nature of Bitcoin return, Eisel et al. (2015) do not propose the classic mean-variance approach applied by Briere et al. (2013), but adopt a Conditional Value-at-Risk framework (CVaR). The results indicate that an investment in Bitcoin increases the CVaR of a portfolio. Nonetheless, this additional risk is overcompensated by high return, leading to better risk-return ratios. This last issue is further extended by Dyhrberg (2015b) who explores the financial asset capabilities of bitcoin using the Generalized Auroregressive Conditional Heteroskedasticity (GARCH) model. Results show that Bitcoins have a few aspects that are similar to gold and the dollar, indicating hedging capabilities and advantages as a medium of exchange. The asymmetric GARCH show that bitcoin may be useful in risk management and ideal for risk-averse investors in anticipation of negative shocks to the market. Overall, one can conclude that Bitcoin has a place in the financial markets and in portfolio management, as it can be considered as something between a fiat currency and a commodity. Conversely, Baur et al. (2018), using the same sample and econometric models of Dyhrberg (2015b), showed that Bitcoin exhibits distinctively different return, volatility and correlation characteristics compared to gold and the US dollar. On the other hand, Baur et al. (2015) argue that Bitcoin is a hybrid between precious metals and conventional currencies. They also highlight its role as a useful diversifier (i.e., uncorrelated with traditional assets) and an investment asset. In another interesting study, Bouri et al. (2017b) investigate the relationship between Bitcoin and commodities by assessing the ability of Bitcoin to act as a diversifier, hedge, or safe haven against daily movements in commodities in general, and energy commodities in particular. Through the use of an Asymmetric Dynamic Conditional Correlation (DCC) model, results show that Bitcoin is a strong hedge and a safe-haven against movements of commodity indices, including energy commodities. Furthermore, when taking in account the December 2013 Bitcoin price crash, results reveal that Bitcoin hedge and safe-haven properties against movements of commodity indices are only present in the pre-crash period, whereas in the post-crash period, Bitcoin is no more than a diversifier. However, Bouoiyour and Selmi (2015) using global macroeconomic and financial indicators and technical drivers, provide insightful evidence that Bitcoin may be used for economic reasons. Furthermore, there is not any sign of being a safe haven or a long-term promise. Our study differs from the previously mentioned studies. In fact, the global financial crisis of 2007–2009 (the “Great Recession”) has simulated considerable interest in defining, measuring and monitoring connectedness among asset classes, markets and countries. As illustrated by this crisis, an important aspect of systemic risk is the propagation of adverse shocks throughout the whole system. As a consequence, a strand of literature that aims at evaluating systemic risk importance and interconnectedness has emerged. In the respective literature, there are many studies done by, among others, Kaul and Sapp (2006), Martin and Diekmann (2007), Baur and McDermott (2010), Baur and Lucey (2010), Beckmann et al. (2015), Bouoiyour and Selmi (2017), Ranaldo and Söderlind (2010), Grisse and Nitschka (2013), Botman et al. (2013), and Ciara (2014), that account for spillover effects and interconnectedness, but only among traditional assets classes. According to this strand of research, our paper builds on and contributes to extending the literature on Bitcoins by assessing interconnectedness within the cryptocurrency market and between Bitcoin price changes and the volatility of traditional asset classes, using within the group of measures in the literature on the spillover index approach.
4. Methodology
Besides assessing the overall error variation in an asset “k” due to shock arising in other asset “j” or leading to shocks to other asset classes, we are also interested in assessing shares of forecast error variation in an asset “k” due to shock to an asset “j” at a specific frequency band. To achieve this, we follow the generalized forecast error variance decomposition methodology by Diebold et al. (2012) and the Barunik et al. (2017).
Let us describe the n-variate stationary process by structural VAR(p) at t = 1,…, T as:
In this equation and below, we define the asset volatility as , where is the daily closing value of the nth asset in the system (e.g., in intra-cryptocurrency market connectedness n = 4) on day t.12
We assume that the roots of lie outside the unit-circle. Under this assumption the VAR process has following MA(∞) representation:
where is an infinite lag polynomial matrix of coefficients.
Let us define the own variance shares as the fractions of the H-step-ahead error variances in forecasting yj that are due to shocks to yj, for j = 1, 2…,n, and across variance shares, or spill over, as the fractions of the H-step-ahead error variances in forecasting yj that are due to shocks to yk, for k = 1,2,…,n, such that . This can be written in the form:
where is an matrix of coefficients corresponding to lag h, and .
The captures the Pearson–Shin GFEVD partial contribution from asset class k to asset class j.
Given that the effect does not add up to one within columns by definition in generalized VAR process of FEVDs, we propose measuring pairwise-directional connectedness , to standardize the effects by:
The total directional connectedness from a variable k to the other variables is then defined as:
Similarly, the total directional connectedness of other variables to j is given by:
The connectedness of the whole system is then defined as the share variances in the forecasts contributed by other than own errors, or equally as the ratio of the sum of the diagonal elements to the sum of the entire matrix:
Tr{.} is the trace operator.
After assessing overall error variation in asset j due to shock arising in an asset k, we now follow Barunik et al. (2017) to evaluate connectedness in the frequency domain. We know that GFEVD is the central part of connectedness, hence we consider a frequency response function that can be obtained from Fourier transform of the coefficients , with .
Formally, let us have a frequency band d = (a, b): a, b . The generalized variance decompositions on frequency band “d” are defined as:
where , denotes the generalized causation spectrum over frequencies ω ∈ , and is a weighting function. In fact, to obtain a natural decomposition of original GFEVD to frequencies, we can simply weight the by the frequency share of the variance of variable j. (Please see Barunik et al. (2017) for more detail).
Denote by “ds” an interval on the real line from the set of intervals that form a partition of the interval , such that and . Due to the linearity of integral and the construction of , we have:
The natural way to describe the time-varying frequency of the connectedness is to consider the spectral representation of GFEVD.13 For that, let us define the scaled generalized variance decomposition on the frequency band d = (a, b): a, b as:
The within connectedness on the frequency band d can be then defined as:
The frequency connectedness on the frequency band d is also defined as:
It is important to note that the within connectedness gives us the connectedness effect that happens within the frequency band and is weighted by the power of the series on the given frequency band exclusively. Moreover, the frequency connectedness decomposes the overall connectedness defined in Equation (3) into distinct parts that, when summed, give the original connectedness measure
5. Data and Descriptive Statistics
In this paper, we investigate whether or not cryptocurrencies are in co-movement over time with each other, and with other markets. For the cryptocurrency market, we use data of four successful cryptocurrencies: Bitcoin (BTC), Ethereum (ETH), Ripple (XRP) and Litecoin (LTC). We also use data of the most active Bitcoin–USD index, a simple average of global Bitcoin/USD exchange prices, produced by Coindesk. Moreover, our data covers the daily return of five popular stock indexes (i.e., SP500, NASDAQ, FTSE100, Hang Seng and Nikkei225) and another five major Forex currencies (i.e., EUR/USD, GBP/USD, USD/JPY, USD/CHF and USD/CAD). For commodity markets, we limit our attention to the daily return of gold and Brent futures contracts launched by COMEX and the London International Petroleum Exchange (IPE), respectively. The data spans the period 7 October, 2010 to 8 February, 2018, with a total of 1918 daily observations. For the computation of volatility, we restrict the analysis to daily absolute returns. The summary statistics of the data can be found in Table 1.

Table 1.
Summary statistics of daily returns related to the Bitcoin index (BTI) and several asset classes.
Following Table 1, the daily mean return is 0.55% for BPI and thus it is the largest average daily return. At the same time, it is observed that its volatility (represented by the standard deviation) is also higher than the volatility of traditional currencies, equities, or commodities. Therefore, this high volatility may prevent the use of cryptocurrency as a currency (Yermack 2015). The direction of skewness is given by the sign. The positive sign is perceived to have a long tail to the right of the distribution, while the negative sign is perceived to have a long tail to the left. From Table 1, the larger positive value of skewness is associated with CAD, followed by BPI. However, the larger negative value is associated with CHF, followed by GBP. This means that there is a great chance that BPI return goes ups more than downs, during our sample period. Note that rational investors value this positively skewed return, which comes from BPI. On the other hand, all volatility series showed a coefficient of kurtosis significantly in excess of the normal distribution reference value. This means that data has a heavy tail. This departure from normality is confirmed by the Jarque–Bera (J–B) test.
The Augmented Dickey–Fuller (ADF) test indicates that the time series of returns are stationary because we reject the null hypothesis of a unit root at 1% level of significance in all cases. The Phillips–Perron (PP) and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) tests also confirm this stationarity. Furthermore, the results of the Lagrange multiplier (LM) test for autoregressive conditional heteroskedastic (ARCH) errors (LM-ARCH test) prove that there is an ARCH effect for almost all series, except the CHF series. Finally, the Q statistics and the p-value reveal the absence of the autocorrelation in the residuals from an AR(1) regression model for BPI and US stock indices.
The descriptive statistics in Table 2 show that the average daily return of the four top cryptocurrencies is positive. The XRP gives the greatest average of daily return. It has also the very high average of daily volatility measured by standard deviation. The XRP followed by LTC seems the riskier digital currencies. More interestingly, we can observe that the skewness is positive for all cryptocurrencies. This led to our precedent notification on BPI that a “rational investor” always prefers a positively skewed distribution to negative distribution. In another term, this result can be probably part of the reason for the latest trend involving using cryptocurrencies to raise money.

Table 2.
Summary statistics of daily returns related to four top cryptocurrencies.
Notice that the Kurtosis value of all cryptocurrencies is above 3. This is consistent with the presence of fat tails in data series and all are not normally distributed.
The results for the ADF test indicate that series are stationary. The PP and KPSS tests confirm also this stationarity. Additionally, the ARCH (LM) test indicates that there is an ARCH effect in almost all series, except the XRP series. Finally, the Q statistics and the p-value show that there is no autocorrelation in the residuals from an AR(1) model for BTC and ETH series.
6. Empirical Results
To explain the dependence of cryptocurrencies on other markets, we investigate here the connectedness among volatility forecasting errors using Diebold et al. (2012) and Barunik et al. (2017). We begin by characterizing volatility spill overs over the digital market as represented by BPI and other financial markets (i.e., Forex, stocks and commodities). Subsequently, we will track volatility spill overs within top digital currencies. Lastly, we report TSI in the lower right corner of Table 3.

Table 3.
Spill over effects between BTI, foreign currencies, stock markets and commodities.
6.1. Directional spill over index
We use VAR (2) approach with 10-days ahead forecasting horizon (h) to construct Table 3. We call this table spill over table. It provides an “input-output” decomposition of the spill over index. For example, the ij-th entry is the estimated contributions to the forecast error variance of index i coming from innovations to index j. Hence, the off-diagonal column sums (labelled contributions to others) and row sums (contributions from others), expressed the directional spill overs.
Panel “a” of Table 3 shows the spill over index for the daily return volatilities among traditional currencies and BPI. Panel “b” is, however, relative to the spill over index between stock indexes and BPI. Concerning Panel c, it reports directional spill overs between the two wide range commodity markets (i.e., gold and Brent oil), and BPI. The TSI in panel “b” appears to have been relatively larger, which indicates that, on average, roughly 30% of the forecast error variance across stock indexes and BPI comes from spill overs. BPI appears as being obviously the tiny and negligible spill over transmitter and recipient of shock channels (i.e., directional spill overs from and to BPI have varied between 0% and 1% over our sample period). Like many analysts, this low connectedness is due to different drivers of returns in the crypto markets (e.g., investor adoption, legal and regulatory developments) versus the stock and bond markets, which are driven more by factors such as economic growth, interest rates and corporate profits. Since cryptocurrency markets are relatively small and lack of economic forces, beside speculations, they will be less connected to the conventional markets.
A comparison of panel “b” with panel “a” or “c” shows that BPI spillover effects are equivalent, ranging mostly from 0% to 1%. For instance, we can learn from panel “a” that innovations to USD/CHF are responsible for 15.20 of the error variance in forecasting 10-days-ahead EUR/USD error variance, but only 0.39 of the error variance in the forecasting 10-days ahead EUR/USD comes from innovations to BPI. That is, volatility spill overs from CHF to EUR are larger than the BPI to EUR. As another example, we see that total volatility spill over from SP500 and NASDAQ to others is much larger than the total return spill overs from BPI to others, and vice versa. The latter suggests that US markets are more transmitters and recipients of shock channels, whereas BPI is less susceptible to global shocks, which indicates that the integration of the digital currency market with other financial markets, is still low for the last decade overall. These findings seem crucial to international investors and portfolio managers, given that uncertainty and investment risks can be reduced significantly by investing in digital currencies.
Table 4 reports the spill over index for the daily return volatilities among the top four cryptocurrencies using VAR (2). For the estimate equation of VAR (2), we suppose that deterministic regressors can be constant (“const”), the trend (“trend”) or “both”. There are also values of forecast error variance to 10 and 50 days ahead. We can see that TSI has a weak value estimated at around 15%. It seems in most cases (i.e., type and number of days ahead) are similar in magnitude. For instance, we can learn from panel “a” that with type “const”. TSI is 17.23 and 15.46 using type “both”, which indicates that these markets are not closely linked with each other. In addition, one can see from Table 4 that BTC hits more other cryptocurrencies. At the same time, it also appears to be the most influenced by shocks of other cryptocurrencies.

Table 4.
Spillover effects within the cryptocurrency market.
We now turn to estimate volatility dynamic connectedness among the top four cryptocurrencies using 50-days rolling window samples. The resulting time series of spill over index are presented in Figure 1. Our first observation reveals that the spill over shape clearly shows that, while there are periods of increased and decreased market interdependence, there are also sudden spikes and dips during our short sample period. This shows that connectedness between cryptocurrencies is dynamic and rises during turmoil periods.
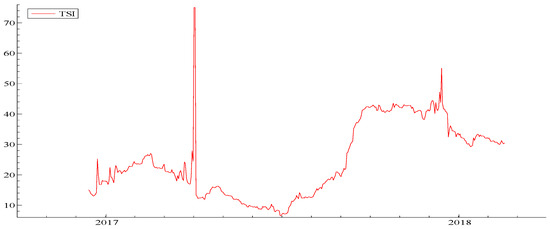
Figure 1.
Dynamic of cryptocurrency spill over indexes: 100-days rolling window.
A natural way to define the frequency dependent connectedness measures is to consider the spectral representation of variance decompositions based on frequency, instead of impulse-responses of shocks. The frequency domain is the natural place to study the long-run, medium-run, or short-run connectedness shifts. In this study, we retain three frequency domains: Freq1: (pi/2, pi), which roughly corresponds to less than 4 days, Freq2: (pi/4, pi/2), which roughly corresponds to 4 days to 10 days and Freq3: (0, pi/4), which roughly corresponds to more than 10 days. Figure 2 presents the results of this frequency-domain analysis.
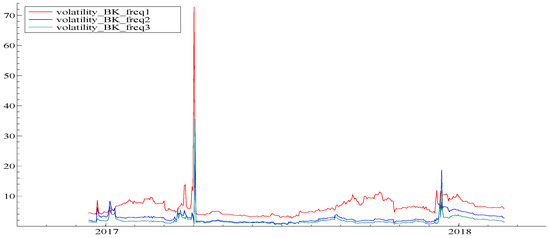
Figure 2.
Time frequency-dynamic of cryptocurrency spill over indexes: window = 100 days and n. ahead = 100 days.
We can see from Figure 2 that the response to return volatility shocks is distributed unevenly over frequency domains. Looking at how the global system is connected at these different frequency domains, we find that the largest total connectedness of cryptocurrencies comes from the short-run frequency (i.e., Freq1). These findings are obviously important and one could not have obtained this with the simple Diebold et al. (2012) method, and it thus highlights the importance of different frequencies that are considered for the analysis.
Referring also to Figure 2, we can show the possible importance of the long and medium run connectedness among cryptocurrencies just during two extreme jambs. As Barunik et al. (2017) shows, the following increases in the long-term connectedness and the declines in short term connectedness can be attributed to change in market participants’ beliefs in created information. In fact, when market participants understand that the information has generated a return shock that would quickly propagate and impact the stability of the system, this can create short-term connectedness. Moreover, the belief in surge volatility persistence can amplify the uncertainty and therefore enhances long term connectedness. These results are in line with the conclusions of Baur et al. (2015), showing that the value of Bitcoin (and “cryptocurrencies” in general) is primarily forced by speculative investors who want to gain experience in new markets and exploit the high return possible because of high volatility.
6.2. Robustness Check
Numerous dependence measures exist in the literature (cf., Joe 1997; Nelsen 2006). To explore the robustness of the results, we simply use Pearson’s product moment coefficient, which indicates the strength and direction of a linear relationship between two random variables. Then, we implement Granger causality tests.
Following Table 5 (panel a), it is found that the correlation coefficients between the major Forex exchange rate and BPI over the sample period are extremely low. In contrast, all other correlation coefficients exhibit a relatively strong relationship with only some exceptions mainly for JPY return with both CAD and GBP return. A similar result is also observed between BPI and stock indexes (panel b) as well as between BPI and gold or Brent oil (panel c). Hence, this analysis shows that Bitcoin does not correlate with the other asset classes mentioned. This can tell us that overall cryptocurrencies do not conform to economic fundamentals, which can reinforce the conclusion that the value of cryptocurrency is mainly based on speculation and betting. Furthermore, bitcoin correlation with core asset classes (i.e., currencies, equities and commodities) is extremely low, implying that it is a favorable diversification instrument. This result is also provided by Dyhrberg (2015b).

Table 5.
Correlation between BTI and other asset classes.
We have observed some interesting patterns in the above analysis. A natural question to ask is whether movements in the return of traditional markets ‘predict’ future changes in returns of digital currencies, and vice versa. For that, we restrict testing the predictability or causality to the Granger causality test as performed by Granger (1969) and Sims (1980). In this interpretation, a variable x causes y if lagged values of x are significant in explaining y in a regression in which lagged values of y are also explanatory variables. It is, of course, possible that causality can exist in both directions. This test can be performed using VAR. Table 6 reports the results of F-statistic for the no Granger causality restrictions imposed on a linear vector autoregressive model (i.e., VAR (2)) under the null hypothesis.

Table 6.
Pairwise Granger causality.
Following Panel “a”, one can show that traditional currencies “do not Granger cause BPI”, except for CAD currency (at a significance level of 10%). In addition, “BPI does not Granger cause” any top traditional currencies with the exception of CHF currency. In regard to panel b of Table 6, we can also see that the hypothesis of stock return that “does not Granger cause BPI” is not statistically satisfied except for the NASDAQ index. As for the causality from BPI to stock return, it is also rejected, except for NASDAQ and FTSE100. Similarly, there is on average no Granger causality between BPI and gold or Brent oil for all cases, except from gold to BPI. From these results, we report that the predictability of many asset classes from BPI is minimal, and vice versa. Turning now to the causality among the four successful cryptocurrencies, (i.e., BTC, ETF, LTC and XRP), the results exhibit that all casual flows are not evident, except the Granger casual flow from XRP to LTC (at a significance level of 5%).
The Granger causality tests also suggest—like the earlier TSI and correlation data—that there is no significant interaction within the nascent market of cryptocurrencies, as well as between BPI and the daily return of different asset classes.
7. Conclusions
In this paper, we have investigated connectedness within the cryptocurrency market, and across BPI and other asset classes such as traditional currencies, stocks and gold or Brent oil. We have used the spill over index approach with the spectral representation of variance decomposition networks as proposed by Diebold et al. (2012) and Barunik et al. (2017). We have shown no significant spillover effects between the nascent market of cryptocurrencies and other asset classes. Hence, we suggest that cryptocurrencies are weakly integrated into the global financial market. They can be interpreted as independent financial instruments that pose little to no systematic risk, which may add to its attractiveness for investors. Concerning the connectedness within the cryptocurrency market, we report a time–frequency–dynamics connectedness nature of the course of the considered period. Moreover, the decomposition of TSI is mostly dominated by short frequency component (2–4 days) leading to the conclusion that this nascent market is highly speculative at present. These findings provide insights for regulators and potential international investors.
As the literature grows, there are different valuation procedures or techniques to model and analyze changes in the volatility of financial assets. The most popular is the Multivariate ARCH type (GARCH) model with DCC correlation or the Spline–GARCH model. Therefore, in the future, we will use one of these methods with the aim of uncovering the connection of assets within other regional and global markets, or industry, and provide grounds for further research in risk management.
Funding
This research received no external funding.
References
- Aftab, Muhammad, Rubi Ahmad, and Izlin Ismail. 2015. Dynamics between currency and equity in Chinese markets. Chinese Management Studies 9: 333–54. [Google Scholar] [CrossRef]
- Ali, Robleh, John Barrdear, Roger Clews, and James Southgate. 2014. The Economics of Digital Currencies. Bank of England Quarterly Bulletin, Q3. Available online: http://www.bankofengland.co.uk/publications/Documents/quarterlybulletin/2014/qb14q3digitalcurrenciesbitcoin1.pdf (accessed on 9 November 2015).
- Antonakakis, Nikolaos, and Konstantinos Vergos. 2013. Sovereign bond yield spillovers in the Euro zone during the financial and debt crisis. Journal of International Financial Markets 26: 258–72. [Google Scholar] [CrossRef]
- Tiwari, Aviral Kumar, Juncal Cunado, Rangan Gupta, and Mark E. Wohar. 2018. Volatility spillovers across Global Asset Classes: Evidence from time and Frequency Domains. The Quarterly Review of Economics and Finance. [Google Scholar] [CrossRef]
- Barber, Simon, Xavier Boyen, Elaine Shi, and Ersin Uzun. 2012. Bitter to Better-How to Make BitCoin a Better Currency. In Financial Cryptography and Data Security. Berlin/Heidelberg: Springer. [Google Scholar]
- Baruník, Jozef, and Tomáš Křehlík. 2017. Measuring the Frequency Dynamics of Financial Connectedness and Systemic Risk. Journal of Financial Econometrics 16: 271–96. [Google Scholar] [CrossRef]
- Baur, Dirk, KiHoon Hong, and Adrian Lee. 2015. Bitcoin: Currency or Asset? Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2736020 (accessed on 22 February 2016).
- Baur, Dirk G., and Brian M. Lucey. 2010. Is Gold a Hedge or a Safe Haven? An Analysis of stocks, Bonds and Gold. Financial Review 45: 217–29. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas K. McDermott. 2010. Is gold a safe haven? International evidence. Journal of Banking & Finance 34: 1886–98. [Google Scholar]
- Baur, Dirk G., Thomas Dimpfl, and Konstantin Kuck. 2018. Bitcoin, gold and the US dollar–A replication and extension. Finance Research Letters 25: 103–10. [Google Scholar] [CrossRef]
- Beckmann, Joscha, Theo Berger, and Robert Czudaj. 2015. Does gold act as a hedge or a safe haven for stocks? A smooth transition approach. Economic Modeling 48: 16–24. [Google Scholar] [CrossRef]
- Bell, Claes. 2013. Bitcoin: Virtual Money or Risky Investment? Available online: https://www.bankrate.com/investing/bitcoin-virtual-money-or-risky-investment/ (accessed on 25 September 2013).
- Botman, Dennis P. J., Irineu E. Carvalho Filho, and Raphael W. Lam. 2013. The Curious Case of the Yen as a Safe Haven Currency: A Forensic Analysis. Available online: https://www.imf.org/external/pubs/ft/wp/2013/wp13228.pdf (accessed on 6 November 2013).
- Bouoiyour, Jamal, and Refk Selmi. 2015. Bitcoin Price: Is it really that New Round of Volatility can be on way? Economics Bulletin 36: 3. [Google Scholar]
- Bouoiyour, Jamal, and Refk Selmi. 2017. Ether: Bitcoin’s Competitor or Ally? Available online: https://arxiv.org/abs/1707.07977 (accessed on 25 July 2017).
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017a. On the hedge and safe haven properties of Bitcoin: Is it really more than a diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Bouri, Elie, Naji Jalkh, Peter Molnár, and David Roubaud. 2017b. Bitcoin for energy commodities before and after the December 2013 crash: diversifier, hedge or a safe haven? Applied Economics 49: 5063–73. [Google Scholar] [CrossRef]
- Briere, Marie, Kim Oosterlinck, and Ariane Szafarz. 2013. Virtual Currency, Tangible Return: Portfolio Diversification with Bitcoins. Journal of Assessment Management 16: 365–73. [Google Scholar] [CrossRef]
- Buchholz, Martis, Jess Delaney, Joseph Warren, and Jeff Parker. 2012. Bits and Bets, Information, Price Volatility, and Demand for BitCoin. Economics. 312. Available online: http://www.bitcointrading.com/ pdf/bitsandbets.pdf (accessed on 5 May 2012).
- Morley, Ciara. 2014. Three Essays on Identifying Safe Haven for Equity Investors. National University of Ireland Maynooth (NUIM), Maynooth, Co. Kildare, Ireland. Available online: http://rian.ie/en/item/view/98385.html (accessed on 8 April 2014).
- Davidian, Marie, and Raymond J. Carroll. 1987. Variance Function Estimation. Journal of the American Statistical Association 82: 1079–91. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2009. Measuring financial asset return and volatility spillovers, with application to global equity markets. The Economic Journal 119: 158–71. [Google Scholar] [CrossRef]
- Diebold, Francis X., and Kamil Yilmaz. 2012. Better to give than to receive: Predictive directional measurement of volatility spillovers. International Journal of Forecasting 28: 57–66. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2015a. Hedging capabilities of Bitcoin. Is it the virtual gold? Finance Research Letters 16: 139–144. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2015b. Bitcoin, gold and the dollar–A GARCH volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Eisel, Alexander, Stephan Gasser, and Karl Weinmayer. 2015. Caveat Emptor: Does Bitcoin Improve Portfolio Diversification? Available online: https://ssrn.com/abstract=2408997 (accessed on 3 June 2015).
- Forsberg, Lars, and Eric Ghysels. 2007. Why Do absolute Returns Predict Volatility so well? Journal of Financial Econometrics 5: 31–67. [Google Scholar] [CrossRef]
- Glaser, Florian, Martin Haferkorn, Moritz Weber, and Kai Zimmermann. 2014. How to price a digital currency? Empirical insights on the influence of media coverage on the Bitcoin bubble. Banking and Information Technology 15: 21–32. [Google Scholar]
- Granger, Clive. 1969. Investigating Causal Relationships by Econometric Models and Cross-Spectral Methods. Econometica 37: 424–38. [Google Scholar] [CrossRef]
- Grinberg, Reuben. 2011. BitCoin: An Innovative Alternative Digital Currency. Hastings Science & Technology Law Journal 4: 159–208. [Google Scholar]
- Grisse, Christian, and Thomas Nitschka. 2013. On Financial Risk and the Safe Haven Characteristics of Swiss Franc Exchange Rates. Swiss National Bank Working Papers. Available online: https://www.sciencedirect.com/science/article/pii/S0927539815000249?via%3Dihub (accessed on 22 March 2015).
- Joe, Harry. 1997. Multivariate Models and Dependence Concepts. London: Chapman & Hall. [Google Scholar]
- Joshi, Leela. 2017. Bitcoin: Real or virtual currency? International Journal of Recent Scientific Research 8: 22354–57. [Google Scholar]
- Kaul, Aditya, and Stephen Sapp. 2006. Y2K fears and safe haven trading of the U.S. dollar. Journal of International Money and Finance 25: 760–79. [Google Scholar] [CrossRef]
- Kerner, Sean Michael. 2014. Why Marc Andreessen is Bullish on Bitcoin. Available online: http://www.eweek.com/cloud/why-marc-andreessen-is-bullish-on-bitcoin (accessed on 2 February 2014).
- Kristoufek, Ladislav. 2013. BitCoin meets Google Trends and Wikipedia: Quantifying the relationship between phenomena of the Internet era. Scientific Reports 3: 1–7. [Google Scholar] [CrossRef] [PubMed]
- Meurers, Martin, and Berend Diekmann. 2007. The US Dollar: Safe Haven, Despite Rising US Current Account Defecit. Deutsche Bank Working Paper Series. Available online: https://www.econstor.eu/dspace/bitstream/10419/21888/1/PROD0000000000214099.pdf (accessed on 6 August 2007).
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://nakamotoinstitute.org/literature/bitcoin/ (accessed on 31 October 2008).
- Nelsen, Roger B. 2006. An Introduction to Copulas, 2nd ed. New York: Springer. [Google Scholar]
- Pesaran, H. Hashem, and Yongcheol Shin. 1998. Generalized impulse response analysis in linear multivariate models. Economics Letters 58: 17–29. [Google Scholar] [CrossRef]
- Ranaldo, Angelo, and Paul Söderlind. 2010. Safe haven currencies. Review of Finance 14: 385–407. [Google Scholar] [CrossRef]
- Gangwal, Shashwat. 2016. Analyzing the Effects of Adding Bitcoin to Portfolio. International Journal of Economics and Management Engineering 10: 3519–32. [Google Scholar]
- Sims, Christopher A. 1980. Macroeconomics and reality. Econometrica 48: 1–48. [Google Scholar] [CrossRef]
- Mikosch, Thomas. 2000. Limit theory for the sample autocorrelations and extremes of a GARCH (1,1) process. Annals of Statistics 28: 1427–51. [Google Scholar]
- Trabelsi, Nader, and Nader Naifar. 2017. Are Islamic stock indexes exposed to systemic risk? Multivariate GARCH estimation of CoVaR. Research in International Business and Finance 42: 727–44. [Google Scholar] [CrossRef]
- van Wijk, Dennis. 2013. What Can be Expected from the BitCoin? Available online: https://thesis.eur.nl/pub/14100/Final-version-Thesis-Dennis-van-Wijk.pdf (accessed on 18 July 2013).
- Wang, Gang-Jin, Chi Xie, Zhi-Qiang Jiang, and H. Eugene Stanley. 2016. Who are the net senders and recipients of volatility spillovers in China’s financial markets? Finance Research Letters 18: 255–62. [Google Scholar] [CrossRef]
- Whelan, Karl. 2013. How Is Bitcoin Different From The Dollar? Available online: https://www.forbes.com/sites/karlwhelan/2013/11/19/how-is-bitcoin-different-from-the-dollar (accessed on 19 November 2013).
- Wu, Chen Y., and Vivek K. Pandey. 2014. The Value of Bitcoin in Enhancing the Efficiency of an Investor’s Portfolio. Journal of Financial Planning 27: 44–52. [Google Scholar]
- Yermack, David. 2015. Is Bitcoin a Real Currency? An Economic Appraisal. NBER Working Paper N. 19747, National Bureau of Economic Research. Available online: https://www.sciencedirect.com/science/article/pii/B9780128021170000023?via%3Dihub (accessed on 5 May 2015).
| 1 | This has given rise also to Islamic products and services (see Trabelsi and Naifar 2017). |
| 2 | Bitcoin is usually labelled as a digital coin or virtual currency, which is BY the people, For the people, Of the people. |
| 3 | Please see document requested by the European Parliament’s Special Committee on Financial Crimes, Tax Evasion and Tax Avoidance, July 2018. |
| 4 | The other existing studies relating to Bitcoins deal with the legalities and technical details associated with Bitcoins. |
| 5 | e.g., CME group has launched in 2017 cryptocurrencies futures contracts. |
| 6 | Market capitalization, price, volume and other Crypto-currency info can be listed on coinmarketcap.com. |
| 7 | Unlike conventional currencies that are designed and controlled by a governing body. |
| 8 | The Bitcoin foundation is a private association that was formed in late 2012, after bitcoin had earned a reputation for criminality and fraud. “The mission of this foundation is to coordinate the efforts of the members of the Bitcoin community, helping to create awareness of the benefits of Bitcoin, how to use it and its related technology requirements, for technologists, regulators, the media and everyone else globally” (see foundation’s global policy). Thus, this association cannot be a legal or a financial regulatory authority responsible for supervising and controlling Law and legal transactions. |
| 9 | Hashing means converting a string of characters of arbitrary length into a fixed length string. |
| 10 | Source: statistic predictions by medium.com. |
| 11 | Please see the article “Bitcoin Regulation in china still unclear, but Chinese exchanges thrive overseas” by Leonhard Weese. Published on forbes.com. |
| 12 | For other advantages of absolute returns one can see Forsberg and Ghysels (2007), Antonakakis and Vergos (2013) and Wang et al. (2016). Indeed, it is well documented in the literature that the use of absolute returns in modeling volatility has some advantages. First of all, absolute returns are more robust than the standard-deviation in the presence of large movements (Davidian and Carroll 1987). In this framework, the standard-deviation may not be investors’ most appropriate measure of risk because it rewards the desirable upside movements as hard as it punishes the undesirable downside movements. Furthermore, absolute return modeling is more reliable than the standard-deviation for the non-existence of a fourth moment commonly associated with financial returns (Thomas 2000). |
| 13 | The spectral representation of Yt at frequency d can be defined as a Fourier transform of MA(∞) filtered series as: . The power spectrum is a key quantity for understanding frequency dynamics, since it describes how the variance of the Yt is distributed over the frequency components d. |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).