Abstract
Bitcoin is an exciting new financial product that may be useful for inclusion in investment portfolios. This paper investigates the implications of replacing gold in an investment portfolio with bitcoin (“digital gold”). Our approach is to use several different multivariate GARCH models (dynamic conditional correlation (DCC), asymmetric DCC (ADCC), generalized orthogonal GARCH (GO-GARCH)) to estimate minimum variance equity portfolios. Both long and short portfolios are considered. An analysis of the economic value shows that risk-averse investors will be willing to pay a high performance fee to switch from a portfolio with gold to a portfolio with bitcoin. These results are robust to the inclusion of trading costs.
JEL Classification:
G11; G17; G32
1. Introduction
Bitcoin is an exciting new financial product that has the potential to disrupt existing economic payment systems. Bitcoin is a peer-to-peer digital cryptocurrency that was launched in 2009 based on an open source project developed by Nakamoto (2008). As of 15 March 2018, a single bitcoin was worth $8014.92, the daily transaction volume was approximately 165,142 and the supply of bitcoins on the network (i.e., have been “mined”) was 16,923,238.1 As a decentralized protocol, Bitcoin is not controlled by any organization or government, but its supply has been set in advance at 21 million bitcoins. The total supply of bitcoin in circulation grows at a predictable rate and is set to reach 21 million by September 2140 (Zohar 2015; Hendrickson et al. 2016).
Bitcoin has on occasion been called digital gold (Popper 2015a, 2015b). Gold is often advocated as a hedge against inflation, a safe haven investment and a way to increase portfolio diversification (Eichengreen 1992). Gold, a mined asset, has been used as a form of currency for much of the history of civilization (Michaud et al. 2006). Interestingly, Bitcoin also uses the mining terminology to describe what “miners” receive once they provide proof-of-work associated with the verification of a transaction and the completion of a block in blockchain (i.e., the decentralized ledger). Bitcoin is possible due to blockchain technology which enables secure electronic transactions without needing a centralized ledger and preventing users from replicating the payment for other uses, also known as the double spending problem (Kiviat 2015; Zohar 2015). The units awarded can be used to make a transaction or invest.
The notion that Bitcoin can replace gold as a hedge against inflation has especially interested people in countries where governments were struggling with hyperinflation. In the mid-2000s for example, Argentine businesses, entrepreneurs and citizens seeking to protect the value of their currency were helpless as inflation rose and the government imposed greater and greater currency controls on the Argentine peso. Although Bitcoin adoption was slow in North America, the same could not be said for Latin America where currency controls were impeding transactions and Bitcoin adoption was growing as people sought both a cheaper way of moving money across international borders and a safe store of value (Popper 2015b). In fact, in a comparison of 16 different currencies, Kim (2017) found bitcoin currency exchange transaction costs to be lower than the retail foreign exchange transaction costs. As a result, Bitcoin has experienced a rapid rise in popularity over the past several years and in December 2017, the CME Group launched bitcoin futures contracts.
Our objective is to examine the impact that replacing gold with bitcoin would have on investment portfolio characteristics and returns. Eliminating a safe haven asset such as gold from an investment portfolio will have implications for risk and return trade-offs, because it reduces diversification. In fact, there is a large literature showing the effectiveness of gold in diversifying portfolio risk (Baur and Lucey 2010; Hillier et al. 2006; Jaffe 1989; Reboredo 2013a, 2013b; Baur and McDermott 2010; Ciner et al. 2013; Beckmann et al. 2015). Gold divestment, therefore, may reduce returns and increase risk. Substituting bitcoin for gold, however, may increase returns and reduce risk. To address whether this is the case, a rigorous empirical analysis using modern portfolio theory is required.
This paper makes three important contributions to the literature. First, we investigate the financial implications of replacing gold in an investment portfolio with bitcoin, using modern portfolio theory. We compare two portfolios: (1) A portfolio that includes gold, and (2) a portfolio that replaces gold with bitcoin. Second, to compare optimal weights for minimum variance equity portfolios subject to a target return, we use three different multivariate GARCH models: dynamic conditional correlation (DCC), asymmetric dynamic conditional correlation (ADCC), and generalized orthogonal GARCH (GO-GARCH). While many papers use DCC and ADCC to estimate optimal portfolio weights, few use GO-GARCH. Given the volatile nature of bitcoin, an analysis that provides more accurate volatility estimates is needed. GO-GARCH not only incorporates persistence in volatility and correlation, as well as time-varying correlation (as do DCC and ADCC), but also allows for spill-over effects in volatility and is closed under linear transformation. Comparing weights computed from three different models demonstrates the robustness of our portfolio results to the choice of GARCH model. Third, we calculate optimal portfolio weights using a fixed-width rolling window, which mitigates the effects of changing dynamics, parameter heterogeneity, and structural change.
The paper is organized as follows. We first present a brief literature review of Bitcoin and its investment potential. We then present our modern portfolio model followed by the methodology, description of the data, empirical results and some robustness analyses. We conclude the paper with some important implications for investors who seek to include bitcoin in their investment portfolios.
2. What Is Bitcoin—Currency or Asset?
The core of Bitcoin’s innovation is blockchain, which forms “an incremental log of all transactions that have ever occurred since the creation of Bitcoin, starting with the “Genesis Block”—the first block in the chain” (Zohar 2015, p. 107). This allows transactions to be processed over a distributed network using public-private key technology, where the sender and the receiver of a transaction use a private key and everyone else on the network uses a public key to verify the legitimacy of the transaction. The public verification system is known as “mining”. Böhme et al. (2015) view the verification system in which users are encouraged to keep the transaction record operational and updated as a public good. Unfortunately, public goods are underprovided unless there are incentives (McNutt 2002). To encourage user participation, users who solve a computationally intensive and random mathematical puzzle associated with the pre-existing contents of a block, known as proof-of-work, are awarded newly minted bitcoins (Böhme et al. 2015). As there is a finite number of bitcoins, the puzzles become more computationally difficult over time.
The advantages of using bitcoin are: (1) as a purely digital currency, Bitcoin allows payments to be sent nearly instantly over the internet for very low fees (Zohar 2015), (2) like cash, bitcoin is nearly anonymous and irreversible once committed, and (3) as there is no controlling organization (private or public), Bitcoin is less open to regulatory oversight (Böhme et al. 2015). The disadvantages of Bitcoin are associated with the fact that it functions outside the purview of financial institutions, governments and without regard to national borders; users of the system are identifiable only by their virtual addresses (Hendrickson et al. 2016). Early adopters of Bitcoin were individuals and businesses who were attracted to the anonymity of the system and the lack of government oversight. Böhme et al. (2015) cite the online sale of narcotics, and gambling as the two of the largest adopters of Bitcoin.
Today, however, businesses are beginning to view Bitcoin as a method to reduce their credit card transaction fees. Such fees can range from 1.65 to 2.71% of transaction sales (Canadian Federation of Independent Business 2018). As of January 2018, companies and organizations such as Overstock.com, KFC Canada, Microsoft, CheapAir.com, Newegg.com, Zynga, Save the Children, and Universidad de las Americas Puebla—just to name a few—accept bitcoin.2 As more and more merchants adjust their payment systems to accept bitcoin, Bitcoin as a method of payment will grow. Consumers, however, may be less inclined to use bitcoin as traditional financial accounts payments can be reversed if an error were to occur whereas it cannot be reversed with bitcoin due to the pseudonymous exchange (Hendrickson et al. 2016).
The question remains as to whether Bitcoin should be considered a currency. Lo and Wang (2014) examine whether Bitcoin can serve as an alternative form of money by evaluating Bitcoin against the three properties of money, namely its ability to act as a medium of exchange, a unit of account and a store of value. In the case of Bitcoin’s ability to act as a medium of exchange, the authors note that bitcoin is not backed by any sovereign entity and therefore its success will be based on its acceptance by private agents. As Bitcoin’s transaction confirmation times decrease (it now takes less than 10 min) and its fees are less than those of other financial intermediaries such as banks and credit card companies, more agents will view this as potential medium of exchange.
Using bitcoin as a unit of account, however, appears to be a problem due to its remarkable volatility. Lo and Wang (2014) argue that despite merchants accepting bitcoin as payment, they continue to post their prices in standard currencies due to bitcoin’s volatility. The store of value function of money, on the other hand, is based on agents’ acceptance that bitcoin’s value will be accepted in the future. Volatility and speculative holdings in bitcoin have suggested that bitcoin may be in a state of speculative play (Glaser et al. 2014). This volatility is catching the attention of market participants who seek to profit from such volatility. This has led to the discussion of the creation of Bitcoin futures contracts (Hopkins 2017) and in December 2017 The CME Group launched bitcoin futures contracts.
Although Bitcoin is seen as a digital currency that can provide a secure, low-cost platform for digital payments (Hendrickson et al. 2016), Glaser et al. (2014) argue that most users of Bitcoin treat their bitcoin investment as a speculative asset rather than as a means of payment. Financial assets allow an investor to diversify her portfolio. An asset can act as a safe haven, a hedge, and/or a diversifier. Bitcoin is highly volatile and (Dyhrberg 2016a) found that bitcoin can be classified somewhere between a currency and a commodity with the associated financial advantages. Dyhrberg (2016b) also suggests that Bitcoin can act as a hedge between UK equities and the US dollar.
Bouri et al. (2017) examine whether bitcoin can be used as a safe haven, diversifier or hedge using daily and weekly data. From a risk perspective, including an asset that is negatively correlated with another decreases risk; the authors, using dynamic conditional correlation models, find that bitcoin can be used as an effective diversifier for most of the cases examined. Using bitcoin as a safe haven, however, was not evidenced in daily movements due perhaps to bitcoin’s speculative nature (Ciaian et al. 2016; Bouri et al. 2017). Zhu et al. (2017) use a vector error correction model to study the dynamic interaction between bitcoin and important economic variables like the US dollar index, stock prices, the Federal Funds Rate, and gold prices. They find that all variables have a long-term influence on bitcoin prices, but the US dollar index has the largest impact, while gold prices have the least. These authors recommend that bitcoin should be treated as a speculative asset rather than a credit currency. Guesmi et al. (2018) use GARCH models to study the usefulness of using Bitcoin to hedge investments in gold, oil and emerging market stocks. All portfolios are two-asset portfolios that include Bitcoin and one other asset. For an emerging market (global market) portfolio, the average optimal portfolio weight for Bitcoin is 0.051 (0.033). Evidence is also presented showing that Bitcoin is a useful hedging instrument.
The question remains as to bitcoin’s contribution to an investor’s portfolio. Is bitcoin an asset that should be added to an investor’s portfolio? Does bitcoin live up to its name as digital gold (Popper 2015b) and can it be a good gold replacement? These are some of the questions we wish to address.
3. Empirical Model
Using modern portfolio theory (Elton and Gruber 1997), we consider an investor who wants to determine the optimal portfolio weights for a minimum variance equity portfolio subject to a target return of μTR. The optimal portfolio weights are found by solving the following optimization problem:
In Equation (1), is the variance-covariance matrix, μ is a vector of mean returns and wt are the portfolio weights. There are no restrictions on short sales. The solution to Equation (1) gives the expression for the optimal portfolio weights:
The optimal portfolio weights depend upon the covariance matrix and the mean returns. The covariance matrix is estimated using three types of multivariate GARCH models. Sample mean returns are used to estimate μ (Fleming et al. 2001).
A GARCH model consists of a mean equation and a variance equation. A vector of n × 1 asset returns is denoted rt. An AR(1) process for the asset returns, rt, conditional on the information set It−1 is written as:
The residuals are modelled as:
where Ht is the conditional covariance matrix of rt and zt is a n × 1 i.i.d. random vector of errors.
One popular and easy approach to estimating optimal portfolio weights is to use a DCC GARCH model to estimate the variance-covariance matrix. Engle (2002) proposed a two-step methodology to estimate dynamic conditional correlations. In the first step, the GARCH parameters are estimated using single equation GARCH models. In the second step, the conditional correlations are estimated using:
Ht is a n × n conditional covariance matrix, Rt is the conditional correlation matrix, and Dt is a diagonal matrix with time-varying standard deviations on the diagonal.
The expressions for h are univariate GARCH models (H is a diagonal matrix). For the GARCH(1,1) model, the elements of Ht can be written as:
Qt is a symmetric positive definite matrix.
is the n × n unconditional correlation matrix of the standardized residuals zi,t (zi,t = εi,t/√hi,t). The parameters θ1 and θ2 are non-negative. These parameters are associated with the exponential smoothing process that is used to construct the dynamic conditional correlations. The DCC model is mean reverting as long as θ1 + θ2 < 1. The correlation estimator is:
The second approach to is to use the ADCC GARCH model of Cappiello et al. (2006) to estimate the variance-covariance matrix. This approach, building upon the work of Glosten et al. (1993), contains an asymmetric term in the variance equation.
The indicator function I(εi,t−1) is equal to one if εi,t−1 < 0 and 0 otherwise. A positive value for d means that negative residuals tend to increase the variance more than positive returns. The asymmetric effect, which is sometimes referred to as the “leverage effect”, is designed to capture an often-observed characteristic of financial assets that an unexpected drop in asset prices tends to increase volatility more than an unexpected increase in asset prices of the same magnitude. This can be interpreted as bad news increasing volatility more than good news.
For the ADCC model, the dynamics of Q are given by:
In the above equation, A, B and G are n × n parameter matrices and are zero-threshold standardized errors, which are equal to zt when less than zero and zero otherwise. The matrices and are the unconditional matrices of zt and , respectively.
The third approach to estimating optimal portfolio weights is to use a GO-GARCH model to estimate the variance-covariance matrix (Van Der Weide 2002). The GO-GARCH model maps a set of asset returns, rt, onto a set of uncorrelated components, zt, using a mapping Z.
The unobserved components, yt, are normalized to have unit variance. Each component of yt can be described by a GARCH process. For example, consider a standard GARCH(1,1) process with a normal distribution.
The index i runs from 1 to n. The unconditional covariance matrix of yt is H0 = I. The conditional covariance matrix of rt is:
The matrix Z maps the uncorrelated components yt to the observed returns rt. There exists an orthogonal matrix U such that:
The matrices P and Λ can be obtained from singular value decomposition on the unconditional variance matrix V. For example, P contains the orthonormal eigenvectors of ZZ′ = V and Λ contains the eigenvalues. The matrix U can be obtained from the conditional variance matrix Vt. Recent work on GO-GARCH is concentrated on finding different ways to parameterize and estimate the matrix U. Boswijk and van der Weide (2006) provide a more detailed discussion of these efforts.
The GO-GARCH model assumes that (1) Z is time invariant, and (2) Ht is a diagonal matrix. An orthogonal GARCH (OGARCH) model is the result when Z is restricted to be orthogonal (Alexander 2001). The OGARCH model can be estimated using principle components on the normalized data and GARCH models estimated on the principle components. This corresponds to U being an identity matrix. In the original formation of the GO-GARCH model, Van Der Weide (2002) uses a 1-step maximum likelihood approach to jointly estimate the rotation matrix and the dynamics. This method, however, is impractical for many assets because the maximum likelihood estimation procedure may fail to converge. The matrix U can also be estimated using nonlinear least squares (Boswijk and van der Weide 2006) and method of moments (Boswijk and van der Weide 2011), both of which involve two-step and three-step estimation procedures. More recently, it has been proposed that U can be estimated by independent component analysis (ICA) (Broda and Paolella 2009; Zhang and Chan 2009) and is the method employed in this paper3.
Asset returns are characterized by autocorrelation, volatility clustering and distributions that are asymmetric and have fat tails. This suggests an AR(1) mean equation for each GARCH model and a distribution that takes into account fat tails. In particular, the DCC and ADCC are each estimated with multivariate Student t (MVT) distributions. The GO-GARCH is estimated with the multivariate affine normal inverse Gaussian (MANIG) distribution. These distributions are useful for modelling data with heavy tails. All estimation is done in R (R Core Team 2015; Ghalanos 2015).
The use of DCC warrants some additional comments. DCC is a very popular multivariate GARCH model. Typing “Dynamic conditional correlation” into Google Scholar on 1 August 2018 returned about 8200 results. Despite the popularity of DCC, there is criticism that DCC is not a true model because it lacks specific technical details (Caporin and McAleer 2013; Aielli 2013). DCC is stated rather than derived, has no moments, does not have testable regularity conditions, and has no asymptotic properties. Caporin and McAleer (2013) argue against the use of DCC as a model because of the lack of moment conditions and asymptotic properties but recommend that DCC may be used as a filter, like EWMA, or as a diagnostic check. Viewed in the context of a filter, DCC may be useful for forecasting dynamic conditional covariances and correlations. We caution, however, that in the absence of any valid moment conditions or asymptotic properties, DCC forecasts may be imprecise and this may affect the estimates of the portfolio returns and any resulting statistical analysis.
Rolling window estimation is used to estimate the GARCH models and construct the portfolio weights. One period ahead conditional expected return and volatility forecasts are required to compute the optimal portfolio weights. For example, consider the case of a fixed window length of 1200 observations. The first 1200 observations are used to estimate the GARCH models and make one period forecasts of the variance-covariance matrix. One period ahead mean values for the returns are calculated from 1200 sample observations. The in sample mean values are used as a naïve forecast for the next period (Fleming et al. 2001). The mean values and covariance matrix are used to construct the one period ahead portfolio weights. Then the process is rolled forward one period by adding on observation and dropping the first observation so that the next estimation period is for observations 2 to 1201. This process is rolled through the data set producing a sequence of one period forecasts for the GARCH variance-covariance matrices, mean values, and portfolio weights. The portfolio weights are used in the construction of equity portfolios.
Equity portfolios are compared using standard risk-return measures like Sharpe Ratios, Omega Ratios, Sortino Ratios, and Information Ratios (Feibel 2003). The Sharpe Ratio measures excess returns relative to risk when risk is measured as the standard deviation. Excess returns are measured relative to a time-independent benchmark. Sharpe value at risk (VaR) and Sharpe expected shortfall (ES) are calculated at 5%. The Sortino Ratio measures excess returns relative to downside semi-variance. The Omega Ratio measures the ratio of probability weighted gains to losses relative to a threshold or benchmark value. Unlike the Sharpe Ratio, which only takes into account the first two moments of a distribution (mean, variance), the Omega Ratio includes information on the mean, variance, skewness, and kurtosis and is therefore well suited for investments with non-normal distribution. The Sharpe Ratio, Sortino Ratio and Omega ratio are estimated using a benchmark value of 1% on an annualized basis. The Information Ratio is similar to the Sharpe Ratio but is calculated as the ratio of the active premium to the tracking error relative to a time-dependent benchmark, which in this paper is the yield on a three-month US T-bill. Statistical significance of Sharpe Ratios are tested using the block bootstrap method of by Ledoit and Wolf (2008).
The performance fee (Δ) approach is used to estimate the economic value of switching between portfolios (Fleming et al. 2001). This approach measures the economic value of different asset allocations. The performance fee, Δ, represents the management fee an investor with a mean variance utility function would be willing to pay to switch from a benchmark portfolio that includes gold to an alternative portfolio that replaces gold for bitcoin without being made worse off in terms of utility. The performance fee is found by solving the following nonlinear equation:
The sample size is T, the portfolio return is rp, the superscripts a and b denote the alternative portfolio and the benchmark portfolio, respectively, and γ denotes the degree of risk relative risk aversion.
Portfolio turnover is used to measure the number of trades per time period and calculate trading costs. Following DeMiguel et al. (2009), the portfolio turnover is calculated as:
where is the portfolio weight in asset j chosen at time t using strategy i and is the portfolio weight in asset j chosen at time t + 1 after rebalancing using strategy i. The portfolio turnover is equal to the sum of the absolute value of the rebalancing trades across the N assets and over the T − τ − 1 trades, normalized by the total number of trading days.
4. Data
Daily stock price data are collected on five exchange traded funds (ETFs) and the price of bitcoin. The ETFs consist of US equities (SPY), US bonds (TLT), US real estate (VNQ), Europe and Far East equities (EFA), and gold (GLD). Ticker symbols are listed in parentheses. These are widely traded ETFs and form the basis of many portfolio allocation strategies. GLD is an ETF backed by physical gold and movements in the price of GLD are meant to reflect movements in the price of gold bullion. ETF data is downloaded from Yahoo Finance and bitcoin prices (BIT) are downloaded from Coindesk. The daily data cover the period of 4 January 2011 to 31 October 20174. The starting period is chosen based on the start of bitcoin trading. Time series plots clearly show that VNQ, TLT, SPY, and EFA display similar upward trending patterns, while GLD has been trending down and BIT displays an exponential growth pattern (Figure 1).
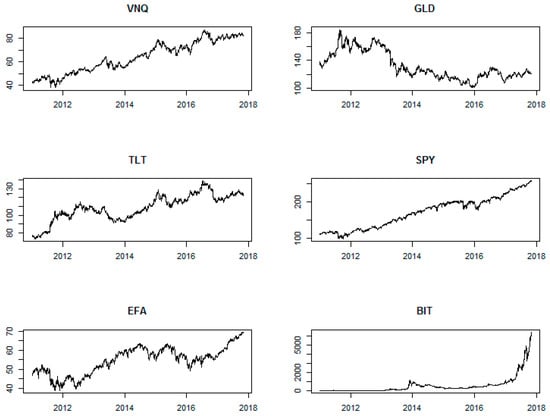
Figure 1.
Time series plots of assets.
Summary statistics for daily returns indicate that, except for GLD, each series has a positive mean and median value (Table 1)5. BIT has the highest average return, while GLD has the lowest. Consistent with the findings of Fry and Cheah (2016), BIT has the highest standard deviation. The coefficient of variation, which is meaningful for positive values, shows that BIT has the least variation, while EFA has the most. Each series has skewness and kurtosis and rejects the null hypothesis of normality, indicating that distributions that take into account fat tails are likely to provide a better fit than a normal distribution. Unit root tests (not reported) indicate that each series is stationary. Correlation coefficients show that SPY, VNQ, and EFA correlate highly with each other (Table 2). TLT correlates negatively with VNQ, SPY, EFA, and BIT, but positively with GLD. Notice that BIT has very low correlation with the other assets, indicating the possible usefulness of bitcoin in diversifying risk. QQ plots show that each series has fat tails, which is common with asset price returns (Figure 2). In Figure 2, the black line is the theoretical quantiles and the circle line is the sample quantiles.

Table 1.
Summary statistics for daily percent returns.

Table 2.
Correlation coefficients for daily percent returns.
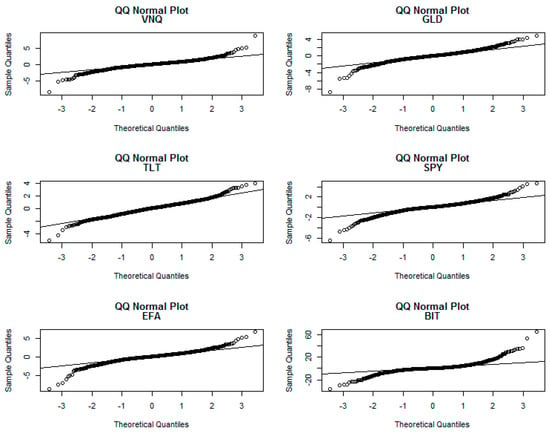
Figure 2.
QQ plots of asset returns.
5. Results
Table 3 shows the average value and standard deviation of the optimal portfolio weights calculated from the BIT and GLD portfolio6. The BIT portfolio consists of SPY, TLT, VNQ, EFA and BIT. The GLD portfolio consists of SPY, TLT, VNQ, EFA and GLD. Portfolio weights are constructed using three GARCH models (DCC, ADCC, and GO). There are no restrictions on short sales. For each GARCH model, portfolios are estimated for a global minimum variance portfolio and annual target returns of 13%, 15%, and 17%. For most assets, portfolio weights calculated from GO have lower standard deviation than those of DCC or ADCC.

Table 3.
Optimal portfolio weights.
Table 4 provides a comparison between the BIT portfolio and the GLD portfolio. For the bitcoin portfolio, and a particular target return, ADCC portfolios have higher risk adjusted measures. For example, for a target return of 15%, DCC-15, ADCC-15, and GO-15 produce Sharpe ratios of 2.089, 2.246, and 2.239, respectively. A similar pattern is observed for the gold portfolio.

Table 4.
Portfolio comparisons.
One of the strongest results from Table 4 is that for a particular target return and GARCH model, the highest risk adjusted returns are observed for the BIT portfolio, indicating that on a risk adjusted basis, the BIT portfolio is preferred over the GLD portfolio. For example, consider the case of estimating portfolio weights using DCC-13. The BIT portfolio has Sortino, Omega, and Information values of 0.170, 0.365, and 1.849, respectively. These values are larger than their corresponding values for the GLD portfolio of 0.156, 0.346, and 1.683, respectively. The results in Table 4 are important in showing that for a particular target return (or minimum variance portfolio) and using a GARCH estimation technique, the bitcoin portfolio is preferred over the gold portfolio.
Equity curves are shown in Figure 3a,b. The bitcoin equity curves for target return portfolios look very similar. Notice that, as expected, portfolios calculated using a target return of 17% have larger final values then portfolios calculated using other target returns. Global minimum variance portfolios have larger drawdowns, which is consistent with the drawdown statistics in Table 4. A similar pattern is observed for the gold portfolio equity curves.
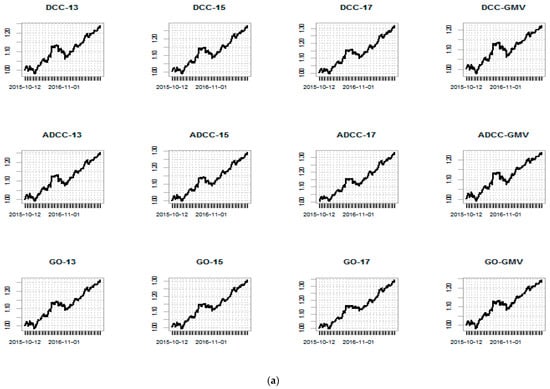
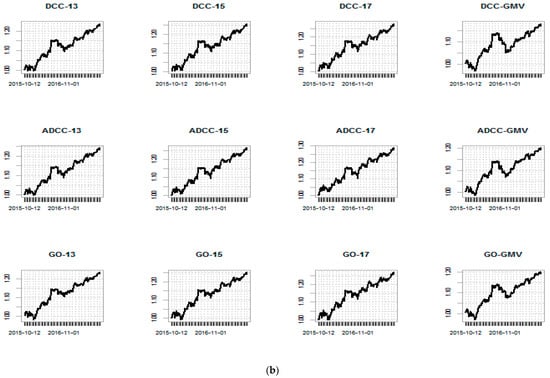
Figure 3.
(a) Equity curves for bitcoin portfolio. (b) Equity curves for gold portfolio.
A statistical comparison between the Sharpe Ratio for the BIT portfolio and the GLD portfolio reveals no statistically significant difference between the Sharpe Ratios (Table 5). Sharpe Ratios, however, focus on the first two moments of the portfolio return distribution and do not take into account other factors like performance fees.

Table 5.
Comparison of Sharpe Ratios.
The performance fees indicate that the economic value an investor places on switching from a GLD portfolio to the BIT portfolio is substantial (Table 6). For example, in the case of a relative risk aversion of 5, the performance fees for GARCH models range between slightly above 28 basis points (DCC-13) to over 400 (GO-17). Performance fees are higher for portfolios with higher target returns.

Table 6.
Performance fees.
In order to make the portfolio comparison more realistic, values for portfolio turnover are constructed (Table 7). Turnover is expressed as the average number of trades per day. For example, for the bitcoin portfolio estimated using DCC-13, a turnover of 0.125 indicates that on average 0.125 trades are made per day. The GO portfolios produce the least turnover. Turnover can be used to estimate trading costs. The turnover values can be annualized by multiplying by 252 to get the number of trades per year and the result multiplied by the trading costs in dollars per trade. These costs are expressed as a percentage of a $1,000,000 portfolio and converted to basis points. As the results in Table 7 show, even with relatively high trading costs of $20 per trade, the total trading costs are less than the performance fee, indicating the benefits of switching to a bitcoin-based portfolio. Notice that portfolios constructed using GO have less transaction costs, which is consistent with GO optimal portfolio weights, for most assets, having a lower standard deviation compared to optimal portfolio weights constructed using either DCC or ADCC.

Table 7.
Turnover and trading costs.
6. Robust Analysis: Long Only Portfolios
The preceding analysis has been conducted assuming short sales are allowed. This section reports on results obtained by assuming long portfolios only. Since the average returns of gold and bitcoin are so different, we only present results on global minimum variance portfolios.
For a particular type of GARCH model, the portfolio with bitcoin produces higher risk-adjusted returns compared to the portfolio with gold (Table 8). Performance fees, the amount an investor would be willing to pay to switch from a portfolio with gold to one with bitcoin are positive and fairly large (Table 9). Transaction costs are smaller than performance fees, indicating that even after adjusting for transaction costs, a risk adverse investor would be willing to pay a fee to switch from a portfolio with gold to one with bitcoin (Table 10). These results for long only portfolios are consistent with our results that allow for short sales.

Table 8.
Portfolio comparisons: Long only.

Table 9.
Performance fees: Long only.

Table 10.
Turnover and trading costs: Long only.
7. Conclusions and Implications
Bitcoin is an exciting new financial product that may be useful for inclusion in investment portfolios. There has been discussion that bitcoin may even by a useful substitute for gold. The purpose of this paper is to investigate the portfolio implications of switching from a portfolio with gold to a portfolio with bitcoin. Given the current interest in Bitcoin investing, this is an important and timely topic to study. Our approach is to use multivariate GARCH models to estimate minimum variance equity portfolios subject to a target return for a US benchmark portfolio that includes gold and a portfolio that substitutes gold for bitcoin. The benchmark portfolio includes US equities, US bonds, US real estate, EAFE equities, and gold. A comparison between these portfolios helps to gain a better understanding of the economic value of substituting bitcoin for gold in an investment portfolio.
Three different multivariable GARCH models (DCC, ADCC, and GO) are used to estimate the optimal portfolio weights. Comparing weights computed from different models demonstrates the robustness of the portfolio results to the choice of GARCH model. Optimal portfolio weights are estimated using rolling window analysis. This mitigates the effects of changing dynamics, parameter heterogeneity, and structural change. For most assets, the optimal portfolio weights estimated from GO have lower standard deviation than those from DCC or ADCC.
Our results show that portfolios with bitcoin rank highest according to risk-adjusted measures such as the Sharpe, Sortino, Omega, and Information ratios. This result is robust to the choice of GARCH model (DCC, ADCC, or GO) used to compute optimal portfolio weights. An analysis of the economic value shows that risk-averse investors will be willing to pay a high performance fee to switch from a portfolio with gold to a portfolio with bitcoin. These results are robust to the inclusion of trading costs. We find that it is possible for an investor to substitute bitcoin for gold in an investment portfolio and achieve a higher risk adjusted return.
While our results on bitcoin investing are encouraging, there are certain limitations that require future research. First, we only have six years of data and more data will be required to test the voracity of our results. Second, in the absence of any valid moment conditions or asymptotic properties DCC forecasts may be imprecise and this may affect the estimates of the portfolio returns and any resulting statistical analysis. Third, as with any new financial asset, the level of widespread adoption will be crucial to its acceptance. Currently, bitcoin is viewed by many investors as a speculative asset and this limits its widespread acceptability. Fourth, bitcoin is in its infancy and the choice of cryptocurrencies is growing. It is not clear if bitcoin will be the preferred cryptocurrency in the future.
Author Contributions
Both authors contributed equally in the preparation of the manuscript.
Funding
This research received no funding.
Acknowledgments
We thank the Editor and two anonymous reviewers for helpful comments.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Aielli, Gian Piero. 2013. Dynamic Conditional Correlation: On Properties and Estimation. Journal of Business & Economic Statistics 31: 282–99. [Google Scholar] [CrossRef]
- Alexander, Carol. 2001. Market Models: A Guide to Financial Data Analysis. Chichester: John Wiley & Sons. [Google Scholar]
- Baur, Dirk G., and Brian M. Lucey. 2010. Is Gold a Hedge or a Safe Haven? An Analysis of Stocks, Bonds and Gold. Financial Review 45: 217–29. [Google Scholar] [CrossRef]
- Baur, Dirk G., and Thomas K. McDermott. 2010. Is Gold a Safe Haven? International Evidence. Journal of Banking & Finance 34: 1886–98. [Google Scholar] [CrossRef]
- Beckmann, Joscha, Theo Berger, and Robert Czudaj. 2015. Does Gold Act as a Hedge or a Safe Haven for Stocks? A Smooth Transition Approach. Economic Modelling 48: 16–24. [Google Scholar] [CrossRef]
- Böhme, Rainer, Nicolas Christin, Benjamin Edelman, and Tyler Moore. 2015. Bitcoin: Economics, Technology, and Governance. Journal of Economic Perspectives 29: 213–38. [Google Scholar] [CrossRef]
- Boswijk, H. Peter, and Roy van der Weide. 2006. Wake Me up before You GO-GARCH. 2006/3. Amsterdam School of Economics. Available online: http://dare.uva.nl/record/390623%5Cnpapers2://publication/uuid/A8691D04-AD04-42B6-8F98-34FD4CA86521 (accessed on 15 March 2018).
- Boswijk, H. Peter, and Roy van der Weide. 2011. Method of Moments Estimation of GO-GARCH Models. Journal of Econometrics 163: 118–26. [Google Scholar] [CrossRef]
- Bouri, Elie, Peter Molnár, Georges Azzi, David Roubaud, and Lars Ivar Hagfors. 2017. On the Hedge and Safe Haven Properties of Bitcoin: Is It Really More than a Diversifier? Finance Research Letters 20: 192–98. [Google Scholar] [CrossRef]
- Broda, Simon A., and Marc S. Paolella. 2009. CHICAGO: A Fast and Accurate Method for Portfolio Risk Calculation. Journal of Financial Econometrics 7: 412–36. [Google Scholar] [CrossRef]
- Canadian Federation of Independent Business. 2018. Regular vs. Premium Credit Card Rate Chart for Small Business. Toronto: CFIB. [Google Scholar]
- Caporin, Massimiliano, and Michael McAleer. 2013. Ten Things You Should Know about the Dynamic Conditional Correlation Representation. Econometrics 1: 115–26. [Google Scholar] [CrossRef]
- Cappiello, Lorenzo, Robert F. Engle, and Kevin Sheppard. 2006. Asymmetric Dynamics in the Correlations of Global Equity and Bond Returns. Journal of Financial Econometrics 4: 537–72. [Google Scholar] [CrossRef]
- Ciaian, Pavel, Miroslava Rajcaniova, and D’Artis Kancs. 2016. The Economics of BitCoin Price Formation. Applied Economics 48: 1799–815. [Google Scholar] [CrossRef]
- Ciner, Cetin, Constantin Gurdgiev, and Brian M. Lucey. 2013. Hedges and Safe Havens: An Examination of Stocks, Bonds, Gold, Oil and Exchange Rates. International Review of Financial Analysis 29: 202–11. [Google Scholar] [CrossRef]
- DeMiguel, Victor, Lorenzo Garlappi, Francisco J. Nogales, and Raman Uppal. 2009. A Generalized Approach to Portfolio Optimization: Improving Performance by Constraining Portfolio Norms. Management Science 55: 798–812. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016a. Bitcoin, Gold and the Dollar—A GARCH Volatility Analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016b. Hedging Capabilities of Bitcoin. Is It the Virtual Gold? Finance Research Letters 16: 139–44. [Google Scholar] [CrossRef]
- Eichengreen, Barry. 1992. Golden Fetters: The Gold Standard and the Great Depression, 1919–1939. New York: Oxford University Press. [Google Scholar]
- Elton, Edwin J., and Martin J. Gruber. 1997. Modern Portfolio Theory, 1950 to Date. Journal of Banking and Finance 21: 1743–59. [Google Scholar] [CrossRef]
- Engle, Robert F. 2002. Dynamic Conditional Correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models. Journal of Business & Economic Statistics 20: 339–50. [Google Scholar] [CrossRef]
- Feibel, Bruce J. 2003. Investment Performance Measurement. Hoboken: John Wiley & Sons. [Google Scholar]
- Fleming, Jeff, Chris Kirby, and Barbara Ostdiek. 2001. The Economic Value of Volatility Timing. The Journal of Finance 56: 329–52. [Google Scholar] [CrossRef]
- Fry, John, and Eng-Tuck Cheah. 2016. Negative Bubbles and Shocks in Cryptocurrency Markets. International Review of Financial Analysis 47: 343–52. [Google Scholar] [CrossRef]
- Ghalanos, Alexios. 2015. Rmgarch: Multivariate GARCH Models. R Package Version 1.2-8. Available online: https://cran.r-project.org/web/packages/rmgarch/index.html (accessed on 15 March 2018).
- Glaser, Florian, Kai Zimmerman, Martin Haferkorn, Moritz Christian Weber, and Michael Siering. 2014. Bitcoin—Asset or Currency? Revealing Users’ Hidden Intentions. Paper presented at Twenty Second European Conference on Information Systems, Tel Aviv, Israel, June 9–14; pp. 1–14. [Google Scholar] [CrossRef]
- Glosten, Lawrence R., Ravi Jagannathan, and David E. Runkle. 1993. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. The Journal of Finance 48: 1779–801. [Google Scholar] [CrossRef]
- Guesmi, Khaled, Samir Saadi, Ilyes Abid, and Zied Ftiti. 2018. Portfolio Diversification with Virtual Currency: Evidence from Bitcoin. International Review of Financial Analysis. [Google Scholar] [CrossRef]
- Hendrickson, Joshua R., Thomas L. Hogan, and William J. Luther. 2016. The Political Economy of Bitcoin. Economic Inquiry 54: 925–39. [Google Scholar] [CrossRef]
- Hillier, David, Paul Draper, and Robert Faff. 2006. Do Precious Metals Shine? An Investment Perspective. Financial Analysts Journal 62: 98–106. [Google Scholar] [CrossRef]
- Hopkins, Jamie. 2017. Bitcoin Might Be A ‘Bubble’ But Digital Currencies Are Not. Forbes, November 29. [Google Scholar]
- Jaffe, Jeffrey F. 1989. Gold and Gold Stocks as Investments for Institutional Portfolios. Financial Analysts Journal 45: 53–59. [Google Scholar] [CrossRef]
- Kim, Thomas. 2017. On the Transaction Cost of Bitcoin. Finance Research Letters 23: 300–5. [Google Scholar] [CrossRef]
- Kiviat, Trevor I. 2015. Beyond Bitcoin: Issues in Regulating Blockchain Transactions. Duke Law Journal 65: 569–608. [Google Scholar] [CrossRef]
- Ledoit, Oliver, and Michael Wolf. 2008. Robust Performance Hypothesis Testing with the Sharpe Ratio. Journal of Empirical Finance 15: 850–59. [Google Scholar] [CrossRef]
- Lo, Stephanie, and J. Christina Wang. 2014. Bitcoin as Money? Federal Reserve Bank of Boston 14: 1–28. [Google Scholar]
- McNutt, Patrick. 2002. The Economics of Public Choice II. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Michaud, By Richard, Robert Michaud, and Katharine Pulvermacher. 2006. Gold as a Strategic Asset. London: World Gold Council. [Google Scholar]
- Nakamoto, Satoshi. 2008. Bitcoin: A Peer-to-Peer Electronic Cash System. Available online: https://bitcoin.org/en/bitcoin-paper (accessed on 15 March 2018).
- Popper, Nathaniel. 2015a. Can Bitcoin Conquer Argentina? The New York Times, April 29. [Google Scholar]
- Popper, Nathaniel. 2015b. Digital Gold: Bitcoin and the Inside Story of Misfits and Millionaires Trying to Reinvent Money. New York: HarperCollins. [Google Scholar]
- R Core Team. 2015. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. Available online: http://www.r-project.org/ (accessed on 15 March 2018).
- Reboredo, Juan C. 2013a. Is Gold a Hedge or Safe Haven against Oil Price Movements? Resources Policy 38: 130–37. [Google Scholar] [CrossRef]
- Reboredo, Juan C. 2013b. Is Gold a Safe Haven or a Hedge for the US Dollar? Implications for Risk Management. Journal of Banking & Finance 37: 2665–76. [Google Scholar] [CrossRef]
- Van Der Weide, Roy. 2002. GO-GARCH: A Multivariate Generalized Orthogonal GARCH Model. Journal of Applied Econometrics 17: 549–64. [Google Scholar] [CrossRef]
- Zhang, Kun, and Laiwan Chan. 2009. Efficient Factor GARCH Models and Factor-DCC Models. Quantitative Finance 9: 71–91. [Google Scholar] [CrossRef]
- Zhu, Yechen, David Dickinson, and Jianjun Li. 2017. Analysis on the Influence Factors of Bitcoin’s Price Based on VEC Model. Financial Innovation 3: 3. [Google Scholar] [CrossRef]
- Zohar, Aviv. 2015. Bitcoin. Communications of the ACM 58: 104–13. [Google Scholar] [CrossRef]
| 1 | Daily data are available at https://blockchain.info/charts. By convention, we use Bitcoin with a capital “B” to denote the Bitcoin network and “bitcoin” with a small “b” to denote the unit of account. |
| 2 | |
| 3 | The rotation matrix U needs to be estimated. For all but a few factors, maximum likelihood is not feasible. For a larger number of factors, alternative estimation methods must be used. ICA is a fast statistical technique for estimating hidden factors in relation to observable data. |
| 4 | Bitcoin price data was from 18 July 2010, but there was not much price variability over the first few months. |
| 5 | Summary statistics are computed using continuously compounded daily returns. Portfolio weights are estimated using discrete returns because discrete returns are additive across assets. The resulting portfolio returns are then converted to continuous returns for the calculation of portfolio summary statistics. |
| 6 | GARCH models are estimated using 1200 observations, and 519 one step forecasts are generated using rolling window estimation. The estimation window of 1200 observations is chosen based on a Monte Carlo comparison of RMSE. GARCH models are refitted every 60 observations. The portfolio results are robust to refits between 40 and 120 observations. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).