Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis
Abstract
:“After Lehman Brothers toppled in September 2008, it took 24 days for US stocks to slide more than 20 per cent into official bear market territory. Bitcoin, the new age cryptocurrency that has been breaking bull market records, did the same on Wednesday in just under six hours”Financial Times—30 November 2017—Bitcoin swings from bull to bear and back in one day
1. Introduction
2. Model
3. Data
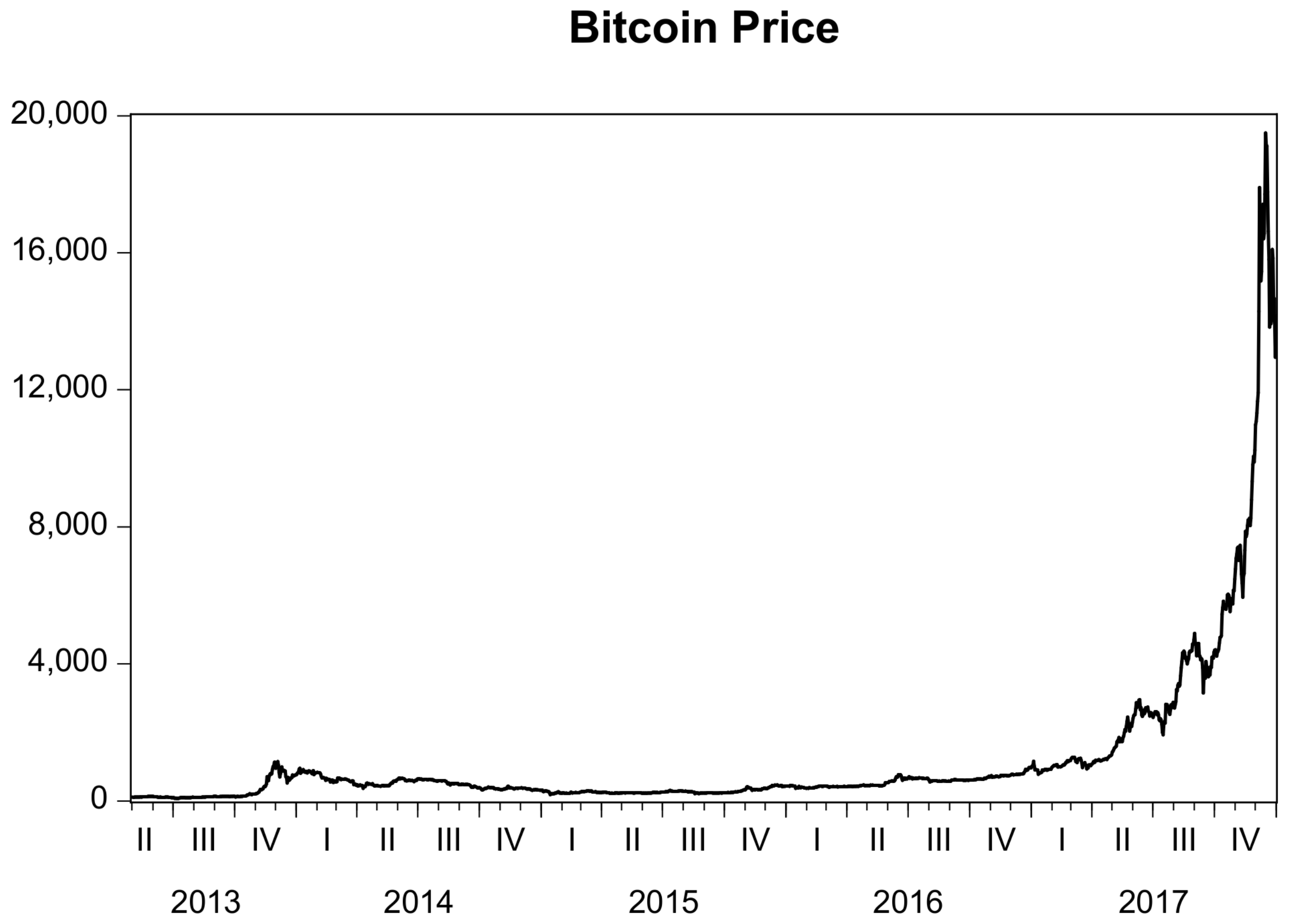
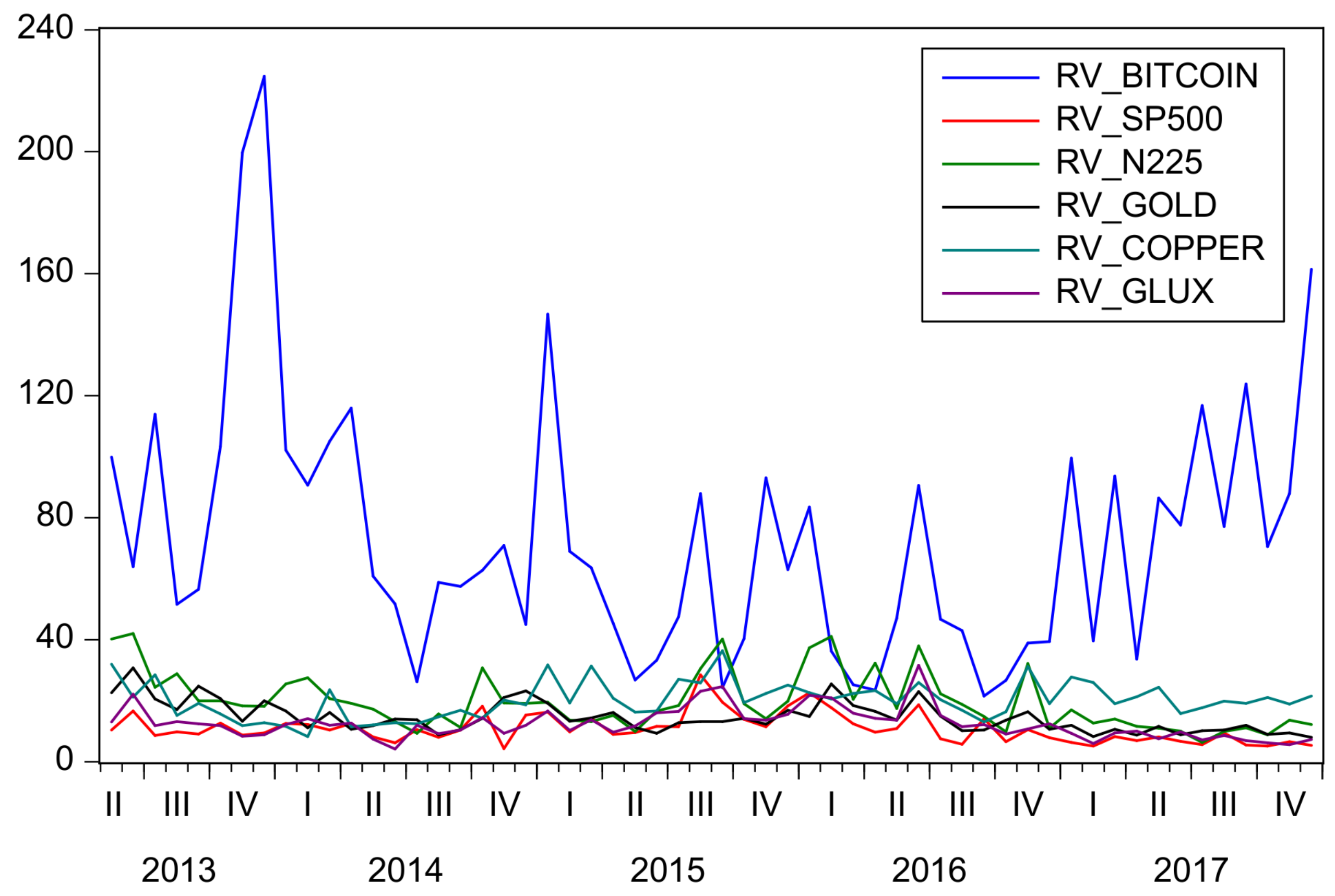
3.1. Data Descriptions
3.2. Summary Statistics
4. Empirical Results
4.1. Macro and Financial Drivers of Long-Term Bitcoin Volatility
4.2. Bitcoin Specific Explanatory Variables
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Al-Khazali, Osamah, Bouri Elie, and David Roubaud. 2018. The impact of positive and negative macroeconomic news surprises: Gold versus Bitcoin. Economics Bulletin 38: 373–82. [Google Scholar]
- Balcilar, Mehmet, Elie Bouri, Rangan Gupta, and David Roubaud. 2017. Can volume predict Bitcoin returns and volatility? A quantiles-based approach. Economic Modelling 64: 74–81. [Google Scholar] [CrossRef]
- Baur, Dirk G., Kihoon Hong, and Adrian D. Lee. 2017. Bitcoin: Medium of Exchange or Speculative Assets? Available online: https://ssrn.com/abstract=2561183 (accessed on 25 April 2018). [CrossRef]
- Bekaert, Geert, Eric Engstrom, and Yuhang Xing. 2009. Risk, uncertainty, and asset prices. Journal of Financial Economics 91: 59–82. [Google Scholar] [CrossRef]
- Bollerslev, Tim, George Tauchen, and Hao Zhou. 2009. Expected stock returns and variance risk premia. Review of Financial Studies 22: 4463–92. [Google Scholar] [CrossRef]
- Bouri, Elie, Georges Azzi, and Anne Haubo Dyhrberg. 2017. On the return-volatility relationship in the Bitcoin market around the price crash of 2013. Economics 11: 1–16. [Google Scholar] [CrossRef]
- Chen, Cathy Y. H., Wolfgang Karl Härdle, Ai Jun Hou, and Weining Wang. 2018. Pricing Cryptocurrency Options: The Case of CRIX and Bitcoin. IRTG 1792 Discussion Paper 2018-004. Berlin: Humboldt-Universität zu Berlin. [Google Scholar]
- Cheah, Eng-Tuck, Tapas Mishra, Mamata Parhi, and Zhuang Zhang. 2018. Long memory interdependency and inefficiency in Bitcoin markets. Economics Letters 167: 18–25. [Google Scholar] [CrossRef]
- Conrad, Christian, and Onno Kleen. 2018. Two Are Better Than One: Volatility Forecasting Using Multiplicative Component GARCH Models. Available online: https://ssrn.com/abstract=2752354 (accessed on 15 October 2017).
- Conrad, Christian, and Karin Loch. 2015. Anticipating long-term stock market volatility. Journal of Applied Econometrics 30: 1090–114. [Google Scholar] [CrossRef]
- D’Amuri, Francesco, and Juri Marcucci. 2017. The predictive power of Google searches in forecasting US unemployment. International Journal of Forecasting 33: 801–16. [Google Scholar] [CrossRef]
- Dyhrberg, Anne Haubo. 2016. Bitcoin, gold and the dollar—A GARCH volatility analysis. Finance Research Letters 16: 85–92. [Google Scholar] [CrossRef]
- Engle, Robert, Michael Fleming, Eric Ghysels, and Giang Nguyen. 2012. Liquidity, Volatility, and Flights to Safety in the U.S. Treasury Market: Evidence from a New Class of Dynamic Order Book Models. FRB of New York Staff Report No. 590. Available online: http://dx.doi.org/10.2139/ssrn.2195655 (accessed on 9 October 2017).
- Engle, Robert F., Eric Ghysels, and Bumjean Sohn. 2013. Stock market volatility and macroeconomic fundamentals. Review of Economics and Statistics 95: 776–97. [Google Scholar] [CrossRef]
- Fang, Libing, Baizhu Chen, Honghai Yu, and Yichuo Qian. 2018. The importance of global economic policy uncertainty in predicting gold futures market volatility: A GARCH-MIDAS approach. Journal of Futures Markets 38: 413–22. [Google Scholar] [CrossRef]
- Katsiampa, Paraskevi. 2017. Volatility estimation for Bitcoin: A comparison of GARCH models. Economics Letters 158: 3–6. [Google Scholar] [CrossRef]
- Kristoufek, Ladislav. 2015. What are the main drivers of the Bitcoin price? Evidence from Wavelet coherence analysis. PLoS ONE 10: e0123923. [Google Scholar] [CrossRef] [PubMed]
- Khuntia, Sashikanta, and J. K. Pattanayak. 2018. Adaptive market hypothesis and evolving predictability of Bitcoin. Economics Letters 167: 26–28. [Google Scholar] [CrossRef]
- Koutmos, Dimitrios. 2018. Bitcoin returns and transaction activity. Economics Letters 167: 81–85. [Google Scholar] [CrossRef]
- Li, Xin, and Chong Alex Wang. 2017. The technology and economic determinants of cryptocurrency exchange rates: The case of Bitcoin. Decision Support Systems 95: 49–60. [Google Scholar] [CrossRef]
- Polasik, Michal, Anna Iwona Piotrowska, Tomasz Piotr Wisniewski, Radoslaw Kotkowski, and Geoffrey Lightfoot. 2015. Price Fluctuations and the Use of Bitcoin: An Empirical Inquiry. International Journal of Electronic Commerce 20: 9–49. [Google Scholar] [CrossRef]
- Schwert, G. William. 1989. Why does stock market volatility change over time? The Journal of Finance 44: 1115–53. [Google Scholar] [CrossRef]
| 1. | All data on data.bitcoinity.org is retrieved directly from exchanges through their APIs and is regularly updated for accuracy. |
| 2. | Note, Quandl’s data source for the BDI is Lloyd’s List. |
| 3. | Fang et al. (2018) investigate whether global economic policy uncertainty predicts long-term gold volatility. We are not aware of any applications of the GARCH-MIDAS to copper returns. |
| 4. | Similarly, Katsiampa (2017) estimates a non-stationary GARCH(1,1) for Bitcoin returns (see his Table 1). See also Chen et al. (2018) for GARCH estimates of Bitcoin volatility. |
| 5. | For example, in a Reuters article from 11 April 2013, it is argued that the Bitcoin “currency has gained in prominence amid the euro zone sovereign debt crisis as more people start to question the safety of holding their cash in the bank. Bitcoins shot up in value in March when investors took fright at Cyprus’ plans to impose losses on bank deposits.” |
| 6. | There is already some evidence that Google searches can be used to forecast macroeconomic variables such as the unemployment rate (see D’Amuri and Marcucci (2017)). |

| Variable | Mean | Min | Max | SD | Skew. | Kurt. | Obs. |
|---|---|---|---|---|---|---|---|
| Panel A: Daily return data | |||||||
| Bitcoin | 0.271 | −26.620 | 35.745 | 4.400 | −0.139 | 11.929 | 1706 |
| S&P 500 | 0.045 | −4.044 | 3.801 | 0.748 | −0.423 | 5.985 | 1176 |
| Nikkei 225 | 0.043 | −8.253 | 7.426 | 1.389 | −0.391 | 7.817 | 1145 |
| Gold | −0.012 | −5.479 | 4.832 | 0.967 | 0.022 | 5.873 | 1177 |
| Copper | −0.004 | −5.126 | 6.594 | 1.323 | 0.018 | 4.812 | 1177 |
| Panel B: Monthly realized volatilities (annualized) | |||||||
| RV-Bitcoin | 73.063 | 21.519 | 224.690 | 42.349 | 1.414 | 5.472 | 56 |
| RV-S&P 500 | 10.879 | 4.219 | 28.435 | 4.825 | 1.263 | 4.909 | 56 |
| RV-Nikkei 225 | 19.701 | 6.336 | 41.969 | 9.328 | 0.981 | 3.039 | 56 |
| RV-Gold | 14.519 | 8.026 | 30.734 | 5.014 | 1.052 | 3.735 | 56 |
| RV-Copper | 20.132 | 8.265 | 36.396 | 6.037 | 0.493 | 2.930 | 56 |
| RV-Glux | 12.469 | 4.087 | 31.537 | 5.114 | 1.359 | 5.536 | 56 |
| Panel C: Monthly explanatory variables | |||||||
| VIX | 14.684 | 9.510 | 28.430 | 3.602 | 1.424 | 5.832 | 56 |
| VRP | 9.819 | −8.337 | 20.299 | 5.837 | −0.463 | 4.538 | 56 |
| Baltic dry index | 983.150 | 306.905 | 2178.059 | 383.597 | 0.774 | 3.613 | 56 |
| RV-Glux | 12.469 | 4.087 | 31.537 | 5.114 | 1.359 | 5.536 | 56 |
| Panel D: Monthly Bitcoin specific explanatory variables | |||||||
| Google Trends (all) | 7.661 | 2.000 | 100.000 | 14.395 | 5.156 | 32.147 | 56 |
| Google Trends (news) | 10.625 | 2.000 | 100.000 | 15.304 | 4.056 | 22.532 | 56 |
| US-TV | 2,308,314 | 603,946 | 4,947,777 | 1,047,524 | 0.573 | 2.686 | 56 |
| CNY-TV | 24,897,595 | 4693 | 173,047,579 | 42,509,087 | 2.180 | 7.056 | 56 |
| RV-Bitcoin | RV-S&P 500 | RV-Nikkei 225 | RV-Gold | RV-Copper | RV-Glux | |
|---|---|---|---|---|---|---|
| RV-Bitcoin | 1.000 | −0.074 | −0.048 | 0.059 | −0.080 | −0.179 |
| RV-S&P 500 | 1.000 | 0.636 | 0.369 | 0.252 | 0.818 | |
| RV-Nikkei 255 | 1.000 | 0.634 | 0.333 | 0.743 | ||
| RV-Gold | 1.000 | 0.220 | 0.469 | |||
| RV-Copper | 1.000 | 0.367 | ||||
| RV-Glux | 1.000 |
| Variable | m | LLF | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| GARCH(1,1) | - | - | 5.4608 | 5.4734 | |||||
| RV-S&P 500 | 5.4182 | 5.4374 | |||||||
| VIX | 5.4285 | 5.4477 | |||||||
| RV-Glux | 5.4208 | 5.4399 | |||||||
| VRP | 5.4126 | 5.4317 | |||||||
| Baltic | 5.3935 | 5.4127 |
| Variable | m | LLF | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| RV-S&P 500 | 2.0371 | 2.0630 | |||||||
| VIX | 2.0270 | 2.0529 | |||||||
| RV-Glux | 2.0425 | 2.0684 | |||||||
| VRP | 2.0405 | 2.0664 | |||||||
| Baltic | 2.0455 | 2.0714 |
| Variable | m | LLF | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| RV-N225 | 3.2489 | 3.2753 | |||||||
| RV-S&P 500 | 3.2335 | 3.2599 | |||||||
| VIX | 3.2265 | 3.2530 | |||||||
| RV-Glux | 3.2425 | 3.2689 | |||||||
| VRP | 3.2437 | 3.2701 | |||||||
| Baltic | 3.2480 | 3.2745 |
| Variable | m | LLF | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| Panel A: Gold | |||||||||
| RV-S&P 500 | 2.6732 | 2.6990 | |||||||
| VIX | 2.6691 | 2.6949 | |||||||
| RV-Glux | 2.6788 | 2.7046 | |||||||
| Panel B: Copper | |||||||||
| RV-S&P 500 | 3.3494 | 3.3753 | |||||||
| Baltic | 3.3493 | 3.3752 | |||||||
| Variable | m | LLF | AIC | BIC | |||||
|---|---|---|---|---|---|---|---|---|---|
| Google Trends (all) | 5.4295 | 5.4486 | |||||||
| Google Trends (news) | 5.4140 | 5.4331 | |||||||
| US-TV | 5.4234 | 5.4431 | |||||||
| CNY-TV | 5.1774 | 5.2011 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conrad, C.; Custovic, A.; Ghysels, E. Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. J. Risk Financial Manag. 2018, 11, 23. https://doi.org/10.3390/jrfm11020023
Conrad C, Custovic A, Ghysels E. Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. Journal of Risk and Financial Management. 2018; 11(2):23. https://doi.org/10.3390/jrfm11020023
Chicago/Turabian StyleConrad, Christian, Anessa Custovic, and Eric Ghysels. 2018. "Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis" Journal of Risk and Financial Management 11, no. 2: 23. https://doi.org/10.3390/jrfm11020023
APA StyleConrad, C., Custovic, A., & Ghysels, E. (2018). Long- and Short-Term Cryptocurrency Volatility Components: A GARCH-MIDAS Analysis. Journal of Risk and Financial Management, 11(2), 23. https://doi.org/10.3390/jrfm11020023







