An Empirical Study on the Impact of Basel III Standards on Banks’ Default Risk: The Case of Luxembourg
Abstract
:1. Introduction
2. Basel III Regulations and the Probability of Default
2.1. Probability of Default, Leverage and Profitability of Banks
2.2. The Basel III Regulations
3. Econometric Specification
4. Data Description
5. Results
5.1. Profitability
5.2. Leverage
5.3. Z-Score
5.4. Robustness: Estimation of the System of Equations
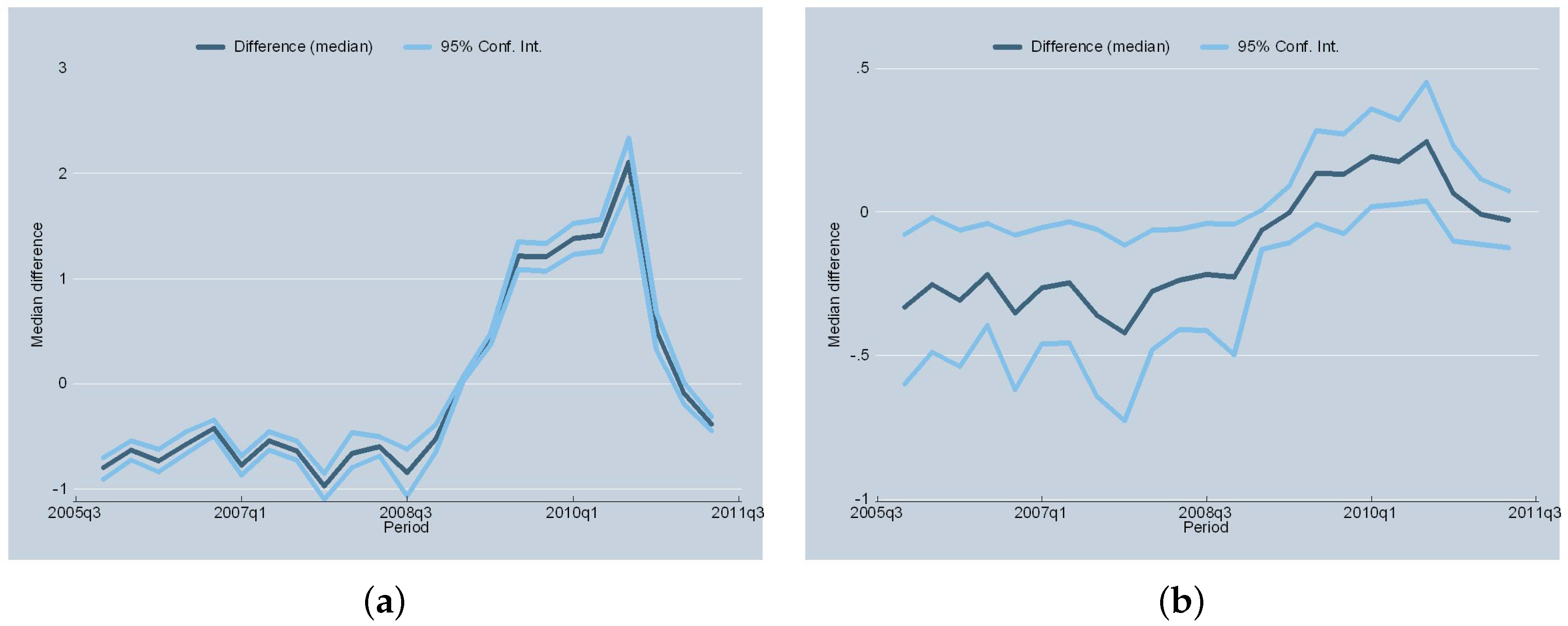
5.5. Simulation Results: When Banks Adhere to the Regulations
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| Variable | Description |
| ROA | Return-On-Assets (after tax results over total assets ratio) times 100 over sd(ROA). |
| sd(ROA) | SD of ROA calculated using an eight-period moving window. |
| LEV | Total assets-to-equity ratio. |
| CAR | Capital-to-Assets Ratio times 100 over sd(ROA). |
| TA | Total Assets. |
| OBSR | Off-Balance Sheet activities over total assets Ratio. |
| LCR | Liquidity Coverage Ratio (Basel III new liquidity standard). |
| NSFR | Net Stable Funding Ratio (Basel III new liquidity standard). |
| HQLAR * | High-Quality Liquid Assets over total assets Ratio. |
| NOR * | Net-Outflows to total assets Ratio. |
| ASFR * | Available Stable Funding to total assets Ratio. |
| RSFR * | Required Stable Funding to total assets Ratio. |
| EFF ** | Gross income over administrative and staff expenses (proxy of efficiency). |
| PLR | Provisions over Loans (proxy of credit risk) Ratio. |
| C | Liquidity crisis dummy variable. It equals one if and zero otherwise. |
| C | Sovereign debt crisis dummy variable. It equals one if and zero otherwise. |
| IR | Short-term Interest Rate, proxied by the Euribor three-month rate. |
| Q | Seasonal dummies (j = 2, 3 and 4). |
References
- Acharya, Viral V., Lasse, H. Pedersen, Philippon Thomas, and Richardson Matthew. 2010. Measuring Systemic Risk. New York: Wiley Online Library. [Google Scholar]
- Adrian, Tobias, and K. Brunnermeier Markus. 2016. CoVaR. The American Economic Review 106: 1705–41. [Google Scholar] [CrossRef]
- Adrian, Tobias, and Shin Song Hyun. 2010. Liquidity and leverage. Journal of Financial Intermediation 19: 418–37. [Google Scholar] [CrossRef]
- Angelini, Paolo, Laurent Clerc, Vasco Cúrdia, Leonardo Gambacorta, Andrea Gerali, Alberto Locarno, Roberto Motto, Werner Roeger, Skander Van den Heuvel, and Jan Vlček. 2011. BASEL III: Long-Term Impact on Economic Performance and Fluctuations. Technical Report. Basel: Bank for International Settlements (BIS). [Google Scholar]
- Athanasoglou, Panayiotis P., Sophocles N. Brissimis, and Matthaios D. Delis. 2008. Bank-specific, industry- specific and macroeconomic determinants of bank profitability. Journal of International Financial Markets, Institutions and Money 18: 121–36. [Google Scholar] [CrossRef]
- Arellano, Manuel, and Stephen Bond. 1991. Some tests of specification for panel data: Monte Carlo evidence and an application to employment equations. The Review of Economic Studies 58: 277–97. [Google Scholar] [CrossRef]
- Arellano, Manuel, and Olympia Bover. 1995. Another look at the instrumental variable estimation of error- components models. Journal of Econometrics 68: 29–51. [Google Scholar] [CrossRef]
- Blundell, Richard, and Stephen Bond. 1998. Initial conditions and moment restrictions in dynamic panel data models. Journal of Econometrics 87: 115–43. [Google Scholar] [CrossRef]
- Brownlees, Christian, and Robert F. Engle. 2016. SRISK: A conditional capital shortfall measure of systemic risk. Review of Financial Studies 30: 48–79. [Google Scholar] [CrossRef]
- BCBS. 2014. Basel III Leverage Ratio Framework and Disclosure Requirements. Technical Report, Bank for International Settlements (BIS). Basel: BCBS (Basel Committee on Banking Supervisors). [Google Scholar]
- BCBS. 2013. LCR: The Liquidity Coverage Ratio and Liquidity Risk Monitoring Tools. Technical Report, Bank for International Settlements (BIS). Basel: BCBS (Basel Committee on Banking Supervisors). [Google Scholar]
- BCBS. 2010a. Basel III: International Framework for Liquidity Risk Measurement, Standards and Monitoring. Rules Text, Bank for International Settlements. Basel: BCBS (Basel Committee on Banking Supervisors). [Google Scholar]
- BCBS. 2010b. Basel III: A Global Regulatory Framework for More Resilient Banks And Banking Systems. Rules Text, Bank for International Settlements. Basel: BCBS (Basel Committee on Banking Supervisors). [Google Scholar]
- Besanko, David, and George Kanatas. 1996. The regulation of bank capital: Do capital standards promote bank safety? Journal of financial intermediation 5: 160–83. [Google Scholar] [CrossRef]
- BCBS. 2010. Results of the Comprehensive Quantitative Impact Study. Technical Report, Bank for International Settlements. Basel: BCBS (Basel Committee on Banking Supervisors). [Google Scholar]
- Berger, Allen N. 1995. The relationship between capital and earnings in banking. Journal of Money, Credit and Banking 27: 432–56. [Google Scholar] [CrossRef]
- Berger, Allen, Gerald Hanweck, and David B. Humphrey. 1987. Competitive viability in banking: Scale, scope, and product mix economies. Journal of Monetary Economics 20: 501–20. [Google Scholar] [CrossRef]
- Berger, Allen N., and Christa H. S. Bouwman. 2010. How Does Capital Affect Bank Performance During Financial Crises? Wharton Financial Institutions Center WP 109: 146–76. [Google Scholar]
- Basurto, Miguel A. Segoviano, and Raphael A. Espinoza. 2011. Probabilities of Default and the Market Price of Risk in a Distressed Economy. IMF Working Paper, April 1. [Google Scholar]
- Berger, Allen N., Leora F. Klapper, and Rima Turk-Ariss. 2009. Bank competition and financial stability. Journal of Financial Services Research 35: 99–118. [Google Scholar] [CrossRef]
- Bikker, Jacob A., and Haixia Hu. 2002. Cyclical patterns in profits, provisioning and lending of banks. DNB Staff Reports 55: 143–175. [Google Scholar]
- Berger, Allen N. 1995. The profit-structure relationship in banking-tests of market-power and efficient-structure hypotheses. Journal of Money, Credit and Banking 27: 404–31. [Google Scholar] [CrossRef]
- Barth, James R., Gerard Caprio Jr., and Ross Levine. 2004. Bank regulation and supervision: What works best? Journal of Financial Intermediation 13: 205–48. [Google Scholar] [CrossRef]
- Bourke, Philip. 1989. Concentration and other determinants of bank profitability in Europe, North America and Australia. Journal of Banking & Finance 13: 65–79. [Google Scholar] [CrossRef]
- Brunnermeier, Markus, Andrew Crockett, Charles Goodhart, Avinash D. Persaud, and Hyun Song Shin. 2009. The Fundamental Principles of Financial Regulation. Technical Report. London: Centre for Economic Policy Research. [Google Scholar]
- Chrystal, Alec, and Paul D. Mizen. 2003. Goodhart’s Law: Its origins, meaning and implications for monetary policy. In Central Banking, Monetary Theory and Practice: Essays In Honour of Charles Goodhart. Cheltenham: Edward Elgar Publishing. [Google Scholar]
- Campbell, John Y., Jens Hilscher, and Jan Szilagyi. 2008. In search of distress risk. The Journal of Finance 63: 2899–939. [Google Scholar] [CrossRef]
- Chan-Lau, Jorge A., and Amadou N. Sy. 2007. Distance-to-default in banking: A bridge too far? Journal of Banking Regulation 9: 14–24. [Google Scholar] [CrossRef]
- Crouhy, Michel, Dan Galai, and Robert Mark. 2000. A comparative analysis of current credit risk models. Journal of Banking & Finance 24: 59–117. [Google Scholar] [CrossRef]
- Demirguc-Kunt, Asli, Enrica Detragiache, and Thierry Tressel. 2008. Banking on the principles: Compliance with Basel Core Principles and bank soundness. Journal of Financial Intermediation 17: 511–42. [Google Scholar] [CrossRef]
- Dietsch, Michel, and Joel Petey. 2002. The credit risk in SME loans portfolios: Modeling issues, pricing, and capital requirements. Journal of Banking & Finance 26: 303–22. [Google Scholar] [CrossRef]
- Duffie, Darrell, and Jun Pan. 1997. An overview of value at risk. The Journal of Derivatives 4: 7–49. [Google Scholar] [CrossRef]
- Demirgüç-Kunt, Ash, and Harry Huizinga. 1999. Determinants of commercial bank interest margins and profitability: Some international evidence. The World Bank Economic Review 13: 379–408. [Google Scholar] [CrossRef]
- Drehmann, Mathias, and Nikola A. Tarashev. 2011. Systemic importance: Some simple indicators. BIS Quarterly Review March: 25–37. [Google Scholar]
- DeNicolo, Gianni. Size, charter value and risk in banking: An international perspective (April 2001). International Finance Discussion Papers, EFA 2001 Barcelona Meetings. FRB International Finance Discussion Paper No. 689.
- Duffie, Darrell, and Kenneth J. Singleton. 2003. Credit Risk: Pricing, Measurement, and Management. Princeton: Princeton University Press. [Google Scholar]
- DeNicolo, Gianni, Jahanara Zaman, Mary G. Zephirin, and Philip F. Bartholomew. 2004. Bank consolidation, internationalization, and conglomeration: Trends and implications for financial risk. Financial Markets, Institutions & Instruments 13: 173–217. [Google Scholar]
- Giordana, Gaston A., and Ingmar Schumacher. 2013. Bank liquidity risk and monetary policy. Empirical evidence on the impact of Basel III liquidity standards. International Review of Applied Economics 27: 633–55. [Google Scholar] [CrossRef]
- Giordana, Gaston, and Ingmar Schumacher. 2012. What are the bank-specific and macroeconomic drivers of banks’ leverage? Evidence from Luxembourg. Empirical Economics 45: 1–24. [Google Scholar] [CrossRef]
- Giordana, Gaston, and Ingmar Schumacher. 2012. An empirical study on the impact of Basel III standards on banks’ default risk: The case of Luxembourg. Banque Centrale du Luxembourg Working Papers 79: 1–31. [Google Scholar]
- Giordana, Gaston Andres. 2016. Welfare and stochastic dominance for the measurement of banks’ domestic systemic importance: Analytical framework and application. International Journal of Finance and Economics 21: 192–208. [Google Scholar] [CrossRef]
- Gennotte, Gerard, and David Pyle. 1991. Capital controls and bank risk. Journal of Banking & Finance 15: 805–24. [Google Scholar] [CrossRef]
- Goddard, John, Phil Molyneux, and John O. S. Wilso. 2004. Dynamics of growth and profitability in banking. Journal of Money, Credit and Banking 36: 1069–90. [Google Scholar] [CrossRef]
- Goddard, John, Phil Molyneux, and John O. S. Wilson. 2004. The profitability of european banks: A cross-sectional and dynamic panel analysis. The Manchester School 72: 363–81. [Google Scholar] [CrossRef]
- Gordy, Michael B. 2000. A comparative anatomy of credit risk models. Journal of Banking & Finance 24: 119–49. [Google Scholar]
- Hamermesh, Daniel S., and Gerard A. Pfann. 1996. Adjustment costs in factor demand. Journal of Economic Literature 34: 1264–92. [Google Scholar]
- Jackson, Patricia, and William Perraudin. 2000. Regulatory implications of credit risk modelling. Journal of Banking & Finance 24: 1–14. [Google Scholar] [CrossRef]
- Jin, Xisong, and Francisco Nadal de Simone. 2011. Market and book based models of probability of default for developing macroprudential policy tools. Banque Centrale du Luxembourg, Working Paper, August 29. [Google Scholar]
- Jin, Xisong, and Francisco Nadal De Simone. 2014. Banking systemic vulnerabilities: A tail-risk dynamic CIMDO approach. Journal of Financial Stability 14: 81–101. [Google Scholar] [CrossRef]
- Judson, Ruth A., and Ann Owen. 1999. Estimating dynamic panel data models: A guide for macroeconomists. Economics Letters 65: 9–15. [Google Scholar] [CrossRef]
- Kopecky, Kenneth J., David Vanhoose, K. Kopecky, and D. VanHoose. 2004. A model of the monetary sector with and without binding capital requirements. Journal of Banking & Finance 28: 633–46. [Google Scholar] [CrossRef]
- Lam, Chun H., and Andrew H. Chen. 1985. Joint effects of interest rate deregulation and capital requirements on optimal bank portfolio adjustments. Journal of Finance 40: 563–75. [Google Scholar] [CrossRef]
- Lucas, Robert E., Jr. 1976. Econometric policy evaluation: A critique. In Carnegie-Rochester Conference Series on Public Policy. New York: Elsevier, vol. 1, pp. 19–46. [Google Scholar]
- Lucas, Robert E., Jr. 1967. Adjustment costs and the theory of supply. The Journal of Political Economy 75: 321–34. [Google Scholar] [CrossRef]
- Maechler, Andrea M., Srobona Mitra, and Delisle Worrell. 2007. Decomposing financial risks and vulnerabilities in Eastern Europe. IMF Working Paper WP/07/ 248: 1–33. [Google Scholar]
- Merton, Robert C. 1974. On the pricing of corporate debt: The risk structure of interest rates. The Journal of Finance 29: 449–70. [Google Scholar] [CrossRef]
- Moore, Kyle, and Chen Zhou. 2013. ‘Too Big to Fail’ or ‘Too Non-Traditional to Fail?’ The Determinants of Banks’ Systemic Importance. MPRA Paper 45589. Munich: University Library of Munich. [Google Scholar]
- Molyneux, Philip, and John Thornton. 1992. Determinants of European bank profitability: A note. Journal of Banking & Finance 16: 1173–78. [Google Scholar] [CrossRef]
- Nickell, Stephen. 1981. Biases in dynamic models with fixed effects. Econometrica: Journal of the Econometric Society 49: 1417–26. [Google Scholar] [CrossRef]
- Richard, Podpiera. 2006. Does Compliance with Basel Core Principles Bring Any Measurable Benefits? IMF Staff Papers 53: 306–25. [Google Scholar]
- Ronald, Anderson, and Suresh Sundaresan. 2000. A comparative study of structural models of corporate bond yields: An exploratory investigation. Journal of Banking & Finance 24: 255–69. [Google Scholar]
- Smirlock, Michael. 1985. Evidence on the (non) relationship between concentration and profitability in banking. Journal of Money, Credit and Banking 17: 69–83. [Google Scholar] [CrossRef]
- Slovik, Patrick, and Boris Cournède. 2011. Macroeconomic Impact of Basel III. OECD Economics Department Working Papers, February 14. [Google Scholar]
- Segoviano, Miguel, and Charles Goodhart. 2009. Banking stability measures. IMF Working Paper, January 1. [Google Scholar]
- Tarashev, Nikola, Claudio Borio, and Kostas Tsatsaronis. 2009. The systemic importance of financial institutions. BIS Quarterly Review September: 75–87. [Google Scholar]
- Tarashev, Nikola, Claudio Borio, and Kostas Tsatsaronis. 2010. Attributing systemic risk to individual institutions. BIS Working Paper 308: 1–29. [Google Scholar] [CrossRef]
- Wagner, Wolf. 2007. The liquidity of bank assets and banking stability. Journal of Banking & Finance 31: 121–39. [Google Scholar] [CrossRef]
- Wolff, Christian C. P., and Nikolaos I. Papanikolaou. 2015. Leverage and Risk in US Commercial Banking in the Light of the Current Financial Crisis. CEPR Discussion Paper DP10890: 1–27. [Google Scholar]
- Windmeijer, Frank. 2005. A finite sample correction for the variance of linear efficient two-step GMM estimators. Journal of econometrics 126: 25–51. [Google Scholar] [CrossRef]
- Zhou, Chen. 2010. Are banks too big to fail? Measuring systemic importance of financial institutions. International Journal of Central Banking 6: 205–50. [Google Scholar] [CrossRef]
| 1. | The BCBS is an international committee constituted by central bank representatives from all around the world and other banking supervisory authorities. It has no legally-binding authority, but provides an international forum of discussion for guidelines and rules for banking supervision that local authorities may implement. |
| 2. | The Z-score index of banks in Luxembourg is calculated by the Central Bank of Luxembourg. Aggregated figures are published annually in the Financial Stability Review. |
| 3. | This dataset is confidential and cannot be distributed. Other available datasets provide a level of granularity far below the one required for a consistent estimate of both ratios. |
| 4. | See Chrystal and Mizen (2003). Goodhart’s law is intimately related to Lucas’ critique formulated later (see Lucas (1976)). |
| 5. | One can find measures based on theoretical models or, alternatively, indicator-based ones that result from aggregating bank-level variables related to the systemic relevance of banks. Some model-based measures are aimed at quantifying the contribution of individual institutions to systemic risk (e.g. Tarashev et al. 2009; Tarashev et al. 2010; Acharya et al. 2010; Adrian and Brunnermeier 2016; Brownlees and Engle 2016). Others focus on interconnectedness externalities (e.g., Segoviano and Goodhart 2009; Zhou 2010; Jin and Nadal De Simone 2014)). |
| 6. | Giordana 2016 shows that indicator-based measures of systemic importance that account for the balance sheet size of banks would increase the welfare gains of capital surcharges. |
| 7. | Other related proxies are Moody’s financial strength ratings (e.g., Demirgüç-Kunt et al. 2008); Merton-KMV model (e.g., Merton 1974; Anderson and Sundaresan 2000); default-mode models (e.g., Dietsch and Petey 2002); value-at-risk models (e.g., Duffie and Pan 1997). For a survey, see Crouhy et al. 2000; for a discussion, see Jackson and Perraudin (2000); for a comparison, see Gordy (2000). |
| 8. | There are no institutions in Luxembourg’s banking sector with stock market quotation. |
| 9. | “Market liquidity is low when it is difficult to raise money by selling the asset at reasonable prices. In other words, market liquidity is low when selling the asset depresses the sale price. When market liquidity is low, it is very costly to shrink a firm’s balance sheet” (Brunnermeier et al. 2009, p. 14). |
| 10. | “Funding liquidity describes the ease with which investors can obtain funding from financiers. Funding liquidity is high when it is easy to raise money” (Brunnermeier et al. 2009, p. 14). |
| 11. | Then, CAR is correlated with and earlier shocks, but is uncorrelated with and subsequent shocks. |
| 12. | This implies that ROA is correlated with and earlier shocks, but is uncorrelated with and future shocks. |
| 13. | As an indicator of credit risk, we also considered the ratio of provisions-to-loans. We did not not retain it in the final specification since the coefficient was not statistically significant. |
| 14. | |
| 15. | The dynamic-panel bias is introduced through correlation between the lagged dependent variable and the fixed effects (Nickell 1981). |
| 16. | The Z-score specification encompasses a proper AR(1) process if it is assumed that |
| 17. | We use the “nlsur” command in Stata 11. |
| 18. | A previous version of this study (Giordana and Schumacher 2012) makes use of the previous LCR definition (see BCBS 2010a). The LCR picture is quite different. |
| 19. | In order to improve the rendering of the estimation results table, ROA and CAR has been multiplied by 100 (in percentage points) when performing the estimation. |
| 20. | There is no clear prediction on the sign of the size-profit relationship. While size certainly accounts for economies or dis-economies of scale, it can be correlated with various financial, legal and political factors that may affect profitability. The empirical evidence is not clear either. For instance, Smirlock (1985) finds a positive and significant relationship while Berger et al. (1987), among others, suggest that increasing the size allows for little cost saving. In a more recent European cross-country study, Goddard et al. (2004) do not find convincing evidence for any consistent or systematic relationship between size and profitability. Likewise, Athanasoglou et al. (2008) show that the effect of bank size on profitability is not important. |
| 21. | Indeed, these costs could be direct and indirect, ranging from haircuts when selling the assets to potential reputation damage. |
| 22. | For a discussion, see Hamermesh and Pfann (1996). The complete simulation model is described in detail in Giordana and Schumacher (2013). |
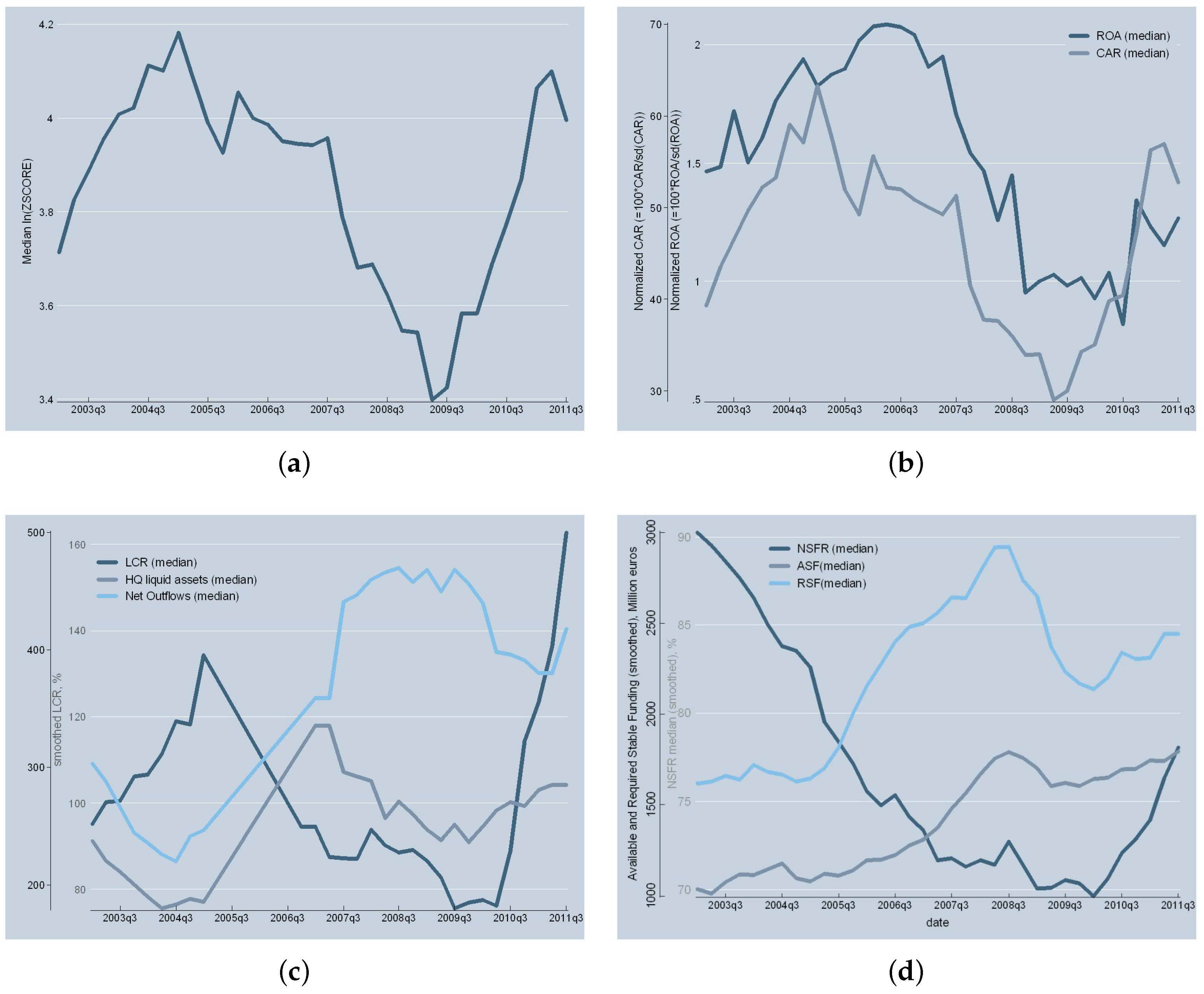
| Variable | Mean | Median | SD | Min | Max |
|---|---|---|---|---|---|
| Z-score * | 3.77417 | 3.83406 | 0.79909 | 1.24833 | 5.59206 |
| ROA ** | 1.85686 | 1.55647 | 1.64330 | −0.47547 | 12.35660 |
| CAR ** | 56.17572 | 44.58117 | 43.66162 | 3.05125 | 265.62676 |
| sd(ROA) | 0.13846 | 0.08951 | 0.16184 | 0.00908 | 2.26599 |
| TA *** | 11.340 | 5.876 | 14.049 | 0.231 | 91.185 |
| OBSR | 0.10523 | 0.04374 | 0.16833 | 0.00000 | 1.17131 |
| LCR | 203.92335 | 115.61707 | 223.44017 | 0.20291 | 998.25783 |
| NSFR | 97.44891 | 75.33648 | 75.59589 | 8.29574 | 513.70575 |
| HQLAR | 0.08339 | 0.04643 | 0.09303 | 0.00014 | 0.69192 |
| NOR | 0.07776 | 0.04650 | 0.10020 | 0.00104 | 0.67377 |
| ASFR | 0.29564 | 0.27947 | 0.15621 | 0.01187 | 0.78054 |
| RSFR | 0.38983 | 0.37706 | 0.19871 | 0.01550 | 0.86704 |
| EFF | 2.43740 | 2.40807 | 0.33262 | 1.60588 | 3.09685 |
| IR | 2.28481 | 2.11150 | 1.30486 | 0.42080 | 4.53940 |
| (1) | (2) | (3) | ||||
|---|---|---|---|---|---|---|
| OLS | FE | SYS-GMM | ||||
| ROA | 0.911 *** | (0.0580) | 0.836 *** | (0.0501) | 0.902 *** | (0.0764) |
| CAR | −0.00313 *** | (0.000720) | −0.00261 ** | (0.00108) | −0.00389 * | (0.00232) |
| ln(LAR) | 0.0270 * | (0.0155) | −0.000621 | (0.0180) | 0.00790 | (0.0202) |
| ln(NOR) | 0.00333 | (0.0160) | −0.0385 | (0.0421) | 0.163 * | (0.0924) |
| ln(ASF) | 0.0958 *** | (0.0307) | 0.0386 | (0.0520) | 0.201 * | (0.107) |
| ln(RSF) | −0.0954 * | (0.0501) | 0.0344 | (0.0650) | −0.108 | (0.106) |
| Size | −0.0123 | (0.0157) | 0.0134 | (0.0628) | 0.437 *** | (0.161) |
| OBSR | −0.0181 | (0.0480) | −0.0503 | (0.0420) | −0.0129 | (0.100) |
| EFF | 0.0774 | (0.0555) | 0.110 * | (0.0611) | 0.177 *** | (0.0427) |
| IR | 0.0708 * | (0.0420) | 0.0947 ** | (0.0433) | 0.137 *** | (0.0474) |
| Cl | −0.175 *** | (0.0515) | −0.187 *** | (0.0542) | −0.299 *** | (0.0700) |
| C | 0.0580 | (0.0676) | 0.0346 | (0.0866) | −0.193 ** | (0.0891) |
| Obs. | 1421 | 1421 | 1421 | |||
| Hansen test, p.v. | 0.991 | |||||
| AR(1) p.v. | 0.000 | |||||
| AR(2) p.v. | 0.301 | |||||
| Groups (Instr.) Nr. | 55 | 55(38) | ||||
| Wald, p.v. | 0.000 | |||||
| (4) | (5) | (6) | ||||
|---|---|---|---|---|---|---|
| OLS | FE | SYS-GMM | ||||
| CAR | 0.660 *** | (0.0592) | 0.456 *** | (0.0697) | 0.647 *** | (0.121) |
| ROA | 6.263 *** | (0.976) | 12.27 *** | (1.994) | 6.161 * | (3.678) |
| ln(LAR) | 1.403 *** | (0.413) | 1.595 ** | (0.715) | 1.013 | (0.646) |
| ln(NOR) | −1.394 ** | (0.625) | 0.0864 | (1.541) | 1.930 | (1.593) |
| ln(ASF) | 2.963 *** | (1.019) | 1.785 | (2.610) | 8.334 *** | (2.878) |
| ln(RSF) | 0.0857 | (1.006) | −0.227 | (2.305) | −0.421 | (2.386) |
| Size | −0.742 | (0.494) | −5.023 | (3.233) | 5.989 | (3.915) |
| EFF | −3.829 ** | (1.607) | −4.339 *** | (1.401) | −11.11 * | (5.727) |
| IR | 1.956 | (1.205) | 1.307 | (1.167) | 1.241 | (1.296) |
| Cl | −2.682 ** | (1.211) | −3.467 * | (1.750) | −3.339 * | (1.814) |
| Cs | 7.362 *** | (2.284) | 8.793 *** | (3.289) | 6.828 ** | (2.843) |
| Obs. | 1421 | 1421 | 1421 | |||
| Hansen test, p.v. | 0.350 | |||||
| AR(1) p.v. | 0.001 | |||||
| AR(2) p.v. | 0.544 | |||||
| Groups (Instr.) Nr. | 55 | 55(49) | ||||
| Wald, p.v. | 0.000 | |||||
| (7) | (8) | (9) | ||||
|---|---|---|---|---|---|---|
| OLS | FE | SYS-GMM | ||||
| ROA | 1.022 | (1.431) | 2.384 | (2.185) | 2.236 * | (1.344) |
| CAR | 0.759 *** | (0.0723) | 0.642 *** | (0.114) | 0.704 *** | (0.0773) |
| ln(HQLAR) | 1.564 *** | (0.489) | 1.047 ** | (0.408) | 1.090 *** | (0.392) |
| ln(NOR) | −0.304 | (0.642) | −1.269 | (1.313) | 2.193 | (1.402) |
| ln(ASFR) | 4.088 *** | (1.221) | 0.455 | (2.082) | 8.384 ** | (3.322) |
| ln(RSFR) | −2.723 ** | (1.270) | 1.447 | (2.138) | −3.015 | (1.882) |
| Size | −0.291 | (0.521) | −3.012 | (2.464) | 3.928 | (2.566) |
| OBSR | −0.534 | (1.426) | −2.346 | (1.979) | −1.807 | (1.209) |
| EFF | −2.059 | (1.940) | −1.258 | (1.998) | −1.966 | (4.608) |
| IR | 2.932 ** | (1.432) | 3.454 ** | (1.545) | 6.714 ** | (3.371) |
| C | −4.560 *** | (1.428) | −5.451 *** | (1.824) | −5.500 ** | (2.681) |
| C | 4.992 * | (2.742) | 5.913 * | (3.287) | 2.355 | (3.672) |
| Obs. | 1421 | 1421 | 1421 | |||
| Hansen test, p.v. | 0.741 | |||||
| AR(1) p.v. | 0.000 | |||||
| AR(2) p.v. | 0.938 | |||||
| Groups (Instr.) Nr. | 55 | 55(58) | ||||
| Wald, p.v. | 0.000 | |||||
| ROA | CAR | Z-score | |||||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | |
| ROA | 1.366 | (0.632) | |||||
| ROA | 0.811 | (0.02) | 2.177 *** | (0.647) | |||
| CAR | −0.002 *** | (0.001) | 0.664 *** | (0.019) | 0.659 *** | (0.021) | |
| ln(HQLAR) | 0.007 | (0.018) | 0.959 * | (0.54) | 0.977 * | (0.577) | |
| ln(NOR) | −0.038 | (0.03) | −1.786 ** | (0.905) | −1.889 ** | (0.964) | |
| ln(ASFR) | 0.016 | (0.061) | 0.436 | (1.832) | 0.478 | (1.957) | |
| ln(RSFR) | 0.035 | (0.053) | 1.039 | (1.587) | 1.134 | (1.693) | |
| Size | 0.02 | (0.049) | −3.85 *** | (1.46) | −3.797 ** | (1.556) | |
| OBSR | 0.014 | (0.031) | 0.036 | (0.082) | |||
| EFF | 0.113 *** | (0.037) | 0.000 | (0.014) | 0.303 ** | (0.134) | |
| IR | 0.118 *** | (0.04) | 3.998 *** | (1.192) | 4.315 *** | (1.269) | |
| C | −0.118 *** | (0.039) | −3.249 *** | (1.157) | −3.566 *** | (1.234) | |
| Cons | −0.18 * | (0.096) | 0.749 | (0.878) | 0.267 | (1.007) | |
| Obs. | 1420 | 1420 | 1420 | ||||
| R.sq | 0.7135 | 0.6723 | 0.6731 | ||||
| Variable | ROA | CAR | Z-score | |||
|---|---|---|---|---|---|---|
| z | P | z | P | z | P | |
| ROA | 30.033 | 0.000 | ||||
| ROA | 25.593 | 0.000 | 1.701 | 0.089 | ||
| CAR | 1.056 | 0.291 | 0.1 | 0.92 | 22.028 | 0.000 |
| ln(LAR) | 0.702 | 0.483 | 3.54 | 0.000 | 1.09 | 0.276 |
| ln(NOR) | 3.132 | 0.002 | 0.974 | 0.33 | 3.524 | 0.000 |
| ln(ASFR) | 2.235 | 0.025 | 2.241 | 0.025 | 2.28 | 0.023 |
| ln(RSFR) | 3.787 | 0.000 | 2.461 | 0.014 | 2.272 | 0.023 |
| Size | 2.676 | 0.007 | 1.52 | 0.129 | 3.97 | 0.000 |
| OBSR | 3.738 | 0.000 | 1.939 | 0.053 | ||
| EFF | 0.874 | 0.382 | 5.295 | 0.000 | 2.694 | 0.007 |
| IR | 0.177 | 0.860 | 3.765 | 0.000 | 1.41 | 0.159 |
| Variable | Mean | Median | SD | Min | Max |
|---|---|---|---|---|---|
| Z-score | 3.708 | 3.810 | 0.855 | 1.735 | 8.522 |
| ROA * | 1.417 | 1.641 | 2.778 | −5.945 | 6.775 |
| CAR * | 72.526 | 53.837 | 67.989 | 4.029 | 726.556 |
| TA ** | 13.527 | 8.686 | 14.729 | 0.284 | 94.160 |
| OBS | 0.001 | 0.000 | 0.003 | 0.000 | 0.024 |
| LCR | 219.275 | 100.000 | 403.724 | 7.011 | 5656.088 |
| NSFR | 2360.512 | 251.332 | 8.27 | 100.000 | 3.03 |
| HQLAR | 0.084 | 0.051 | 0.098 | 0.001 | 0.731 |
| NOR | 0.058 | 0.030 | 0.074 | 0.001 | 0.545 |
| ASFR | 0.233 | 0.226 | 0.128 | 0.011 | 0.669 |
| RSFR | 0.338 | 0.331 | 0.175 | 0.010 | 0.770 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giordana, G.A.; Schumacher, I. An Empirical Study on the Impact of Basel III Standards on Banks’ Default Risk: The Case of Luxembourg. J. Risk Financial Manag. 2017, 10, 8. https://doi.org/10.3390/jrfm10020008
Giordana GA, Schumacher I. An Empirical Study on the Impact of Basel III Standards on Banks’ Default Risk: The Case of Luxembourg. Journal of Risk and Financial Management. 2017; 10(2):8. https://doi.org/10.3390/jrfm10020008
Chicago/Turabian StyleGiordana, Gastón Andrés, and Ingmar Schumacher. 2017. "An Empirical Study on the Impact of Basel III Standards on Banks’ Default Risk: The Case of Luxembourg" Journal of Risk and Financial Management 10, no. 2: 8. https://doi.org/10.3390/jrfm10020008
APA StyleGiordana, G. A., & Schumacher, I. (2017). An Empirical Study on the Impact of Basel III Standards on Banks’ Default Risk: The Case of Luxembourg. Journal of Risk and Financial Management, 10(2), 8. https://doi.org/10.3390/jrfm10020008





