Reconstruction Optimization Algorithm of 3D Temperature Distribution Based on Tucker Decomposition
Abstract
1. Introduction
2. Fundamental Measurement Principles
2.1. Tucker Decomposition Reconstruction Algorithm
2.2. Missing Datasets Reconstruction Algorithm
- A prior dataset with temperature loss is obtained, where represents a three-dimensional temperature distribution with missing data at different locations under various operating conditions;
- Average the temperature of in the 1-mode direction, and use the average to complete the missing temperature data in the 1-mode direction vector;
- The dataset after completion is denoted as , and the core tensor and the corresponding reconstruction coefficient tensor along the 1-mode direction are calculated by Tucker decomposition. The and the original actual measurement data are substituted into the reconstruction algorithm to calculate the coefficient 1-mode decomposition factor vector . The temperature field in the missing dataset is reconstructed by using and to complete the missing data in with the calculated results;
- The dataset completed by step 3 is denoted as , and the tucker algorithm is used to calculate the core tensor and the corresponding reconstruction coefficient tensor expanded along the 1-mode direction. If , the iterative convergence is determined. If it does not converge, continue to put and the actual measurement data before the completion into the reconstruction algorithm to calculate the coefficient 1-modulus decomposition factor vector , and use and to reconstruct the temperature field distribution in the missing dataset. The missing data in are completed by the calculated values, and the completed dataset is recorded as ;
- Repeat calculation in step 4 until the convergence conditions are met;
- Taking the mth iteration dataset , which satisfies the convergence condition as the final complement prior dataset, the three-dimensional temperature field is reconstructed by .
2.3. Reconstruction Result Error
3. Verification and Analysis Based on Numerical Simulation
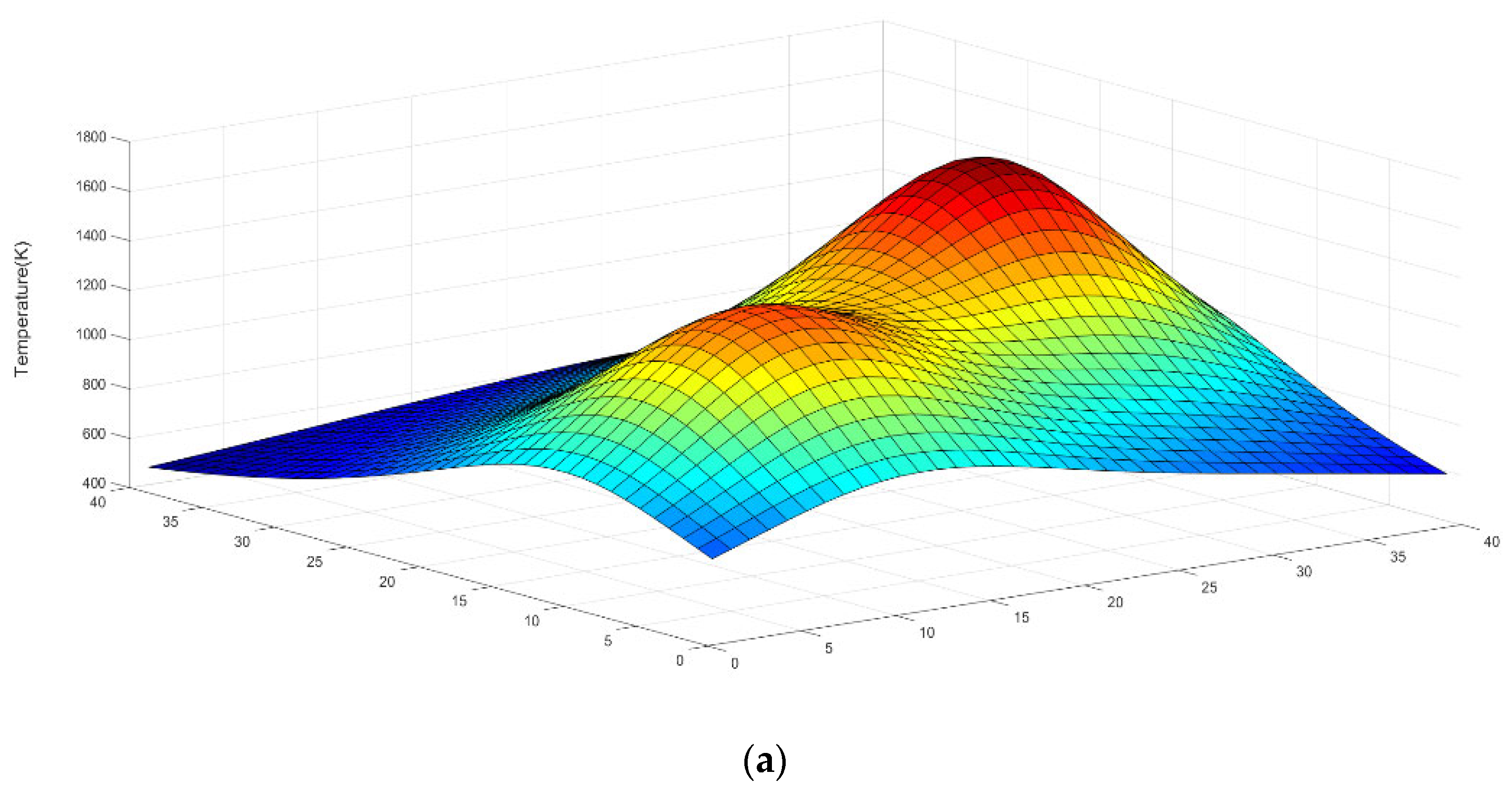
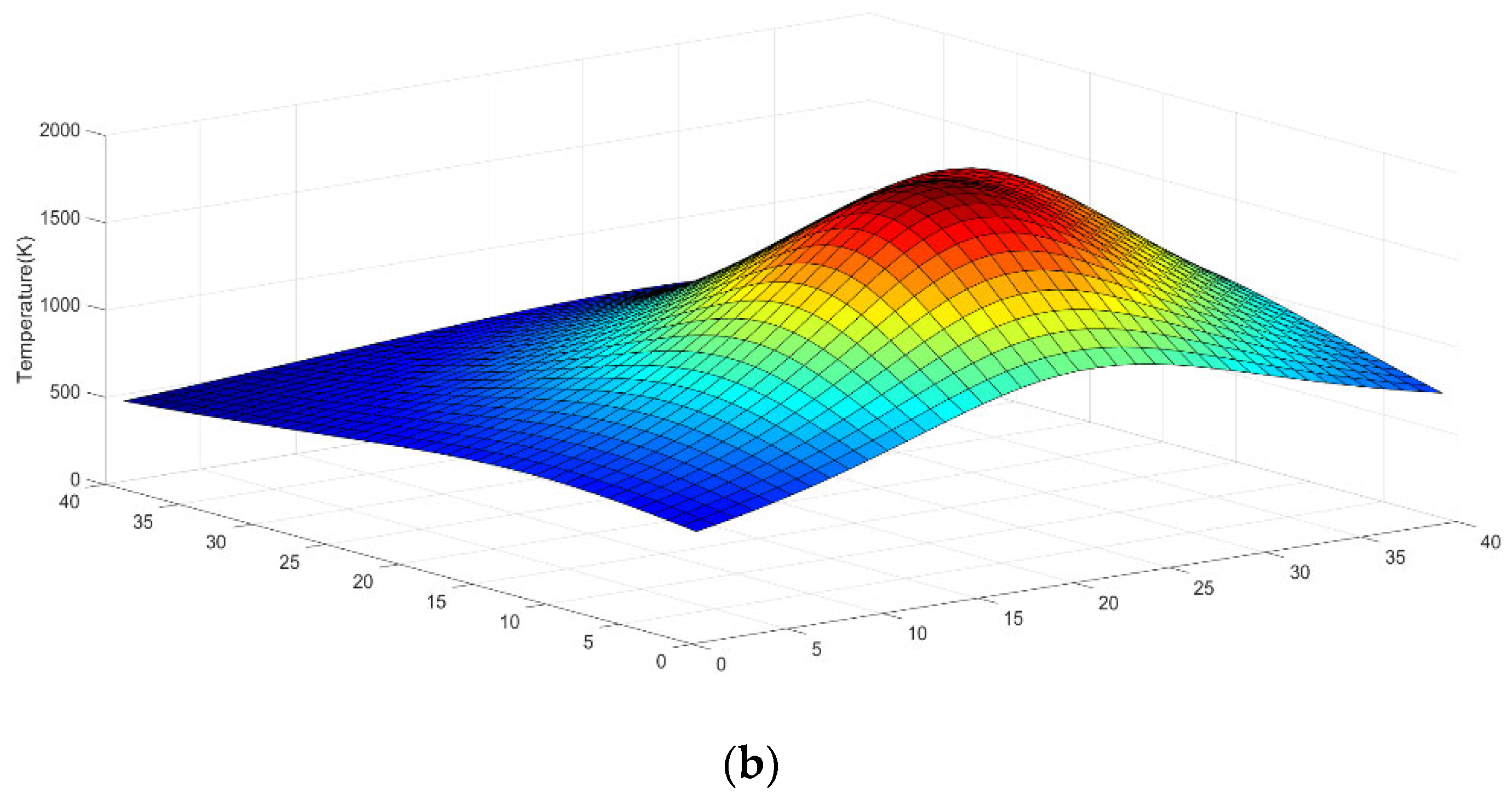
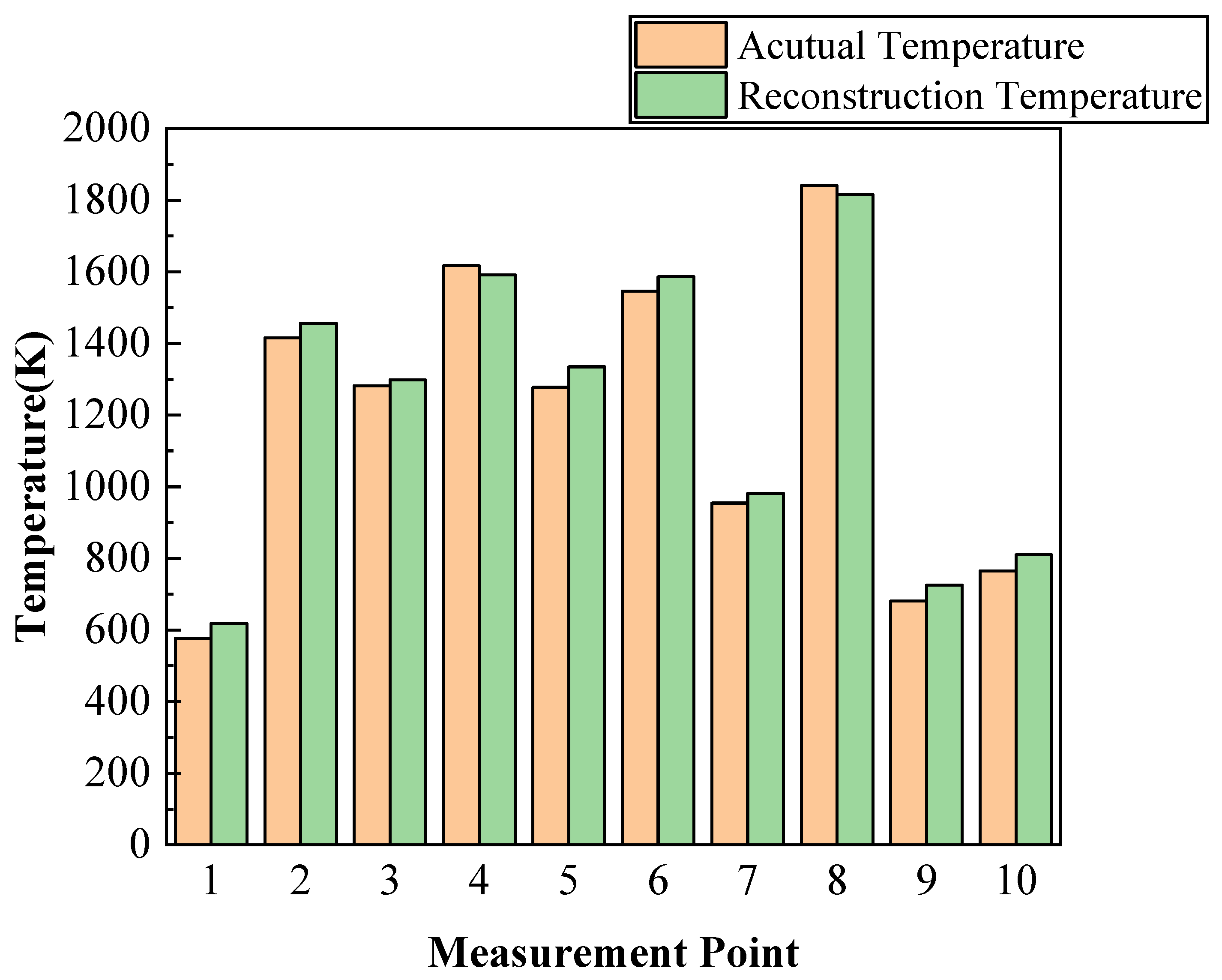
3.1. Temperature Distribution Reconstruction and Simulation Condition Setting
3.2. Data Analysis and Discussion
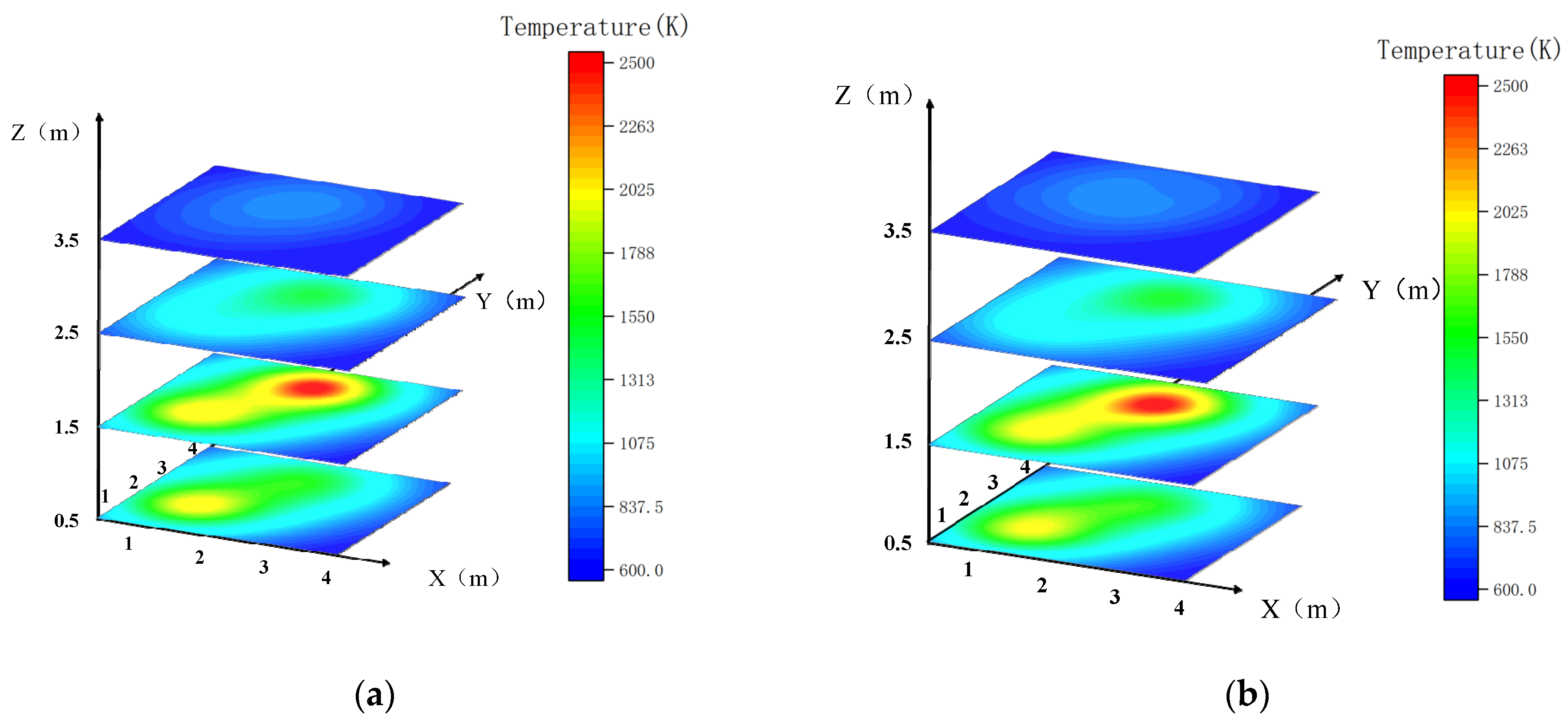
3.3. Temperature Distribution Reconstruction with Data Missing
4. Reconstruction Parameters Optimization of Tucker Decomposition
4.1. Influence of Core Tensor Dimension
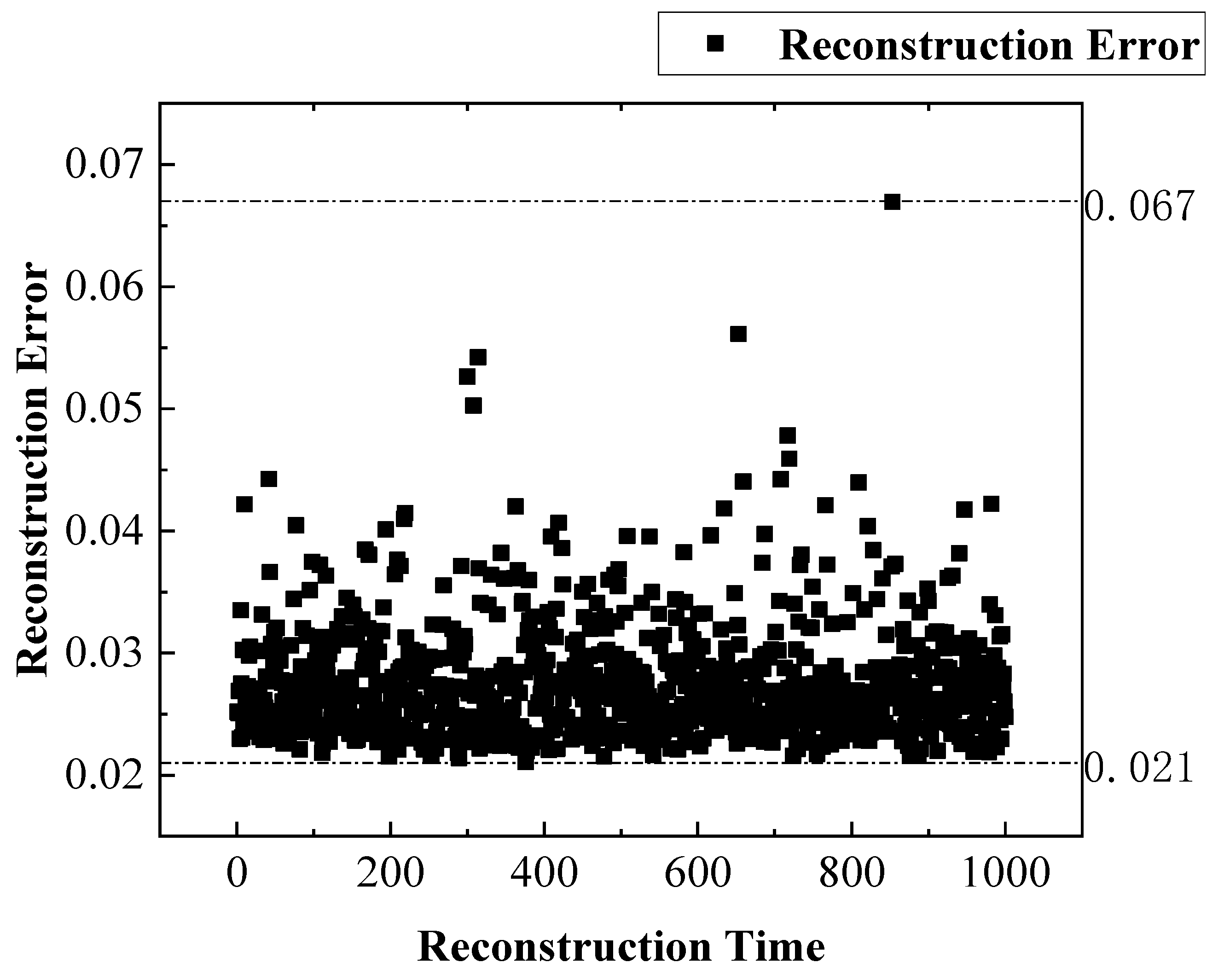
4.2. Effect of Measuring Point Number
- Using different numbers of measuring points (10–25), the measuring points are randomly selected to construct a measurement matrix, and the temperature measured is extracted from the test condition data;
- The feature vector is obtained by the Tucker decomposition of the empirical dataset. The optimized core tensor and temperature measurement are used to reconstruct the temperature distribution, and the reconstruction error is calculated;
- Repeat the first two steps 1000 times to obtain a general conclusion.
4.3. Effect of Measuring Point Arrangement on Reconstruction Accuracy
- All positions are traversed to calculate the number of conditions, and find the location with the smallest number of conditions as the first optimized measurement point;
- Retain the first optimized measurement point, traverse the remaining position, calculate the corresponding condition number together with the first optimized measurement position, and take the position with the smallest condition number as the second optimized measurement position;
- Repeat step 2 until all measuring points are optimized.
- The initial optimization condition number obtained by the greedy algorithm is set as the judgment basis, and the corresponding measuring point arrangement is taken as the starting position;
- Generate a new arrangement in a random step length near the preliminary optimized position of measuring points;
- Calculate the condition number corresponding to the new measuring point arrangement. If the condition number is less than the judgment basis, the condition number is used as a new judgment basis, the corresponding measuring point position is updated to a new starting position, and the calculation in Step (2) is repeated. If the condition number is greater than the criterion, repeat Step (2) directly;
- Set the optimization calculation step; if in the calculation step and the judgment basis has remained unchanged, that is, the judgment basis for local optimum, stop the optimization calculation.
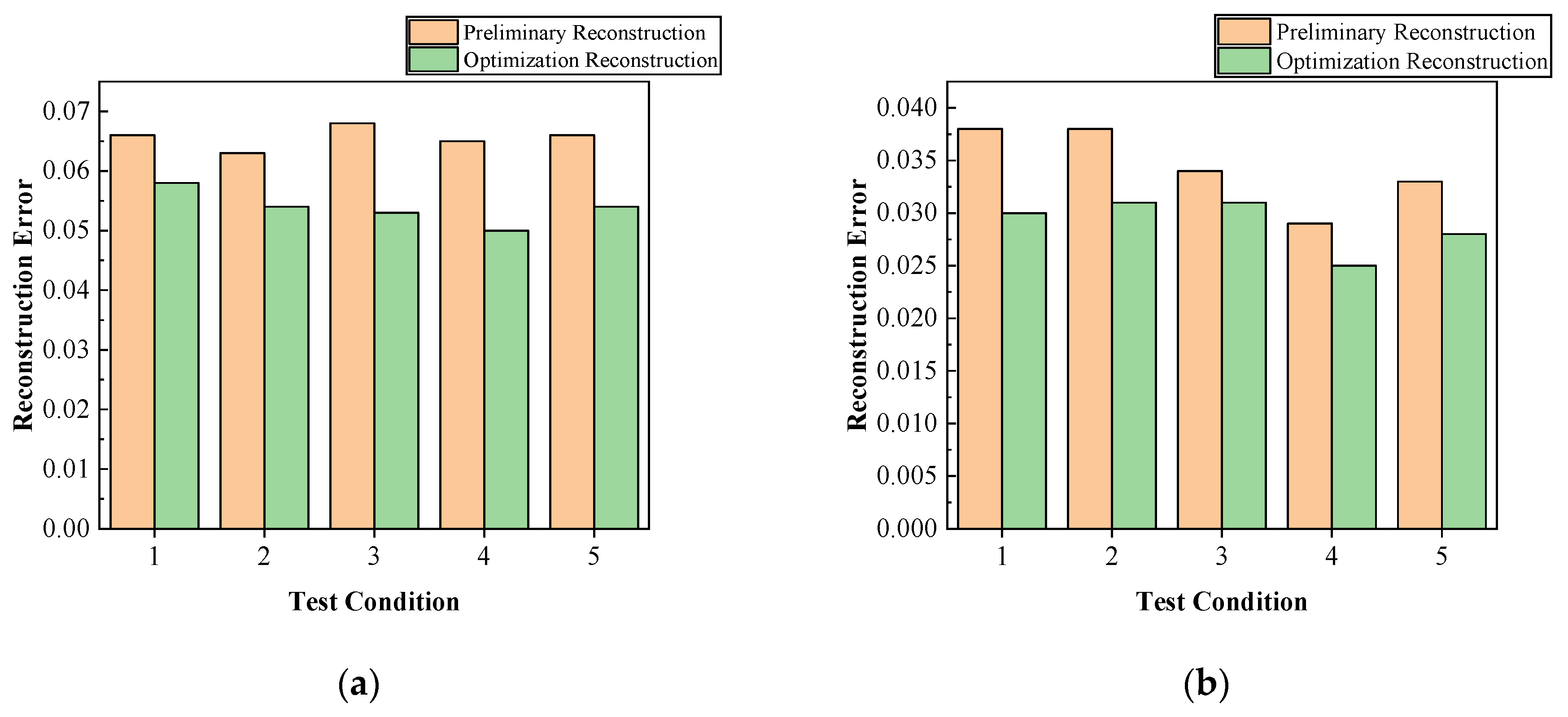
5. Optimization Effect Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yang, W.; Xue, B.; Wang, C. Image Super Resolution Reconstruction Based MCA and PCA Dimension Reduction. Adv. Mol. Imaging 2018, 8, 82144. [Google Scholar] [CrossRef]
- Tucker, L.R. Implications of factor analysis of three-way matrices for measurement of change. Probl. Meas. Chang. 1963, 15, 122–137. [Google Scholar]
- Maldonado-Chan, M.; Mendez-Vazquez, A.; Guardado-Medina, R.O. Multimodal tucker decomposition for gated rbm inference. Appl. Sci. 2021, 11, 7397. [Google Scholar] [CrossRef]
- Li, R.; Pan, Z.; Wang, Y.; Wang, P. The correlation-based tucker decomposition for hyperspectral image compression. Neurocomputing 2021, 419, 357–370. [Google Scholar] [CrossRef]
- Marmoret, A.; Cohen, J.E.; Bertin, N.; Bimbot, F. Uncovering audio patterns in music with Nonnegative Tucker Decomposition for structural segmentation. arXiv 2021, arXiv:2104.08580. [Google Scholar]
- Karami, A.; Yazdi, M.; Asli, A.Z. Noise Reduction of Hyperspectral Images Using Kernel Non-Negative Tucker Decomposition. IEEE J. Sel. Top. Signal Process. 2011, 5, 487–493. [Google Scholar] [CrossRef]
- Zhang, J.; Han, Y.; Jiang, J. Tucker decomposition-based tensor learning for human action recognition. Multimedia Syst. 2015, 22, 343–353. [Google Scholar] [CrossRef]
- Zhao, M.; Li, W.; Li, L.; Ma, P.; Cai, Z.; Tao, R. Three-Order Tensor Creation and Tucker Decomposition for Infrared Small-Target Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5900511. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, S.; Chen, M.; Zhang, Y.; Yao, P. Application of Tucker Decomposition in Temperature Distribution Reconstruction. Appl. Sci. 2022, 12, 2749. [Google Scholar] [CrossRef]
- Qin, L.; Liu, S.; Kang, Y.; Yan, S.A.; Schlaberg, H.I.; Wang, Z. Wind velocity distribution reconstruction using CFD database with Tucker decomposition and sensor measurement. Energy 2018, 167, 1236–1250. [Google Scholar] [CrossRef]
- Hou, Z.; Li, W.; Tao, R.; Du, Q. Three-Order Tucker Decomposition and Reconstruction Detector for Unsupervised Hyperspectral Change Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6194–6205. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Plemmons, R.J. Tensor methods for hyperspectral data analysis: A space object material identification study. J. Opt. Soc. Am. A 2008, 25, 3001–3012. [Google Scholar] [CrossRef] [PubMed]
- Everson, R.; Sirovich, L. Karhunen-Loeve procedure for gappy data. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1995, 12, 1657–1664. [Google Scholar] [CrossRef]
- Zhang, X. Matrix Analysis and Application; Tsinghua University Press: Beijing, China, 2013; pp. 453–471. [Google Scholar]
- Polansky, J.; Wang, M. Proper Orthogonal Decomposition as a technique for identifying two-phase flow pattern based on electrical impedance tomography. Flow Meas. Instrum. 2017, 53, 126–132. [Google Scholar] [CrossRef]
- Tsamardinos, I.; Brown, L.E.; Aliferis, C.F. The max-min hill-climbing Bayesian network structure learning algorithm. Mach. Learn. 2006, 65, 31–78. [Google Scholar] [CrossRef]

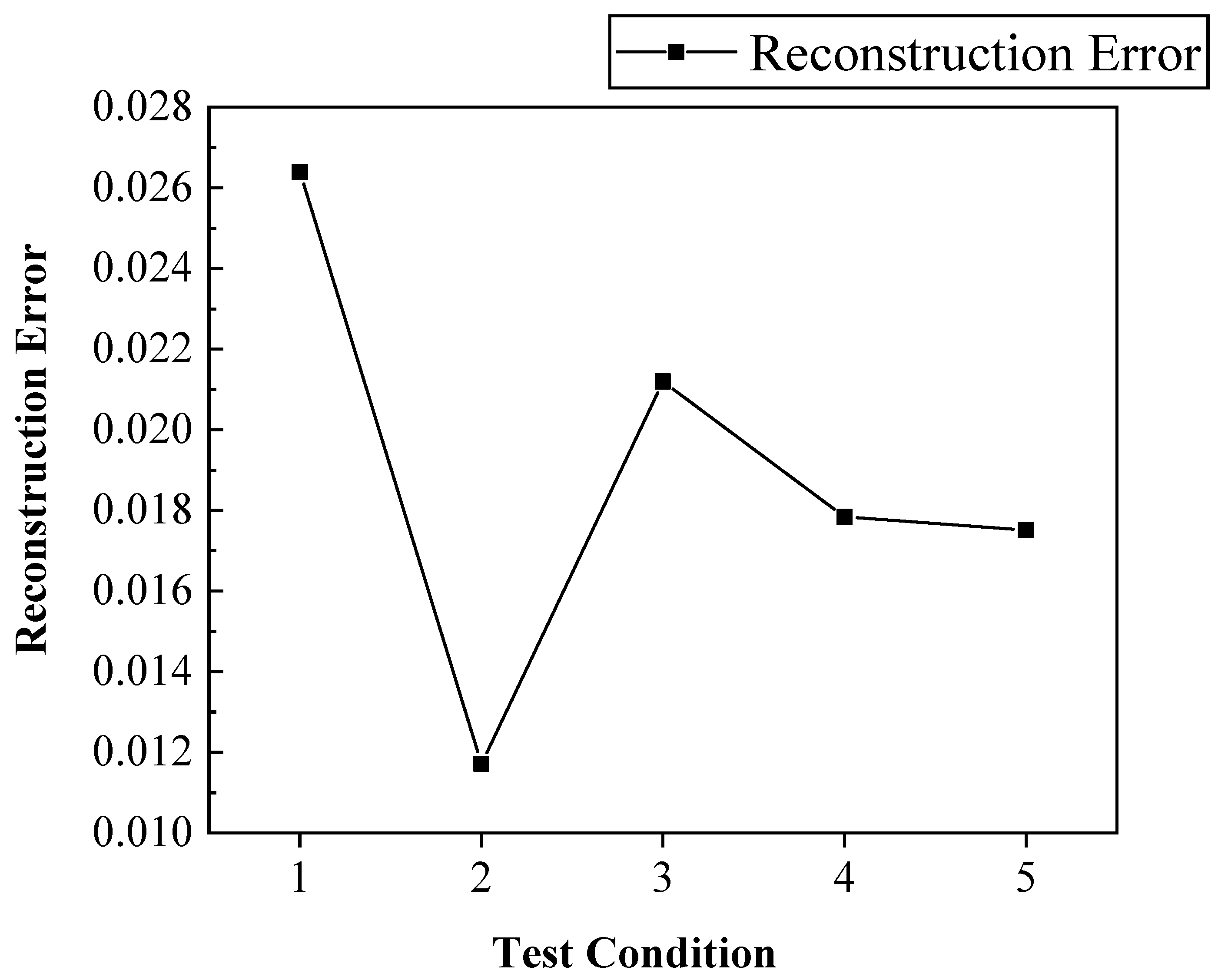
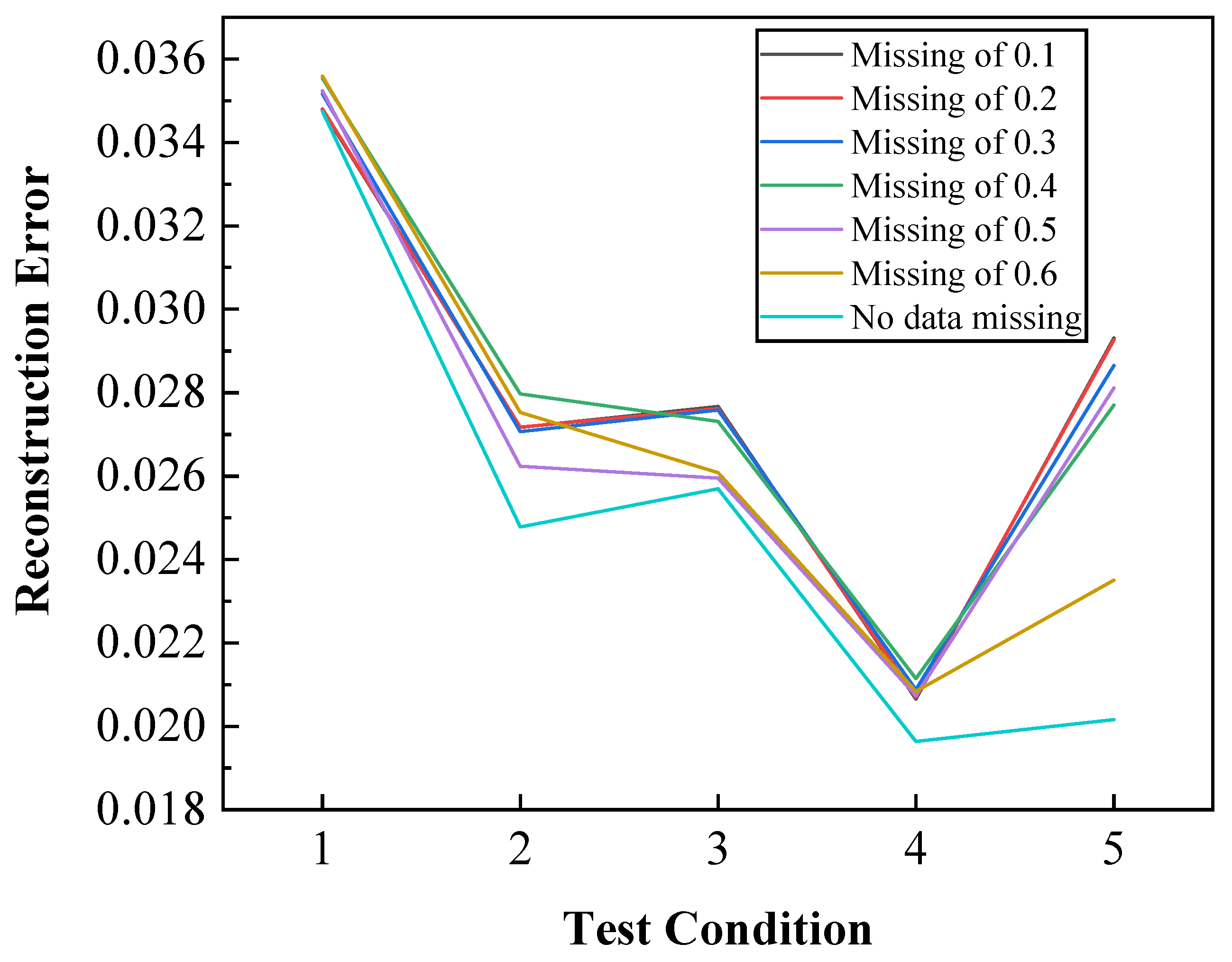

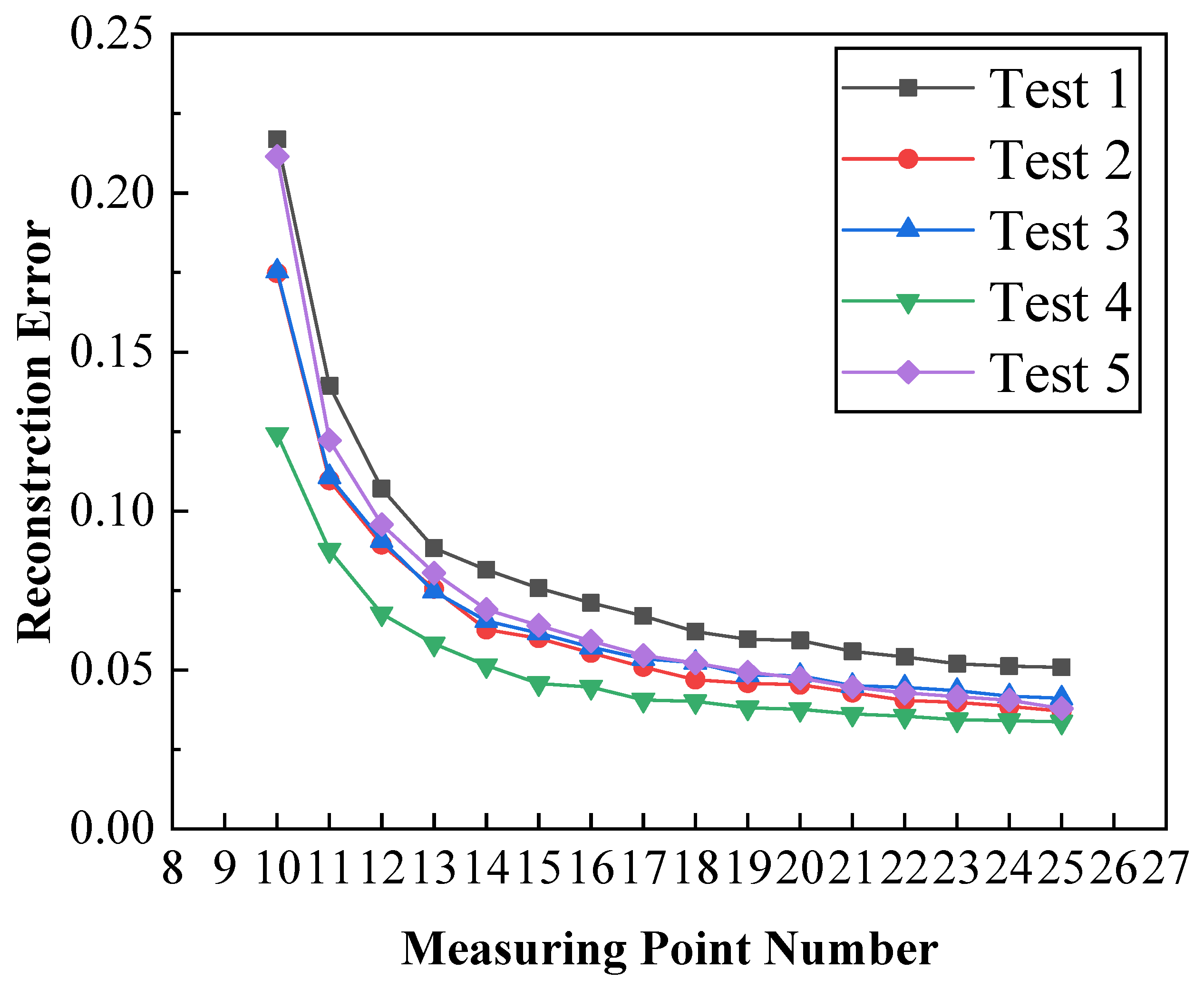
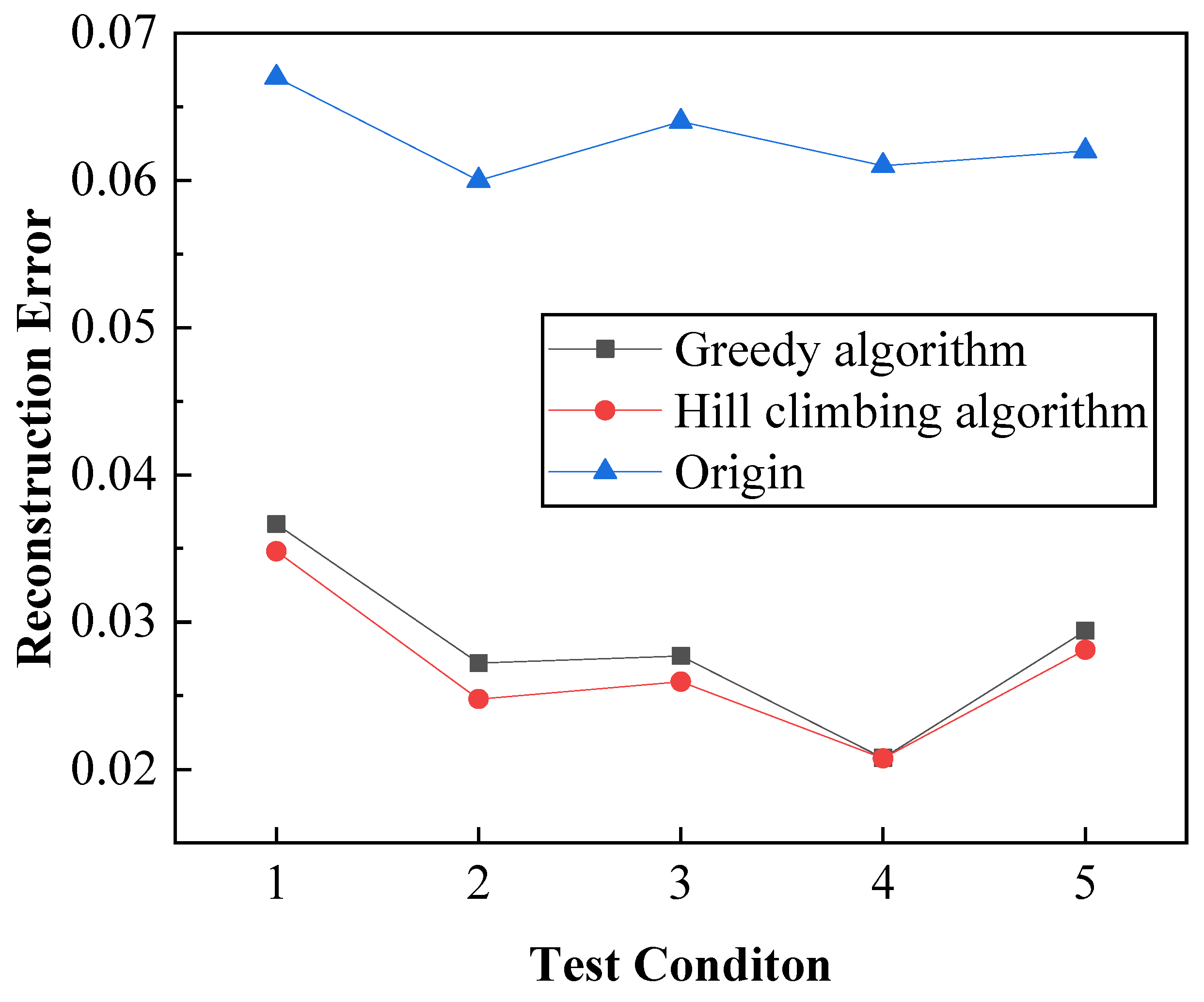

| Working Condition | Boundary Condition (a) | Boundary Condition (b) | Boundary Condition (c) | Boundary Condition (d) |
|---|---|---|---|---|
| Test Condition 1 | 821 | 1159 | 0.6 | 1.5 |
| Test Condition 2 | 1394 | 1569 | 1.1 | 2.2 |
| Test Condition 3 | 1521 | 17.7 | 2.5 | 3.6 |
| Test Condition 4 | 1777 | 1353 | 3.5 | 2.8 |
| Test Condition 5 | 1827 | 1973 | 1.2 | 3.1 |
| Arrangement | Reconstruction Error(%) |
|---|---|
| 1 | 3.1 |
| 2 | 11.7 |
| 3 | 6.78 |
| 4 | 9.2 |
| 5 | 18.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Liu, S.; Zhang, Y.; Yao, P. Reconstruction Optimization Algorithm of 3D Temperature Distribution Based on Tucker Decomposition. Appl. Sci. 2022, 12, 10814. https://doi.org/10.3390/app122110814
Liu Z, Liu S, Zhang Y, Yao P. Reconstruction Optimization Algorithm of 3D Temperature Distribution Based on Tucker Decomposition. Applied Sciences. 2022; 12(21):10814. https://doi.org/10.3390/app122110814
Chicago/Turabian StyleLiu, Zhaoyu, Shi Liu, Yaofang Zhang, and Pengbo Yao. 2022. "Reconstruction Optimization Algorithm of 3D Temperature Distribution Based on Tucker Decomposition" Applied Sciences 12, no. 21: 10814. https://doi.org/10.3390/app122110814
APA StyleLiu, Z., Liu, S., Zhang, Y., & Yao, P. (2022). Reconstruction Optimization Algorithm of 3D Temperature Distribution Based on Tucker Decomposition. Applied Sciences, 12(21), 10814. https://doi.org/10.3390/app122110814





