Explicit Solutions of MHD Flow and Heat Transfer of Casson Fluid over an Exponentially Shrinking Sheet with Suction
Abstract
:1. Introduction
2. Mathematical Model
3. Explicit Solutions
3.1. and
3.2. and
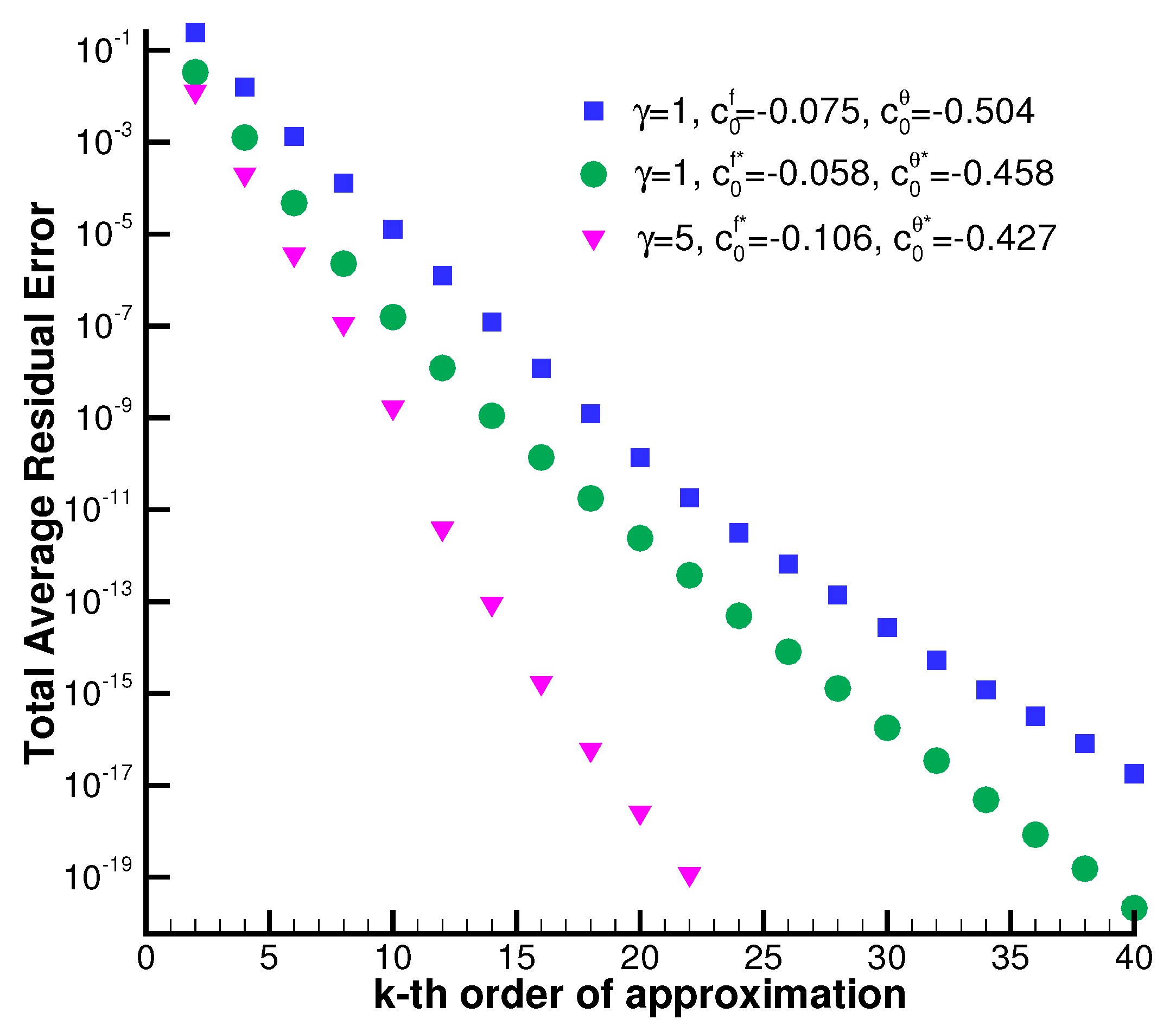
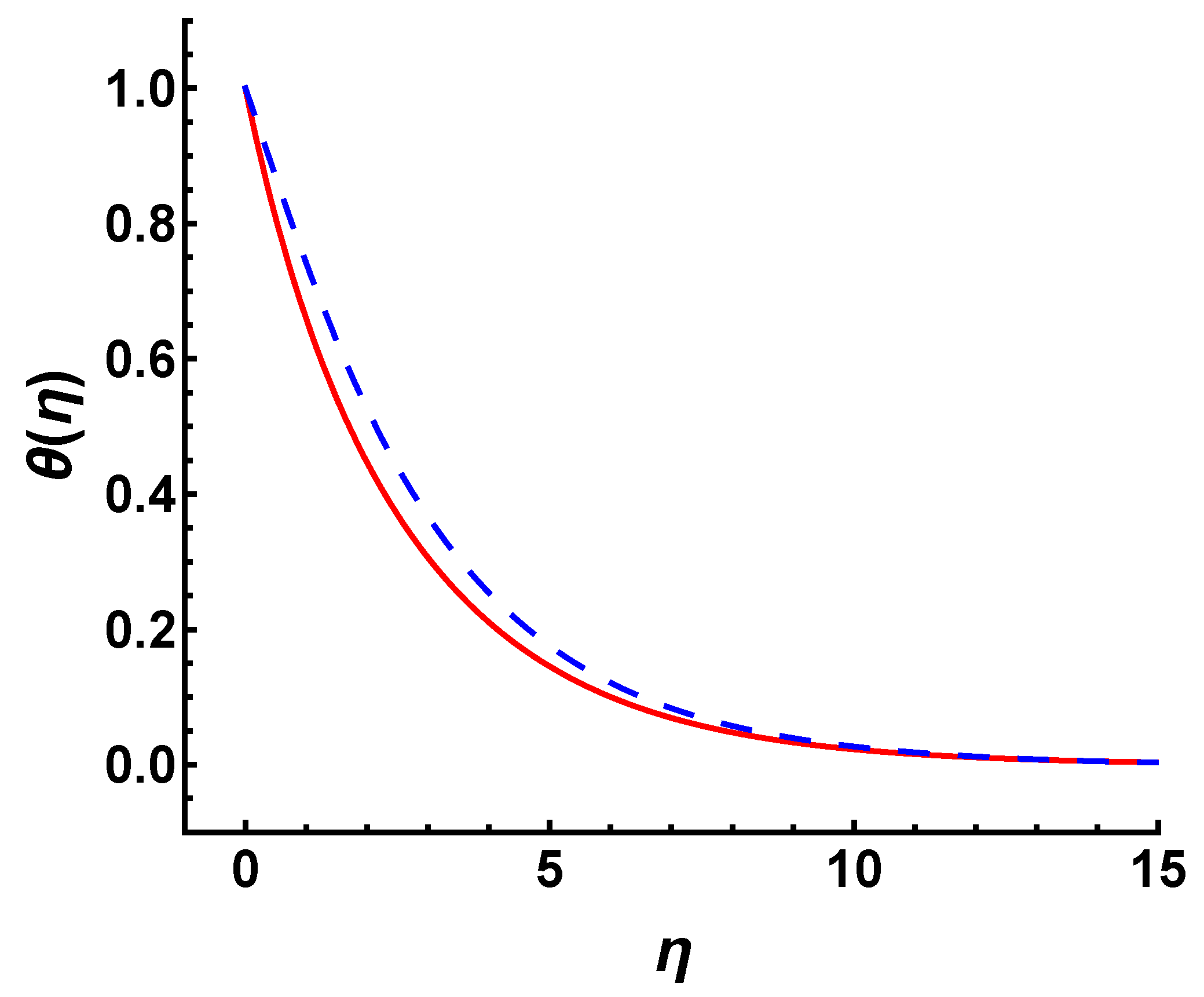
4. Convergence Test
5. Discussions
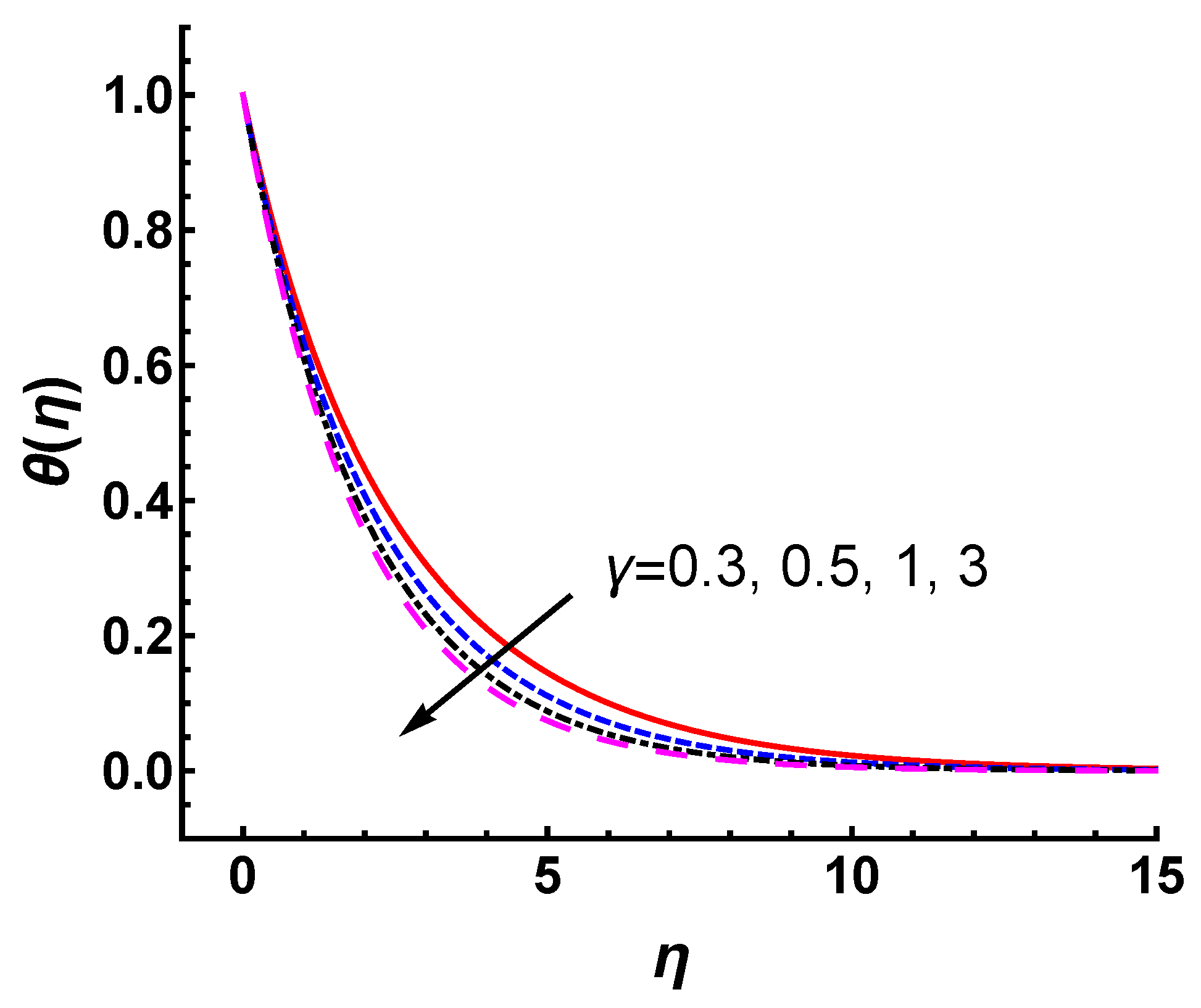
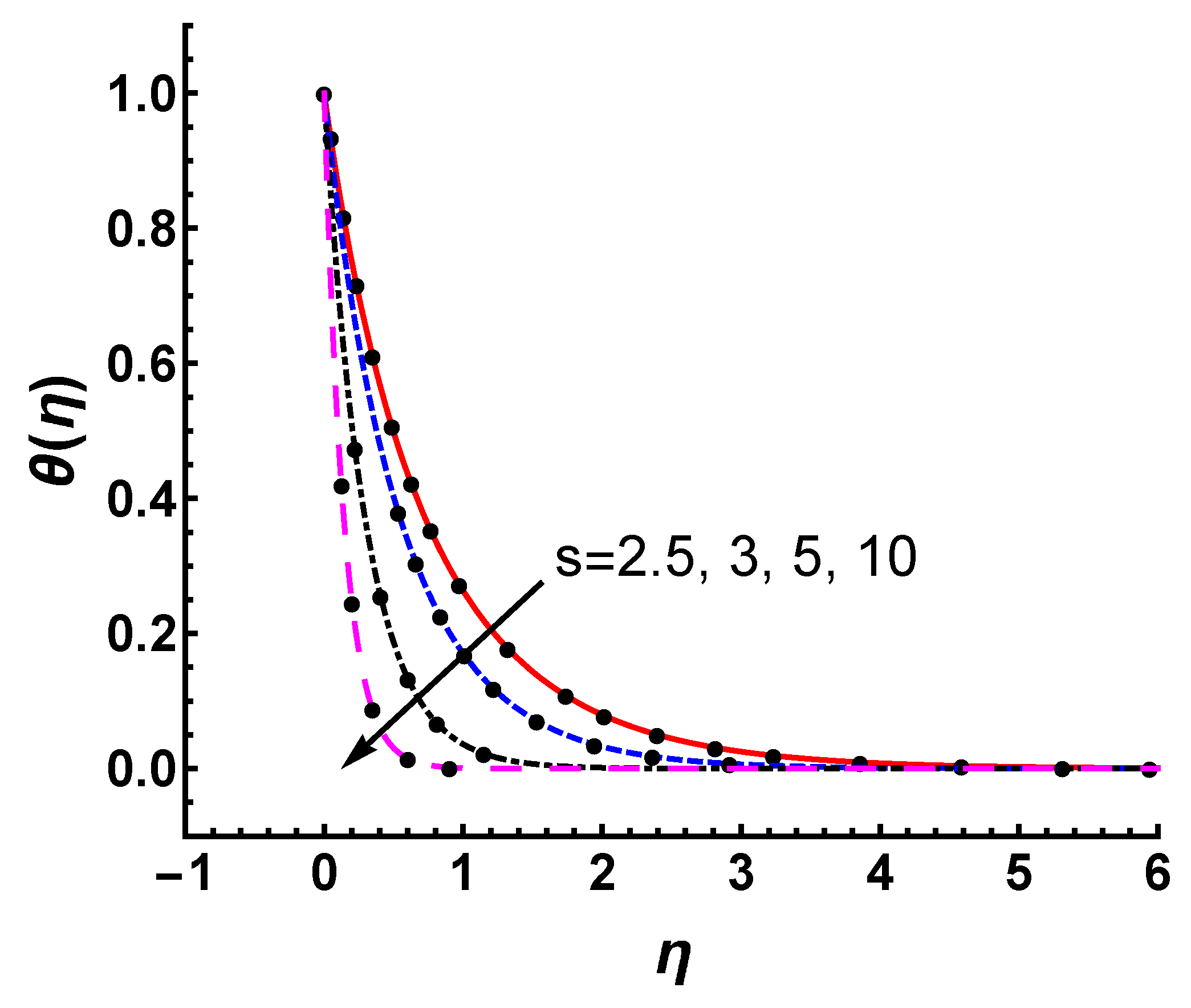
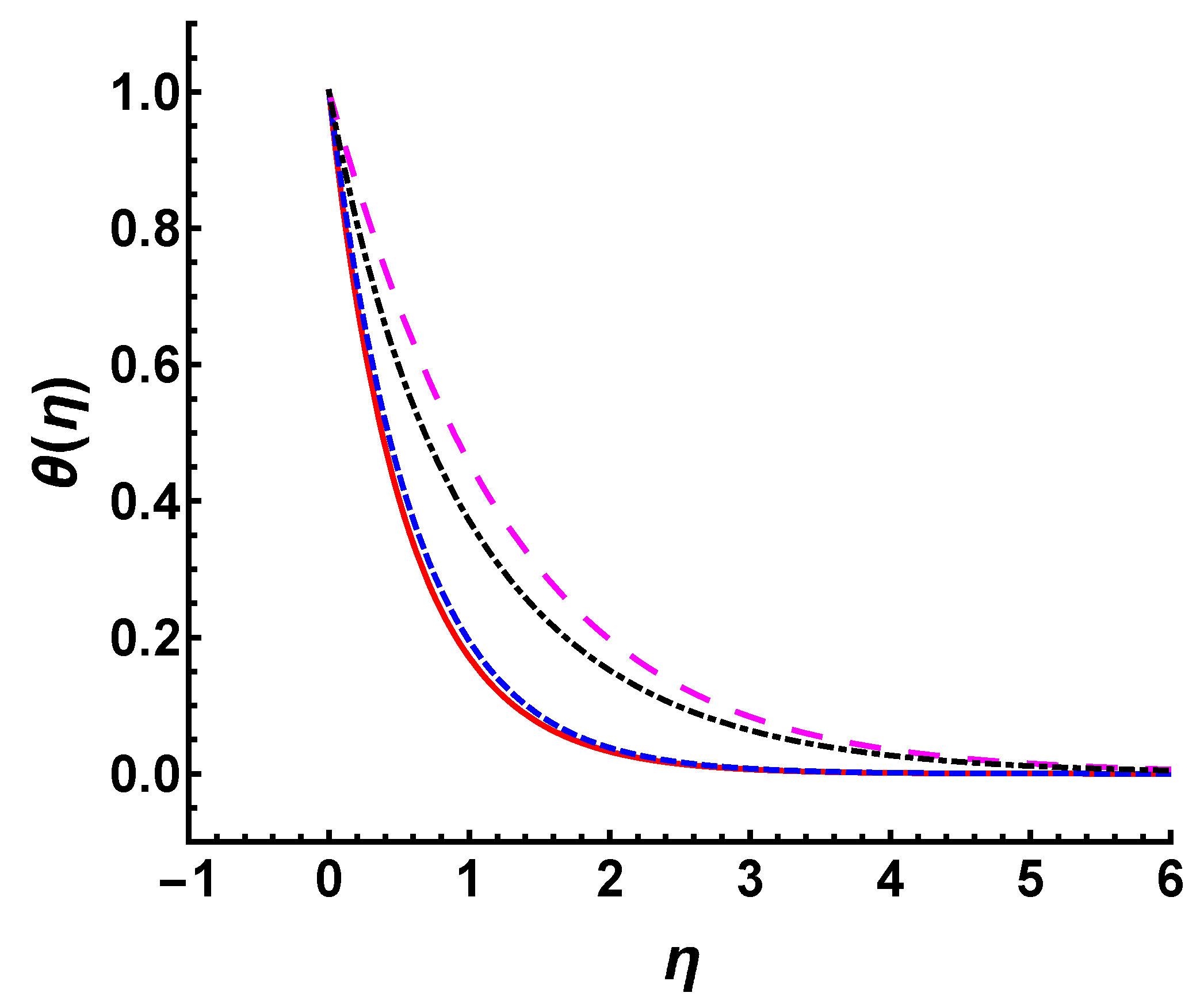
5.1. Effect of
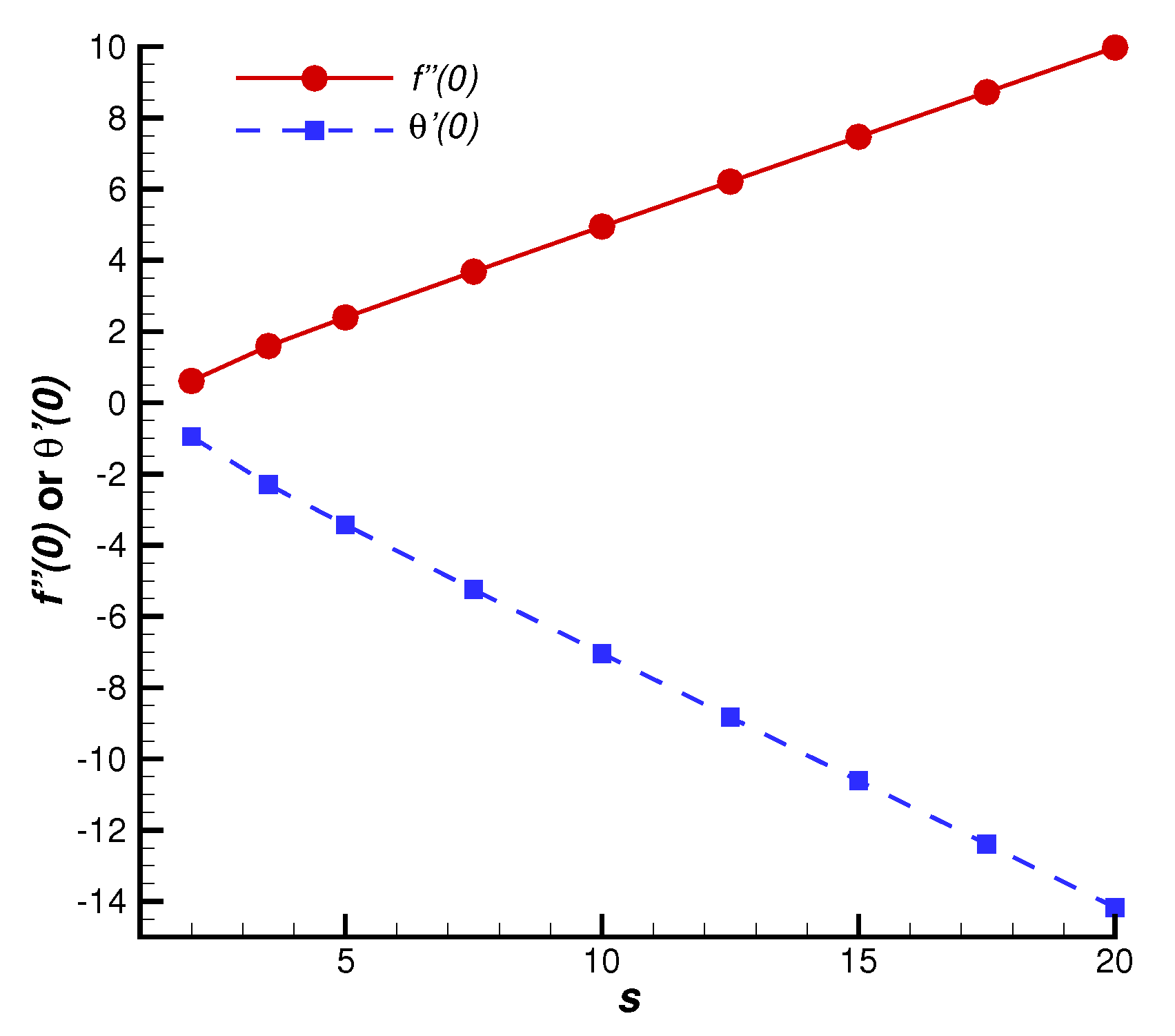
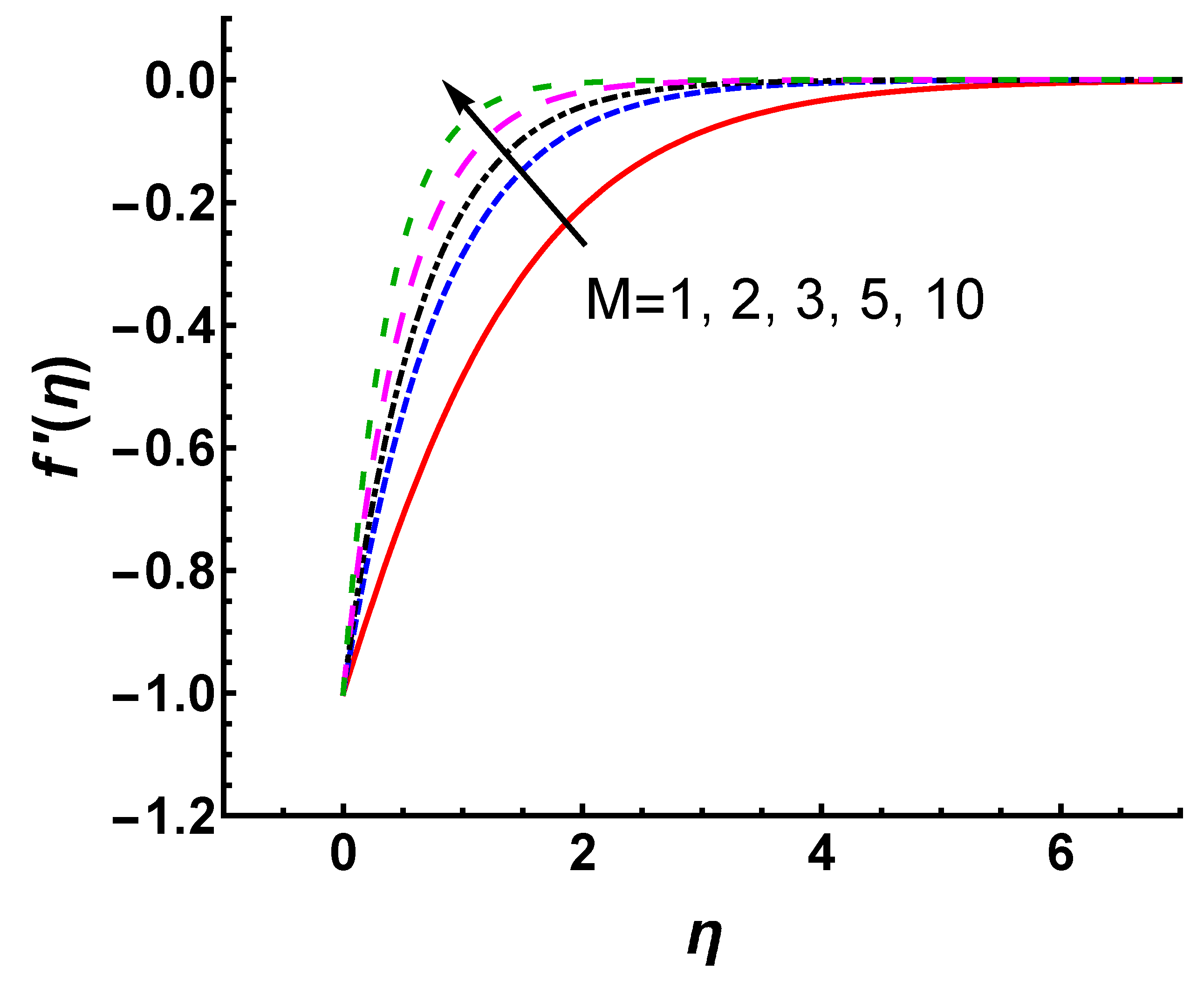
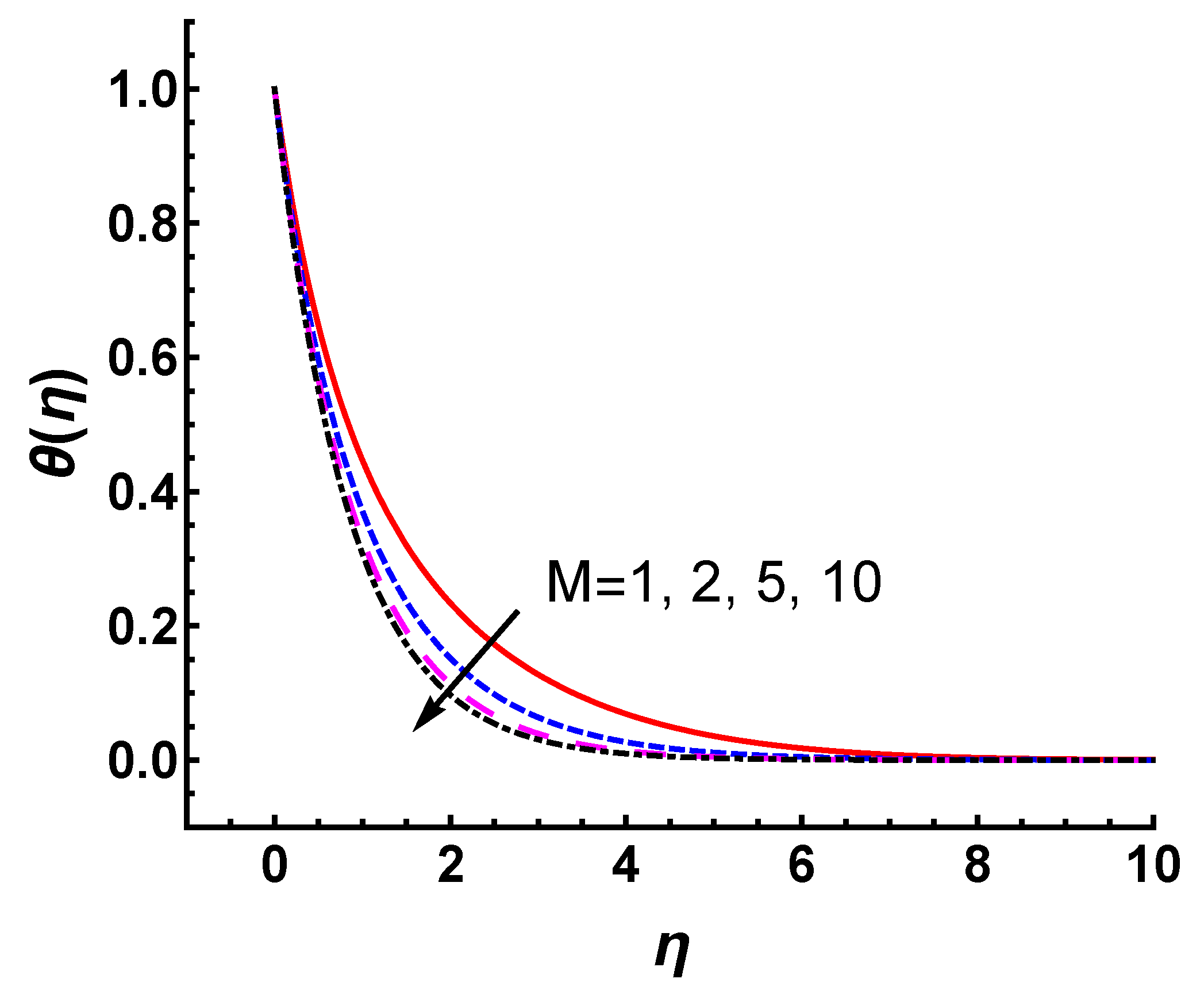
5.2. Effects of M and s
5.3. Effect of
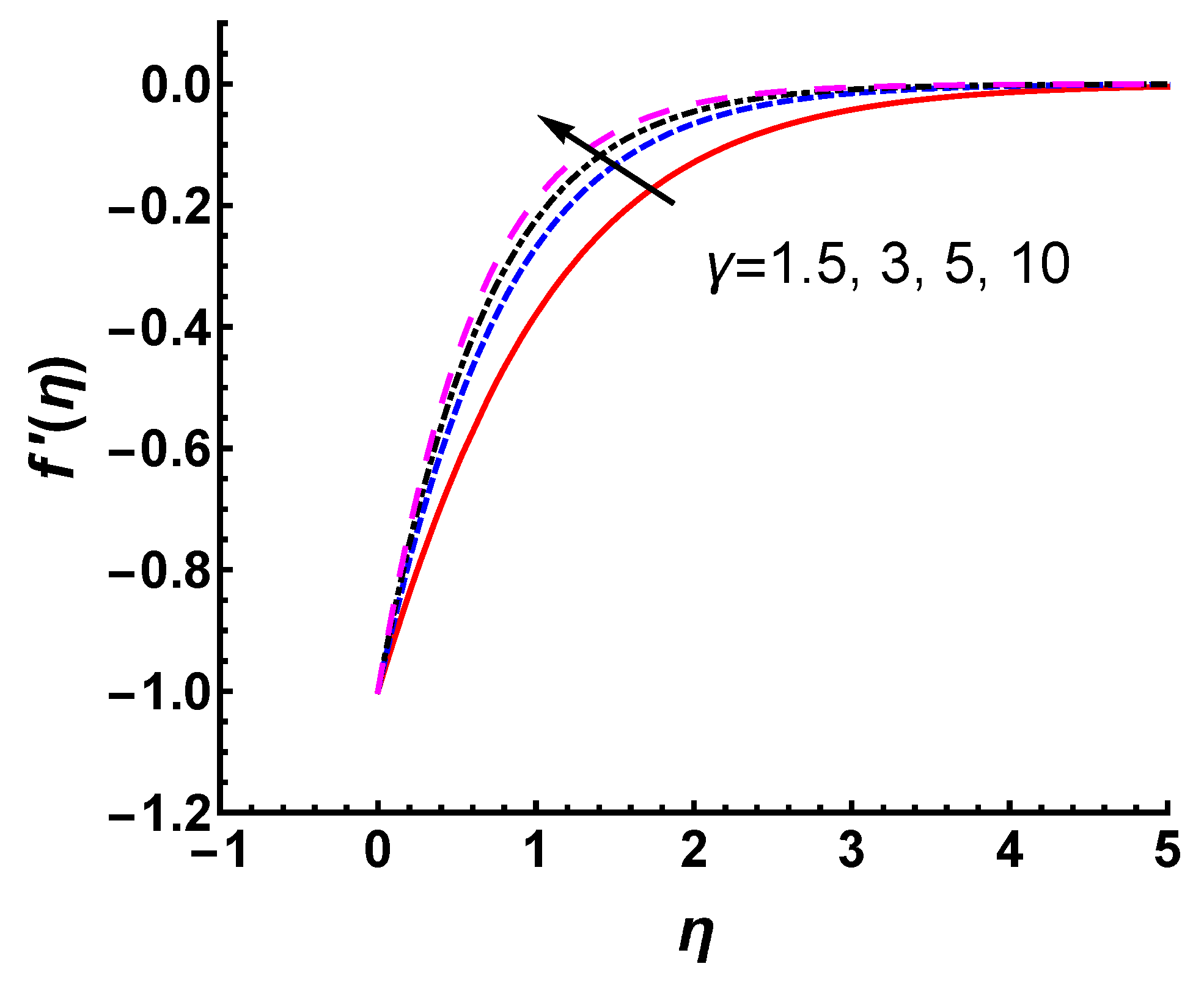
5.4. Analysis of and
6. Conclusions
- The explicit analytic solutions of and are obtained and valid in the whole region .
- The important quantities and related to the skin friction coefficient and local Nusselt number are derived in an explicit form.
- The convergent analytic solutions are in good agreement with the numerical solutions. The rapid decrease in squared residual error ensures the accuracy of the homotopy approximation.
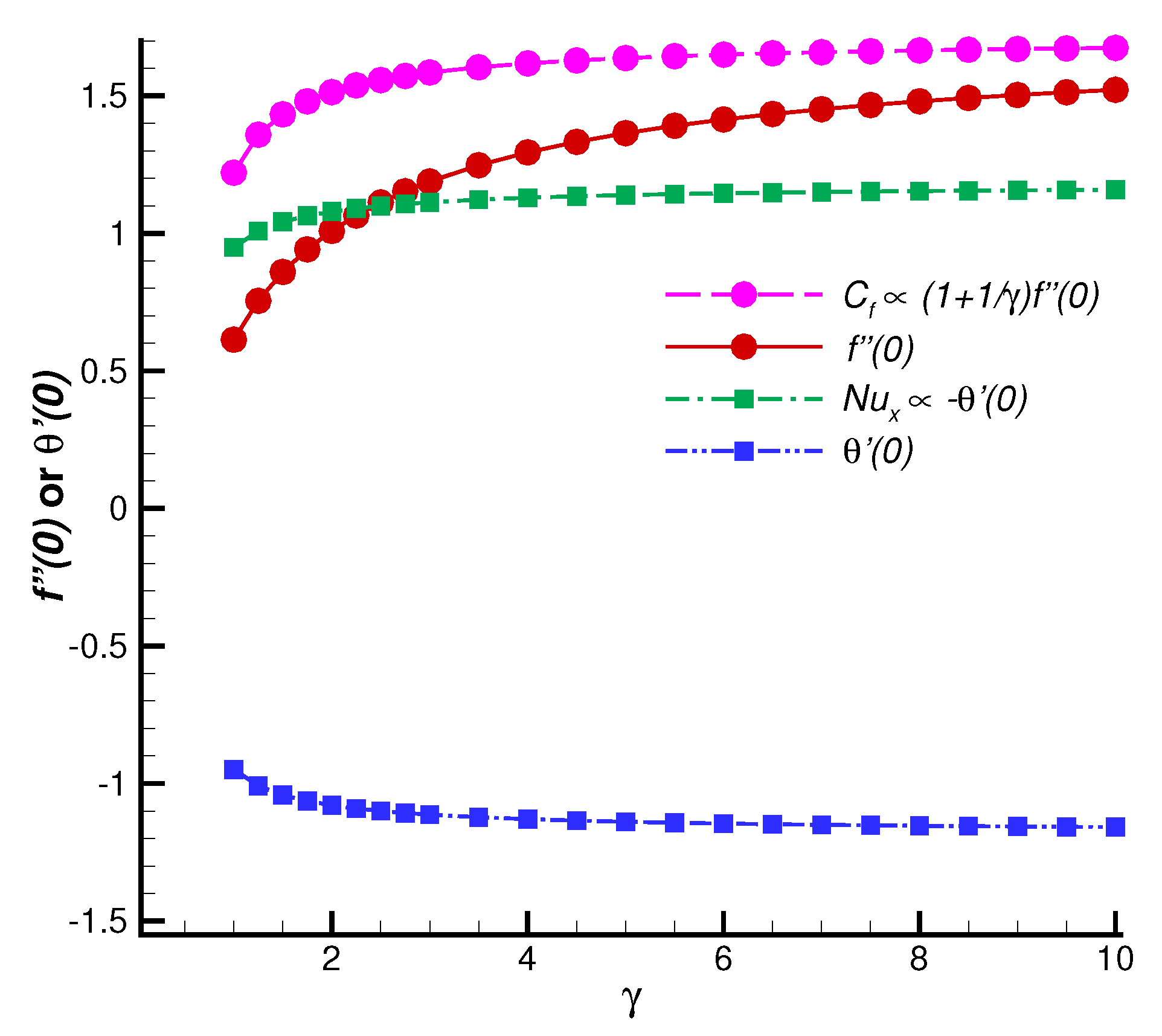
- An increase in the Casson fluid parameter suppresses the magnitude of velocity profile due to the reduced yield stress as increases. This leads to a thinner momentum boundary layer thickness. The velocity profile magnitude is found to decrease with increasing for both stretching and shrinking surfaces.
- The temperature profile decreases slightly with increasing values of in the current case, which decreases the thermal boundary layer thickness.
- The magnitudes of and decrease significantly with increases in the magnetic interaction parameter M and suction parameter s.
- The velocity and thermal boundary layer thicknesses decrease as M and s increase. The presence of a magnetic field force opposite to the velocity and suction reduces the momentum and thermal thickness of the boundary layer.
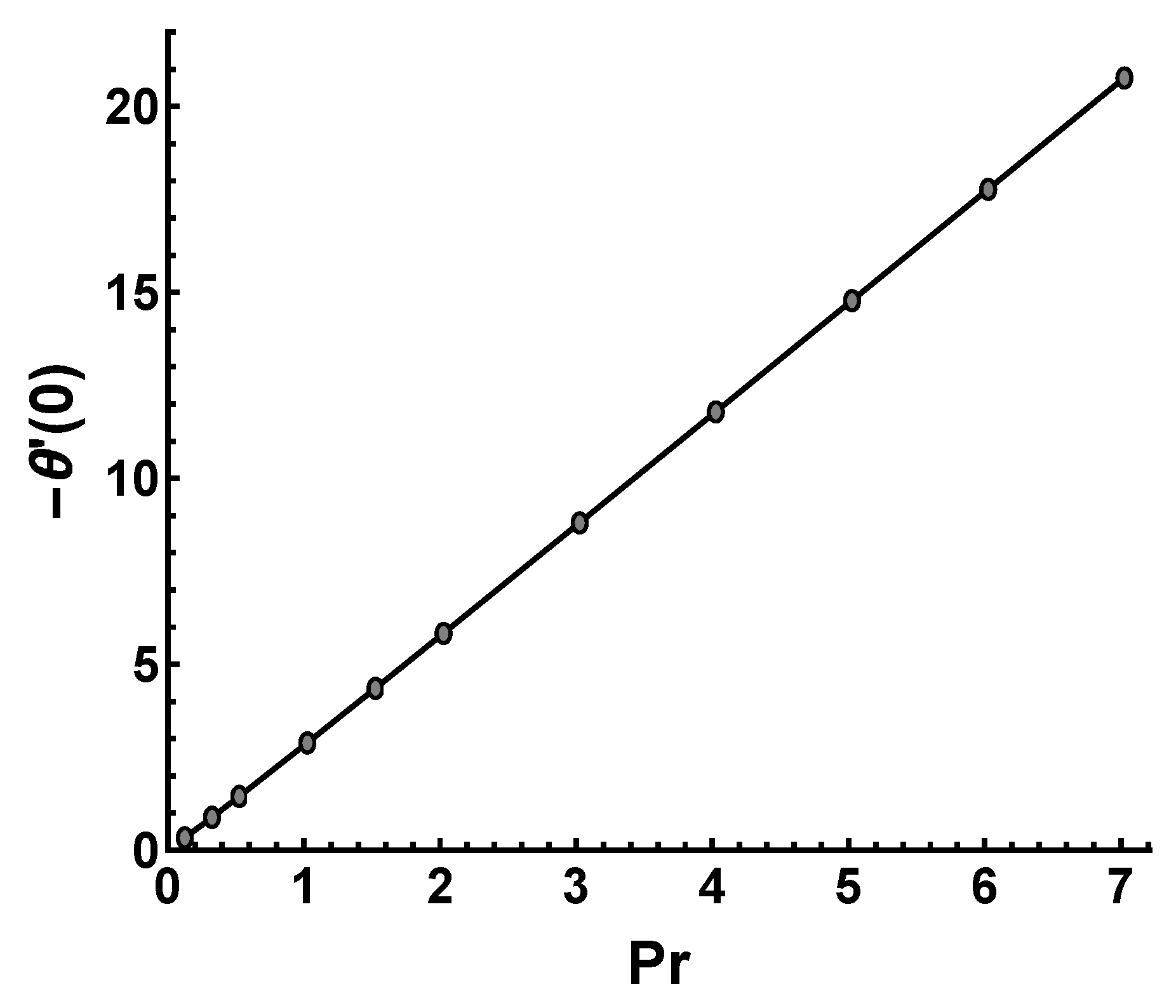
- The temperature profile and thermal boundary layer thickness decrease with increasing values of Prandtl number . The heat diffuses faster corresponding to the higher thermal conductivity for a small value of .
- and exhibit a linearly increasing trend as s becomes stronger.
- and increase nonlinearly with increases in and M.
- The wall heat transfer rate increases linearly as increases, as a result, also increases linearly.
- Compared with the constant wall temperature condition, the exponentially increasing wall temperature with x raises the temperature of the fluid within the boundary layer and leads to increased thickness of the thermal boundary layer.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. The Related Coefficients in
Appendix B. The Related Coefficients in
References
- Ryutova, M.; Tarbell, T. MHD Shocks and the Origin of the Solar Transition Region. Phys. Rev. Lett. 2003, 90, 191101. [Google Scholar] [CrossRef] [PubMed]
- Takahashi, R.; Brennan, D.P.; Kim, C.C. Kinetic Effects of Energetic Particles on Resistive MHD Stability. Phys. Rev. Lett. 2009, 102, 135001. [Google Scholar] [CrossRef]
- Stawarz, J.E.; Pouquet, A. Small-scale behavior of Hall magnetohydrodynamic turbulence. Phys. Rev. E 2015, 92, 063102. [Google Scholar] [CrossRef] [PubMed]
- Miura, H.; Yang, J.G.; Gotoh, T. Hall magnetohydrodynamic turbulence with a magnetic Prandtl number larger than unity. Phys. Rev. E 2019, 100, 063207. [Google Scholar] [CrossRef] [PubMed]
- Klein, R.; Pothérat, A. Appearance of Three Dimensionality in Wall-Bounded MHD Flows. Phys. Rev. Lett. 2010, 104, 034502. [Google Scholar] [CrossRef] [PubMed]
- Reddy, K.S.; Fauve, S.; Gissinger, C. Instabilities of MHD flows driven by traveling magnetic fields. Phys. Rev. Fluids 2018, 3, 063703. [Google Scholar] [CrossRef]
- Camobreco, C.J.; Pothérat, A.; Sheard, G.J. Transition to turbulence in quasi-two-dimensional MHD flow driven by lateral walls. Phys. Rev. Fluids 2021, 6, 013901. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Layek, G.C.; Samad, S.A. Study of MHD boundary layer flow over a heated stretching sheet with variable viscosity. Int. J. Heat Mass Transf. 2005, 48, 4460–4466. [Google Scholar] [CrossRef]
- Kerrache, N.; Bouaziz, M.N. Suction/injection effects on MHD free convection boundary flow in a darciam-forchheimer porous medium. Adv. Appl. Fluid Mech. 2017, 20, 561–578. [Google Scholar]
- Saadatmandi, A.; Sanatkar, Z. Collocation method based on rational Legendre functions for solving the magneto-hydrodynamic flow over a nonlinear stretching sheet. Appl. Math. Comput. 2018, 323, 193–203. [Google Scholar] [CrossRef]
- Ponalagusamy, R.; Priyadharshini, S. Pulsatile MHD flow of a Casson fluid through a porous bifurcated arterial stenosis under periodic body acceleration. Appl. Math. Comput. 2018, 333, 325–343. [Google Scholar] [CrossRef]
- Asifa, P.K.; Shah, Z.; Watthayu, W.; Anwar, T. Radiative MHD unsteady Casson fluid flow with heat source/sink through a vertical channel suspended in porous medium subject to generalized boundary conditions. Phys. Scr. 2021, 96, 075213. [Google Scholar] [CrossRef]
- Kumar, M.; Mondal, P.K. Bejan’s flow visualization of buoyancy-driven flow of a hydromagnetic Casson fluid from an isothermal wavy surface. Phys. Fluids 2021, 33, 093113. [Google Scholar] [CrossRef]
- Kandelousi, M.S.; Ameen, S.; Akhtar, M.S.; Shin, H.S. Nanofluid Flow in Porous Media; IntechOpen: London, UK, 2020. [Google Scholar]
- Nadeema, S.; Haqa, R.U.; Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. B 2012, 19, 1550–1553. [Google Scholar] [CrossRef]
- Liao, S. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; Chapman and Hall/CRC: New York, NY, USA, 2003. [Google Scholar]
- Liao, S. Notes on the homotopy analysis method: Some definitions and theorems. Commun. Nonlinear Ence Numer. Simul. 2009, 14, 983–997. [Google Scholar] [CrossRef]
- Liao, S. Homotopy Analysis Method in Nonlinear Differential Equations; Springer-Verlag GmbH: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Vajravelu, K.; Van Gorder, R.A. Nonlinear Flow Phenomena and Homotopy Analysis: Fluid Flow and Heat Transfer; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Yu, Q. Wavelet-based homotopy method for analysis of nonlinear bending of variable-thickness plate on elastic foundations. Thin-Walled Struct. 2020, 157, 107105. [Google Scholar] [CrossRef]
- Ramzan, M.; Bilal, M.; Chung, J.D.; Lu, D.C.; Farooq, U. Impact of generalized Fourier’s and Fick’s laws on MHD 3D second grade nanofluid flow with variable thermalconductivity and convective heat and mass conditions. Phys. Fluids 2017, 29, 093102. [Google Scholar] [CrossRef]
- Xu, D.L.; Liu, Z. A study on nonlinear steady-state waves at resonance in water of finite depth by the amplitude-based Homotopy Analysis Method. J. Hydrodyn. 2020, 32, 888–900. [Google Scholar] [CrossRef]
- Liu, L.; Rana, J.; Liao, S. Analytical solutions for the hydrogen atom in plasmas with electric, magnetic, and Aharonov-Bohm flux fields. Phys. Rev. E 2021, 103, 023206. [Google Scholar] [CrossRef]
- Yang, X.Y.; Li, Y. On bi-chromatic steady-state gravity waves with an arbitrary included angle. Phys. Fluids 2022, 34, 032107. [Google Scholar] [CrossRef]
- Sardanyés, J.; Rodrigues, C.; Januário, C.; Martins, N.; Gil-Gómez, G.; Duarte, J. Activation of effector immune cells promotes tumor stochastic extinction: A homotopy analysis approach. Appl. Math. Comput. 2015, 252, 484–495. [Google Scholar] [CrossRef] [Green Version]
- Nassar, C.J.; Revelli, J.F.; Bowman, R.J. Application of the homotopy analysis method to the Poisson-Boltzmann equation for semiconductor devices. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 2501–2512. [Google Scholar] [CrossRef]
- Liao, S.J. An explicit, totally analytic approximate solution for Blasius’ viscous flow problems. Int. J. Non Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Farooq, U.; Zhao, Y.L.; Hayat, T.; Alsaedi, A.; Liao, S.J. Application of the HAM-based Mathematica package BVPh 2.0 on MHD Falkner–Skan flow of nano-fluid. Comput. Fluids 2015, 111, 69–75. [Google Scholar] [CrossRef]
- Mustafa, M.; Hayat, T.; Pop, I.; Hendi, A. Stagnation-Point Flow and Heat Transfer of a Casson Fluid towards a Stretching Sheet. Z. Naturforschung A 2015, 67, 70–76. [Google Scholar] [CrossRef]
- Ali, A.; Zaman, H.; Abidin, M.Z.; Naeemullah; Shah, S.I.A. Analytic Solution for Fluid Flow over an Exponentially Stretching Porous Sheet with Surface Heat Flux in Porous Medium by Means of Homotopy Analysis Method. Am. J. Comput. Math. 2015, 5, 224–238. [Google Scholar] [CrossRef]
- Bhattacharyya, K. Boundary Layer Flow and Heat Transfer over an Exponentially Shrinking Sheet. Chin. Phys. Lett. 2011, 28, 074701. [Google Scholar] [CrossRef]
- Kierzenka, J.; Shampine, L.F. A BVP Solver Based on Residual Control and the Matlab PSE. ACM Trans. Math. Softw. 2001, 27, 299. [Google Scholar] [CrossRef]
- Pramanik, S. Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Eng. J. 2014, 5, 205–212. [Google Scholar] [CrossRef] [Green Version]



| Parameters | |||||
|---|---|---|---|---|---|
| HAM | Num | HAM | Num | ||
| M | 2 | 1.18455279 | 1.184553 | −1.10536254 | −1.105533 |
| 3 | 1.47878566 | 1.478786 | −1.14720967 | −1.147279 | |
| 5 | 1.89590282 | 1.895903 | −1.18877394 | −1.188803 | |
| 10 | 2.60700267 | 2.607003 | −1.23492995 | −1.234942 | |
| 1 | 0.61356181 | 0.613026 | −0.94909557 | −0.944217 | |
| 3 | 1.18865714 | 1.188657 | −1.11302087 | −1.113159 | |
| 5 | 1.36433170 | 1.364332 | −1.13918925 | −1.139268 | |
| 10 | 1.52194504 | 1.521945 | −1.15851866 | −1.158571 | |
| s | 2.5 | 1.00391561 | 1.003915 | −1.48397701 | −1.483987 |
| 3 | 1.31012112 | 1.310121 | −1.90669518 | −1.906695 | |
| 5 | 2.39570505 | 2.395705 | −3.42764833 | −3.427648 | |
| 10 | 4.94949146 | 4.949491 | −7.04073641 | −7.040736 | |
| Parameters | |||
|---|---|---|---|
| 0.1 | 0.2664 | 0.23258 | |
| 0.2 | 0.53845 | 0.47562 | |
| 0.5 | 1.37692 | 1.24919 | |
| 1 | 2.81671 | 2.62471 | |
| 4 | 11.71837 | 11.42673 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, J.; Liao, S. Explicit Solutions of MHD Flow and Heat Transfer of Casson Fluid over an Exponentially Shrinking Sheet with Suction. Nanomaterials 2022, 12, 3289. https://doi.org/10.3390/nano12193289
Liu L, Li J, Liao S. Explicit Solutions of MHD Flow and Heat Transfer of Casson Fluid over an Exponentially Shrinking Sheet with Suction. Nanomaterials. 2022; 12(19):3289. https://doi.org/10.3390/nano12193289
Chicago/Turabian StyleLiu, Ling, Jing Li, and Shijun Liao. 2022. "Explicit Solutions of MHD Flow and Heat Transfer of Casson Fluid over an Exponentially Shrinking Sheet with Suction" Nanomaterials 12, no. 19: 3289. https://doi.org/10.3390/nano12193289
APA StyleLiu, L., Li, J., & Liao, S. (2022). Explicit Solutions of MHD Flow and Heat Transfer of Casson Fluid over an Exponentially Shrinking Sheet with Suction. Nanomaterials, 12(19), 3289. https://doi.org/10.3390/nano12193289







