Influence of the Algorithmization Process on the Mathematical Competence: A Case Study of Trainee Teachers Assessing ABN- and CBC-Instructed Schoolchildren by Gamification

Abstract

In this manuscript, schoolchild mathematical competencies have been assessed by using educational gamification methodologies; specifically, Educational Escape Rooms (EER). To ease the interpretation of results, Spanish schoolchildren trained by using two different methodologies (ABN and CBC) were selected to participate in the experience. The gamified environment used as assessment tool was co-designed by trainee teachers, on-service teachers, and university researchers. The design was implemented in different educational centers and the results were transcribed to deliver a didactic analysis. Among the findings of this study, we uncovered: (i) the reduction of the math anxiety, (ii) the different performance of the schoolchild involved—ABN students show an additional and positive 10% development of certain mathematical competences—and (iii) a positive didactic-mathematic development of the participant trainee teachers.

1. Introduction

Each academic year, thousands of students initiate a new educational stage in the frame of a highly qualified and strongly competitive working market. Because of this environment, the educational system has been forced to make changes on how teaching is delivered to the students. Therefore, education in the 21st century is not only focused on creating rational, critical citizens but is also focused on developing specific abilities, which are required in the 21st century working market. Consequently, formative institutions are fitting their educational projects to adjust to the new, changing realities of the 21st century world.

Among the key abilities required for the 21st century labor market we find problem-solving skills [1], which requires of two major competences: observation and critical thinking skills. The observation skill refers to collecting data, understanding, and interpreting the meaning of the information using all the senses. Critical thinking involves the individual’s ability to do the following: conceptualizing, logical reasoning, applying strategy, analytical thinking, decision making, and synthesizing to solve any problem.

However, in the formative/educational context, most educational institutions still focus on the mechanization of abilities. As a response to this reality, innovative methodologies have been proposed to boost some of the key elements for the development of the problem-solving skills (particularly numerical thinking). In the frame of Spanish-speaking educational systems, one of such innovative methodologies is the ABN method [2] (Open Number-Based, by its Spanish acronym); which has been widely compared [3] to the more conventional and wide-spread CBC method (Closed Digit-Based, by its Spanish acronym).

In this regard, if problem-solving skills are significant, the way these skills are assessed is no less so. In fact, assessing is one of the main roles of the mathematics teacher [4], and the way assessment is delivered might have an impact on the performance of the students themselves. Indeed, it has been already demonstrated that evaluation is the most common cause of mathematics anxiety [5] for all age groups [6]. Thus, the literature concludes [7] that traditional forms of evaluation have obvious limitations:

• Traditional evaluation does not consider the growth and development of students and can limit their progress.
• It can be frustrating: traditional evaluation pushes educators to accurately summarize student achievement with simple numerical grades and a few words of condensed feedback.
• The assessment of students’ higher order thinking skills (problem solving, attitudes, and other skills) cannot be easily quantified by a simple numerical grade.
• Most traditional assessment systems do not involve discussions, class-projects, and other programs designed to encourage students to deliver materials, products, or other content which could be used by the teacher to observe, measure, and track the students’ knowledge.

Therefore, it is convenient to propose new ways for evaluating the abilities of interest previously presented. Furthermore, it has also been demonstrated that mathematics anxiety has its own specificities and can be treated by modifying the way in which students are assessed [8]. In this regard, a written exam can be stressful for anyone taking it; thus, contributing to the increase in mathematics anxiety and affecting the students’ performance. In this regard, it has been suggested that “…there is simply less worry (…) when facilitating a level playing field during exams” [8]. By utilizing these precedents, the present study proposes exploring new forms of evaluation using game-based learning methodologies that, because of the similarities with problem-based learning strategies [9], allow the creation of more suitable learning and assessment scenarios in terms of context, resources, and content to be evaluated [10].

To this end, we propose using educational gamification strategies to assess mathematical competences related to numerical thinking. In order to give meaning to the previously presented discussion, the proposed experience was implemented in educational institutions that used different math-teaching methodologies (ABN and CBC, respectively). We choose to compare both methodologies because it has been demonstrated that mathematics anxiety also is closely related to arithmetic-related abilities [11]. So, the way in which such abilities are developed should also be considered a matter of research. Finally, as trainee teachers’ instructors, we are conscious of the historical difficulty and bad relationship with mathematics (sometimes addressing mathematics anxiety) that future teachers have. So, we proposed a way for trainee teachers to interact with in-service teachers by co-designing gamified assessing tools, so that the evaluation of the mathematical competencies becomes accessible for all (trainee teachers and primary school students). Our hope is not only to provide trainee teachers with a picture of what the mathematical competencies are but also to influence the future educational context (emphasizing that the focus should not be on the mechanization of abilities but on the development of problem-solving skills).

Summarizing, this study aims to test the efficiency of gamified methodologies (educational escape rooms, in our case) to assess the mathematical competency. To ease this, students taught with different methodologies (ABN and CBC), which are supposed to present different problem-solving skills, were selected. The final application of this study is to provide alternative evaluation tools that do not increase math anxiety of students. The aims are listed as follows:

• 1—Exploring the possibilities and limitations of alternative assessment methodologies based on games.
• 2—Using educational gamification methodologies to assess mathematical competences related to numerical thinking.
• 3—Discussing the relation between arithmetic-related skills and the algorithmization methodology (CBC vs. ABN)
• 4—Promoting future teachers’ professional knowledge and skills, particularly those related to assessment of the mathematical competencies.

2. Background and Framework

In the frame of Piaget’s theory [12,13,14], children aged 7 to 11 are expected to remain in a “concrete operational stage” from a cognitive point of view, evolving to a formal operation stage at ages 12 and up. So, in the context of this theory, mathematical cognition is developed by physically interacting with the environment, discussing with peers, and delivering generalizations about the experience (i.e., the mathematization of the environment). This perspective has been more recently detailed by Clements and Sarama [15], who, in summary, suggest a learning trajectory with a progressive abstraction process by starting with concrete experiences.

However, it has been found [16] that teachers tend to teach arithmetic-related knowledge from a purely abstract perspective (i.e., not supported by concrete experiences or manipulatives). However, a mathematics teacher should make an effort to provide a context to the knowledge [17]. In this regard, a mathematician does not communicate results as they are found. Rather, they reorganize such results, modify them in a general manner, and deliver knowledge with a communicable, decontextualized, depersonalized, and timeless structure [18].

On the other hand, Brousseau’s theory (as cited in the literature [4]) states that the teacher should first carry out inverse work through the repersonalization and recontextualization of knowledge—by giving meaning to the knowledge to be taught through contextualized situations. If the personalization phase has worked properly, then students should not know that they have “produced” new knowledge that will be applicable to other situations. To transform their answers into knowledge, they must, with the help of the teacher, personalize and contextualize the knowledge that they have produced in order to recognize something general and universal in what they have achieved (reusable knowledge).

2.1. The Mathematical Competence

Mathematical competence was defined in the European Recommendations for Learning [19] as “the ability to develop and apply mathematical thinking to solve a range of problems in everyday situations” and is considered of key importance for lifelong learning within European countries. There are several approaches to studying and modeling mathematical competences. Here we will present two wide-spread and well considered models as the basis of our own analysis model.

The first model to be presented is that of Niss [20], who presented mathematical competencies as essentially being cognitive constructs. In doing so, Niss argues that the significance of the affective, dispositional, and volitional factors of mathematical mastery and learning were not disregarded, but he considered that these factors were of a different nature to the ones taken into account in his framework. Niss ([20], p.20) states that:

“(…) the core of a mathematical competency is the enactment of mathematics in contexts and situations that present a certain kind of challenge. In other words, a competency focuses on aspects of actively doing mathematics. In contradistinction, knowing mathematics means to be in possession of factual knowledge about mathematical definitions, concepts, results (propositions and theorems), algorithms, formulae, theories and so on and so forth”

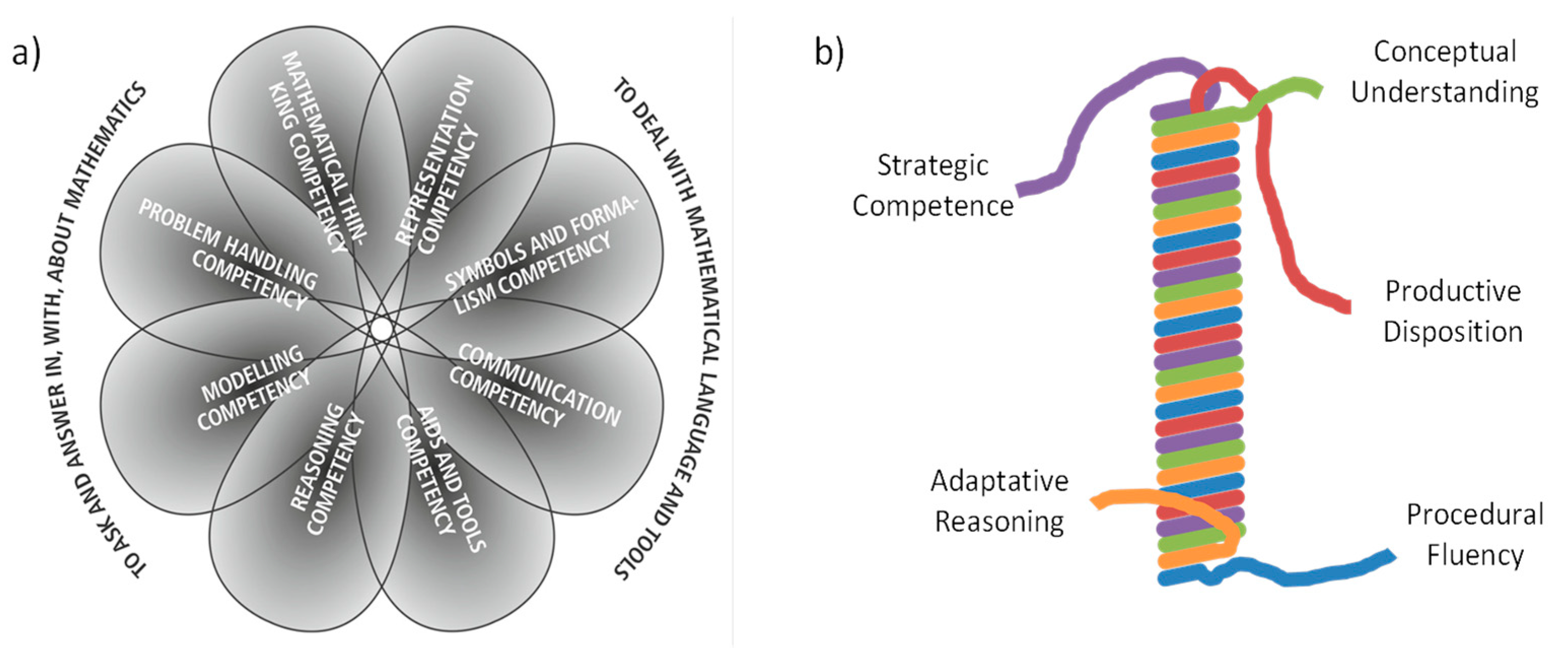
A visual representation of the eight mathematical competencies described by Niss is presented in Figure 1a.

On the other hand, Kilpatrick’s vision of the mathematical competence [21] uses the term “proficiency” because it should include not only skill and understanding but other qualities as well. He uses the metaphor of a rope woven of strands, with the five strands to be developed in concert and not one before or after the other. The rope model (see Figure 1b) could then be used to define learning goals for all students, and a variation of the model could be used to discuss proficiency in teaching. Kilpatrick [21] states that:

“These strands—interwoven and interdependent—describe a set of knowledge, skills, abilities, and beliefs based on a body of research in cognitive psychology and mathematics education (and build a picture of a mathematically proficient student)”

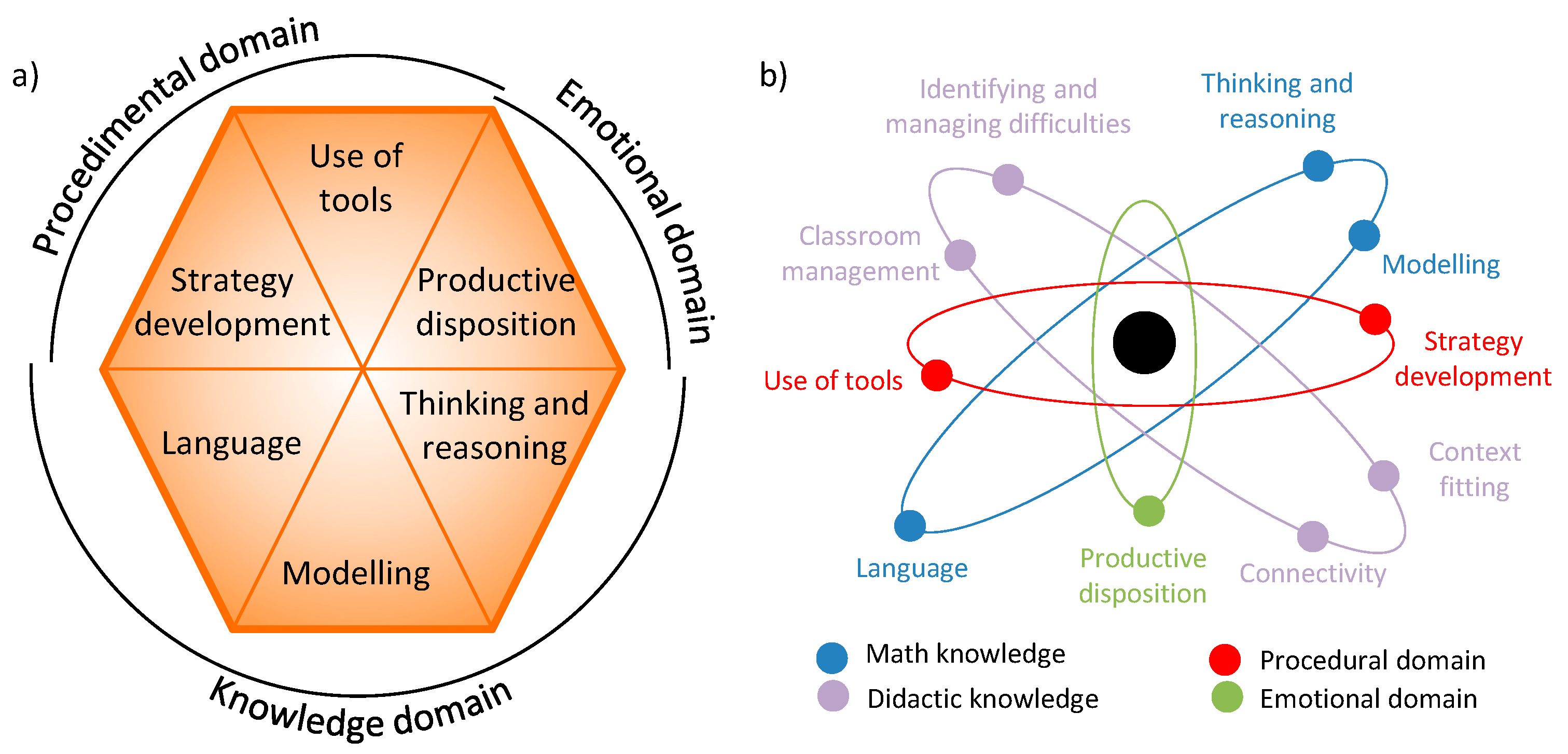
So, Kilpatrick’s model considers “emotional” factors but pays less attention to specific knowledge/procedural items. A combination of both visions allows an accurate categorization of the authors’ own vision of the mathematical competence. Such a perspective is summarized on a visual representation of this model (presented in Figure 2a), which would be composed by:

• Thinking and reasoning: being able to relate to and pose the kinds of generic questions that are characteristic of mathematics and relate to the nature of answers that may be expected of such questions. This competency involves both constructively providing the justification of mathematical claims and critically analyzing and assessing existing or proposed justifications.
• Modelling: being able to develop mathematical models and to critically evaluate and analyze proposed models.
• Strategy development: being able to formulate, represent, and solve mathematical problems within and across a variety of mathematical domains, as well as being able to critically analyze and evaluate one’s own and others’ attempted solutions to problems. This competence also involves the ability to carry out procedures flexibly, accurately, efficiently, and appropriately.
• Language: this ability involves the use of mathematical symbols, formalisms, and communication. This competence is related with the ability to deal with mathematical symbols, symbolic expressions, and transformations, as well as with the rules and formalisms that govern them. This skill is also related to the ability to engage in written, oral, visual, or gestural mathematical communication, in different genres, styles, and registers.
• Use of tools: This competency focuses on dealing with material aids and tools for mathematical activity, ranging from concrete physical objects and instruments, specially designed papers and charts, to a wide spectrum of digital technologies designed to represent and facilitate mathematical work.
• Productive disposition: The regular inclination to see mathematics as rational, practical, and beneficial, accompanied with a belief in constancy and one’s own performance. This competence also involves the resiliency to errors and mistakes and the ability to learn from them.

2.2. Didactic–Mathematic Knowledge and Teachers in Formation

TEDS-M’s recent report [22] highlights worrisome data: in-service teachers’ specific lack on mathematical and didactical knowledge. As the cited report states, the lack of teachers’ professional competence also influences students’ skill to codify, handle, and depict mathematics in a variety of contexts [23]. Therefore, trainee teachers should have specific academic educations in mathematics (the TEDS-M report evidenced that countries with a specific teacher academic education in mathematics demonstrate better performances). As a first step of this specific academic education, we proposed a mentoring program to co-design didactical situations in touch with in-service teachers and schoolchildren. The co-design approach is used to conform innovative assignments jointly developed by in-service schoolteachers, students, and the authors of this manuscript (researchers and lecturers at a University). As the literature states [24], a participatory design process should be based on a question to be solved, whose treatment could be supported and enhanced using virtual learning networks. With the aim of respecting such principles, the procedure carried out in this research involved the creation of a small “designer team” (comprising three students). To enhance the process, such a “designer team” should be involved in the creation of problems, activities, tasks, tests, narratives, etc., which are considered when designing an Educational Escape Room (EER).

This methodology constitutes a service-learning approach, i.e., an experiential education approach that is premised on “reciprocal learning”, suggesting that since learning flows from service activities, both those who provide the service and receive it “learn” from the experience [25].

Finally, the specific competencies of the trainee teachers were analyzed by using a simplified model based on the discussions presented in the literature [26], which has been already successfully applied to similar experiments [10]. The selected model is schematically presented in Figure 2b. The professional competencies here analyzed consider the two key aspects of professional knowledge: mathematical and didactic knowledge.

2.3. Algorithmization and Methodologies

Algorithmizing is the process of converting an informal description of a procedure into a collection of ordered steps that solve a mathematical problem, i.e., a precise step-by-step plan for a computational procedure that possibly begins with an input value and yields an output value in a finite number of steps. It is related to the mathematical competencies of mathematical language, thinking, reasoning, and strategy development (as presented in the previous section). To develop the early “algorithmization” skill, the two main methodologies wide-spread in the Spanish educational system are described as follows:

2.3.1. The CBC Method

CBC is the Spanish acronym for “closed, based in digits”, and is coincident with the traditional U.S. algorithm. Concerning the U.S. algorithm, many published studies have reported the effectiveness of this algorithm, concluding that “traditional algorithms do not encourage students’ autonomous thinking, since they are based on memory processes and certain predetermined steps” [27]. However, this algorithm is by far the most used and wide-spread in the Spanish educational system. Indeed, the traditional U.S. algorithm used for addition and subtraction is powerful, elegant, efficient, yet simple. It requires little understanding of mathematics beyond single-digit calculations and an ability to memorize a set of procedures. Historically known as “shopkeeper math”, the U.S. algorithm was used widely by early merchants who did not need any depth of mathematical understanding.

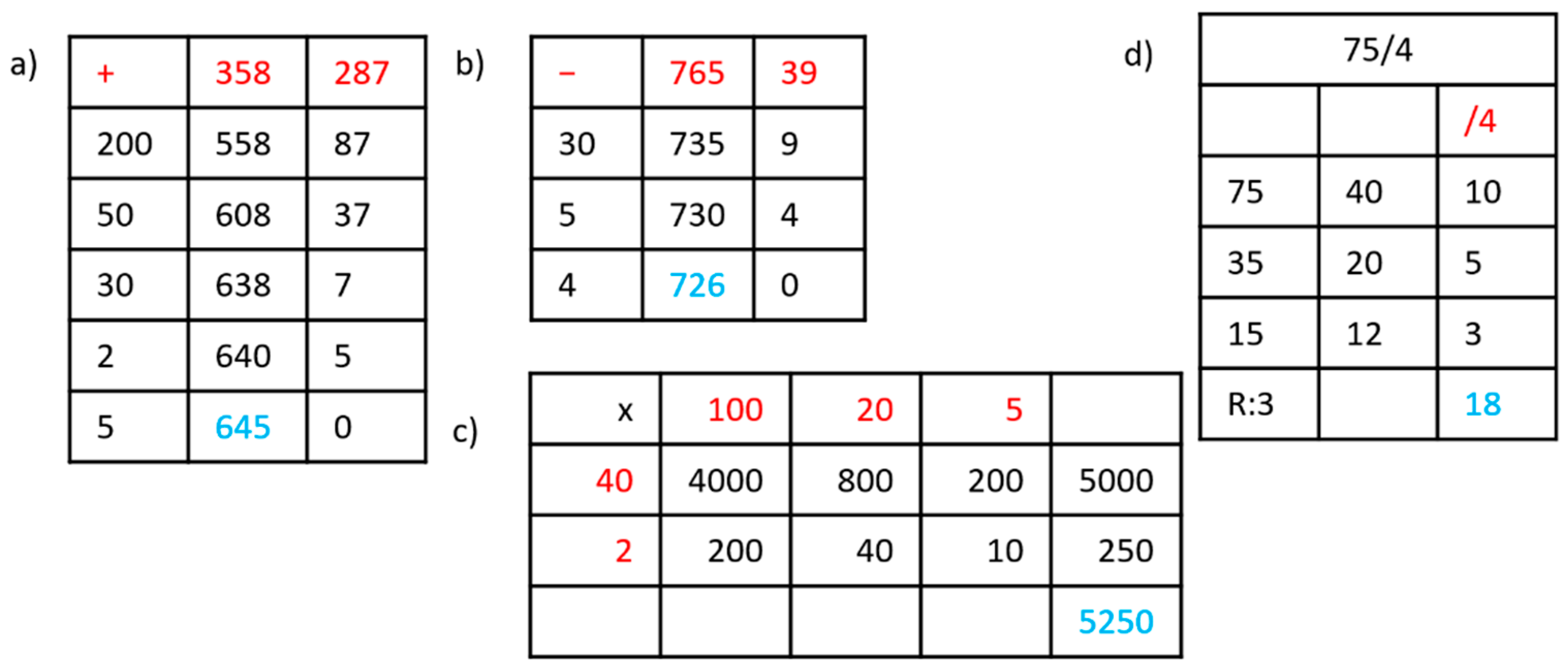
Figure 3 shows an example of each basic operation when using the CBC algorithm. The algorithm for each operation on the traditional U.S./CBC algorithm requires proper digit alignment and works as follows:

• Addition: The traditional method computes two numbers by adding their single digits from right to left. If the sum of the digits is greater than 9, then a carry-over occurs. The carry-over is placed over the next digit group. The carry-over is then included in the next groups sum.
• Subtraction: The minuend and subtrahend are stacked vertically with place values aligned and the digits in each column are subtracted, working column by column from the right. If a digit in the subtrahend is larger than the corresponding digit in the minuend, then a 10 is “borrowed” from the next column to the left.
• Multiplication: First, the two numbers are aligned so that the places are in the same column. Next, the value of the multiplier is multiplied to each digit of the multiplicand by its place. The results are aligned based on their places and added to obtain the final product.
• Division: Perform division requires the construction of a tableau. The divisor is separated from the dividend by a vertical bar and the dividend is separated from the quotient by an overbar. The steps are as follows: Take the first digit of the dividend from the left. Check if this digit is greater than or equal to the divisor. Then divide it by the divisor and write the answer on top as the quotient. Subtract the result from the digit and write the difference below. Bring down the next digit of the dividend (if present).

Detractors of the CBC algorithm argue that students using this algorithm might lose their number sense (as students are able to operate with no understanding of the place value of numbers). Indeed, the main argument is that “Memorized procedures send the wrong message to young mathematicians, who will become the future’s innovators and problem solvers” [28]. Furthermore, this algorithm leaves no freedom for students to explore ways to solve the operation and is based on memory process and predetermined steps.

This algorithm is based on the abacus and, while it can be taught in a meaningful way, mathematics teachers tend to teach decontextualized mathematics [22], so that students perceive mathematics as useless knowledge which operates as a black box; thus, inducing a lack of interest [4]. In fact, children tend to abandon their own efforts to make sense of mathematics when they are introduced to a systematic procedure and, in the process, lose the opportunity to flexibly compute and comprehend the strategies of others. The significant work of Kamii et al. [29] found that the rote learning of traditional algorithms can actually interfere with a child’s development of number sense. However, this algorithm could be preferred by a person who likes procedures or patterns.

2.3.2. The ABN Method

ABN is the Spanish acronym for “Open, based in numbers” [2], and its algorithm is also known as the box method or the grid method. This algorithm works by breaking a number and rearranging it in a grid. The associated methodology is widely used in elementary schools, serving as starting point for elementary students because breaking down numbers is a more logical approach. It is based on the “expanded methods” designed to support children by offering connections between mental processes and written algorithms [30].

This method can be defined as a calculation and problem-solving routine, with some specific characteristics [31]. It works on numbering as the basis for mathematical learning and support for calculation and problem solving. The ABN method is expected to promote natural and open learning through which students can solve operations and problems in different ways, considering the individual progress of each student. On the other hand, the ABN method is based on the “Realistic Mathematics Teaching” (RMT) approach created through the ideas of Freudenthal (as cited in the literature [32]). So (if well conducted), it trends to result in the meaningful understanding of mathematical operations.

Figure 4 shows an example of each basic operation by using the ABN algorithm. The algorithm for each operation on the box/grid/ABN algorithm works as follows:

• Addition: The basic idea of the addition is to accumulate one addend with the other. Once fully accumulated, the new addend provides the result.
• Subtraction: In subtraction, three different basic models are used, the “descending or ascending ladder format” being the most common. This format only uses two columns. In the first, the partial amounts are collocated. In the second, the progress is represented until the desired amount is obtained.
• Multiplication: The first step is to break down the numbers as a sum of numbers. Afterwards, these addends are arranged in a grid and each addend is multiplied by another. Finally, all the results inside the box are added to obtain the product.
• Division: Division allows different adaptation levels and the breakdown of the calculations. This algorithm consists of three columns. The first, on the left, represents the total amounts to be distributed. The second, in the center, represents the accurate distribution of the amounts. The column on the right represents the partial quotients. The sum of these represents the total quotient and the amount in the first column is the remainder.

Detractors of this methods argues that the solution process is slower than the traditional method and requires additional skills to solve operations (which should be considered when attempting straightforward operations). However, this algorithm could be preferred by someone who wants a more logical approach to solve operations.

2.4. Assessment by Educational Games

In connection to the previously discussed mathematical competency, assessment in modern education is understood as a form of diagnosis and control, rather than the traditional vision of classifying and qualifying students. The diagnosis makes possible the identification, discrimination, understanding, and characterization of the factors that trigger learning difficulties. Therefore, the main purpose is to identify and record shortcomings in the development of the teaching–learning process, so that such leaks can be fixed through the systematic monitoring and by maintaining teacher–student interaction. On the other hand, the “classification” function of the assessment is mainly focused on classifying of a student according to the level of achievement reached in comparison with, for example, the class group. Corresponding to these functions, three types of evaluation are distinguished:

• The diagnostic evaluation: which implies an evaluation “at the beginning of the course”, with the intention of verifying whether the students have mastery of the prerequisites needed. The purpose of the diagnostic evaluation would not only be an instrument to determine “pass or fail” but be a tool which can be used to define adequate references for learning.
• The formative evaluation: which is the control function that is carried out throughout the course to verify whether the students are reaching the foreseen expected objectives. It is mainly through this type of evaluation that the student knows their errors and finds stimuli for systematic study. Formative evaluation is connected to feedback procedures mechanisms since it allows the detection and identification of deficiencies.
• The summative evaluation: which occurs after the action (that is, after the results have been recorded). This is usually a time-specific evaluation, such as one carried out at the end of a teaching unit, trimester, semester, or cycle.

According to the definition of formative evaluation, it can take various forms as long as certain principles are recognized and respected (the detection of deficiencies, feedback, etc.). It is easy to export these principles to a gamified system where players are monitored and their progress is tracked. On the other hand, a common complaint from students is that the evaluation is usually delivered too late and perceived as very slow (it takes place at the end of the academic year). In contrast, in the world of gaming, live evaluation is in the very essence of the method.

Assessment principles for gaming have been widely discussed in the literature [33], and it is well known that the specific shape of the “triangle of assessment”—cognition, tasks, and context [34]—depends on the type of game. In this regard, tools for evaluating mathematical competencies by using games have been already designed by using commercial games [35]; so, there is no novelty in using games to evaluate mathematical competence. However, most of these assessment methods are based on digital tools and board games (as far as the authors know), while the use of educational escape rooms to assess the mathematical competencies is still a novel topic. 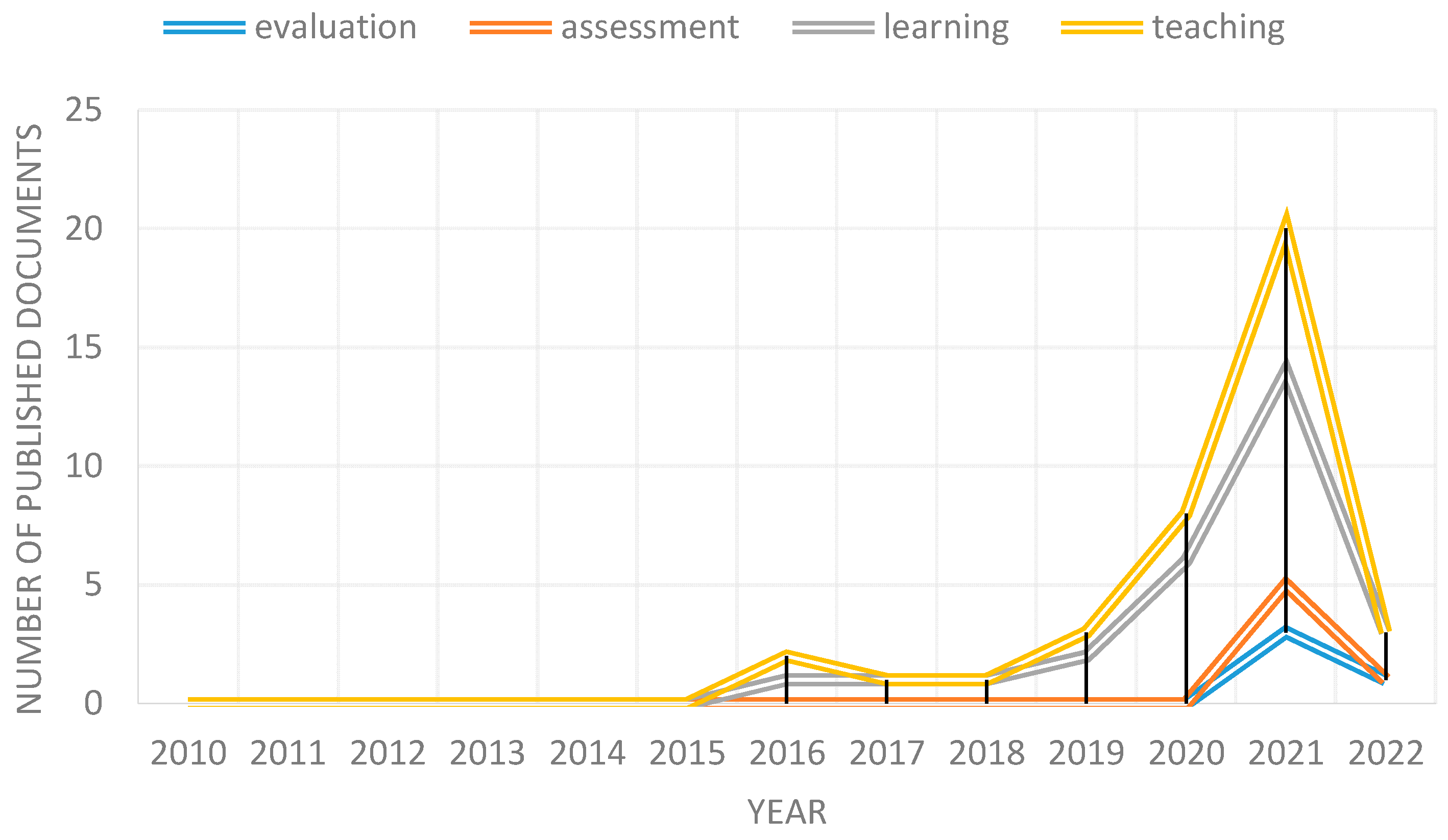Indeed, educational escape rooms have recently been evidenced to be powerful vehicles for teaching mathematics [9,36]; but little to no research has been focused on educational escape rooms for mathematical competence assessment purposes. To prove this, we used the Scopus database, looking for “mathematics” + “escape rooms” in article titles, abstracts, or keywords with their contents specific to learning, teaching, and assessment (we also used “evaluation” in order to consider synonyms). Results are shown in Figure 5, where a clear lack of research regarding assessment is evidenced.

So, in the authors’ opinions, there is room for research on the use of educational escape rooms to assess mathematical competencies. Furthermore, we consider that the specific characteristics of educational escape rooms [37] (in terms of isolation, dynamism, communication, performance, and more) have a positive impact in terms of formative outcomes.

3. Materials and Methods

In this section we present the research methodology, which includes the set of techniques and methods used to carry out the planned research tasks. In this study, we deliver a case study of the use of gamified learning scenarios proposed as a tool with which to carry out a formative and contextualized evaluation.

3.1. Formative and Contextualized Evaluation: The Educational Escape Rooms (EER)

To carry out a formative and contextualized evaluation, we proposed the creation of an immersive scenario in which students could be actively involved. To this end, we decided to use an educational escape room game model. Such a methodology has already been demonstrated as a valid vehicle for teaching/learning mathematics (as shown in Section 2.3). In this environment, a group of students are locked in a room in which they will have to unravel a narrative that will connect the different tests and questions in order to obtain the key that allows them to leave the abovementioned room within a certain timeframe. In this scenario, the students should remain isolated from the outside world; however, they have radio-communication with the outside world (in this case, the outside guidance was provided by both the researcher in charge of this document and the in-service teacher of the students involved). The interventions were monitored by video and audio, with hidden cameras placed in the room. Thus, a monitoring and feedback mechanism was created, recording students’ errors, and creating a stimulating environment that motivates the student to continue striving to overcome their deficiencies.

The activities of the room were designed to take 45 min of work, comprising three major connected activities (minor activities, with no mathematical relevance, were also used in the EER to boost motivation). The first activity was used to introduce the narrative of the room, as well as to present the skills required to unravel a conventional escape room. So, this first activity was not used to assess the mathematical competence but to teach students how the game works in terms of mechanics, materials, communication, and other inner dynamics.

Once the first activity was solved, students obtained the first digit of a 3 digit code that would be used to open a padlock and obtain the key that opens the room. The second and third activities should be solved in a specific order, because the third activity provides paper and pencil (and the second activity was designed to test mental calculation). The narrative of the room guides the students to the right sequence, all the activities should be solved to obtain the access code to the final key that unlocks the room. The experience was designed to specifically assess mathematical competencies related to algorithmization, mathematization of situations, mind calculations, and number sense.

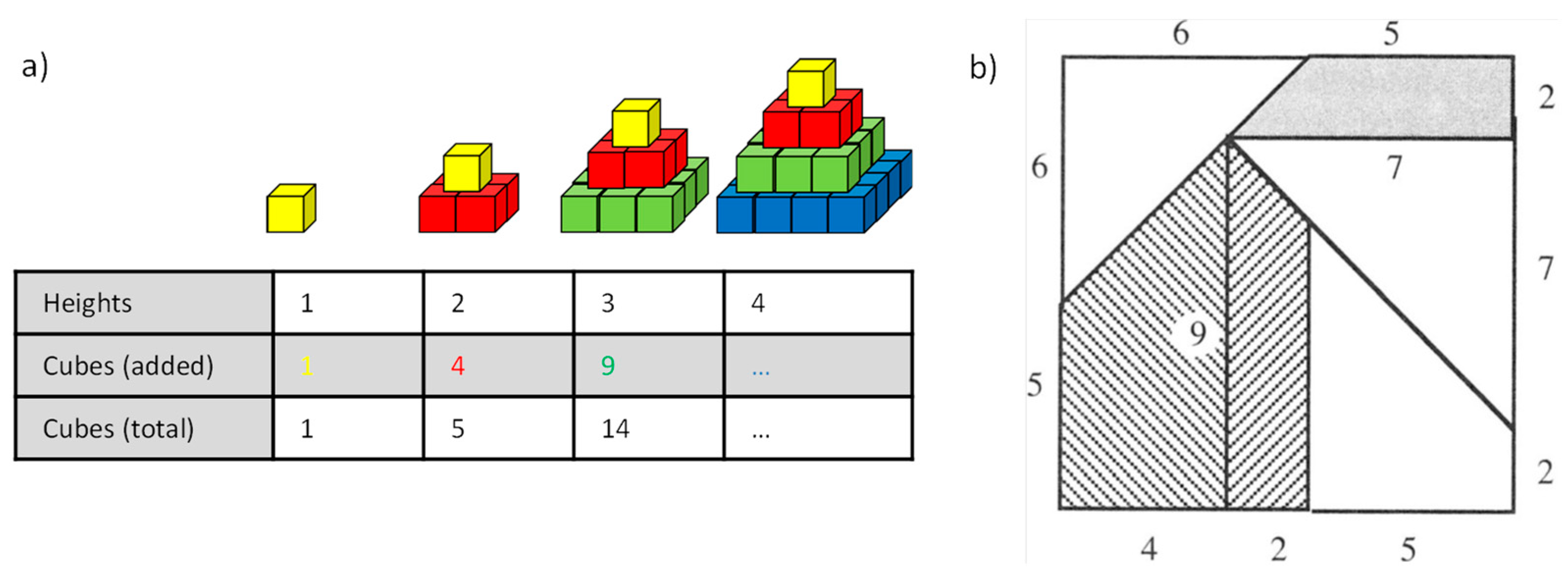
Activity 2 consisted of reproducing a pyramidal pattern, extending the pattern to 11 levels, and then providing the total number of cubes used to build the 11-level-tall pyramid (see Figure 6a). Students were provided with a set of 300 cubes, which were less than the amount needed to build the 11 levels, so that strategy development and mental calculation was expected to be mobilized. The total number of 506 cubes that would be used to build the final pyramid provided a code that was used in the game.

Activity 3 comprised a minor adaptation of the “puzzle enlargement” activity designed by Brousseau [38]. Minor modifications to fit to the narrative were made, in this case, the enlargement of the figure makes the vertex coincide with specific locations on a map. As the original figure was smaller than the provided map, students were invited to enlarge the original figure through following a single clue: “The segment that measures 4 cm on the model will measure 7 cm on your reproduction. I shall give a puzzle to each group of four or five students, but every student will do at least one piece or a group of two will do two. When you have finished, you must be able to reconstruct figures that are exactly the same as the model” (see Figure 6b). As students were provided with scissors, pencils papers and rulers, this activity was designed to be the last of the experience. In this case, the calculations involve a multiplication with decimals (so pencil and paper could be used to aid in the calculation). The enlargement factor of 1.75 provides a code to be used in the EER.

3.2. Data Collection and Analysis Method

The data collection was carried out by audio and video recording, with several hidden cameras located at key points of the learning scenario. Students were recorded by hidden cameras in two different spots of the room (so that no area was out of view), resulting in audio and video data of each experience. Immediately after the experience, students were asked about the educational escape room content (in terms of joy, difficulties, and knowledge).

A transcription of the experiences was made so that didactic analysis methodology [39] could be applied to extract the information needed to determine the degree of activation of certain skills and knowledge.

Didactic analysis is a familiar denomination used in didactic aspect of mathematical research and it includes a set of notions and mechanisms of analysis commonly used by research groups. Here, Font’s model [40] has been used to analyze conceptual and procedural aspects (because of the agreement between our research and the criteria behind Font’s model [41]). Additionally, a brief analysis of the didactic suitability of the formative process has been carried out using a model [42] that agrees with Font’s (sharing the same archetype). Aside from this didactic analysis, the schoolchildren were interviewed immediately after each experience. A competency rubric, designed following Miller’s pyramid, was used to assess the mathematical competence of students (provided in ANNEX 1, see Supplementary Materials).

The experiences were designed as pilot experiments and were implemented during the year 2021 in three educational centers (two schools and one college) in the Spanish province of Cadiz; with the participation of a total of 56 students from the 6th year of Primary Education (approx. 12 years old) and 25 students from the first year of ESO (approx. 13 years old). The educational centers were selected based on a clear distinction in the teaching methodology applied to the development of numerical and arithmetic thinking. The teams of players were composed of between 4 and 6 students grouped heterogeneously. The sample was composed of 23 ABN students and 58 CBC students.

Regarding the trainee teachers involved, three student teachers participated in the mentoring program (two of them were 4th year students undertaking a primary education degree and one of them was a student in a secondary education Master’s degree). They contacted in-service teachers due to the internship stage and used the opportunity to identify common difficulties. The design of the implemented experience was an agreement between the three student teachers, the in-service teachers, and the university researchers. These student teachers were assessed by using a competency rubric (provided in ANNEX 2, see Supplementary Materials); furthermore, the results of their cooperation in the mentoring program were included in their final degree theses and evaluated by a committee.

Online and face-to-face meetings with the researchers in charge (authors of the manuscript) were scheduled in order to provide feedback to the students. Moreover, virtual meetings with in-service teachers at the school were also scheduled to verify that the designed EERs fit their needs, as well as to plan different implementations. The activities presented in this manuscript were co-designed by the researcher in charge and by a group of student-teachers at the University of Cadiz as part of a mentoring program that has already delivered good results in terms of the promotion of professional skills and knowledge [10].

4. Results and Discussion

Due to extension limitations, we focused the study on the analysis of only three transcripts of the relevant activities that composed the whole EER. The selected transcripts were representative of most of the groups. Finally, due to the composition of the sample, the experience was delivered to 5 ABN groups and 12 CBC groups of 4–5 students.

4.1. Solving the Pyramidal Pattern

In this section we present a transcription of two selected experiences (which are representative of the whole experience) of how students solved the pyramidal pattern presented in Figure 6a in the frame of the educational escape room. An extract of the students’ conversation is presented in each section. It should be noted that students were not provided with pencil and paper to carry out the involved calculations.

A fragment from the conversations of one of the game groups is here presented, these dialogues take place just after having read the card corresponding to the activity (all the players begin to handle cubes to assemble the pyramid).

4.1.1. CBC-Instructed Students

• S1: (Giving instructions) We have to assemble eleven.
• S2: (Joining cubes, once having built 5 floors) But it has to be with less cubes… because it has to be like that (points to the draw).
• S1: No, it’s even bigger, it’s up to eleven.
• S3: (After a few minutes) It’s just that we have not enough, there are no more cubes.
• S2: Still two floors remaining, we will have to make it bigger.
• S1: Oh look!… we already have nine floors (dismantles the pyramid), so we are missing these two floors (builds floors 10 and 11).
• S3: (Consulting by radio) I think that we miss some cubes, we have not enough.
• GM: (Confirming that they have understood the activity correctly) That is what the game consists of: deducing the number of cubes that you would have to use.
• S1: Wait, I’m trying!
• S2: Maybe you have to skip those floors.
• S3: It’s just that you don’t have to do it that way, it’s a pyramid and that’s not a pyramid (referring to the fact that only floors 10 and 11 have been built).
• S2: (Checking on the radio) This is impossible!
• GM: No, it’s not impossible. You must think. Let’s see, how many cubes do you have now assembled?
• S1: (After a while, by radio) I had counted 221.
• GM: Ahm, and what do you plan to do now?
• S1: Well, build up to 9 and count, right?
• GM: Try and tell me.
• S1: (Assembling the pyramid up to 9 levels) I think I got it.
• S4: But there are leftover cubes.
• S3: It’s okay, it’s a pyramid.
• GM: How many cubes do you have?
• S1: Ugh… wait (disassembling and counting, they make a mistake in the count and have to reassemble and recount) 285 cubes.
• GM: Well, what do you plan to do now?
• S1: Add with those from before.
• GM: How many were there?
• The students do not remember the number of cubes corresponding to floors 10 and 11. To prevent frustration, after a moment of pause, we provide the number by radio.
• S2: Oh ok, so it’s 285 + 221.
• S3: I have already understood.
• S4: Done! (claps his hands).
• Having no paper support to carry out the operation, they submit (by radio) quantities more or less close to the solution, waiting for radio confirmation.
• GM: I’m not going to confirm the result. You have a lock to enter the result and check if it is correct.
• The students manipulate the lock for a few minutes. The conversation is incomprehensible (they are all talking at the same time and wearing COVID-19 masks), but the recorded video indicates that they try several times by entering numbers close to the solution (506) until the lock opens.

Most of the CBC groups (10/12) attempted to solve the activity exclusively in a manipulative way. That is, by building the 11-level pyramid and counting the cubes which compose it (since they had enough cubes to build up to the 9-level pyramid, this procedure was slow but feasible). Even so, approximately half of the groups of players involved (5/12) failed to physically build the pyramid (as presented in Figure 7b) by not identifying each of the floors of the structure as squares.

In the conversation (lines 1–3), it can be seen how some students do not understand what is asked in the problem. According to Font’s model [40], this denotes a lack of mathematical practice, in that they proceed to act with no analysis of the problem. In the presented transcription, the first (and only) strategy was to try to solve the problem manipulatively and proceed to count the cubes used. Upon encountering obstacles due to the lack of pieces, only one person in this group proposes breaking down the problem in such a way that it can be solved with the cubes provided (lines 6–16). It is also evidenced that students avoid mental calculation as much as possible (lines 30–32). It is detected that the material has served to develop strategies to simplify the problem, but it is also evident that the students prefer not to carry out mental calculation, instead pretending that the teacher validated (by radio transmission) the results that they were suggesting (until they “get” the correct one).

4.1.2. ABN-Instructed Students

• At first, they realize that they have to find a code, but they do not fully understand the instructions: they hesitate between the total number of cubes or the cubes that are added to the provided drawing. The GM asks and cross-questions until they are clear about what is being asked of them.
• GM: How many heights does the problem ask you for?
• S2: Eleven.
• GM: And for eleven heights, how many cubes do you need?
• S2: …nine…
• S3: (building the pyramid up to 4 levels) Oh! Oh, wait. For 4 heights there are 16 cubes. (Talking to a peer) Ask her: for 5 steps we need 25 cubes?
• GM: Yes, now you could build another height. Do you need to build it?
• S2: Twenty-five!
• GM: Come on, now with 6 steps.
• S2: Well 25 + 6!
• S3: No.
• S2: Why not? (he starts counting, builds the 6th floor, talks to S2, and discards his initial idea).
• S2: (By radio) 36 steps?
• GM: Steps or cubes?
• S2: … cubes. Okay, thirty-six cubes for six steps.
• S1: Look! (pointing to the pyramid) 2 × 2 = 4, 3 × 3 = 9, 4 × 4 = 16, 5 × 5 = 25.
• S3: Yes, I knew that too.
• S2: 7 × 7!
• S4: What do you have to multiply?
• S3: By the same number.
• GM: So for 11 steps?
• S2: 11 × 11 = 121 (mental calculation).
• S1: That’s the code!
• They enter the code in the lock, but it does not work. They seem frustrated. They consult by radio if they have made a mistake when calculating. The GM invites them to read the statement of the problem again, where it is specified that they must calculate the total number of cubes (and not those of a specific plant).
• S1: Ok, so let’s slowly add 1 + … 2 × 2 = 4, 5… 06.
• The work is distributed, one is calculating the cubes of the next floor and the others count the accumulated cubes until reaching the solution.

While similar difficulties to those of the CBC group are observed (particularly regarding the intention to solve the problem in an exclusively manipulative way). Approximately 4/5 of the groups developed a strategy to solve the problem in a similar way to the one transcribed below. Of course, errors also occur in the construction of the pyramid.

In the presented situation, students confused steps (floors/levels) with cubes and, at first, they focused on the number of cubes that they are adding (lines 13–16). This group found a pattern of square numbers once they built the pyramid up to the 4th floor and (line 16), consequently, they focused on developing the pattern found. When entering the code into the lock, they expected it to be correct (11 × 11 = 121), but it did not open and they seemed frustrated (line 24). We had to invite them to read the statement aloud again and ask “what they are being asked for”, until they realized that they were being asked for the total number of cubes in the pyramid. In general, these children showed a level of mathematical practice similar to those of the CBC group but they developed (cooperative) mental calculation strategies to solve the problem without having to build the complete pyramid.

4.2. Solving the Puzzle Enlargement

When opening the box, students were provided with the original figure (printed on yellow paper), the map, rulers, pencils, and a set of sheets (red sheets, grid sheets, and clear white sheets). The transcribed experience follows a CBC group, but no significant differences were identified in the ABN groups.

• Students read the instructions and clear the table to allocate the sections of the maps: the vertex of the augmented figure reveals some key positions on the map, but the size of provided figure does not fit with the map.
• S1: What about if we cut this (referring to the original figure) and put here the triangle (i.e., in the map). Ask the teacher, can we cut the figure?
• S2: Wait, wait! Don’t cut it… we shall cut the whole square (i.e., the whole figure, which is printed on yellow paper).
• Students manipulate and cut the original figure into its components. Then try to fit it to the map by separating the pieces.
• S3: This is so hard!
• S1: Shut up! (She takes all the figures and re-builds the original puzzle).
• Students use the provided red paper to reproduce copies of the original figure with no augmentation and share a copy with all the members of the group.
• One of the students (S4) starts testing random numbers on the padlock.
• S2: Ok, you can try, but we must do the calculation… teacher said.
• S1: Maybe we can fit the whole square with the map
• They use the red papers to build a square that fits with the provided map and allocate the original figure next to the new structure.
• S2: Now it is said that we have to change 4 to 7.
• Students augments the edge of the figure, but they do not enlarge the rest of the figure (see Figure 8).
• S2: We have to enlarge all the figure.
• Students try to enlarge the figure by adding 3 cm to each section of the perimeter. However, they realize that this is not going to solve the problem when drawing the augmented figure on a sheet.
• S1: I surrender
• GM (by radio): What happens?
• S2: The augmented figure doesn’t fit to the map.
• GM: Why?
• S2: Because adding 3 to each figure doesn’t work
• GM: Adding? That’s the way you enlarge? Let’s think… you’ve a smartphone, right? When using the camera to zoom in “ten times”, what is shown on the screen?
• S2: ×10… oh!
• Student suddenly cuts radio communication and explains to their peers.
• S2: We have to multiply by tens.
• Students try to multiply by tens, but quickly realize that 10 is not the augmentation ratio. Now they are conscious that “they have to multiply” and start searching for the augmentation ratio.
• S1: Maybe we can see the percentage 3 on 7 is a (doing the calculation) … uf!… way too complex.
• S2: Maybe using a rule of three? We went from 4 to 7 by adding 3.
• GM (by radio): do not use additions…
• S3: And how do we go from 4 to 7 with no additions
• S1: Multiplying 7 by something?
• Students finally use pencil and paper to divide 7/4; getting 1.75
• S1: This is much easier than with percentages.
• S2: Ok, so let’s enlarge all figures
• Students distributes the original figures and try to enlarge each single figure, they sometime fail when calculations have to be traduced to a geometric figure; but finally they manage to build the enlarged figure.

In this situation, students seem to have a better understanding of the goal of the problem (enlarging the figure) and could also self-validate the augmentation of the figure. So, the performance in terms of mathematical practice and reasoning seems to improve during the Escape Room experience; they are learning by doing mathematics. All the groups failed when enlarging the original figure and all the groups tried to “add 3” rather than calculating the scale to augment the figure (line 15). Once they were asked about “how to augment a figure”, they realized that the enlargement should be proportional (in the transcribed text, the teacher used the analogy of a camera zoom, see line 21).

A collection of failures is presented in Figure 8a. Despite the many fails evidenced, students seemed to engage with the problem and stay focused on the game, trying to solve the puzzle both in a manipulative and abstract way (see Figure 8b). On the other hand, all the groups used paper and pencil to solve the calculation. When questioned about this at the end of the experience the most common answer was that “decimals are too difficult for mental calculations”.

While the presented fragment demonstrates with the CBC group experience, no meaningful differences with ABN students were identified. ABN students show the same difficulties and face the same obstacles. They also refuse the use of mental calculations and prefer the use of paper and pencil when provided.

4.3. Outcomes of the Two Methods

By using the scores registered using the rubrics provided in ANNEX 1, a chi-square test of independence was carried out. The null hypothesis postulates that the use of the ABN method and the development of a specific sub-competence are not related (i.e., they are independent). The alternative hypothesis considered that the use of the ABN method and the development of a specific sub-competency are associated (i.e., they are not independent). It has to be noticed that the rubric used to assess schoolchildren (ANNEX 1) was coded so that 1 = does not know and 5 = does know. Results of the chi-square test are presented in

Table 1. Chi-square values obtained for each subcompetence.

Dimension	Subcompetence	Χ2
Cognitive	Language	0.41
	Modelling	12.05
	Thinking and reasoning	4.87
Procedural	Use of tools	21.92
	Strategy development	7.67
Emotional	Productive disposition	3.02

. A chi-square critical value of 3.84 was obtained.

Attending to the results presented in Table 1, and as χ² corresponding to mathematical language can be considered as 0, one can conclude that there is no relation with the ABN–CBC methodology when considering the development of the mathematical language (i.e., the development of the mathematical language is independent of the methodology). However, this is not the case for other subcompetencies as, for example, the “modelling” skill. Indeed, it can be considered that the use of the ABN methodology boosts the skills related to the construction of mathematical models (as well as to critically analyze and evaluate existing or proposed models) in connection with the use of tools.

The positive progress of the “strategy development” of ABN students is also remarkable. One can conclude that the use of the ABN method is not independent of the development of, at least, the skills related to mathematical modeling, the use of tools, and strategy development.

On the other hand,

Table 2. Mean scores (using the ANNEX 1 rubric) obtained by ABN–CBC schoolchildren.

	Competence
	Language	Modelling	Thinking	Tools	Strategy	Disposition
ABN (P.E.)	3.22	3.39	3.17	3.87	3.26	3.61
CBC (P.E.)	3.29	2.76	2.94	3.53	2.82	3.59
CBC (S.E)	3.12	2.96	2.76	3.2	2.8	3.2

shows the mean scoring of CBC–ABN schoolchildren. It should be noted that the score obtained in the abovementioned competences of modelling, the use of tools, and strategy development are consistent with the conclusions of the χ² test. It can also be observed that the development of the “use of tools” competency seems to worsen not only in CBC students but also in secondary education (S.E.).

Finally, concerning the performance of the methods, one can conclude that the ABN method is at least 10% more efficient in developing the “modelling”, “use of tools”, and “strategy development” competences. The authors would also like to highlight the satisfactory progress of the “productive disposition” of the participants, which scores over 3, considering that the maximum scoring on the related item is 4. So, a good performance of the EER is determined and no mathematical anxiety was induced during the experience.

4.4. Profits for Student Teachers

Student teachers’ professional development was analyzed by using a simplified model (presented in Section 2). Of course, there are deeper and more complex models (such as MTSK model [43], for example). However, such models are difficult to approach for those not specifically instructed on the model. The selected model was chosen for its simplicity, comprehensibility, and accessibility (even for non-specialized researchers), while being useful for the research in didactic of the mathematics. According to this, the design, implementation, and analysis of the complete experience has mobilized several professional competencies. First, trainee teachers were conventionally evaluated in order to attain an idea of their mathematics-related capabilities. They were also evaluated in the same manner at the end of the formative process. In doing so, we found:

• Math knowledge: A meaningful improvement on the procedures for solving mathematic problems was demonstrated, showing a positive development in their capabilities to think and reason about mathematics. They also slightly improved their abilities regarding mathematical models, while no improvement in the use of mathematic language was detected.
• Didactic knowledge: In this regard, trainee teachers had to identify schoolchild difficulties during the “practicum” stage and then develop an educational escape room to manage such difficulties. As the escape room was co-designed, no clear information was obtained. However, participating in the development of the experience improved trainee teachers’ skills for making connections in mathematics as well as integrating mathematics with other fields. They all were able to manage the situation with the schoolchildren, negotiating, provoking, or giving clues to unravel the experience.
• Procedural domain: This was the dimension with the best performance. Student teachers showed meaningful improvement in their abilities for using tools to “make mathematics”. In the same way, they all seem to have gained flexibility and have promoted their abilities to stablish generalizations (so that they were able to develop strategies for solving math problems with improved fluency).
• Emotional domain: Student teachers were already well disposed towards mathematics prior to the mentoring program, so no meaningful improvements regarding this aspect was detected.

Student teachers were taught in ABN and CBC methodologies prior to the experience and had to deliver a text comparing both methodologies and identifying weakness and strengths of both mathematical methods. It has to be highlighted that a proper design of the activities included in the EER should be accompanied by an analysis of the possible difficulties which may emerge during the experience. Such activities should be designed to allow children to reach an autonomous solution of the problem, displacing the “center of gravity” from the teacher to the student.

As this research focuses on the “assessor” role of the trainee teachers, reaching an adequate degree of development of their own mathematic competence was a pivot point. As seen, mathematics knowledge of the trainee teachers involved was promoted during the experience. On the other hand, by the end of the experience, the involved student teachers were interviewed and asked about the experience in terms of professional didactic–mathematic knowledge. They all stated that they felt much more confident in their capabilities to instruct mathematics, showing enthusiasm towards mathematics learning, and improving self-belief for being able to adapt educational environments; finally, they all confessed to be more passionate about presenting innovative practices to a class. These findings agree well with those available in the literature [44].

Finally, we would like to highlight that no quantitative or qualitative research was carried to reach these conclusions. Rather, the participant trainee teachers delivered a final degree thesis (or a final Master’s thesis, depending on the student), which was delivered and presented in a thesis viva. The theses were scored 9.5, 9.3, and 8 (out of a maximum score of 10) by the committees, so the works of the student were well ranked and considered suitable to be stored and made available in the university repository. This was the main marker used to assess the performance of the participant trainee teachers.

5. Conclusions

This manuscript reports on a case study of the implementation of mathematic educational escape rooms (experiences were delivered to schoolchildren taught by using different methodologies—ABN and CBC). To do so, extracts of the in-game conversations were recorded and analyzed. The experiences were co-designed by trainee teachers, in service teachers, and university researchers. So, this study affects all the corners of the educational environment.

Regarding the original objectives and from the point of view of the schoolchild, during the interview they stated that they had enjoyed the escape room experience and had not felt “assessment pressure” (O1). They felt some urgency because they wanted to “win the game”, but all the groups felt far less anxiety than in a written exam. With respect to the CBC groups, it has been demonstrated that they prefer not to perform mental calculations, and they were also not familiar with most manipulative materials (they stated that they did not use manipulatives in conventional lessons). They were able to solve the problems with a reasonable amount of guidance and clues, but they encountered difficulties when asked to identify patterns and regularities. Overall, CBC students show insufficient development in productive disposition, the use of tools, modelling, and strategy development; however, they show an adequate development in language and reasoning.

During the experience, the activation of two major skills could be seen: observation and critical thinking (as the students had to collect data, as well as understanding and interpreting the meaning of the information). So, we consider that the EER design is well suited to the original aim of “strengthening the problem-solving skill” (so it can be used to assess mathematical competencies, Aim 2).

On the other hand, ABN students showed similar results with respect to mental calculations (they preferred using paper and pencil), but they also showed a higher ability to carry out mental calculations when mandatory. ABN students were more familiar with tools and manipulatives (they stated that the use of such tools occurred “sometimes” in conventional lessons). As in the case of the CBC students, they were able to solve the problems with a reasonable amount of guidance and clues, but they showed fewer difficulties in identifying patterns. Overall, ABN students showed insufficient development of modelling, mathematic language, and strategy development; however, they show an adequate development on productive disposition, the use of tools, and reasoning (this fulfills Aim 3). In this regard, ABN students showed a positive 10% additional performance of certain mathematical competences.

We conclude that schoolchildren tended to show some degree of math-phobia, mainly due to evaluations but also due to a lack of comprehension of what are they really doing when solving an operation. By using the grid//ABN method, schoolchildren could easily attain a deeper comprehension of what is being carried out. The ABN method might not be “easier” for schoolchildren but might be more adequate for developing the mathematical competences.

Finally, regarding Aim 4, student teachers involved in the experience specifically mentioned the value of interacting with “real children” and with in-service teachers. They also state that co-designing the experience was a valuable learning opportunity and we were able to verify that some professional competencies were successfully developed during the experience (especially those concerning didactic knowledge).

To close this section, and as a note for the future; families and educational institutions have greatly valued the interventions of this project. Indeed, both demand more interventions. Families and in-service teachers stated that schoolchildren greatly enjoyed the experience while doing mathematics. As a final reflection, the authors would like to emphasize that these studies need to be more extensive, by including a larger number of students, in order to carry out statistical analyses which allow a proper characterization of the outcomes of the methodologies. In this study, we demonstrated that educational escape rooms can be used as assessment tools (replacing traditional tests that induce mathematics anxiety in students). Once this step is taken, implementing EER in conventional courses and gathering as many participants as possible should be the next research phase.