1. Introduction
In many fields of applied sciences, such as engineering, medicine, insurance, economics, and marketing, studying and analyzing count data play a significant role. Count data sets are often modeled using a Poisson distribution. However, the Poisson distribution cannot handle overdispersed data sets. Overdispersion occurs when the variance exceeds the mean. As a consequence, many researchers have developed mixed-Poisson distributions to provide alternative models for overdispersed count data, including [
1,
2,
3,
4]. Recent studies in this area are [
5,
6,
7], among others. When using count data as a response variable, Poisson regression is a popular model. It is assumed that the dependent variable’s mean and variance are both identical in the Poisson regression model. There is a lot of evidence to support the overdispersion that the count data sets exhibit. Thus, the Poisson regression’s theoretical premise is practically violated. In the beginning, negative binomial regression (NB) was employed to model overdispersion in the context of count regression. The Poisson-transmuted exponential linear model was introduced by [
2] and applied to healthcare data sets. The generalized Poisson–Lindley linear model was introduced by [
8], who showed that generalized Poisson–Lindley linear models provide better modeling abilities than Poisson and NB regression models when there is an overdispersion of data.
There are many instances of integer-valued time series in the real world, such as the number of births at a hospital in successive months, the number of accidents, the number of patients, the number of chromosome exchanges in cells, and so on. As an inaugural approach, refs. [
9,
10,
11] proposed a stochastic model for integer-valued time series called INAR(1)P for a first-order non-negative integer-valued autoregressive process with Poisson innovations. As time series of counts mostly exhibit overdispersion, the Poisson distribution is no longer applicable to the INAR(1) process. To overcome this issue, researchers have proposed different INAR(1) processes with flexible innovation distributions. Consequently, Aghababaei Jazi et al. [
12] proposed an INAR(1) process with geometric innovations (INAR(1)G), Altun E. [
5] presented an INAR(1) process with new Poisson weighted exponential innovation distribution (INAR(1)PWE),Altun et al. [
13] introduced an INAR(1) process with Poisson quasi-xgamma innovations (INAR(1)PQX), and so on. Although these methods are excellent for overdispersed time series count data sets, they have significant drawbacks in real-world applications. By discovering more INAR(1) models, more opportunities will be available for optimally fitting real data sets by choosing those models that are most appropriate for each situation.
Therefore, this paper provide new facts on what we call a two-parameter mixed-Poisson distribution, namely the Poisson extended exponential (PEE) distribution, obtained by compounding the Poisson distribution with the extended exponential (EE) distribution proposed by [
14]. The EE distribution is obtained by mixing exponential and gamma distributions. The probability density function (pdf) of the EE distribution is given by
It is sometimes denoted as EE
to specify the parameters. This distribution also appears in a different form in [
15], presented as a two-parameter Lindley distribution. Recent statistical literature has paid a lot of attention to the EE distribution. As a result of this, an EE regression model was proposed by [
16] in which the reparameterization of the EE model based on the mean is performed. In addition, de Andrade et al. [
17] proposed the exponentiated generalized EE distribution. Refs. [
18,
19] also showed the novelty and possibility of EE distribution through their study of different generalizations of the EE model. The PEE distribution appears in [
20] under a discrete two-parameter Poisson–Lindley distribution version. However, to the best of our knowledge, some of these aspects are understudied, and the goal of this research is to rehabilitate them from applied perspectives. In particular, the appealing applicability and competence of the EE regression model inspired us to present a two-parameter mixed-Poisson distribution created by compounding Poisson with the EE distribution and elucidating its regression characteristics and associated INAR(1) process.
In the rest of the paper, the sections are arranged as follows.
Section 2 presents the PEE distribution and explores some of its statistical properties. The finite sample performance of the estimation method is examined in
Section 3 with a simulation study for the maximum likelihood estimation of the model parameters. A regression model is discussed in
Section 4. The INAR(1)PEE process is developed in
Section 5 using PEE innovations. An empirical analysis of three real data sets is conducted in
Section 6 to prove that the proposed model is useful when compared to some existing models. In
Section 7, a few concluding remarks are presented.
2. The Poisson Extended Exponential Distribution
In the new formulation, Poisson distribution is compounded with EE distribution to produce a mixed-Poisson distribution, which is known as the PEE distribution. Let the random variable
X follow the PEE distribution which holds the following stochastic representation:
P
and
EE
, where
and
. Then the unconditional probability mass function (pmf) of
X has the following form:
In fact, by construction, the random variable X has the Poisson distribution with a parameter , and we assume that the parameter represents a random variable with the EE distribution. Then, the unconditional distribution of X is obtained by the classical method of compounding, which gives
The gamma function was used here and the relation = , for any positive integer m.
The discrete two-parameter Poisson–Lindley distribution proposed by [
20] has the same pmf but had a different support for the parameters, i.e.,
, and merely explored its various distributional characteristics. In contrast to [
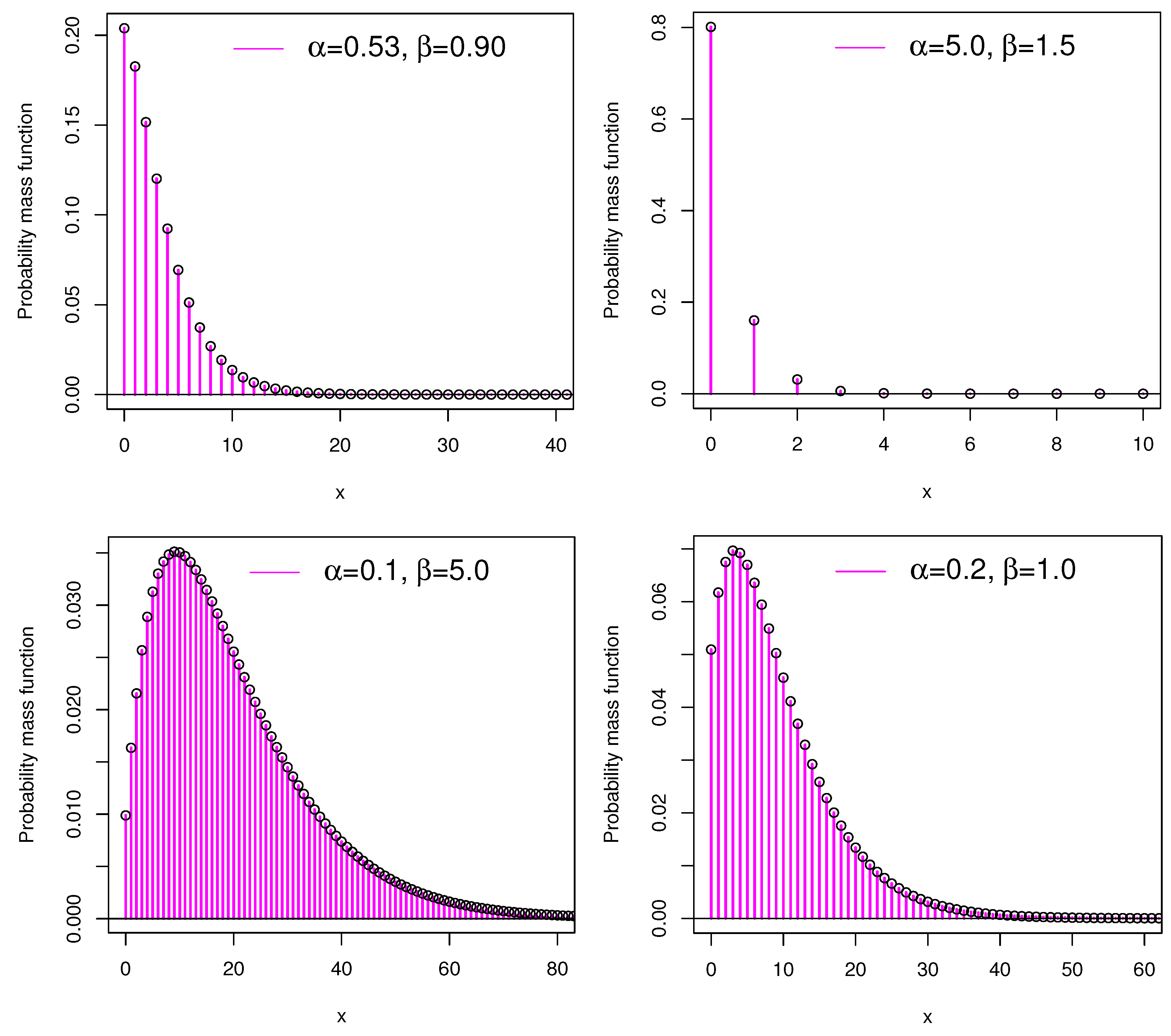
20], our applied work is more focused on the count regression model and the accompanying INAR(1) process, which are of current interest. Our theoretical work adds more aspects to the aforementioned study. Different pmf shapes are presented in
Figure 1 for several parameter combinations of PEE distribution. The figure unequivocally demonstrates that the PEE distribution is right skewed.
2.1. Moments, Skewness and Kurtosis
Some results that can be derived from [
20] are now presented in this portion. The probability-generating function for a random variable
X with the PEE distribution is provided by
for
. Correspondingly, the moment-generating function of
X is given by
for
. Let
r be a positive integer. The
rth factorial moment of a random variable
X with the PEE distribution is given by
That is, in accordance with the definition of the rth factorial moment, we have
From the last equality, (
5) is determined by applying the relation,
,
r being a positive integer. The first four non-central moments are derived as
and
The variance of
X is given by
The explicit versions of measures such as skewness and kurtosis of
X can be found using the following formulas:
and
respectively.
2.2. Dispersion Index and Coefficient of Variation
The dispersion index (DI) of the PEE distribution is given by
As a complementary measure, the coefficient of variation (CV) of the PEE distribution is given by
Now,
Table 1 and
Table 2 provide some numerical values for the PEE distribution’s mean, variance, and DI for a variety of parameter configurations. For the values considered, we check the mean, variance, and DI of the PEE distribution, and it is inferred that the DI of the PEE distribution is always greater than one, clearly showing overdispersion.
5. INAR(1) Model with PEE Innovations
The INAR(1) process is widely used in the modeling of time series of counts in several scientific disciplines, including actuarial, finance, and medical. By applying the binomial thinning operator, INAR(1) differs from the first-order autoregressive process (AR(1)). The INAR(1) process is given by
where
, and the innovation process is denoted by
which are independent and identically distributed (iid) integer-valued random variables having mean,
and variance,
The binomial thinning operator is denoted by the symbol ∘ and is defined as
where
is the sequence of Bernoulli random variables with probability
For the INAR(1) process, the one-step transition probability matrix is given by
where
There are many examples in real life where these types of stochastic processes play a role, including the number of passengers each year, the growth of bacteria each day, the number of scientific books cited, and many more. Here, a new INAR(1) process is introduced by assuming that the
innovations follow a PEE distribution. The one-step transition probability of the INAR(1)PEE model is given by
So, hereafter, the described process will be called the INAR(1)PEE process.
Weiss C.H. [
21] provide the mean, variance, and DI of
by using the mean, variance, and DI of the innovation distribution. For the INAR(1)PEE process, they are
and
According to [
21,
22], the conditional expectation and variance of the INAR(1)PEE process are given by
and
respectively.
5.1. Estimation
The conditional maximum likelihod (CML), conditional least squares (CLS), and Yule–Walker (YW) methods are used to obtain the unknown parameters of the INAR(1) process.
5.1.1. Conditional Maximum Likelihood
The complicated form of the likelihood function resulting from the usual maximum likelihood method motivated the researchers to use the CML method instead of maximum likelihood. The knowledge of the transition probabilities is sufficient for the creation of likelihood in the CML technique since conditioning on the first observation results in a simple form of the likelihood, whereas there is no such conditioning present in the traditional maximum likelihood approach. The conditional log-likelihood function for the INAR(1)PEE process of the random sample
based on associated observations
is given by
where
is fixed, and
is given by (
13). By the maximization of (
19), the CML estimates are obtained by using the
constrOptim function of R.
5.1.2. Conditional Least Squares
The below function is minimized to obtain the CLS estimates of the parameters of the INAR(1) process
5.1.3. Yule–Walker
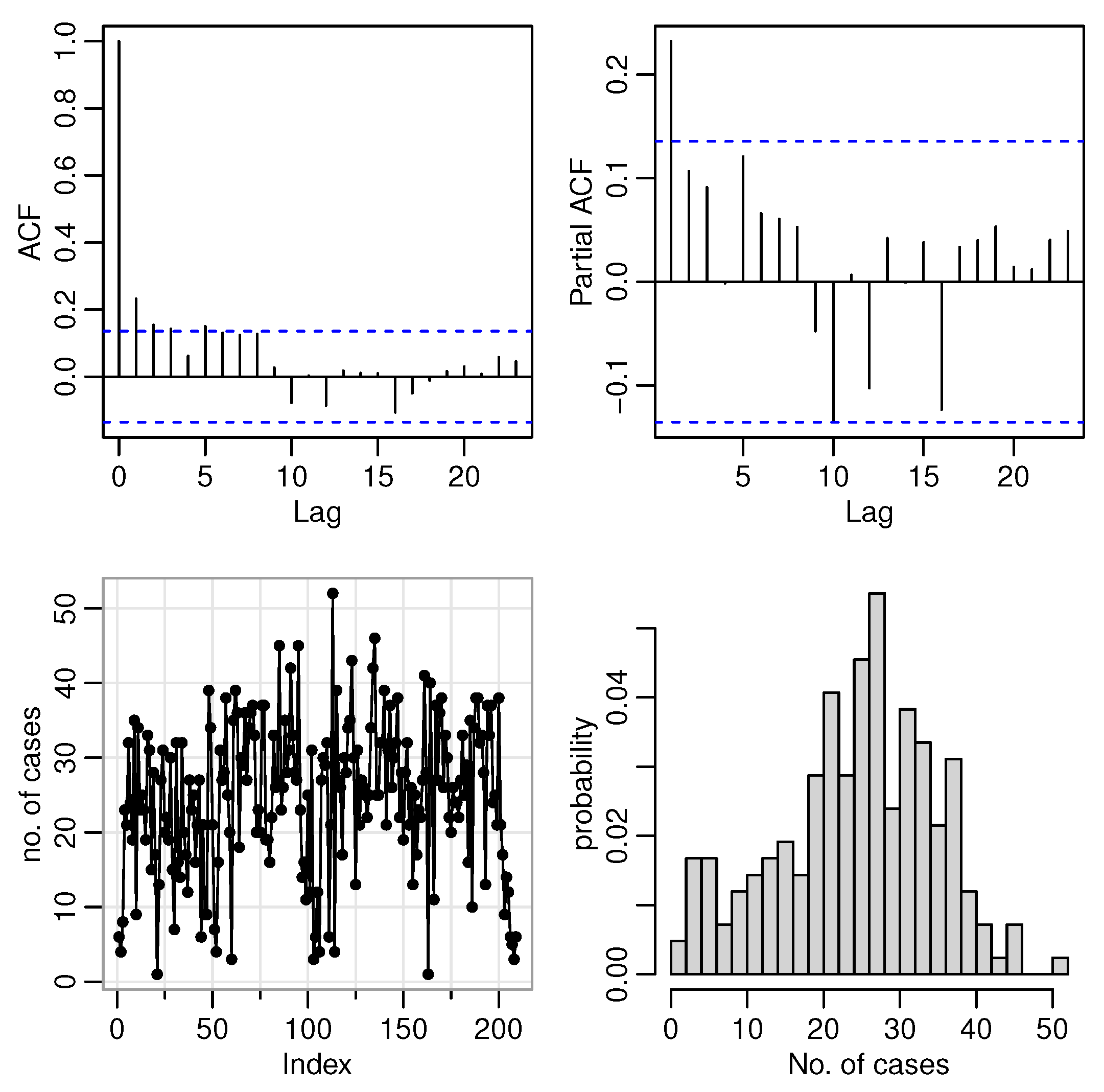
As a result of the YW approach, the theoretical moments as well as the empirical ones are solved synchronously. Given that the autocorrelation function (ACF) of the INAR(1) process at lag
is
, the YW estimate of
p is given by
where
Now, the theoretical mean is solved with their empirical equivalents to derive the YW estimates of
and
. More precisely, when the theoretical mean equated with the empirical mean, we obtain
By substituting (
21) in (
16) and equating it with the sample dispersion,
is obtained.
5.2. Simulation
A simulation study was performed to check the finite sample performance of the CML, CLS, and YW estimates. In this regard, the number of replications is chosen as
for different sample sizes,
50, 100, 200, 300, and 500. The two parameter vectors used here are (
) and (
). The simulation results are interpreted based on the biases and MSEs. The R-code is given in
Appendix A.
Table 6 and
Table 7 show the results. The biases and MSEs of the CML estimates are the smallest when the three estimation methods are compared, and the CML estimation approach outperforms the others. The CML estimation approach is then applied.