Abstract
This paper addresses the modification of the F-test for count data following the Poisson distribution. The F-test when the count data are expressed in intervals is considered in this paper. The proposed F-test is evaluated using real data from climatology. The comparative study showed the efficiency of the F-test for count data under neutrosophic statistics over the F-test for count data under classical statistics.
1. Introduction
The F-test for two counts obtained from the Poisson distribution has been applied for the testing of the hypothesis that two counts differ significantly vs. the alternative hypothesis that there are two counts that do not differ significantly. The F-test for two counts is used to test whether the two counts exposed to different conditions (respectively) are significantly different (see Kanji [1]). The F-test works when the sample is obtained under the same conditions. This type of test is applied for testing the occurrence of counts in a fixed time and when the time interval is different. The details of the F-test when the counts are obtained from the Poisson distribution can be found in Kanji [1]. A powerful test for comparing the means of the Poisson distribution was presented by Krishnamoorthy and Thomson [2]. The application of the count data in the field of education was studied by Hilbe [3]. The application and goodness-of-fit test were studied by Puig and Weiß [4]. Various applications of this kind of test can be seen in [5,6,7,8,9,10].
Weather and wind forecasting and estimation are conducted using statistical models. The statistical tests are applied for testing the significance of the models used in the estimation and forecasting of wind speed. For the applications of statistical techniques and methods, the reader may refer to [11,12,13,14,15,16,17,18,19,20].
The F-test for two counts under classical statistics is usually applied when counts from the Poisson distribution are sure, certain, and determinate. Viertl [21] stated that “statistical data are frequently not precise numbers but more or less non-precise, also called fuzzy. Measurements of continuous variables are always fuzzy to a certain degree”. When the count data are recorded in an interval such as the minimum count and the maximum count, the F-test for two counts cannot be applied. In such a situation, the statistical test designed under fuzzy logic can be applied. The application of statistical tests under fuzzy logic can be seen in [22,23,24,25,26,27,28,29].
The idea of neutrosophic logic was introduced by Smarandache [30]. The efficiency of neutrosophic logic can be found in Smarandache [31]. Some applications of the neutrosophic logic were described in [32,33,34,35,36]. Neutrosophic statistics with applications were discussed by Smarandache [37]. The statistical methods to deal with neutrosophic numbers were discussed by Chen et al. [38,39]. Aslam [40] introduced the F-test to perform an analysis of the variance test. Various neutrosophic tests with applications can be seen in [41,42].
Generally, the F-test under classical statistics is applied for testing the equality of variance of two population variances. The existing F-test for two counts (Poisson distribution) is applied when counts are determined or all parameters involved are certain. The F-test under classical statistics cannot be utilized when counts are recorded in an interval. According to the literature, to the best of the author’s knowledge, no F-test for two counts (Poisson distribution) can be found when counts are recorded in the interval. The main focus of the paper was to develop the F-test under neutrosophic statistics when two counts are modeled from a Poisson distribution. Data from the weather department are applied for the illustration of the proposed F-test for counts. It is expected that the proposed F-test for counts is more efficient than the existing F-test for counts under classical statistics.
2. Methods
Kanji [1] reported the F-test when two counts follow a Poisson distribution. Kanji [1] presented the statistical test when counts are obtained in a fixed time and obtained over different time intervals. Mathematical proofs of the F-test for two counts when the number of events occurring in a fixed time and different periods of time are shown in the Appendix A (Theorems A1 and A2). Let us assume that and are two neutrosophic counts consisting of determinate and indeterminate parts. For the measure of and indeterminacy in counts, see [43,44,45,46,47,48,49].
Theorem 1.
The statistic in neutrosophic form when counts are obtained in the same period of time is given as
Proof.
The basic operation on neutrosophic numbers can be performed as described below.
Let and for be neutrosophic numbers obtained from the neutrosophic F-distribution (see [37]). According to [38], the following operation can be performed on the neutrosophic numbers:
or
Suppose that is the lower value, is the upper value of the neutrosophic form, and is the measure of indeterminacy.
According to [1,37,38] and Theorems A1 and A2, we have
i.e.,
Note that and are the lower and upper counts of the first population, respectively, and and are the lower and upper counts of the second population, respectively.
Using the basic operation, the neutrosophic form of can be written as
or
where presents the neutrosophic F-distribution degree of freedom. □
Theorem 2.
To test the null hypothesis that, the F-test, say , is given as .
Proof.
Let and be count in intervals for the first and the second populations, respectively. Let and be the neutrosophic forms of these counts, where and are the measures of indeterminacy for counts in population 1 and population 2, respectively. By following Theorems A1 and A2, we can proceed as described below.
From [1], the F-test for classical statistics is given by
The F-test, say , under neutrosophic statistics is given by
The F-test under indeterminacy is expressed as
□
Suppose that the first population mean is and the second population mean is . To test the null hypothesis that , the F-test, say , based on neutrosophic counts and is defined as
The statistic is modeled by a neutrosophic F-distribution with degrees of freedom (see Aslam [50]). The statistic in neutrosophic form can be expressed as
The proposed statistic is a generalization of the existing F-test for two counts of data. The statistic presents the existing F-test for two counts of data. Note that presents the indeterminate part, and is a measure of uncertainty associated with . The proposed statistic becomes the existing statistic when.
Theorem 3.
The proposed statistic in neutrosophic form over the different periods of timeandis given as
Proof.
Let and be different times with counting rates and , respectively. Suppose that is the lower value, is the upper value of the neutrosophic form, and is the measure of indeterminacy.
According to [1,37] and Theorems 1 and 2, we have
and
i.e.,
Note that and are the lower and upper counts of the first population, respectively, and and are the lower and upper counts of the second population, respectively.
Using the basic operation, the neutrosophic form of can be written as
or
where presents the neutrosophic F-distribution with degrees of freedom. □
Theorem 4.
The statistic over different periods of timeandand counting ratesandis given by
Proof.
According to [1] and Theorems A1 and A2, the F-test for classical statistics is given by
The F-test, say , under neutrosophic statistics is given by
The F-test under indeterminacy is expressed as
when two counts are observed over diverse periods of time and, with the counting rates and . The proposed statistic is defined as
The proposed statistic in neutrosophic form can be expressed as
□
The existing F-test is a special case of the proposed statistic . The statistic presents the existing F-test for two counts of data. Note that presents the indeterminate part and is a measure of the uncertainty associated with . The proposed statistic becomes the existing statistic when .
3. Application
The US daily and monthly weather recorded data which broke records are used to show the application of the proposed F-test. The daily or monthly records are noted in intervals rather than the exact number. The record weather data follow a Poisson distribution as these are count data; the events are independent, the average rate of record broken data during the specified time can be calculated, and two records are assumed to be not noted in the same time period. The low minimum, low maximum, high minimum, and high maximum data for daily and monthly records were accessed on 7 January 2021, through https://www.ncdc.noaa.gov/cdo-web/datatools/records. The daily record and monthly record data are presented in Table 1 and Table 2, respectively (see Aslam [50]). The weather data in intervals can be adequately analyzed using the proposed F-test as compared to the F-test under classical statistics. Table 1 and Table 2 indicate that the record-breaking data were recorded for the same time periods (daily records/monthly records); therefore, the statistic can be suitably applied when . In Table 1 and Table 2, the values of are also shown. The proposed test for the daily records (last 30 days) was implemented according to the following steps:

Table 1.
US daily records.

Table 2.
US monthly records.
- Step-1
- State vs. .
- Step-2
- Let = 5% and the corresponding critical value at be 1 using the F-table from Kanji [1].
- Step-3
- For the last 30 days, the values of are calculated as .
- Step-4
- Accept as .
The computed value of falls in the acceptance region, which leads to acceptance of the null hypothesis with the conclusion that there is no significant difference between the two counts for less than 30 days. Similarly, the other results for US daily and monthly records can be interpreted.
4. Comparative Study
A statistical test based on neutrosophic statistics has an edge over the statistical test based on classical statistics. Therefore, in this section, a comparison of the proposed F-test with the existing F-test is presented. The proposed F-test consists of two parts known as the determinate and indeterminate parts, with the latter having the measure of indeterminacy. The proposed F-test is reduced to the existing F-test when record data are measured as exact values. The neutrosophic analysis for the last 30 days and the last 365 days is shown in Table 3 (see Aslam [50]).

Table 3.
Neutrosophic analysis of two datasets.
For example, the neutrosophic form of the statistic for the records of the last 365 days (US daily record) is expressed as . This neutrosophic form has two parts. The first part 0.4421 denotes the values of statistics under classical statistics. The second value denotes the indeterminate part, and = 0.2611 is the measure of indeterminacy associated with the test. Note here that the proposed F-test is reduced to the F-test under classical statistics when = 0. From the analysis, it can be noted that the proposed F-test provides the values of the test statistic in the interval from 0.4221 to 0.5713 rather than the exact value. From this study, it is clear that the existing F-test gives the determinate value of the statistics while the proposed F-test for two counts from the Poisson distribution gives the values in the interval, in addition to information about the measure of indeterminacy.
Another advantage of the proposed test over the existing F-test is that, when = 5%, the probability of rejecting when it is true is 0.05, the probability of accepting is 0.95, and the measure of uncertainty/indeterminacy associated with the test is 0.2611. This is the case of paraconsistent probability where the total probability (0.05 + 0.95 + 0.2611 = 1.2611) lies in intervals from 1 and 3 (see Smarandache [37]). For the proposed test, the total probability associated with the test can be greater than 1; however, for the existing test, the total probability associated with the test is always equal to 1. Therefore, the proposed test is more informative than the existing F-test in terms of the probability associated with the test.
5. Power of the Test
In this section, we compare the performance of the proposed test with the existing F-test for counts in terms of the power of the test by following Aslam [51]. Suppose that and are the type-I error (the chance of rejecting when it is true) and type-II error (the probability of accepting when it is false), respectively. Let be the power of the test. A simulation study was performed to calculate the power of the test for various values of . The values of the power of the test of the proposed F-test for counts when = 0.05 are shown in Table 4. The values of the power of the test of the proposed F-test for counts when = 0.01 are shown in Table 5. The simulation process to calculate the power of the proposed test is explained as follows:

Table 4.
The values of the power of the test when = 0.05.

Table 5.
The values of power of the test when = 0.01.
- Generate 100 values of counting data at various values of .
- Specify the values of = 0.01 and = 0.05 and select the corresponding table values using the F-table from Kanji [1].
- Compute the test statistic and record the number of values accepting and not accepting .
- The power of the test can be computed from the ratio of values accepting to the total number of replications.
In Table 4 and Table 5 the first value when presents the power of the test under classical statistics. From Table 4 and Table 5, it can be seen that, as the values of increased, the values of the power of the test also increased. For example, from Table 4, it can be noted that the value of the power of the test was [0.90, 0.90] when and the value of the power of the test was [0.90, 0.97] when. The curves of power of the proposed F-test for counts are shown in Figure 1 and Figure 2. Figure 1 and Figure 2 also show that as the values of increased, the values of the power of the test also increased.
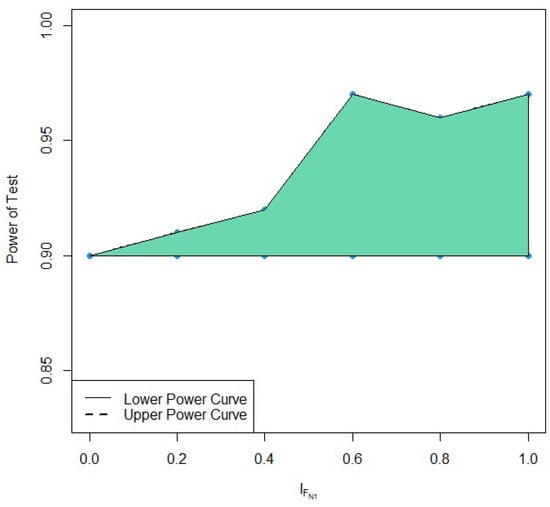
Figure 1.
The curve of the power of the test when = 0.05.

Figure 2.
The curve of the power of the test when = 0.01.
6. Concluding Remarks
The modification of the F-test for two counts of data came from the Poisson distribution presented in the paper. The mathematical proofs to the equations under neutrosophic statistics were added. The theoretical and application studies showed that the proposed F-test for two counts of data is a generalization of the existing F-test. From the analysis, it was noted that the proposed F-test performed better than the existing F-test in terms of information and probabilities associated with the test. The proposed F-test can be extended using a double sampling scheme for future research.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is taken from https://www.ncdc.noaa.gov/cdo-web/datatools/records (accessed on 4 July 2022).
Acknowledgments
The author is deeply thankful to the editor and reviewers for their valuable suggestions to improve the quality and presentation of the paper.
Conflicts of Interest
The author declare no conflict of interest.
Appendix A
Theorem A1.
Show that
Proof.
From Cox (1953), in direct Poisson sampling, the number of events occurring in a fixed time is recorded, whereby we have
and
According to Cox (1953), “if we wish to make an approximation to probability (no. of events > n) in which the number of events is treated as a continuous variate, it is reasonable to take a quantity intermediate between above equations”. A natural choice is
i.e., we calculate probabilities as if is distributed as
As mentioned in Cox (1953), “the suggestion is that, if we observe n events in a fixed time t, we may work approximately as if is fixed and is distributed as . The remainder of the paper is concerned with the consequences using the above equation”. If we sample two populations with rates of occurrence ,, and if we observe , events in times ,, then, “ is distributed as ”.
We can write that
is distributed approximately as F with degrees of freedom. Thus, we may test the hypothesis that by referring to
Hence, Theorem A1 is proven.
Note: In Kanji [1], the formulas should be read as above. □
Theorem A2.
Show that
Proof.
By following Theorem 1 and Kanji [1], we can write that
is distributed approximately as F with degrees of freedom. Thus, we may test the hypothesis that when by referring to
Hence, Theorem A2 is proven. □
References
- Kanji, G.K. 100 Statistical Tests; Sage: Thousand Oaks, CA, USA, 2006. [Google Scholar]
- Krishnamoorthy, K.; Thomson, J. A more powerful test for comparing two Poisson means. J. Stat. Plan. Inference 2004, 119, 23–35. [Google Scholar] [CrossRef]
- Hilbe, J.M. The statistical analysis of count data/El análisis estadístico de los datos de recuento. Cult. Educ. 2017, 29, 409–460. [Google Scholar] [CrossRef]
- Puig, P.; Weiß, C.H. Some goodness-of-fit tests for the Poisson distribution with applications in Biodosimetry. Comput. Stat. Data Anal. 2020, 144, 106878. [Google Scholar] [CrossRef]
- White, G.C.; Bennetts, R.E. Analysis of Frequency Count Data Using the Negative Binomial Distribution. Ecology 1996, 77, 2549–2557. [Google Scholar] [CrossRef]
- Coxe, S.; West, S.G.; Aiken, L.S. The Analysis of Count Data: A Gentle Introduction to Poisson Regression and Its Alternatives. J. Pers. Assess. 2009, 91, 121–136. [Google Scholar] [CrossRef]
- Salinas-Rodriguez, A.; Manrique-Espinoza, B.; Sosa-Rubi, S.G. Statistical analysis for count data: Use of healthcare services applications. Salud Publica Mex. 2009, 51, 397–406. [Google Scholar]
- Pham, T.V.; Jimenez, C.R. An accurate paired sample test for count data. Bioinformatics 2012, 28, i596–i602. [Google Scholar] [CrossRef]
- Hawinkel, S.; Rayner, J.C.W.; Bijnens, L.; Thas, O. Sequence count data are poorly fit by the negative binomial distribution. PLoS ONE 2020, 15, e0224909. [Google Scholar] [CrossRef]
- Böhning, D.; Sangnawakij, P. Count outcome meta-analysis for comparing treatments by fusing mixed data sources: Comparing interventions using across report information. Adv. Stat. Anal. 2021, 105, 75–85. [Google Scholar] [CrossRef]
- Akpinar, E.K.; Akpinar, S. A statistical analysis of wind speed data used in installation of wind energy conversion systems. Energy Convers. Manag. 2005, 46, 515–532. [Google Scholar] [CrossRef]
- Yilmaz, V.; Çelik, H.E. A Statistical Approach to Estimate the Wind Speed Distribution: The Case of Gelibolu Region. Doğuş Üniversitesi Derg. 2008, 9, 122–132. [Google Scholar] [CrossRef]
- Ali, S.; Lee, S.-M.; Jang, C.-M. Statistical analysis of wind characteristics using Weibull and Rayleigh distributions in Deokjeok-do Island—Incheon, South Korea. Renew. Energy 2018, 123, 652–663. [Google Scholar] [CrossRef]
- Arias-Rosales, A.; Osorio-Gómez, G. Wind turbine selection method based on the statistical analysis of nominal specifications for estimating the cost of energy. Appl. Energy 2018, 228, 980–998. [Google Scholar] [CrossRef]
- Akgül, F.G.; Şenoğlu, B. Comparison of wind speed distributions: A case study for Aegean coast of Turkey. Energy Sources Part A Recover. Util. Environ. Eff. 2019, 1–18. [Google Scholar] [CrossRef]
- Haq, M.A.U.; Rao, G.S.; Albassam, M.; Aslam, M. Marshall-Olkin Power Lomax distribution for modeling of wind speed data. Energy Rep. 2020, 6, 1118–1123. [Google Scholar] [CrossRef]
- Bludszuweit, H.; Dominguez-Navarro, J.A.; Llombart, A. Statistical Analysis of Wind Power Forecast Error. IEEE Trans. Power Syst. 2008, 23, 983–991. [Google Scholar] [CrossRef]
- Brano, V.L.; Orioli, A.; Ciulla, G.; Culotta, S. Quality of wind speed fitting distributions for the urban area of Palermo, Italy. Renew. Energy 2011, 36, 1026–1039. [Google Scholar] [CrossRef]
- Katinas, V.; Gecevicius, G.; Marciukaitis, M. An investigation of wind power density distribution at location with low and high wind speeds using statistical model. Appl. Energy 2018, 218, 442–451. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M.R. An improved process monitoring by mixed multivariate memory control charts: An application in wind turbine field. Comput. Ind. Eng. 2020, 142, 106343. [Google Scholar] [CrossRef]
- Viertl, R. Univariate statistical analysis with fuzzy data. Comput. Stat. Data Anal. 2006, 51, 133–147. [Google Scholar] [CrossRef]
- Filzmoser, P.; Viertl, R. Testing hypotheses with fuzzy data: The fuzzy p-value. Metrika 2004, 59, 21–29. [Google Scholar] [CrossRef]
- Tsai, C.-C.; Chen, C.-C. Tests of quality characteristics of two populations using paired fuzzy sample differences. Int. J. Adv. Manuf. Technol. 2006, 27, 574–579. [Google Scholar] [CrossRef]
- Taheri, S.M.; Arefi, M. Testing fuzzy hypotheses based on fuzzy test statistic. Soft Comput. 2008, 13, 617–625. [Google Scholar] [CrossRef]
- Jamkhaneh, E.B.; Ghara, A.N. Proceedings of the 2010 International Conference on Intelligent Computing and Cognitive Informatics, Kuala Lumpur, Malaysia, 22–23 June 2010; IEEE: Piscataway Township, NY, USA; pp. 86–89.
- Chachi, J.; Taheri, S.M.; Viertl, R. Testing Statistical Hypotheses Based on Fuzzy Confidence Intervals. Austrian J. Stat. 2012, 41, 267–286. [Google Scholar] [CrossRef]
- Kalpanapriya, D.; Pandian, P. Statistical hypotheses testing with imprecise data. Appl. Math. Sci. 2012, 6, 5285–5292. [Google Scholar]
- Montenegro, M.; Casals, M.A.R.; Lubiano, M.A.A.; Gil, M.A.A. Two-sample hypothesis tests of means of a fuzzy random variable. Inf. Sci. 2001, 133, 89–100. [Google Scholar] [CrossRef]
- Park, S.; Lee, S.-J.; Jun, S. Patent Big Data Analysis using Fuzzy Learning. Int. J. Fuzzy Syst. 2017, 19, 1158–1167. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy. Neutrosophic Probability, Set, and Logic, ProQuest Information & Learning; Infinite Study: Ann Arbor, MI, USA, 1998; Volume 105, pp. 118–123. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral, And Neutrosophic Probability; Infinite Study: Ann Arbor, MI, USA, 2011. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. Correlation Coefficient of Interval Neutrosophic Set. Appl. Mech. Mater. 2013, 436, 511–517. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A. NCM: Neutrosophic c-means clustering algorithm. Pattern Recognit. 2015, 48, 2710–2724. [Google Scholar] [CrossRef]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F. Bipolar Neutrosophic Minimum Spanning Tree; Infinite Study: Ann Arbor, MI, USA, 2018. [Google Scholar]
- Abdel-Baset, M.; Chang, V.; Gamal, A. RETRACTED: Evaluation of the green supply chain management practices: A novel neutrosophic approach. Comput. Ind. 2019, 108, 210–220. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, M.; Elhoseny, M.; Son, L.H.; Chiclana, F.; Zaied, A.E.-N.H. Cosine similarity measures of bipolar neutrosophic set for diagnosis of bipolar disorder diseases. Artif. Intell. Med. 2019, 101, 101735. [Google Scholar] [CrossRef] [PubMed]
- Smarandache, F. Introduction to Neutrosophic Statistics; Infinite Study: Ann Arbor, MI, USA, 2014. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Du, S. Scale Effect and Anisotropy Analyzed for Neutrosophic Numbers of Rock Joint Roughness Coefficient Based on Neutrosophic Statistics. Symmetry 2017, 9, 208. [Google Scholar] [CrossRef]
- Chen, J.; Ye, J.; Du, S.; Yong, R. Expressions of Rock Joint Roughness Coefficient Using Neutrosophic Interval Statistical Numbers. Symmetry 2017, 9, 123. [Google Scholar] [CrossRef]
- Aslam, M. Neutrosophic analysis of variance: Application to university students. Complex Intell. Syst. 2019, 5, 403–407. [Google Scholar] [CrossRef]
- Aslam, M.; Albassam, M. Application of Neutrosophic Logic to Evaluate Correlation between Prostate Cancer Mortality and Dietary Fat Assumption. Symmetry 2019, 11, 330. [Google Scholar] [CrossRef]
- Aslam, M. A new method to analyze rock joint roughness coefficient based on neutrosophic statistics. Measurement 2019, 146, 65–71. [Google Scholar] [CrossRef]
- Ye, J. Multiple-attribute group decision-making method under a neutrosophic number environment. J. Intell. Syst. 2016, 25, 377–386. [Google Scholar] [CrossRef]
- Liu, P.; Liu, X. The neutrosophic number generalized weighted power averaging operator and its application in multiple attribute group decision making. Int. J. Mach. Learn. Cybern. 2018, 9, 347–358. [Google Scholar] [CrossRef]
- Zheng, E.; Teng, F.; Liu, P. Multiple attribute group decision-making method based on neutrosophic number generalized hybrid weighted averaging operator. Neural Comput. Appl. 2017, 28, 2063–2074. [Google Scholar] [CrossRef]
- Pramanik, S.; Roy, R.; Roy, T.K. Teacher Selection Strategy Based on Bidirectional Projection Measure in Neutrosophic Number Environment. In Neutrosophic Operational Research; Smarandache, F., Abdel-Basset, M., El-Henawy, I., Eds.; Pons Publishing House: Bruxelles, Belgium, 2017; Volume 2, ISBN 978-1-59973-537-5. [Google Scholar]
- Maiti, I.; Mandal, T.; Pramanik, S. Neutrosophic goal programming strategy for multi-level multi-objective linear programming problem. J. Ambient Intell. Humaniz. Comput. 2019, 11, 3175–3186. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S.; Giri, B.C.; Smarandache, F. NN-Harmonic Mean Aggregation Operators-Based MCGDM Strategy in a Neutrosophic Number Environment. Axioms 2018, 7, 12. [Google Scholar] [CrossRef]
- Pramanik, S.; Banerjee, D. Neutrosophic number goal programming for multi-objective linear programming problem in neutrosophic number environment. MOJ Curr. Res. Rev. 2018, 1, 135–141. [Google Scholar] [CrossRef][Green Version]
- Aslam, M. RETRACTED ARTICLE: Neutrosophic statistical test for counts in climatology. Sci. Rep. 2021, 11, 17806. [Google Scholar] [CrossRef]
- Aslam, M. Enhanced statistical tests under indeterminacy with application to earth speed data. Earth Sci. Inform. 2021, 14, 1261–1267. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).