The Health Effects of Climate Change: A Survey of Recent Quantitative Research
Abstract
:1. Introduction: Some Facts and Opinions on the Relationship Between Climate Change and Health
- Time series models, among which ARMAX (Auto Regressive Moving Average with exogenous variables) models, ECM (Error Correction Models), and non-parametric forecasting models such as single and double exponential smoothing, Holt-Winters methods (additive, no seasonal, multiplicative);
- Panel data and spatial models, such as fixed and random effects models, dynamic panel data models, spatial lag and spatial error models;
- Non-statistical approaches, such as Integrated Assessment Models (IAMs), Computable General Equilibrium (CGE) models, Global Trade Analysis Project Models (GTAP), and Comparative Risk Assessments (CRA).
2. Quantitative Models for the Relationship Between Climate Change and Health: Methods and Examples
2.1. Time Series Models
2.1.1. Methods

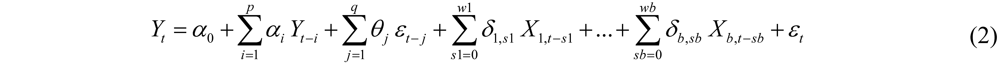

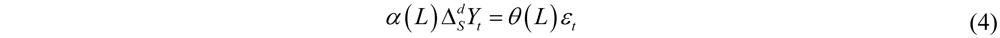
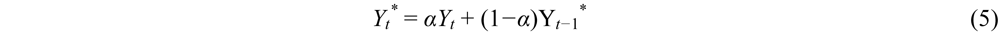
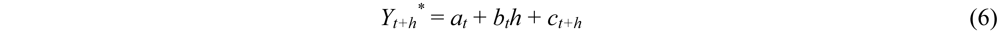

2.1.2. Examples
2.2. Panel Data and Spatial Models
2.2.1. Methods
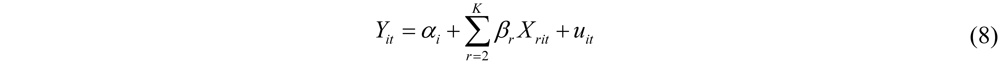
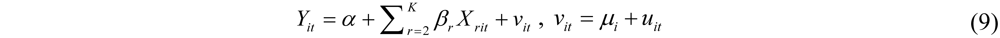
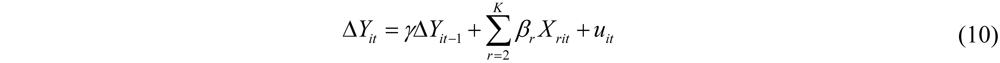
2.2.2. Examples
2.3. Non-Statistical Approaches
2.3.1. General Equilibrium Models: Methods and Examples
2.3.2. Comparative Risk Analyses: Methods and Examples
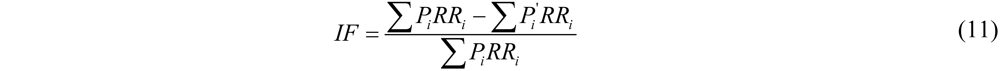
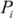 is the proportion of population in the exposure category,
is the proportion of population in the exposure category, 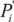 is an alternative proportion and
is an alternative proportion and 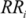 is the relative risk exposure at category i compared to the reference level.
is the relative risk exposure at category i compared to the reference level.3. Integrating Results from Multiple Quantitative Studies: The Case of Malaria
3.1. Time Series Studies
3.2. Cross-Section and Panel Data Studies
3.3. Non-Statistical Studies: General Equilibrium
4. Using Quantitative Results Toward Managing Human Health
4.1. The Economics of Climate Change
4.2. Managing the Health Effects of Climate Change
4.3. Developing Diseases and Early Warning Systems
5. Conclusions
- – The attribution of weather-related disasters to climate change, as no consensus estimate of the global attribution has yet been made;
- – Estimate of economic losses today, as the current models are forward looking;
- – Regional analysis, as the understanding of the human impact at regional level is often very limited but also crucial to guide effective adaptation interventions.
References and Notes
- Prüss-Üstün, A.; Corvalán, C.F. Preventing Disease Through Healthy Environments. Towards an Estimate of the Environmental Burden of Disease; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- World Health Organization (WHO), Climate Change and Human Health. Risks and Responses; McMicheal, A.J.; Campbell-Lendrum, D.H.; Corvalan, C.F.; Ebi, K.L.; Githeko, A.K.; Scheraga, J.D.; Woodward, A. (Eds.) WHO: Geneva, Switzerland, 2003.
- Additional aspects such as characteristics of the dependent and independent variables, number and type of countries investigated, data frequency, temporal period spanned by the analysis, and robustness of the empirical findings are examined.
- Steenland, K.; Burnett, C.; Lalich, N.; Ward, E.; Hurrell, J. Dying for work: The magnitude of U.S. mortality from selected causes of death associated with occupation. Am. J. Ind. Med. 2003, 43, 461–482. [Google Scholar] [CrossRef]
- Nurminem, M.; Karjalainen, A. Epidemiologic estimate of the proportion of fatalities related to occupational factors in Finland. Scand. J. Work Environ. Health 2001, 27, 161–213. [Google Scholar]
- Olsen, O.; Kristensen, T.S. Impact of work environment on cardiovascular diseases in Denmark. J. Epidemiol. Community Health 1991, 45, 4–9. [Google Scholar]
- Githeko, A.; Ndegwa, W. Predicting malaria epidemics in the Kenyan highlands using climate data: A tool for decision-makers. Global Change Hum. Health 2001, 2, 54–63. [Google Scholar]
- Patz, J.A.; Strzepek, K.; Lele, S.; Hedden, M.; Greene, S.; Noden, B.; Hay, S.I.; Kalkstein, L.; Beier, J.C. Predicting key malaria transmission factors, biting and entomological inoculation rates, using modeled soil moisture in Kenya. Trop. Med. Int. Health 1998, 3, 818–827. [Google Scholar] [CrossRef]
- Bouma, M.J.; van der Kaay, H.J. The El Niño southern oscillation and the historic malaria epidemics on the Indian Subcontinent and Sri Lanka: An early warning system for future epidemics? Trop. Med. Int. Health 1996, 1, 86–96. [Google Scholar] [CrossRef]
- Akthar, R.; McMichael, A.J. Rainfall and malaria outbreaks in western Rajasthan. Lancet 1996, 348, 1457–1458. [Google Scholar]
- Bouma, M.J.; Dye, C. Cycles of malaria associated with El Niño in Venezuela. J. Am. Med. Assoc. 1997, 278, 1772–1774. [Google Scholar]
- Lütkepohl, H.; Krätzig, M. Applied Time Series Econometrics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ghysels, E.; Osborn, D.R.; Rodrigues, P.M.M. Seasonal Nonstationarity and Near-nonstationarity. In A Companion to Theoretical Econometrics; Baltagi, B.H., Ed.; Blackwell: Oxford, UK, 2003; pp. 655–677, Chapter 31. [Google Scholar]
- Mills, T.C. Modelling Trends and Cycles in Economic Time Series; Palgrave McMillan: Basingstoke, UK, 2003. [Google Scholar]
- Chaves, L.F.; Pascual, M. Climate cycles and forecasts of cutaneous leishmaniasis, a nonstationary vector-borne disease. PLoS Med. 2006, 3, e295. [Google Scholar]
- Chaves, L.F.; Pascual, M. Comparing models for early warning systems of neglected tropical diseases. PLoS Negl. Trop. Dis. 2007, 1, e33. [Google Scholar]
- Chaves, L.F.; Cohen, J.M.; Pascual, M.; Wilson, M.L. Social exclusion modifies climate and deforestation impacts on a vector-borne disease. PLoS Negl. Trop. Dis. 2008, 2, e176. [Google Scholar]
- Chaves, L.F. Climate and recruitment limitation of hosts: The dynamics of American cutaneous leishmaniasis seen through semi-mechanistic seasonal models. Ann. Trop. Med. Parasitol. 2009, 103, 221–234. [Google Scholar]
- Medina, D.C.; Findley, S.E.; Guindo, B.; Doumbia, S. Forecasting non-stationary diarrhea, acute respiratory infection, and malaria time-series in Niono, Mali. PLoS One 2007, 2, e1181. [Google Scholar]
- Curriero, F.C.; Heiner, K.S.; Samet, J.M.; Zeger, S.L.; Strug, L.; Patz, J.A. Temperature and mortality in 11 cities of the eastern United States. Am. J. Epidemiol. 2002, 155, 80–87. [Google Scholar]
- Shakoor, H.; Armstrong, B.; Baccini, M.; Biggeri, A.; Bisanti, L.; Russo, A.; Paldy, A.; Menne, B.; Kosatsky, T. Impact of high temperature on mortality: Is there an added heat wave effect? Epidemiology 2006, 17, 632–638. [Google Scholar]
- Keatinge, W.R.; Donaldson, G.C.; Cordioli, E.; Martinelli, M.; Kunst, A.E.; Mackenbach, J.P.; Nayha, S.; Vuori, I. Heat related mortality in warm and cold regions of Europe: Observational study. Br. Med. J. 2000, 321, 670–673. [Google Scholar]
- Rodò, X.; Pascual, M.; Fuchs, G.; Faruque, A.S.G. ENSO and cholera: A nonstationary link related to climate change? Proc. Natl. Acad. Sci. USA 2002, 99, 12901–12906. [Google Scholar]
- Pascual, M.; Rodó, X.; Ellner, S.P.; Colwell, R.; Bouma, M.J. Cholera dynamics and El Niño-Southern oscillation. Science 2000, 289, 1766–1769. [Google Scholar]
- Pascual, M.; Chaves, L.F.; Cash, B.; Rodò, X.; Yunus, M. Predicting endemic cholera: The role of climate variability and disease dynamics. Clim. Res. 2008, 36, 131–140. [Google Scholar]
- Codeco, C.T.; Lele, S.; Pascual, M.; Bouma, M.; Ko, A.I. A Stochastic model for ecological systems with strong nonlinear response to environmental drivers: Application to two water-borne diseases. J. R. Soc. Interface 2008, 5, 247–252. [Google Scholar]
- Koelle, K.; Rodo, X.; Pascual, M.; Yunus, M.; Mostafa, G. Refractory periods and climate forcing in cholera dynamics. Nature 2005, 436, 696–700. [Google Scholar]
- Hashizume, M.; Faruque, A.S.G.; Wagatsuma, Y.; Hayashi, T.; Armstrong, B. Cholera in bangladesh climatic components of seasonal variation. Epidemiology 2010, 21, 706–710. [Google Scholar]
- Baltagi, B.H. Econometric Analysis of Panel Data, 2nd ed; Wiley: Chichester, UK, 2001. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Kluwer Academic: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Cattaneo, C. Spatial Econometrics. A Primer; Internal Lecture; Fondazione Eni Enrico Mattei: Milano, Italy, 2008. [Google Scholar]
- Cattaneo, C.; Manera, M.; Scarpa, E. Industrial coal demand in China: A provincial analysis. Resource Energ. Econ. 2011, 33, 12–35. [Google Scholar]
- Rupasingha, A.; Goetz, S.J.; Debertin, D.L.; Pagoulatos, A. The environmental kuznets curve for U.S. Counties: A spatial econometric analysis with extension. Pap. Reg. Sci. 2004, 83, 407–424. [Google Scholar] [CrossRef]
- Salomon, J.A.; Murray, C.J.L. The Epidemiologic transition revisited: Compositional models for causes of death by age and sex. Popul. Dev. Rev. 2002, 28, 205–228. [Google Scholar]
- Omran, A.R. The epidemiologic transition: A theory of the epidemiology of population change. Milbank Mem. Fund Q. 1971, 49, 509–538. [Google Scholar]
- Conrad, K. Computable General Equilibrium Models for Environmental Economics and Policy Analysis. In Handbook of Environmental and Resource Economics; van den Bergh, J.C.J.M., Ed.; Edward Elgar: Cheltenam, UK, 2002; pp. 1060–1087, Chapter 69. [Google Scholar]
- Martens, W.J.M. Climate change, thermal stress and mortality changes. Soc. Sci. Med. 1998, 46, 331–344. [Google Scholar]
- Tol, R.S.J. Estimates of the damage costs of climate change. Part 1: Benchmark estimates. Environ. Resource Econ. 2002, 21, 47–73. [Google Scholar] [CrossRef]
- Bosello, F.; Roson, R.; Tol, R.S.J. Economy-wide estimates of the implications of climate change: Human health. Ecol. Econ. 2006, 58, 579–591. [Google Scholar]
- Martin, P.H.; Lefebvre, M.G. Malaria and climate: Sensitivity of malaria potential transmission to climate. Ambio 1995, 24, 200–207. [Google Scholar]
- Morita, T.; Kainuma, M.; Harasawa, H.; Kai, K.; Dong-Kun, L.; Matsuoka, Y. Asian-Pacific Integrated Model for Evaluating policy Options to Reduce Greenhouse Gas Emissions and Global Warming Impacts; AIM Interim Paper; National Institute for Environmental Studies: Tsukuba, Japan, 1994. [Google Scholar]
- Hertel, T.W.; Tsigas, M. Primary Factors Shares. In Global Trade, Assistance, and Production: The GTAP 5 Data Base; Dimaranan, B.V., McDougall, R.A., Eds.; Center for Global Trade Analysis, Purdue University: West Lafayette, IN, USA, 2002. [Google Scholar]
- IMAGE, The IMAGE 2.2 Implementation of the SRES Scenarios; RIVM CD-ROM Publication 481508018: Bilthoven, The Netherlands, 2001.
- Ackerman, F.; Stanton, E. Can Climate Change Save Lives? A Comment on ‘Economy-Wide Estimates of the Implications of Climate Change: Human Health’; Working Paper No. 06-05; Global Development and Environment Institute, Tufts University: Medford, MA, USA, 2006. [Google Scholar]
- Martens, W.J.M. Health and Climate Change: Modeling the Impacts of Global Warming and Ozone Depletion; Earthscan Publications Ltd.: London, UK, 1998. [Google Scholar]
- De Dube, R.K.; Prakasa Rao, G.S. Extreme weather events over India in the last 100 years. J. Ind. Geophys. Union 2005, 9, 173–187. [Google Scholar]
- Stern, N. The Economics of Climate Change.The Stern Review; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Ezzati, M.; Lopez, A.D.; Rodgers, A.; Vander Hoorn, S.; Murray, C.J. Comparative Risk Assessment Collaborating Group. Selected major risk factors and global and regional burden of disease. Lancet 2002, 360, 1347–1360. [Google Scholar]
- Kovats, R.S.; Campbell-Lendrum, D.; Matthies, F. Climate change and human health: Estimating avoidable deaths and disease. Risk Anal. 2005, 25, 1409–1418. [Google Scholar]
- McMichael, A.J.; Campbell-Lendrum, D.; Kovats, S.; Edwards, S.; Wilkinson, P.; Wilson, T.; Nicholls, R.; Hales, S.; Tanser, F.; Le Sueur, D.; et al. Global Climate Change. In Comparative Quantification of Health Risks. Global and Regional Burden of Disease Attributable to Selected Major Risk Factors; Ezzati, M., Lopez, A.D., Rodgers, A., Murray, C.J.L., Eds.; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Hijioka, Y.; Takahashi, K.; Matsuoka, Y.; Harasawa, H. Impact of global warming on waterborne disease. J. Jpn. Soc. Water Environ. 2002, 25, 647–652. [Google Scholar]
- Lindsay, S.W.; Birley, M.H. Climate change and malaria transmission. Ann. Trop. Med. Parasitol. 1996, 90, 573–588. [Google Scholar]
- Chaves, L.F.; Koenraadt, C.J.M. Climate change and highland malaria: Fresh air for a hot debate. Q. Rev. Biol. 2010, 85, 27–55. [Google Scholar]
- Freeman, T.; Bradley, M. Temperature is predictive of severe malaria years in Zimbabwe. Trans. R. Soc. Trop. Med. Hyg. 1996, 90, 232. [Google Scholar]
- Freeman, T. Malaria Outbreaks. A Review of the Epidemiology of Malaria Transmission and Distribution in Zimbabwe and the Relationship of Malaria Outbreaks to Preceding Meteorological Conditions; Deutsche Gesellschaft für Technische Zusammenarbeit (GTZ): Harare, Zimbabwe, 1995. [Google Scholar]
- Tulu, A.N. Determinants of Malaria Transmission in the Highlands of Ethiopia. The Impact of Global Warming on Morbidity and Mortality Ascribed to Malaria; London School of Hygiene and Tropical Medicine: London, UK, 1996. [Google Scholar]
- Loevinsohn, M.E. Climatic warming and increased malaria incidence in Rwanda. Lancet 1994, 343, 714–718. [Google Scholar]
- Bouma, M.J.; Dye, C.; van der Kaay, H.J. Falciparum malaria and climate change in the north west frontier province of Pakistan. Am. J. Trop. Med. Hyg. 1996, 55, 131–137. [Google Scholar]
- Matola, Y.G.; White, G.B.; Magayuka, S.A. The changed pattern of malaria endemicity and transmission at amano in the eastern Usambara mountains, north-eastern Tanzania. J. Trop. Med. Hyg. 1987, 90, 127–134. [Google Scholar]
- Malakooti, M.A.; Biomndo, K.; Shanks, G.D. Reemergence of epidemic highland malaria in the highlands of western Kenya. Emerg. Infect. Dis. 1997, 4, 671–676. [Google Scholar]
- Entomological inoculation rate is the product of the human-biting rate and the proportion of female mosquitoes carrying infective parasites in their salivary glands ready to be delivered to the next host.
- Patz, J.A.; Lindsay, S.W. New challenges, new tools: The impact of climate change on infectious diseases. Curr. Opin. Microbiol. 1999, 2, 445–451. [Google Scholar]
- Pascual, M.; Ahumada, J.A.; Chaves, L.F.; Rodò, X.; Bouma, M.J. Malaria resurgence in the east african highlands: Temperature trends revisited. Proc. Natl. Acad. Sci. USA 2006, 103, 5829–5834. [Google Scholar]
- Shanks, G.D.; Hay, S.I.; Stern, D.I.; Biomdo, K.; Snow, R.W. Meteorologic influences on plasmodium falciparum malaria in the highland tea estates of Kericho, western Kenya. Emerg. Infect. Dis. 2002, 8, 1–10. [Google Scholar]
- Kazembe, L.N.; Kleinschmidt, I.; Sharp, B.L. Patterns of malaria-related hospital admissions and mortality among malawian children: An example of spatial modelling of hospital register data. Malar. J. 2006, 5, 93. [Google Scholar]
- Kazembe, L.N. Spatial modelling and risk factors of malaria incidence in northern Malawi. Acta Trop. 2007, 102, 126–137. [Google Scholar]
- Bhattacharya, S.; Sharma, C.; Dhiman, R.C.; Mitra, A.P. Climate change and malaria in India. Curr. Sci. 2006, 90, 369–375. [Google Scholar]
- Dhiman, R.C.; Pahwa, S.; Dash, A.P. Climate change and malaria in India: Interplay between temperatures and mosquitoes. Reg. Health Forum 2008, 12, 1. [Google Scholar]
- Lindsay, S.W.; Martens, W.J.M. Malaria in the African highlands: Past, present and future. Bull. World Health Organ. 1998, 76, 33–45. [Google Scholar]
- The studies by [63,64,69], analyze the (re)emergence of malaria in regions once free of this disease risks. These contribution add to a vast literature on the epidemics of malaria. This includes: studies of the highlands of Kenya, Madagascar, Burundi and Irian Jaya, Indonesia (e.g., [71-79]). Other analyses include the studies by [80,81] on epidemics in Manyuchi dam, Zimbabwe and Ethiopia, respectively.
- Kigotho, A.W. Services stretched as malaria reaches Kenyan highlands. Lancet 1997, 350, 422. [Google Scholar]
- Khaemba, B.M.; Mutani, A.; Bett, M.K. Studies of anopheline mosquitoes transmitting malaria in a newly developed highland urban area: A case study of Moi university and its environs. East Afr. Med. J. 1994, 71, 159–164. [Google Scholar]
- Fontaine, R.E.; Najjar, A.E.; Prince, J.S. The 1958 malaria epidemic in Ethiopia. Am. J. Trop. Med. Hyg. 1961, 10, 795–803. [Google Scholar]
- de Zulueta, J. Malaria and ecosystems: From Prehistory to post eradication. Parassitologia 1994, 36, 7–15. [Google Scholar]
- Fontenielle, D.; Lepers, J.P.; Campbell, G.H.; Coluzzi, M.; Rakotoarivony, I.; Coulanges, P. Malaria transmission and vector biology in Manarintsoa, high plateaux of Madagascar. Am. J. Trop. Med. Hyg. 1990, 43, 107–115. [Google Scholar]
- Mouchet, J.; Laventure, S.; Blanchy, S.; Fioramonti, R.; Rakotonjanabelo, A.; Rabarison, P.; Sircoulon, J.; Roux, J. La reconquete des hautes terres de madagascar par le paludisme. Bull. Soc. Pathol. Exot. 1997, 90, 162–168. [Google Scholar]
- Marimbu, J.; Ndayiragije, A.; Le Bras, M.; Chaperon, J. Environnement et paludisme au burundi. A propos d’une epidemie de paludisme dans une region montagneuse non endémique. Bill. Soc. Pathol. Exot. 1993, 86, 399–401. [Google Scholar]
- Anthony, R.L.; Bangs, M.J.; Hamzah, N.; Basri, H.; Purnomo; Subianto, B. Heightened transmission of stable malaria in an isolated population in the highlands of Irian Jaya, Indonesia. Am. J. Trop. Med. Hyg. 1992, 47, 346–356. [Google Scholar]
- Bangs, M.J.; Rusmiarto, S.; Anthony, R.L. Malaria transmission by anopheles punctulatus in the highlands of Irian Jaya, Indonesia. Ann. Trop. Med. Parasit. 1995, 90, 29–38. [Google Scholar]
- Freeman, T. Manyuchi Dam Malaria Outbreak; Gesellschaft für Technische Zusammenarbeit (GTZ): Harare, Zimbabwe, 1994. [Google Scholar]
- Woube, M. Geographical distribution and dramatic increases in incidences of malaria: Consequences of the resettlement scheme in Gambela, SW Ethiopia. Indian J. Malariol. 1997, 34, 140–163. [Google Scholar]
- Martens, W.J.M.; Jetten, T.H.; Rotmans, J.; Niessen, L.W. Climate change and vector-borne diseases: A global modelling perspective. Global Environ. Change 1995, 5, 195–209. [Google Scholar]
- The total damage evaluated in terms of loss of life caused by climate change is estimated to range from US$ 6 billion to US$ 88 billion (1990 dollar prices) [84]. In terms of disability adjusted life years (DALYs) the loss has been estimated around 5.5 million in year 2000 [85].
- Intergovernmental Panel on Climate Change (IPCC), Climate Change 2007: Impacts, Adaptation and Vulnerability; WHO: Geneva, Switzerland, Working Group II Contribution to the IPCC.
- Costello, A.; Abbas, M.; Allen, A.; Ball, S.; Bell, S.; Bellamy, R.; Friel, S.; Groce, N.; Johnson, A.; Kett, M.; et al. Managing the Health Effects of Climate Change. Lancet 2009, 373, 1693–1733. [Google Scholar]
- World Health Organization (WHO), Sixty-First World Health Assembly; WHO: Geneva, Switzerland, 2008.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Grasso, M.; Manera, M.; Chiabai, A.; Markandya, A. The Health Effects of Climate Change: A Survey of Recent Quantitative Research. Int. J. Environ. Res. Public Health 2012, 9, 1523-1547. https://doi.org/10.3390/ijerph9051523
Grasso M, Manera M, Chiabai A, Markandya A. The Health Effects of Climate Change: A Survey of Recent Quantitative Research. International Journal of Environmental Research and Public Health. 2012; 9(5):1523-1547. https://doi.org/10.3390/ijerph9051523
Chicago/Turabian StyleGrasso, Margherita, Matteo Manera, Aline Chiabai, and Anil Markandya. 2012. "The Health Effects of Climate Change: A Survey of Recent Quantitative Research" International Journal of Environmental Research and Public Health 9, no. 5: 1523-1547. https://doi.org/10.3390/ijerph9051523
APA StyleGrasso, M., Manera, M., Chiabai, A., & Markandya, A. (2012). The Health Effects of Climate Change: A Survey of Recent Quantitative Research. International Journal of Environmental Research and Public Health, 9(5), 1523-1547. https://doi.org/10.3390/ijerph9051523




