1. Introduction
Two of the major risk factors for cardiovascular disease are obesity and diabetes, and analysis of geographic patterning in the variation and interrelation of these two major conditions is important for ensuring that resources for prevention and care match need and are effectively targeted. The close link between obesity and diabetes is well established [
1,
2], and increases in the prevalence of obesity and overweight are a major factor in the growth of diabetes [
3,
4]. In the US there is evidence of wide geographic contrasts in the prevalence of both obesity and diabetes, and of clear differences in relative risk between age and ethnic groups, and between socioeconomic groups [
5,
6].
It is important to establish whether geographic variations are simply the result of differences between populations in their age, social and ethnic composition (compositional effects), or whether there are distinct geographic effects that account for part of the variation. The distinct impacts of area on health, and also those of interactions between area variables and individual level risk factors, are often denoted as ”contextual variation”. Thus, area-based measures of socioeconomic status may affect health outcomes even after control for individual risks [
7–
10], while interactions between geography and individual risk factors are exemplified by the study of Subramanian
et al. [
11], which considers ”geographic variation in the individual relationship between race/ethnicity and mortality”. In the present paper, contextual variation is assessed by the significance (after allowing for major individual level risk factors) of both known area variables, and latent area effects, on chances of diabetes and/or excess weight.
This paper develops a multilevel multinomial regression model for diabetes and weight category as joint outcomes. The model framework allows for subject level risk factors, and contextual (area) effects including known area influences (e.g., poverty, race composition, and population density), and unmeasured area influences at two levels (county and state). The latter are modelled using a latent variable approach that results in a summary index of latent contextual effects shared across multinomial outcomes. Because of clustering in both diseases, the latent variables are assumed to be spatially structured [
12].
A case study application is based on the 2007 Behavioral Risk Factor Surveillance System (BRFSS) survey, which is an annual random-digit-dialed telephone survey to determine the prevalence among adults (ages 18 and over) of major illnesses and health risk behaviors. The results described in this paper are based on 128,150 male respondents to the 2007 BRFSS, and living in the continental United States. The main object is to demonstrate unique aspects of the methodology such as the use of a common spatial factor with a multinomial health outcome, and within a multilevel analysis that also allows for the impact of individual risk factors. The method transfers straightforwardly to other cross-sectional settings, including (say) joint obesity-diabetes prevalence for females in 2007, and no distinct methodological elements would be involved in considering females. Therefore the analysis is confined to males. Distinct methods would certainly be involved if time were introduced as an extra feature (e.g., how has the joint obesity-diabetes multilevel relationship evolved since 2000), but this is left for another study.
Obesity is defined as a body mass index over 30, based on self-reported height and weight, with overweight defined as BMI between 25 and 29.9. To determine diabetes status, respondents were asked “Have you ever been told by a doctor that you have diabetes?”, encompassing both types of diabetes. Women with gestational diabetes were excluded. The BRFSS does include other questions on diabetes such as age of onset, and whether or not taking insulin; answers to these questions have been combined in some studies [
13] to informally differentiate diabetes 1 (onset before age 30 combined with current insulin use) from diabetes 2. However, for the majority (94%) of diabetic survey subjects who have onset after age 30, obesity is an established risk factor for diabetes.
2. Multinomial Regression Combining Individual and Geographic Risk Factors
A multinomial response is involved when there are three or more sub-categories of a single condition, or may be obtained by combining sub-categories over two or more conditions. In the present BRFSS case study, the response yi (i = 1,.., n) is based on combining sub-categories of two conditions: there are J + 1 = 6 categories defined by diabetic status and weight status, namely diabetic and obese (y = 1), diabetic and overweight (y = 2), diabetic and normal weight (y = 3), non-diabetic and obese (y = 4), non-diabetic and overweight (y = 5), and non-diabetic and normal weight (y = 6). So categories 1 to 5 all show some form of morbidity relative to the final non-morbid category who are normal weight and not diabetic.
A multinomial regression is applied with the final (non-morbid) category as reference, so that
where the
φij are
J regression terms. Let
dij = 1 if subject
i is in the
jth category. Then for equally weighted subjects the likelihood
L would take the form
with log-likelihood
However, with population survey data, such as the BRFSS [
14], it is necessary also to incorporate survey weights
wi for respondents
i to account for differential response between demographic groups and regions. Then a weighted likelihood
Lw is obtained as
with weighted log-likelihood
Three classes of predictors are used in the multinomial regression defined by (1.1)–(1.2), and with weighted likelihood as in (3.1)–(3.2). As well as subject level risk variables
R, the regression model includes known geographic influences
GK, and latent geographic influences,
GL, so the regression terms have the generic form
φij =
φij(
R,
GK,
GL).
Predictor effects are modelled either as fixed or random effects, in a form of general linear mixed model, in particular one with a multinomial outcome [
15]. Random effects are used to pool strength (e.g., over areas or age groups) and to incorporate anticipated correlations in the age or spatial profiles of prevalence for categories
j = 1,...,
J (see
Appendix 1). For example, while the levels of the different combinations of diabetic and weight status are different (e.g., obesity without diabetes is much more common than diabetes with normal weight), one would expect their age profiles to be similar (
i.e., correlated).
3. Subject Level Predictors
There has been extensive research on variations in obesity and diabetes over demographic and socioeconomic categories, such as age, socioeconomic status and race. A pronounced gradient in diabetes prevalence by age is reported by CDC [
16], though obesity may reduce slightly among the very old. Paeratakul
et al. [
5] also report impacts of socioeconomic status (SES) on obesity and its comorbidities. For example, obese subjects with lower education reported higher rates of diabetes compared to those with higher education; these differentials were more marked than those between high and low income individuals; see Table 3 in Paeratakul
et al. [
5]. Freudenberg & Ruglis [
17] argues that ”although education is highly correlated with income and occupation, evidence suggests that education exerts the strongest influence on health”, and Zhang
et al. [
18] and Maty
et al. [
19] also argue the benefit of using education as a measure of SES risk. For the 2007 BRFSS data,
Table 1 shows morbidity rates due to obesity/overweight and/or diabetes by education level, namely percentages of subjects at each education level located in the six diabetic-weight categories (including the reference category). Higher levels of combined morbidity, namely suffering diabetes combined with obesity or overweight, occur for the less well educated. For example, 5.6% of subjects with less than high school education (namely, 794 of 14,158 survey participants at this education level) are obese and diabetic, compared to 3.2% of college graduates (namely, 1562 of 48186 survey participants at this education level).
Ethnic group variability in levels of obesity and diabetes are well established. Paeratakul
et al. [
5] found the prevalence of overweight and obesity to be higher among black and Hispanic groups compared to whites, and the prevalence of obesity comorbidities (including diabetes) was also found to be higher in blacks than whites. For the 2007 BRFSS data,
Table 2 shows morbidity rates due to obesity/overweight and/or diabetes by race, namely percentages of subjects in the six diabetic-weight categories. Compared to other races, black non-Hispanics are more likely to be located in the first two categories, and also have the highest proportion who are both obese and non-diabetic. The other race category (penultimate column in
Table 2) has a relatively high proportion who are diabetic but of normal weight. As Zhang
et al. [
18] mention, racial disparities in diabetes are not entirely explained by racial/ethnic differences in the prevalence of common risk factors such as obesity: racial differences in diabetes risk remain after controlling for body mass and socioeconomic status. Hence cross tabulation such as in
Table 2 does not control for interrelations between risk factors (e.g., between race and education), and a regression is required.
Subject level risks are here represented in the regression terms
φij by:
overall intercepts (αj),
differential risks by ethnic group r, namely r = 1 for white non-Hispanic, r = 2 for black, r = 3 for Hispanic, and r = 4 for other races (mainly American Asians and native Americans); these are modelled as fixed effects within each φij, with unknown parameters βjr, r = 2, 3, 4, and with βj1 = 0 as reference under an identifying corner constraint;
differential risks by education attainment e, namely e = 1 for less than high school; e = 2 for high school graduate; e = 3 for some college or technical school; and e = 4 for college graduate; these are also modelled as fixed effects, with unknowns γje, e = 2,.., 4, and γj1 = 0 as reference;
differential risks by age group
a = 1,..,
A (with
A = 12 for ages 18–24, 25–29, 30–34, .., 70–74, and 75+), represented by unknowns
ηja. These are modelled using a random effects approach that allows correlation in the age profiles over the first
J prevalence categories (see
Appendix 1); an identifying constraint is applied that ensures these effects sum to zero within outcomes, so that
.
4. Area Level Predictors
Health disparities not explained by population composition (
i.e., by considering subject level risk factors alone) may be linked to area effects. For example, Do
et al. [
20] seek to estimate the share of racial health disparities that can be explained by differences in residential context. There are a wide range of potential area level risk factors for obesity, diabetes and related conditions that have been suggested or applied in the literature. These include area poverty and income levels [
21], area racial composition [
22,
23], climate [
24], income inequality [
25,
26], social cohesion [
27,
28], type of place (e.g., level of urbanicity) [
29–
31], and urban sprawl [
32–
34].
As to geographic effects in the BRFSS, these are defined by the lowest spatial scale identified by that study, namely the county of residence. In fact this means that there are two potentially relevant spatial divisions for the BRFSS data considered here, namely states and counties. There are 3,110 counties across the mainland US, albeit varying considerably in population size. The choice of known area predictors (
GK) in the current study is defined partly by availability of a complete and contemporary profile of county level indicators; for example, some studies suggest potential effects of environmental pollution on diabetes [
35,
36], but a comprehensive US wide index of environmental quality is not available at county level.
Known county level predictors included in the regression in this paper are 2007 county poverty rate x1c (as a proportion between 0 and 1), county population density x2c (logarithmically transformed), and binary indicators (x3c, x4c, x5c) for counties with proportions in the top decile of county population who are black, Hispanic and other nonwhite. Thus the 311 counties with proportions black exceeding the 90th percentile (over all 3,110 continental counties) are coded x3c = 1, and other counties coded zero, x3c = 0. All these variables have the advantage of being updateable between censuses, whereas a number of more complex indices (urban sprawl, social cohesion, etc) rely on 2,000 census variables in their construction. There are therefore five county predictors, each with outcome specific effects. These are represented by fixed effect parameters (δj1, δj2, δj3, δj4, δj5), for categories j = 1, .., J, applying to the five county level predictors {xjc, j = 1, .., 5; c = 1, .., 3110}.
To account for unmeasured (i.e., omitted) area effects (GL), a latent variable strategy is adopted. Given considerable evidence of spatial clustering in high levels of diabetes and obesity, this feature should be incorporated in the latent variable specification. One option is a separate random effect for each area and each outcome, but this would involve heavy parameterisation. The object of the method adopted here is a parsimonious summary of risks that tend to produce the well known clustering of both high obesity/overweight and high diabetes in certain parts of the US (e.g., in the South East and Appalachians).
Specifically, a spatially correlated county effect
vc for counties
c = 1,..., 3110 is adopted with loadings
λj defining the impact of the shared county effect on weight-diabetes category
j (see
Appendix 1 for the form of the spatial dependence). A second set of spatially structured random effects
us is defined according to state
s of residence (
s = 1,.., 49 including District of Columbia), with loadings
κj defining the impact of that effect on category
j. The latter model relatively broad scale and unmeasured effects for states. Identifiability is obtained by setting the first category loadings to 1, namely
λ1 =
κ1 = 1, so that the conditional variances of
vc and
us are unknowns.
Let
Ci and
Si denote the county and state of residence for respondents
i = 1,..,
n where
n = 128, 150, and let {
ai,
ri,
ei} denote the age, race and education status of individual respondents. Then the regression terms
φij (
i = 1,..
n; j = 1,..,
J) defining the multinomial logit regression are represented in full form as:
Thus the model provides estimates both of the impacts of individual level risk factors and of area effects. Let
Sc ∈ (1,..., 49) denote the state that county
c is located in. Then the composite county latent effect for joint prevalence category
j is defined by the sum
and will incorporate both localized county effects, but also distinctive state level influences. In particular, the total county effect for obesity and diabetes combined is
5. Modelling Strategy and Distinct Geographic Effects
A major question of interest in multilevel modelling of health data is the presence (or otherwise) of distinct area effects, both effects of known area indicators (such as county poverty or population density) and effects of latent unmeasured area characteristics [
20,
37]. The presence of geographic contrasts is apparent from
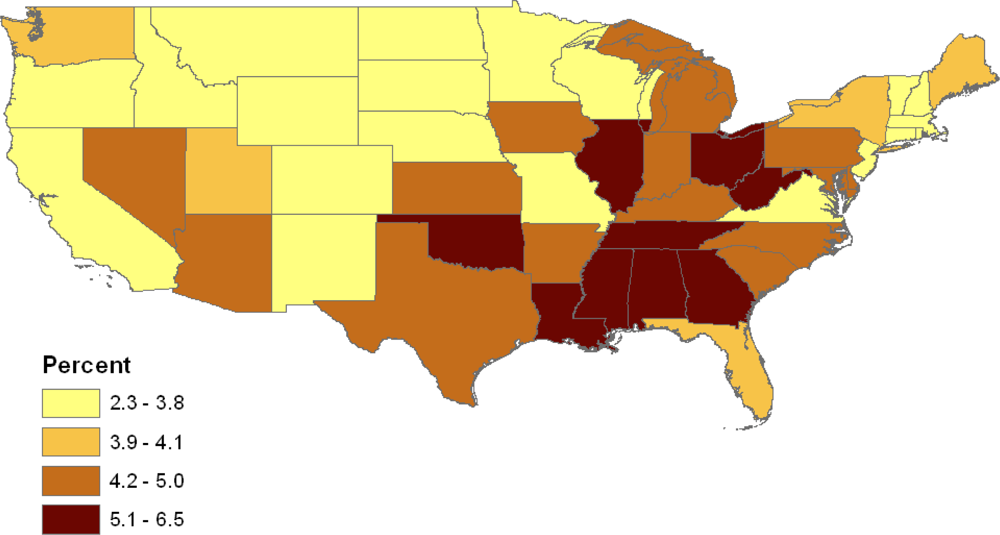
Table 3, which contains age standardized prevalence rates (as percents) for the six conditions by state; the nine census divisions of the states are also listed. For example, the highest rates of obesity & diabetes combined exceed 5.5% (e.g., in Tennessee, Mississippi, and Illinois) while the lowest rates are under 3%, for example, in Colorado and Montana (see
Figure 1). Such variation may be due largely to differences in population composition, or there may be substantial area effects, and the role of such area effects is assessed here by using an incremental modelling strategy. Distinct area effects (sometimes called contextual effects), due either to known area covariates or latent area effects, are those remaining after the influence on prevalence of individual level attributes has been controlled for.
Thus a baseline model estimates county level prevalence rates from a reduced version of the full model (4), including only subject level age and latent county and state effects. The resulting estimates of county prevalences of the different weight-diabetes categories are adjusted for age [
38], but not for population differences in race and education composition, or for the effect of measured county level factors. Thus the baseline model (model 1) involves the regression terms
which account for the differing age composition of survey subjects in different areas. Defining
age standardised proportions in counties
c = 1,.., 3110, for the
J + 1 = 6 weight-diabetes categories are then estimated as
A second model (model 2) adds the effect of measured area predictors, namely county poverty, race composition and population density to the baseline model. Thus in model 2
Age standardised prevalence rates by county and category under model 2 are estimated via
, where now
These models are compared to the full model (model 3) including all subject level predictors (age, race, education) and both types of area effect (known and latent), namely
Of particular interest are changes in the level of variance of the latent area effects as county predictors and individual risk variables are added to the model. Also of interest are changes in the impact (and statistical significance) of known area predictors when individual level risk variables are added. For example, are there distinct county poverty effects on prevalence after individual level race and education level are allowed for?
6. Case Study Application
Fitting of the regression models and assessment of their goodness of fit follows a Bayesian approach. A Bayesian strategy is advantageous for estimating models with several sets of random effects, including random effects which are spatially clustered, especially when the responses (as here) are not continuous variables but discrete, namely a multinomial category. Under the Bayesian approach, prior densities are specified on all parameters in the model, and final (or posterior) estimates of parameters are based on the combination of the data likelihood and the prior densities.
Estimation uses iterative Monte Carlo Markov Chain (MCMC) sampling methods [
39], as provided in the WINBUGS program [
40]. Goodness of fit is assessed by a measure of fit that penalizes model complexity, known as the Deviance Information Criterion or
DIC [
41]. The
DIC is obtained as the average deviance, using the definition (3.2), plus a measure of complexity. Lower values of the
DIC indicate better fitting models. Posterior summaries of parameters are based on the 2
nd half of runs of 10,000 iterations, using two chains starting from dispersed starting values. Convergence was achieved in all models using Brooks-Gelman-Rubin criteria [
42].
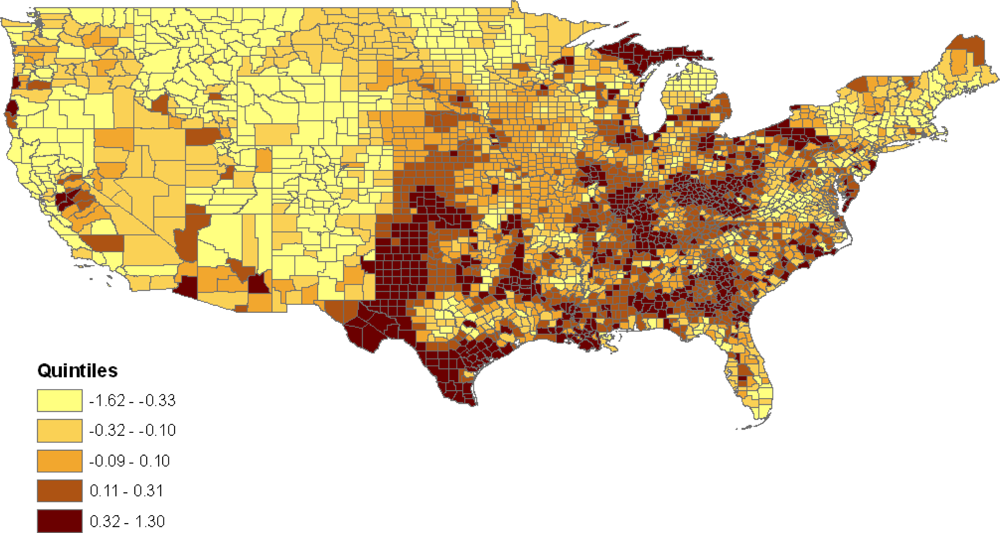
Figure 2 maps the composite latent county effects
t1c =
vc +
uSc from the baseline model 1 (these are posterior means from the MCMC sample). For example,
c = 1 for Autauga County in Alabama, and Alabama is the first state alphabetically among the 49 states in the analysis, so
Sc =
S1 = 1. The effects
t1c summarise varying risks for the jointly obese-diabetic condition between counties before controlling for factors such as county poverty and race composition. They show higher risks in the East South Central states (Kentucky, Tennessee, Alabama, Mississippi), and in some East North Central states (e.g., Illinois, Ohio) [
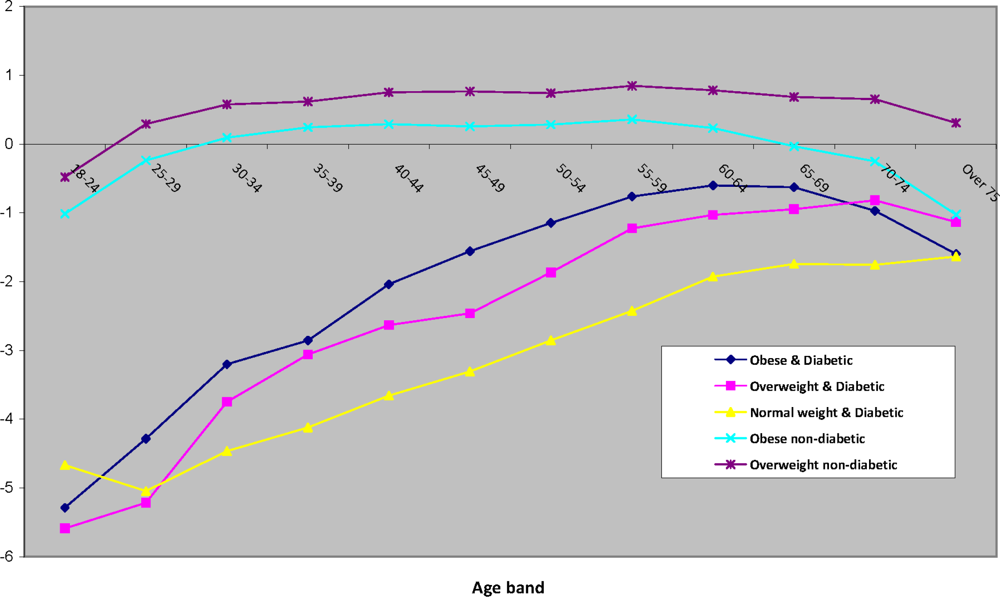
43]. Model 1 also provides age profiles for the five diagnostic groups, plotted in
Figure 3 as log-odds coefficients relative to the reference category. An increasing prevalence with age is confined to the categories obese & diabetic, overweight & diabetic, and normal weight & diabetic.
One useful feature of this initial analysis is that the county effects can be profiled against known county and state level characteristics. For example,
Figure 4 shows the profile of the average
t1c according to county poverty decile (defined by grouping counties into ten categories according to their ranked poverty rates).
Table 4 compares the fit from the baseline model against the other two models, and also presents the variances of the latent spatial effects. These need to account for differential loadings {
λj,
κj} of the area effects by category (see
Table 5), and for the distribution of subjects between categories, and are obtained marginally as
var(
λjvCi +
κjuSi). It can be seen that adding known area predictors in Model 2 results in improved fit (a reduced DIC), and also in a (relatively slight) reduction in the variance of the latent spatial effects.
Table 6 contains the
δjk coefficients from model 2 (
j = 1,..,
J; k = 1,.., 5). It can be seen that the county poverty rate has a strong influence in raising chances of being both obese and diabetic (the first category). It is also an important positive influence on area relativities in the joint normal weight-diabetic category, and on obesity without diabetes. As
Table 3 shows, the latter condition applies to around 22% of the US male population and occurs across relatively evenly the age spectrum.
Table 6 also shows (via the coefficients
δj2) higher rates of morbidity in lower density areas, typically non-metropolitan areas, for four of the five categories. This is consistent with findings that lower density areas, with greater sprawl and lower ”walkability”, have higher rates of obesity and overweight [
44]. The exception to this effect is diabetes combined with normal weight, which is higher in more densely populated areas. As to effects of county ethnic structure, high concentrations of blacks or Hispanics remain a positive influence on the three morbidity categories involving diabetes, even after controlling for county poverty.
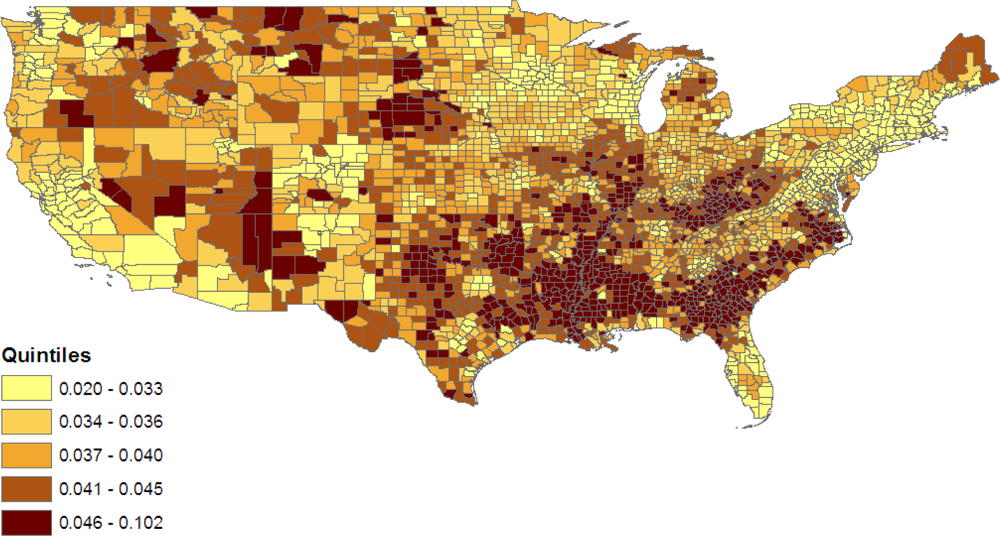
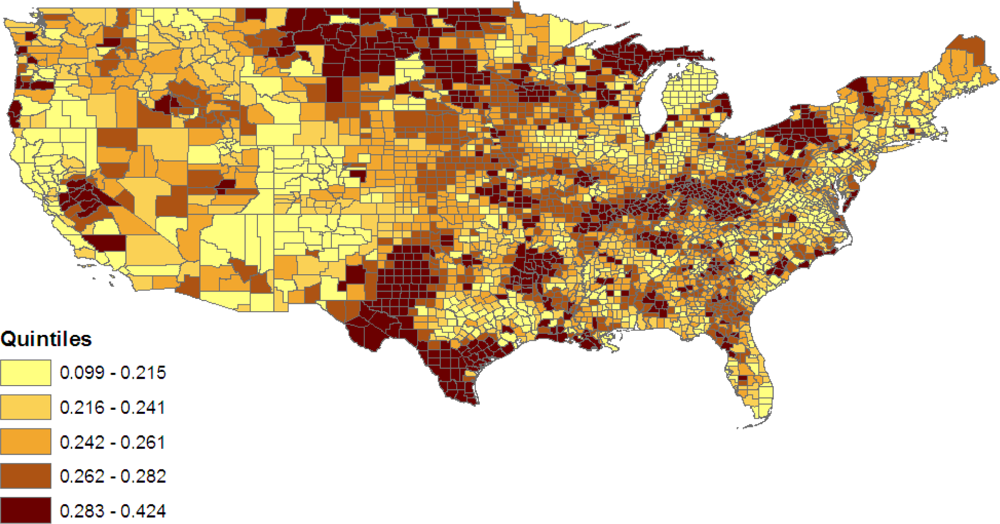
Figure 5 maps county level variations in proportions jointly obese & diabetic from model 2, namely
where the
ωcj are as in (10). The role of county poverty in defining levels of the joint obese-diabetic category under model 2 results in isolated high prevalence clusters in West North Central states such as North Dakota, Montana and Nebraska. These may, for example, be low income rural areas or counties with concentrations of native Americans [
45].
Figure 6 maps variations in the prevalence of obesity without diabetes, namely
The geographic pattern of this condition broadly resembles that of the rarer joint obese-diabetic condition; the state level correlation between these two sets of prevalence rates is 0.50.
As might be expected, combining individual and county level predictors in model 3 produces the lowest DIC and a reduced spatial variance, though over 80% in the baseline spatial variance remains unexplained.
Table 7 summarises the effects of individual level risk factors under model 3, in terms of relativities between education and race groups for each of the five morbidity categories. These are represented by the education parameters
γje (
e = 2,.., 4), and race parameters
βjr (
r = 2, 4); the reference coefficient for education is
γj1 = 0 for less than high school, and the reference coefficient for education is
βj1 = 0 for white non-Hispanics.
A notable feature from the education parameters is the lower morbidity among college graduates. Generally, morbidity is greater for subjects with lower education attainment, except for the overweight-non diabetic category.
The race parameters in
Table 7 show that black and Hispanic males have higher morbidity than white non-Hispanic males for all conditions. By contrast, other ethnicity (primarily Asian Americans and native Americans) enhances only the rate of diabetes without obesity. This is consistent with the original survey data (see
Table 2) which shows that other ethnic groups have the highest proportion of all race groups in the non-morbid (normal weight, non-diabetic) category. The high rate of diabetes without excess weight among asian Americans has been shown by other studies [
43,
46]. Although other studies [
47] show high obesity among native Americans, the results in
Table 7 suggest this may to a considerable extent be explained by socioeconomic status (as measured by education) and by area effects.
Table 8 contains the
δjk coefficients relating to county level predictors under model 3. The effects of county poverty rate remain pronounced, and are in fact enhanced for the joint obese-diabetic and obese-non-diabetic categories. The significantly higher prevalence of all conditions (except diabetic normal weight) in lower density counties is also still evident. Thus the effects of known area predictors have been largely maintained after allowing for subject level race and education, established as major individual level risk factors for the two conditions [
48]. The reduction (relatively slight) in the variance of latent area effects (see
Table 4) under model 3 may then be mainly attributable to control for population composition.
7. Conclusion
This paper has considered an approach to modelling prevalence variations in diseases or conditions considered jointly, taking account of both area effects and characteristics of survey subjects. The influence of area is represented partly by known variables (e.g., county poverty), and partly by spatially clustered latent area influences. The application has focussed on the joint prevalence of diabetes and weight status, so providing a geographic perspective on weight-related diabetes prevalence. However, the approach is generic and potentially extends to more than two conditions.
Geographic variability in chronic conditions whether considered singly or jointly will partly reflect variations in the socio-demographic characteristics of area populations, sometimes termed ‘compositional’ effects [
49]. However, a number of studies find evidence for prevalence variations between different areas even after controlling for population composition, illustrating what are sometimes termed ‘contextual’ effects [
50]. The present study adds to this evidence by showing enduring geographic contrasts in prevalence of different joint obesity-diabetes categories after taking account of individual level age, race and education status.
In the present paper contextual effects have been represented by shared latent effects over the joint obesity-diabetes categories. These are spatially structured random effects for counties and states, and the consistently positive loadings in
Table 5 demonstrate that a shared univariate effect is appropriate. Elaborations to the model presented above are possible, such as ethnic group differentiation in age or education gradients, or additional subject level predictors, though those included (age, race, education) are established as the major dimensions of variation for diabetes and obesity [
5,
48]. One might also assume spatially varying impacts of the known area predictors, such as the county poverty rate [
51].