On the Effects of Clothing Area Factor and Vapour Resistance on the Evaluation of Cold Environments via IREQ Model

Abstract

The IREQ (Insulation REQuired) index is the only reliable and effective model for predicting and evaluating the protection given by a clothing ensemble in cold environments. Even with the growth of studies aimed at assessing the thermophysical characteristics of clothing, IREQ remained unaltered from Holmér’s original formulation four decades prior. This paper focuses on the effect of the evaluation of the clothing area factor and the resultant vapour resistance on the assessment of cold environments via IREQ. Obtained results reveal meaningful variations in the duration limit exposure (up to 5 h), whereas IREQ values remain unchanged. Observed phenomena could be interesting when discussing the revision of the ISO 11079 standard, which prescribes using IREQ for the determination and interpretation of cold stress.

1. Introduction

1.1. Background

As observed by Petersson et al. [1], despite the increased interest in heat stress due to global warming, in temperate climates, the mortality is still higher in winter than in summer [2,3]. Cold exposure is typical in some outdoor work environments, including open pit miners, oil and gas industry workers, foresters, soldiers, construction and road industry personnel and occurs indoors in several industrial activities (e.g., milk, fish, meat industry, food distribution and pharmaceutical units) [4,5,6]. The most common problems/illnesses associated with cold exposure include hypothermia, pain in the extremities up to frostbite, impaired mobility and operational capacity due to the weight of clothing, and reduced physical capacity of the body [4,7,8,9,10].

The increased interest in occupational safety and health gave rise to the update of the legislation [11] and the promotion of public awareness, education and investigation in this field and in the formulation of a three-phase strategy called SOBANE (Screening, OBservation, ANalysis, Expertise) [6,12,13], which inspired the ISO 15265 [14] and, specifically for cold environments, the ISO 15743 [15]. This standard reports models and methods for cold-risk assessment and management, a checklist for identifying cold-related problems at work, a methodology based on subjective analysis aimed at identifying those individuals with symptoms that increase their cold sensitivity, and guidelines on how to apply thermal standards and other validated scientific methods when assessing cold-related risks. As far as the evaluation of the cooling of the body as a whole, ISO 15743 recommends the evaluation of the Insulation Required IREQ [16,17,18], which is also used by ISO 15265 to assess the class of risk in cold environments both in the short and long term.

Forty years after its formulation, several investigations based on physiological, objective and subjective analyses demonstrate the reliability of the IREQ model [19,20,21,22,23], even if compared with other available models [24,25]. Most specifically, studies carried out during military operations reveal that clothes worn by soldiers exhibit thermal insulation values generally in agreement with IREQ or slightly higher, leading to a slight increase (1 °C) in the core temperature [19,20]. Other studies seem to confirm that the claim of operators exposed to cold conditions is typically due to behavioural issues: workers prefer to wear lighter clothes to increase the ease of movement [22,23] and often do not accurately capture the correlation between the cold protection provided by clothing and the environmental conditions [26].

Other criticisms about IREQ focused on a lack of a database of experimental investigations as the basis of its validation [27,28,29,30], the impossibility of considering short time exposure and variations in work intensity [31], and some inconsistencies in its calculation by software due to systematic errors [32]. In addition, the influence of wind action and body movements on clothing insulation and vapour resistance values relies on algorithms that differ from those reported in ISO 9920 [33,34].

Finally, recent experimental studies focused on the determination of the clothing area factor as a function of the basic clothing insulation have resulted in the formulation of new and more robust algorithms. These algorithms represent an advancement compared to those prescribed by existing standards in the field of physical environment ergonomics [35,36], but their influence on the IREQ formulation has yet to be investigated.

1.2. Aim of This Paper

Despite its limitations, the IREQ model remains the only tool for evaluating global and local cooling in cold environments. That is why it is used by ISO standard 11079, which deals with the assessment of cold environments in occupational health and industrial hygiene, and to combine weather forecasting with personal factors to offer guidance on the risks of daily cold exposures [1]. The model, unchanged since 1993, suffers from significant drawbacks. Its implementation is inconsistent, and its underlying rationale fails to reflect recent advancements in clothing thermophysical properties research and standardization. Notably, the model lacks the new algorithms for calculating clothing area factor and evaporative resistance, leaving these crucial aspects unaddressed.

The aim of this paper is to verify to what extent the evaluation of these two quantities influences the body heat storage rate and the exposure duration limit D_lim. The results obtained will constitute solid arguments for revising the IREQ model and the current ISO standard 11079 and implementing more reliable software.

The next section aims to help readers understand the IREQ model’s rationale and its detailed application. Subsequently, it will address the open issues and relevant literature that motivate the present investigation.

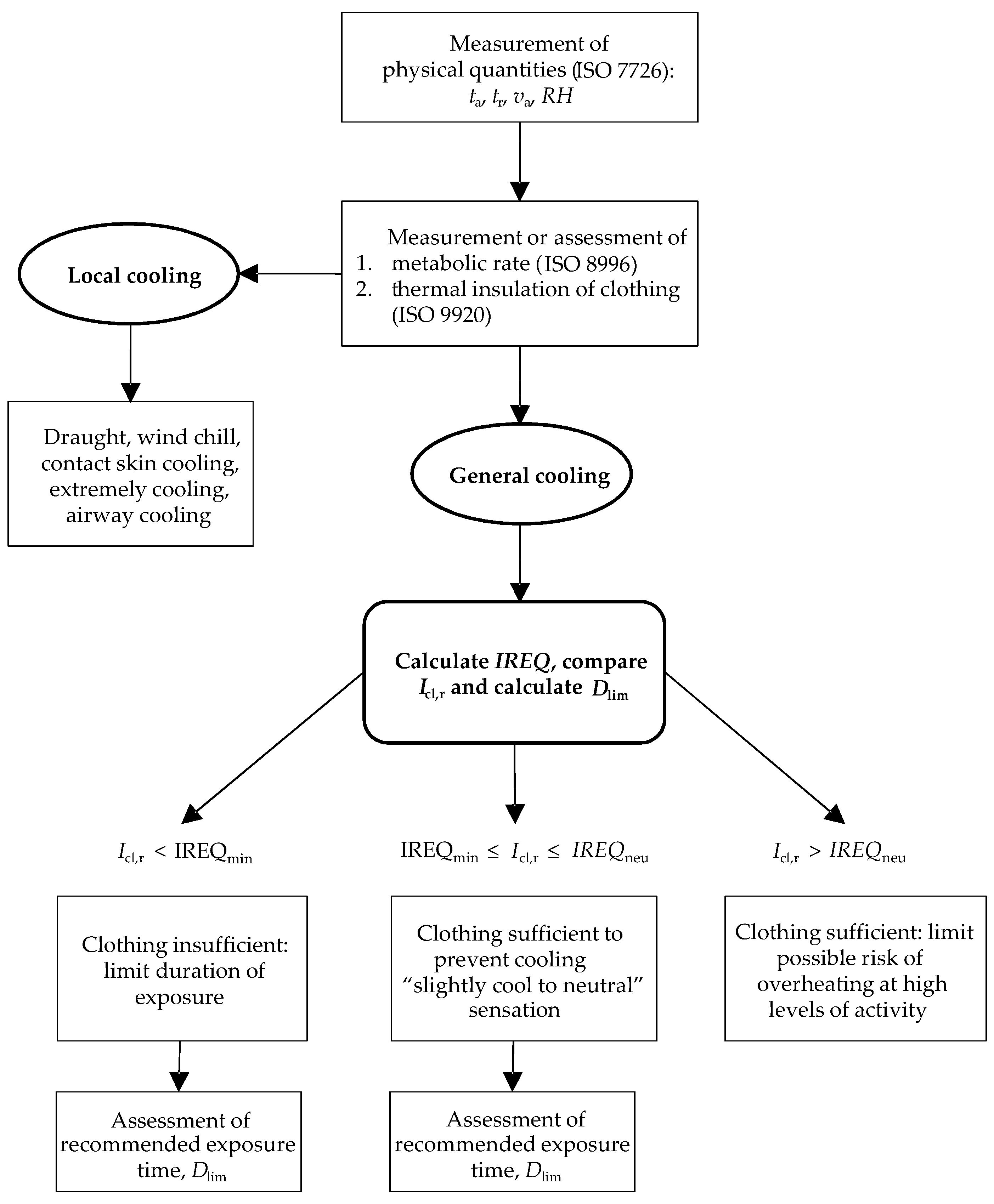
2. The IREQ Model

2.1. Model Features

IREQ represents the clothing insulation value needed to maintain the body heat balance. It is calculated from the well-known heat balance equation on the human body [35].

$$M-W=E_{\mathrm{res}}+C_{\mathrm{res}}+E+K+R+C+S$$

(1)

where

C convective heat flow, W m⁻²;

C_res respiratory convective heat flow, W m⁻²;

E evaporative heat flow at the skin, W m⁻²;

E_res respiratory evaporative heat flow, W m⁻²;

K conductive heat flow, W m⁻²;

M metabolic rate, W m⁻²;

R radiative heat flow, W m⁻²;

S body heat storage rate, W m⁻²;

W rate of mechanical power, W m⁻².

By assuming negligible the contribution of the heat transfer by conduction (K = 0), under steady conditions (S = 0), Equation (1) can be arranged as

$$R+C=M-W-E_{\mathrm{res}}-C_{\mathrm{res}}-E$$

(2)

Convective, radiative and evaporative heat flows can be calculated as follows:

$$C=f_{\mathrm{cl}}{h}_{\mathrm{c}}\left(t_{\mathrm{cl}}-t_{\mathrm{a}}\right)$$

(3)

$$R=f_{\mathrm{cl}}{\epsilon }_{\mathrm{cl}}{\displaystyle \frac{A_{\mathrm{r}}}{A_{\mathrm{Du}}}}\left[{\left(t_{\mathrm{cl}}+273\right)}^4-{\left(t_{\mathrm{r}}+273\right)}^4\right]$$

(4)

$$E=w{\displaystyle \frac{p_{\mathrm{sk},\mathrm{s}}-p_{\mathrm{a}}}{R_{e,T,r}}}$$

(5)

where

A_r effective radiating area of a body, m²;

A_Du Du Bois body surface area, m²;

f_cl clothing area factor, ND;

h_c convective heat transfer coefficient, W m⁻² K⁻¹;

p_a water vapour partial pressure, kPa;

p_sk,s saturated water vapour pressure at skin temperature, kPa;

t_a air temperature, °C;

t_cl clothing surface temperature, °C;

t_r mean radiant temperature, °C;

R_e,T,r resultant evaporative resistance of clothing and boundary air layer, m² kPa W⁻¹;

w skin wittedness, ND;

ε_cl emissivity of the clothing surface, ND.

On the basis of Equations (1) and (2), IREQ can be finally obtained by means of this equation:

$$IREQ={\displaystyle \frac{t_{\mathrm{sk}}-t_{\mathrm{cl}}}{R+C}}$$

(6)

Equation (6) contains two unknown variables: IREQ and the clothing surface temperature t_cl; therefore, it has to be solved for t_cl by means of an iterative numerical procedure (see Appendix A for related details).

As the primary goal of the IREQ model is to analyze whether the clothing ensemble worn by the subject provides enough insulation to sustain the heat balance with no storage (S = 0), the resultant clothing insulation I_cl,r covering the body under the current situation should be calculated and then compared with IREQ. The calculation of I_cl,r value is obtained by the resultant clothing insulation value and the resultant boundary layer thermal insulation according to Equations (7)–(10) as indicated by the ISO standards 9920 [34] and 11079 [18].

$$I_{\mathrm{cl},\mathrm{r}}=I_{\mathrm{T},\mathrm{r}}-{\displaystyle \frac{I_{\mathrm{a},\mathrm{r}}}{f_{\mathrm{cl}}}}$$

(7)

$$I_{\mathrm{T},\mathrm{r}}=I_T\left[0.54e^{\left(0.075\cdot \ln a_{\mathrm{p}}-0.15v_{\mathrm{a}}-0.22v_{\mathrm{w}}\right)}-0.06\cdot \ln a_{\mathrm{p}}+0.5\right]$$

(8)

$$I_{\mathrm{a},\mathrm{r}}=0.092e^{\left(-0.15v_{\mathrm{a}}-0.22v_{\mathrm{w}}\right)}-0.0045$$

(9)

$$I_{\mathrm{T}}=I_{\mathrm{cl}}+{\displaystyle \frac{I_{\mathrm{a}}}{f_{\mathrm{cl}}}}$$

(10)

where

a_p air permeability of outer fabric, L s⁻¹ m⁻²;

I_a static boundary layer thermal insulation, m² K W⁻¹;

I_a,r resultant boundary layer thermal insulation, m² K W⁻¹;

I_cl basic clothing insulation, m² K W⁻¹;

I_cl,r resultant clothing insulation, m² K W⁻¹;

I_T basic total insulation, m² K W⁻¹;

I_T,r resultant total insulation, m² K W⁻¹;

v_a air velocity, m s⁻¹;

v_w walking speed, m s⁻¹;

I_a = 0.085 m² K W⁻¹.

The walking seed value, if unknown, can be calculated as follows [34]:

$$v_{\mathrm{w}}=0.0052\left(M-58.2\right)$$

(11)

Equations (8) and (9) apply for 0.4 m s⁻¹ ≤ v_a ≤ 18 m s⁻¹ and 0 m s⁻¹ ≤ v_w ≤ 1.2 m s⁻¹.

Regarding the IREQ interpretation criteria, there are two possibilities:

• IREQ < I_cl,r: there is no risk for cold. However, if IREQ << I_cl,r, then there may be a risk of overheating and excess sweating, which may lead to discomfort and cold-related issues later.
• IREQ > I_cl,r: worker safety is not necessarily guaranteed. More specifically, if the body heat loss is within 144 kJ m⁻², there is no risk to health, provided that the extremities are properly protected. However, if this limit for heat loss is exceeded, it is necessary to assess the maximum safe exposure time.

In situation (2), for low strain conditions, it may be sufficient to have thermal insulation that satisfies the balance, IREQ_neu, or it may be necessary to have thermal insulation that guarantees safety even for high strain, IREQ_min. In both cases, duration-limited exposure D_lim should be calculated based on acceptable levels of body cooling:

$$D_{\lim }=-{\displaystyle \frac{Q_{\lim }}{S}}$$

(12)

The heat storage rate S in Equation (12) can be obtained from Equations (1) (K = 0) and (6) (IREQ = I_cl,r) by an iterative procedure. In Figure 1, the procedure for calculating and interpreting IREQ is shown, while suggested physiological criteria for the determination of IREQ and D_lim are reported in

Table 1. Suggested physiological criteria for the determination of IREQ and D_lim [18].

Quantity	Low Strain	High Strain
IREQ	Neutral (IREQneu)	Minimal (IREQmin)
tsk	35.7–0.0285·M	33.34–0.0354·M
w	w = 0.001·M	0.06
Dlim	Short	Long
Qlim (kJ m−2)	144	144

.

2.2. Open Issues

Since 1993, knowledge in the field of cold thermal environments has advanced, but the only modification to the IREQ model has been the introduction of special algorithms for accounting for the effect of wind action and body movements on the basic clothing insulation values. In contrast, two fundamental aspects remain unexplored: the clothing area factor f_cl, systematically investigated in [36], and the evaluation of the resultant (or dynamic) vapour resistance of clothing.

The clothing area factor f_cl is defined as the ratio of the outer surface area of the clothed body to the surface area of the body. Its evaluation is a crucial step of the IREQ model because it affects convective, radiative, and evaporative heat losses, and total clothing insulation [18,34]. f_cl is usually measured by different methods (e.g., photographic method, 3D scanning) [37,38,39] or evaluated with empirical equations as a function of the clothing insulation. These equations were derived using typical clothing for moderate and hot environments, like in [37,38] and [39], respectively, and may not be adequate in the case of highly insulating clothing [36]. The only equation for protective clothing against the cold is the one developed in early 2000 in Finland by SubZero project [40,41].

The accuracy of most common formulas for evaluating f_cl from the basic clothing insulation I_cl has been discussed in a paper by Kuklane and Toma [36], who considered a set of measurement carried out on 14 clothing ensembles designed for ambulance personnel covering clothing insulation values from 0.53 to 3.19 clo measured according to ISO 15831 [42]. The clothing area factors were measured with the photographic method [43]. Obtained values were then compared with those predicted by the equations summarized in

Table 2. Some clothing area factor formulas considered by Kuklane and Toma [36]. I_cl is expressed in m² K W⁻¹.

Equation	Equation Number	References
1.0 + 1.97 Icl	(13)	[18,44]
1.0 + 1.197 Icl	(14)	[45]
1.0 + 0.97 Icl	(15)	[46]
1.05 + 0.645 Icl	(16)	[40,41,47]
1.0 + 1.81 Icl	(17)	[34]
1.0 + 0.85 IT	(18)	[40,41]
1.01 +1.599 Icl	(19)	[48]
1.0 + 1.697 Icl	(20)	[48]
1.04 + 0.85 IT	(21)	[36]
1.657 Icl0.1546	(22)	[36]

.

Additional datasets of f_cl measurements were considered [41] to avoid a one-sided discussion on the topic.

Obtained results [36] demonstrate that all formulas for evaluating the clothing area factor return reliable results for western type and industrial clothing if I_cl ≤ 1.5 clo. For I_cl > 2.0 clo, the equations typically used in the standards (Equations (13), (16) and (17)) and the ones suggested by Smallcombe et al. (Equations (19) and (20)) return an overestimation of the clothing area factor. The calculation accuracy by these equations in the range 1.5 < I_cl ≤ 2 clo may still be acceptable, while equations (Equations (16), (18) and (21)) are highly accurate for I_cl > 2.0 clo. For modern clothing systems based on Western industrial clothing, Equation (22) gives the best fit but requires additional validation on other clothing ensembles. However, as the authors observe [36], a separate question is if and how much different approaches of f_cl calculation affect IREQ prediction outcome [18,49].

The second issue discussed in [32] deals with the calculation of the resultant total vapour resistance of clothing R_e,T,r which accounts for the effects of body movements and wind action.

Consistently with ISO 9920 [34,50,51] and ISO 7933 [44], the resultant vapour total clothing resistance can be calculated by multiplying the static R_e,T value given by Equation (23) with a correction factor CorrE (as a function of the relative air velocity v_ar and the walking speed v_w) according to Equation (24).

$$R_{e,T}={\displaystyle \frac{I_T}{i_{m}L}}$$

(23)

with i_m = 0.38, L = 16.5 K kPa⁻¹ and I_T given by Equation (7).

$$R_{eT,r}=R_{e,T}\cdot CorrE$$

(24)

with, optionally,

$$CorrE=\exp \left[-0.468\left({\mathrm{v}}_{\mathrm{ar}}-0.15\right)+0.080{\left({\mathrm{v}}_{\mathrm{ar}}-0.15\right)}^2-0.874v_w+0.358v_w^2\right]$$

(25)

or

$$CorrE=0.3-0.5Corr{I}_T+1.2Corr{I}_T^2$$

(26)

and

$$Corr{I}_T={\displaystyle \frac{I_{T,r}}{I_T}}$$

(27)

and 0.15 m s⁻¹ ≤ v_ar ≤ 3.5 m s⁻¹, 0 m s⁻¹ ≤ v_w ≤ 1.2 m s⁻¹.

CorrI_T can be calculated with different equations [34,52] as a function of the total clothing insulation as follows.

Normal or light clothing (e.g., 0.6 clo < I_cl < 1.4 clo or 1.2 clo < I_T < 2.0 clo):

$$Corr{I}_T=e^{\left[-0.281\cdot \left(v_{ar}-0.15\right)+0.044\cdot {\left(v_{ar}-0.15\right)}^2-0.492v_w+0.176v_w^2\right]}$$

(28)

Specialized, insulating, cold weather clothing (e.g I_T > 2 clo):

$$\mathrm{Corr}{I}_T=e^{\left\{\left[-0.0512\cdot \left(v_{ar}-0.4\right)+0.794\cdot {10}^{-3}\cdot {\left(v_{ar}-0.4\right)}^2-0.0639v_w\right]\cdot a{p}^{0.144}\right\}}$$

(29)

It is essential to note that more recent algorithms for evaluating R_e,T,r are not available in the literature. Specifically, more recent algorithms [53] focus on local R_e,T,r values to be used in multi-node models [54].

Unlike ISO 9920, the ISO TR 11079: 1993 [49] calculated the resultant vapour resistance by Equation (30):

$$R_{eT,r}={\displaystyle \frac{i_m}{L}}\left({\displaystyle \frac{I_a}{f_{cl}}}+I_{cl,r}\right)$$

(30)

with

$$I_{cl,r}=\left\{\begin{array}{l}\begin{array}{cccc}0.90I_{cl}& & if& M<100 W{m}^{-2}\end{array}\\ \begin{array}{cccc}0.75I_{cl}& & if& M\ge 100 W{m}^{-2}\end{array}\end{array}\right.$$

(31)

Fifteen years later, ISO 11079:2007 also applied correction to the basic air boundary layer insulation I_a and introduced the resultant air boundary layer insulation I_a,r and calculates R_e,T,r by means of Equation (32):

$$R_{e,T,r}={\displaystyle \frac{i_m}{L}}\left({\displaystyle \frac{I_{a,r}}{f_{cl}}}+I_{cl,r}\right)={\displaystyle \frac{i_m}{L}}{I}_{T,r}$$

(32)

Consequently, if Equations (32) and (27) are considered, the correction factor to apply to the static vapour clothing resistance is the same correction factor for the basic total insulation:

$$R_{eT,r}=R_{e,T}\cdot Corr{I}_T$$

(33)

This means that the effect of wind and body movements results in the same decrease in clothing vapour resistance R_e,T and total clothing insulation I_T (e.g., CorrE = CorrI_T). This assumption is inconsistent with measurements analyzed by Havenith et al. [50] who observed a higher reduction in vapour resistance than in total insulation values for three clothing ensembles (1: underwear, trousers, sweater; 2: 1 + cotton coverall; 3: 1 + impermeable coverall).

The approach of the current version of ISO 11079 in dealing with the resultant vapour resistance brings to different values, as observed in previous papers by our team [32,52]. More specifically, R_eT,r values calculated according to Equation (33) are higher than 50% of those calculated according to Equation (24) (air velocity and walking speed values under 2.5 m s⁻¹ and 0.6 m s⁻¹, respectively) [52]. Such an occurrence could indicate a significant underestimation of latent heat loss through the skin, which has not yet been explored regarding its impact on IREQ and D_lim values. In contrast, the effects of various approaches to addressing the resultant vapour resistance have only been examined in the context of predicting heat stress conditions using the PHS model [52,55].

3. Methods

The investigation discussed here has been carried out numerically using special software developed in MATLAB (version: 9.13.0) [56], which allows the evaluation of indoor thermal environments [57]. The software section devoted to cold stress assessment via IREQ was specifically designed based on the JAVA Applet available online, corrected by all bugs previously highlighted by our research team [32]. To improve accessibility for users, as performed by other research groups [58], the four MATLAB functions implementing the IREQ model are provided in Appendix B (from Appendix B.1, Appendix B.2, Appendix B.3, Appendix B.4 and Appendix B.5).

Concerning the effect of the clothing area factor on the assessment of cold stress conditions according to ISO 11079, we focused on the equations considered by Kuklane and Toma [36] summarized in Table 2. The analysis consists of two steps:

• Identification of the equations which return the highest and lowest f_cl values, respectively.
• Evaluation and comparison of IREQ and D_lim values using the equations identified in the previous step, consistently with low strain (neutral) and high strain (minimal) criteria within the range of subjective (metabolic rate and basic clothing insulation) and physical (air temperature, air velocity, relative humidity and mean radiant temperature) variables considered by ISO 11079.

In the second part of this paper, the analysis deals with the effect of the resultant clothing vapour resistance by comparing IREQ and D_lim values calculated by Equations (24) and (33), respectively.

The reference conditions for IREQ, D_lim, and resultant total evaporative resistance were consistent with those adopted by the figures reported in the ISO 11079 standard [18]. They are summarized in

Table 3. Experimental conditions for the evaluation of the effect of f_cl formulas on IREQ and D_lim calculations. ⁽*⁾ Air temperature and mean radiant temperature are assumed to be equal; ⁽**⁾ I_cl values of 0.5, 3.0, and 3.5 clo have not been considered in simulations with M = 175 W m⁻².

Variable	Units	Values	Number of Conditions
IREQ calculations
ta	°C	from −50 to 10 (step 10 °C)	7
RH	%	50	1
tr	°C	from −50 to 10 (step 10 °C)	7
va	m s−1	0.5, 1.0, 1.5, 2, 5, 10, 18	7
M	W m−2	70, 90, 115, 145, 175, 200, 230, 260	8
ap	L m−2 s−1	8	1
Number of simulations			2744
Dlim calculations
ta (*)	°C	from −50 to 10 (step 10 °C)	7
RH	%	50	1
va	m s−1	0.5, 1.0, 1.5, 2.0, 5.0, 10, 18	7
M	W m−2	90, 115, 145, 175	4
Icl	clo	0.5 (**), 1.0, 1.5, 2.0, 2.5, 3.0 (**), 3.5 (**)	7
ap	L s−1 m−2	8	1
Number of simulations			1225

and

Table 4. Experimental conditions for the evaluation of the effect of the calculation of the resultant total evaporative resistance on IREQ and D_lim calculations. ⁽*⁾ Air temperature and mean radiant temperature are assumed to be equal; ⁽**⁾ I_cl values of 0.5, 3.0, and 3.5 clo have not been considered in simulations with M = 175 W m⁻².

Variable	Units	Values	Number of Conditions
ta (*)	°C	from −50 to 10 (step 10 °C)	7
RH	%	50	1
va	m s−1	from 0.5 to 3.5 (step 0.5 m s−1)	7
M	W m−2	90, 175	2
Icl	clo	0.5 (**), 1.0, 1.5, 2.0, 2.5, 3.0 (**), 3.5 (**)	7
ap	L m−2 s−1	8	1
Number of simulations			539

, respectively.

The effect of clothing area factor has been studied within the following limits of the main parameters as recommended by ISO 11079:

• Air temperature: t_a < 10 °C;
• Air velocity: 0.4 < v_a < 18 m/s;
• Basic clothing insulation, I_cl ≥ 0.5 clo.

The analysis of the effect of the calculation of the resultant total evaporative resistance was limited to v_a = 3.5 m s⁻¹ according to the range of applicability of the algorithms recommended by ISO 9920 [34].

4. Results and Discussion

4.1. The Effect of Clothing Area Factor

4.1.1. Preliminary Observations

In Figure 2, the values of clothing area factor calculated using Equations (13)–(22) are depicted, and the percentage difference with respect to Equation (16) is shown.

Three main groups of formulas can be identified, which provide the highest (A), the lowest (B) and intermediate (C) values of clothing area factor:

• Group A formulas (Equations (13), (17), (19) and (20)) that include ISO 11079 (Equation (13)), ISO 9920 (Equation (17)), and ISO 7933 (Equation (17)) return f_cl values higher than 25% (50%) for I_cl = 2.0 clo (I_cl = 4.0 clo) if compared with Equation (16), which returns the lowest values.
• Group B formulas (Equations (15), (18) and (21)) return f_cl values not higher than 10% if compared with those calculated by Equation (16).
• Group C formulas exhibit intermediate behaviour if compared with Equation (16). More particularly, Equation (14) returns f_cl values not higher than 20%, whereas Equation (22) behaves like group A formulas for I_cl < 1.0 clo, then reaches a maximum of 10.6% for I_cl = 2 clo, and finally overestimates f_cl by 6.2% for I_cl = 4.0 clo.

According to the observation above, the analysis of the effect of the clothing area factor on the calculation of IREQ and D_lim values will be focused on the following:

• Equation (13), which returns the highest f_cl values and is adopted by ISO 11079.
• Equation (16), which returns the lowest f_cl values and is chosen as the basis for comparisons.
• Equation (22), which despite requiring further validation, is a better fit for the experimental f_cl values measured on professional modular clothing system for ambulance personnel, which is meant to provide thermal comfort over a wide range of climatic conditions from hot summer days to extremely cold Nordic winters [36].

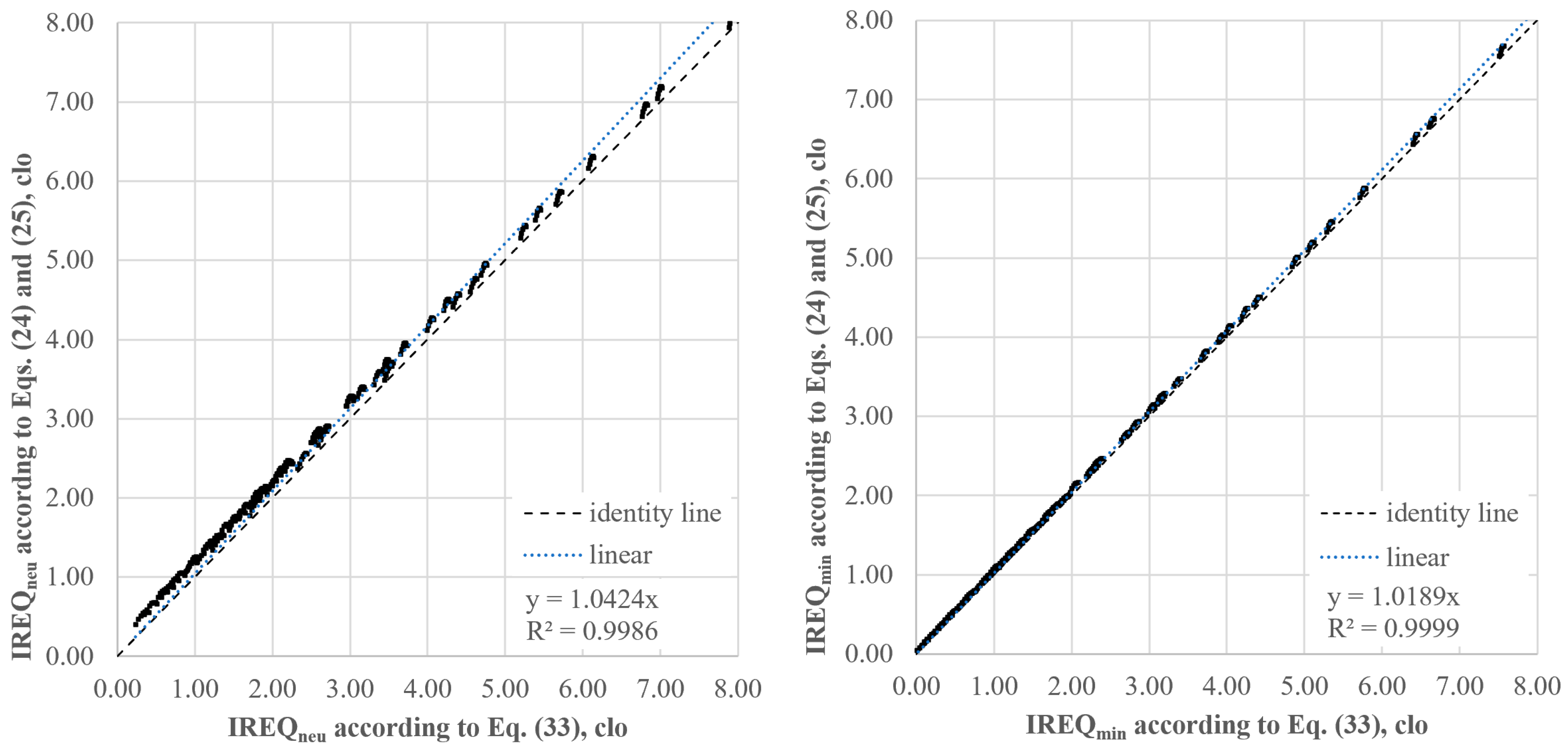
4.1.2. Effect of Clothing Area Factor on IREQ Values

Figure 3 shows the effect of f_cl calculations on IREQ_min and IREQ_neu values in the entire range of parameters considered (2744 conditions).

All data quite overlap on the identity line (y = x) with R² values exceeding 0.999 and slopes a few less than 1: 0.9838 and 0.9842 in the worst cases, that means a negligible underestimation of IREQ values of 1.6% in the case of Equations (16) and (22). This phenomenon is quite surprising when we consider that for I_cl = 4.0 clo, Equation (13) yields f_cl values that are 50% higher than those predicted by Equation (16). In contrast, Equations (16) and (22) produce similar results, with a difference not higher than 10% in the range from 0.5 to 4.0 clo.

This behaviour is due to the structure of Equation (2), which results in two effects which do not affect both the numerator and denominator of Equation (4):

1.

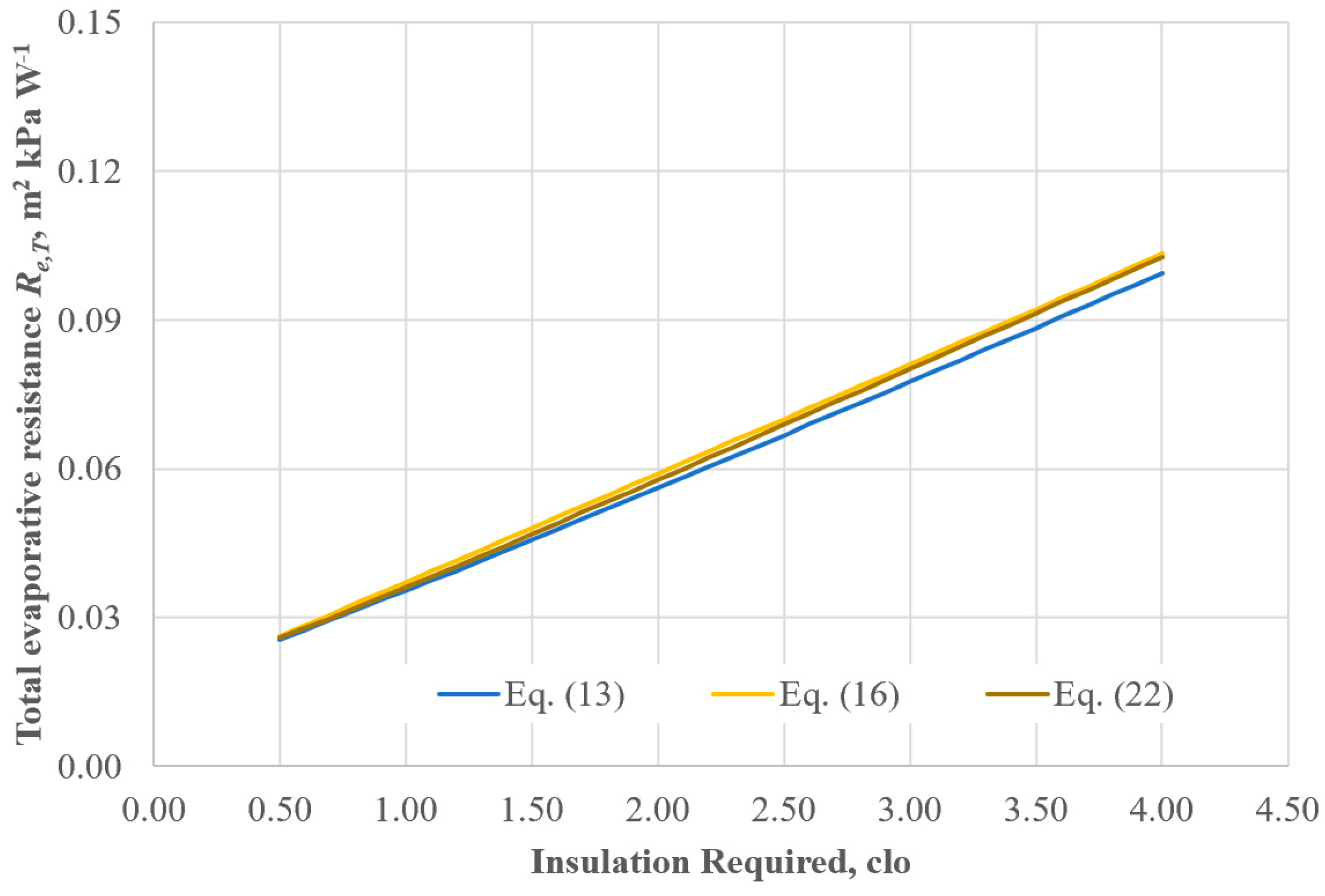
The right side of Equation (2) (dry heat loss) is scarcely affected by the different formulas used for the evaluation of f_cl. This is because the only term at the right side of Equation (2) affected by the clothing area factor is the evaporative heat flow E being related to the resultant total evaporative resistance of clothing according to Equations (5) and (32) with I_cl,r = IREQ. Now, the total evaporative resistance of clothing and air boundary layer is quite unaffected by the formula adopted for f_cl calculation, as shown in Figure 4.

In fact, according to Equations (13) and (23) for low IREQ values, e.g., <1.0 clo, the f_cl variation is not excessive, at 15% at least according to Figure 2, whereas for higher IREQ values, the meaningful variation of f_cl values (see Figure 2) related to the different formula is meaningfully softened by the low value of the air boundary layer insulation, I_a = 0.085 m² K W⁻¹. As an example, for IREQ = 4 clo, f_cl values given by Equations (16) and (13) are 1.45 and 2.22 (+53%), respectively, while corresponding R_e,T values are almost the same (0.099 and 0.102 m² kPa W⁻¹).

2.

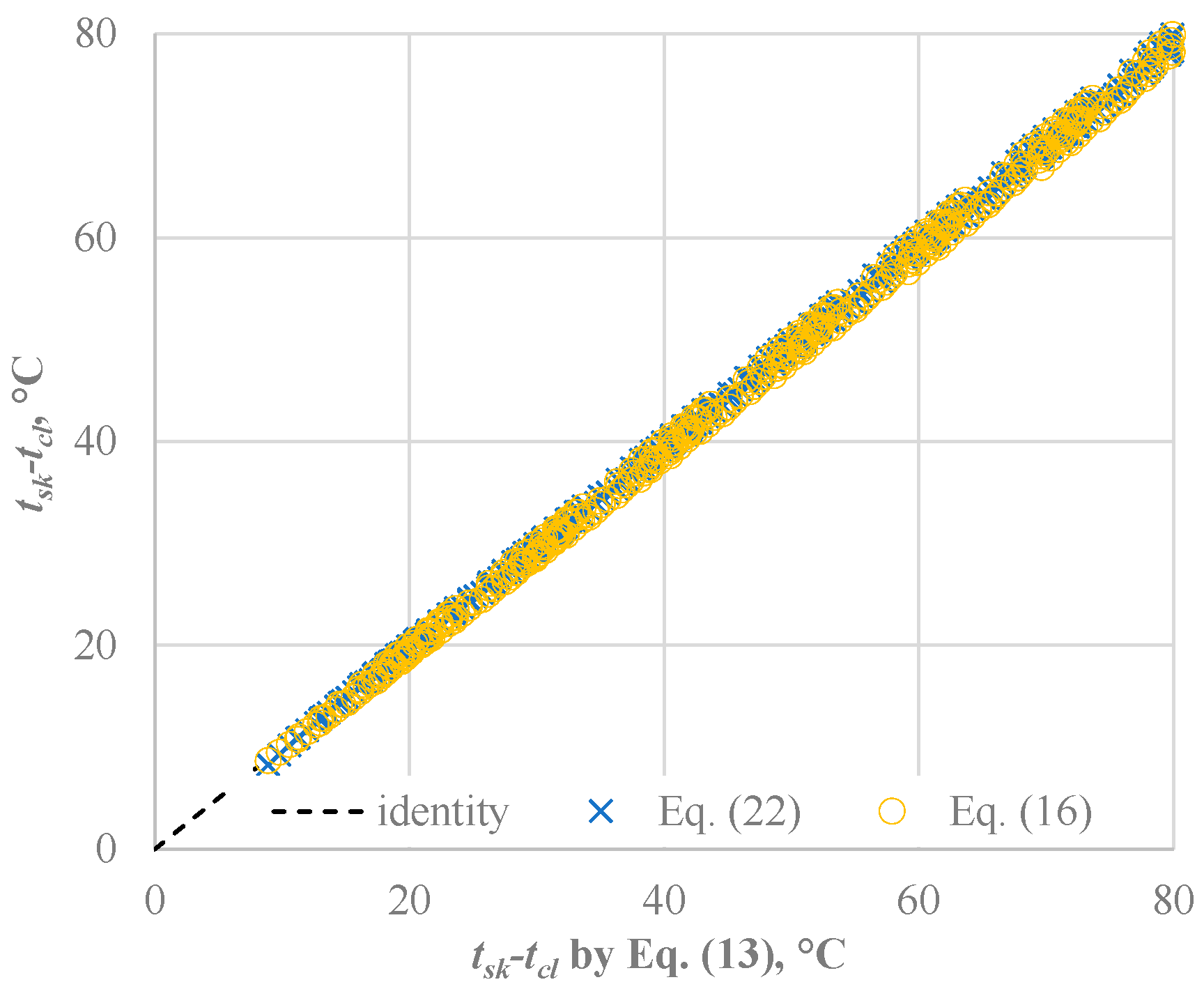
The clothing surface temperature is scarcely affected by the errors induced by the use of the different formulas for f_cl calculation as confirmed by data shown in Figure 5.

This is the trivial consequence of the presence of the clothing insulation layer of the body surface. More particularly, the value of the difference t_sk-t_cl is close to the difference between the mean skin temperature—which is only affected by the metabolic rate, as shown in Table 1.

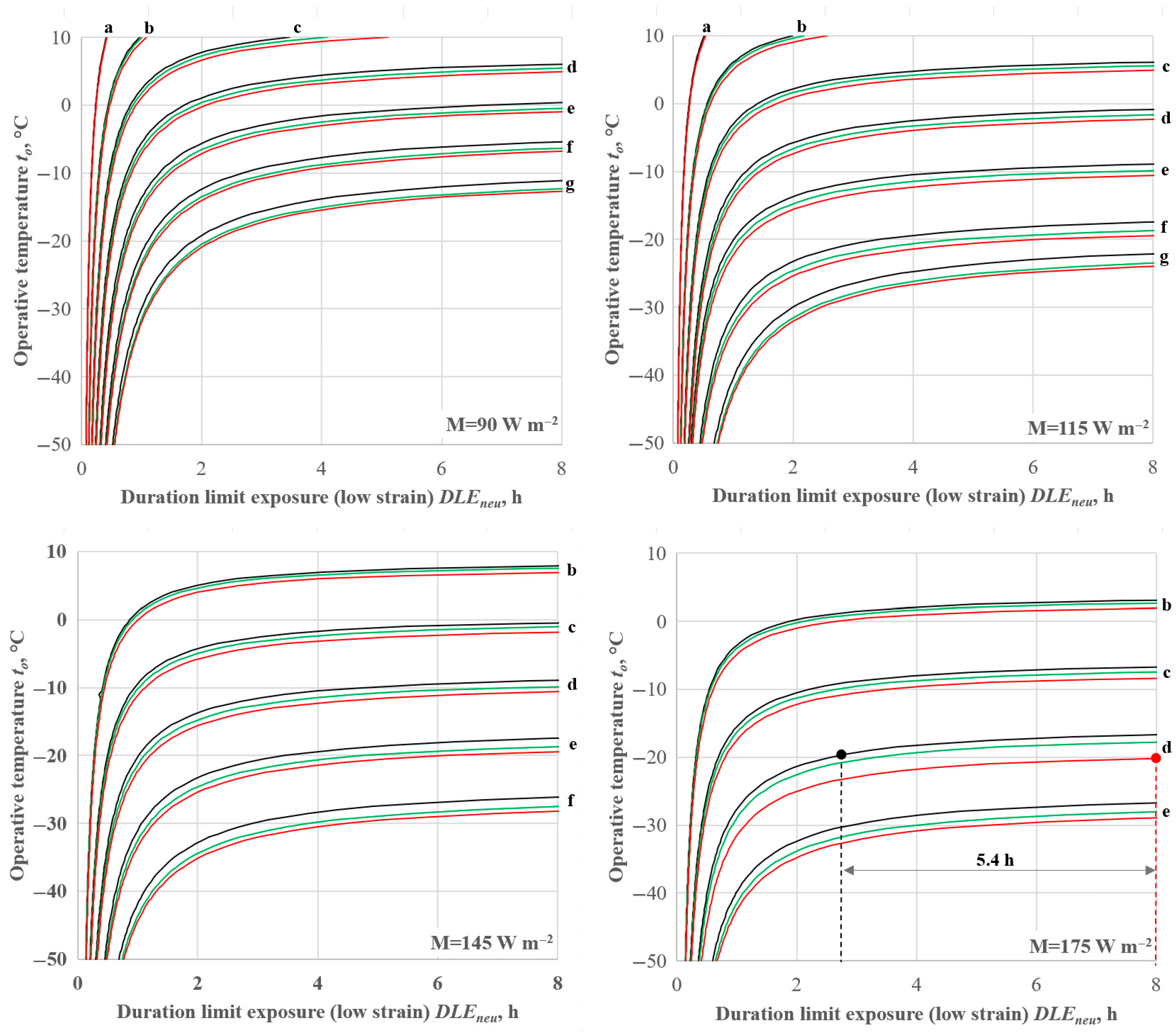
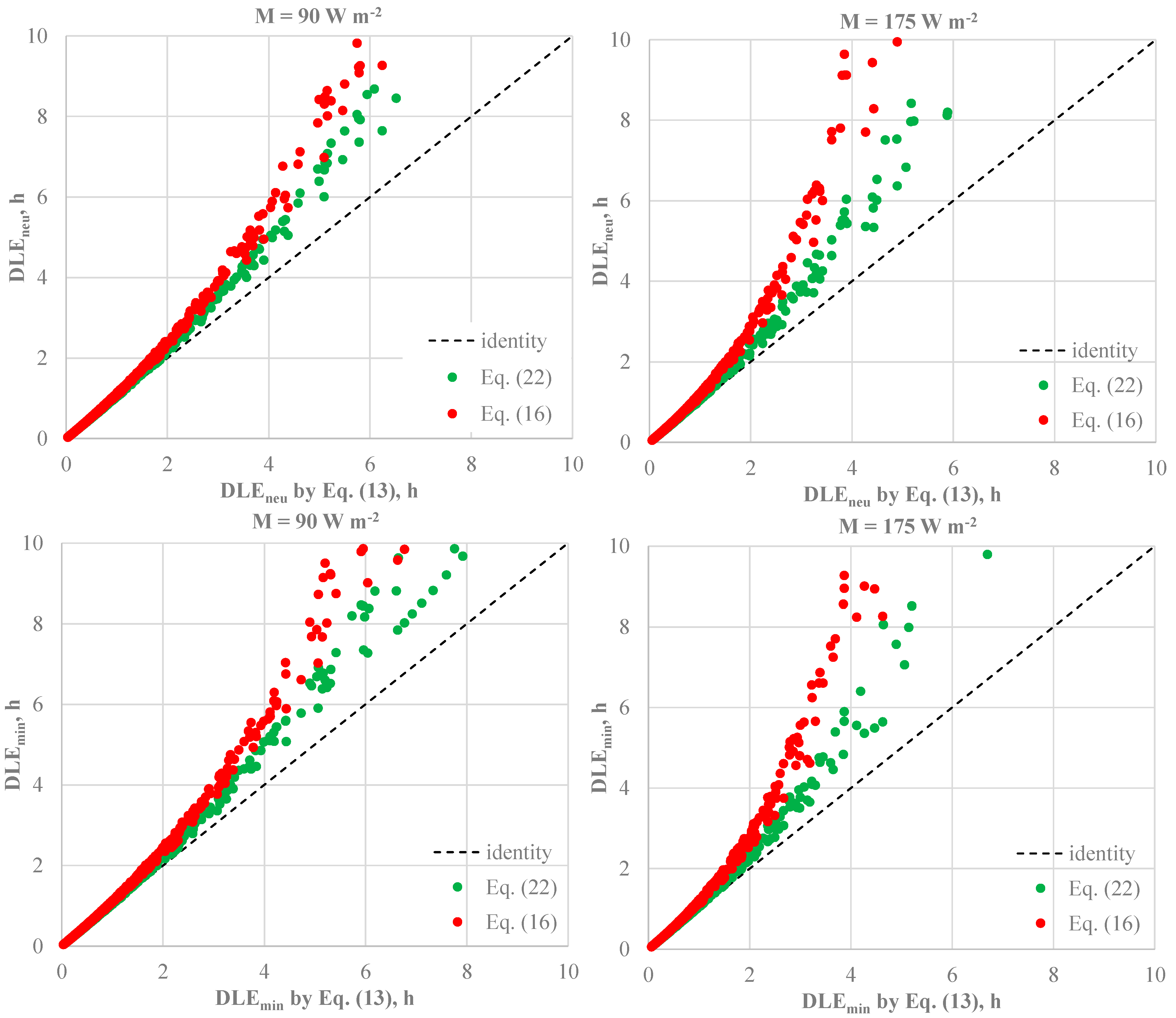
4.1.3. Effect of Clothing Area Factor on D_lim Values

The trends depicted in Figure 6 prove that the D_lim values predicted with Equations (16) and (22) are systematically higher than those calculated with Equation (13), actually adopted by the IREQ model [18].

The reason for this behaviour is that the clothing area factor directly affects the body heat storage rate by increasing the dry heat loss R + C and the evaporative term E. More specifically, R, C and E increase as the clothing area factor increases according to Equations (3)–(5) and (32). Consequently, the body heat storage rate increases in modulus with the consequent decrease in the D_lim value, according to Equations (34) and (12), respectively.

$$S=M-W-\left(E_{res}+C_{res}+E+R+C\right)$$

(34)

From the quantitative perspective, the difference in D_lim values obtained with Equations (16) and (22) is related to the value of the heat storage rate value. More particularly, for high values of the heat storage rate (e.g., at low operative temperature, clothing insulation or low metabolic rate), D_lim is lowest, and even important variations in f_cl do not affect the results. This means that for short-term exposures (e.g., at high values of the heat storage rate S), the effect of the clothing area factor is negligible. In contrast, for lower values of the module of the heat storage rate, D_lim is higher. Therefore, the differences are magnified exceeding 5 h in case of Equation (16) as depicted in Figure 6 and Figure 7, which also reports DLE_min values.

Equation (22) shows lower overestimation of D_lim values due to the non-linear behaviour observed in Figure 2. However, for D_lim > 4 h, it returns D_lim values 3 h higher than those calculated with Equation (10).

Based on observed behaviours, it is important to define if Equation (16) or Equation (22) can be adopted by the revision of ISO 11079. On the one hand, Equations (16) and (22) yield more reliable values for the clothing area factor f_cl [36] compared to traditional formulas such as Equation (13), which is currently employed by the IREQ model as specified in the latest ISO 11079 standard [18,59,60]. However, despite their improved accuracy, these equations negatively affect the evaluation of D_lim—particularly during long-term exposure assessments at the verification stage when the resultant clothing insulation I_cl,r falls below the minimum required insulation IREQ_min (Figure 1). This issue arises from their tendency to underestimate the heat storage rate S, leading to safety concerns. Therefore, given the limited influence of the f_cl algorithms on IREQ calculations during the design phase—where a clothing ensemble with predefined insulation must be specified—and the absence of physiological validation of the model, we recommend that no changes be made to the current standard.

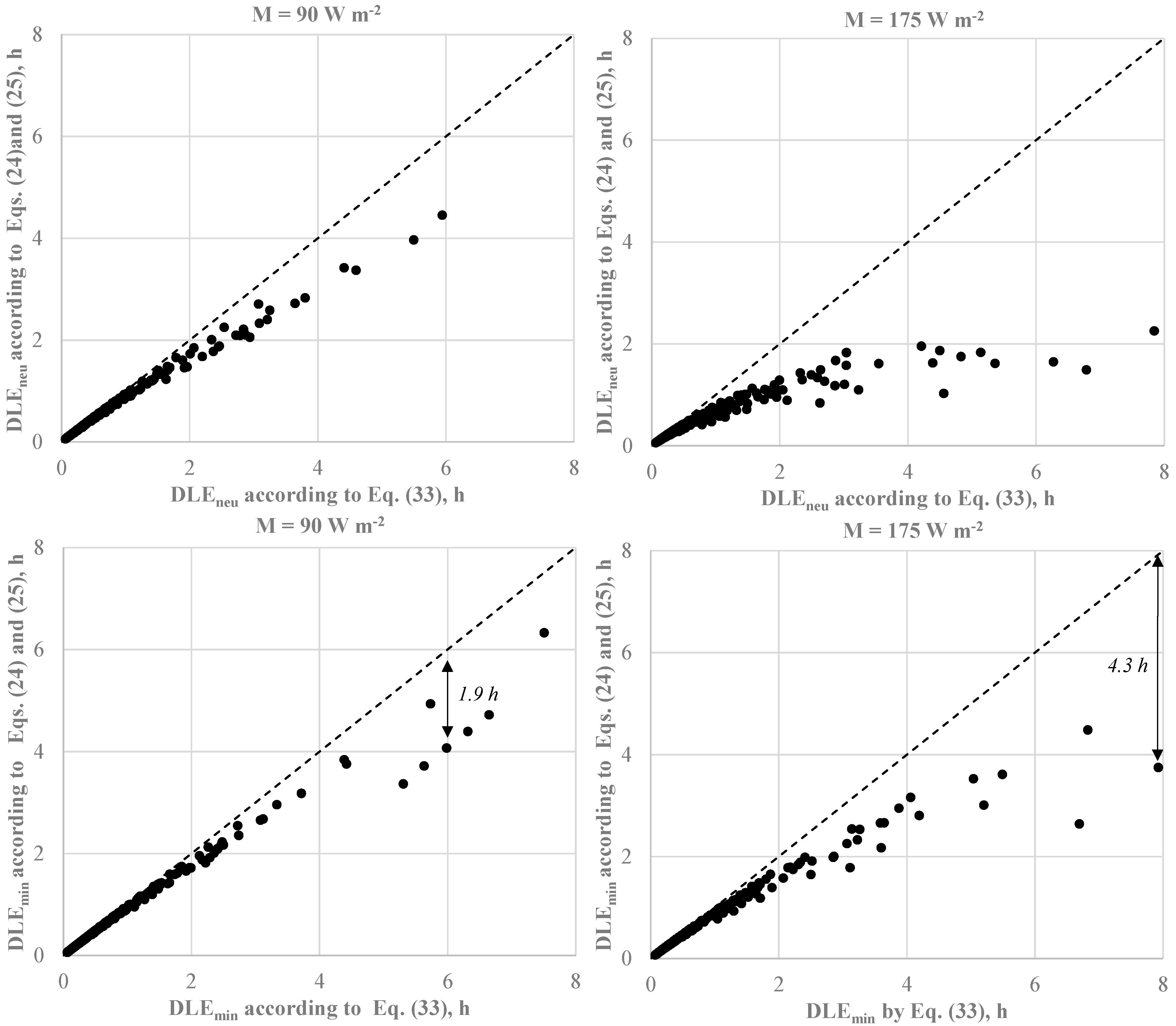
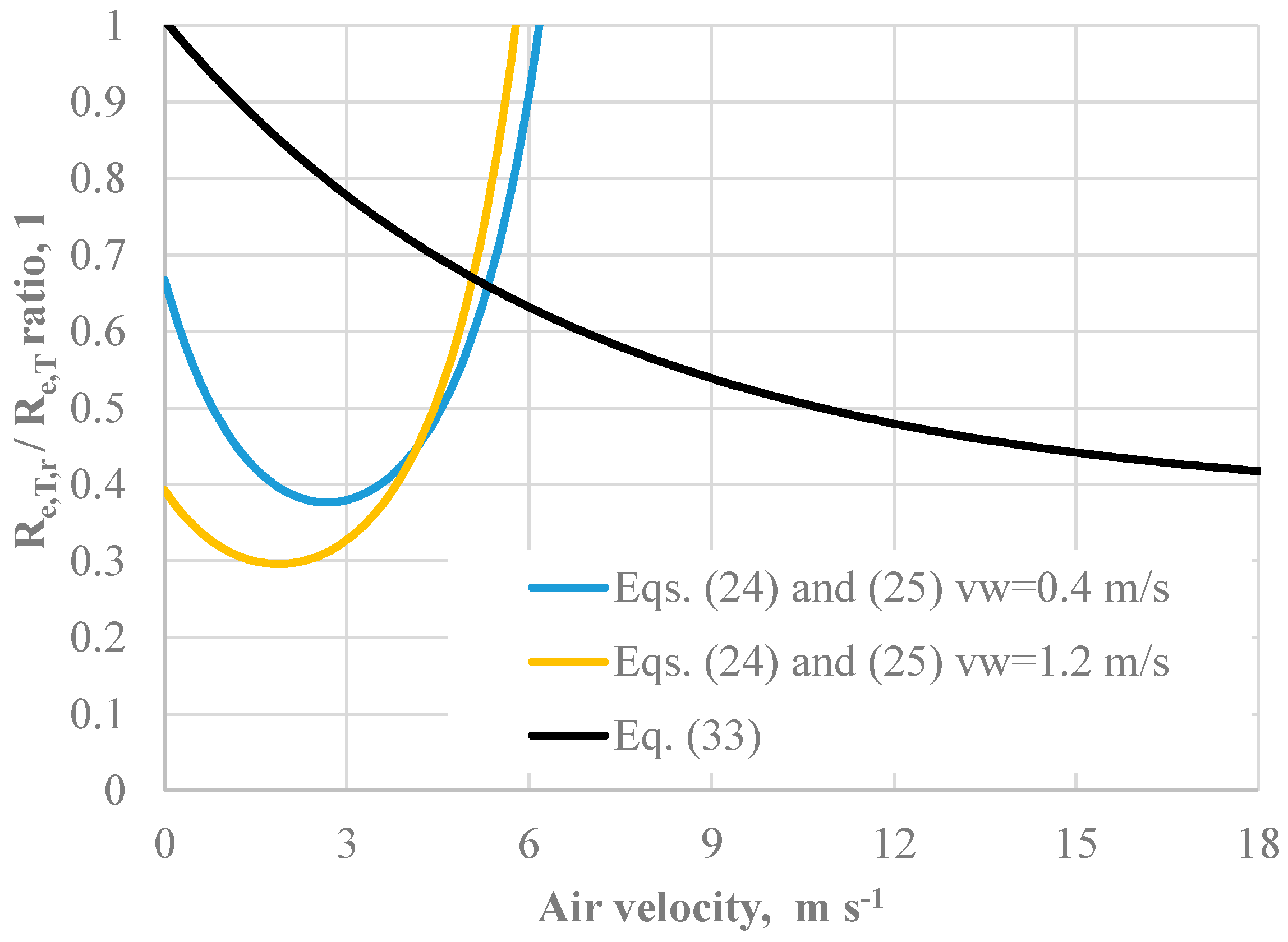
4.2. The Effect of Resultant Vapour Resistance

Although the R_e,T,r values calculated by Equations (33) and (24) with CorrE given by Equation (25) can be meaningfully different—as remarked in a previous investigation by our team [32]—the effect of the calculation of the resultant total vapour resistance on both IREQ values is not meaningful, as depicted in Figure 8.

The values of the slopes of the regression lines for IREQ_neu (1.042) and IREQ_min (1.019) demonstrate that the underestimation of the vapour resistance resulting from the application of Equations (24) and (25) [31] and then the higher value of the evaporative heat loss leads to some overestimation IREQ_neu values. More particularly, according to our calculations, this phenomenon is more pronounced in the range of operative temperature from 0 to 10 °C or in the case of high metabolic rate values (175 W m⁻²). For the highest activity level, the effect of the lower vapour resistance is amplified by a higher value of the skin wettedness (as a function of the metabolic rate as in Table 2), resulting in a high evaporative heat loss as quantified by the right side of Equation (5).

In contrast, IREQ_min values are less affected by the value of the R_e,T,r as the slope of the regression line confirms. This is mainly due to the constant value of the skin wettedness (w = 0.06) under high strain conditions (see Table 1).

Similarly to what was observed for the effect of the clothing area factor, the impact of the different algorithms for calculating the resultant vapour resistance is more pronounced in cold stress conditions (e.g., when I_cl,r is less than IREQ). This is quite surprising if we consider that under cold exposures, the evaporative term in the heat balance equation on the human body is less significant than the dry heat loss (R + C). More particularly, the differences are more pronounced for long-term exposures and high metabolic rates, as depicted in Figure 9, which reveals a systematic underestimation of D_lim by Equation (15). This is the trivial consequence of the higher R_eT,r value returned by Equation (33) resulting in a lower evaporative heat loss and, finally, higher value of the body heat storage S.

The underestimation of D_lim values obtained by Equation (33) is more pronounced for exposures over two hours, typical of long-term risks as claimed by ISO 15265 [14,61]. More particularly, for M = 90 W m⁻² and both physiological criteria reported in Table 1 (low and high strain), Equation (33) overestimated D_lim values by about 2 h (from 1.9 to 2.1 h). For M = 175 W m⁻², meaningful differences have been observed in the range of DLE_neu values from 2 to 4 h with a maximum overestimation of DLE_min of 5.2 h. Except for a couple of conditions (overestimation of 4.3 h about), DLE_min trend is similar to that observed at lower metabolic rate.

The results mentioned above seem astonishing in cold environments, considering the reduced significance of the evaporative term in the heat balance equation. To understand this apparent inconsistency, a detailed analysis of the contribution of the evaporative term in Equation (34) is necessary. More specifically, according to data in

Table 5. Effect of the calculation of the resultant vapour resistance on the evaporative heat flow at the skin E and the body heat storage rate S as a function of the air temperature, clothing insulation and metabolic rate under low strain conditions (Table 1). v_a = 0.5 m s⁻¹; RH = 50%, ap = 8 L s⁻¹ m⁻². Positive values of the body heat storage rate have not been reported.

to (°C)	E (W m−2)		Δ (%)	S (W m−2)		Δ (%)	E (W m−2)		Δ (%)	S (W m−2)		Δ (%)
	Equation (33)	Equations (24) and (25)		Equation (33)	Equations (24) and (25)		Equation (33)	Equations (24) and (25)		Equation (33)	Equations (24) and (25)
	M = 90 W m−2						M = 175 W m−2
Icl = 1.0 clo
−50	13.9	18.7	34.1	−337	−341	1.4	24.9	48.0	92.5	−284	−307	8
−40	13.9	18.6	34.1	−288	−293	1.6	24.9	47.9	92.5	−232	−255	10
−30	13.9	18.6	34.1	−239	−244	2.0	24.8	47.8	92.5	−180	−203	13
−20	13.8	18.5	34.1	−190	−195	2.5	24.6	47.4	92.5	−128	−151	18
−10	13.6	18.2	34.1	−141	−146	3.3	24.2	46.6	92.5	−76	−98.2	30
0	13.1	17.5	34.1	−92	−97	4.8	23.2	44.7	92.5	−23	−44.3	94
10	12.2	16.4	34.1	−42	−47	9.9	21.5	41.3	92.5	-	-	-
Icl = 1.5 clo
−50	10.5	14.1	34.1	−236	−239	1.5	18.9	36.3	92.5	−178	−196	10
−40	10.5	14.1	34.1	−199	−202	1.8	18.8	36.3	92.5	−139	−156	13
−30	10.5	14.1	34.1	−162	−165	2.2	18.8	36.2	92.5	−99	−116	18
−20	10.4	14.0	34.1	−125	−128	2.9	18.6	35.9	92.5	−59	−76.6	29
−10	10.3	13.8	34.1	−88	−91	4.0	18.3	35.2	92.5	−20	−36.5	87
0	9.9	13.3	34.1	−50	−54	6.7	17.6	33.8	92.5	-	-	-
10	9.3	12.4	34.1	−12	−15	25.7	16.2	31.3	92.5	-	-	-
Icl = 2.0 clo
−50	8.4	11.3	34.1	−174	−177	1.7	15.1	29.1	92.5	−113	−127	12
−40	8.4	11.3	34.1	−144	−147	2.0	15.1	29.1	92.5	−81	−95	17
−30	8.4	11.3	34.1	−114	−117	2.5	15.1	29.0	92.5	−49	−63	28
−20	8.4	11.2	34.1	−84	−87	3.4	15.0	28.8	92.5	−17	−31	81
−10	8.2	11.0	34.1	−54	−57	5.2	14.7	28.3	92.5	-	-	-
0	7.9	10.7	34.1	−24	−27	11.2	14.1	27.1	92.5	-	-	-
10	7.4	10.0	34.1	-	-	-	13.0	25.1	92.5	-	-	-
Icl = 2.5 clo
−50	7.0	9.4	34.1	−132	−134	1.8	12.6	24.2	92.5	−69	−81	17
−40	7.0	9.4	34.1	−107	−109	2.2	12.6	24.2	92.5	−42	−54	28
−30	7.0	9.4	34.1	−82	−84	2.9	12.5	24.2	92.5	−15	−27	76
−20	7.0	9.3	34.1	−57	−59	4.2	12.5	24.0	92.5	-	-	-
−10	6.9	9.2	34.1	−32	−34	7.3	12.2	23.5	92.5	-	-	-
0	6.6	8.9	34.1	−7	−9	33.5	11.7	22.6	92.5	-	-	-
10	6.2	8.3	34.1	-	-	-	10.9	20.9	92.5	-	-	-

, for low clothing insulation and operative temperature values (e.g., highest values of the heat body storage rate), even significant variations in the evaporative heat loss (+34.1% for M = 90 W m⁻²) do not result in appreciable variations in S values.

In fact, the modulus of the body heat storage S increases less than 4.2% for t_o ≤ −20 °C. In contrast, for M = 175 W m⁻², the evaporative heat loss variation (+92.5%) due to the lower R_e,T,r value obtained with Equations (24) and (25) results in a 10% increase in S even for t_o = −50 °C.

Based upon the findings above, using Equation (24) with CorrE given by Equation (25) in IREQ calculations is not recommendable. The reasons are mainly twofold. Above all, Equation (25) has been validated just for v_a < 3.5 m s⁻¹, while the current version of IREQ works for v_a < 18 m/s. In addition, the application of Equation (25) over its validation range could bring physical inconsistencies. This is mainly because, as shown in Figure 10, it exhibits a minimum and exceeds the unitary value at high air velocity.

Eventually, Equations (24) and (25) could be recommended in the range of air velocity from 0 to 3.5 m s⁻¹.

5. Conclusions

Despite some limitations, the IREQ model formulated by Holmér in the late 1980s remains the reference method for evaluating global cooling in extreme cold environments. Over the past forty years, the only meaningful modification to the original model consisted of the equations for calculating the resultant clothing insulation to be compared with the IREQ value. In contrast, the calculation of the clothing area factor (affecting the dry heat loss and the vapour resistance) and the resultant vapour resistance (affecting the evaporative heat loss) remain unchanged.

Consistently with the issue highlighted in this paper, totally focused on the effects of the new algorithms for the calculation of the clothing area factor f_cl and the resultant vapour resistance, we can schematically state the following:

• Despite the meaningful underestimation of the clothing area factor calculated with the most recent algorithms developed on an experimental basis, the effects on the neutral and minimum IREQ values are negligible. Different f_cl formulas return the same IREQ values. This phenomenon is only an apparent inconsistency as, under equilibrium conditions (no heat accumulated in the body), the only term affecting the heat balance equation on the human body is the evaporative heat loss that is scarcely affected by f_cl, especially for high clothing insulation values.
• The clothing area factor meaningfully affects the duration limit exposure under long-term risk conditions (D_lim > 2 h and I_cl,r < IREQ_min). More particularly, as f_cl increases, both dry and latent heat losses increase with the consequent increase in the modulus of the body heat storage rate. Consequently, the most recent formula proposed by Kuklane and Toma (lower f_cl, then lower dry heat loss) [36] returns higher D_lim values (up to 5 h) if compared with those calculated consistently with the actual version of ISO 11079 standard.
• The effect of the resultant vapour resistance calculation is similar to that observed in the case of f_cl. IREQ values are not meaningfully affected even by meaningful differences in the vapour resistance and the evaporative loss, whereas D_lim values calculated using the actual version of ISO 11079 can be significantly higher than those calculated consistently with the algorithms recommended by ISO 9920 but validated for air velocity values lower than 3.5 m s⁻¹.

Based on the results from the present study, we recommend leaving the actual implementation of the IREQ model unchanged unless new experimental evidence demonstrates to modify the evaluation of the resultant clothing thermophysical quantities. If on one side, the most recent studies provide more accurate algorithms for evaluating the clothing area factor as a function of the clothing insulation, then on the other side, their effects on the total and the resultant clothing insulations are unknown. In addition, the algorithms for evaluating the resultant vapour resistance provided by ISO 9920 do not cover the entire range of application of the ISO 11079 in terms of air velocity (18 m s⁻¹) and return unacceptable physical inconsistencies when forced over their validation range. Maintaining the current calculation is the most effective approach. Its familiarity ensures easy adoption and understanding among occupational hygienists and environmental ergonomists, who may not grasp intricate changes, especially when the practical effects are negligible.

The results from the present investigation require further validation on an experimental basis, which is difficult to carry out due to the lack of a systematic database of physiological measurements collected in the field or the laboratory (as in the case of extreme hot environments). However, it is important to highlight that the current version of IREQ also lacks experimental validation. So, the obtained results, despite being numerical, provide robust evidence for contributing to its improvement and address further research to focus better on the measurement and evaluation of clothing area factor and resultant vapour resistance for clothing ensembles of interest in cold exposures. This also applies to other indices, such as the Predicted Mean Vote (PMV) and the Predicted Heat Stress (PHS), which use different algorithms for evaluating the clothing area factor and the resultant vapour resistance if compared with those recommended by ISO 9920.

In the immediate future, the development of this research will proceed along two parallel paths. Firstly, new experimental measurements will be conducted on mobile mannequins to determine the optimal method for calculating dynamic vapour resistance in severe cold environments. Additionally, significant efforts will be made to address the validation and refinement of the IREQ model. Specifically, physiological measurements will be performed under both laboratory and field conditions. Furthermore, the IREQ model will be validated by comparing its predicted values for heat storage rate and duration limit exposure with those obtained from the most advanced thermo-physiological models, such as Fiala Ergonsim, THERMODE, and JOS-3.