Deep Learning-Based Road Traffic Noise Annoyance Assessment
Abstract
1. Introduction
2. Subjective Listening Experiment and Dataset Construction
2.1. Listening Experiment Dataset
2.2. Listening Experiment Settings
2.3. Listening Experiment Results
2.4. Extended Dataset
3. Research Method
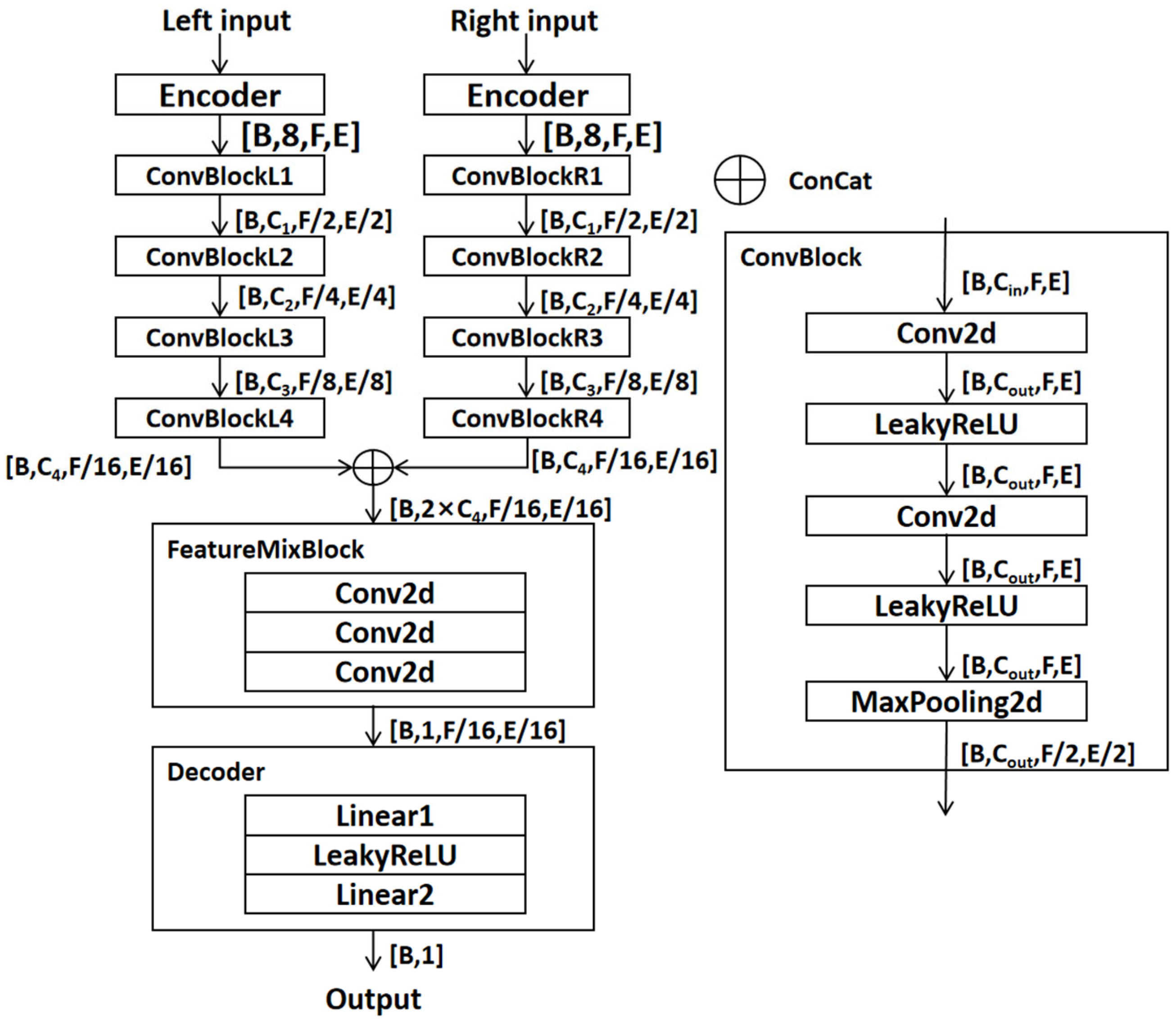
3.1. Model Architecture
3.1.1. Encoder
3.1.2. Convolutional Downsampling Module
3.1.3. Feature Fusion Module
3.1.4. Decoder
3.2. Model Parameter Setting and Optimization
4. Experimental Results and Analysis
4.1. Pre-Training Stage
4.1.1. Pre-Training Dataset Setup
4.1.2. Pre-Training Model Results
4.2. Formal Training Stage
4.2.1. Formal Training Dataset Setup
4.2.2. Formal Training Results and Comparison
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ouis, D. Annoyance from road traffic noise: A review. J. Environ. Psychol. 2001, 21, 101–120. [Google Scholar] [CrossRef]
- Moudon, A.V. Real noise from the urban environment: How ambient community noise affects health and what can be done about it. Am. J. Prev. Med. 2009, 37, 167–171. [Google Scholar] [CrossRef]
- Kujawa, S.G.; Liberman, M.C. Adding Insult to Injury: Cochlear Nerve Degeneration after “Temporary” Noise-Induced Hearing Loss. J. Neurosci. Off. J. Soc. Neurosci. 2009, 29, 14077. [Google Scholar] [CrossRef] [PubMed]
- Stansfeld, S.; Haines, M.; Brown, B. Noise and health in the urban environment. Rev. Environ. Health 2000, 15, 43–82. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Sun, B.; Chen, L. An optimization model for planning road networks that considers traffic noise impact. Appl. Acoust. 2022, 192, 108693. [Google Scholar] [CrossRef]
- Jin, J.; Zhu, C.; Wu, R.; Liu, Y.; Li, M. Comparative noise reduction effect of sound barrier based on statistical energy analysis. J. Comput. Methods Sci. Eng. 2021, 21, 737–745. [Google Scholar] [CrossRef]
- Stansfeld, S.A.; Haines, M.M.; Berry, B.; Burr, M. Reduction of road traffic noise and mental health: An intervention study. Noise Health 2009, 11, 169–175. [Google Scholar] [CrossRef]
- Langdon, F.J. Noise nuisance caused by road traffic in residential areas: Part I. J. Sound Vib. 1976, 47, 243–263. [Google Scholar] [CrossRef]
- Jakovljevic, B.; Paunovic, K.; Belojevic, G. Road-traffic noise and factors influencing noise annoyance in an urban population. Environ. Int. 2009, 35, 552–556. [Google Scholar] [CrossRef]
- Marquis-Favre, C.; Premat, E.; Aubrée, D.; Vallet, M. Noise and its Effects—A Review on Qualitative Aspects of Sound. Part I: Notions and Acoustic Ratings. Acta Acust. United Acust. 2005, 91, 613–625. [Google Scholar]
- Schomer, P.D. Criteria for assessment of noise annoyance. Noise Control Eng. J. 2005, 53, 125–137. [Google Scholar] [CrossRef]
- Carletti, E.; Pedrielli, F.; Casazza, C. Annoyance prediction model for assessing the acoustic comfort at the operator station of compact loaders. In Proceedings of the 16th International Congress on Sound and Vibration, Krakow, Poland, 5–9 July 2009. [Google Scholar]
- Morel, J.; Marquis-Favre, C.; Gille, L.A. Noise annoyance assessment of various urban road vehicle pass-by noises in isolation and combined with industrial noise: A laboratory study. Appl. Acoust. 2016, 101, 47–57. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, R.; Ying, S.; Shu, H. A new noise annoyance measurement metric for urban noise sensing and evaluation. In Proceedings of the ICASSP 2017–2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Lopez-Ballester, J.; Pastor-Aparicio, A.; Segura-Garcia, J.; Felick-Castell, S. Computation of Psycho-Acoustic Annoyance Using Deep Neural Networks. Appl. Sci. 2019, 9, 3136. [Google Scholar] [CrossRef]
- Shu, H.; Song, Y.; Zhou, H. RNN based noise annoyance measurement for urban noise evaluation. In Proceedings of the Tencon IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017. [Google Scholar]
- Bravo-Moncayo, L.; Lucio-Naranjo, J.; Chavez, M.; Pavon-Garcia, I.; Garzon, C. A machine learning approach for traffic-noise annoyance assessment. Appl. Acoust. 2019, 156, 262–270. [Google Scholar] [CrossRef]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Xiong, H.; He, Q. A Comprehensive Survey on Transfer Learning. Proc. IEEE 2019, 109, 43–76. [Google Scholar] [CrossRef]
- Pan, S.J.; Qiang, Y. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Niu, S.; Liu, Y.; Wang, J.; Liu, Y.; Song, H. A Decade Survey of Transfer Learning (2010–2020). IEEE Trans. Artif. Intell. 2020, 1, 151–166. [Google Scholar] [CrossRef]
- Zwicker, E.; Fastl, H. Psychoacoustics: Facts and Models; Springer: New York, NY, USA, 1999. [Google Scholar]
- Lample, G.; Conneau, A. Cross-lingual Language Model Pretraining. In Proceedings of the Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Sounds Idealgeneral6000. Available online: www.sound-ideas.com/Product/42/General-Series-6000 (accessed on 14 February 2023).
- Song Meter 4. Available online: https://www.wildlifeacoustics.com/products/song-meter-sm4 (accessed on 26 February 2023).
- RME Fireface, II. Available online: https://www.rme-audio.de/fireface-ufx-ii.html (accessed on 26 February 2023).
- HD 600. Available online: https://www.sennheiser-hearing.com/zh-CN/p/hd-600/ (accessed on 26 February 2023).
- ISO/TS 15666-2021; Acoustics: Assessment of Noise Annoyance by Means of Social and Socio-Acoustic Surveys. International Organization for Standardization: Geneva, Switzerland, 2021. Available online: https://www.iso.org/standard/74048.html (accessed on 15 February 2023).
- Mortensen, F.; Poulsen, T. Annoyance of Low Frequency Noise and Traffic Noise. Low Freq. Noise Vib. Act. Control 2001, 20, 193–196. [Google Scholar] [CrossRef]
- Soares, F.; Freitas, E.; Cunha, C.; Silva, C.; Lamas, J.; Mouta, S.; Santos, J. Traffic noise: Annoyance assessment of real and virtual sounds based on close proximity measurements. Transp. Res. Part D Transp. Environ. 2017, 52, 399–407. [Google Scholar] [CrossRef]
- Steinbach, L.; Altinsoy, M.E. Prediction of annoyance evaluations of electric vehicle noise by using artificial neural networks. Appl. Acoust. 2019, 145, 149–158. [Google Scholar] [CrossRef]
- Ascigil-Dincer, M.; Demirkale, S.Y. Model development for traffic noise annoyance prediction. Appl. Acoust. 2021, 177, 107909. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, K.; Li, H.; Chen, X.; Dong, N. The effects of rating scales and individual characteristics on perceived annoyance in laboratory listening tests. Appl. Acoust. 2023, 202, 109137. [Google Scholar] [CrossRef]
- Tristán-Hernández, E.; Pavón, I.; Campos-Canton, I.; Kolosovas-Machuca, E. Evaluation of Psychoacoustic Annoyance and Perception of Noise Annoyance Inside University Facilities. Int. J. Acoust. Vib. 2016, 23, 3–8. [Google Scholar]
- Eggenschwiler, K.; Heutschi, K.; Taghipour, A.; Pieren, R.; Gisladottir, A. Urban design of inner courtyards and road traffic noise: Influence of façade characteristics and building orientation on perceived noise annoyance. Build. Environ. 2022, 224, 109526. [Google Scholar] [CrossRef]
- Killengreen, T.F.; Olafsen, S. Response to noise and vibration from roads and trams in Norway. In Proceedings of the International Congress on Acoustics (ICA), Gyeongju, Republic of Korea, 24–28 October 2022. [Google Scholar]
- Wu, C.; Wu, F.; Huang, Y. One Teacher is Enough? Pre-trained Language Model Distillation from Multiple Teachers. In Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021; Association for Computational Linguistics: Cedarville, OH, USA, 2021; pp. 4408–4413. [Google Scholar] [CrossRef]
- Zheng, S.; Suo, H.; Chen, Q. PRISM: Pre-trained Indeterminate Speaker Representation Model for Speaker Diarization and Speaker Verification. arXiv 2022, arXiv:2205.07450. [Google Scholar]
- Rajagopal, A.; Nirmala, V. Convolutional Gated MLP: Combining Convolutions & gMLP. arXiv 2021, arXiv:2111.03940. [Google Scholar]
- Dai, X.; Yin, H.; Jha, N.K. Incremental Learning Using a Grow-and-Prune Paradigm with Efficient Neural Networks. IEEE Trans. Emerg. Top. Comput. 2020, 10, 752–762. [Google Scholar] [CrossRef]
- Li, X.L.; Liang, P. Prefix-Tuning: Optimizing Continuous Prompts for Generation. In Proceedings of the The 11th International Joint Conference on Natural Language Processing, Virtual Event, 1–6 August 2021. [Google Scholar]
- Liu, S.; Ye, H.; Jin, K.; Cheng, H. CT-UNet: Context-Transfer-UNet for Building Segmentation in Remote Sensing Images. Neural Process. Lett. 2021, 53, 4257–4277. [Google Scholar] [CrossRef]
- Yu, G.; Li, A.; Wang, H.; Wang, Y.; Ke, Y.; Zheng, C. DBT-Net: Dual-branch federative magnitude and phase estimation with attention-in-attention transformer for monaural speech enhancement. IEEE ACM Trans. Audio Speech Lang. Process. 2022, 30, 2629–2644. [Google Scholar] [CrossRef]
- Zheng, C.; Wang, M.; Li, X.; Moore, B.C.J. A deep learning solution to the marginal stability problems of acoustic feedback systems for hearing aids. J. Acoust. Soc. Am. 2022, 152, 3616–3634. [Google Scholar] [CrossRef]
- Bojesomo, A.; Al Marzouqi, H.; Liatsis, P. SwinUNet3D–A Hierarchical Architecture for Deep Traffic Prediction using Shifted Window Transformers. arXiv 2023, arXiv:2201.06390. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. arXiv 2015, arXiv:1505.04597. [Google Scholar]
- Lecun, Y.; Bottou, L. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Li, Q.; Shen, L. Neuron segmentation using 3D wavelet integrated encoder–decoder network. Bioinformatics 2022, 38, 809–817. [Google Scholar] [CrossRef]
- Available online: https://github.com/search?q=Unet (accessed on 26 February 2023).
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization—Computer Science. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; The MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Zhihua, Z. Machine Learning; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- MNIST. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 4 March 2023).
- Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
- Rice, J.A. Mathematical Statistics and Data Analysis. Math. Gaz. 1988, 72, 426. [Google Scholar]
- Schneider, P.; Scherg, M.; Dosch, H.G.; Specht, H.J.; Gutschalk, A.; Rupp, A. Morphology of Heschl’s gyrus reflects enhanced activation in the auditory cortex of musicians. Nat. Neurosci. 2002, 5, 688–694. [Google Scholar] [CrossRef]
- Barker, R.A.; Anderson, J.R.; Meyer, P.; Dick, D.J.; Scolding, N.J. Microangiopathy of the brain and retina with hearing loss in a 50 year old woman: Extending the spectrum of Susac’s syndrome. J. Neurol. Neurosurg. Psychiatry 1999, 66, 641–643. [Google Scholar] [CrossRef]
- Zekveld, A.A.; Kramer, S.E.; Festen, J.M. Cognitive load during speech perception in noise: The influence of age, hearing loss, and cognition on the pupil response. Ear Hear. 2011, 32, 498–510. [Google Scholar] [CrossRef]
- Schneider, B.A.; Daneman, M.; Murphy, D.R.; See, S.K. Listening to discourse in distracting settings: The effects of aging. Psychol. Aging 2015, 30, 28–35. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, H.J.; Dobie, R.A.; Losonczy, K.G.; Themann, C.L.; Flamme, G.A. Declining Prevalence of Hearing Loss in US Adults Aged 20 to 69 Years. Otolaryngol. Head Neck Surg. 2016, 143, 274–285. [Google Scholar] [CrossRef] [PubMed]


| Annoyance Interval | The Number of Noise Samples |
|---|---|
| [0,1) | 0 |
| [1,2) | 1 |
| [2,3) | 17 |
| [3,4) | 72 |
| [4,5) | 95 |
| [5,6) | 239 |
| [6,7) | 266 |
| [7,8) | 186 |
| [8,9) | 72 |
| [9,10) | 1 |
| Total | 949 |
| Psychoacoustic Annoyance Interval | The Number of Noise Samples |
|---|---|
| [0,10] | 544 |
| (11,20] | 1994 |
| (20,30] | 3412 |
| (30,40] | 2494 |
| (40,50] | 2727 |
| (50,60] | 1832 |
| (60,70] | 2377 |
| (70,80] | 1356 |
| (80,90] | 280 |
| (90,100] | 9 |
| total | 17,025 |
| Network | Layer | Input Size | Output Size | Kernel | Stride | Padding |
|---|---|---|---|---|---|---|
| Encoder | Conv2d | 1 × 1499 × 257 | 8 × 1499 × 257 | (1,1) | (1,1) | (0,0) |
| ConvBlock1 | Conv2d + LeakyReLU | 8 × 1499 × 257 | 32 × 1499 × 257 | (3,3) | (1,1) | (1,1) |
| Conv2d + LeakyReLU | 32 × 1499 × 257 | 32 × 1499 × 257 | (3,3) | (1,1) | (1,1) | |
| Maxpooling2d | 32 × 1499 × 257 | 32 × 749 × 128 | (2,2) | (2,2) | (0,0) | |
| ConvBlock2 | Conv2d + LeakyReLU | 32 × 749 × 128 | 64 × 749 × 128 | (3,3) | (1,1) | (1,1) |
| Conv2d + LeakyReLU | 64 × 749 × 128 | 64 × 749 × 128 | (3,3) | (1,1) | (1,1) | |
| Maxpooling2d | 64 × 749 × 128 | 64 × 374 × 64 | (2,2) | (2,2) | (0,0) | |
| ConvBlock3 | Conv2d + LeakyReLU | 64 × 374 × 64 | 32 × 374 × 64 | (3,3) | (1,1) | (1,1) |
| Conv2d + LeakyReLU | 32 × 374 × 64 | 32 × 374 × 64 | (3,3) | (1,1) | (1,1) | |
| Maxpooling2d | 32 × 374 × 64 | 32 × 187 × 32 | (2,2) | (2,2) | (0,0) | |
| CovBlock4 | Conv2d + LeakyReLU | 32 × 187 × 32 | 8 × 187 × 32 | (3,3) | (1,1) | (1,1) |
| Conv2d + LeakyReLU | 8 × 187 × 32 | 8 × 187 × 32 | (3,3) | (1,1) | (1,1) | |
| Maxpooling2d | 8 × 187 × 32 | 8 × 93 × 16 | (2,2) | (2,2) | (0,0) | |
| Concat | Concat | (8 × 93 × 16,8 × 93 × 16) | 16 × 93 × 16 | None | None | None |
| FeatureMixBlock | Conv2d | 16 × 93 × 16 | 16 × 93 × 16 | (3,3) | (1,1) | (1,1) |
| Conv2d | 16 × 93 × 16 | 8 × 93 × 16 | (3,3) | (1,1) | (1,1) | |
| Conv2d | 8 × 93 × 16 | 1 × 93 × 16 | (3,3) | (1,1) | (1,1) | |
| Decoder | Linear1 + LeakyReLU | 1 × 93 × 16 | 1 × 93 × 1 | 16 | None | None |
| Squeeze | 1 × 93 × 1 | 1 × 93 | None | None | None | |
| Linear2 | 1 × 93 | 1 × 1 | 93 | None | None |
| Annoyance Interval | The Number of Noise Samples |
|---|---|
| [2,3) | 3 |
| [3,4) | 21 |
| [4,5) | 28 |
| [5,6) | 81 |
| [6,7) | 68 |
| [7,8) | 53 |
| [8,9) | 26 |
| Total | 280 |
| Annoyance Intervals | MAE | ||||||
|---|---|---|---|---|---|---|---|
| Artificial Neural Network | Linear | Lasso | Ridge | Direct | Total-Tuning | Fine-Tuning | |
| [2,3) | 3.22 | 2.86 | 3.01 | 2.89 | 1.63 | 0.77 | 0.77 |
| [3,4) | 2.61 | 1.76 | 1.95 | 1.83 | 0.96 | 0.41 | 0.36 |
| [4,5) | 1.66 | 1.00 | 1.10 | 1.01 | 0.41 | 0.41 | 0.32 |
| [5,6) | 0.79 | 0.32 | 0.32 | 0.31 | 0.42 | 0.39 | 0.48 |
| [6,7) | 0.26 | 0.55 | 0.52 | 0.56 | 0.57 | 0.40 | 0.43 |
| [7,8) | 0.76 | 0.91 | 0.98 | 0.99 | 0.63 | 0.54 | 0.53 |
| [8,9) | 1.71 | 1.69 | 1.77 | 1.82 | 0.66 | 0.49 | 0.43 |
| Mean error | 0.99 | 0.82 | 0.84 | 0.85 | 0.57 | 0.45 | 0.46 |
| Algorithms | Mean Error | PCC | SCC |
|---|---|---|---|
| Artificial Neural Network | 0.99 | 0.46 | 0.47 |
| Linear Regression | 0.82 | 0.58 | 0.69 |
| Lasso Regression | 0.84 | 0.54 | 0.67 |
| Ridge Regression | 0.85 | 0.54 | 0.67 |
| Direct | 0.57 | 0.87 | 0.87 |
| Total-tuning | 0.45 | 0.92 | 0.91 |
| Fine-tuning | 0.46 | 0.93 | 0.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Wang, X.; Yuan, M.; Hu, W.; Hu, X.; Lu, K. Deep Learning-Based Road Traffic Noise Annoyance Assessment. Int. J. Environ. Res. Public Health 2023, 20, 5199. https://doi.org/10.3390/ijerph20065199
Wang J, Wang X, Yuan M, Hu W, Hu X, Lu K. Deep Learning-Based Road Traffic Noise Annoyance Assessment. International Journal of Environmental Research and Public Health. 2023; 20(6):5199. https://doi.org/10.3390/ijerph20065199
Chicago/Turabian StyleWang, Jie, Xuejian Wang, Minmin Yuan, Wenlin Hu, Xuhong Hu, and Kexin Lu. 2023. "Deep Learning-Based Road Traffic Noise Annoyance Assessment" International Journal of Environmental Research and Public Health 20, no. 6: 5199. https://doi.org/10.3390/ijerph20065199
APA StyleWang, J., Wang, X., Yuan, M., Hu, W., Hu, X., & Lu, K. (2023). Deep Learning-Based Road Traffic Noise Annoyance Assessment. International Journal of Environmental Research and Public Health, 20(6), 5199. https://doi.org/10.3390/ijerph20065199







