Future Projection of Extreme Precipitation Indices over the Qilian Mountains under Global Warming
Abstract
1. Introduction
2. Data and Methods
2.1. Description of the Study Area
2.2. Observations and CMIP6 Model Outputs
2.3. Extreme Precipitation Indices
2.4. Bias Correction Algorithm
2.5. Model Evaluation Metrics
2.5.1. Statistical Metrics
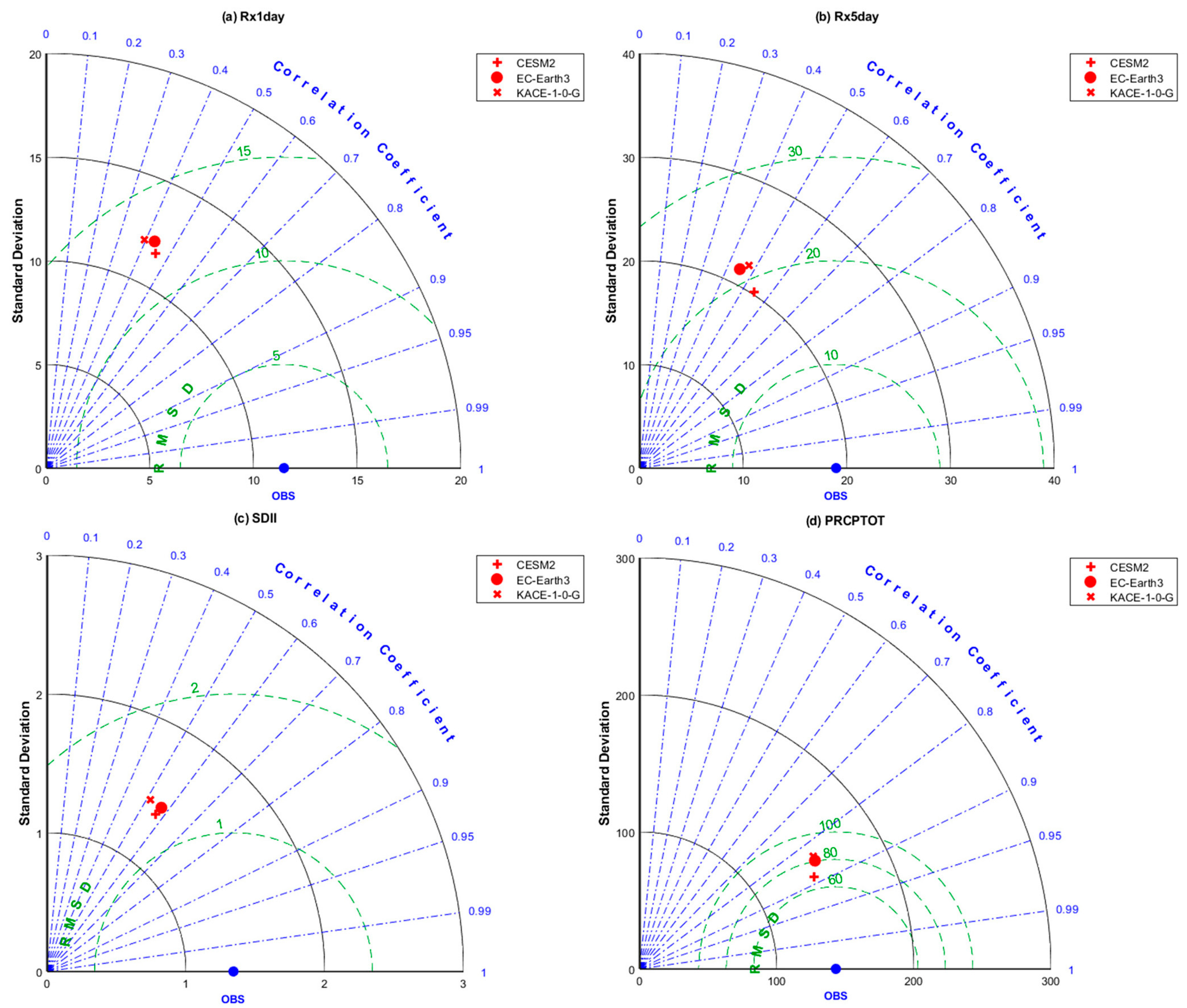
2.5.2. Taylor Diagram
2.5.3. Inter-Annual Variability Skill Score
3. Model Evaluation
3.1. Evaluation of the Spatial Interpolation
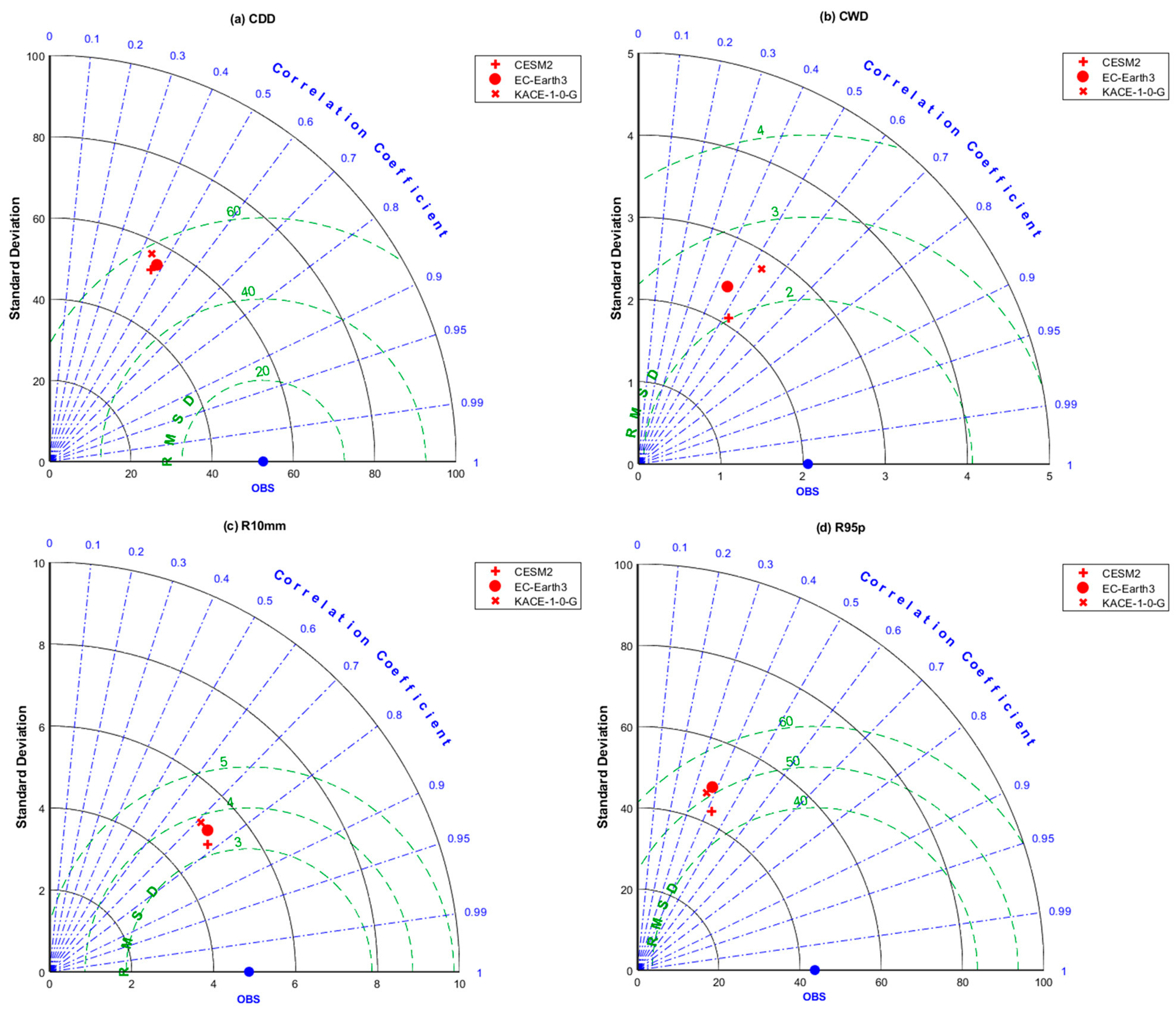
3.2. Evaluation of Spatial Variation in Extreme Precipitation Indices
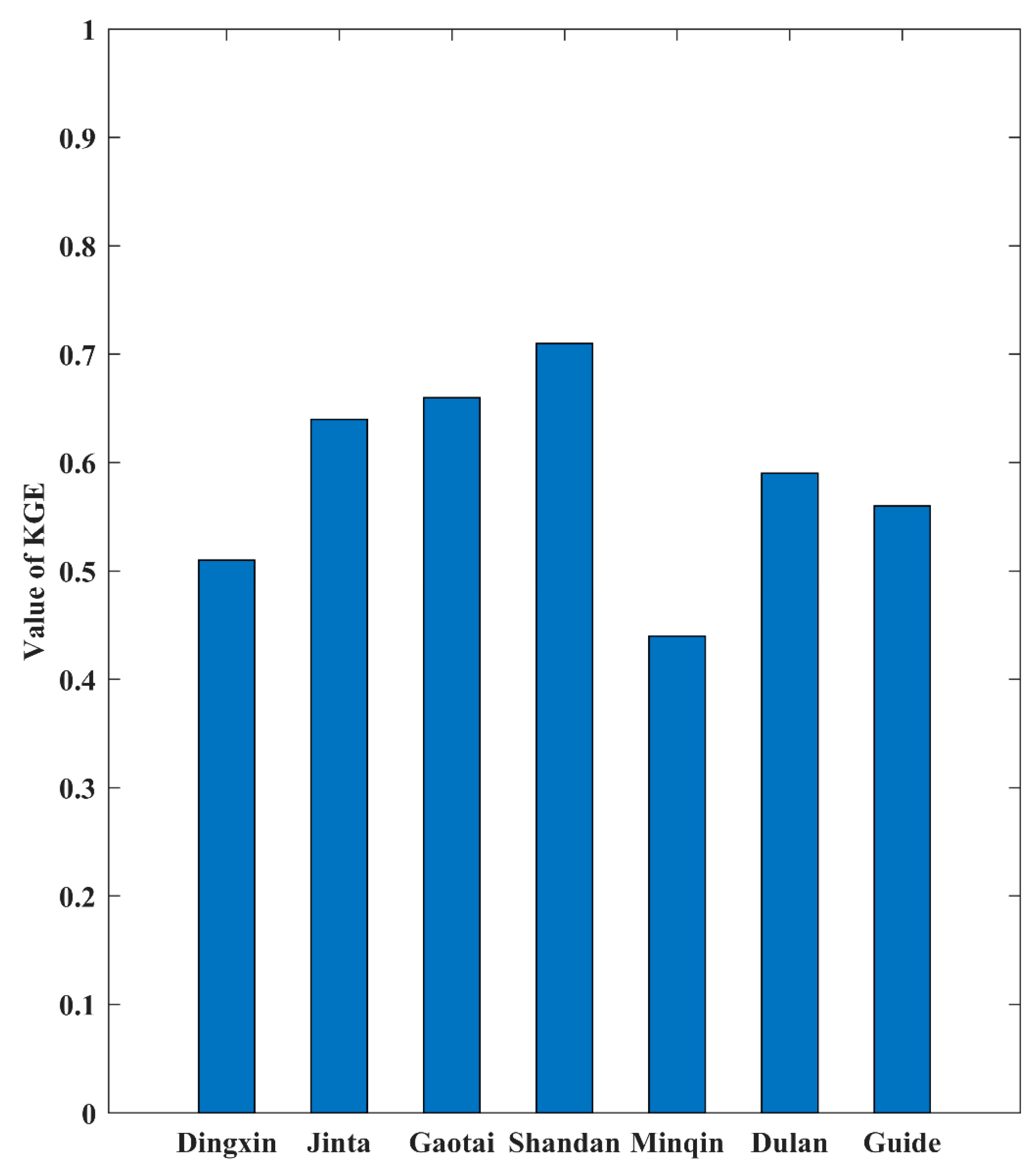
3.3. Evaluation of Inter-Annual Variability in Extreme Precipitation Indices
4. Future Projection
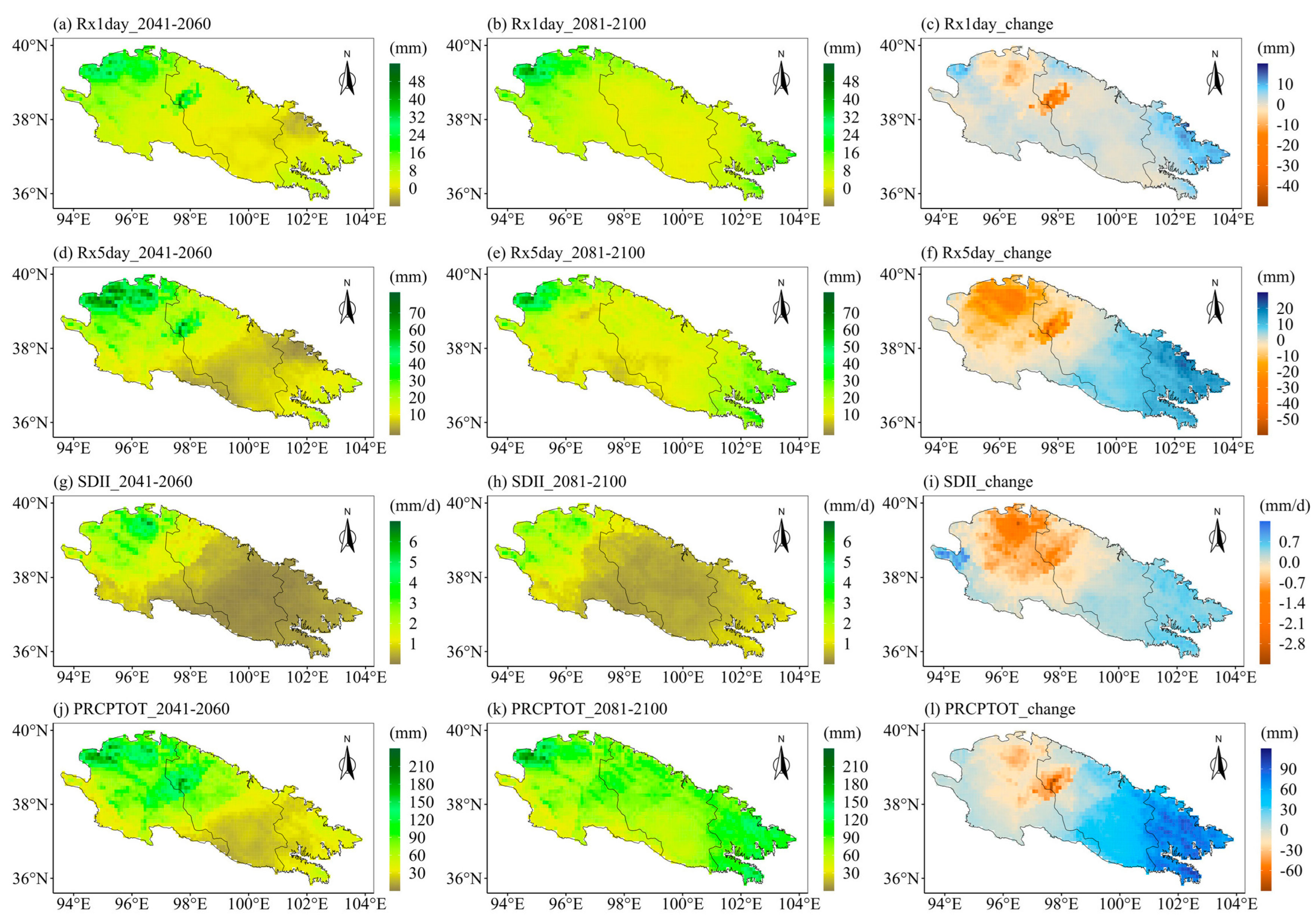
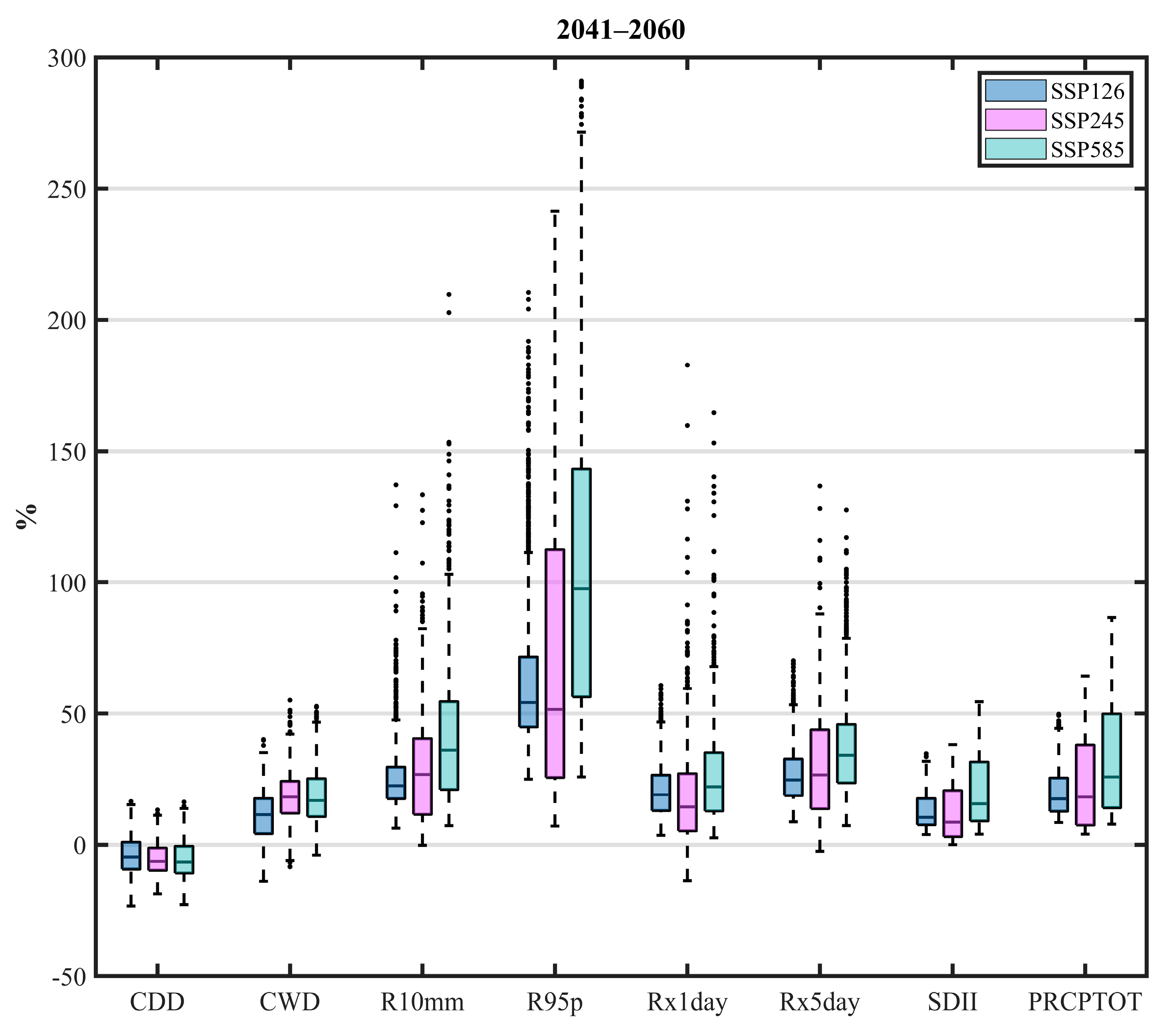
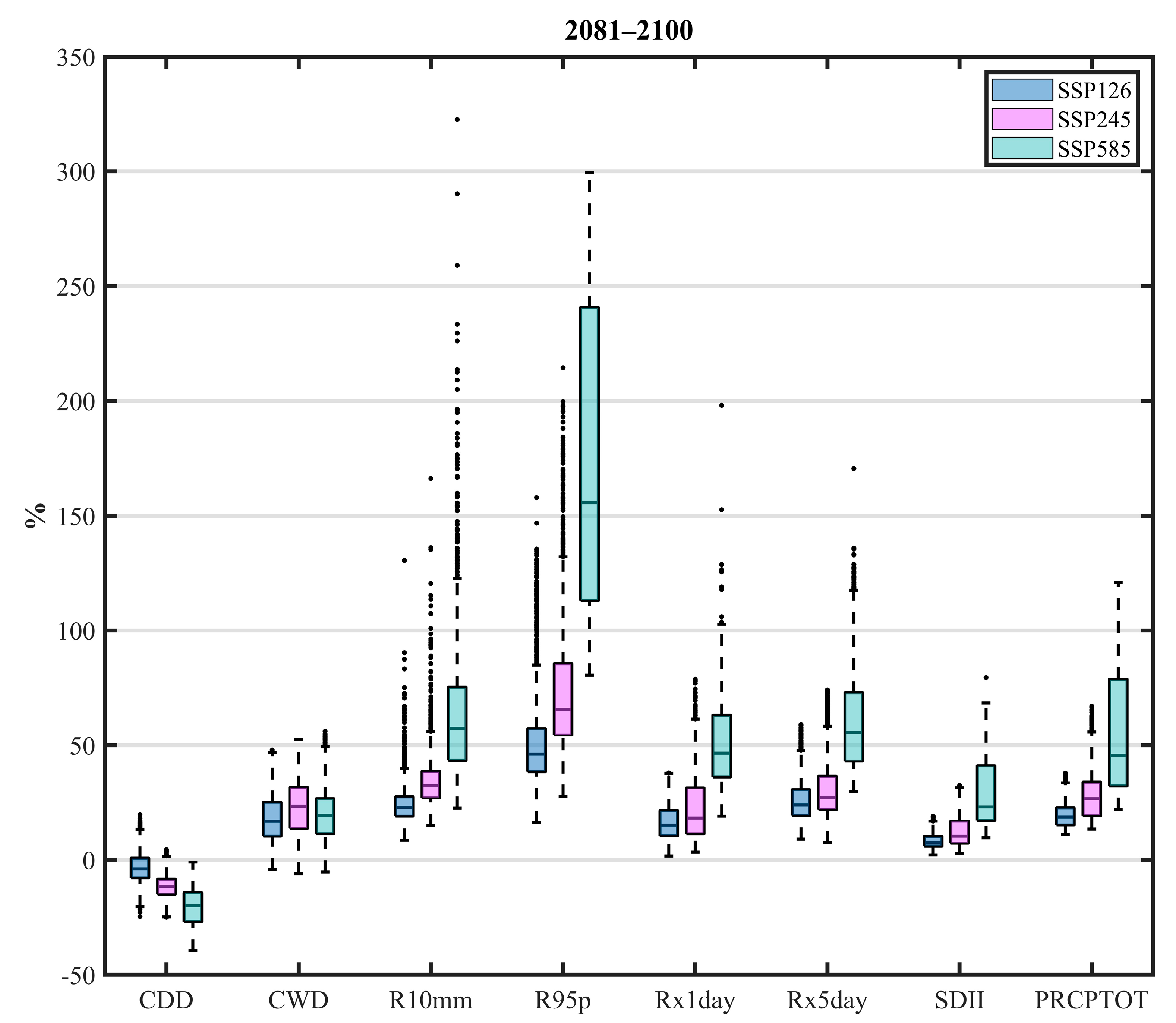
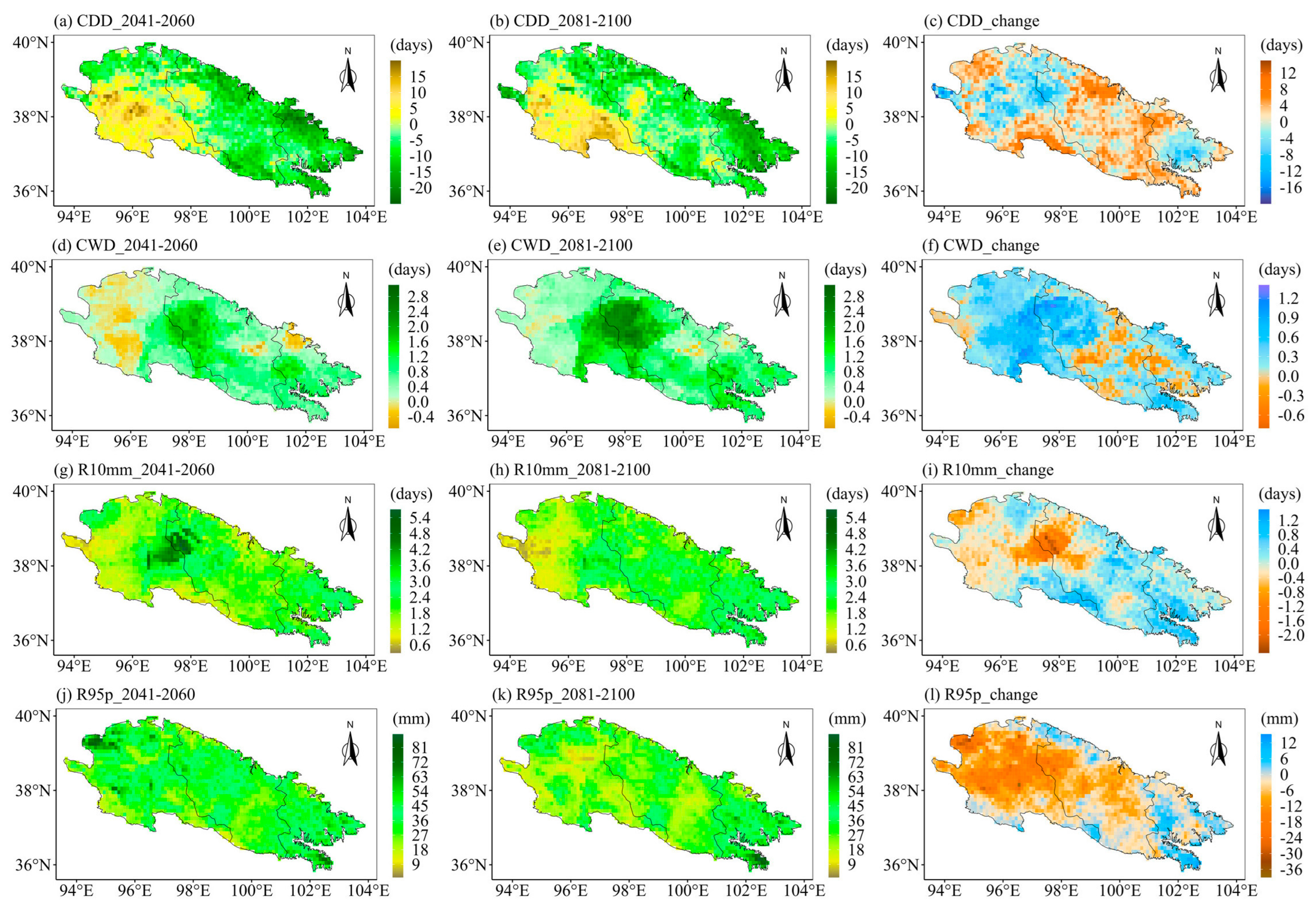
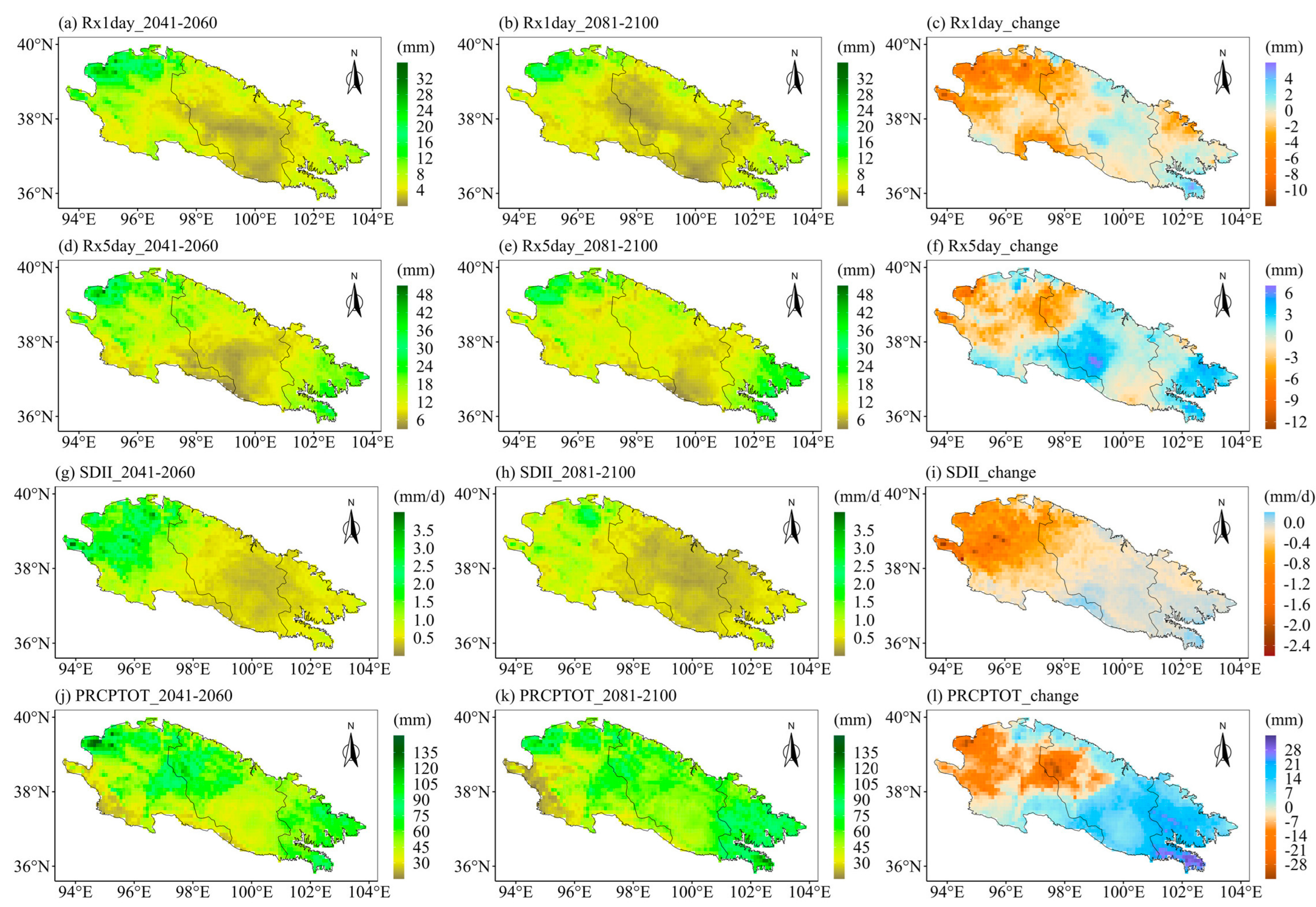
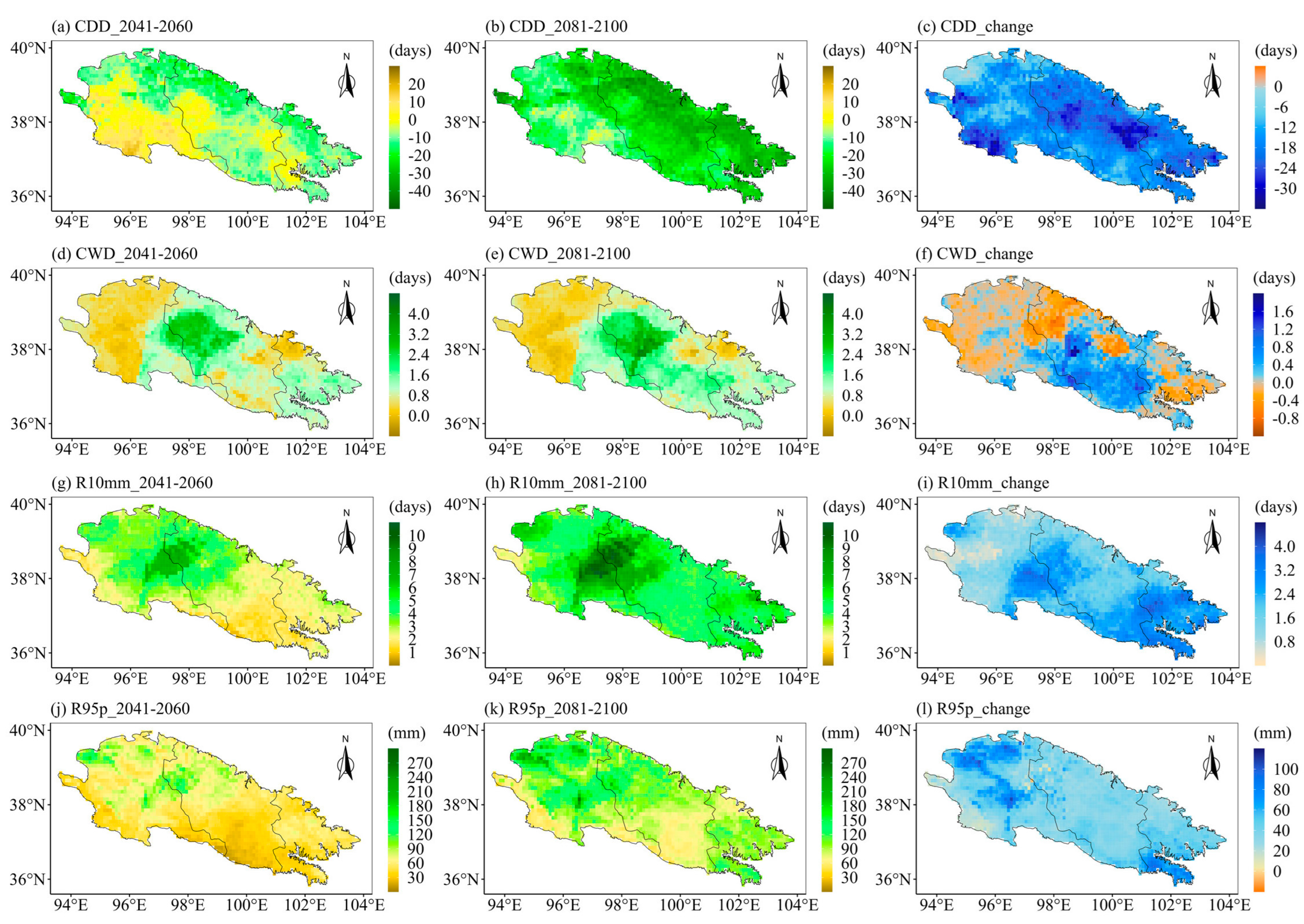
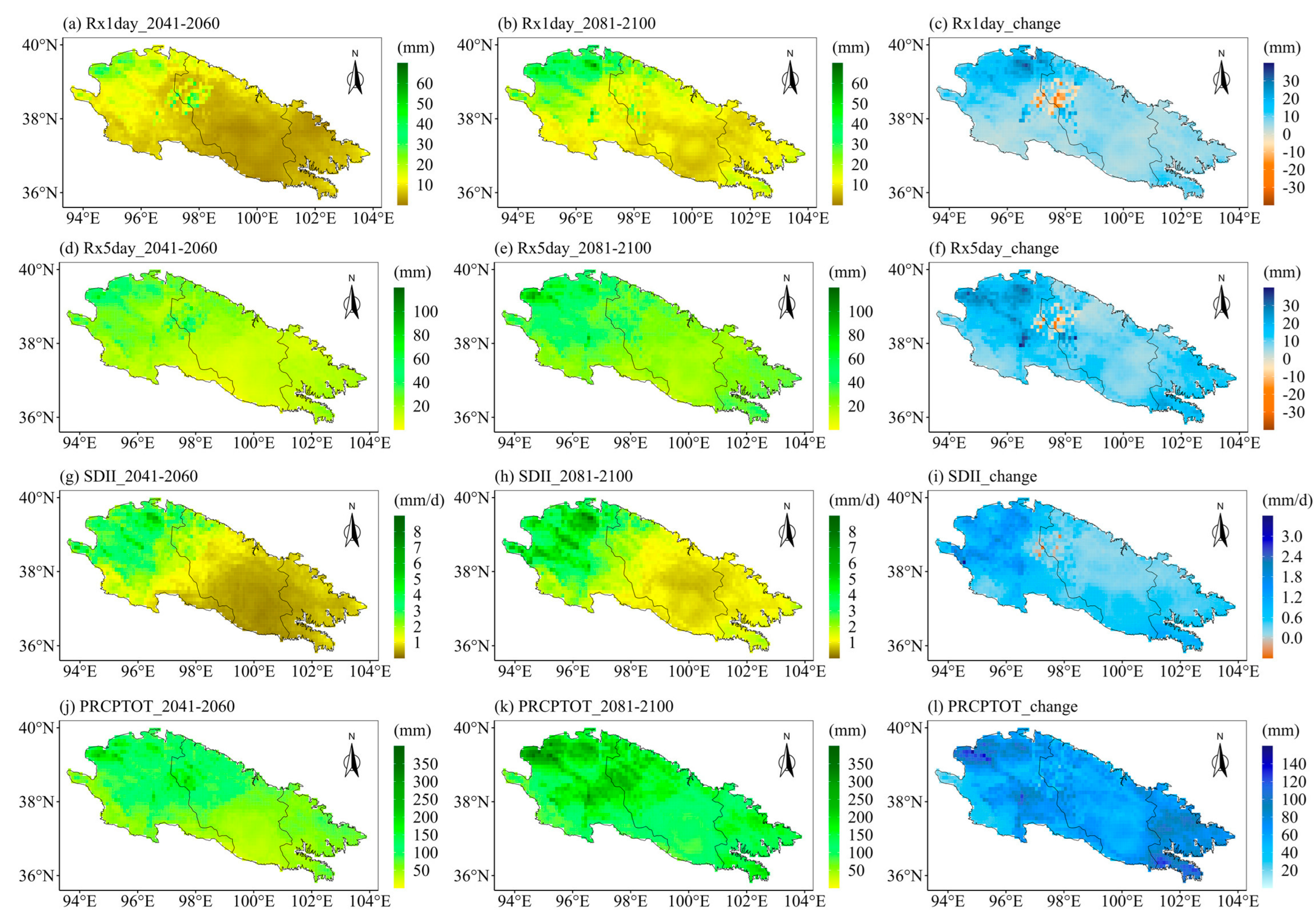
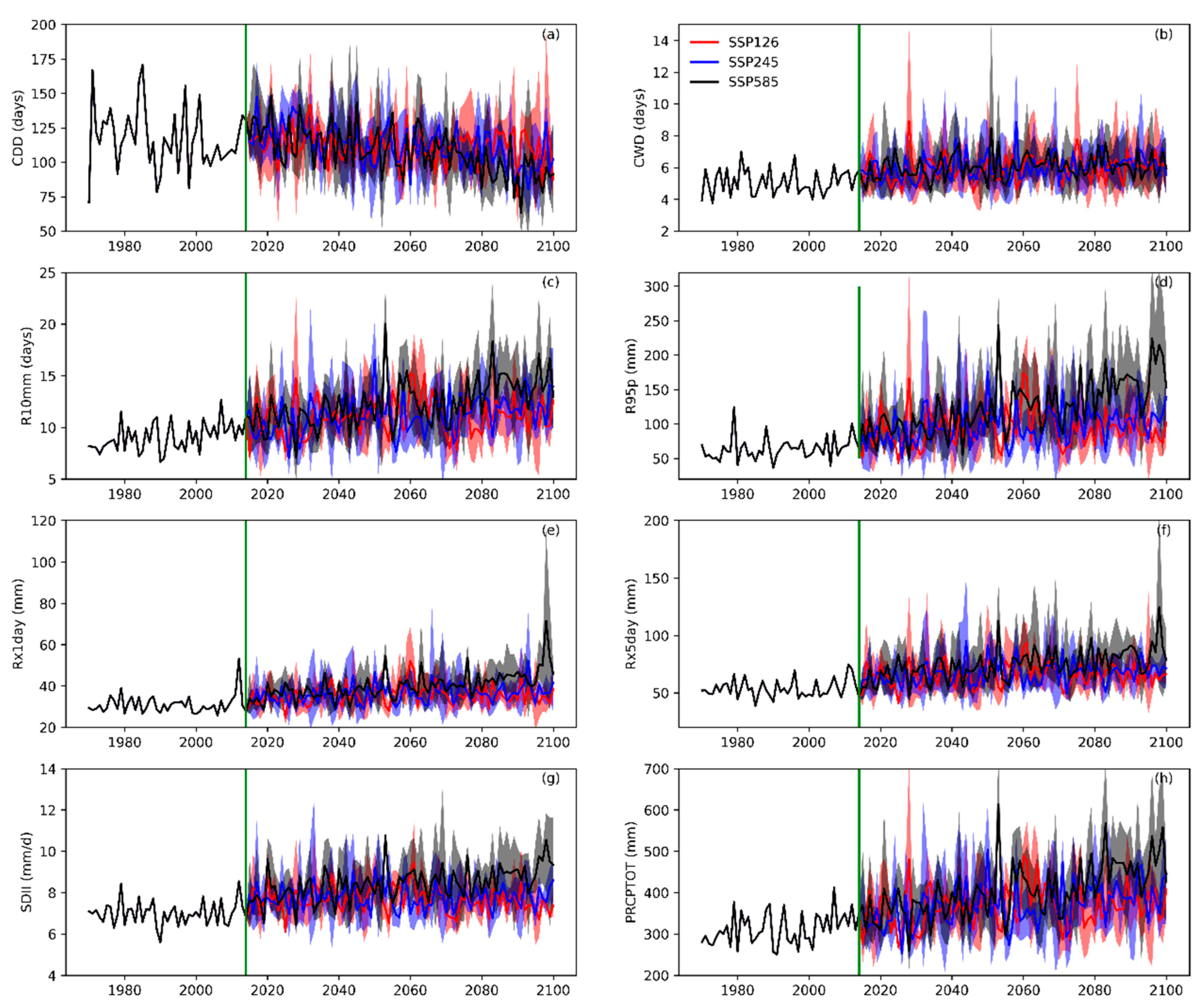
4.1. Future Projection of the Eight Extreme Precipitation Indices
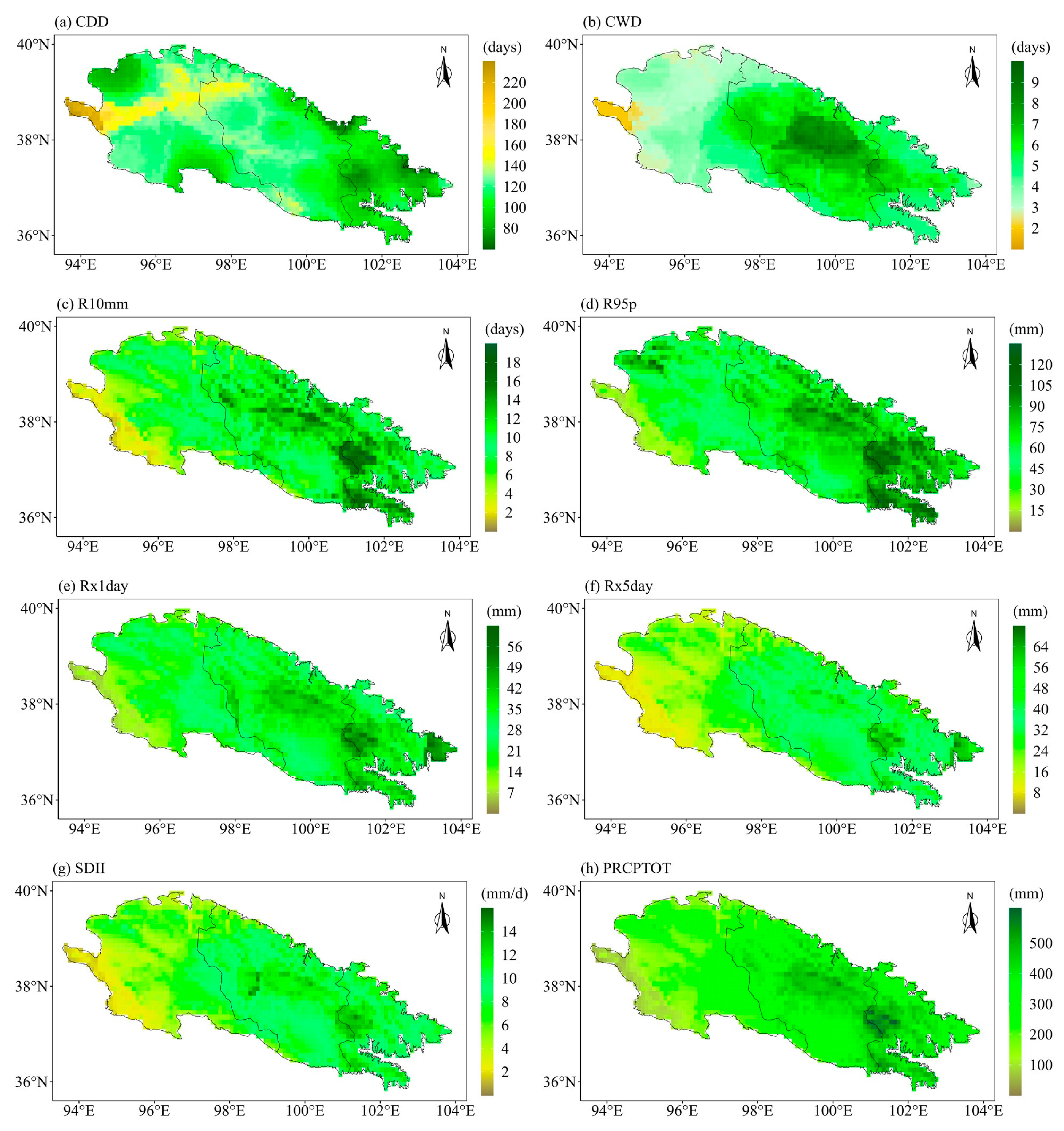
4.2. Spatial Variations of the Future Extreme Precipitation Indices
4.3. Inter-Annual Variations of the Future Extreme Precipitation Indices
5. Discussion
5.1. Comparison with Other Similar Studies
5.2. Relationship between Future Precipitation and Altitude
5.3. Biases and Deficiencies in the Projection of Extreme Precipitation
6. Conclusions
- (1)
- On the whole, the corrected CMIP6 models are able to simulate the changes of extreme precipitation indices over the Qilian Mountains in the historical period, but there are still large errors in the simulation of some indices (CDD, R95p, and Rx1day). The CMIP6 models performed well in the simulations of R10mm and PRCPTOT, and the results correlated well with the observed values. CESM2 displays better simulation performance for extreme precipitation indices in the Qilian Mountains as compared to the other two CMIP6 models.
- (2)
- The CDD of the Qilian Mountains is likely to decrease in the middle and end of the 21st century under different SSPs. The remaining seven indices in the Qilian Mountains under the three SSPs will increase in both periods (2041–2060 and 2081–2100). Moreover, the changes in the eight extreme precipitation indices will increase with the enhancement of the SSP scenario. The growth rate of precipitation in the Qilian Mountains during the 21st century under SSP585 is significantly higher than the other two SSP scenarios. The increment in precipitation over the Qilian Mountains mainly comes from the increase in heavy precipitation.
- (3)
- The Qilian Mountains will become wetter in the 21st century, especially in the central and eastern regions. The precipitation intensity and total precipitation of the Qilian Mountains will maintain continuous growth in the middle and end of the 21st century under SSP585 scenario, which is different from SSP126. The western Qilian Mountains are likely to witness the largest increase in precipitation intensity and total precipitation in the middle and end of the 21st century under SSP585.
- (4)
- The inter-annual variation in the drought index (CDD) shows strong volatility both in the historical period and in the future. The remaining seven extreme precipitation indices show a fluctuating upward trend under different SSPs in the 21st century. In addition, the precipitation increment of the Qilian Mountains will increase with the altitude in the middle and end of the 21st century. In the 21st century, the change in precipitation at the high-altitude area of the Qilian Mountains will have an important impact on glacier mass balance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| No. | Station Name | Station-ID | Long (dd) | Lat (dd) | Elevation (m) |
|---|---|---|---|---|---|
| 1 | Dunhuang | 52418 | 94.68 | 40.15 | 1139.0 |
| 2 | Guazhou | 52424 | 95.78 | 40.53 | 1170.9 |
| 3 | Yumen | 52436 | 97.03 | 40.27 | 1526.0 |
| 4 | Subei | 52515 | 94.87 | 39.52 | 2137.2 |
| 5 | Jiuquan | 52533 | 98.48 | 39.77 | 1477.2 |
| 6 | Lenghu | 52602 | 93.20 | 38.45 | 2770.0 |
| 7 | Tuole | 52633 | 98.25 | 38.49 | 3367.0 |
| 8 | Sunan | 52643 | 99.62 | 38.83 | 2311.8 |
| 9 | Yeniugou | 52645 | 99.36 | 38.26 | 3314.0 |
| 10 | Zhangye | 52652 | 100.28 | 39.08 | 1461.1 |
| 11 | Minle | 52656 | 100.82 | 38.43 | 2281.4 |
| 12 | Qilian | 52657 | 100.15 | 38.11 | 2787.4 |
| 13 | Yongchang | 52674 | 101.97 | 38.23 | 2093.9 |
| 14 | Wuwei | 52679 | 102.67 | 37.92 | 1540.2 |
| 15 | Da Qaidam | 52713 | 95.21 | 37.51 | 3173.2 |
| 16 | Delingha | 52737 | 97.23 | 37.22 | 2981.5 |
| 17 | Tianjun | 52745 | 99.02 | 37.30 | 3417.8 |
| 18 | Gangca | 52754 | 100.08 | 37.20 | 3301.5 |
| 19 | Menyuan | 52765 | 101.37 | 37.23 | 2850.0 |
| 20 | Gulang | 52784 | 102.90 | 37.47 | 2072.4 |
| 21 | Wushaoling | 52787 | 102.87 | 37.20 | 3045.1 |
| 22 | Jingtai | 52797 | 104.03 | 37.11 | 1630.9 |
| 23 | Chaka | 52842 | 99.05 | 36.47 | 3087.6 |
| 24 | Gonghe | 52856 | 100.37 | 36.16 | 2835.0 |
| 25 | Xining | 52866 | 101.45 | 36.44 | 2295.2 |
| 26 | Ledu | 52874 | 102.38 | 36.48 | 1981.9 |
| 27 | Minhe | 52876 | 102.51 | 36.19 | 1813.9 |
| 28 | Yongdeng | 52885 | 103.26 | 36.75 | 2118.8 |
| 29 | Dingxin | 52446 | 99.52 | 40.30 | 1177.4 |
| 30 | Jinta | 52447 | 98.88 | 40.00 | 1270.5 |
| 31 | Gaotai | 52546 | 99.83 | 39.37 | 1332.2 |
| 32 | Shandan | 52661 | 101.08 | 38.80 | 1765.5 |
| 33 | Minqin | 52681 | 103.08 | 38.63 | 1367.5 |
| 34 | Dulan | 52836 | 98.06 | 36.18 | 3189.0 |
| 35 | Guide | 52868 | 101.26 | 36.02 | 2237.1 |
References
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change. 2021. Available online: https://www.ipcc.ch/report/sixth-assessmentreport-working-group-i/ (accessed on 5 October 2021).
- Shiu, C.J.; Liu, S.C.; Fu, C.; Dai, A.; Sun, Y. How much do precipitation extremes change in a warming climate? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci. 2013, 6, 181–185. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Montanari, A. Global and regional increase of precipitation extremes under global warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Giorgi, F. Thirty years of regional climate modeling: Where are we and where are we going next? J. Geophys. Res. Atmos. 2019, 124, 5696–5723. [Google Scholar] [CrossRef]
- Li, Y.; Qin, X.; Liu, Y.; Jin, Z.; Liu, J.; Wang, L.; Chen, J. Evaluation of long-term and high-resolution gridded precipitation and temperature products in the Qilian Mountains, Qinghai-Tibet Plateau. Front. Environ. Sci. 2022, 10, 609. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Lin, P.; He, Z.; Du, J.; Chen, L.; Zhu, X.; Li, J. Recent changes in daily climate extremes in an arid mountain region, a case study in northwestern China’s Qilian Mountains. Sci. Rep. 2017, 7, 2245. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T. Increasing impacts from extreme precipitation on population over China with global warming. Sci. Bull. 2020, 65, 243–252. [Google Scholar] [CrossRef]
- Chen, H.; Sun, J.; Chen, X.; Zhou, W. CGCM projections of heavy rainfall events in China. Int. J. Climatol. 2012, 32, 441–450. [Google Scholar] [CrossRef]
- Prein, A.F.; Rasmussen, R.M.; Ikeda, K.; Liu, C.; Clark, M.P.; Holland, G.J. The future intensification of hourly precipitation extremes. Nat. Clim. Chang. 2017, 7, 48–52. [Google Scholar] [CrossRef]
- Chen, H. Projected change in extreme rainfall events in China by the end of the 21st century using CMIP5 models. Chin. Sci. Bull. 2013, 58, 1462–1472. [Google Scholar] [CrossRef]
- Yang, K.; Jiang, D. Interannual climate variability change during the Medieval Climate Anomaly and Little Ice Age in PMIP3 last millennium simulations. Adv. Atmos. Sci. 2017, 34, 497–508. [Google Scholar] [CrossRef]
- Li, W.; Jiang, Z.; Xu, J.; Li, L. Extreme precipitation indices over China in CMIP5 models. Part II: Probabilistic projection. J. Clim. 2016, 29, 8989–9004. [Google Scholar] [CrossRef]
- Watterson, I.G.; Rafter, T. The distribution of daily rainfall in Australia and simulated future changes. J. South. Hemis. Earth Syst. Sci. 2017, 67, 160–180. [Google Scholar] [CrossRef]
- Lee, Y.; Paek, J.; Park, J.S.; Boo, K.O. Changes in temperature and rainfall extremes across East Asia in the CMIP5 ensemble. Theor. Appl. Climatol. 2020, 141, 143–155. [Google Scholar] [CrossRef]
- Tang, B.; Hu, W.; Duan, A. Future projection of extreme precipitation indices over the Indochina Peninsula and South China in CMIP6 models. J. Clim. 2021, 34, 8793–8811. [Google Scholar] [CrossRef]
- Huai, B.; Wang, J.; Sun, W.; Wang, Y.; Zhang, W. Evaluation of the near-surface climate of the recent global atmospheric reanalysis for Qilian Mountains, Qinghai-Tibet Plateau. Atmos. Res. 2021, 250, 105401. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Tong, Y.; Gao, X.; Han, Z.; Xu, Y.; Xu, Y.; Giorgi, F. Bias correction of temperature and precipitation over China for RCM simulations using the QM and QDM methods. Clim. Dyn. 2021, 57, 1425–1443. [Google Scholar] [CrossRef]
- Whetton, P.; Macadam, I.; Bathols, J.; O’Grady, J. Assessment of the use of current climate patterns to evaluate regional enhanced greenhouse response patterns of climate models. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Guo, W.; Liu, S.; Xu, J.; Wu, L.; Shangguan, D.; Yao, X.; Wei, J.; Bao, W.; Yu, P.; Liu, Q.; et al. The Second Chinese Glacier Inventory: Data, Methods and Results. J. Glaciol. 2015, 61, 357–372. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Feng, J.Y.; Bai, H.Z.; Zhao, J.H.; Xu, X.H. A Study of Atmospheric Water Cycle over the Qilian Mountains (I): Variation of Annual Water Vapor Transport. J. Glaciol. Geocryol. 2014, 36, 1079–1091. [Google Scholar]
- Wang, H.; Chen, Y.; Chen, Z. Spatial distribution and temporal trends of mean precipitation and extremes in the arid region, northwest of China, during 1960–2010. Hydrol. Process. 2013, 27, 1807–1818. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, S.; Ding, Y.J.; Wang, J.; Han, H.; Xu, J.; Zhao, C.; Guo, W.; Shangguan, D. Modeling hydrologic response to climate change and shrinking glaciers in the highly Glacierized Kunma Like River Catchment, Central Tian Shan. J. Hydrometeorol. 2015, 16, 2383–2402. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Chen, T.; Zheng, G.; Wang, Y.; Jiang, L.; De Maeyer, P. Assessment of CMIP6 in simulating precipitation over arid Central Asia. Atmos. Res. 2021, 252, 105451. [Google Scholar] [CrossRef]
- O’Neill, B.C.; Tebaldi, C.; van Vuuren, D.P.; Eyring, V.; Friedlingstein, P.; Hurtt, G.; Knutti, R.; Kriegler, E.; Lamarque, J.-F.; Lowe, J.; et al. The Scenario Model Intercomparison Project (ScenarioMIP) for CMIP6. Geosci. Model Dev. 2016, 9, 3461–3482. [Google Scholar] [CrossRef]
- Eyring, V.; Cox, P.M.; Flato, G.M.; Gleckler, P.J.; Abramowitz, G.; Caldwell, P.; Collins, W.D.; Gier, B.K.; Hall, A.D.; Hoffman, F.M.; et al. Taking climate model evaluation to the next level. Nat. Clim. Chang. 2019, 9, 102–110. [Google Scholar] [CrossRef]
- Karl, T.R.; Nicholls, N.; Ghazi, A. Clivar/GCOS/WMO workshop on indices and indicators for climate extremes workshop summary. In Weather and Climate Extremes: Changes, Variations and a Perspective from the Insurance Industry; Springer: Berlin/Heidelberg, Germany, 1999; pp. 3–7. [Google Scholar]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar]
- Dong, T.; Dong, W. Evaluation of extreme precipitation over Asia in CMIP6 models. Clim. Dyn. 2021, 57, 1751–1769. [Google Scholar] [CrossRef]
- Akinsanola, A.A.; Ongoma, V.; Kooperman, G.J. Evaluation of CMIP6 models in simulating the statistics of extreme precipitation over Eastern Africa. Atmos. Res. 2021, 254, 105509. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A global, continental, and regional analysis of changes in extreme precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
- Fauzi, F.; Kuswanto, H.; Atok, R.M. Bias correction and statistical downscaling of earth system models using quantile delta mapping (QDM) and bias correction constructed analogues with quantile mapping reordering (BCCAQ). J. Phys. Conf. Ser. 2020, 1538, 012050. [Google Scholar] [CrossRef]
- Xavier AC, F.; Martins, L.L.; Rudke, A.P.; de Morais MV, B.; Martins, J.A.; Blain, G.C. Evaluation of Quantile Delta Mapping as a bias-correction method in maximum rainfall dataset from downscaled models in São Paulo state (Brazil). Int. J. Climatol. 2022, 42, 175–190. [Google Scholar] [CrossRef]
- Kim, Y.T.; Lima, C.H.; Kwon, H.H. Kriging Approach to Quantile Delta Mapping (QDM) for Spatial Downscaling of Climate Change Scenario. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 3–8 May 2020; p. 20829. [Google Scholar]
- Kim, S.; Joo, K.; Kim, H.; Shin, J.Y.; Heo, J.H. Regional quantile delta mapping method using regional frequency analysis for regional climate model precipitation. J. Hydrol. 2021, 596, 125685. [Google Scholar] [CrossRef]
- Olsson, J.; Berggren, K.; Olofsson, M.; Viklander, M. Applying climate model precipitation scenarios for urban hydrological assessment: A case study in Kalmar City, Sweden. Atmos. Res. 2009, 92, 364–375. [Google Scholar] [CrossRef]
- Willems, P.; Vrac, M. Statistical precipitation downscaling for small-scale hydrological impact investigations of climate change. J. Hydrol. 2011, 402, 193–205. [Google Scholar] [CrossRef]
- Wood, A.W.; Leung, L.R.; Sridhar, V.; Lettenmaier, D.P. Hydrologic implications of dynamical and statistical approaches to downscaling climate model outputs. Clim. Chang. 2004, 62, 189–216. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Liu, J.; Shangguan, D.; Liu, S.; Ding, Y.; Wang, S.; Wang, X. Evaluation and Comparison of CHIRPS and MSWEP Daily-Precipitation Products in the Qinghai-Tibet Plateau during the Period of 1981–2015. Atmos. Res. 2019, 230, 104634. [Google Scholar] [CrossRef]
- He, Q.; Yang, J.; Chen, H.; Liu, J.; Ji, Q.; Wang, Y.; Tang, F. Evaluation of Extreme Precipitation Based on Three Long-Term Gridded Products over the Qinghai-Tibet Plateau. Remote Sens. 2021, 13, 3010. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Chen, W.; Jiang, Z.; Li, L. Probabilistic projections of climate change over China under the SRES A1B scenario using 28 AOGCMs. J. Clim. 2011, 24, 4741–4756. [Google Scholar] [CrossRef]
- Wang, G.; Zhang, Q.; Yu, H.; Shen, Z.; Sun, P. Double increase in precipitation extremes across China in a 1.5 °C/2.0 °C warmer climate. Sci. Total Environ. 2020, 746, 140807. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, Y.; Fang, G.; Xia, Z.; Yang, Y.; Duan, W.; Xia, Q.; Li, S. Future changes in extreme precipitation from 1.0 °C more warming in the Tienshan Mountains, Central Asia. J. Hydrol. 2022, 612, 128269. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, F. Future changes in extreme precipitation in central Asia with 1.5–4 °C global warming based on Coupled Model Intercomparison Project Phase 6 simulations. Int. J. Climatol. 2022, 42, 8509–8525. [Google Scholar] [CrossRef]
- Liu, S.; Ding, Y.; Shangguan, D.; Zhang, Y.; Li, J.; Han, H.; Wang, J.; Xie, C. Glacier retreat as a result of climate warming and increased precipitation in the Tarim river basin, northwest China. Ann. Glaciol. 2006, 43, 91–96. [Google Scholar] [CrossRef]
- Fujita, K. Influence of precipitation seasonality on glacier mass balance and its sensitivity to climate change. Ann. Glaciol. 2008, 48, 88–92. [Google Scholar] [CrossRef]
- Ding, Y.J. Precipitation conditions for the development of the present glaciers on the Norhtern Slope of Karakorum. GeoJournal 1991, 25, 243–248. [Google Scholar] [CrossRef]
- Jin, Z.; Zhao, Q.; Qin, X.; Zhang, J.; Zhang, H.; Qin, J.; Qin, Y.; Li, H.; Chen, J.; Liu, Y.; et al. Quantifying the impact of landscape changes on hydrological variables in the alpine and cold region using hydrological model and remote sensing data. Hydrol. Process. 2021, 35, e14392. [Google Scholar] [CrossRef]



| Model Name | Institute and Country | Resolution (lat × lon) |
|---|---|---|
| CESM2 | National Center for Atmospheric Research (NCAR), USA | 0.938° × 1.25° |
| EC-Earth3 | EC-Earth-Consortium, Europe | 0.703° × 0.703° |
| KACE-1-0-G | National Institute of Meteorological Sciences/Korea Meteorological Administration (NIMS-KMA), Republic of Korea | 1.25° × 1.875° |
| Index | Descriptive Name | Definition | Units |
|---|---|---|---|
| CDD | Consecutive dry days | Maximum number of consecutive dry days (when precipitation < 1.0 mm) | days |
| CWD | Consecutive wet days | Maximum annual number of consecutive wet days (when precipitation ≥ 1.0 mm) | days |
| R10mm | Number of heavy rain days | Number of days when precipitation ≥ 10 mm | days |
| R95p | Total annual precipitation from heavy rain days | Annual sum of daily precipitation > 95th percentile | mm |
| Rx1day | Max 1-day precipitation | Maximum 1-day precipitation total | mm |
| Rx5day | Max 5-day precipitation | Maximum 5-day precipitation total | mm |
| SDII | Daily precipitation intensity | Annual total precipitation divided by the number of wet days (when total precipitation ≥ 1.0 mm) | mm/d |
| PRCPTOT | Annual total wet-day precipitation | Sum of daily precipitation ≥ 1.0 mm | mm |
| Index | CESM2 | EC-Earth3 | KACE-1-0-G | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CC | RMSE | MAE | BIAS | CC | RMSE | MAE | BIAS | CC | RMSE | MAE | BIAS | |
| CDD | 0.15 | 75.81 | 59.93 | −48.08 | 0.35 | 70.68 | 56.74 | −37.55 | 0.26 | 76.42 | 60.96 | −49.55 |
| CWD | 0.28 | 6.76 | 5.23 | 118.44 | 0.46 | 5.09 | 3.51 | 71.24 | 0.31 | 5.16 | 3.85 | 79.96 |
| R10mm | 0.63 | 12.34 | 9.56 | 149.99 | 0.64 | 4.21 | 3.09 | −20.34 | 0.54 | 5.00 | 3.64 | −13.13 |
| R95p | 0.38 | 124.06 | 95.02 | 183.50 | 0.42 | 50.28 | 37.11 | 13.58 | 0.35 | 53.01 | 39.21 | 19.69 |
| Rx1day | 0.36 | 19.16 | 15.27 | 53.11 | 0.36 | 13.06 | 9.38 | −27.05 | 0.32 | 13.05 | 9.34 | −29.25 |
| Rx5day | 0.42 | 41.39 | 33.68 | 81.28 | 0.43 | 20.32 | 15.00 | −8.26 | 0.40 | 19.32 | 14.40 | −12.07 |
| SDII | 0.45 | 1.41 | 1.10 | 1.33 | 0.39 | 2.08 | 1.72 | −31.75 | 0.45 | 2.00 | 1.65 | −31.06 |
| PRCPTOT | 0.71 | 412.36 | 346.68 | 148.20 | 0.83 | 124.39 | 90.59 | 21.61 | 0.70 | 166.61 | 125.08 | 36.41 |
| Index | CESM2 * | EC-Earth3 * | KACE-1-0-G * | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CC | RMSE | MAE | BIAS | CC | RMSE | MAE | BIAS | CC | RMSE | MAE | BIAS | |
| CDD | 0.47 | 54.64 | 42.61 | −1.12 | 0.48 | 55.04 | 42.03 | −0.78 | 0.44 | 58.20 | 43.82 | 3.40 |
| CWD | 0.53 | 2.02 | 1.43 | −0.89 | 0.45 | 2.45 | 1.74 | 14.57 | 0.53 | 2.62 | 1.89 | 22.56 |
| R10mm | 0.78 | 3.27 | 2.37 | −0.35 | 0.74 | 3.60 | 2.61 | 1.20 | 0.71 | 3.82 | 2.78 | −0.24 |
| R95p | 0.42 | 46.64 | 34.37 | −2.77 | 0.38 | 51.65 | 37.12 | 2.55 | 0.36 | 51.04 | 37.15 | −2.56 |
| Rx1day | 0.45 | 12.07 | 8.35 | −0.73 | 0.43 | 12.59 | 8.52 | −1.87 | 0.39 | 12.93 | 8.99 | −2.03 |
| Rx5day | 0.55 | 18.70 | 13.77 | 1.51 | 0.45 | 21.47 | 15.51 | 6.83 | 0.48 | 21.45 | 15.73 | 8.13 |
| SDII | 0.57 | 1.27 | 0.95 | −0.39 | 0.57 | 1.29 | 0.96 | −1.76 | 0.52 | 1.38 | 1.04 | −1.80 |
| PRCPTOT | 0.88 | 69.18 | 51.98 | 0.30 | 0.85 | 80.57 | 58.91 | 1.68 | 0.84 | 83.99 | 62.64 | 0.91 |
| Index | SSP126 | SSP245 | SSP585 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 2041–2060 | 2081–2100 | Change | 2041–2060 | 2081–2100 | Change | 2041–2060 | 2081–2100 | Change | |
| CDD | −4.25 | −3.56 | 0.68 | −6.07 | −12.83 | −6.76 | −6.13 | −23.02 | −16.89 |
| CWD | 0.62 | 0.94 | 0.32 | 1.00 | 1.26 | 0.26 | 0.98 | 1.09 | 0.11 |
| R10mm | 2.09 | 2.10 | 0.01 | 2.23 | 2.93 | 0.70 | 3.14 | 5.17 | 2.03 |
| R95p | 35.76 | 29.75 | −6.01 | 37.77 | 43.93 | 6.16 | 57.68 | 101.44 | 43.77 |
| Rx1day | 6.52 | 5.17 | −1.35 | 6.10 | 7.27 | 1.17 | 8.08 | 15.90 | 7.82 |
| Rx5day | 13.77 | 13.63 | −0.14 | 16.74 | 16.17 | −0.58 | 19.46 | 31.47 | 12.01 |
| SDII | 0.94 | 0.60 | −0.34 | 0.97 | 0.92 | −0.05 | 1.49 | 2.12 | 0.63 |
| PRCPTOT | 55.90 | 58.35 | 2.45 | 61.99 | 81.55 | 19.56 | 84.75 | 151.15 | 66.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Qin, X.; Jin, Z.; Liu, Y. Future Projection of Extreme Precipitation Indices over the Qilian Mountains under Global Warming. Int. J. Environ. Res. Public Health 2023, 20, 4961. https://doi.org/10.3390/ijerph20064961
Li Y, Qin X, Jin Z, Liu Y. Future Projection of Extreme Precipitation Indices over the Qilian Mountains under Global Warming. International Journal of Environmental Research and Public Health. 2023; 20(6):4961. https://doi.org/10.3390/ijerph20064961
Chicago/Turabian StyleLi, Yanzhao, Xiang Qin, Zizhen Jin, and Yushuo Liu. 2023. "Future Projection of Extreme Precipitation Indices over the Qilian Mountains under Global Warming" International Journal of Environmental Research and Public Health 20, no. 6: 4961. https://doi.org/10.3390/ijerph20064961
APA StyleLi, Y., Qin, X., Jin, Z., & Liu, Y. (2023). Future Projection of Extreme Precipitation Indices over the Qilian Mountains under Global Warming. International Journal of Environmental Research and Public Health, 20(6), 4961. https://doi.org/10.3390/ijerph20064961






