Analysing the Effect of Energy Intensity on Carbon Emission Reduction in Beijing
Abstract
1. Introduction
2. Literature Review
3. Data and Methodology
3.1. Estimation of Carbon Emissions
3.2. Models
3.2.1. The Decomposition Method
3.2.2. The Econometric Model
3.3. Data and Variables
4. Empirical Results
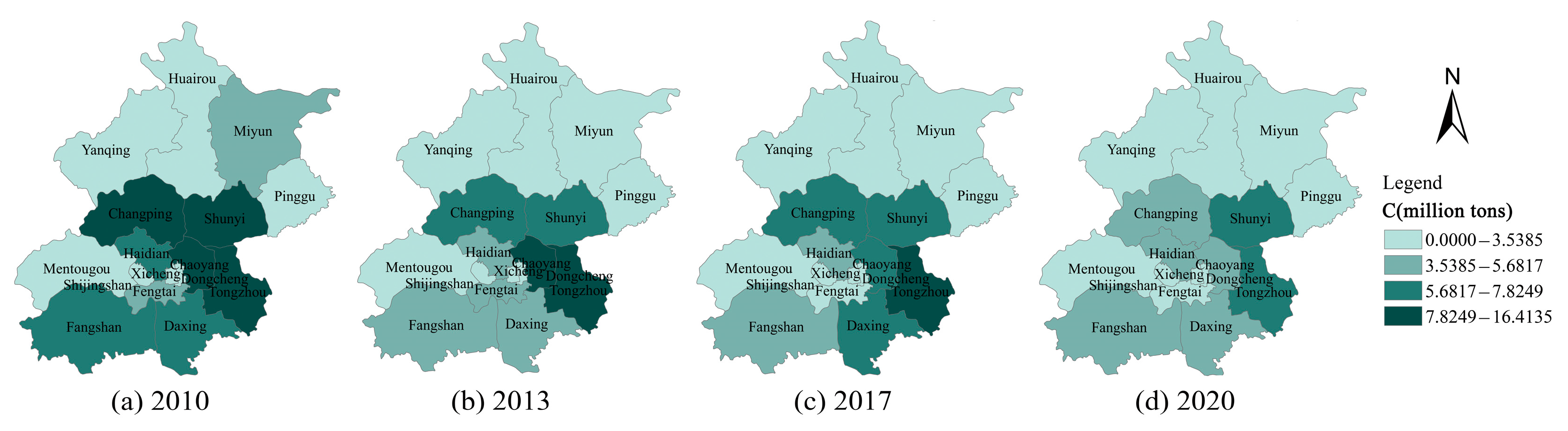
4.1. Decomposition Analysis of the Driving Factors for Carbon Emissions
4.2. Analysis of the Spatial Spill over Effects
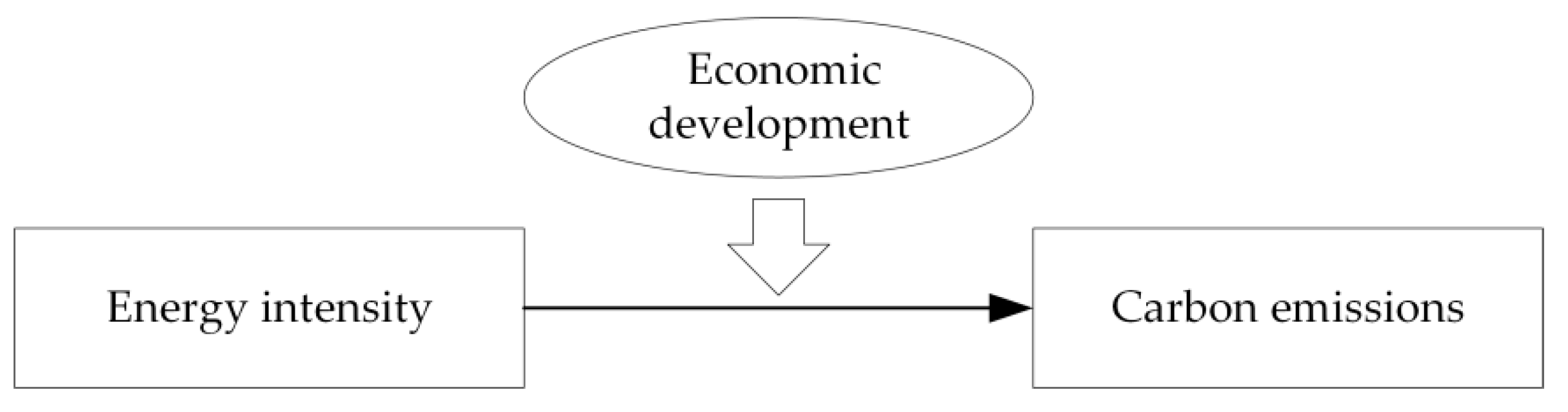
4.3. Influence Mechanism Analysis
5. Discussion and Conclusions
5.1. Discussion
5.2. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liobikiene, G.; Butkus, M. Determinants of greenhouse gas emissions: A new multiplicative approach analysing the impact of energy efficiency, renewable energy, and sector mix. J. Clean. Prod. 2021, 309, 127233. [Google Scholar] [CrossRef]
- Ou, X.M.; Yuan, Z.Y.; Peng, T.D.; Sun, Z.Q.; Zhou, S. The low-carbon transition toward sustainability of regional coal-dominated energy consumption structure: A case of Hebei province in China. Sustainability 2017, 9, 1184. [Google Scholar] [CrossRef]
- Töbelmann, D.; Wendler, T. The impact of environmental innovation on carbon dioxide emissions. J. Clean. Prod. 2020, 244, 118787. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Li, H.; Zhang, Z.H.; Zhang, Y.F.; Wang, S.; Liu, Y. Decomposition and scenario analysis of CO2 emissions in China’s power industry: Based on LMDI method. Nat. Hazards 2017, 86, 645–668. [Google Scholar] [CrossRef]
- Adedoyin, F.; Ozturk, I.; Abubakar, I.; Kumeka, T.; Folarin, O.; Bekun, F.V. Structural breaks in CO2 emissions: Are they caused by climate change protests or other factors? J. Environ. Manag. 2020, 266, 110628. [Google Scholar] [CrossRef]
- Cosmas, N.C.; Chitedze, I.; Mourad, K.A. An econometric analysis of the macroeconomic determinants of carbon dioxide emissions in Nigeria. Sci. Total Environ. 2019, 675, 313–324. [Google Scholar] [CrossRef]
- Oreskes, N. Beyond the ivory tower—The scientific consensus on climate change. Science 2004, 306, 1686. [Google Scholar] [CrossRef]
- Udara Willhelm Abeydeera, L.H.; Wadu Mesthrige, J.; Samarasinghalage, T.I. Global research on carbon emissions: A scientometric review. Sustainability 2019, 11, 3972. [Google Scholar] [CrossRef]
- Wang, G.F.; Liao, M.L.; Jiang, J. Research on agricultural carbon emissions and regional carbon emissions reduction strategies in China. Sustainability 2020, 12, 2627. [Google Scholar] [CrossRef]
- Ullah, I.; Ali, S.; Shah, M.H.; Yasim, F.; Rehman, A.; Al-Ghazali, B.M. Linkages between trade, CO2 emissions and healthcare spending in China. Int. J. Environ. Res. Public Health 2019, 16, 4298. [Google Scholar] [CrossRef]
- Cui, G.; Yu, Y.; Zhou, L.; Zhang, H. Driving forces for carbon emissions changes in Beijing and the role of green power. Sci. Total Environ. 2020, 728, 138688. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Li, M.; Xue, J.; Liu, Y. Evaluation of effectiveness of China’s carbon emissions trading scheme in carbon mitigation. Energy Econ. 2020, 90, 104872. [Google Scholar] [CrossRef]
- Xu, L.; Fan, M.; Yang, L.; Shao, S. Heterogeneous green innovations and carbon emission performance: Evidence at China’s city level. Energy Econ. 2021, 99, 105269. [Google Scholar] [CrossRef]
- Feng, J.C.; Zeng, X.L.; Yu, Z.; Tang, S.; Li, W.C.; Xu, W.J. Status and driving forces of CO2 emission of the national low carbon pilot: Case study of Guangdong province during 1995–2015. Energy Procedia 2019, 158, 3602–3607. [Google Scholar] [CrossRef]
- Zhou, Q.; Yabar, H.; Mizunoya, T.; Higano, Y. Exploring the potential of introducing technology innovation and regulations in the energy sector in China: A regional dynamic evaluation model. J. Clean. Prod. 2016, 112, 1537–1548. [Google Scholar] [CrossRef]
- Huang, R.; Zhang, S.; Wang, P. Key areas and pathways for carbon emissions reduction in Beijing for the “Dual Carbon” targets. Energy Policy 2022, 164, 112873. [Google Scholar] [CrossRef]
- Xue, Q.; Feng, S.; Chen, K.; Li, M. Impact of digital finance on regional carbon emissions: An empirical study of sustainable development in China. Sustainability 2022, 14, 8340. [Google Scholar] [CrossRef]
- Huang, J.; Du, D.; Hao, Y. The driving forces of the change in China’s energy intensity: An empirical research using DEA-Malmquist and spatial panel estimations. Econ. Model. 2017, 65, 41–50. [Google Scholar] [CrossRef]
- Pan, X.; Wei, Z.; Han, B.; Shahbaz, M. The heterogeneous impacts of interregional green technology spillover on energy intensity in China. Energy Econ. 2021, 96, 105133. [Google Scholar] [CrossRef]
- Wang, Q.; Chiu, Y.H.; Chiu, C.R. Driving factors behind carbon dioxide emissions in China: A modified production-theoretical decomposition analysis. Energy Econ. 2015, 51, 252–260. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, T. Impacts of energy-related CO2 emissions: Evidence from under developed, developing and highly developed regions in China. Ecol. Indic. 2015, 50, 186–195. [Google Scholar] [CrossRef]
- Zhang, C.; Su, B.; Zhou, K.; Yang, S. Decomposition analysis of China’s CO2 emissions (2000–2016) and scenario analysis of its carbon intensity targets in 2020 and 2030. Sci. Total Environ. 2019, 668, 432–442. [Google Scholar] [CrossRef] [PubMed]
- Latief, R.; Kong, Y.; Javeed, S.A.; Sattar, U. Carbon emissions in the SAARC countries with causal effects of FDI, economic growth and other economic factors: Evidence from dynamic simultaneous equation models. Int. J. Environ. Res. Public Health 2021, 18, 4605. [Google Scholar] [CrossRef]
- Hussain, I.; Wang, H.; Safdar, M.; Ho, Q.B.; Wemegah, T.D.; Noor, S. Estimation of Shipping Emissions in Developing Country: A Case Study of Mohammad Bin Qasim Port, Pakistan. Int. J. Environ. Res. Public Health 2022, 19, 11868. [Google Scholar] [CrossRef] [PubMed]
- Azarkamand, S.; Wooldridge, C.; Darbra, R. Review of initiatives and methodologies to reduce CO2 emissions and climate change effects in ports. Int. J. Environ. Res. Public Health 2020, 17, 3858. [Google Scholar] [CrossRef] [PubMed]
- Moutinho, V.; Moreira, A.C.; Silva, P.M. The driving forces of change in energy-related CO2 emissions in Eastern, Western, Northern and Southern Europe: The LMDI approach to decomposition analysis. Renew. Sustain. Energy Rev. 2015, 50, 1485–1499. [Google Scholar] [CrossRef]
- Xu, S.C.; He, Z.X.; Long, R.Y. Factors that influence carbon emissions due to energy consumption in China: Decomposition analysis using LMDI. Appl. Energy 2014, 127, 182–193. [Google Scholar] [CrossRef]
- Wu, Y.; Tam, V.W.Y.; Shuai, C.; Shen, L.; Zhang, Y.; Liao, S. Decoupling China’s economic growth from carbon emissions: Empirical studies from 30 Chinese provinces (2001–2015). Sci. Total Environ. 2019, 656, 576–588. [Google Scholar] [CrossRef]
- Mousavi, B.; Lopez, N.S.A.; Biona, J.B.M.; Chiu, A.S.F.; Blesl, M. Driving forces of Iran’s CO2 emissions from energy consumption: An LMDI decomposition approach. Appl. Energy 2017, 206, 804–814. [Google Scholar] [CrossRef]
- Sumabat, A.K.; Lopez, N.S.; Yu, K.D.; Hao, H.; Li, R.; Geng, Y.; Chiu, A.S.F. Decomposition analysis of Philippine CO2 emissions from fuel combustion and electricity generation. Appl. Energy 2016, 164, 795–804. [Google Scholar] [CrossRef]
- Doganlar, M.; Mike, F.; Kizilkaya, O.; Karlilar, S. Testing the long-run effects of economic growth, financial development and energy consumption on CO2 emissions in Turkey: New evidence from RALS cointegration test. Environ. Sci. Pollut. Res. 2021, 28, 32554–32563. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Yu, H.; Liu, Q.; Li, Y.; Li, L.; Dong, H.; Adenutsi, C.D. Identifying the key driving factors of carbon emissions in ‘Belt and Road Initiative’ countries. Sustainability 2022, 14, 9104. [Google Scholar] [CrossRef]
- Ertugrul, H.M.; Cetin, M.; Seker, F.; Dogan, E. The impact of trade openness on global carbon dioxide emissions: Evidence from the top ten emitters among developing countries. Ecol. Indic. 2016, 67, 543–555. [Google Scholar] [CrossRef]
- Du, Q.; Lu, X.; Li, Y.; Wu, M.; Bai, L.; Yu, M. Carbon emissions in China’s construction industry: Calculations, factors and regions. Int. J. Environ. Res. Public Health 2018, 15, 1220. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, S.; Li, R. Determinants of decoupling economic output from carbon emission in the transport sector: A comparison study of four municipalities in China. Int. J. Environ. Res. Public Health 2019, 16, 3729. [Google Scholar] [CrossRef]
- Ogungbile, A.J.; Shen, G.Q.; Wuni, I.Y.; Xue, J.; Hong, J. A Hybrid Framework for Direct CO2 Emissions Quantification in China’s Construction Sector. Int. J. Environ. Res. Public Health 2021, 18, 11965. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mandaraka, M. Decomposition analysis for assessing the progress in decoupling industrial growth from CO2 emissions in the EU manufacturing sector. Energy Econ. 2007, 29, 636–664. [Google Scholar] [CrossRef]
- Kopidou, D.; Diakoulaki, D. Decomposing industrial CO2 emissions of Southern European countries into production- and consumption-based driving factors. J. Clean. Prod. 2017, 167, 1325–1334. [Google Scholar] [CrossRef]
- Lin, B.; Benjamin, N.I. Influencing factors on carbon emissions in China transport industry. A new evidence from quantile regression analysis. J. Clean. Prod. 2017, 150, 175–187. [Google Scholar] [CrossRef]
- Akbostanci, E.; Tunc, G.I.; Turut-Asik, S. CO2 emissions of Turkish manufacturing industry: A decomposition analysis. Appl. Energy 2011, 88, 2273–2278. [Google Scholar] [CrossRef]
- Li, T.; Baležentis, T.; Makutėnienė, D.; Streimikiene, D.; Kriščiukaitienė, I. Energy-related CO2 emission in European Union agriculture: Driving forces and possibilities for reduction. Appl. Energy 2016, 180, 682–694. [Google Scholar] [CrossRef]
- O’Mahony, T. Decomposition of Ireland’s carbon emissions from 1990 to 2010: An extended Kaya identity. Energy Policy 2013, 59, 573–581. [Google Scholar]
- Han, H.; Zhong, Z.; Guo, Y.; Xi, F.; Liu, S. Coupling and decoupling effects of agricultural carbon emissions in China and their driving factors. Environ. Sci. Pollut. Res. 2018, 25, 25280–25293. [Google Scholar] [CrossRef] [PubMed]
- Lin, B.; Long, H. Emissions reduction in China’s chemical industry—Based on LMDI. Renew. Sustain. Energy Rev. 2016, 53, 1348–1355. [Google Scholar] [CrossRef]
- Li, H.; Mu, H.; Zhang, M.; Li, N. Analysis on influence factors of China’s CO2 emissions based on Path–STIRPAT model. Energy Policy 2011, 39, 6906–6911. [Google Scholar] [CrossRef]
- Wang, S.; Shi, C.; Fang, C.; Feng, K. Examining the spatial variations of determinants of energy-related CO2 emissions in China at the city level using Geographically Weighted Regression Model. Appl. Energy 2019, 235, 95–105. [Google Scholar] [CrossRef]
- Shahbaz, M.; Loganathan, N.; Muzaffar, A.T.; Ahmed, K.; Ali Jabran, M. How urbanization affects CO2 emissions in Malaysia? The application of STIRPAT model. Renew. Sustain. Energy Rev. 2016, 57, 83–93. [Google Scholar] [CrossRef]
- Shahbaz, M.; Nasir, M.A.; Roubaud, D. Environmental degradation in France: The effects of FDI, financial development, and energy innovations. Energy Econ. 2018, 74, 843–857. [Google Scholar] [CrossRef]
- Wang, Y.; Liao, M.; Wang, Y.; Xu, L.; Malik, A. The impact of foreign direct investment on China’s carbon emissions through energy intensity and emissions trading system. Energy Econ. 2021, 97, 105212. [Google Scholar] [CrossRef]
- Li, K.; Fang, L.; He, L. The impact of energy price on CO2 emissions in China: A spatial econometric analysis. Sci. Total Environ. 2020, 706, 135942. [Google Scholar] [CrossRef]
- Li, W.; Sun, W.; Li, G.; Jin, B.; Wu, W.; Cui, P.; Zhao, G. Transmission mechanism between energy prices and carbon emissions using geographically weighted regression. Energy Policy 2018, 115, 434–442. [Google Scholar] [CrossRef]
- Salahuddin, M.; Habib, M.A.; Al-Mulali, U.; Ozturk, I.; Marshall, M.; Ali, M.I. Renewable energy and environmental quality: A second-generation panel evidence from the Sub Saharan Africa (SSA) countries. Environ. Res. 2020, 191, 110094. [Google Scholar] [CrossRef] [PubMed]
- Sharif, A.; Raza, S.A.; Ozturk, I.; Afshan, S. The dynamic relationship of renewable and nonrenewable energy consumption with carbon emission: A global study with the application of heterogeneous panel estimations. Renew. Energy 2019, 133, 685–691. [Google Scholar] [CrossRef]
- Meng, Z.; Wang, H.; Wang, B. Empirical analysis of carbon emission accounting and influencing factors of energy consumption in China. Int. J. Environ. Res. Public Health 2018, 15, 2467. [Google Scholar] [CrossRef]
- Zeng, S.; Li, G.; Wu, S.; Dong, Z. The impact of green technology innovation on carbon emissions in the context of carbon neutrality in China: Evidence from spatial spillover and nonlinear effect analysis. Int. J. Environ. Res. Public Health 2022, 19, 730. [Google Scholar] [CrossRef]
- Pan, X.; Guo, S.; Xu, H.; Tian, M.; Pan, X.; Chu, J. China’s carbon intensity factor decomposition and carbon emission decoupling analysis. Energy 2022, 239, 1221752. [Google Scholar] [CrossRef]
- Wu, S.; Ding, S. Efficiency improvement, structural change, and energy intensity reduction: Evidence from Chinese agricultural sector. Energy Econ. 2021, 99, 105313. [Google Scholar] [CrossRef]
- Ang, B.W.; Liu, F.L. A new energy decomposition method: Perfect in decomposition and consistent in aggregation. Energy 2001, 26, 537–548. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, Q. Examining the driving factors of urban residential carbon intensity using the LMDI method: Evidence from China’s county-level cities. Int. J. Environ. Res. Public Health 2021, 18, 3929. [Google Scholar] [CrossRef]
- Dong, F.; Gao, X.; Li, J.; Zhang, Y.; Liu, Y. Drivers of China’s industrial carbon emissions: Evidence from joint PDA and LMDI approaches. Int. J. Environ. Res. Public Health 2018, 15, 2712. [Google Scholar] [CrossRef]
- Wang, W.; Chen, H.; Wang, L.; Li, X.; Mao, D.; Wang, S. Exploration of spatio-temporal characteristics of carbon emissions from energy consumption and their driving factors: A case analysis of the Yangtze River Delta, China. Int. J. Environ. Res. Public Health 2022, 19, 9483. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Jiang, H.; Sun, R.; Dong, X. Driving forces and mitigation potential of global CO2 emissions from 1980 through 2030: Evidence from countries with different income levels. Sci. Total Environ. 2019, 649, 335–343. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.M.; Chongbo, W. Estimating energy-related CO2 emission growth in Bangladesh: The LMDI decomposition method approach. Energy Strategy Rev. 2020, 32, 100565. [Google Scholar] [CrossRef]
- Wang, X.; Yan, L. Driving factors and decoupling analysis of fossil fuel related-carbon dioxide emissions in China. Fuel 2020, 314, 122869. [Google Scholar] [CrossRef]
- Yang, J.; Cai, W.; Ma, M.; Li, L.; Liu, C.; Ma, X.; Li, L.; Chen, X. Driving forces of China’s CO2 emissions from energy consumption based on Kaya-LMDI methods. Sci. Total Environ. 2020, 711, 134569. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, X.; Zhang, M.; Feng, Y.; Liu, Y.; Wen, J.; Liu, L. Influencing factors of carbon emissions in transportation industry based on CD function and LMDI decomposition model: China as an example. Environ. Impact Assess. Rev. 2021, 90, 106623. [Google Scholar] [CrossRef]
- Liu, W.; Jia, Z.; Du, M.; Dong, Z.; Pan, J.; Li, Q.; Pan, L.; Umole, C. Influencing factors and contribution analysis of CO2 emissions originating from final energy consumption in Sichuan Province, China. Reg. Sustain. 2022, 3, 356–372. [Google Scholar] [CrossRef]
- Gu, S.; Fu, B.; Thriveni, T.; Fujita, T.; Ahn, J.W. Coupled LMDI and system dynamics model for estimating urban CO2 emission mitigation potential in Shanghai, China. J. Clean. Prod. 2019, 240, 118034. [Google Scholar] [CrossRef]
- Chen, L.; Xu, L.; Xu, Q.; Yang, Z. Optimization of urban industrial structure under the low-carbon goal and the water constraints: A case in Dalian, China. J. Clean. Prod. 2016, 114, 323–333. [Google Scholar] [CrossRef]
- Namahoro, J.P.; Wu, Q.; Zhou, N.; Xue, S. Impact of energy intensity, renewable energy, and economic growth on CO2 emissions: Evidence from Africa across regions and income levels. Renew. Sustain. Energy Rev. 2021, 147, 111233. [Google Scholar] [CrossRef]
- Wu, R.; Wang, J.; Wang, S.; Feng, K. The drivers of declining CO2 emissions trends in developed nations using an extended STIRPAT model: A historical and prospective analysis. Renew. Sustain. Energy Rev. 2021, 149, 111328. [Google Scholar] [CrossRef]
- IPCC. Guidelines for National Greenhouse Gas Inventories. Intergovernmental Panel on Climate Change. Available online: https://www.ipcc-nggip.iges.or.jp/public/2006gl/index.html (accessed on 20 December 2022).
- Zheng, J.; Mi, Z.; Coffman, D.M.; Milcheva, S.; Shan, Y.; Guan, D.; Wang, S. Regional development and carbon emissions in China. Energy Econ. 2019, 81, 25–36. [Google Scholar] [CrossRef]
- Auffhammer, M.; Carson, R.T. Forecasting the path of China’s CO2 emissions using province-level information. J. Environ. Econ. Manag. 2008, 55, 229–247. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Spatial econometric modeling of origin-destination flows. J. Reg. Sci. 2008, 48, 941–967. [Google Scholar] [CrossRef]
- Anselin, L. Lagrange multiplier test diagnostics for spatial dependence and spatial heterogeneity. Geogr. Anal. 1988, 20, 1–17. [Google Scholar] [CrossRef]
- Wang, D.; Han, B. Effects of indigenous R&D and foreign spillover on energy intensity in China. J. Renew. Sustain. Energy 2017, 9, 035901. [Google Scholar]
- Brondino, G. Productivity growth and structural change in China (1995–2009): A subsystems analysis. Struct. Chang. Econ. Dyn. 2019, 49, 183–191. [Google Scholar] [CrossRef]
- Shen, X.; Lin, B. Does industrial structure distortion impact the energy intensity in China? Sustain. Prod. Consum. 2021, 25, 551–562. [Google Scholar] [CrossRef]
- Wu, N.; Liu, Z. Higher education development, technological innovation and industrial structure upgrade. Technol. Forecast. Soc. Chang. 2021, 162, 120400. [Google Scholar] [CrossRef]
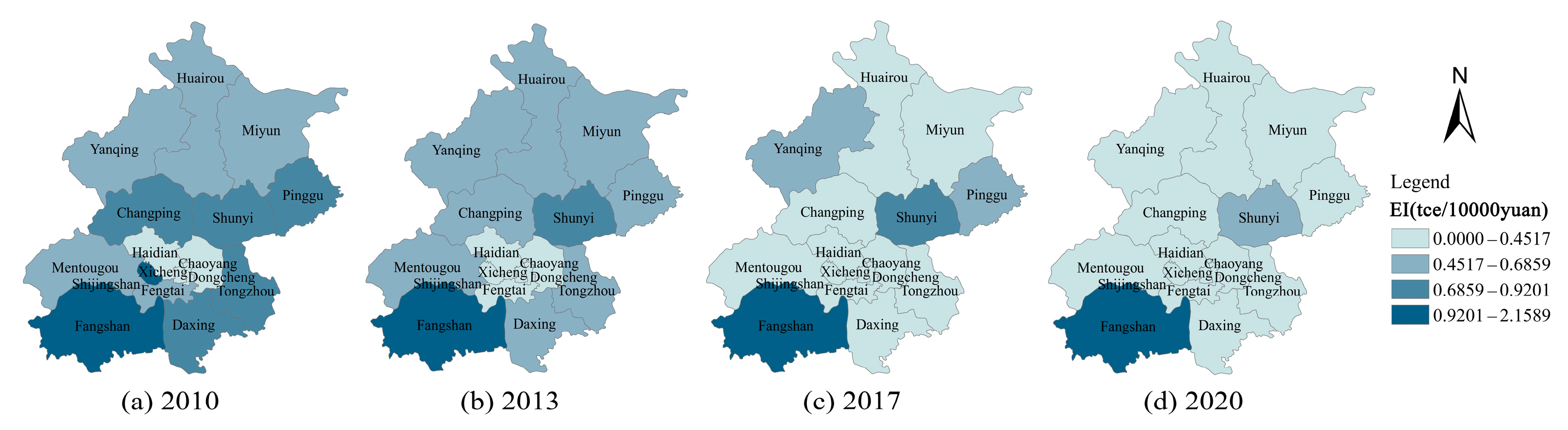
| Energy Type | NCV (kJ/kg, m3) | CEF (kg/GJ) | COF | CO2 Emission Factor (kg/kg, m3) |
|---|---|---|---|---|
| Raw Coal | 20,908 | 26.37 | 0.94 | 1.9003 |
| Cleaned Coal | 26,344 | 25.41 | 0.98 | 2.4044 |
| Briquettes | 20,908 | 33.56 | 0.9 | 2.3183 |
| Coke | 28,435 | 29.42 | 0.93 | 2.8604 |
| Gasoline | 43,070 | 18.90 | 0.98 | 2.9251 |
| Kerosene | 43,070 | 19.60 | 0.98 | 3.0179 |
| Diesel Oil | 42,652 | 20.20 | 0.98 | 3.0959 |
| Fuel Oil | 41,816 | 21.10 | 0.98 | 3.1705 |
| Liquefied Petroleum Gas | 50,179 | 17.20 | 0.98 | 3.1013 |
| Refinery Gas | 45,998 | 18.20 | 0.98 | 3.0082 |
| Other Petroleum Products | 41,816 | 20.00 | 0.98 | 3.0052 |
| Natural Gas | 38,931 | 15.32 | 0.99 | 2.165 |
| Variable | Variable Declaration | Mean | S.D. | Min | Max |
|---|---|---|---|---|---|
| C | Carbon emissions | 4.1772 | 3.2368 | 0.4504 | 16.4133 |
| EI | Energy intensity | 0.5070 | 0.3997 | 0.0717 | 2.5358 |
| ECO | Economic level | 9.4305 | 8.4998 | 2.1347 | 45.7600 |
| POP | Population size | 5198.0800 | 7265.4570 | 157.0000 | 25,787.0000 |
| TEC | Technology innovation | 9741.3130 | 15,999.3000 | 41.0000 | 95,140.0000 |
| STR | Industrial structure | 4.8740 | 6.7654 | 0.5018 | 39.4860 |
| OPE | Foreign direct investment | 74,246.9100 | 168,205.0000 | 100.0000 | 1,161,083.0000 |
| Year | Total | Agricultural Sector | Manufacturing Sector | Construction Sector | Transport Sector | Services Sector |
|---|---|---|---|---|---|---|
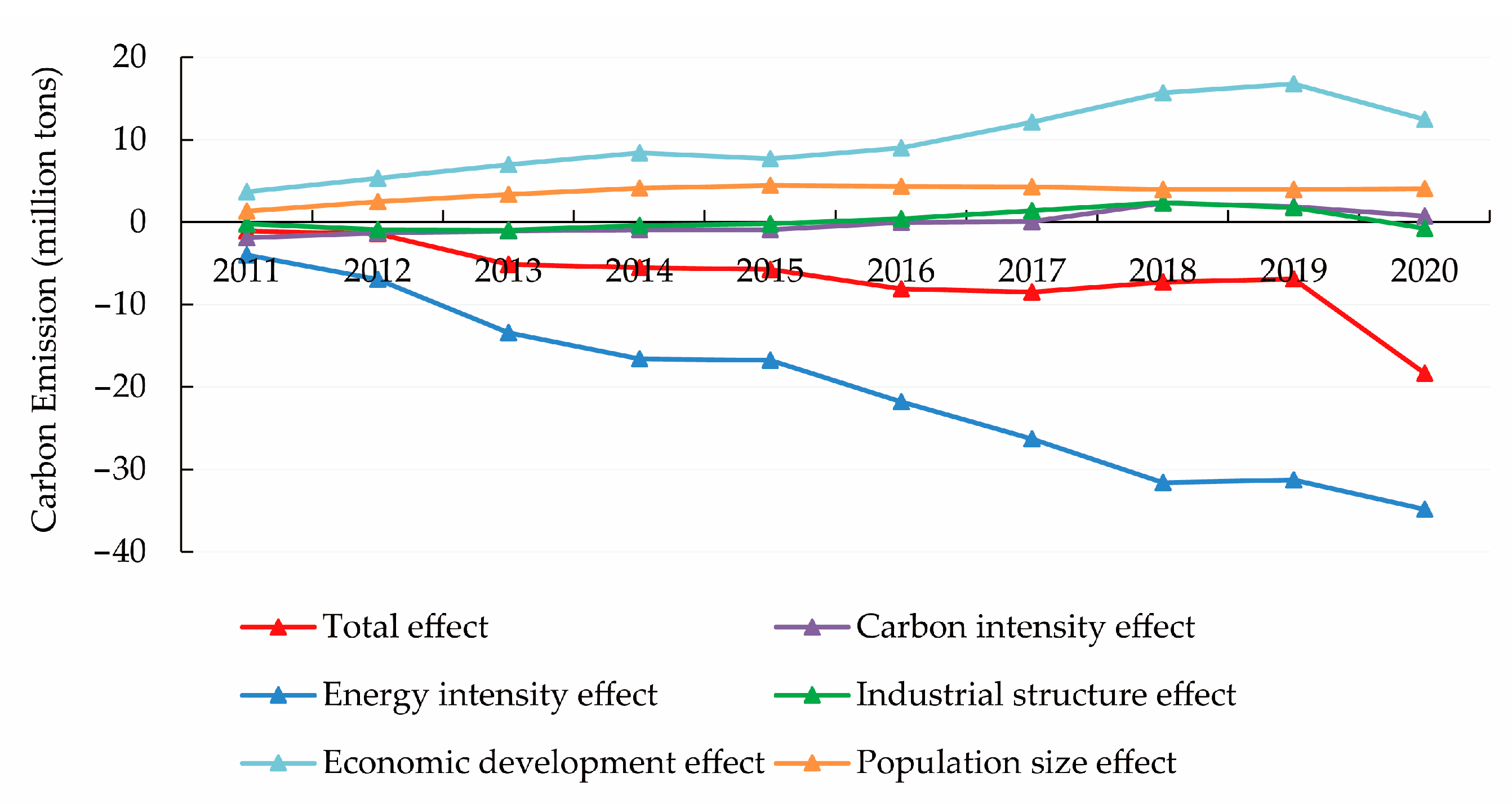
| 2011 | −3.9866 | −0.1326 | −2.2607 | −0.5006 | −0.9087 | −0.1841 |
| 2012 | −6.9693 | −0.3201 | −4.8342 | −0.8725 | −0.6462 | −0.2963 |
| 2013 | −13.4180 | −0.4522 | −10.6408 | −1.2674 | −0.4512 | −0.6064 |
| 2014 | −16.5955 | −0.5422 | −13.0116 | −1.3233 | −0.9756 | −0.7428 |
| 2015 | −16.7543 | −0.5376 | −13.5302 | −1.3913 | −0.7250 | −0.5701 |
| 2016 | −21.8109 | −0.6199 | −17.6826 | −1.6281 | −1.0958 | −0.7845 |
| 2017 | −26.3147 | −0.7786 | −20.0379 | −1.7720 | −2.6203 | −1.1058 |
| 2018 | −31.6305 | −0.9436 | −22.0394 | −1.9362 | −4.0165 | −2.6948 |
| 2019 | −31.2980 | −0.9374 | −21.9902 | −2.0865 | −3.3859 | −2.8979 |
| 2020 | −34.8172 | −0.9352 | −21.4063 | −2.2916 | −7.1460 | −3.0381 |
| Year | Total | Agricultural Sector | Manufacturing Sector | Construction Sector | Transport Sector | Services Sector |
|---|---|---|---|---|---|---|
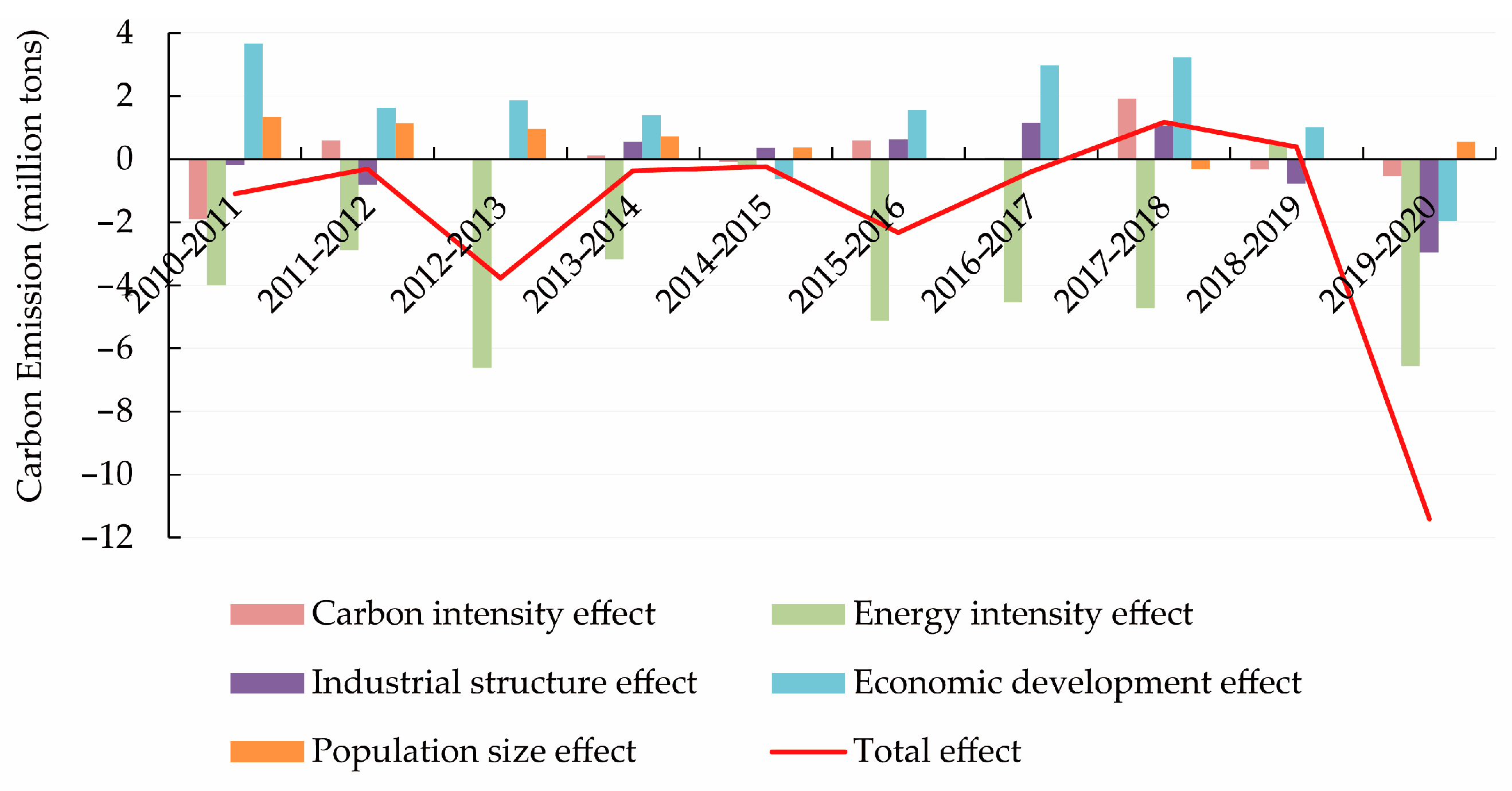
| 2010–2011 | −3.9866 | −0.1326 | −2.2607 | −0.5006 | −0.9087 | −0.1841 |
| 2011–2012 | −2.8818 | −0.1901 | −2.4889 | −0.3732 | 0.2804 | −0.1101 |
| 2012–2013 | −6.6117 | −0.1348 | −5.9625 | −0.4142 | 0.2207 | −0.3210 |
| 2013–2014 | −3.1770 | −0.1080 | −2.3464 | −0.0339 | −0.5449 | −0.1439 |
| 2014–2015 | −0.2493 | −0.0285 | −0.6582 | −0.0537 | 0.2873 | 0.2038 |
| 2015–2016 | −5.1235 | −0.1095 | −4.1827 | −0.1853 | −0.3915 | −0.2544 |
| 2016–2017 | −4.5331 | −0.1876 | −2.1919 | −0.1004 | −1.6905 | −0.3628 |
| 2017–2018 | −4.7154 | −0.1708 | −1.1599 | −0.1553 | −1.5027 | −1.7266 |
| 2018–2019 | 0.4854 | −0.0241 | 0.0848 | −0.1545 | 0.8100 | −0.2307 |
| 2019–2020 | −6.5568 | −0.0098 | −0.2858 | −0.3328 | −5.4760 | −0.4525 |
| Year | CE | EI | ||||||
|---|---|---|---|---|---|---|---|---|
| I | sd (I) | z | p | I | sd (I) | z | p | |
| 2010 | 0.2090 | 0.1290 | 2.1480 | 0.0160 | 0.0500 | 0.1220 | 0.9620 | 0.1680 |
| 2011 | 0.2090 | 0.1270 | 2.1610 | 0.0150 | 0.0870 | 0.1080 | 1.4260 | 0.0770 |
| 2012 | 0.2080 | 0.1270 | 2.1670 | 0.0150 | 0.0990 | 0.1080 | 1.5280 | 0.0630 |
| 2013 | 0.2070 | 0.1260 | 2.1700 | 0.0150 | 0.1720 | 0.1090 | 2.1920 | 0.0140 |
| 2014 | 0.2160 | 0.1280 | 2.2170 | 0.0130 | 0.1790 | 0.1100 | 2.2310 | 0.0130 |
| 2015 | 0.2220 | 0.1290 | 2.2400 | 0.0130 | 0.1790 | 0.1110 | 2.2070 | 0.0140 |
| 2016 | 0.2340 | 0.1310 | 2.2980 | 0.0110 | 0.1980 | 0.1170 | 2.2550 | 0.0120 |
| 2017 | 0.2410 | 0.1320 | 2.3350 | 0.0100 | 0.1820 | 0.1180 | 2.1100 | 0.0170 |
| 2018 | 0.2480 | 0.1330 | 2.3720 | 0.0090 | 0.1370 | 0.1170 | 1.7440 | 0.0410 |
| 2019 | 0.2390 | 0.1340 | 2.2810 | 0.0110 | 0.1380 | 0.1160 | 1.7740 | 0.0380 |
| 2020 | 0.2370 | 0.1350 | 2.2490 | 0.0120 | 0.1220 | 0.1040 | 1.8100 | 0.0350 |
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| lnEI | 0.1470 *** | 0.2346 *** | 0.0471 * | 0.1398 *** | 0.0872 *** | 0.1222 *** |
| (0.0389) | (0.0354) | (0.0280) | (0.0246) | (0.0299) | (0.0361) | |
| lnECO | −0.3885 *** | 0.0515 | −0.0019 | −0.1964 *** | −0.0518 | −0.2281 *** |
| (0.0712) | (0.0678) | (0.0575) | (0.0469) | (0.0645) | (0.0834) | |
| lnPOP | 0.0128 | 0.5597 *** | 0.2917 *** | 0.2902 *** | 0.3062 *** | 0.2540 * |
| (0.1335) | (0.1041) | (0.0948) | (0.0865) | (0.1051) | (0.1412) | |
| lnTEC | −0.0523 * | 0.0124 | −0.0730 *** | 0.0077 | −0.0655 *** | −0.0801 *** |
| (0.0267) | (0.019) | (0.0185) | (0.0174) | (0.0201) | (0.0241) | |
| lnSTR | 0.0198 | 0.1413 *** | −0.0103 | 0.0873 *** | 0.0014 | −0.0600 |
| (0.0392) | (0.032) | (0.0272) | (0.0252) | (0.0057) | (0.0435) | |
| lnOPE | 0.0074 | −0.0022 | 0.0037 | −0.0024 | −0.0189 | −0.0023 |
| (0.0075) | (0.0047) | (0.0052) | (0.0048) | (0.0298) | (0.0064) | |
| ρ | 0.7239 *** | 0.7216 *** | 0.7431 *** | 0.5847 *** | ||
| (0.0605) | (0.0552) | (0.0498) | (0.0624) | |||
| λ | 0.5233 *** | |||||
| (0.1145) | ||||||
| n | 176 | 176 | 176 | 176 | 176 | 176 |
| R2 | 0.8603 | 0.8534 | 0.8842 | 0.8536 | 0.8793 | 0.8517 |
| AIC | −394.4919 | −279.7437 | −484.4979 | −499.8542 | −452.1035 | −416.9191 |
| BIC | −372.2985 | −244.8684 | −459.1340 | −474.4903 | −426.7397 | −391.5553 |
| Short-Term | Long-Term | |||||
|---|---|---|---|---|---|---|
| Direct | Indirect | Total | Direct | Indirect | Total | |
| lnEI | 0.3416 *** | 0.9530 *** | 1.2947 *** | 0.3687 *** | 1.1909 *** | 1.5596 *** |
| (0.0619) | (0.3411) | (0.3961) | (0.0739) | (0.4890) | (0.5563) | |
| lnECO | 0.0307 | −0.2252 | −0.1945 | 0.0265 | −0.2613 | −0.2349 |
| (0.0770) | (0.3249) | (0.3728) | (0.0829) | (0.4053) | (0.4621) | |
| lnPOP | 0.7203 *** | 1.3587 * | 2.0789 ** | 0.7642 *** | 1.7477 | 2.5119 ** |
| (0.1504) | (0.7821) | (0.8993) | (0.1756) | (1.0989) | (1.2460) | |
| lnTEC | 0.0284 | 0.1450 | 0.1734 | 0.0322 | 0.1779 | 0.2101 |
| (0.0254) | (0.1238) | (0.1432) | (0.0285) | (0.1609) | (0.1840) | |
| lnSTR | 0.1618 *** | 0.1727 | 0.3344 ** | 0.1686 *** | 0.2336 | 0.4023 * |
| (0.0366) | (0.1440) | (0.1665) | (0.0399) | (0.1922) | (0.2196) | |
| lnOPE | 0.0000 | 0.0203 | 0.0203 | 0.0004 | 0.0237 | 0.0241 |
| (0.0070) | (0.0293) | (0.0349) | (0.0076) | (0.0365) | (0.0429) | |
| Moderating Effect Test | Threshold Effect Test | |||||
|---|---|---|---|---|---|---|
| lnEI | 0.1481 *** | p value | ||||
| (0.0376) | Single | 0.0867 | lnEI * I (Th < q) | 0.2152 *** | ||
| lnECO | −0.2912 *** | (0.0350) | ||||
| (0.0743) | Double | 0.1767 | lnEI * I (Th ≥ q) | 0.3003 *** | ||
| lnEI·lnECO | 0.0754 *** | (0.0354) | ||||
| (0.0218) | Triple | 0.1800 | ||||
| lnPOP | −0.1475 | lnPOP | 0.2264 * | |||
| (0.1370) | (0.1157) | |||||
| lnTEC | −0.0837 *** | Threshold | q1 | 2.7868 | lnTEC | −0.1376 *** |
| (0.0273) | (0.0194) | |||||
| lnSTR | 0.0181 | q2 | 3.3539 | lnSTR | −0.0765 ** | |
| (0.0379) | (0.0368) | |||||
| lnOPE | 0.0112 | q3 | 1.7495 | lnOPE | 0.0146 * | |
| (0.0073) | (0.0076) | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zeng, S.; Li, T.; Peng, Q.; Irfan, M. Analysing the Effect of Energy Intensity on Carbon Emission Reduction in Beijing. Int. J. Environ. Res. Public Health 2023, 20, 1379. https://doi.org/10.3390/ijerph20021379
Li G, Zeng S, Li T, Peng Q, Irfan M. Analysing the Effect of Energy Intensity on Carbon Emission Reduction in Beijing. International Journal of Environmental Research and Public Health. 2023; 20(2):1379. https://doi.org/10.3390/ijerph20021379
Chicago/Turabian StyleLi, Gen, Shihong Zeng, Tengfei Li, Qiao Peng, and Muhammad Irfan. 2023. "Analysing the Effect of Energy Intensity on Carbon Emission Reduction in Beijing" International Journal of Environmental Research and Public Health 20, no. 2: 1379. https://doi.org/10.3390/ijerph20021379
APA StyleLi, G., Zeng, S., Li, T., Peng, Q., & Irfan, M. (2023). Analysing the Effect of Energy Intensity on Carbon Emission Reduction in Beijing. International Journal of Environmental Research and Public Health, 20(2), 1379. https://doi.org/10.3390/ijerph20021379









