Quantifying Social Interventions for Combating COVID-19 via a Symmetry-Based Model
Abstract
1. Introduction
2. Mathematical Model
2.1. Symmetry Analysis
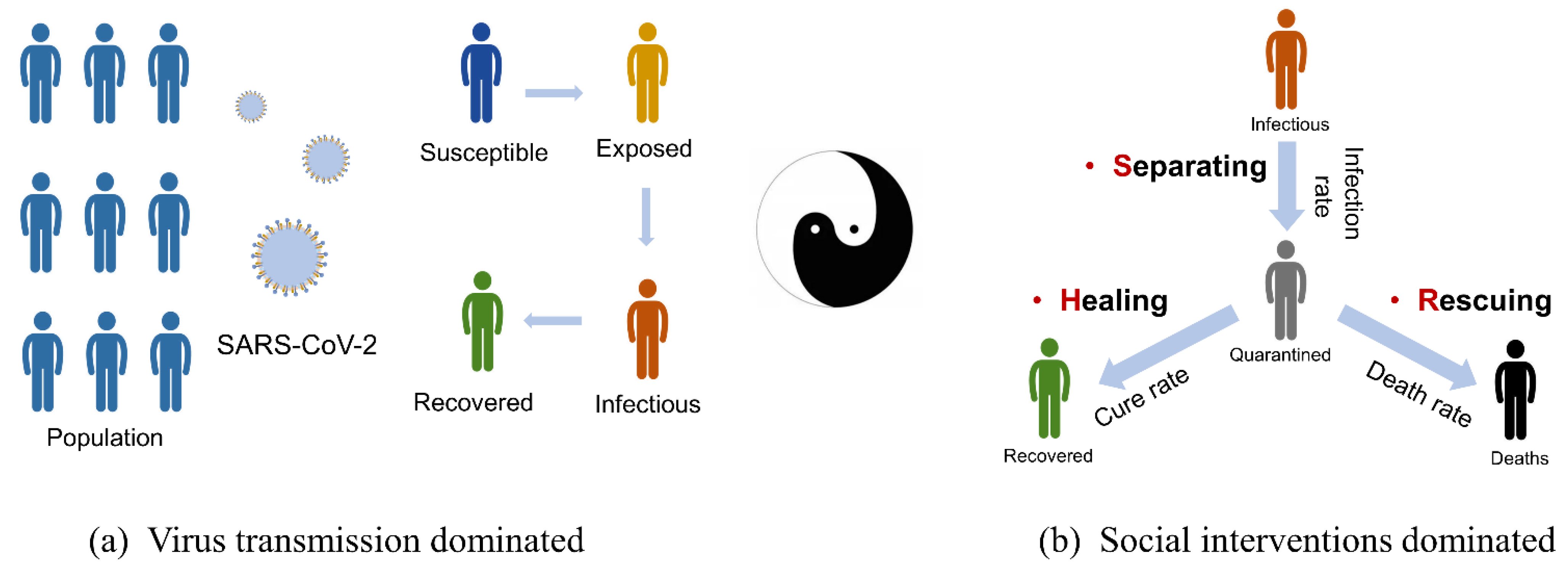
2.1.1. Virus Transmission
2.1.2. Social Interventions
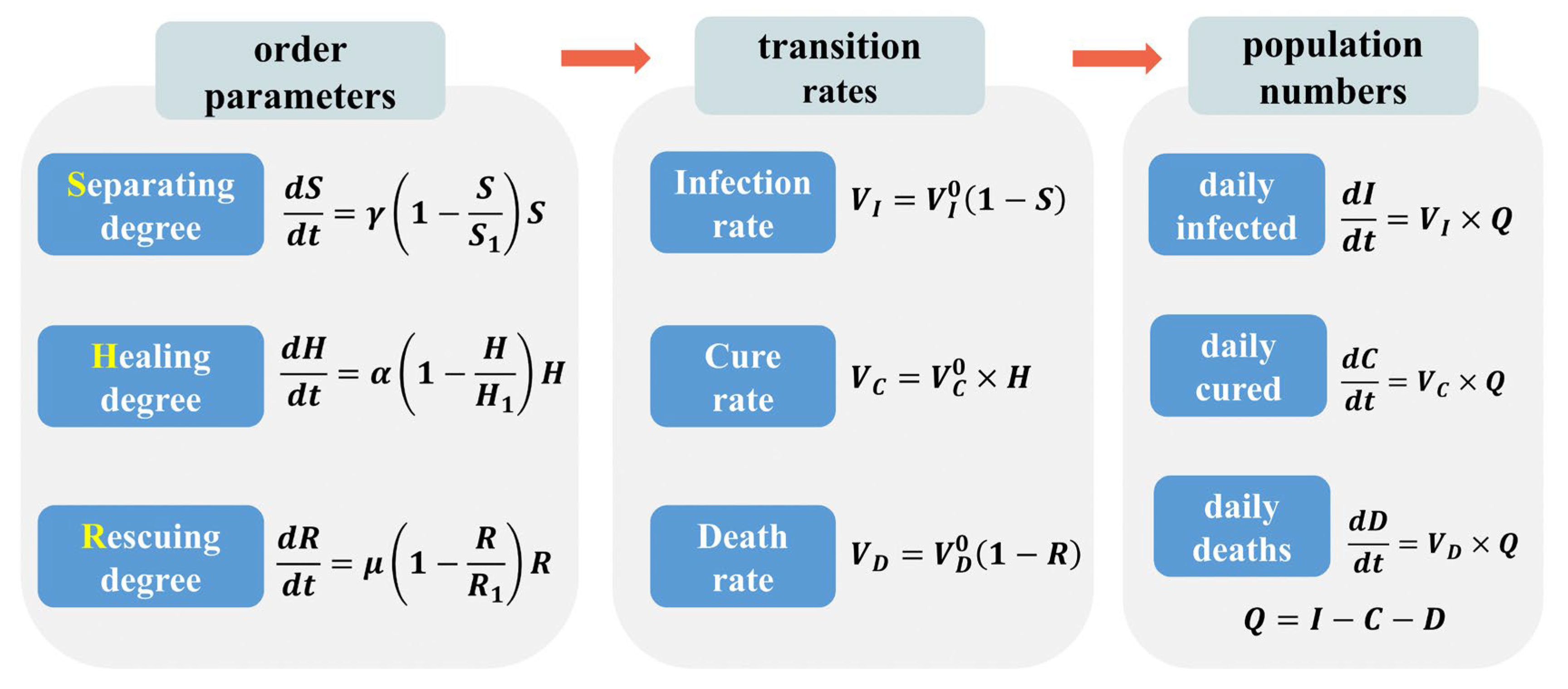
2.2. SHR Model
2.3. Analytic Solution
2.4. Parameter Determination
3. Results
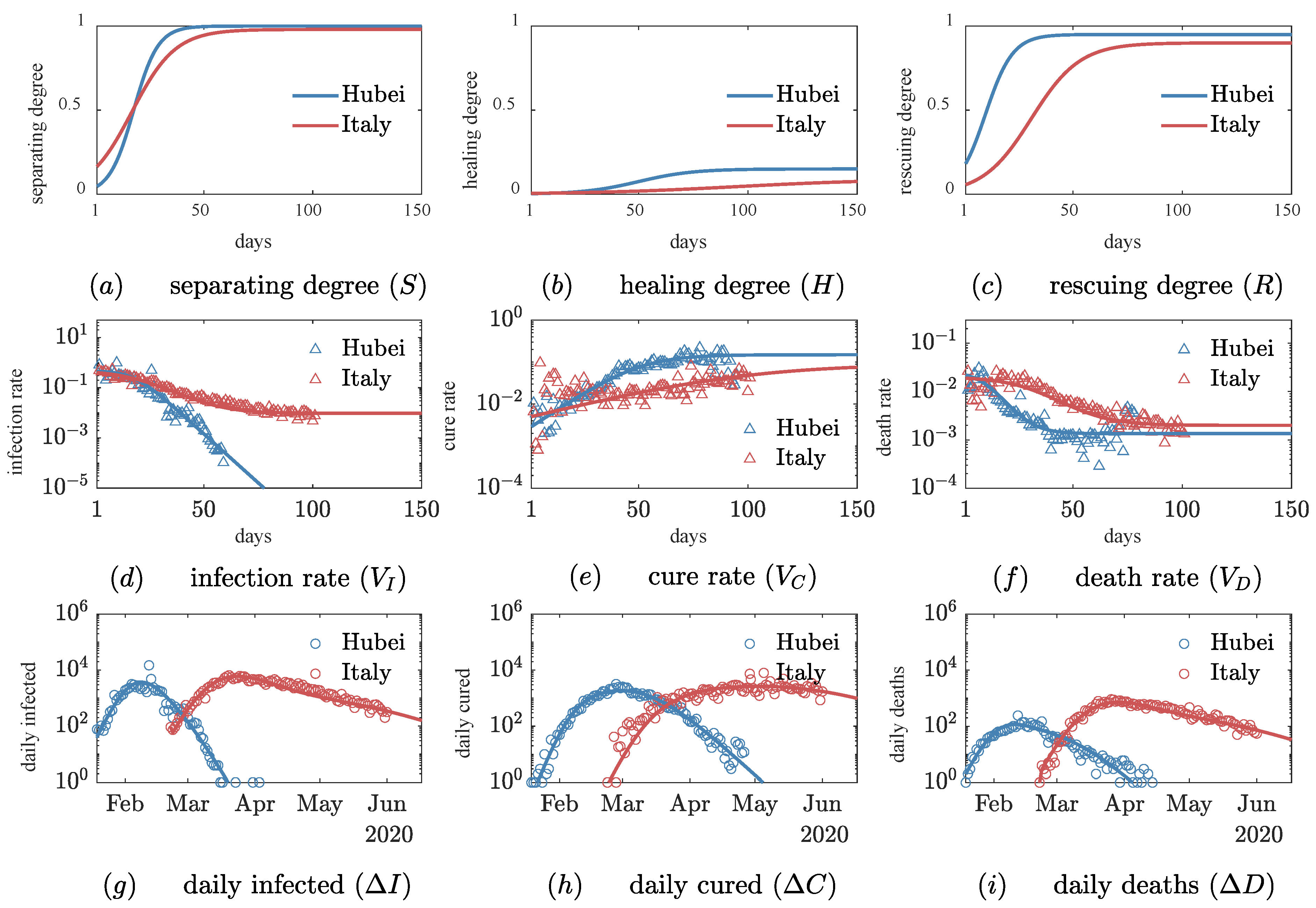
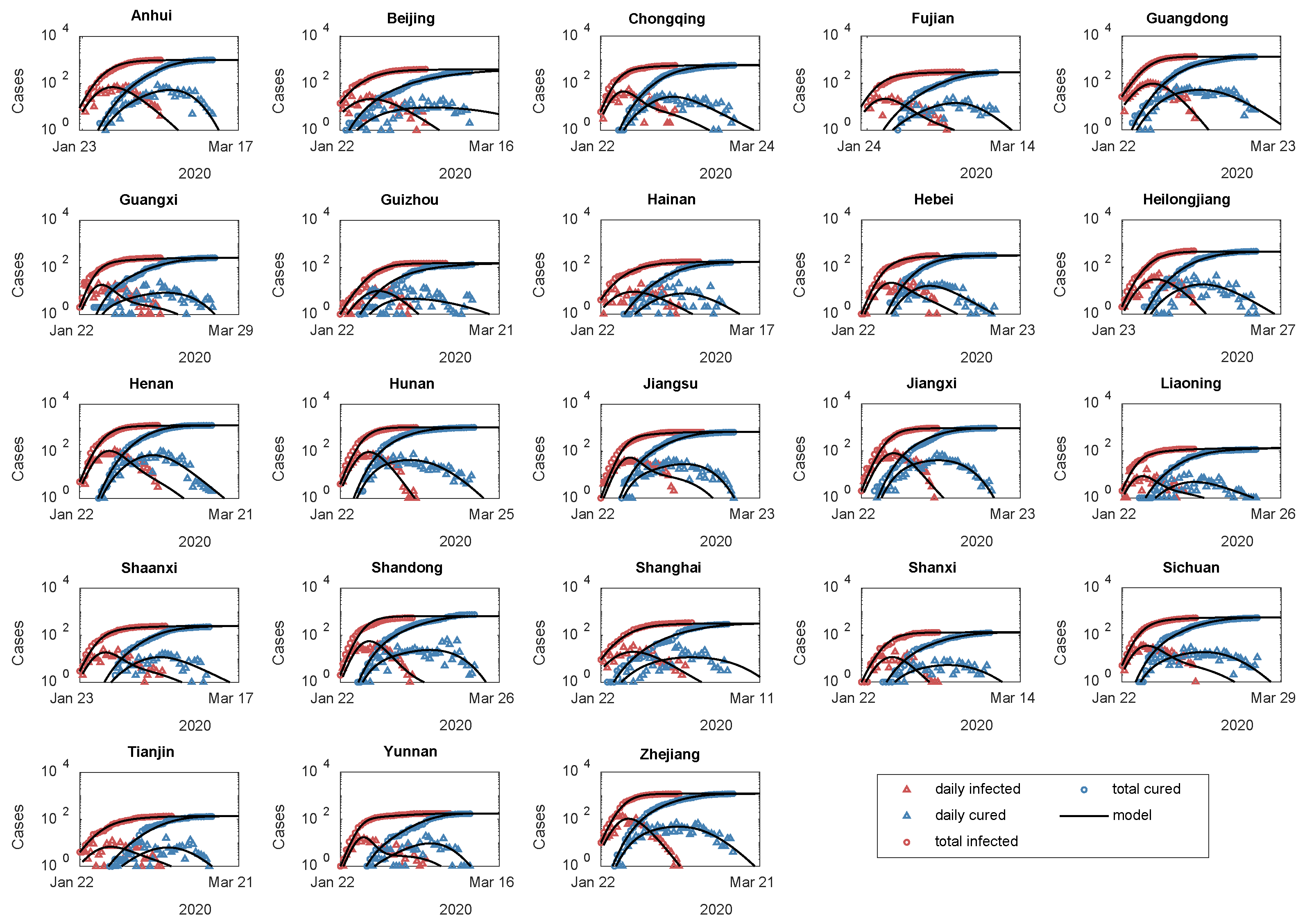
3.1. Quantitative Comparison of Social Intervention Degrees
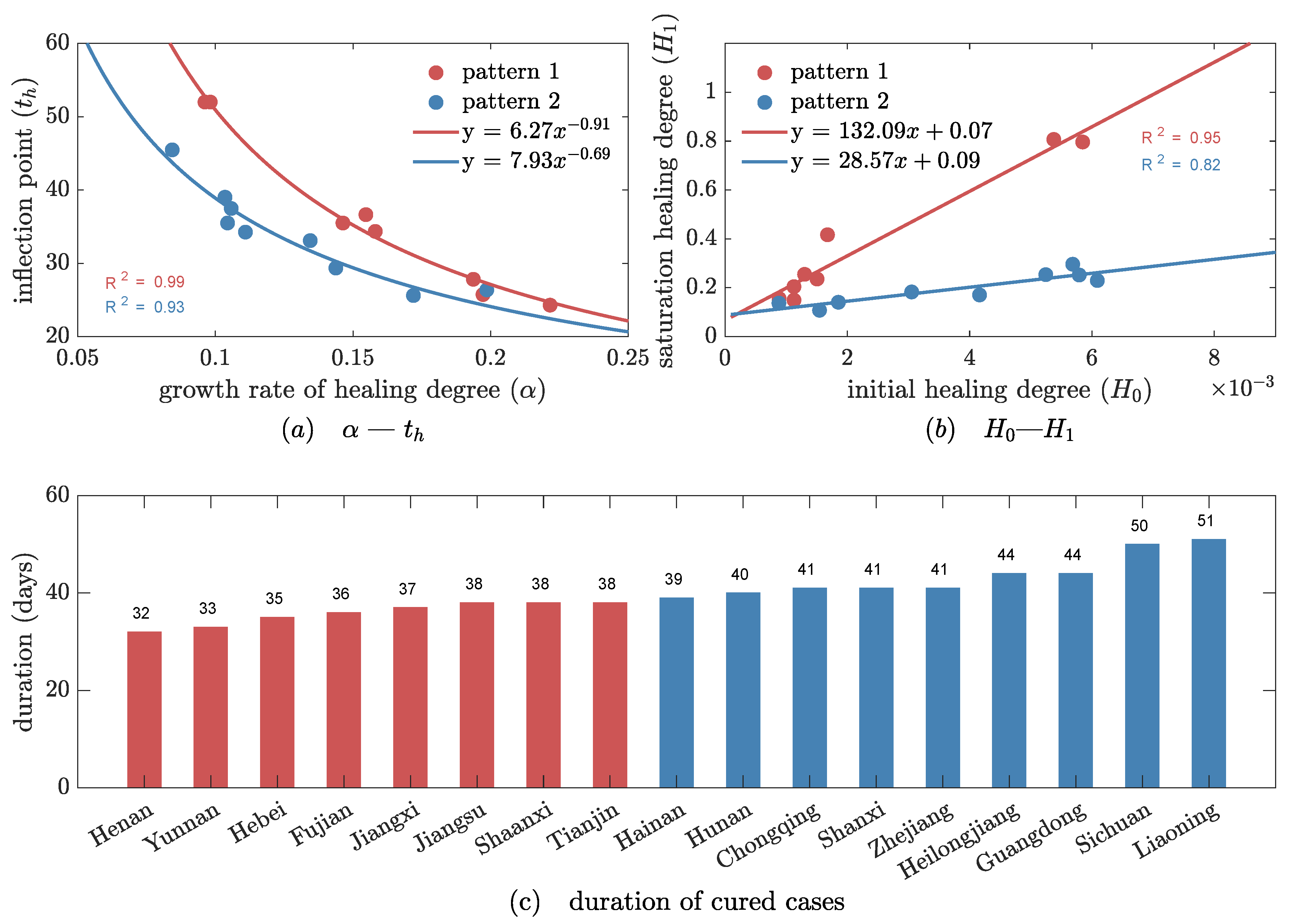
3.2. Two Evolutionary Patterns of Healing Degree in 23 Areas
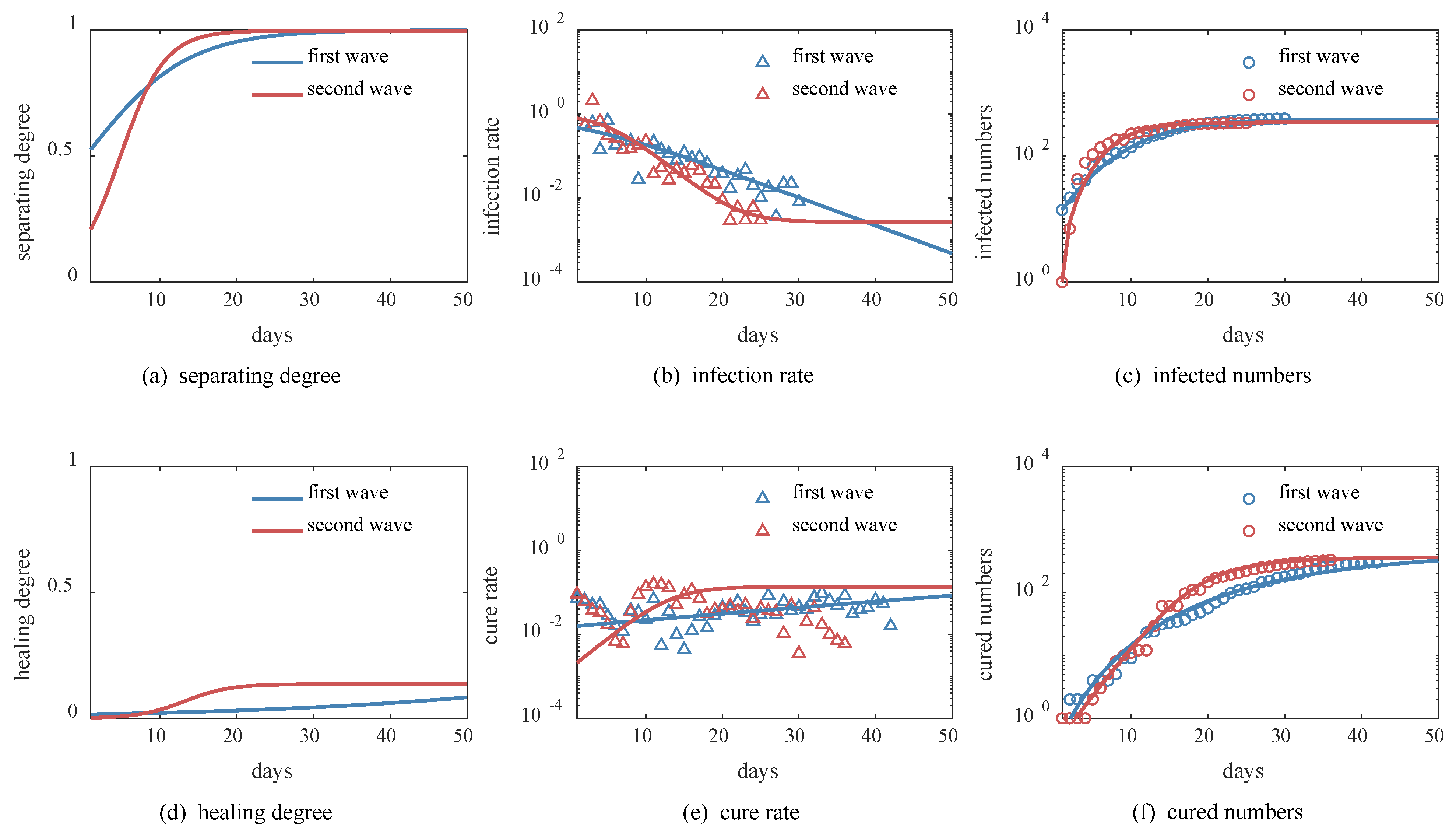
3.3. Beijing’s Successful Experiences in Two Waves
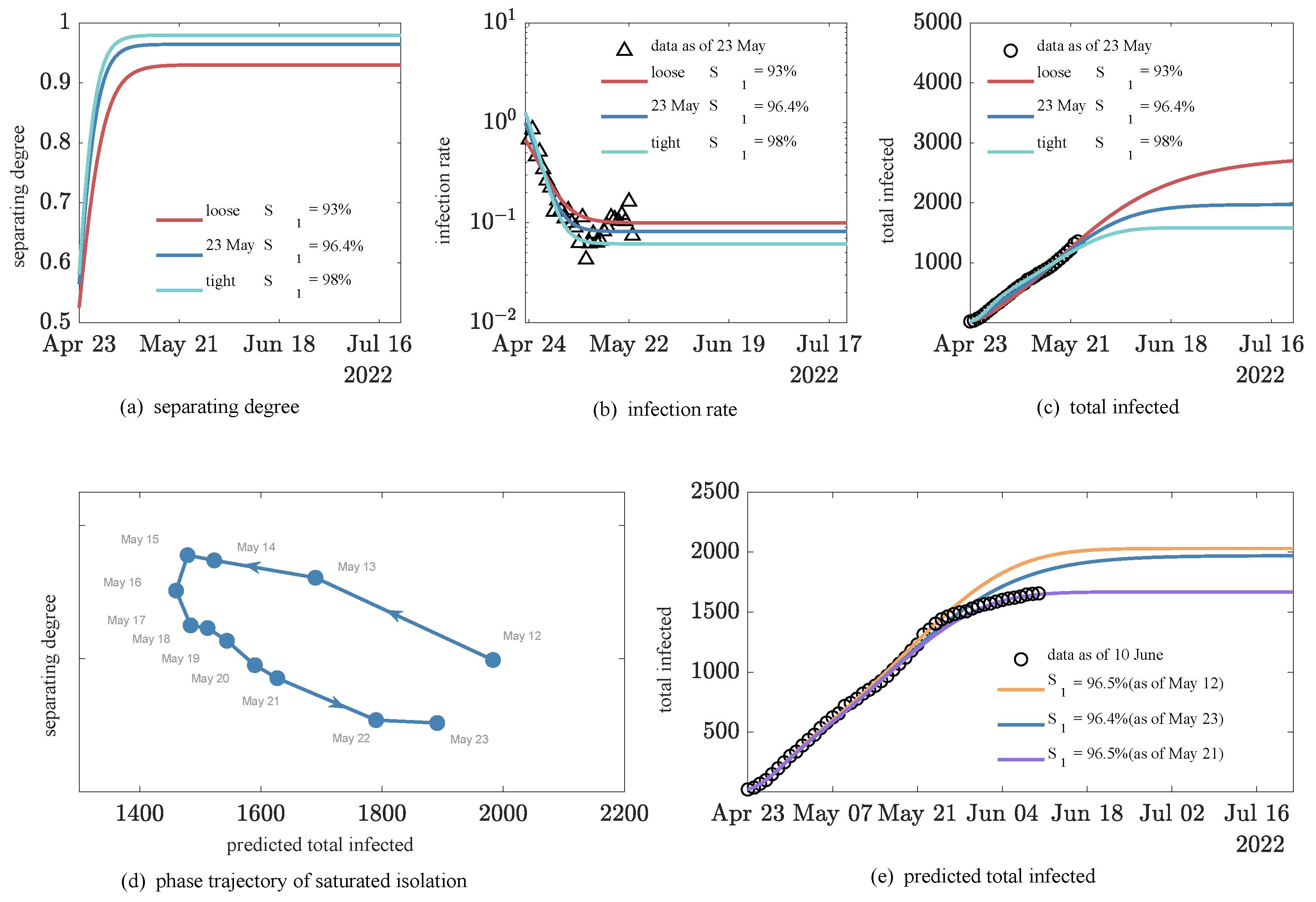
3.4. Simulation of the Impact of Dynamic Back-to-Zero Policy
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adam, D. Special report: The simulations driving the world’s response to COVID-19. Nature 2020, 580, 316–318. [Google Scholar] [CrossRef] [PubMed]
- Else, H. COVID in Papers: A Torrent of Science. Nature 2020, 588, 553. [Google Scholar] [CrossRef] [PubMed]
- Dietz, K.; Heesterbeek, J.A.P. Daniel Bernoulli’s epidemiological model revisited. Math. Biosci. 2002, 180, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; Mckendrick, A.G.A. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. A Math. Phys. Eng. Sci. 1927, 115, 700–721. [Google Scholar]
- Mahmud, A.; Lim, P.Y. Applying the SEIR Model in Forecasting The COVID-19 Trend in Malaysia: A Preliminary Study. medRxiv 2020. [Google Scholar] [CrossRef]
- Labadin, J.; Hong, B.H. Transmission Dynamics of COVID-19 in Malaysia Prior to the Movement Control Order. medRxiv 2020. [Google Scholar] [CrossRef]
- Peng, L.; Yang, W.; Zhang, D.; Zhuge, C.; Hong, L. Epidemic analysis of COVID-19 in China by dynamical modeling. medRxiv 2020. [Google Scholar] [CrossRef]
- Liu, X.; Huang, J.; Li, C.; Zhao, Y.; Wang, D.; Huang, Z.; Yang, K. The role of seasonality in the spread of COVID-19 pandemic. Environ. Res. 2021, 195, 110874. [Google Scholar] [CrossRef]
- López, L.; Rodó, X. The end of social confinement and COVID-19 re-emergence risk. Nat. Hum. Behav. 2020, 4, 746–755. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef]
- Chen, T.; Rui, J.; Wang, Q.; Zhao, Z.; Cui, J.-A.; Yin, L. A mathematical model for simulating the transmission of Wuhan novel Coronavirus. bioRxiv 2020. [Google Scholar] [CrossRef]
- Chen, Y.; Cheng, J.; Jiang, Y.; Liu, K. A time delay dynamical model for outbreak of 2019-nCoV and the parameter identification. J. Inverse Ill-Posed Probl. 2020, 28, 243–250. [Google Scholar] [CrossRef]
- Yang, Z.; Zeng, Z.; Wang, K.; Wong, S.-S.; Liang, W.; Zanin, M.; Liu, P.; Cao, X.; Gao, Z.; Mai, Z.; et al. Modified SEIR and AI prediction of the epidemics trend of COVID-19 in China under public health interventions. J. Thorac. Dis. 2020, 12, 165–174. [Google Scholar] [CrossRef] [PubMed]
- Cao, S.-L.; Feng, P.-H.; Shi, P.-P. Study on the epidemic development of COVID-19 in Hubei province by a modified SEIR model. J. Zhejiang Univ. Med. Sci. 2020, 49, 178–184. [Google Scholar]
- Tianyu, Zeng; Yunong, Zhang; Zhenyu, Li; Xiao, Liu; Qiu, B. Predictions of 2019-nCoV Transmission Ending via Comprehensive Methods. arXiv 2020, arXiv:2002.04945. [Google Scholar]
- Wang, Y.; Wang, P.; Zhang, S.; Pan, H. Uncertainty Modeling of a Modified SEIR Epidemic Model for COVID-19. Biology 2022, 11, 1157. [Google Scholar] [CrossRef] [PubMed]
- Jung, S.; Kim, J.-H.; Hwang, S.-S.; Choi, J.; Lee, W. Modified susceptible–exposed–infectious–recovered model for assessing the effectiveness of non-pharmaceutical interventions during the COVID-19 pandemic in Seoul. J. Theor. Biol. 2023, 557, 111329. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, D.; Peng, L.; Zhuge, C.; Hong, L. Rational evaluation of various epidemic models based on the COVID-19 data of China. Epidemics 2021, 37, 100501. [Google Scholar] [CrossRef]
- Tang, B.; Bragazzi, N.L.; Li, Q.; Tang, S.; Xiao, Y.; Wu, J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov). Infect. Dis. Model. 2020, 5, 248–255. [Google Scholar] [CrossRef]
- Godio, A.; Pace, F.; Vergnano, A. SEIR Modeling of the Italian Epidemic of SARS-CoV-2 Using Computational Swarm Intelligence. Int. J. Environ. Res. Public Health 2020, 17, 3535. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, X.; Liu, F.; Zhu, G.; Wang, L. Prediction of the COVID-19 spread in African countries and implications for prevention and control: A case study in South Africa, Egypt, Algeria, Nigeria, Senegal and Kenya. Sci. Total Environ. 2020, 729, 138959. [Google Scholar] [CrossRef]
- Olivier, L.E.; Craig, I.K. An epidemiological model for the spread of COVID-19: A South African case study. arXiv 2020, arXiv:2005.08012. [Google Scholar]
- Mangoni, L.; Pistilli, M. Epidemic Analysis of COVID-19 in Italy by Dynamical Modelling; Social Science Electronic Publishing: Rochester, NY, USA, 2020. [Google Scholar]
- Cheynet, E. Generalized SEIR Epidemic Model (Fitting and Computation). Available online: https://zenodo.org/record/3911854#collapseCitations (accessed on 25 March 2022).
- Li, W.; Gong, J.; Zhou, J.; Fan, H.; Qin, C.; Gong, Y.; Hu, W.B. The Analysis of Patterns of Two COVID-19 Outbreak Clusters in China. Int. J. Environ. Res. Public Health 2022, 19, 4876. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Xie, R.; Dong, X.; Li, J.; Peng, P.; Dr Santibanez Gonzalez, E. SEIR-FMi: A coronavirus disease epidemiological model based on intra-city movement, inter-city movement and medical resource investment. Comput. Biol. Med. 2022, 149, 106046. [Google Scholar] [CrossRef] [PubMed]
- Hatami, F.; Chen, S.; Paul, R.; Thill, J.-C. Simulating and Forecasting the COVID-19 Spread in a U.S. Metropolitan Region with a Spatial SEIR Model. Int. J. Environ. Res. Public Health 2022, 19, 15771. [Google Scholar] [CrossRef]
- Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.; Cuomo-Dannenburg, G.; et al. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College London: London, UK, 2020; pp. 1–20. [Google Scholar]
- Read, J.M.; Bridgen, J.R.E.; Cummings, D.A.T.; Ho, A.; Jewell, C.P. Novel coronavirus 2019-nCoV (COVID-19): Early estimation of epidemiological parameters and epidemic size estimates. Philos. Trans. R. Soc. B Biol. Sci. 2021, 376, 20200265. [Google Scholar] [CrossRef]
- Wu, J.T.; Leung, K.; Leung, G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: A modelling study. Lancet 2020, 395, 689–697. [Google Scholar] [CrossRef]
- Landau, L.D. On the theory of phase transitions. Zh.Eksp.Teor.Fiz. 1937, 7, 19–32. [Google Scholar] [CrossRef]
- Zhang, L.; She, Y.-R.; She, G.-H.; Li, R.; She, Z.-S. The cross-scale correlations between individuals and nations in COVID-19 mortality. Sci. Rep. 2022, 12, 13895. [Google Scholar] [CrossRef]
- She, Z.-S.; Chen, X.; Hussain, F. Quantifying wall turbulence via a symmetry approach: A Lie group theory. J. Fluid Mech. 2017, 827, 322–356. [Google Scholar] [CrossRef]
- Chen, X.; Hussain, F.; She, Z.-S. Quantifying wall turbulence via a symmetry approach. Part 2. Reynolds stresses. J. Fluid Mech. 2018, 850, 401–438. [Google Scholar] [CrossRef]
- Li, R.; She, Z.-S. Unified energy law for fluctuating density wave orders in cuprate pseudogap phase. Commun. Phys. 2022, 5, 13. [Google Scholar] [CrossRef]
- Gu, Q. Mathematical Methods for Physics; Science Press: Beijing, China, 2012. [Google Scholar]
- Pelinovsky, E.; Kurkin, A.; Kurkina, O.; Kokoulina, M.; Epifanova, A. Logistic equation and COVID-19. Chaos Solitons Fractals 2020, 140, 110241. [Google Scholar] [CrossRef]
- Consolini, G.; Materassi, M. A stretched logistic equation for pandemic spreading. Chaos Solitons Fractals 2020, 140, 110113. [Google Scholar] [CrossRef] [PubMed]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Health Commission of Hubei Province. Preventing and Controlling SARS-CoV-2 Pneumonia Outbreaks. Available online: https://wjw.hubei.gov.cn/ (accessed on 1 October 2020).
| Order Parameters | Model Parameters | Hubei | Italy | |
|---|---|---|---|---|
| Separating degree () | Initial infection rate | 0.48 ± 0.01 | 0.48 ± 0.02 | |
| Growth rate of separating degree | 0.18 ± 0.02 | 0.10 ± 0.02 | ||
| Saturation value of separating degree | 1.00 ± 0.00 | 0.98 ± 0.01 | ||
| Time up to midpoint of | 17.8 ± 0.4 | 17.0 ± 1.0 | ||
| Healing degree () | Growth rate of healing degree | 0.08 ± 0.01 | 0.03 ± 0.01 | |
| Saturation value of healing degree | 0.15 ± 0.01 | 0.09 ± 0.04 | ||
| Time up to midpoint of | 50 ± 2 | 96 ± 20 | ||
| Rescuing degree () | Initial death rate | 0.03 ± 0.01 | 0.03 ± 0.01 | |
| Growth rate of rescuing degree | 0.16 ± 0.06 | 0.09 ± 0.03 | ||
| Saturation value of rescuing degree | 0.95 ± 0.02 | 0.80 ± 0.10 | ||
| Time up to midpoint of | 9 ± 5 | 32 ± 18 | ||
| Infected | Duration | ||||
|---|---|---|---|---|---|
| 0.27 ± 0.09 | 6.5 ± 2.7 | 0.12 ± 0.05 | 43.4 ± 18.9 | 528 ± 395 | 27 ± 5 |
| Wave | Infected | Duration | |||
|---|---|---|---|---|---|
| First | 0.15 | 53% | 0.04 | 395 | 30 |
| Second | 0.35 | 21% | 0.34 | 335 | 25 |
| Infected | |||||
|---|---|---|---|---|---|
| 0.33 ± 0.01 | 56.2% ± 0.1% | 96.5% ± 0.1% | 0.071 ± 0.005 | 1.8% ± 0.1% | 1631 ± 166 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; She, G.-H.; She, Y.-R.; Li, R.; She, Z.-S. Quantifying Social Interventions for Combating COVID-19 via a Symmetry-Based Model. Int. J. Environ. Res. Public Health 2023, 20, 476. https://doi.org/10.3390/ijerph20010476
Zhang L, She G-H, She Y-R, Li R, She Z-S. Quantifying Social Interventions for Combating COVID-19 via a Symmetry-Based Model. International Journal of Environmental Research and Public Health. 2023; 20(1):476. https://doi.org/10.3390/ijerph20010476
Chicago/Turabian StyleZhang, Lei, Guang-Hui She, Yu-Rong She, Rong Li, and Zhen-Su She. 2023. "Quantifying Social Interventions for Combating COVID-19 via a Symmetry-Based Model" International Journal of Environmental Research and Public Health 20, no. 1: 476. https://doi.org/10.3390/ijerph20010476
APA StyleZhang, L., She, G.-H., She, Y.-R., Li, R., & She, Z.-S. (2023). Quantifying Social Interventions for Combating COVID-19 via a Symmetry-Based Model. International Journal of Environmental Research and Public Health, 20(1), 476. https://doi.org/10.3390/ijerph20010476






