Suburban Road Networks to Explore COVID-19 Vulnerability and Severity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Source
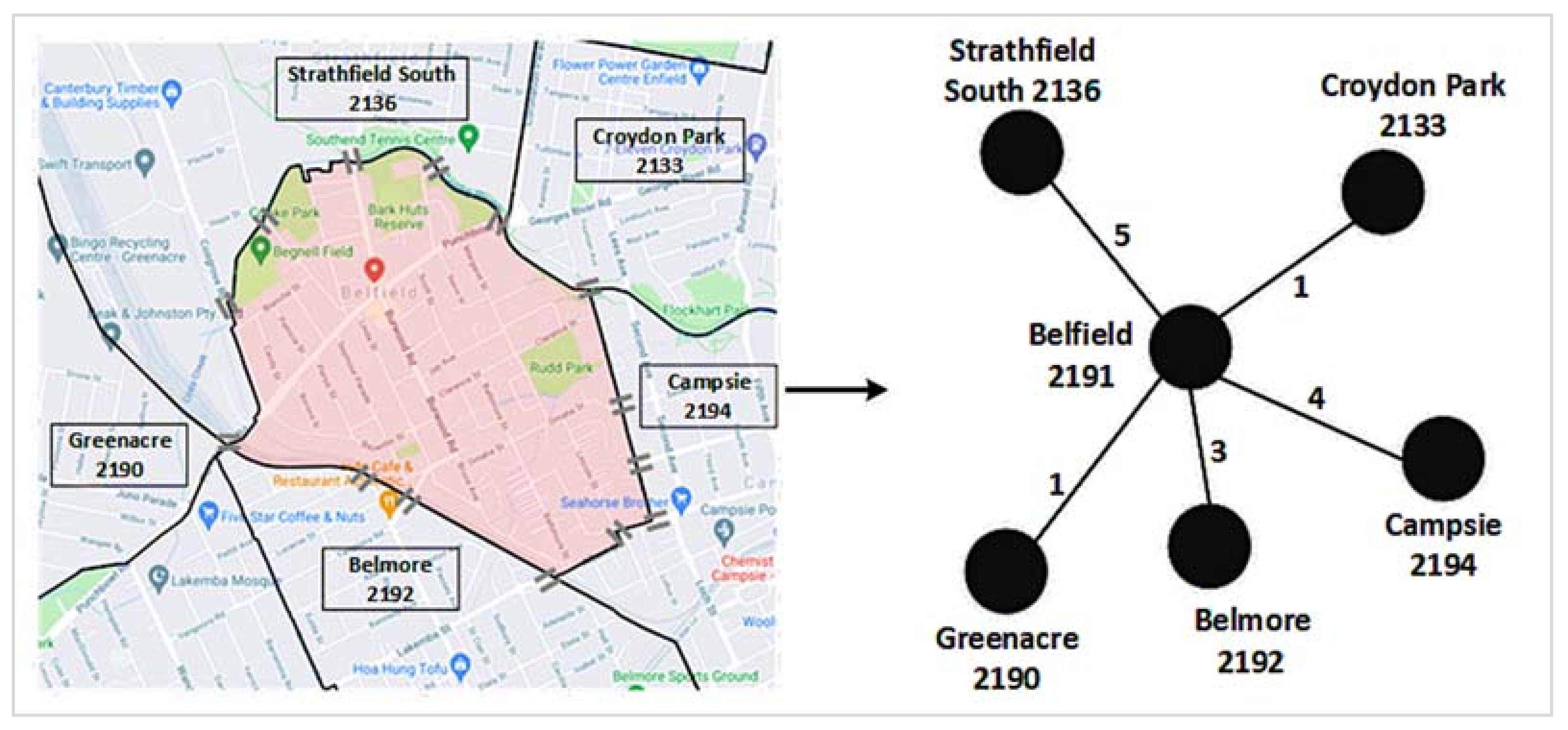
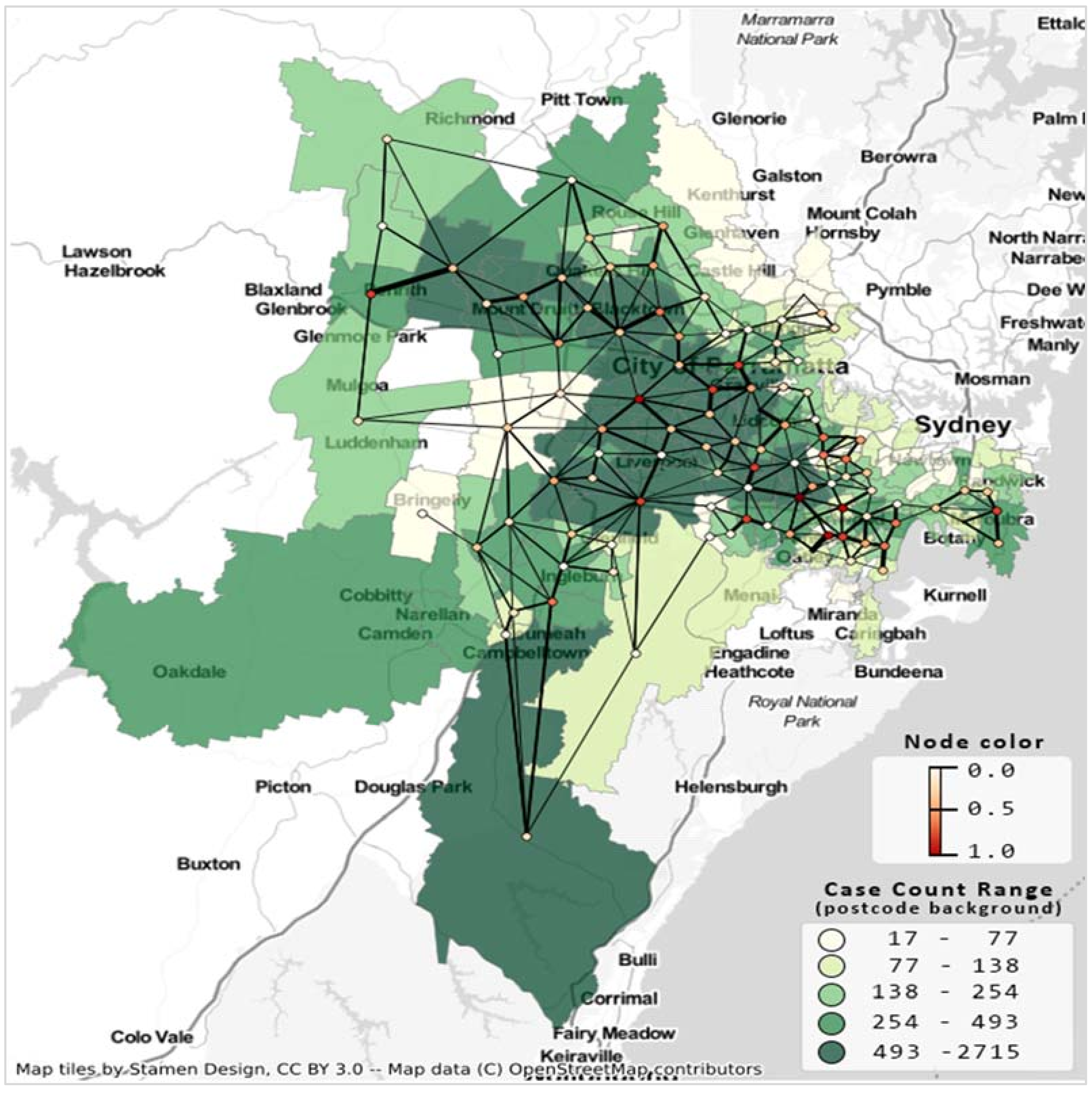
2.2. Suburban Road Network: Construction and Analysis
2.3. COVID-19 Vulnerability and Severity
3. Results
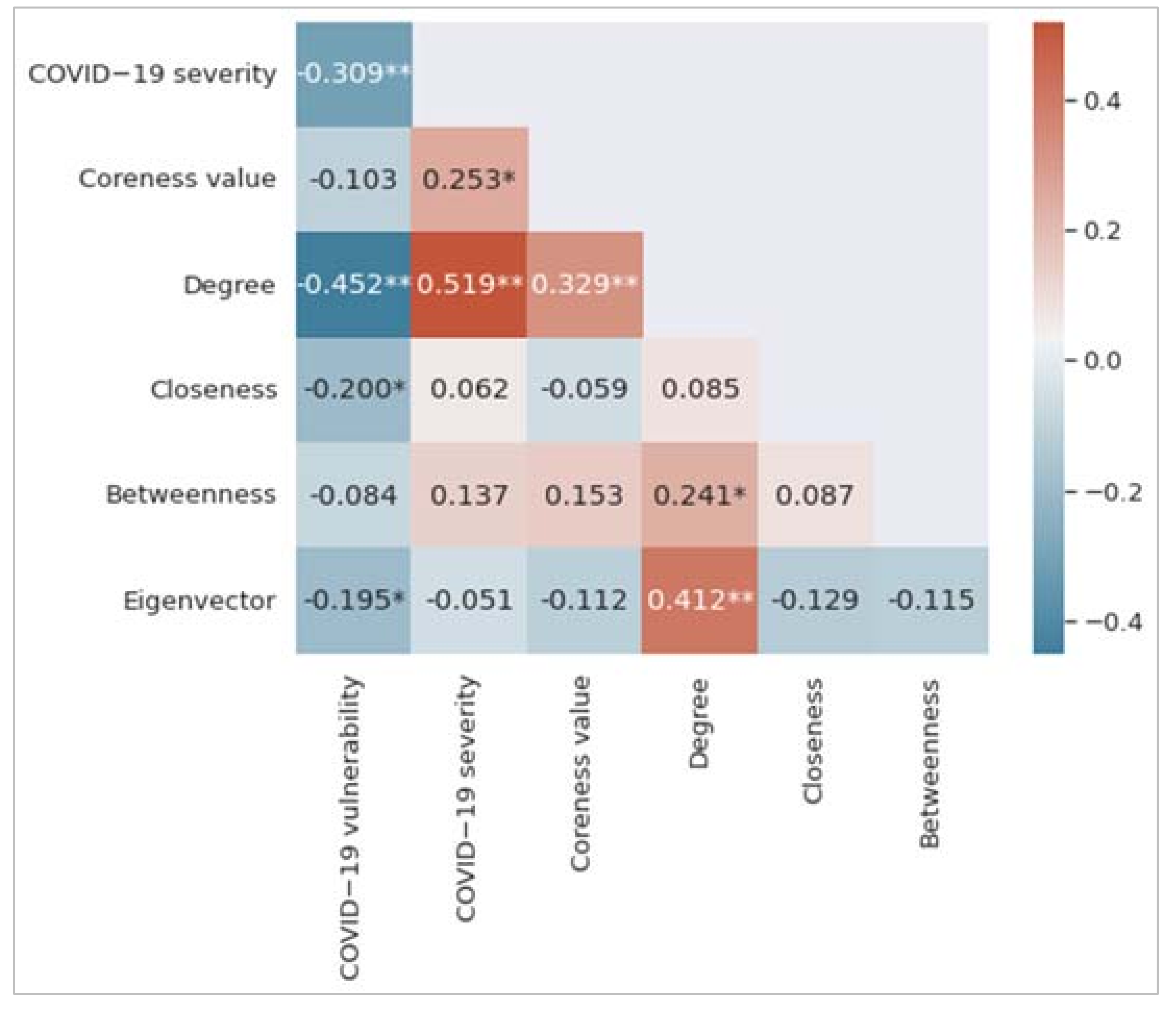
3.1. Correlation Results
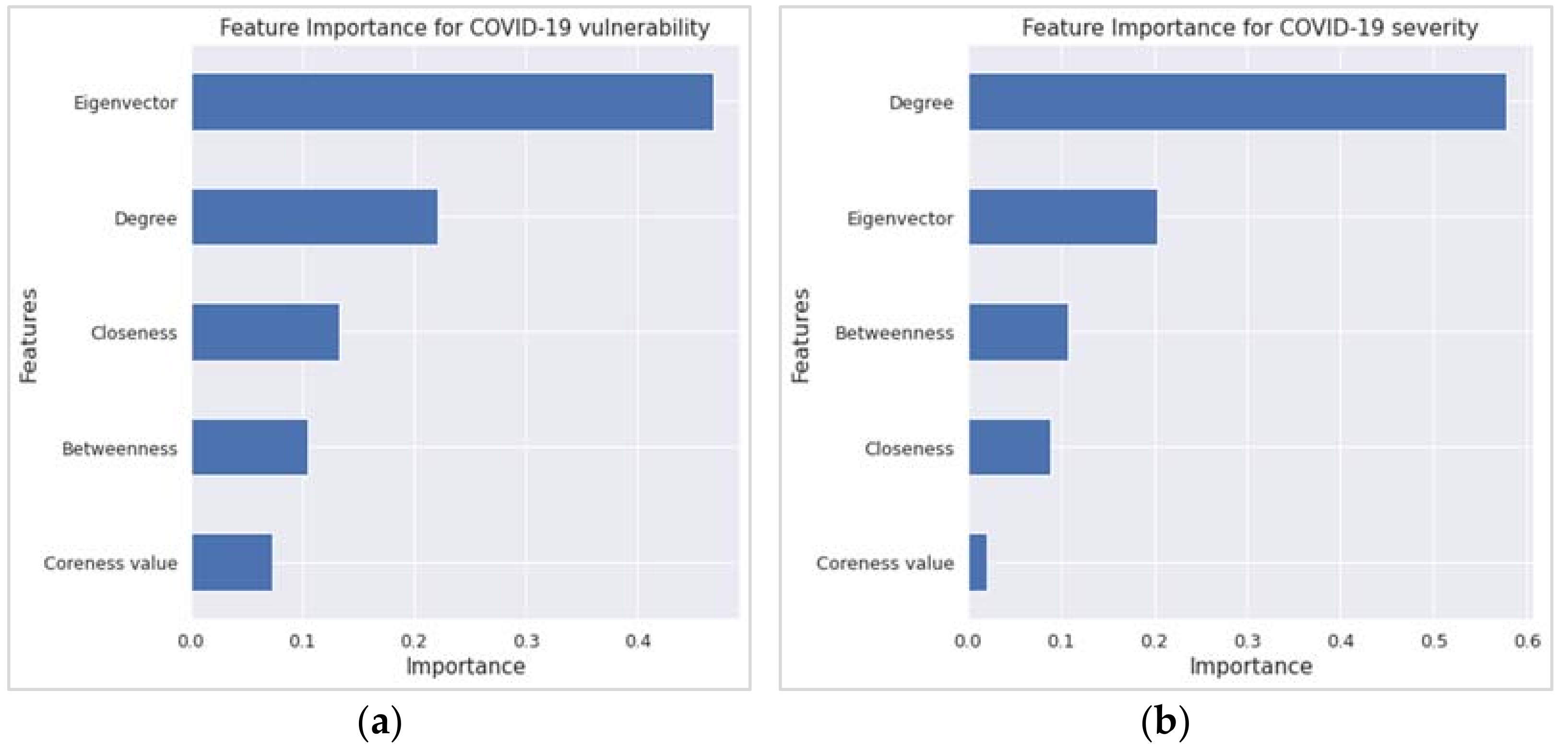
3.2. Regression Results
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Smith, J.A.; Judd, J. COVID-19: Vulnerability and the power of privilege in a pandemic. Health Promot. J. Aust. 2020, 31, 158. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Data. NSW. Available online: https://data.nsw.gov.au (accessed on 4 February 2022).
- Zhou, P.; Yang, X.-L.; Wang, X.-G.; Hu, B.; Zhang, L.; Zhang, W.; Si, H.-R.; Zhu, Y.; Li, B.; Huang, C.-L.; et al. A pneumonia outbreak associated with a new coronavirus of probable bat origin. Nature 2020, 579, 270–273. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mehra, M.R.; Desai, S.S.; Kuy, S.; Henry, T.D.; Patel, A.N. Cardiovascular disease, drug therapy, and mortality in COVID-19. N. Engl. J. Med. 2020, 382, 102. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Karakiulakis, G.; Roth, M. Are patients with hypertension and diabetes mellitus at increased risk for COVID-19 infection? Lancet Respir. Med. 2020, 8, 21. [Google Scholar] [CrossRef]
- Plough, A.; Bristow, B.; Fielding, J.; Caldwell, S.; Khan, S. Pandemics and health equity: Lessons learned from the H1N1 response in Los Angeles County. J. Public Health Manag. Pract. 2011, 17, 20–27. [Google Scholar] [CrossRef]
- Lagarde, M.; Palmer, N. The impact of user fees on access to health services in low-and middle-income countries. Cochrane Database Syst. Rev. 2011, 4, 1–60. [Google Scholar] [CrossRef] [Green Version]
- Adebayo, E.F.; Uthman, O.A.; Wiysonge, C.S.; Stern, E.A.; Lamont, K.T.; Ataguba, J.E. A systematic review of factors that affect uptake of community-based health insurance in low-income and middle-income countries. BMC Health Serv. Res. 2015, 15, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Currie, G.; Delbosc, A. Exploring public transport usage trends in an ageing population. Transportation 2010, 37, 151–164. [Google Scholar] [CrossRef]
- Bezyak, J.L.; Sabella, S.A.; Gattis, R.H. Public transportation: An investigation of barriers for people with disabilities. J. Disabil. Policy Stud. 2017, 28, 52–60. [Google Scholar] [CrossRef]
- Kayman, H.; Ablorh-Odjidja, A. Revisiting public health preparedness: Incorporating social justice principles into pandemic preparedness planning for influenza. J. Public Health Manag. Pract. 2006, 12, 373–380. [Google Scholar] [CrossRef]
- Hutchins, S.S.; Fiscella, K.; Levine, R.S.; Ompad, D.; McDonald, M. Protection of racial/ethnic minority populations during an influenza pandemic. Am. J. Public Health 2009, 99, S261–S270. [Google Scholar] [CrossRef] [PubMed]
- Brooks, S.K.; Webster, R.K.; Smith, L.E.; Woodland, L.; Wessely, S.; Greenberg, N.; Rubin, G.J. The psychological impact of quarantine and how to reduce it: Rapid review of the evidence. Lancet 2020, 395, 912–920. [Google Scholar] [CrossRef] [Green Version]
- Huremović, D. Psychiatry of Pandemics: A Mental Health Response to Infection Outbreak; Springer: New York, NY, USA, 2019. [Google Scholar]
- Tiwari, A.; Dadhania, A.V.; Ragunathrao, V.A.B.; Oliveira, E.R. Using machine learning to develop a novel COVID-19 vulnerability index (C19VI). Sci. Total Environ. 2021, 773, 145650. [Google Scholar] [CrossRef] [PubMed]
- Tuli, S.; Tuli, S.; Tuli, R.; Gill, S.S. Predicting the growth and trend of COVID-19 pandemic using machine learning and cloud computing. Internet Things 2020, 11, 100222. [Google Scholar] [CrossRef]
- Prout, T.A.; Zilcha-Mano, S.; Doorn, K.A.-V.; Békés, V.; Christman-Cohen, I.; Whistler, K.; Kui, T.; Di Giuseppe, M. Identifying predictors of psychological distress during COVID-19: A machine learning approach. Front. Psychol. 2020, 11, 3063. [Google Scholar] [CrossRef]
- Hernandez-Matamoros, A.; Fujita, H.; Hayashi, T.; Perez-Meana, H. Forecasting of COVID-19 per regions using ARIMA models and polynomial functions. Appl. Soft Comput. 2020, 96, 106610. [Google Scholar] [CrossRef]
- Swaraj, A.; Verma, K.; Kaur, A.; Singh, G.; Kumar, A.; de Sales, L.M. Implementation of stacking based ARIMA model for prediction of COVID-19 cases in India. J. Biomed. Inform. 2021, 121, 103887. [Google Scholar] [CrossRef]
- Hssayeni, M.D.; Chala, A.; Dev, R.; Xu, L.; Shaw, J.; Furht, B.; Ghoraani, B. The forecast of COVID-19 spread risk at the county level. J. Big Data 2021, 8, 99. [Google Scholar] [CrossRef]
- Kim, M.; Kang, J.; Kim, D.; Song, H.; Min, H.; Nam, Y.; Park, D.; Lee, J.G. Hi-COVIDNet: Deep learning approach to predict inbound COVID-19 patients and case study in South Korea. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual, 6–10 July 2020. [Google Scholar]
- Badr, H.S.; Du, H.; Marshall, M.; Dong, E.; Squire, M.M.; Gardner, L.M. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1247–1254. [Google Scholar] [CrossRef]
- Chang, S.; Pierson, E.; Koh, P.W.; Gerardin, J.; Redbird, B.; Grusky, D.; Leskovec, J. Mobility network models of COVID-19 explain inequities and inform reopening. Nature 2021, 589, 82–87. [Google Scholar] [CrossRef]
- Block, P.; Hoffman, M.; Raabe, I.J.; Dowd, J.B.; Rahal, C.; Kashyap, R.; Mills, M.C. Social network-based distancing strategies to flatten the COVID-19 curve in a post-lockdown world. Nat. Hum. Behav. 2020, 4, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Hou, X.; Gao, S.; Li, Q.; Kang, Y.; Chen, N.; Chen, K.; Rao, J.; Ellenberg, J.S.; Patz, J.A. Intracounty modeling of COVID-19 infection with human mobility: Assessing spatial heterogeneity with business traffic, age, and race. Proc. Natl. Acad. Sci. USA 2021, 118, 24. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Yang, S.; Yang, H. Statistical analysis of spatial network characteristics in relation to COVID-19 transmission risks in US counties. In Proceedings of the 43rd Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Guadalajara, Mexico, 26–30 July 2021. [Google Scholar]
- Lu, J.; Lin, A.; Jiang, C.; Zhang, A.; Yang, Z. Influence of transportation network on transmission heterogeneity of COVID-19 in China. Transp. Res. Part C Emerg. Technol. 2021, 129, 103231. [Google Scholar] [CrossRef]
- COVID-19 Data and Statistics. Available online: https://www.nsw.gov.au/covid-19/stay-safe/data-and-statistics (accessed on 4 February 2022).
- Australian Bureau of Statistics: 2016 Census QuickStats. Available online: https://quickstats.censusdata.abs.gov.au/census_services/getproduct/census/2016/quickstat/POA2190?opendocument (accessed on 4 February 2022).
- Wasserman, S.; Faust, K. Social Network Analysis: Methods and Applications; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Conger, A.J. A revised definition for suppressor variables: A guide to their identification and interpretation. Educ. Psychol. Meas. 1974, 34, 35–46. [Google Scholar] [CrossRef]
- ABC News. What’s Within 10 km of Your Sydney Home? Here’s Where You Can and Can’t Go Under New COVID Restrictions for Parts of NSW. 2021. Available online: https://www.abc.net.au/news/2021-07-09/sydney-lockdown-covid-10-km-calculator/100281718 (accessed on 4 February 2022).
| Coefficient | t-Value | p-Value | |
|---|---|---|---|
| Constant | 41.468 | 13.80 | 0.000 |
| Coreness | 4.579 | 0.279 | 0.781 |
| Degree | −3175.511 | −4.380 | 0.000 |
| Closeness | −8667.510 | −2.054 | 0.042 |
| Betweenness | 22.737 | 0.360 | 0.720 |
| Eigenvector | −3.761 | −0.296 | 0.768 |
| Coefficient | t-Value | p-Value | |
|---|---|---|---|
| Constant | −80.131 | −0.97 | 0.334 |
| Coreness | −0.098 | 0.000 | 1.000 |
| Degree | 1.46 × 105 | 7.342 | 0.000 |
| Closeness | −5.25× 104 | −0.452 | 0.652 |
| Betweenness | −1423.047 | −0.819 | 0.415 |
| Eigenvector | −1379.437 | −3.944 | 0.000 |
| Multiple Linear Regression | Random Forest Regression | |
|---|---|---|
| COVID-19 vulnerability | 23.30% | 82.44% |
| COVID-19 severity | 35.80% | 91.51% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Uddin, S.; Khan, A.; Lu, H.; Zhou, F.; Karim, S. Suburban Road Networks to Explore COVID-19 Vulnerability and Severity. Int. J. Environ. Res. Public Health 2022, 19, 2039. https://doi.org/10.3390/ijerph19042039
Uddin S, Khan A, Lu H, Zhou F, Karim S. Suburban Road Networks to Explore COVID-19 Vulnerability and Severity. International Journal of Environmental Research and Public Health. 2022; 19(4):2039. https://doi.org/10.3390/ijerph19042039
Chicago/Turabian StyleUddin, Shahadat, Arif Khan, Haohui Lu, Fangyu Zhou, and Shakir Karim. 2022. "Suburban Road Networks to Explore COVID-19 Vulnerability and Severity" International Journal of Environmental Research and Public Health 19, no. 4: 2039. https://doi.org/10.3390/ijerph19042039
APA StyleUddin, S., Khan, A., Lu, H., Zhou, F., & Karim, S. (2022). Suburban Road Networks to Explore COVID-19 Vulnerability and Severity. International Journal of Environmental Research and Public Health, 19(4), 2039. https://doi.org/10.3390/ijerph19042039








