Assessment of the Best FEA Failure Criteria (Part II): Investigation of the Biomechanical Behavior of Dental Pulp and Apical-Neuro-Vascular Bundle in Intact and Reduced Periodontium
Abstract
1. Introduction
2. Materials and Methods
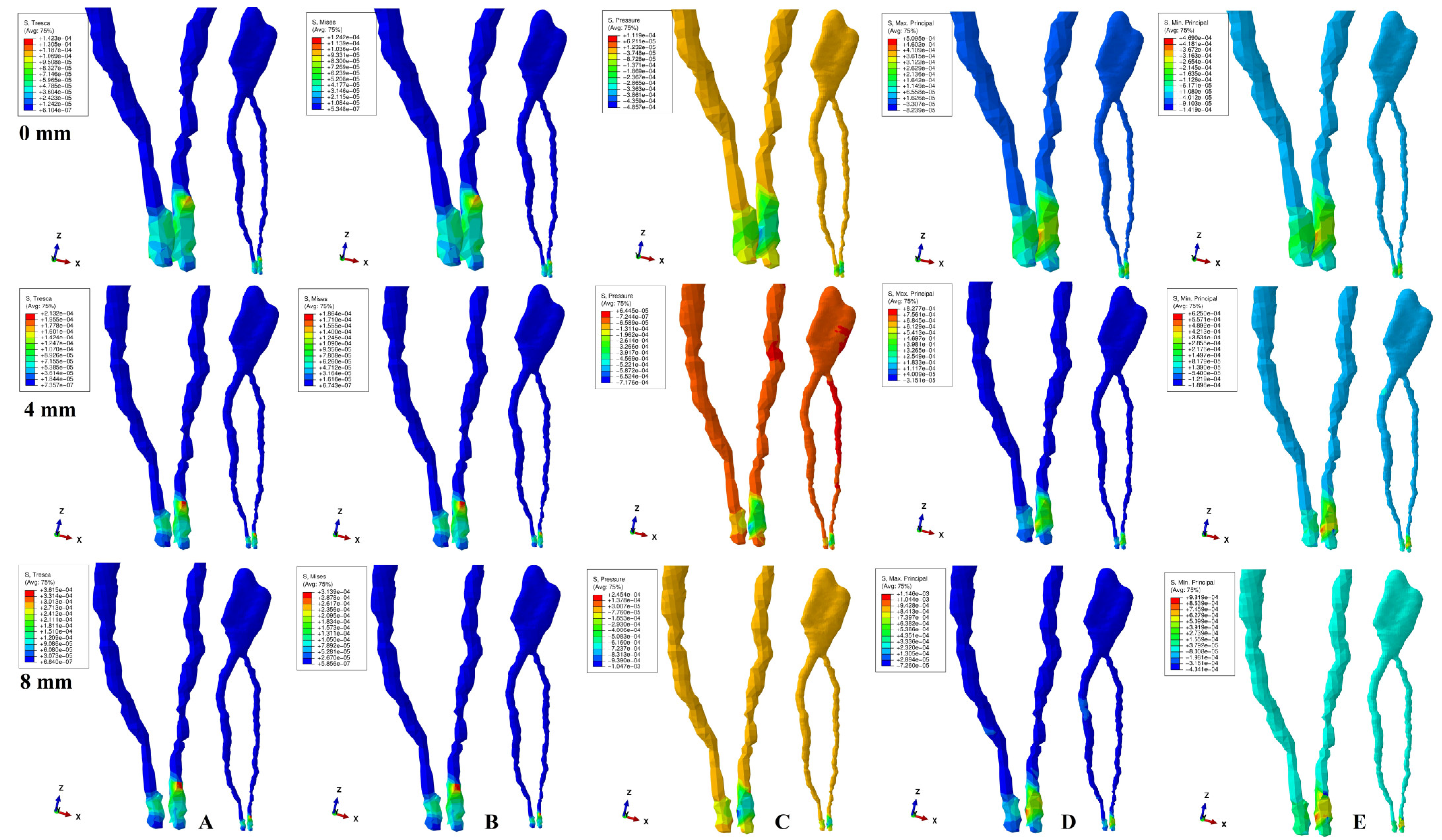
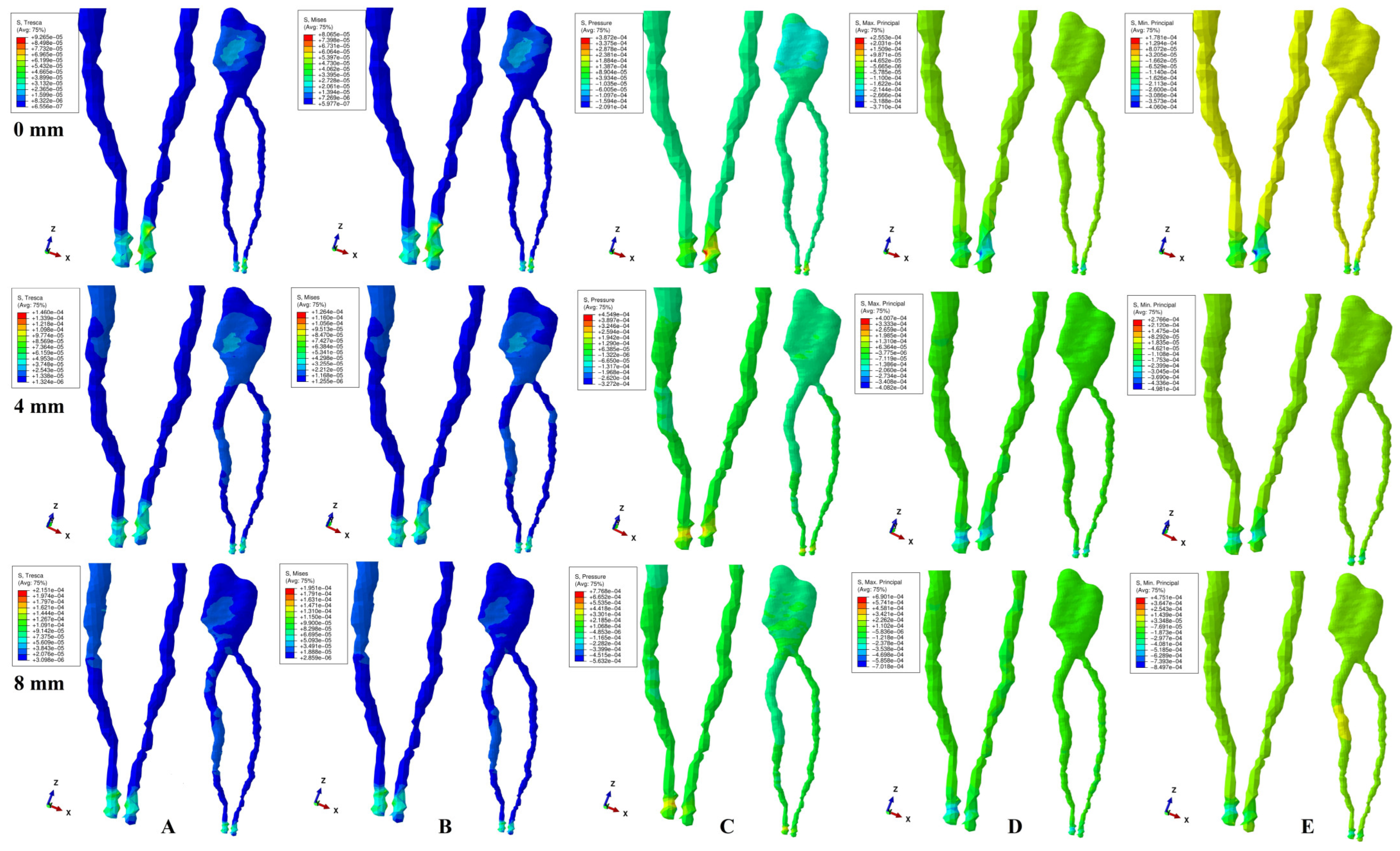
3. Results
4. Discussion
5. Conclusions
- 0.5 N of the orthodontic force is safe of any ischemic and necrotic risks up to 8 mm of periodontal breakdown, with rotation the most invasive (translation the least), and apical NVB more prone to ischemia than dental pulp. However, limited ischemic areas are also visible in the coronal and radicular pulp for translational and rotational movements.
- A clear difference between failure criteria when analyzing the dental pulp and NVB cannot be proved based only on the correlation between the FEA quantitative results and MHP. Nonetheless, the difference could rely on the type of analyzed material (i.e., ductile vs. brittle, with dental pulp, apical NVB and periodontal ligament having ductile resemblance), thus the choice should consider this issue. Tresca and VM’s failure criteria (adequate for the analysis of ductile materials) supplied comparable results and the lowest amount of stress.
- To obtain a clear image of the biomechanical behavior of tissues under orthodontic movements in a reduced periodontium, correlations with the other components of periodontium, such as PDL, should be considered.
6. Practitioner Points
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Moga, R.A.; Buru, S.M.; Olteanu, C.D. Assessment of the Best FEA Failure Criteria (Part I): Investigation of the Biomechanical Behavior of PDL in Intact and Reduced Periodontium. Int. J. Environ. Res. Public Health 2022, 19, 12424. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Buru, S.M.; Chiorean, C.G. Overall stress in periodontal ligament under orthodontic movement during a periodontal breakdown. Am. J. Orthod. Dentofac. Orthop. 2022, 161, e127–e135. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Buru, S.M.; Chiorean, C.G.; Cosgarea, R. Compressive stress in periodontal ligament under orthodontic movements during periodontal breakdown. Am. J. Orthod. Dentofac. Orthop. 2021, 159, e291–e299. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Cosgarea, R.; Buru, S.M.; Chiorean, C.G. Finite element analysis of the dental pulp under orthodontic forces. Am. J. Orthod. Dentofac. Orthop. 2019, 155, 543–551. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Fukasawa, S. Is Inflammation a Friend or Foe for Orthodontic Treatment?: Inflammation in Orthodontically Induced Inflammatory Root Resorption and Accelerating Tooth Movement. Int. J. Mol. Sci. 2021, 22, 2388. [Google Scholar] [CrossRef] [PubMed]
- Ricucci, D.; Siqueira, J.F., Jr.; Rôças, I.N. Pulp Response to Periodontal Disease: Novel Observations Help Clarify the Processes of Tissue Breakdown and Infection. J. Endod. 2021, 47, 740–754. [Google Scholar] [CrossRef] [PubMed]
- Minch, L.E.; Sarul, M.; Nowak, R.; Kawala, B.; Antoszewska-Smith, J. Orthodontic intrusion of periodontally-compromised maxillary incisors: 3-dimensional finite element method analysis. Adv. Clin. Exp. Med. 2017, 26, 829–833. [Google Scholar] [CrossRef] [PubMed]
- Weissheimer, T.; Silva, E.; Pinto, K.P.; Só, G.B.; Rosa, R.A.; Só, M.V.R. Do orthodontic tooth movements induce pulp necrosis? A systematic review. Int. Endod. J. 2021, 54, 1246–1262. [Google Scholar] [CrossRef]
- Vitali, F.C.; Cardoso, I.V.; Mello, F.W.; Flores-Mir, C.; Andrada, A.C.; Dutra-Horstmann, K.L.; Duque, T.M. Effect of orthodontic force on dental pulp histomorphology and tissue factor expression. Angle Orthod. 2021, 91, 830–842. [Google Scholar] [CrossRef] [PubMed]
- Vermiglio, G.; Centofanti, A.; Matarese, G.; Militi, A.; Matarese, M.; Arco, A.; Nicita, F.; Cutroneo, G. Human Dental Pulp Tissue during Orthodontic Tooth Movement: An Immunofluorescence Study. J. Funct. Morphol. Kinesiol. 2020, 5, 65. [Google Scholar] [CrossRef]
- Proffit, W.R.F.H.; Sarver, D.M.; Ackerman, J.L. (Eds.) Contemporary Orthodontics, 5th ed.; Elsevier: St. Louis, MO, USA, 2012. [Google Scholar]
- Hohmann, A.; Wolfram, U.; Geiger, M.; Boryor, A.; Sander, C.; Faltin, R.; Faltin, K.; Sander, F.G. Periodontal ligament hydrostatic pressure with areas of root resorption after application of a continuous torque moment. Angle Orthod. 2007, 77, 653–659. [Google Scholar] [CrossRef]
- Hohmann, A.; Wolfram, U.; Geiger, M.; Boryor, A.; Kober, C.; Sander, C.; Sander, F.G. Correspondences of hydrostatic pressure in periodontal ligament with regions of root resorption: A clinical and a finite element study of the same human teeth. Comput. Methods Programs Biomed. 2009, 93, 155–161. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.; Tambe, A.A.; Maeda, Y.; Wada, M.; Gonda, T. Finite element analysis of dental implants with validation: To what extent can we expect the model to predict biological phenomena? A literature review and proposal for classification of a validation process. Int. J. Implant Dent. 2018, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.L.Y.; Peng, W.; Dong, H.Y.; Zhang, J.X. A biomechanical case study on the optimal orthodontic force on the maxillary canine tooth based on finite element analysis. J. Zhejiang Univ. Sci. B 2018, 7, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Hemanth, M.; Deoli, S.; Raghuveer, H.P.; Rani, M.S.; Hegde, C.; Vedavathi, B. Stress Induced in the Periodontal Ligament under Orthodontic Loading (Part I): A Finite Element Method Study Using Linear Analysis. J. Int. Oral Health 2015, 7, 129–133. [Google Scholar]
- Hemanth, M.; Deoli, S.; Raghuveer, H.P.; Rani, M.S.; Hegde, C.; Vedavathi, B. Stress Induced in Periodontal Ligament under Orthodontic Loading (Part II): A Comparison of Linear Versus Non-Linear Fem Study. J. Int. Oral Health 2015, 7, 114–118. [Google Scholar] [PubMed]
- Wang, S.; Sun, J.; Yu, Y.Y. Influence of proximal two-wall bone defect on periodontal ligament stresses under normal occlusal forces. Zhonghua Kou Qiang Yi Xue Za Zhi = Zhonghua Kouqiang Yixue Zazhi = Chin. J. Stomatol. 2018, 53, 448–452. [Google Scholar]
- Wu, J.; Liu, Y.; Li, B.; Wang, D.; Dong, X.; Sun, Q.; Chen, G. Numerical simulation of optimal range of rotational moment for the mandibular lateral incisor, canine and first premolar based on biomechanical responses of periodontal ligaments: A case study. Clin. Oral Investig. 2021, 25, 1569–1577. [Google Scholar] [CrossRef]
- Wu, J.; Liu, Y.; Wang, D.; Zhang, J.; Dong, X.; Jiang, X.; Xu, X. Investigation of effective intrusion and extrusion force for maxillary canine using finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 1294–1302. [Google Scholar] [CrossRef]
- Roscoe, M.G.; Cattaneo, P.M.; Dalstra, M.; Ugarte, O.M.; Meira, J.B.C. Orthodontically induced root resorption: A critical analysis of finite element studies’ input and output. Am. J. Orthod. Dentofac. Orthop. 2021, 159, 779–789. [Google Scholar] [CrossRef]
- Shaw, A.M.; Sameshima, G.T.; Vu, H.V. Mechanical stress generated by orthodontic forces on apical root cementum: A finite element model. Orthod. Craniofacial Res. 2004, 7, 98–107. [Google Scholar] [CrossRef] [PubMed]
- Toms, S.R.; Eberhardt, A.W. A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am. J. Orthod. Dentofac. Orthop. 2003, 123, 657–665. [Google Scholar] [CrossRef] [PubMed]
- Geramy, A.; Faghihi, S. Secondary trauma from occlusion: Three-dimensional analysis using the finite element method. Quintessence Int. 2004, 35, 835–843. [Google Scholar] [PubMed]
- Geramy, A. Initial stress produced in the periodontal membrane by orthodontic loads in the presence of varying loss of alveolar bone: A three-dimensional finite element analysis. Eur. J. Orthod. 2002, 24, 21–33. [Google Scholar] [CrossRef]
- Perez-Gonzalez, A.; Iserte-Vilar, J.L.; Gonzalez-Lluch, C. Interpreting finite element results for brittle materials in endodontic restorations. Biomed. Eng. Online 2011, 10, 44. [Google Scholar] [CrossRef]
- Hussein Mahmood Ghuloom, K.; Mascarenhas, R.; Parveen, S.; Husain, A. Finite element analysis of orthodontically induced stress in the periodontal ligament of the maxillary first molar with simulated bone loss. J. Comput. Methods Sci. Eng. 2017, 17, 243–252. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, J.; Weinkamer, R.; Darendeliler, M.A.; Swain, M.V.; Sue, A.; Zheng, K.; Li, Q. In vivo effects of different orthodontic loading on root resorption and correlation with mechanobiological stimulus in periodontal ligament. J. R. Soc. Interface 2019, 16, 20190108. [Google Scholar] [CrossRef]
- Aprile, P.; Kelly, D.J. Hydrostatic Pressure Regulates the Volume, Aggregation and Chondrogenic Differentiation of Bone Marrow Derived Stromal Cells. Front. Bioeng. Biotechnol. 2020, 8, 619914. [Google Scholar] [CrossRef]
- Merdji, A.; Mootanah, R.; Bachir Bouiadjra, B.A.; Benaissa, A.; Aminallah, L.; Ould Chikh el, B.; Mukdadi, S. Stress analysis in single molar tooth. Mater. Sci. Eng. C Mater. Biol. Appl. 2013, 33, 691–698. [Google Scholar] [CrossRef]
- Javed, F.; Al-Kheraif, A.A.; Romanos, E.B.; Romanos, G.E. Influence of orthodontic forces on human dental pulp: A systematic review. Arch. Oral Biol. 2015, 60, 347–356. [Google Scholar] [CrossRef]
- Bauss, O.; Rohling, J.; Meyer, K.; Kiliaridis, S. Pulp vitality in teeth suffering trauma during orthodontic therapy. Angle Orthod. 2009, 79, 166–171. [Google Scholar] [CrossRef] [PubMed]
- Bauss, O.; Rohling, J.; Rahman, A.; Kiliaridis, S. The effect of pulp obliteration on pulpal vitality of orthodontically intruded traumatized teeth. J. Endod. 2008, 34, 417–420. [Google Scholar] [CrossRef] [PubMed]
- Bauss, O.; Schäfer, W.; Sadat-Khonsari, R.; Knösel, M. Influence of orthodontic extrusion on pulpal vitality of traumatized maxillary incisors. J. Endod. 2010, 36, 203–207. [Google Scholar] [CrossRef] [PubMed]
- Bauss, O.; Röhling, J.; Sadat-Khonsari, R.; Kiliaridis, S. Influence of orthodontic intrusion on pulpal vitality of previously traumatized maxillary permanent incisors. Am. J. Orthod. Dentofac. Orthop. 2008, 134, 12–17. [Google Scholar] [CrossRef] [PubMed]




| Material | Young’s Modulus, E (GPa) | Poisson Ratio, ʋ | Refs. |
|---|---|---|---|
| Enamel | 80 | 0.33 | [1,2,3,4] |
| Dentin/Cementum | 18.6 | 0.31 | [1,2,3,4] |
| Pulp/apical NVB | 0.0021 | 0.45 | [1,2,3,4] |
| PDL | 0.0667 | 0.49 | [1,2,3,4] |
| Cortical bone | 14.5 | 0.323 | [1,2,3,4] |
| Trabecular bone | 1.37 | 0.3 | [1,2,3,4] |
| Bracket (Cr-Co) | 218 | 0.33 | [1,2,3,4] |
| Resorption (mm) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intrusion | Tresca | NVB | 1.16 | 1.40 | 1.65 | 1.89 | 2.13 | 2.50 | 2.88 | 3.25 | 3.62 |
| 0.5 N | c | 0.12 | 0.14 | 0.15 | 0.17 | 0.18 | 0.21 | 0.25 | 0.28 | 0.31 | |
| VM | NVB | 0.94 | 1.18 | 1.40 | 1.63 | 1.86 | 2.18 | 2.59 | 2.73 | 3.14 | |
| c | 0.11 | 0.12 | 0.14 | 0.15 | 0.16 | 0.19 | 0.22 | 0.24 | 0.27 | ||
| Pressure | NVB | 4.36 | 4.94 | 5.45 | 5.98 | 6.52 | 7.52 | 8.50 | 9.48 | 10.47 | |
| c | 0.37 | 0.44 | 0.52 | 0.59 | 0.66 | 0.97 | 1.29 | 1.59 | 1.90 | ||
| S1 | NVB | −3.70 | −4.27 | −4.83 | −5.40 | −5.96 | −6.64 | −7.33 | −8.01 | −8.69 | |
| c | 0.41 | 0.45 | 0.48 | 0.52 | 0.55 | 0.64 | 0.73 | 0.82 | 0.91 | ||
| S3 | NVB | −4.60 | −4.98 | −5.37 | −5.75 | −6.13 | −6.96 | −7.78 | −8.61 | −9.43 | |
| c | 0.33 | 0.34 | 0.34 | 0.35 | 0.35 | 0.45 | 0.54 | 0.63 | 0.73 | ||
| Extrusion | Tresca | NVB | 1.20 | 1.40 | 1.65 | 1.89 | 2.13 | 2.50 | 2.88 | 3.25 | 3.62 |
| 0.5 N | c | 0.12 | 0.14 | 0.15 | 0.17 | 0.18 | 0.21 | 0.25 | 0.28 | 0.31 | |
| VM | NVB | 0.94 | 1.18 | 1.40 | 1.63 | 1.86 | 2.18 | 2.59 | 2.73 | 3.14 | |
| c | 0.11 | 0.12 | 0.14 | 0.15 | 0.16 | 0.19 | 0.22 | 0.24 | 0.27 | ||
| Pressure | NVB | −4.36 | −4.94 | −5.45 | −5.98 | −6.52 | −7.52 | −8.50 | −9.48 | −10.47 | |
| c | −0.37 | −0.44 | −0.52 | −0.59 | −0.66 | −0.97 | −1.29 | −1.59 | −1.90 | ||
| S1 | NVB | 4.21 | 4.97 | 5.74 | 6.50 | 7.26 | 7.82 | 8.38 | 8.93 | 9.49 | |
| c | −0.83 | −0.92 | −1.02 | −1.12 | 1.19 | 1.24 | 1.29 | 1.34 | 1.39 | ||
| S3 | NVB | 4.69 | 5.09 | 5.48 | 5.86 | 6.25 | 7.14 | 8.04 | 8.93 | 9.82 | |
| c | −0.40 | −0.44 | −0.47 | −0.51 | −0.54 | −0.61 | −0.68 | −0.74 | −0.80 | ||
| Translation | Tresca | NVB | 0.93 | 1.06 | 1.20 | 1.33 | 1.46 | 1.63 | 1.81 | 1.98 | 2.15 |
| 0.5 N | c | 0.16 | 0.18 | 0.21 | 0.23 | 0.25 | 0.26 | 0.28 | 0.29 | 0.30 | |
| VM | NVB | 0.81 | 0.92 | 1.04 | 1.15 | 1.26 | 1.43 | 1.61 | 1.78 | 1.95 | |
| c | 0.21 | 0.22 | 0.23 | 0.24 | 0.25 | 0.25 | 0.26 | 0.26 | 0.26 | ||
| Pressure | NVB | 3.87 | 4.05 | 4.24 | 4.41 | 4.59 | 5.39 | 6.19 | 6.98 | 7.77 | |
| c | −0.56 | −0.58 | −0.60 | −0.62 | 0.64 | 0.75 | 0.86 | 0.96 | 1.07 | ||
| S1 | NVB | −3.29 | −3.51 | −3.74 | −3.98 | −4.18 | −4.89 | −5.61 | −6.32 | −7.03 | |
| c | 0.41 | 0.47 | 0.53 | 0.58 | 0.64 | 0.71 | 0.78 | 0.84 | 0.91 | ||
| S3 | NVB | −4.06 | −4.29 | −4.52 | −4.75 | −4.98 | −5.87 | −6.75 | −7.63 | −8.50 | |
| c | −0.17 | −0.17 | −0.18 | −0.18 | 0.18 | 0.22 | 0.26 | 2.93 | 0.33 | ||
| Rotation | Tresca | NVB | 1.43 | 1.51 | 2.01 | 2.52 | 3.45 | 3.87 | 4.28 | 4.70 | 5.11 |
| 0.5 N | c | 0.25 | 0.27 | 0.29 | 0.30 | 0.32 | 0.36 | 0.40 | 0.44 | 0.47 | |
| VM | NVB | 1.25 | 1.62 | 1.98 | 2.34 | 2.71 | 2.89 | 3.08 | 3.26 | 3.44 | |
| c | 0.22 | 0.24 | 0.25 | 0.27 | 0.28 | 0.32 | 0.37 | 0.41 | 0.45 | ||
| Pressure | NVB | 5.71 | 6.64 | 7.55 | 8.47 | 9.39 | 10.55 | 11.72 | 12.88 | 14.03 | |
| c | 2.69 | 2.82 | 2.94 | 3.06 | 3.17 | 3.55 | 3.94 | 4.32 | 4.70 | ||
| S1 | NVB | −5.55 | −6.63 | −7.78 | −8.89 | −10.00 | −11.20 | −12.40 | −13.59 | −14.79 | |
| c | 0.94 | 1.47 | 2.00 | 2.52 | 3.05 | 3.46 | 3.87 | 4.28 | 4.69 | ||
| S3 | NVB | −6.03 | −7.14 | −8.25 | −9.35 | −10.46 | −11.75 | −13.04 | −14.34 | −15.62 | |
| c | 0.63 | 0.78 | 0.94 | 1.09 | −1.23 | −1.37 | −1.52 | −1.66 | −1.80 | ||
| Tipping | Tresca | NVB | 1.22 | 1.52 | 1.81 | 2.11 | 2.40 | 2.74 | 3.07 | 3.41 | 3.74 |
| 0.5 N | c | 0.21 | 0.22 | 0.23 | 0.23 | 0.24 | 0.26 | 0.29 | 0.30 | 0.32 | |
| VM | NVB | 1.06 | 1.32 | 1.57 | 1.83 | 2.08 | 2.39 | 2.70 | 3.00 | 3.30 | |
| c | 0.18 | 0.18 | 0.19 | 0.19 | 0.19 | 0.22 | 0.24 | 0.27 | 0.29 | ||
| Pressure | NVB | 4.38 | 5.14 | 5.92 | 6.68 | 7.45 | 8.24 | 9.03 | 9.81 | 10.60 | |
| c | 1.88 | 1.95 | 2.02 | 2.08 | 2.15 | 2.21 | 2.28 | 2.34 | 2.40 | ||
| S1 | NVB | −4.26 | −4.67 | −5.08 | −5.49 | −6.97 | −7.61 | −8.26 | −8.90 | −9.54 | |
| c | −0.84 | −1.16 | −1.47 | −1.79 | 2.10 | 2.56 | 3.03 | 3.49 | 3.95 | ||
| S3 | NVB | −4.71 | −5.32 | −5.93 | −6.53 | −7.14 | −8.12 | −9.11 | −10.09 | −11.07 | |
| c | −0.42 | −0.50 | −0.58 | −0.66 | −0.74 | 0.76 | 0.78 | 0.79 | 0.80 |
| Resorption (mm) | Intact Periodontium | 8 mm Reduced Periodontium | |
|---|---|---|---|
| Intrusion | Tresca | NVB | NVB |
| 0.5 N | Von Mises | NVB | NVB |
| Pressure | NVB | NVB | |
| S1 | Max. Princ. | NVB | NVB |
| S3 | Min. Princ. | NVB | NVB |
| Extrusion | Tresca | NVB | NVB |
| 0.5 N | Von Mises | NVB | NVB |
| Pressure | NVB | NVB | |
| S1 | Max. Princ. | NVB | NVB |
| S3 | Min. Princ. | NVB | NVB |
| Translation | Tresca | NVB, C, r | NVB, c |
| 0.5 N | Von Mises | NVB, C, r | NVB, c |
| Pressure | NVB | NVB, c | |
| S1 | Max. Princ. | NVB | NVB |
| S3 | Min. Princ. | NVB | NVB, r |
| Rotation | Tresca | NVB, c | NVB |
| 0.5 N | Von Mises | NVB, c | NVB |
| Pressure | NVB, | NVB | |
| S1 | Max. Princ. | NVB, | NVB |
| S3 | Min. Princ. | NVB, c | NVB, r |
| Tipping | Tresca | NVB | NVB |
| 0.5 N | Von Mises | NVB | NVB |
| Pressure | NVB | NVB | |
| S1 | Max. Princ. | NVB | NVB |
| S3 | Min. Princ. | NVB | NVB |
| FEA Criterion | Studies | Force, Movement, Stress, NVB and PDL |
|---|---|---|
| Von Mises | Moga et al. (2019) [4], lower premolar | 0.2 N intrusion; 0.5 KPa NVB |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | 0.6 N extrusion; 1.5 KPa NVB | |
| No bone loss | 1.2 N translation; 1.9 KPa NVB | |
| 0.6 N rotation; 1.5 KPa NVB | ||
| 0.6 N tipping; 1.2 KPa NVB | ||
| 8 mm bone loss | 0.2 N intrusion; 1.4 KPa NVB | |
| 0.6 N extrusion; 4.1 KPa NVB | ||
| 1.2 N translation; 4.7 KPa NVB | ||
| 0.6 N rotation; 5.4 KPa NVB | ||
| 0.6 N tipping; 3.9 KPa NVB | ||
| Toms et al. (2003) [23], lower premolar, 5205 nodes and 1674 elements | 1 N extrusion; a-8 KPa; c-7.75 KPa | |
| No bone loss | ||
| Merdji et al. (2013) [30], lower molar, 557,974 elements | 10 N intrusion; a-29.48 KPa | |
| No bone loss | 3 N tipping; a-8.96 KPa | |
| 3 N translation; a-6.78 KPa | ||
| Shaw et al. (2004) [22], upper incisor, 20,582 nodes and 11,924 elements | ? N extrusion-intrusion a-2 KPa | |
| No bone loss | ? N tipping a-1 KPa | |
| Roscoe et al. (2021) [21], premolar, 1.67 million elements | 0.25 N intrusion; a/c-1.1 KPa | |
| No bone loss | 0.25 N tipping; a/c-2.9 KPa | |
| Moga et al. (2022) [2], lower premolar, 0.2–1.2 N | 0.2 N intrusion; a-0.44 KPa, c-1.51 KPa | |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | 0.6 N extrusion; a-1.33 KPa, c-5.18 KPa | |
| No bone loss | 1.2 N translation; a-3.58 KPa, c-28.06 KPa | |
| 0.6 N rotation; a-2.02 KPa, c-15.91 KPa | ||
| 0.6 N tipping; a-1.34 KPa, c-10.52 KPa | ||
| 8 mm bone loss | 0.2 N intrusion; a-1.22 KPa, c-4.76 KPa | |
| 0.6 N extrusion; a-5.42 KPa, c-21.39 KPa | ||
| 1.2 N translation; a-26.28 KPa, c-117 KPa | ||
| 0.6 N rotation; a-17.86 KPa, c-71.06 KPa | ||
| 0.6 N tipping; c-7.29 KPa, c-43.19 KPa | ||
| Moga et al. (2022) [1], lower premolar, 0.5 N | Intrusion; a-2.17 KPa, c-4.32 KPa | |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | Extrusion, a-2.17 KPa, c-4.85 KPa | |
| No bone loss | Translation; a-1.49 KPa, c-14.59 KPa | |
| Rotation; a-1.68 KPa, c-14.80 KPa | ||
| Tipping, a-1.12 KPa, c-9.85 KPa | ||
| 8 mm bone loss | Intrusion; a-6 KPa, c-11.19 KPa | |
| Extrusion; a-6 KPa, c-16.34 KPa | ||
| Translation; a-5.49KPa, c-54.44 KPa | ||
| Rotation; a-7.49 KPa, c-66.46 KPa | ||
| Tipping; a-6 KPa, c-33 KPa | ||
| Tresca | Moga et al. (2022) [1], lower premolar, 0.5 N | Intrusion; a-2.50 KPa, c-4.97 KPa |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | Extrusion; a-2.50 KPa, c-5.59 KPa | |
| No bone loss | Translation; a-1.68 KPa, c-16.37 KPa | |
| Rotation, a-1.94 KPa, c-17.17 KPa | ||
| Tipping; a-1.29 KPa, c-11.36 KPa | ||
| 8 mm bone loss | Intrusion; a-6.85 KPa, c-13.66 KPa | |
| Extrusion, a-6.87 KPa, c-18.75 KPa | ||
| Translation; a-6.31 KPa, c-62.57 KPa | ||
| Rotation; a-8.23 KPa, c-73 KPa | ||
| Tipping; a-6.89 KPa, c-37.42 KPa | ||
| S1–S3 | Toms et al. (2003) [23], lower premolar, 5205 nodes; 1674 elements, 1 N | Extrusion; S1: a-36 KPa, c-(−2.69 KPa) |
| No bone loss | Extrusion; S3: a-28.49 KPa, c-(−11.6 KPa) | |
| Moga et al. (2021) [3], lower premolar 0.2–1.2 N | 0.2 N intrusion; S3: a-(−1.74 KPa), c-(−1.74 KPa) | |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | 0.6 N extrusion; S3: a-14.1 KPa, c-27.99 KPa | |
| No bone loss | 1.2 N translation; S3: a-(−97.79 KPa), c-93 KPa | |
| 0.6 N rotation; S3: a-(−56.27 KPa), c-68.07 KPa | ||
| 0.6 N tipping; S3: a-(−18.53 KPa), c-28.89 KPa | ||
| 8 mm bone loss | 0.2 N intrusion; S3: a-(−21.26 KPa), c-(−8.8 KPa) | |
| 0.6 N extrusion; S3: a-64.15 KPa, c-82.83 KPa | ||
| 1.2 N translation; S3: a-(−292 KPa), c-260 KPa | ||
| 0.6 N rotation; S3: a-(−290 KPa), c-170 KPa | ||
| 0.6 N tipping; S3: a-(−109 KPa), c-(−109 KPa) | ||
| Geramy et al. (2004) [24], upper central incisor | Tipping; S1: a-78 KPa, c-(−23.6 KPa) | |
| 378,884 nodes, 32,768 elements, 1 N | Tipping; S3: a-(–74 KPa), c-(−28 KPa) | |
| No bone loss | ||
| 8 mm bone loss | Tipping; S1: a-881 KPa, c-(−395 KPa) | |
| Tipping; S3: a-740 KPa, c-(−491 KPa) | ||
| Geramy et al. (2002) [25], upper central incisor | Tipping; S1: a-(−37 KPa), c-55 KPa | |
| 726 nodes, 475 elements, 1 N | Tipping; S3: a-39 KPa, c-(−75 KPa) | |
| No bone loss | ||
| Intrusion; S1: a-26 KPa, c-(−9 KPa) | ||
| Intrusion; S3: a-(−29 KPa), c-(−12 KPa) | ||
| 8 mm bone loss | Tipping; S1: a-(−440 KPa), c-(−288 KPa) | |
| Tipping; S3: a-(−475 KPa), c-300 KPa | ||
| Intrusion; S1: a-(–43 KPa), c-19 KPa | ||
| Intrusion; S3: a-(–47 KPa), c-(−23 KPa) | ||
| Hemanth et al. (2015) [16,17], upper central incisor | 0.2 N intrusion; S1: c-1 KPa | |
| 239,666 nodes, 148,097 elements. | 1 N tipping; S1: a-(−16.4 KPa) | |
| No bone loss | ||
| 0.2 N intrusion; S3: a-(−13.37 KPa) | ||
| 1 N tipping; S3: a-16.4 KPa | ||
| Roscoe et al. (2021) [21], premolar, 1.67 million elements | 0.25 N intrusion; a/c-5.3 KPa | |
| No bone loss | 0.25 N tipping; a/c-7.3 KPa | |
| Pressure | Moga et al. (2022) [1], lower premolar, 0.5 N | Intrusion; a-(−13.68 KPa), c-18.86 KPa |
| 5.06–6.05 million elements; 0.96–1.07 million nodes | Extrusion; a-13.68 KPa, c-19.1 KPa | |
| No bone loss | Translation; a-(−28.21 KPa), c-(−79.1 KPa) | |
| Rotation, a-(−34.3 KPa), c-(−85.3 KPa) | ||
| Tipping; a-13.75 KPa, c-33 KPa | ||
| 8 mm bone loss | Intrusion; a-(−30 KPa), c-60.8 KPa | |
| Extrusion, a-30 KPa, c-60.3 KPa | ||
| Translation; a-103.8 KPa, c-(−129 KPa) | ||
| Rotation; a-97.6 KPa, c-(−162 KPa) | ||
| Tipping; a-71.3 KPa, c-129 KPa | ||
| Hohmann et al. (2009) [13], upper premolar, 0.5 N | Intrusion, a-(4.7 KPa–9.95 TPa), c-4.7 KPa | |
| PDL 195,881 elements, tooth 711,114 elements | ||
| No bone loss | ||
| Hohmann et al. (2007) [12], upper premolar 3 N | Tipping; a-38.84 KPa, c-(−68 KPa) | |
| PDL 152,776 elements, tooth 56,454 elements | ||
| No bone loss | ||
| Wu et al. (2018) [15], upper canine | optimal force: tipping 0.28–0.44 N, translation 1.1–1.37 N | |
| PDL 1263, elements, tooth 1928 elements | rotation 1.7–2.1 N, extrusion 0.38–0.4 N | |
| No bone loss | ||
| Wu et al. (2021) [19], lower incisor, canine, premolar | optimal force: rotation 2.2–2.3 N, 3–3.1 N, 2.8–2.9 N | |
| PDL 3032, 3416, 3851 elements, bone 5692 elements | ||
| No bone loss | ||
| Wu et al. (2019) [20], upper canine | optimal force: intr. 0.8–0.9 N, extr. 2.3–2.6 N | |
| PDL 2272, elements, tooth 2101 elements | ||
| No bone loss | ||
| Roscoe et al. (2021) [21], premolar, 1.67 million elements, 0.25 N | Intrusion; a/c-(−4.7 KPa) | |
| No bone loss | Tipping; a/c-(−5.8 KPa) | |
| Zhong et al. (2019) [28], lower premolar, PDL 17,575 elements, 0.25 N | Tipping; a/c-(10–20 KPa) | |
| No bone loss |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moga, R.A.; Buru, S.M.; Olteanu, C.D. Assessment of the Best FEA Failure Criteria (Part II): Investigation of the Biomechanical Behavior of Dental Pulp and Apical-Neuro-Vascular Bundle in Intact and Reduced Periodontium. Int. J. Environ. Res. Public Health 2022, 19, 15635. https://doi.org/10.3390/ijerph192315635
Moga RA, Buru SM, Olteanu CD. Assessment of the Best FEA Failure Criteria (Part II): Investigation of the Biomechanical Behavior of Dental Pulp and Apical-Neuro-Vascular Bundle in Intact and Reduced Periodontium. International Journal of Environmental Research and Public Health. 2022; 19(23):15635. https://doi.org/10.3390/ijerph192315635
Chicago/Turabian StyleMoga, Radu Andrei, Stefan Marius Buru, and Cristian Doru Olteanu. 2022. "Assessment of the Best FEA Failure Criteria (Part II): Investigation of the Biomechanical Behavior of Dental Pulp and Apical-Neuro-Vascular Bundle in Intact and Reduced Periodontium" International Journal of Environmental Research and Public Health 19, no. 23: 15635. https://doi.org/10.3390/ijerph192315635
APA StyleMoga, R. A., Buru, S. M., & Olteanu, C. D. (2022). Assessment of the Best FEA Failure Criteria (Part II): Investigation of the Biomechanical Behavior of Dental Pulp and Apical-Neuro-Vascular Bundle in Intact and Reduced Periodontium. International Journal of Environmental Research and Public Health, 19(23), 15635. https://doi.org/10.3390/ijerph192315635







