Influence of the Backward Fall Technique on the Sagittal Linear Acceleration of the Head during a Fall
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Material
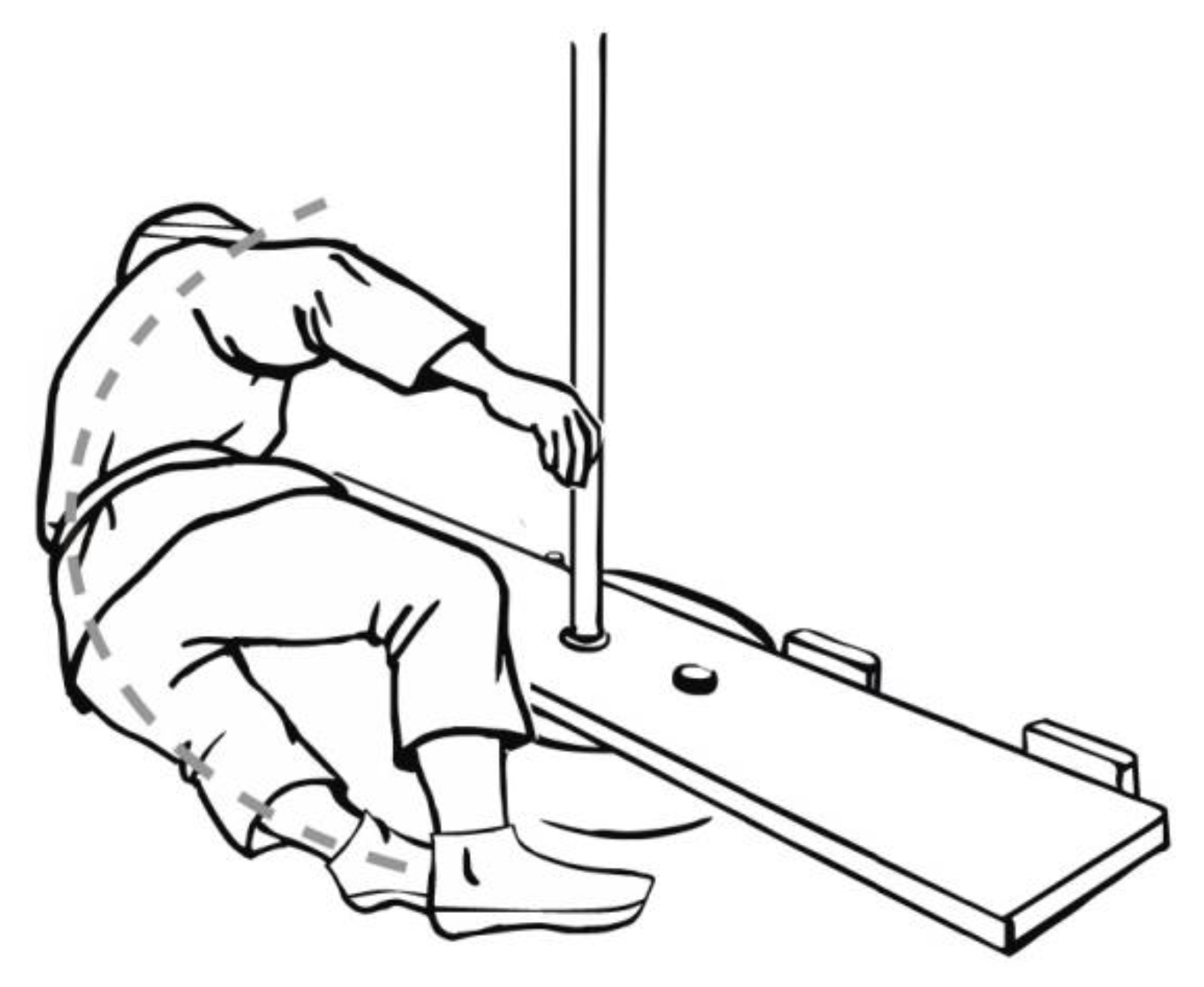
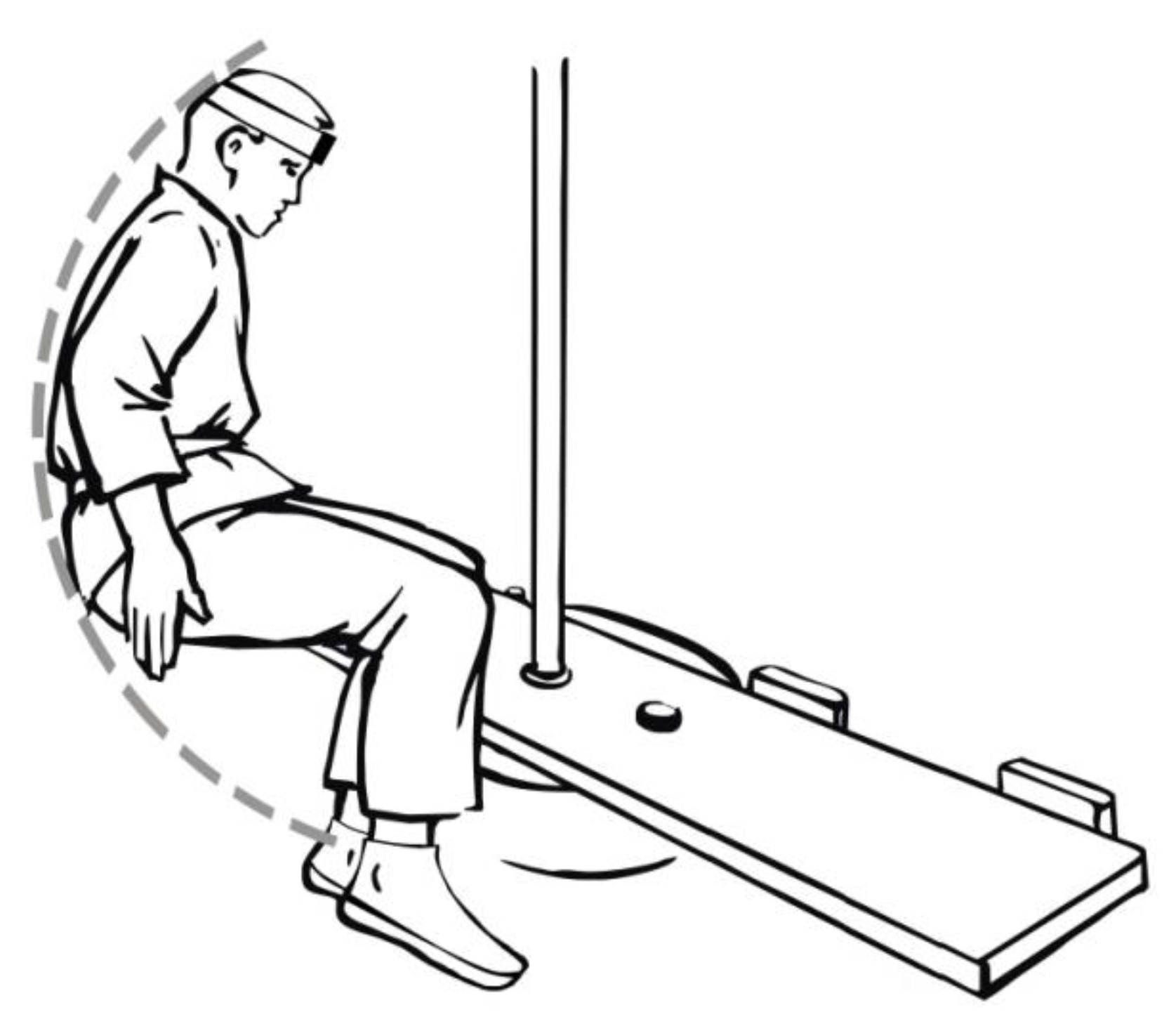
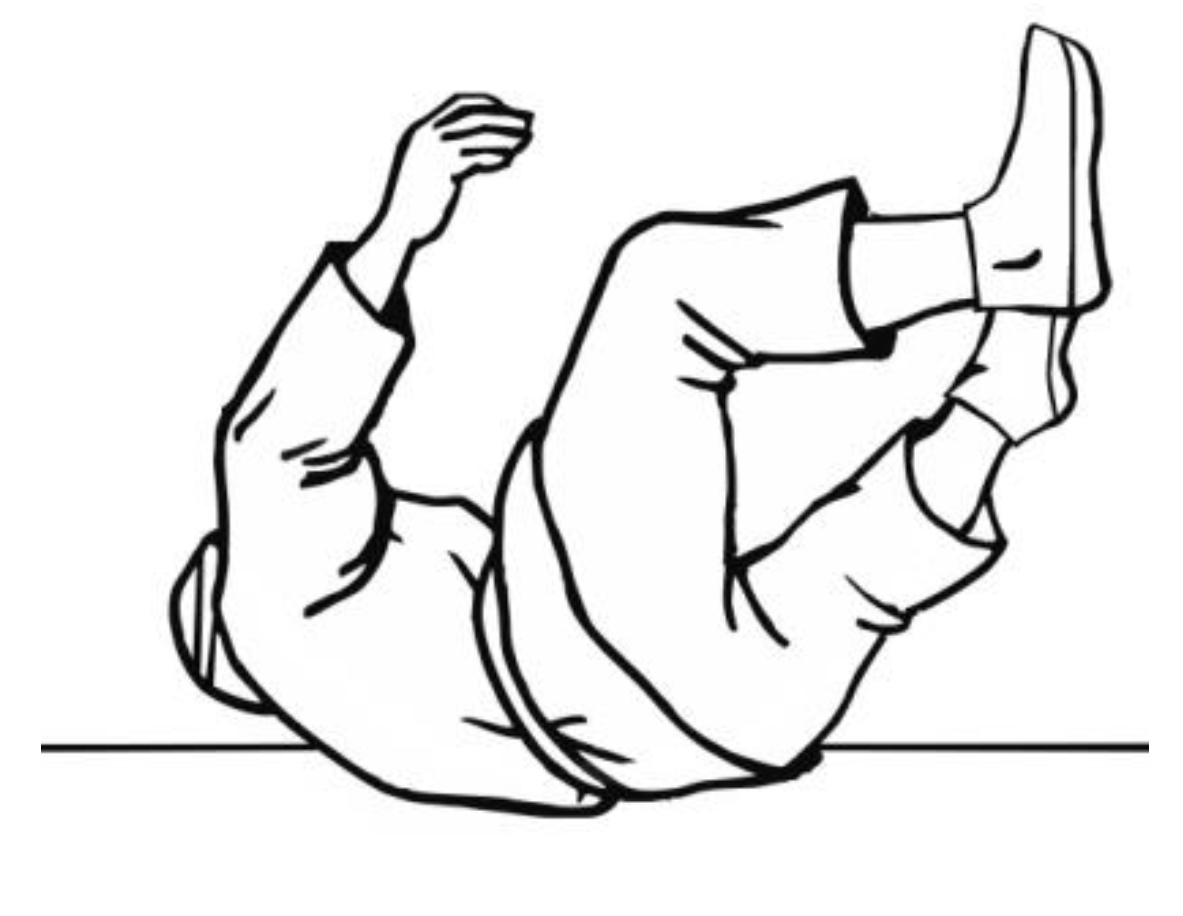
2.2. Research Method
2.3. Statistical Methods
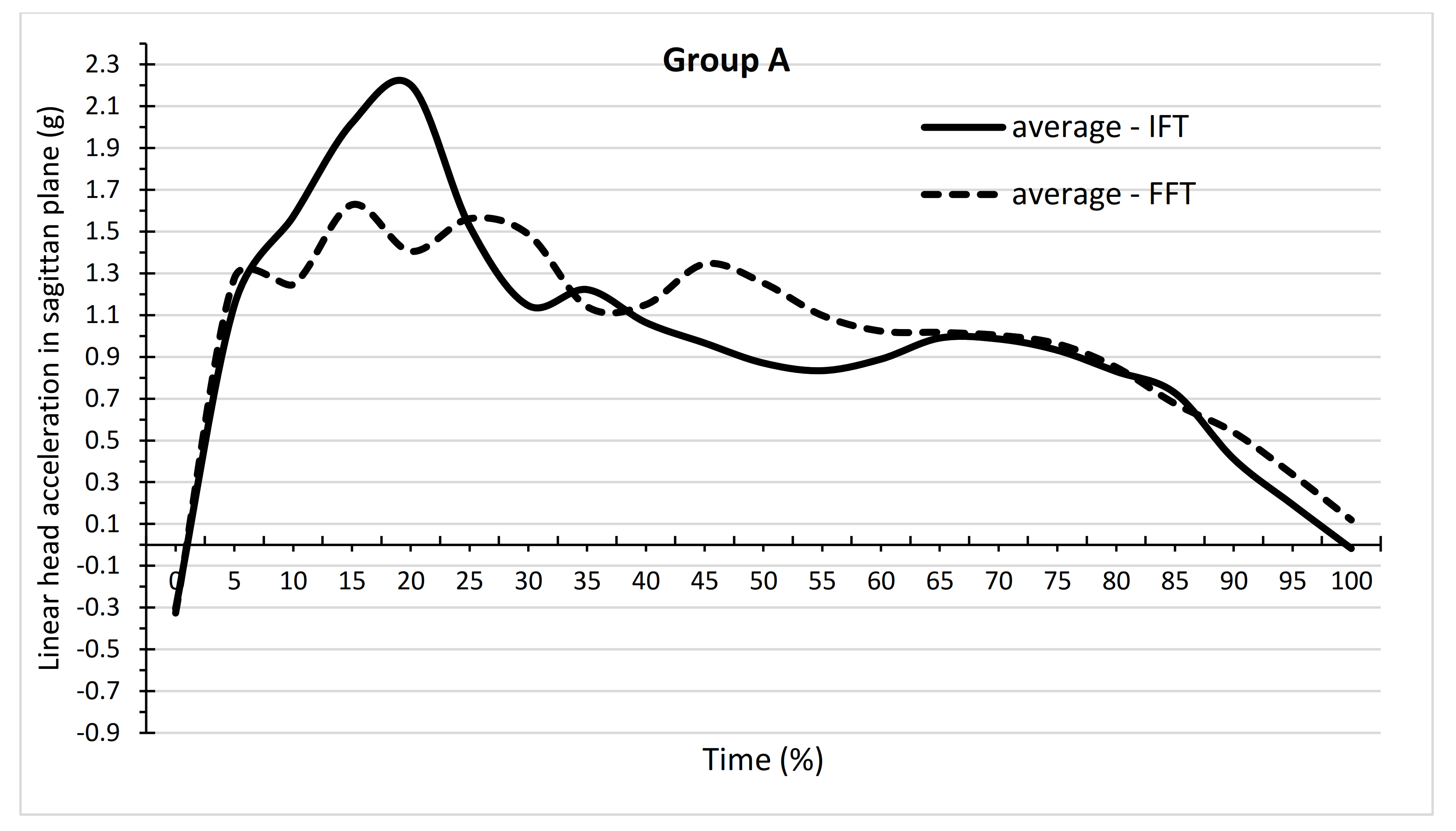
3. Results
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yoshida, S. A Global Report on Falls Prevention. Epidemiology of Falls Geneva: World Health Organization. 2007. Available online: https://www.who.int/ageing/projects/1.Epidemiologyoffallsinolderage.pdf (accessed on 15 October 2021).
- World Health Organization. Violence and Injury Prevention and Disability. 2020. Available online: https://www.who.int/violence_injury_prevention/other_injury/falls/en/ (accessed on 15 October 2021).
- Hsu, I.L.; Li, C.Y.; Chu, D.C.; Chien, L.C. An Epidemiological Analysis of Head Injuries in Taiwan. Int. J. Environ. Res. Public Health 2018, 15, 2457. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Y.; Peng, X.; Guo, Z. Biomechanical analysis of C4-C6 spine segment considering anisotropy of annulus fibrosus. Biomed. Tech. 2013, 58, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Montemurro, N.; Perrini, P.; Mangini, V.; Galli, M.; Papini, A. The Y-shaped trabecular bone structure in the odontoid process of the axis: A CT scan study in 54 healthy subjects and biomechanical considerations. J. Neurosurg. Spine 2019, 30, 585–592. [Google Scholar] [CrossRef] [PubMed]
- Mroczkowski, A.; Sikorski, M.M. The susceptibility to body injuries during a fall and abilities related to motor coordination of children aged 10 to 12. Arch. Budo Sci. Martial Arts Extrem. Sports 2015, 11, 65–71. [Google Scholar]
- Kalina, R.M.; Barczyński, B.J. EKO-AGRO-FITNESS original author continuous program of health-oriented and ecological education in the family, among friends or individually implemented—Ihe premises and assumptions. Arch. Budo 2010, 6, 179–184. [Google Scholar]
- Simpson, J.M. Elderly People at Risk of Fall The Role of Muscle Weakness. Physiotherapy 1993, 79, 831–835. [Google Scholar] [CrossRef]
- Prevention, O.F.; Panel, O.S. Guideline for the Prevention of Falls in Older Persons. J. Am. Geriatr. Soc. 2001, 49, 664–672. [Google Scholar] [CrossRef]
- Kallin, K.; Jensen, J.; Olsson, L.L.; Nyberg, L.; Gustafson, Y. Why the elderly fall in residential care facilities, and suggested remedies. J. Fam. Pract. 2004, 53, 41–52. [Google Scholar]
- Bhatt, T.; Pai, Y.C. Generalization of Gait Adaptation for Fall Prevention: From Moveable Platform to Slippery Floor. J. Neurophysiol. 2009, 101, 948–957. [Google Scholar] [CrossRef] [Green Version]
- Owings, T.M.; Pavol, M.J.; Grabiner, M.D. Mechanisms of failed recovery following postural perturbations on a motorized treadmill mimic those associated with an actual forward trip. Clin. Biomech. 2001, 16, 813–819. [Google Scholar] [CrossRef]
- Grabiner, M.D.; Donovan, S.; Bareither, M.L.; Marone, J.R.; Hamstra-Wright, K.; Gatts, S.; Troy, K.L. Trunk kinematics and fall risk of older adults: Translating biomechanical results to the clinic. J. Electromyogr. Kinesiol. 2008, 18, 197–204. [Google Scholar] [CrossRef]
- Mroczkowski, A.; Mosler, D. Diagnosis of Motor Habits during Backward Fall with Usage of Rotating Training Simulator. In Sport and Exercise Science; Merc, M., Ed.; InTech: London, UK, 2018. [Google Scholar] [CrossRef]
- Kalina, R.M.; Barczyński, B.J.; Klukowski, K.; Langfort, L.; Gasienica-Walczak, B. The method to evaluate the susceptibility to injuries during the fall—Validation procedure of the specific motor test. Arch. Budo 2011, 7, 201–215. [Google Scholar]
- Meng, L.; Ceccarelli, M.; Yu, Z.; Chen, X.; Huang, Q. An experimental characterization of human falling down. Mech. Sci. 2017, 8, 79–89. [Google Scholar] [CrossRef]
- Meng, L.; Yu, Z.; Chen, X.; Ceccarelli, M.; Huang, Q. A Falling Motion Strategy for Humanoids Based on Motion Primitives of Human Falling. In Advances in Service and Industrial Robotics. Proceedings of the 26th International Conference on Robotics in Alpe-Adria-Danube Region. RAAD; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Meng, L.; Ceccarelli, M.; Yu, Z.; Chen, X.; Huang, Q. Gait Transition Between Standing and Falling Down for a Humanoid Robot. In Advances in Mechanism and Machine Science, Mechanisms and Machine Science; Springer Nature Switzerland AG: Cham, Switzerland, 2019; Volume 73. [Google Scholar] [CrossRef]
- Ceccarelli, M. Design and Operation of Humanoid Robots with Incipient Fall Detection. BMSTU J. Mech. Eng. 2021, 1, 11–15. [Google Scholar] [CrossRef]
- Available online: http://smaes.archbudo.com/page/display/id/11/title/relative-immobility/ (accessed on 15 October 2021).
- Mroczkowski, A. Factors putting the head at the risk of injury during backward fall. Ido Mov. Culture. J. Martial Arts Anthropol. 2021, 21, 19–27. [Google Scholar] [CrossRef]
- Mroczkowski, A. Susceptibility to Head Injury during Backward Fall with Side Aligning of the Body. Appl. Sci. 2020, 22, 8239. [Google Scholar] [CrossRef]
- Tan, J.; Robinovitch, S.; Warnick, B. Wrist impact velocities are smaller in forward falls than backward falls from standing. J. Biomech. 2006, 39, 1804–1811. [Google Scholar] [CrossRef]
- Toronjo-Hornillo, L.; DelCastillo-Andrés, Ó.; Campos-Mesa, M.; Díaz Bernier, V.; Zagalaz Sánchez, M. Effect of the Safe Fall Programme on Children’s Health and Safety: Dealing Proactively with Backward Falls in Physical Education Classes. Sustainability 2018, 10, 1168. [Google Scholar] [CrossRef] [Green Version]
- DelCastillo-Andrés, Ó.; Toronjo-Hornillo, L.; Rodríguez-López, M.; Castañeda-Vázquez, C.; Campos-Mesa, M. Children’s Improvement of a Motor Response during Backward Falls through the Implementation of a Safe Fall Program. Int. J. Environ. Res. Public Health 2018, 15, 2669. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Andrés, O.D.; Toronjo-Hornillo, L.; Moya-Martínez, I.; Campos-Mesa, M. Propuesta de un programa de prevención de lesiones en voleibol femenino infantil y cadete. SPORT TK-Rev. EuroAm. Cienc. Deporte 2019, 27, 7–12. [Google Scholar] [CrossRef]
- Mroczkowski, A. Rotating training simulator—An apparatus used for determining the moment of inertia, assisting learning various motor activities during rotational movements and simulating falls imposed by internal force. Arch. Budo Sci. Martial Arts Extrem. Sports 2014, 10, 69–74. [Google Scholar]
- Koshida, S.; Ishii, T.; Matsuda, T.; Hashimoto, T. Biomechanics of the judo backward breakfall: Comparison between experienced and novice judokas. Arch. Budo 2014, 10, 187–194. [Google Scholar]
- Available online: http://www.letsense.net/free4act_eng.php (accessed on 15 October 2021).
- Feldman, F.; Robinovitch, S.N. Reducing hip fracture risk during sideways falls: Evidence in young adults of the protective effects of impact to the hands and stepping. J. Biomech. 2007, 40, 2612–2618. [Google Scholar] [CrossRef]
- Mroczkowski, A. Motor safety of a man during a fall. Arch. Budo 2015, 11, 293–303. [Google Scholar]
- Michnik, R.; Jurkojć, J.; Wodarski, P.; Mosler, D.; Kalina, R.M. Similarities and differences of body control during professional, externally forced fall to the side performed by men aged 24 and 65 years. Arch. Budo 2014, 10, 233–243. [Google Scholar]
- Groen, B.E.; Smulders, E.; de Kam, D.; Duysens, J.; Weerdesteyn, V. Martial arts fall training to prevent hip fractures in the elderly. Osteoporos. Int. 2009, 21, 215–221. [Google Scholar] [CrossRef]
- Groen, B.E.; Weerdesteyn, V.; Duysens, J. Martial arts fall techniques decrease the impact forces at the hip during sideways falling. J. Biomech. 2007, 40, 458–462. [Google Scholar] [CrossRef]
- Weerdesteyn, V.; Groen, B.E.; van Swigchem, R.; Duysens, J. Martial arts fall techniques reduce hip impact forces in naive subjects after a brief period of training. J. Electromyogr. Kinesiol. 2008, 18, 235–242. [Google Scholar] [CrossRef]
- Mroczkowski, A. Susceptibility to fall injury in students of Physical Education practising handball. Arch. Budo Sci. Martial Arts Extrem. Sports 2018, 14, 109–115. [Google Scholar]
- Momola, I.; Cynarski, W.J. Safe falls in the lessons of physical education. Ido Mov. Cult. J. Martial Arts Anthropol. 2006, 124–131. Available online: http://imcjournal.com/index.php/en/volume-vii-2007/contents-vol-vii/797-safe-falls-in-the-lessons-of-physical-education (accessed on 15 October 2021).
- Cynarski, W.J.; Sieber, L.; Szajna, G. Martial arts in physical culture. Ido Mov. Cult. J. Martial Arts Anthropol. 2014, 14, 39–45. [Google Scholar] [CrossRef]
- Reguli, Z.; Senkyr, J.; Vit, M. Questioning the Concept of General Falling Techniques. In Proceedings of the 1st World Congress on Health and Martial Arts in Interdisciplinary Approach, HMA 2015, Czestochowa, Poland, 17–19 September 2015; pp. 63–67. [Google Scholar]
- Mroczkowski, A.; Hes, B. Motor safety during trampolining. Arch. Budo Sci. Martial Arts Extrem. Sports 2015, 11, 57–64. [Google Scholar]
- Cham, R.; Redfern, M. Heel contact dynamics during slip events on level and inclined surfaces. Saf. Sci. 2002, 40, 559–576. [Google Scholar] [CrossRef]

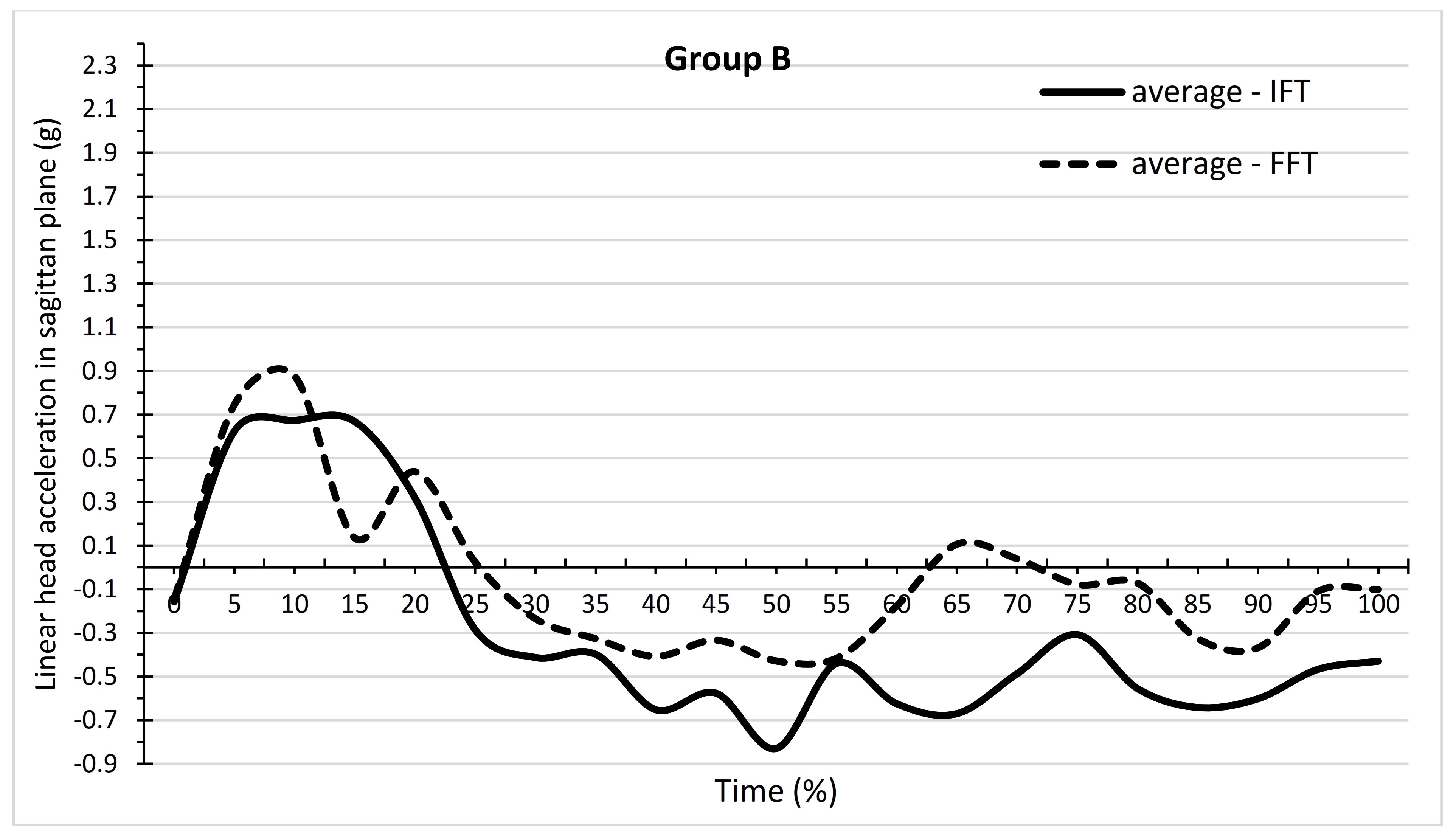
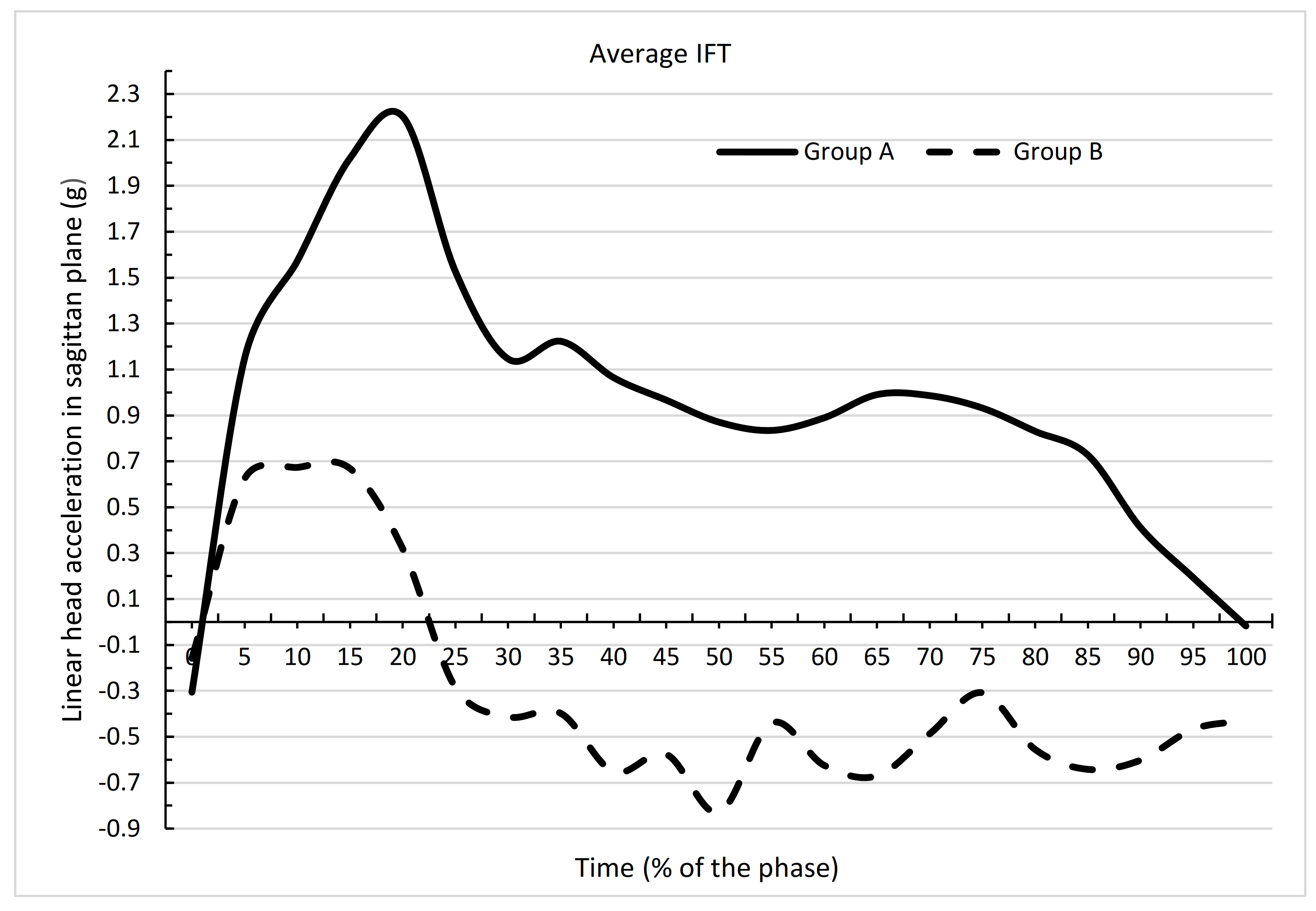
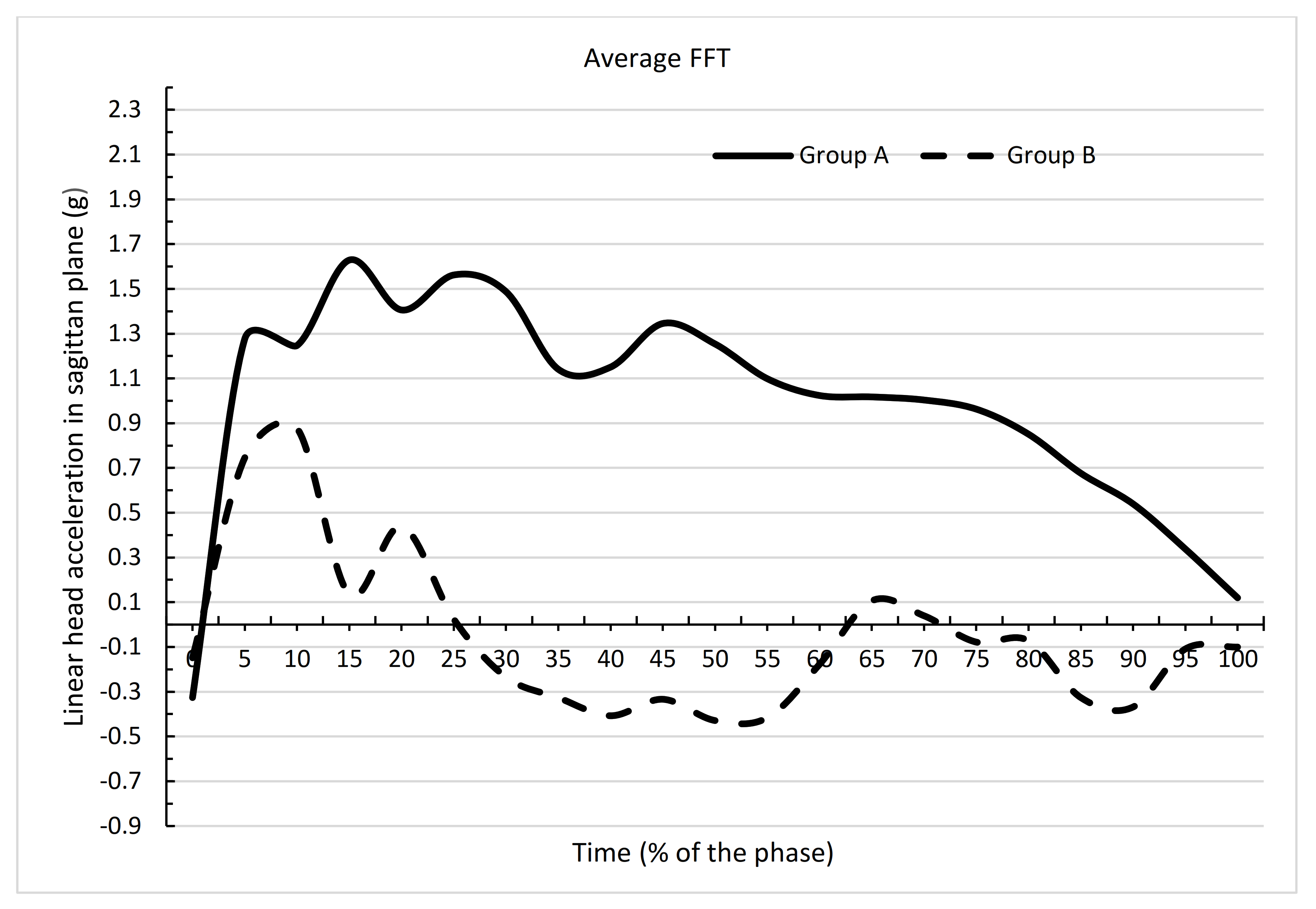
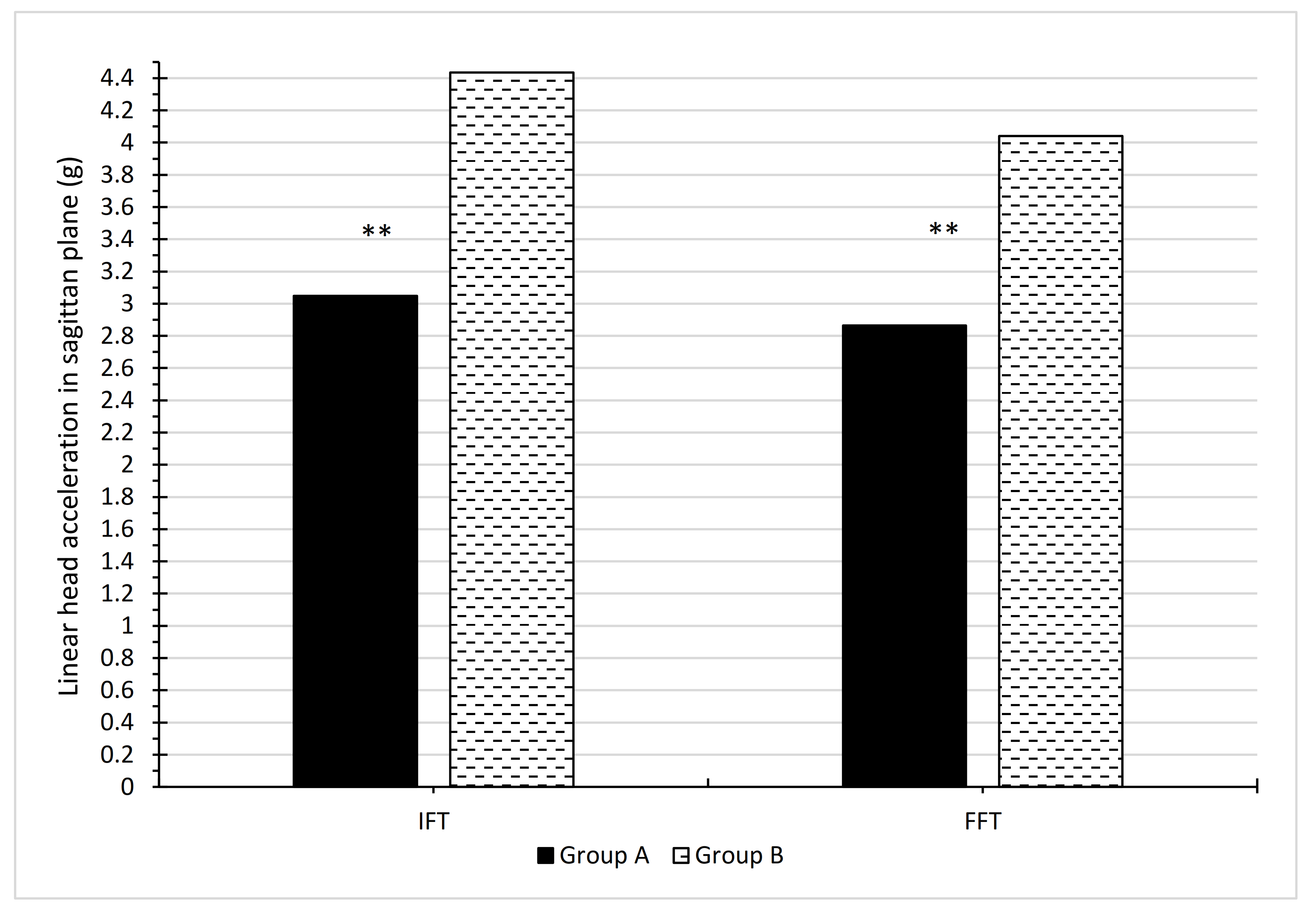
| Time (%) | n(A) | Mean A IFT | SDA IFT | minA IFT | maxA IFT | Mean A FFT | SDA FFT | minA FFT | maxA FFT | Difference (IFT–FFT) | t | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 19 | −0.31 | 0.33 | −0.86 | 0.12 | −0.33 | 0.37 | −1.21 | 0.24 | 0.02 | 0.25 | 0.8023 |
| 5 | 19 | 1.15 | 0.43 | 0.42 | 1.72 | 1.28 | 0.89 | −0.02 | 3.04 | −0.13 | −0.78 | 0.4397 |
| 10 | 19 | 1.57 | 0.63 | 0.77 | 2.90 | 1.25 | 0.58 | 0.33 | 2.59 | 0.33 | 1.94 | 0.0603 |
| 15 | 19 | 2.02 | 0.97 | 0.69 | 3.92 | 1.63 | 1.04 | 0.40 | 3.36 | 0.39 | 1.72 | 0.0938 |
| 20 | 19 | 2.20 | 0.88 | 0.84 | 3.79 | 1.41 | 0.81 | 0.31 | 3.39 | 0.80 | 4.50 | 0.0001 |
| 25 | 19 | 1.53 | 0.59 | 0.72 | 2.66 | 1.56 | 0.53 | 0.61 | 2.51 | −0.04 | −0.24 | 0.8142 |
| 30 | 19 | 1.15 | 0.47 | 0.50 | 2.20 | 1.49 | 0.41 | 0.93 | 2.31 | −0.34 | −2.37 | 0.0234 |
| 35 | 19 | 1.22 | 0.70 | 0.68 | 3.23 | 1.14 | 0.47 | 0.49 | 2.46 | 0.08 | 0.40 | 0.6889 |
| 40 | 19 | 1.06 | 0.76 | 0.19 | 3.14 | 1.15 | 0.54 | 0.44 | 2.31 | −0.09 | −0.41 | 0.6809 |
| 45 | 19 | 0.97 | 0.51 | 0.17 | 2.28 | 1.35 | 0.58 | 0.65 | 2.43 | −0.38 | −2.66 | 0.0116 |
| 50 | 19 | 0.87 | 0.35 | 0.15 | 1.31 | 1.25 | 0.50 | 0.65 | 2.40 | −0.38 | −3.54 | 0.0011 |
| 55 | 19 | 0.83 | 0.37 | 0.03 | 1.35 | 1.10 | 0.38 | 0.62 | 2.55 | −0.26 | −3.24 | 0.0026 |
| 60 | 19 | 0.89 | 0.43 | −0.23 | 1.24 | 1.02 | 0.41 | 0.50 | 2.48 | −0.13 | −0.97 | 0.3376 |
| 65 | 19 | 0.99 | 0.54 | −0.12 | 2.12 | 1.02 | 0.35 | 0.61 | 2.30 | −0.03 | −0.20 | 0.8443 |
| 70 | 19 | 0.99 | 0.38 | 0.11 | 1.58 | 1.00 | 0.38 | 0.33 | 2.28 | −0.02 | −0.16 | 0.8730 |
| 75 | 19 | 0.93 | 0.41 | 0.01 | 1.39 | 0.96 | 0.45 | 0.19 | 2.34 | −0.03 | −0.27 | 0.7868 |
| 80 | 19 | 0.83 | 0.52 | −0.13 | 1.41 | 0.85 | 0.44 | 0.10 | 2.00 | −0.02 | −0.19 | 0.8507 |
| 85 | 19 | 0.73 | 0.41 | 0.09 | 1.35 | 0.68 | 0.43 | −0.07 | 1.39 | 0.05 | 0.53 | 0.6021 |
| 90 | 19 | 0.41 | 0.51 | −0.51 | 1.21 | 0.54 | 0,57 | −0.70 | 1.42 | −0.13 | −1.32 | 0.1942 |
| 95 | 19 | 0.19 | 0.42 | −0.65 | 0.69 | 0.34 | 0,56 | −0.82 | 0.98 | −0.14 | −1.95 | 0.0596 |
| 100 | 19 | −0.02 | 0.31 | −0.50 | 0.39 | 0.12 | 0.59 | −1.10 | 1.06 | −0.14 | −1.56 | 0.1272 |
| Mean | 21 | 0.96 | 0.59 | 0.11 | 1.91 | 0.99 | 0.49 | 0.15 | 2.18 | −0.03 | −0.48 | 0.6397 |
| Time (%) | n(B) | Mean B IFT | SDB IFT | minB IFT | maxB IFT | Mean B FFT | SDB FFT | minB FFT | maxB FFT | Difference (IFT-FFT) | t | p |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 22 | −0.16 | 0.32 | −0.80 | 0.59 | −0.15 | 0.37 | −1.46 | 0.32 | −0.01 | −0.13 | 0.9002 |
| 5 | 22 | 0.62 | 0.42 | −0.12 | 1.84 | 0.75 | 0.52 | −0.18 | 1.74 | −0.12 | −0.79 | 0.4319 |
| 10 | 22 | 0.67 | 0.46 | −0.57 | 1.41 | 0.88 | 0.71 | −0.72 | 2.88 | −0.20 | −1.31 | 0.1981 |
| 15 | 22 | 0.67 | 0.69 | −0.92 | 1.91 | 0.14 | 1.10 | −2.87 | 1.93 | 0.53 | 2.52 | 0.0155 |
| 20 | 22 | 0.32 | 0.91 | −2.25 | 1.92 | 0.44 | 0.84 | −1.16 | 2.03 | −0.12 | −0.73 | 0.4705 |
| 25 | 22 | −0.29 | 1.25 | −4.51 | 1.64 | 0.02 | 0.98 | −2.03 | 2.07 | −0.31 | −2.22 | 0.0316 |
| 30 | 22 | −0.41 | 1.31 | −3.29 | 2.32 | −0. 23 | 1.00 | −2.63 | 1.39 | −0.18 | −1.33 | 0.1911 |
| 35 | 22 | −0.40 | 1.03 | −2.42 | 1.51 | −0.33 | 0.76 | −1.49 | 1.37 | −0.07 | −0.38 | 0.7064 |
| 40 | 22 | −0.65 | 1.00 | −2.91 | 1.05 | −0.41 | 0.88 | −1.51 | 2.16 | −0.24 | −1.28 | 0.2085 |
| 45 | 22 | −0.58 | 1.10 | −3.66 | 0.68 | −0.33 | 1.12 | −2.71 | 1.87 | −0.24 | −1.83 | 0.0740 |
| 50 | 22 | −0.83 | 1.81 | −6.85 | 2.99 | −0.43 | 1.05 | −2.05 | 1.14 | −0.40 | −3.98 | 0.0003 |
| 55 | 22 | −0.44 | 1.17 | −2.74 | 2.84 | −0.42 | 0.93 | −2.44 | 0.86 | −0.02 | −0.31 | 0.7586 |
| 60 | 22 | −0.62 | 1.25 | −4.74 | 1.49 | −0.18 | 1.18 | −2.71 | 2.08 | −0.45 | −3.49 | 0.0011 |
| 65 | 22 | −0.67 | 1.56 | −3.77 | 2.59 | 0.11 | 1.52 | −2.44 | 3.12 | −0.78 | −6.16 | 0.0000 |
| 70 | 22 | −0.49 | 1.43 | −2.32 | 2.80 | 0.04 | 1.29 | −2.16 | 2.47 | −0.53 | −5.22 | 0.0000 |
| 75 | 22 | −0.31 | 1.30 | −2.13 | 2.90 | −0.08 | 1.46 | −3.19 | 2.96 | −0.23 | −2.19 | 0.0344 |
| 80 | 22 | −0.56 | 0.98 | −1.92 | 1.72 | −0.07 | 1.52 | −2.50 | 3.04 | −0.48 | −4.93 | 0.0000 |
| 85 | 22 | −0.64 | 1.09 | −3.82 | 1.27 | −0.33 | 1.25 | −2.21 | 2.28 | −0.32 | −3.48 | 0.0012 |
| 90 | 22 | −0.60 | 0.92 | −2.55 | 1.27 | −0.37 | 1.27 | −3.12 | 1.26 | −0.23 | −2.60 | 0.0127 |
| 95 | 22 | −0.47 | 0.93 | −2.28 | 1.52 | −0.11 | 0.92 | −1.57 | 1.72 | −0.36 | −5.18 | 0.0000 |
| 100 | 22 | −0.43 | 0.71 | −1.21 | 1.14 | −0.10 | 0.64 | −1.10 | 1.02 | −0.33 | −4.04 | 0.0002 |
| Mean | 21 | −0.30 | 0.46 | −2.66 | 1.78 | −0.06 | 0.36 | −2.01 | 1.89 | −0.24 | −4.37 | 0.0003 |
| Time % | n(A) | Mean A IFT | n(B) | Mean B IFT | Difference | t | p |
|---|---|---|---|---|---|---|---|
| 0 | 19 | −0.3058 | 22 | −0.1582 | −0.1476 | −1.4671 | 0.1504 |
| 5 | 19 | 1.1481 | 22 | 0.6240 | 0.5241 | 3.9438 | 0.0003 |
| 10 | 19 | 1.5723 | 22 | 0.6734 | 0.8989 | 5.3038 | 0.0000 |
| 15 | 19 | 2.0201 | 22 | 0.6685 | 1.3516 | 5.2061 | 0.0000 |
| 20 | 19 | 2.2017 | 22 | 0.3189 | 1.8828 | 6.6956 | 0.0000 |
| 25 | 19 | 1.5264 | 22 | −0.2857 | 1.8121 | 5.7865 | 0.0000 |
| 30 | 19 | 1.1457 | 22 | −0.4130 | 1.5587 | 4.9036 | 0.0000 |
| 35 | 19 | 1.2225 | 22 | −0.3981 | 1.6206 | 5.8129 | 0.0000 |
| 40 | 19 | 1.0647 | 22 | −0.6523 | 1.170 | 6.1118 | 0.0000 |
| 45 | 19 | 0.9664 | 22 | −0.5764 | 1.5428 | 5.6043 | 0.0000 |
| 50 | 19 | 0.8705 | 22 | −0.8298 | 1.7003 | 4.0229 | 0.0003 |
| 55 | 19 | 0.8343 | 22 | −0.4401 | 1.2743 | 4.5545 | 0.0001 |
| 60 | 19 | 0.8895 | 22 | −0.6248 | 1.5143 | 5.0081 | 0.0000 |
| 65 | 19 | 0.9904 | 22 | −0.6701 | 1.6605 | 4.4106 | 0.0001 |
| 70 | 19 | 0.9859 | 22 | −0.4872 | 1.4732 | 4.3587 | 0.0001 |
| 75 | 19 | 0.9318 | 22 | −0.3080 | 1.2398 | 3.9781 | 0.0003 |
| 80 | 19 | 0.8305 | 22 | −0.5550 | 1.3855 | 5.5299 | 0.0000 |
| 85 | 19 | 0.7274 | 22 | −0.6419 | 1.3693 | 5.1634 | 0.0000 |
| 90 | 19 | 0.4114 | 22 | −0.6020 | 1.0135 | 4.2703 | 0.0001 |
| 95 | 19 | 0.1933 | 22 | −0.4670 | 0.6603 | 2.8623 | 0.0067 |
| 100 | 19 | −0.0174 | 22 | −0.4295 | 0.4122 | 2.3446 | 0.0242 |
| Mean | 21 | 0.9624 | 21 | −0.2978 | 1.2602 | 7.6760 | 0.0000 |
| Time % | n(A) | Mean A FFT | n(B) | Mean B FFT | Difference | t | p |
|---|---|---|---|---|---|---|---|
| 0 | 19 | −0.3263 | 22 | −0.1486 | −0.1777 | −1.5300 | 0.1341 |
| 5 | 19 | 1.2763 | 22 | 0.7450 | 0.5313 | 2.3693 | 0.0229 |
| 10 | 19 | 1.2469 | 22 | 0.8772 | 0.3698 | 1.8084 | 0.0783 |
| 15 | 19 | 1.6287 | 22 | 0.1350 | 1.4936 | 4.4549 | 0.0001 |
| 20 | 19 | 1.4056 | 22 | 0.4385 | 0.9670 | 3.7489 | 0.0006 |
| 25 | 19 | 1.5620 | 22 | 0.0243 | 1.5377 | 6.1193 | 0.0000 |
| 30 | 19 | 1.4874 | 22 | −0.2348 | 1.7222 | 6.9948 | 0.0000 |
| 35 | 19 | 1.1408 | 22 | −0.3268 | 1.4676 | 7.2863 | 0.0000 |
| 40 | 19 | 1.1502 | 22 | −0.4075 | 1.5578 | 6.6970 | 0.0000 |
| 45 | 19 | 1.3452 | 22 | −0.3338 | 1.6790 | 5.8729 | 0.0000 |
| 50 | 19 | 1.2539 | 22 | −0.4289 | 1.6828 | 6.3553 | 0.0000 |
| 55 | 19 | 1.0986 | 22 | −0.4166 | 1.5152 | 6.6199 | 0.0000 |
| 60 | 19 | 1.0235 | 22 | −0.1775 | 1.2009 | 4.2072 | 0.0001 |
| 65 | 19 | 1.0172 | 22 | 0.1063 | 0.9110 | 2.5542 | 0.0147 |
| 70 | 19 | 1.0034 | 22 | 0.0392 | 0.9642 | 3.1325 | 0.0033 |
| 75 | 19 | 0.9626 | 22 | −0.0784 | 1.0410 | 2.9801 | 0.0049 |
| 80 | 19 | 0.8505 | 22 | −0.0720 | 0.9225 | 2.5477 | 0.0149 |
| 85 | 19 | 0.6761 | 22 | −0.3263 | 1.0024 | 3.3145 | 0.0020 |
| 90 | 19 | 0.5391 | 22 | −0.3685 | 0.9077 | 2.8794 | 0.0064 |
| 95 | 19 | 0.3378 | 22 | −0.1091 | 0.4469 | 1.8428 | 0.0730 |
| 100 | 19 | 0.1195 | 22 | −0.1005 | 0.2199 | 1.1301 | 0.2653 |
| Mean | 21 | 0.9904 | 21 | −0.0554 | 1.0458 | 7.8742 | 0.0000 |
| Variable | N | Mean | Minimum | Maximum | Std Deviat. |
|---|---|---|---|---|---|
| A IFT | 19 | 3.047947 | 1.496000 | 4.570000 | 0.916093 |
| A FFT | 19 | 2.865105 | 1.662000 | 4.600000 | 0.796852 |
| B IFT | 22 | 4.434295 | 2.414000 | 9.694000 | 1.463410 |
| B FFT | 22 | 4.039909 | 2.786000 | 6.164000 | 0.902734 |
| Mean Group A | Mean Group B | t | p | |
|---|---|---|---|---|
| A IFT vs. B IFT | 3.048 | 4.434 | −3.566 | 0.000976 |
| A FFT vs. B FFT | 2.865 | 4.040 | −4.385 | 0.000085 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mroczkowski, A. Influence of the Backward Fall Technique on the Sagittal Linear Acceleration of the Head during a Fall. Int. J. Environ. Res. Public Health 2022, 19, 753. https://doi.org/10.3390/ijerph19020753
Mroczkowski A. Influence of the Backward Fall Technique on the Sagittal Linear Acceleration of the Head during a Fall. International Journal of Environmental Research and Public Health. 2022; 19(2):753. https://doi.org/10.3390/ijerph19020753
Chicago/Turabian StyleMroczkowski, Andrzej. 2022. "Influence of the Backward Fall Technique on the Sagittal Linear Acceleration of the Head during a Fall" International Journal of Environmental Research and Public Health 19, no. 2: 753. https://doi.org/10.3390/ijerph19020753
APA StyleMroczkowski, A. (2022). Influence of the Backward Fall Technique on the Sagittal Linear Acceleration of the Head during a Fall. International Journal of Environmental Research and Public Health, 19(2), 753. https://doi.org/10.3390/ijerph19020753






