Location Optimization of COVID-19 Vaccination Sites: Case in Hillsborough County, Florida
Abstract
:1. Introduction
2. Method
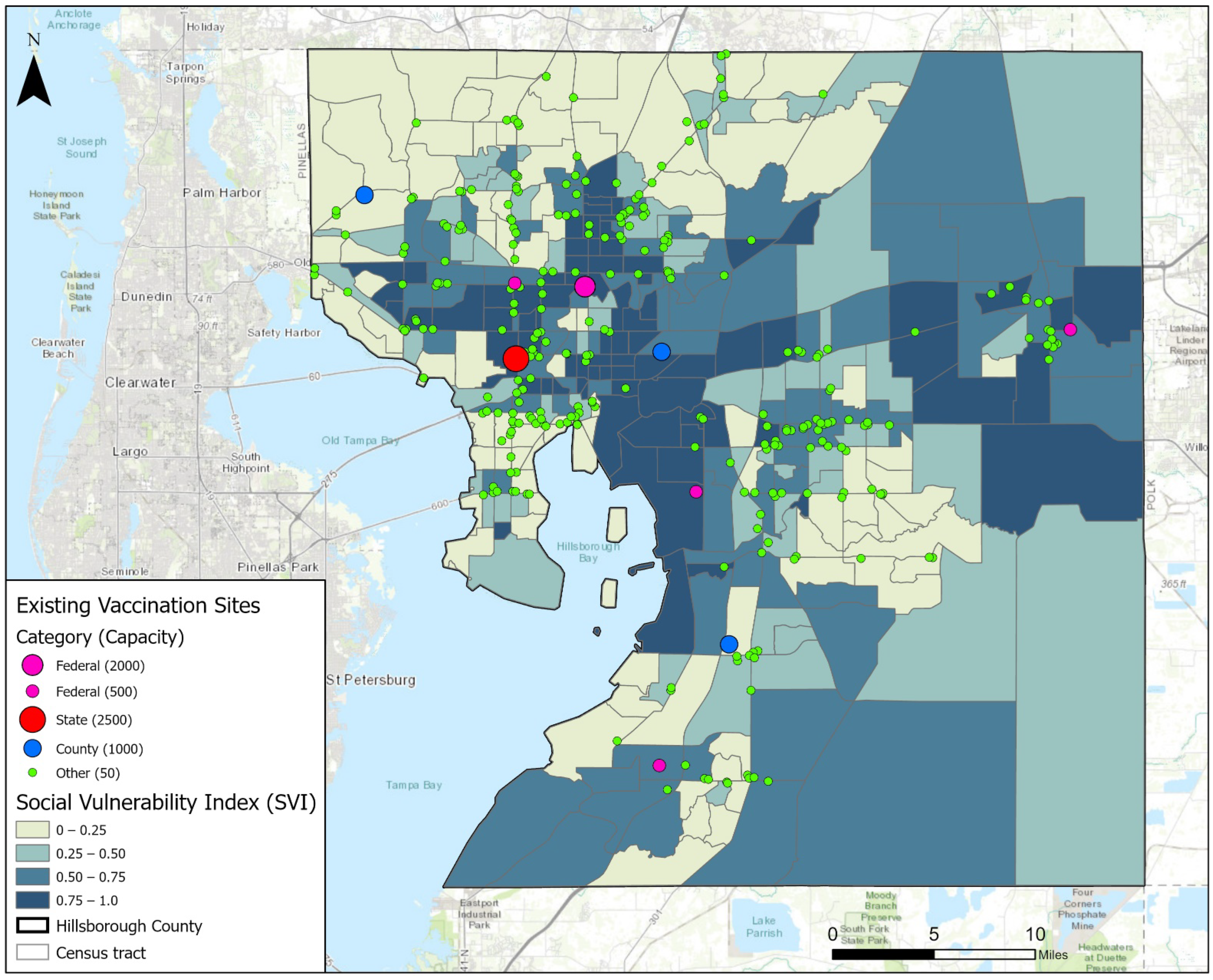
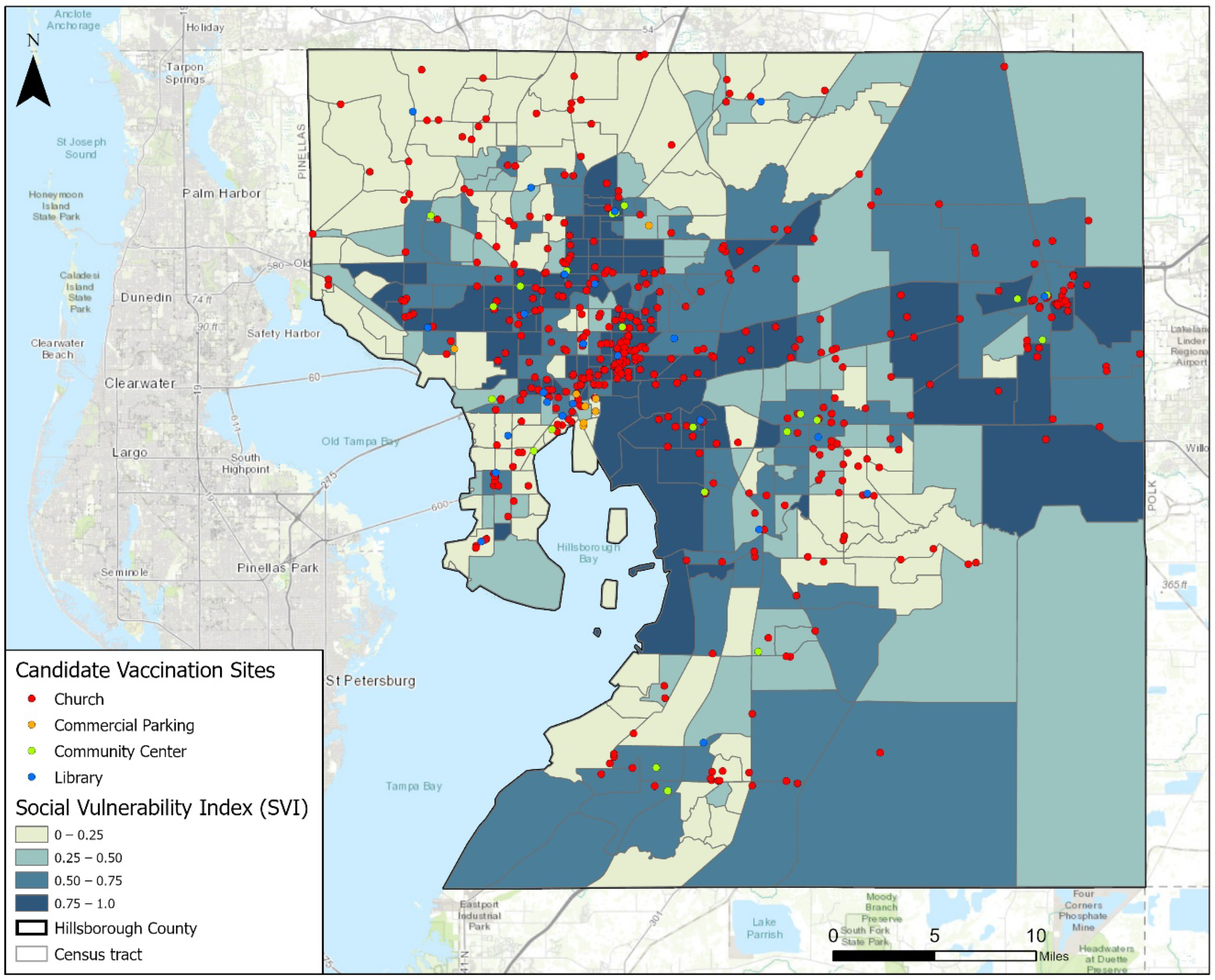
2.1. Study Area and Data Collection
2.2. Two-Step MCLP Model
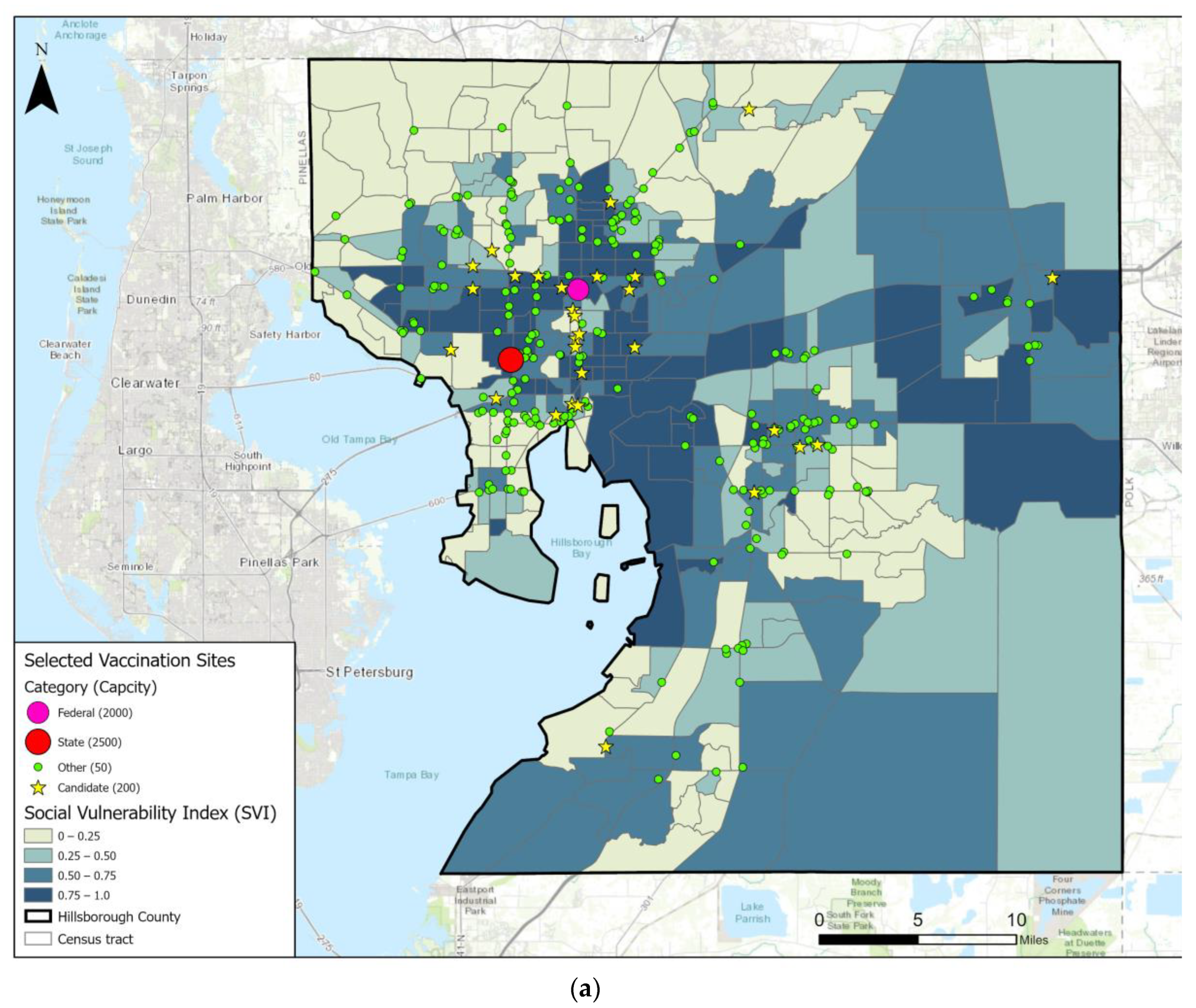
3. Results and Discussions
3.1. Reserved Vaccines for the Vulnerable
3.2. Constraint B
3.3. Capacities of Candidate Sites
3.4. Constraints C and D
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Patel, J.A.; Nielsen, F.B.H.; Badiani, A.A.; Assi, S.; Unadkat, V.A.; Patel, B.; Ravindrane, R.; Wardle, H. Poverty, inequality and COVID-19: The forgotten vulnerable. Public Health 2020, 183, 110. [Google Scholar] [CrossRef]
- Biden, J.R., Jr. National Strategy for the COVID-19 Response and Pandemic Preparedness: January 2021; Simon and Schuster: New York, NY, USA, 2021. [Google Scholar]
- National Academies of Sciences, Engineering, and Medicine. Framework for Equitable Allocation of COVID-19 Vaccine; National Academies Press: Washington, DC, USA, 2020. [Google Scholar]
- Schmidt, H.; Weintraub, R.; Williams, M.A.; Miller, K.; Buttenheim, A.; Sadecki, E.; Wu, H.; Doiphode, A.; Nagpal, N.; Gostin, L.O.; et al. Equitable allocation of COVID-19 vaccines in the United States. Nat. Med. 2021, 27, 1298–1307. [Google Scholar] [CrossRef]
- Cabanilla, K.I.M.; Enriquez, E.A.T.; Mendoza, R.; Mendoza, V.M.P. Optimal Selection of COVID-19 Vaccination Sites at the Municipal Level. medRxiv 2021. [Google Scholar] [CrossRef]
- Bertsimas, D.; Digalakis, V., Jr.; Jacquillat, A.; Li, M.L.; Previero, A. Where to locate COVID-19 mass vaccination facilities? Nav. Res. Logist. 2022, 69, 179–200. [Google Scholar]
- Tao, R.; Downs, J.; Beckie, T.M.; Chen, Y.; McNelley, W. Examining spatial accessibility to COVID-19 testing sites in Florida. Ann. GIS 2020, 26, 319–327. [Google Scholar] [CrossRef]
- Church, R.; ReVelle, C. The maximal covering location problem. In Papers of the Regional Science Association; Springer: Berlin, Germany, 1974; Volume 32, pp. 101–118. [Google Scholar]



| Case No. | Description | S in Constraint A | M in Constraint B | Selected Existing Sites | Selected Candidate Sites | Z in Objective | SVI~Drive | SVI~Walk |
|---|---|---|---|---|---|---|---|---|
| 0 | The real situation | 23,500 | 300 | 289 | 0 | 15,571,906 | 0.191 | −0.03 (N/S) |
| 1 | 0% Reserved | 23,500 | 300 | 234 | 37 | 16,463,086 | 0.227 | 0.376 |
| 2 | 10% Reserved | 23,500 | 300 | 239 | 37 | 16,432,874 | 0.229 | 0.381 |
| 3 | 20% Reserved | 23,500 | 300 | 242 | 35 | 16,346,930 | 0.238 | 0.376 |
| 4 | 30% Reserved | 23,500 | 300 | 234 | 37 | 16,203,260 | 0.255 | 0.381 |
| 5 | 30% Reserved for step1 | 23,500 | 300 | 238 | 36 | 16,199,157 | 0.218 | 0.370 |
| Case No. | Description | S in Constraint A | M in Constraint B | Selected Existing Sites | Selected Candidate Sites | Z in Objective | SVI~Drive | SVI~Walk |
|---|---|---|---|---|---|---|---|---|
| 4a | 30% Reserved | 23,500 | 100 | 254 | 32 | 29,741,147 | 0.264 | 0.373 |
| 4 | 30% Reserved | 23,500 | 300 | 234 | 37 | 16,203,260 | 0.255 | 0.381 |
| 4b | 30% Reserved | 23,500 | 500 | 162 | 55 | 10,344,833 | 0.238 | 0.377 |
| Case No. | Description | S in Constraint A | M in Constraint B | Candidate Site Capacity | Selected Existing Sites | Selected Candidate Sites | Z in Objective | SVI~Drive | SVI~Walk |
|---|---|---|---|---|---|---|---|---|---|
| 4c | 30% Reserved | 23,500 | 300 | 50 | 112 | 212 | 16,956,177 | 0.305 | 0.395 |
| 4 | 30% Reserved | 23,500 | 300 | 200 | 234 | 37 | 16,203,260 | 0.255 | 0.381 |
| 4d | 30% Reserved | 23,500 | 300 | 500 | 242 | 14 | 15,568,174 | 0.241 | 0.376 |
| 4e | 30% Reserved | 23,500 | 300 | 1000 | 232 | 7 | 15,407,636 | 0.232 | 0.371 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Tao, R.; Downs, J. Location Optimization of COVID-19 Vaccination Sites: Case in Hillsborough County, Florida. Int. J. Environ. Res. Public Health 2022, 19, 12443. https://doi.org/10.3390/ijerph191912443
Chen Y, Tao R, Downs J. Location Optimization of COVID-19 Vaccination Sites: Case in Hillsborough County, Florida. International Journal of Environmental Research and Public Health. 2022; 19(19):12443. https://doi.org/10.3390/ijerph191912443
Chicago/Turabian StyleChen, Yuzhou, Ran Tao, and Joni Downs. 2022. "Location Optimization of COVID-19 Vaccination Sites: Case in Hillsborough County, Florida" International Journal of Environmental Research and Public Health 19, no. 19: 12443. https://doi.org/10.3390/ijerph191912443
APA StyleChen, Y., Tao, R., & Downs, J. (2022). Location Optimization of COVID-19 Vaccination Sites: Case in Hillsborough County, Florida. International Journal of Environmental Research and Public Health, 19(19), 12443. https://doi.org/10.3390/ijerph191912443







