A Simple Index of Lake Ecosystem Health Based on Species-Area Models of Macrobenthos
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
2.2. Index Development
- (1)
- O/E-SA index
- (2)
- O/E-RF indices
- (3)
- Other indices
3. Results
3.1. Taxonomic Composition
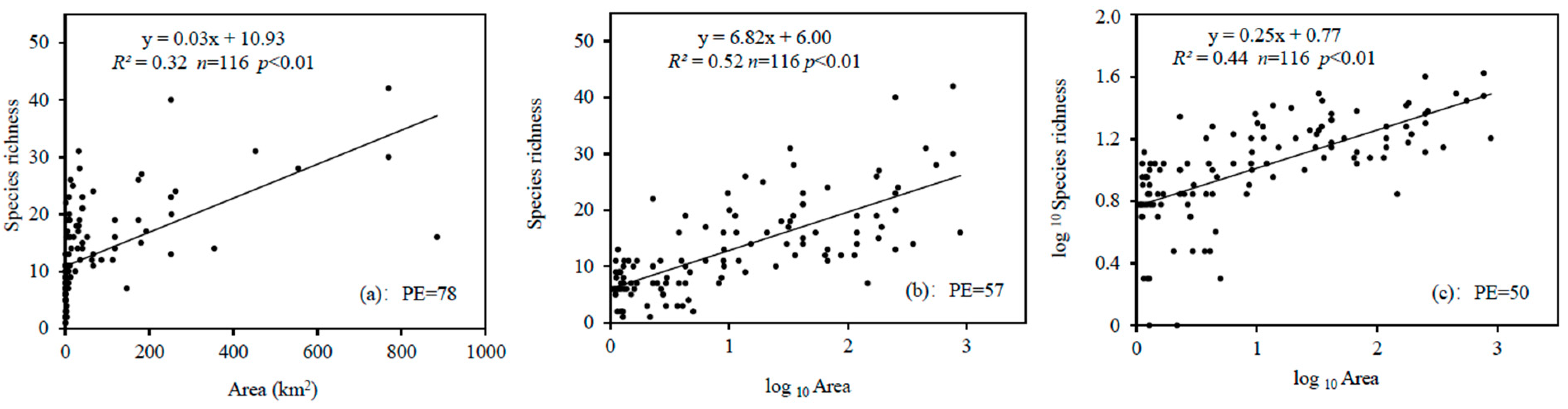
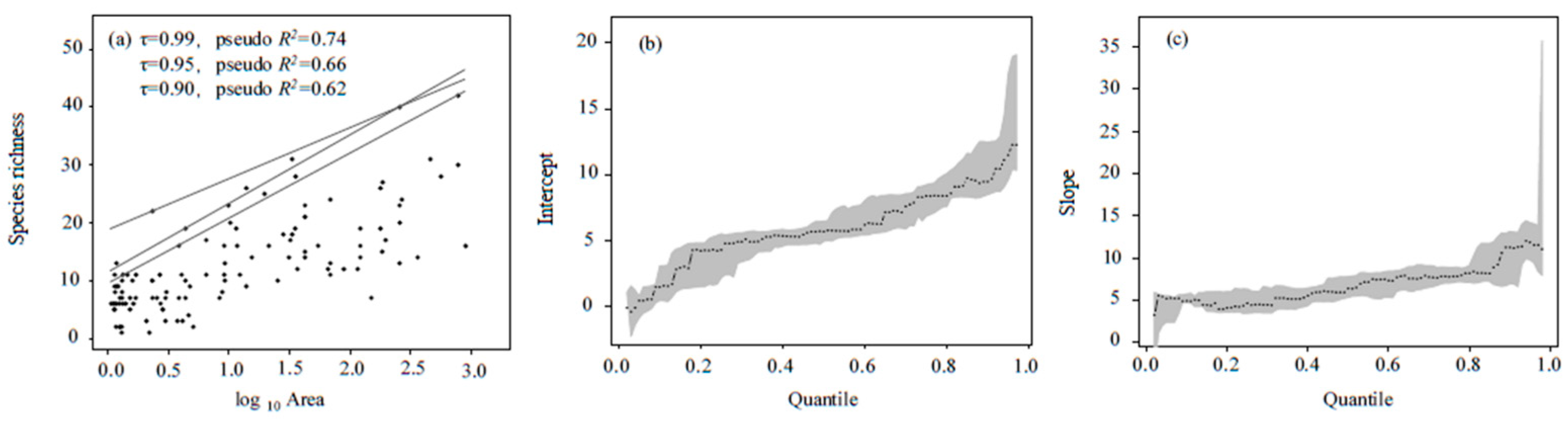
3.2. O/E-SA Modeling
3.3. O/E-RF Modeling
3.4. Comparison of INDICES
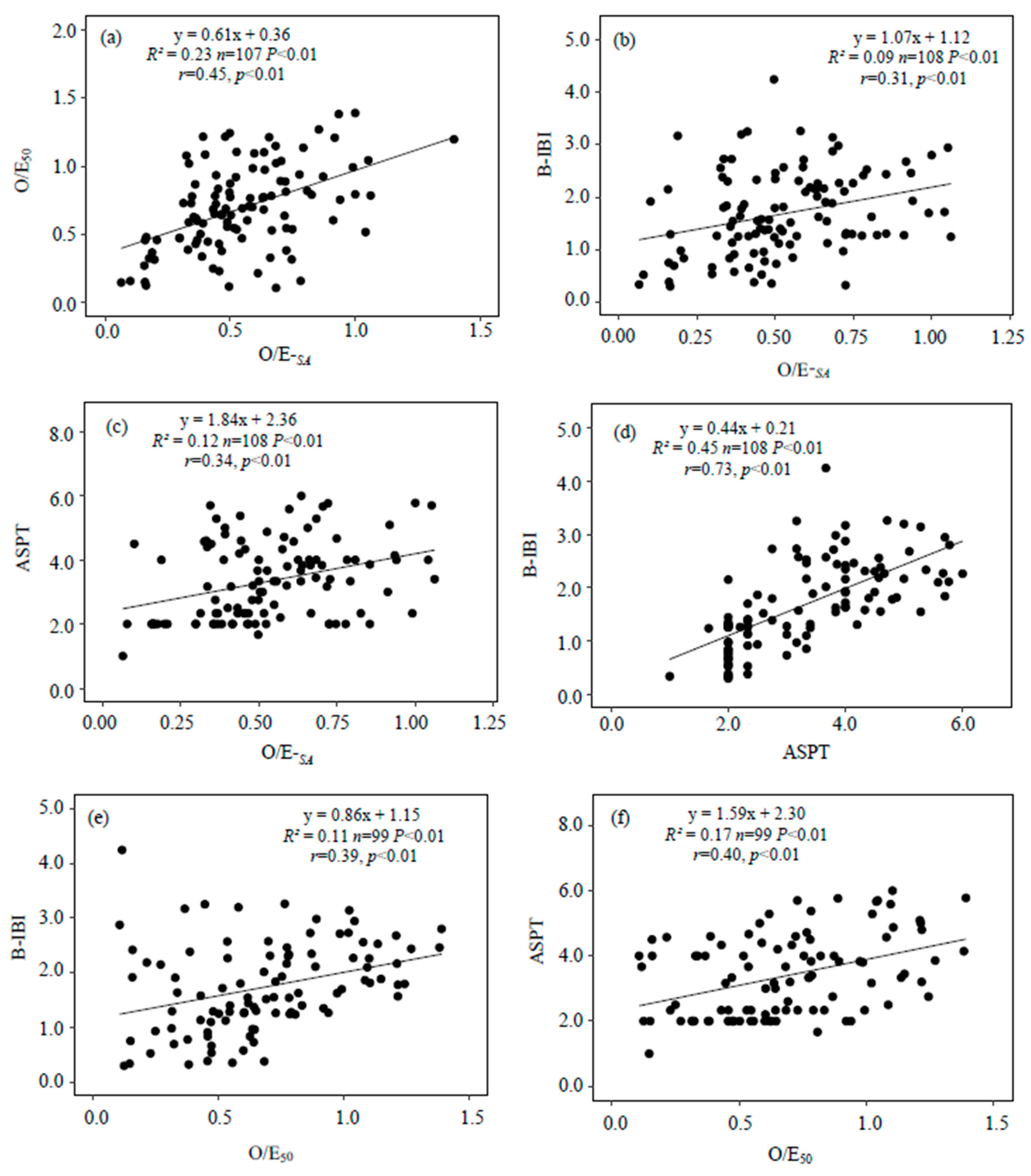
3.4.1. Relationships between O/E-SA and Other Indices
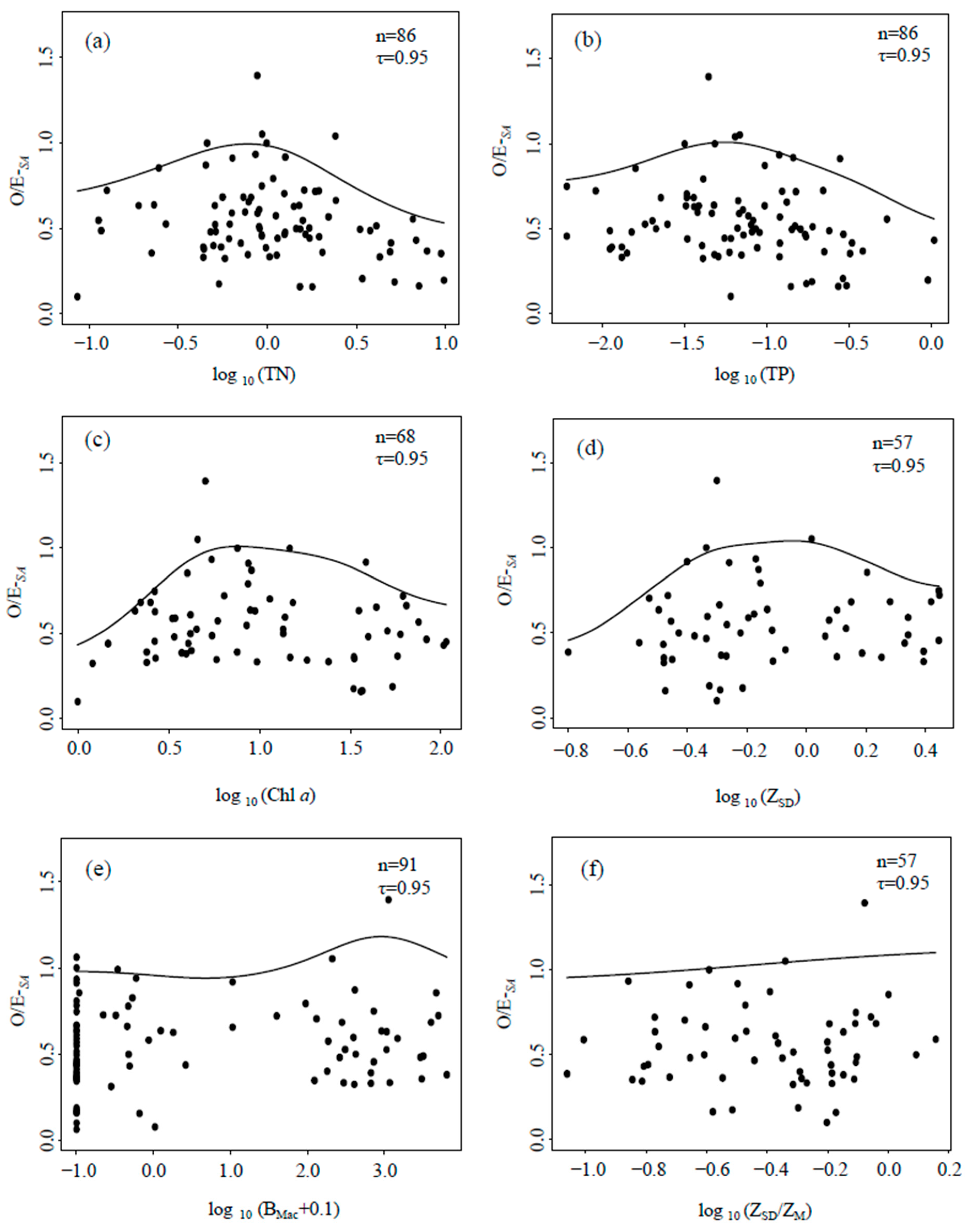
3.4.2. Relationships between Macrobenthos Indices and Eutrophication Metrics
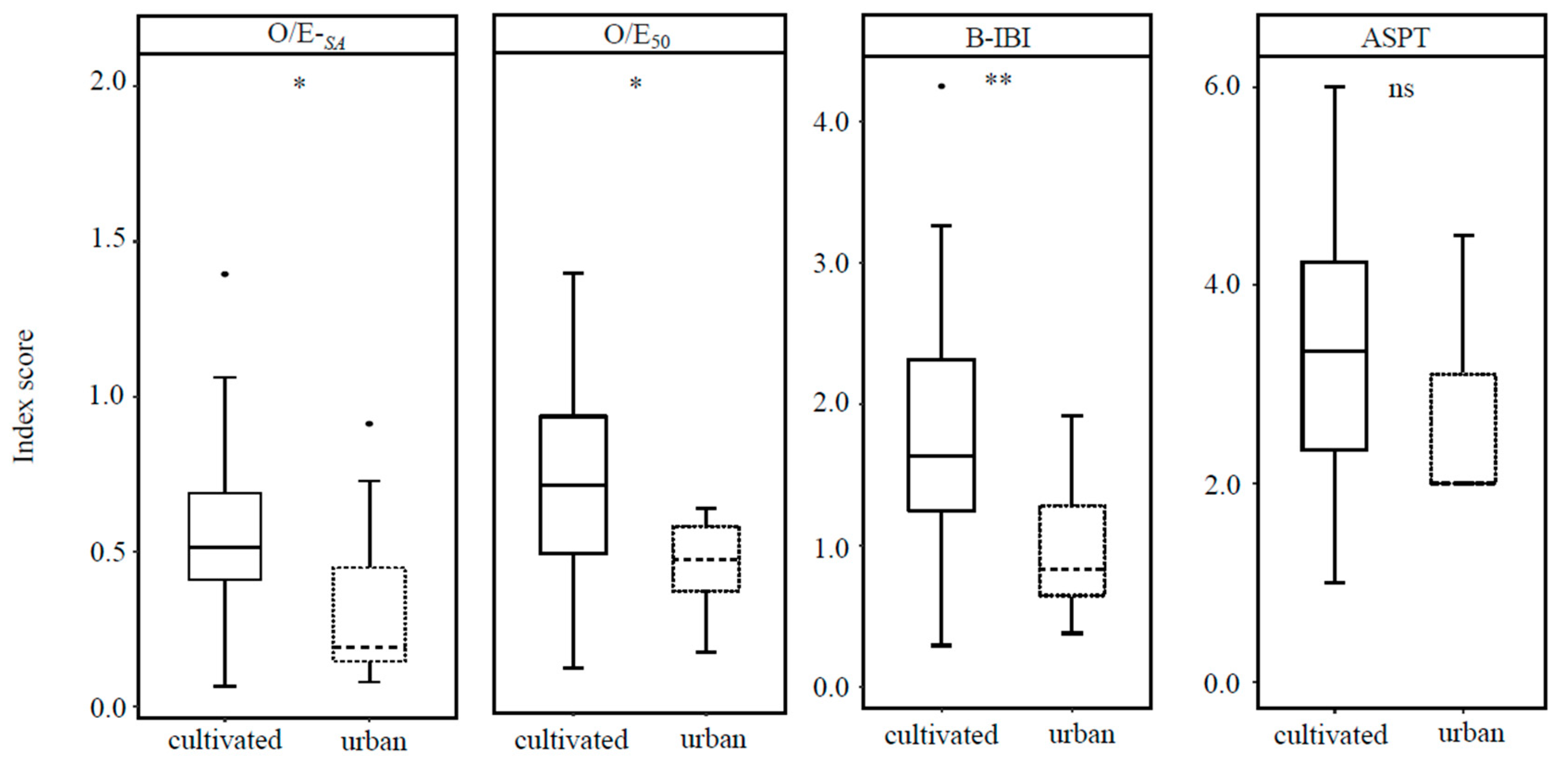
3.4.3. Comparison of Macrobenthos Index Scores in Cultivated and Urban Lakes
4. Discussion
4.1. O/E-SA Is a Simple and Reliable Index for Lake Biological Assessment
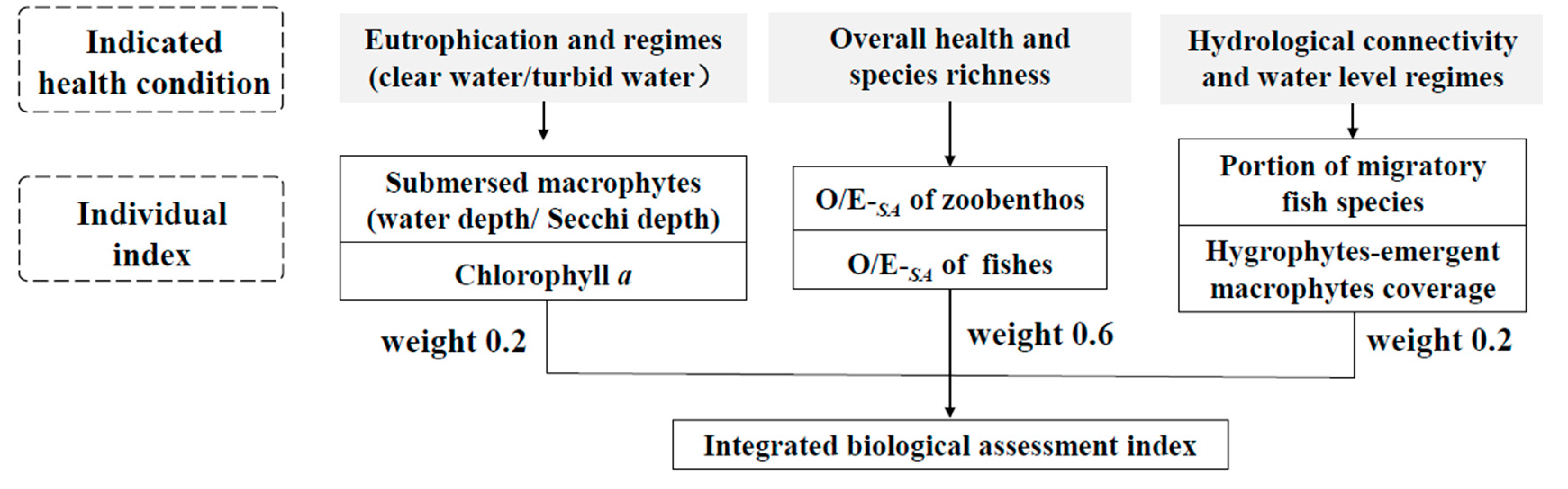
4.2. Constructing an Integrated Biological Assessment Index for Lakes
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, H.Z.; Liu, X.Q.; Wang, H.J. The Yangtze River Floodplain: Threats and Rehabilitation. In Fishery Resources, Environment, and Conservation in the Mississippi and Yangtze; Chen, Y., Chapman, D.C., Jackson, J.R., Chen, D., Li, Z., Killgore, K.J., Phelps, Q., Eggleton, M.A., Eds.; American Fisheries Society Symposium 84; American Fisheries Society: Maryland, MD, USA, 2016; Volume 84, pp. 263–291. [Google Scholar]
- SEPA; AQSIQ. Environmental Quality Standards for Surface Water: GB3838–2002; China Environmental Science Press: Beijing, China, 2002. [Google Scholar]
- Hughes, R.M.; Noss, R.F. Biological Diversity and Biological Integrity: Current Concerns for Lakes and Streams. Fisheries 1992, 17, 11–19. [Google Scholar] [CrossRef]
- Chen, K. Incorporating functional traits to enhance multimetric index performance and assess land use gradients. Sci. Total Environ. 2019, 691, 1005–1015. [Google Scholar] [CrossRef]
- Klemm, D.J.; Blocksom, K.A.; Fulk, F.A.; Herlihy, A.T.; Hughes, R.M.; Kaufmann, P.R.; Peck, D.V.; Stoddard, J.L.; Thoeny, W.T.; Griffith, M.B.; et al. Development and evaluation of a Macroinvertebrate Biotic Integrity Index (MBII) for regionally assessing Mid-Atlantic Highlands Streams. Environ. Manag. 2003, 31, 656–669. [Google Scholar] [CrossRef]
- Ruaro, R.; Gubiani, É.A.; Hughes, R.M.; Mormul, R.P. Global trends and challenges in multimetric indices of biological condition. Ecol. Indic. 2020, 110, 105862. [Google Scholar] [CrossRef]
- Beck, M.W.; Hatch, L.K. A review of research on the development of lake indices of biotic integrity. Environ. Rev. 2009, 17, 21–44. [Google Scholar] [CrossRef]
- Kuehne, L.M.; Olden, J.D.; Strecker, A.L.; Lawler, J.J.; Theobald, D.M. Past, present, and future of ecological integrity assessment for fresh waters. Front. Ecol. Environ. 2017, 15, 197–205. [Google Scholar] [CrossRef]
- Albrecht, J.; Peters, M.K.; Becker, J.N.; Behler, C.; Classen, A.; Ensslin, A.; Ferger, S.W.; Gebert, F.; Gerschlauer, F.; Helbig-Bonitz, M.; et al. Species richness is more important for ecosystem functioning than species turnover along an elevational gradient. Nat. Ecol. Evol. 2021, 5, 1582–1593. [Google Scholar] [CrossRef]
- Gaston, K. Global patterns in biodiversity. Nature 2000, 405, 220–227. [Google Scholar] [CrossRef]
- Gotelli, N.J.; Colwell, R.K. Quantifying biodiversity: Procedures and pitfalls in the measurement and comparison of species richness. Ecol. Lett. 2001, 4, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Cairns, J.; McCormick, P.V.; Niederlehner, B.R. A proposed framework for developing indicators of ecosystem health. Hydrobiologia 1993, 263, 1–44. [Google Scholar] [CrossRef]
- De Jonge, M.; Van de Vijver, B.; Blust, R.; Bervoets, L. Responses of aquatic organisms to metal pollution in a lowland river in Flanders: A comparison of diatoms and macroinvertebrates. Sci. Total Environ. 2008, 407, 615–629. [Google Scholar] [CrossRef]
- Hurlbert, S.H. The Nonconcept of Species Diversity: A Critique and Alternative Parameters. Ecology 1971, 52, 577–586. [Google Scholar] [CrossRef]
- Koperski, P.; Meronka, R. Environmental quality of a stream can be better predicted by phylogenetic than by taxonomic diversity. Knowl. Manag. Aquat. Ecosyst. 2017, 418, 16. [Google Scholar] [CrossRef] [Green Version]
- Stoddard, J.L.; Larsen, D.P.; Hawkins, C.P.; Johnson, R.K.; Norris, R.H. Setting expectations for the ecological condition of running waters the concept of reference condition. Ecol. Appl. 2006, 16, 1267–1276. [Google Scholar] [CrossRef]
- Hering, D.; Feld, C.K.; Moog, O.; Ofenbock, T. Cook book for the development of a Multimetric Index for biological condition of aquatic ecosystems: Experiences from the European AQEM and STAR projects and related initiatives. Hydrobiologia 2006, 566, 311–324. [Google Scholar] [CrossRef]
- Clarke, R.T.; Wright, J.F.; Furse, M.T. RIVPACS models for predicting the expected macroinvertebrate fauna and assessing the ecological quality of rivers. Ecol. Model. 2003, 160, 219–233. [Google Scholar] [CrossRef]
- Hawkins, C.P.; Norris, R.H.; Hogue, J.N.; Feminella, J.W. Development and evaluation of predictive models for measuring the biological integrity of streams. Ecol. Appl. 2000, 10, 1456–1477. [Google Scholar] [CrossRef]
- Clarke, R.T.; Murphy, J.F. Effects of locally rare taxa on the precision and sensitivity of RIVPACS bioassessment of freshwaters. Freshwat. Biol. 2006, 51, 1924–1940. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Chen, Q.W.; YU, H.Y.; Wang, B.X.; Jin, X.W.; Wang, Y.Y.; Xu, R.J.; Cai, K. Methods and prospects of index of biological integrity used for China river ecological health assessment. China Environ. Sci. 2018, 38, 1589–1600. [Google Scholar]
- Fausch, K.D.; Karr, J.R.; Yant, P.R. Regional Application of an Index of Biotic Integrity Based on Stream Fish Communities. Trans. Am. Fish. Soc. 1984, 113, 39–55. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Z.; Yuan, S.; Wang, H. A novel methodology for the assessment of water level requirements in shallow lakes. Ecol. Eng. 2017, 102, 31–38. [Google Scholar] [CrossRef]
- Morse, J.C.; Yang, L.F.; Tian, L.X. Aquatic Insects of China Useful for Monitoring Water Quality; Hohai University Press: Nanjing, China, 1994. [Google Scholar]
- Wang, H.Z. Studies on Taxonomy, Distribution and Ecology of Microdrile Oligochaetes of China, with Description of Two New Species from the Vicinity of the Great Wall Station of China, Antarctica; Higher Education: Beijing, China, 2002. [Google Scholar]
- Wang, H.J.; Pan, B.Z.; Liang, X.M.; Wang, H.Z. Gastropods on Submersed Macrophytes in Yangtze Lakes: Community Characteristics and Empirical Modelling. Int. Rev. Hydrobiol. 2006, 91, 521–538. [Google Scholar] [CrossRef]
- Huang, X.F.; Chen, W.M.; Cai, Q.M. Survey, Observation and Analysis of Lake Ecology; Standards Press of China: Beijing, China, 1999. [Google Scholar]
- Canfield, D.E.J. Prediction of chlorophyll a concentrations in Florida lakes: The importance of phosphorus and nitrogen. Water Resour. Bull. 1983, 19, 255–262. [Google Scholar] [CrossRef]
- Hawkins, C.P.; Carlisle, D.M. Use of Predictive Models for Assessing the Biological Integrity of Wetlands and Other Aquatic Habitats. In Bioassessment and Management of North American Freshwater Wetlands; John Wiley & Son: New York, NY, USA, 2001; pp. 59–83. [Google Scholar]
- Van Sickle, J.; Hawkins, C.P.; Larsen, D.P.; Herlihy, A.T. A null model for the expected macroinvertebrate assemblage in streams. J. N. Am. Benthol. Soc. 2005, 24, 178–191. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Armitage, P.D.; Moss, D.; Wright, J.F.; Furse, M.T. The performance of a new biological water quality score system based on macroinvertebrates over a wide range of unpolluted running-water sites. Water Res. 1983, 17, 333–347. [Google Scholar] [CrossRef]
- Zhang, J.W.; Cai, K.; Yu, H.Y.; Jiang, Y.W.; Li, X.W.; Zhou, S.L.; Xie, Z.C.; Wang, Y.Y.; Jin, X.W.; Wang, B.X. Establishment of Chinese Macroinvertebrate Score Index and Water Quality Boundary. Environ. Monit. China 2018, 34, 10–18. (In Chinese) [Google Scholar] [CrossRef]
- Barbour, M.T.; Gerritsen, J.; Griffith, G.E.; Frydenborg, R.; McCarron, E.; White, J.S.; Bastian, M.L. A framework for biological criteria for Florida streams using benthic macroinvertebrates. J. N. Am. Benthol. Soc. 1996, 15, 185–211. [Google Scholar] [CrossRef]
- Hawkins, C.P.; Cao, Y.; Roper, B. Method of predicting reference condition biota affects the performance and interpretation of ecological indices. Freshw. Biol. 2010, 55, 1066–1085. [Google Scholar] [CrossRef]
- Lemm, J.U.; Feld, C.K.; Birk, S. Diagnosing the causes of river deterioration using stressor-specific metrics. Sci. Total Environ. 2019, 651, 1105–1113. [Google Scholar] [CrossRef]
- Dodson, S.I.; Arnott, S.E.; Cottingham, K.L. The relationship in lake communities between primary productivity and species richness. Ecology 2000, 81, 2662–2679. [Google Scholar] [CrossRef]
- Karr, J.R. Assessment of Biotic Integrity Using Fish Communities. Fisheries 1981, 6, 21–27. [Google Scholar] [CrossRef]
- Heatherly, T.; Whiles, M.R.; Knuth, D.; Garvey, J.E. Diversity and community structure of littoral zone macroinvertebrates in southern Illinois reclaimed surface mine lakes. Am. Midl. Nat. 2005, 154, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Porst, G.; Bader, S.; Munch, E.; Pusch, M. Sampling approaches for the assessment of shoreline development based on littoral macroinvertebrates: The case of Lake Werbellin, Germany. Fundam. Appl. Limnol. 2012, 180, 123–131. [Google Scholar] [CrossRef]
- Birk, S.; Bonne, W.; Borja, A.; Brucet, S.; Courrat, A.; Poikane, S.; Solimini, A.; van de Bund, W.; Zampoukas, N.; Hering, D. Three hundred ways to assess Europe’s surface waters: An almost complete overview of biological methods to implement the Water Framework Directive. Ecol. Indic. 2012, 18, 31–41. [Google Scholar] [CrossRef]
- Chen, K.; Hughes, R.M.; Wang, B. Effects of fixed-count size on macroinvertebrate richness, site separation, and bioassessment of Chinese monsoonal streams. Ecol. Indic. 2015, 53, 162–170. [Google Scholar] [CrossRef]
- Borja, A.; Tunberg, B.G. Assessing benthic health in stressed subtropical estuaries, eastern Florida, USA using AMBI and M-AMBI. Ecol. Indic. 2011, 11, 295–303. [Google Scholar] [CrossRef]
- Hering, D.; Borja, A.; Jones, J.I.; Pont, D.; Boets, P.; Bouchez, A.; Bruce, K.; Drakare, S.; Hanfling, B.; Kahlert, M.; et al. Implementation options for DNA-based identification into ecological status assessment under the European Water Framework Directive. Water Res. 2018, 138, 192–205. [Google Scholar] [CrossRef]
- Pawlowski, J.; Kelly-Quinn, M.; Altermatt, F.; Apotheloz-Perret-Gentil, L.; Beja, P.; Boggero, A.; Borja, A.; Bouchez, A.; Cordier, T.; Domaizon, I.; et al. The future of biotic indices in the ecogenomic era: Integrating (e)DNA metabarcoding in biological assessment of aquatic ecosystems. Sci. Total Environ. 2018, 637–638, 1295–1310. [Google Scholar] [CrossRef]
- Whittier, T.R.; Halliwell, D.B.; Paulsen, S.G. Cyprinid distributions in Northeast USA lakes: Evidence of regional-scale minnow biodiversity losses. Can. J. Fish. Aquat. Sci. 1997, 54, 1593–1607. [Google Scholar] [CrossRef]
- Whittier, T.R.; Kincaid, T.M. Introduced Fish in Northeastern USA Lakes: Regional Extent, Dominance, and Effect on Native Species Richness. Trans. Am. Fish. Soc. 1999, 128, 769–783. [Google Scholar] [CrossRef]
- Wang, H.J.; Wang, H.Z.; Liang, X.M.; Wu, S.K. Total phosphorus thresholds for regime shifts are nearly equal in subtropical and temperate shallow lakes with moderate depths and areas. Freshw. Biol. 2014, 59, 1659–1671. [Google Scholar] [CrossRef] [Green Version]
| Reference Site | Test Site | |||||
|---|---|---|---|---|---|---|
| Mean | Precision SD | Bias RF% Var | Mean | Sensitivity %NRC | Responsiveness t-Value | |
| O/E0 | 0.99 | 0.33 | 9.52 | 0.54 | 1.00 | 6.96 |
| O/E0-null | 1.00 | 0.37 | 19.33 | 0.54 | 1.00 | 8.46 |
| O/E50 | 1.02 | 0.18 | 0.00 | 0.61 | 0.99 | 8.29 |
| O/E50-null | 1.00 | 0.17 | 4.51 | 0.67 | 0.95 | 8.85 |
| O/E-SA | 1.00 | 0.20 | 0.42 | 0.74 | 0.99 | 3.94 |
| B-IBI | 1.00 | 0.26 | 3.53 | 0.64 | 0.94 | 5.23 |
| ASPT | 1.00 | 0.37 | 3.84 | 0.70 | 0.97 | 4.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; He, Y.; Zhao, Y.; Chen, K.; Cui, Y.; Wang, H. A Simple Index of Lake Ecosystem Health Based on Species-Area Models of Macrobenthos. Int. J. Environ. Res. Public Health 2022, 19, 9678. https://doi.org/10.3390/ijerph19159678
Wu J, He Y, Zhao Y, Chen K, Cui Y, Wang H. A Simple Index of Lake Ecosystem Health Based on Species-Area Models of Macrobenthos. International Journal of Environmental Research and Public Health. 2022; 19(15):9678. https://doi.org/10.3390/ijerph19159678
Chicago/Turabian StyleWu, Junyan, Yajing He, Yongjing Zhao, Kai Chen, Yongde Cui, and Hongzhu Wang. 2022. "A Simple Index of Lake Ecosystem Health Based on Species-Area Models of Macrobenthos" International Journal of Environmental Research and Public Health 19, no. 15: 9678. https://doi.org/10.3390/ijerph19159678
APA StyleWu, J., He, Y., Zhao, Y., Chen, K., Cui, Y., & Wang, H. (2022). A Simple Index of Lake Ecosystem Health Based on Species-Area Models of Macrobenthos. International Journal of Environmental Research and Public Health, 19(15), 9678. https://doi.org/10.3390/ijerph19159678







