Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm
Abstract
1. Introduction
- Is it possible to utilize a GP algorithm to obtain the symbolic expression for each U.S. state based on latitude and longitude of the central location of that state and the number of days since the outbreak began for the estimation of the number confirmed, deceased and recovered patients with high accuracy?
- Based on the obtained symbolic expressions for the estimation of the number of confirmed, deceased and recovered patients for each U.S. state, is it possible to formulate the symbolic expressions for the estimation of the number of confirmed, deceased and recovered patients for the entire U.S. with high accuracy?
- Is it possible to utilize three symbolic expressions for the estimation of the number confirmed, deceased and recovered patients for the entire U.S. to formulate symbolic expression for estimation of the epidemiology curve for the entire U.S. with high accuracy?
2. Materials and Methods
2.1. Dataset Description
2.2. Genetic Programming Algorithm
Fitness Function
- Crossover is taking two selected solutions and combining them into a new, children, solution (influenced by the crossover coefficient).
- Mutation is randomly modifying an existing solution from the previous and copying it to the current generation (influenced by the subtree, hoist and point mutation coefficients).
- Reproduction is copying the solutions from the previous to the current generation without modification (influenced by the maximal sample’s coefficient).
2.3. Epidemiology Curve
3. Results and Discussion
3.1. Symbolic Expression for Estimation of the Number of Confirmed Patients for Each State and the Entire U.S.
3.2. Symbolic Expression for Estimation of the Number of Deceased Patients for Each State and the Entire U.S.
3.3. Symbolic Expression for Estimation of the Number of Recovered Patients for Each State and the Entire U.S.
Symbolic Expression for Estimation of Epidemiology Curve for the Entire U.S.
3.4. Sensitivity Analysis
3.5. Discussion
4. Conclusions
- The GP algorithm can be utilized to obtain symbolic expressions for each U.S. state based on the latitude and longitude of their central location and day as an input variable to estimate the number of confirmed/deceased/recovered patients for the aforementioned state.
- The obtained symbolic expressions for the estimation of the number of confirmed/deceased/recovered patients for each state can be summed to obtain the symbolic expression for the estimation of the number of confirmed/deceased/recovered patients for the entire U.S. with high accuracy.
- Symbolic expressions for the estimation of the number of confirmed, deceased and recovered patients of the entire U.S. can be combined to obtain the symbolic expression for the estimation of the epidemiology curve with very high accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Tables of Results and Hyperparameters for Each State
Appendix A.1. Table of Results and Hyperparameters for Confirmed Patients
| Federal State | GP Paramters (Population size, Number of Generations, Tournament Selection, Tree Depth, Crossover Coefficient, Subtree Mutation Coefficient, Point Mutation Coefficient, Hoist Mutation Coefficient, Maximum Samples, Constant Range, Parsimony Coefficeint) | Score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alabama | 211 | 174 | 49 | (5, 11) | 0.92 | 0.0086 | 0.0377 | 0.0348 | 0.74 | 0.97 | (−70,101.14, 63,475.94) | 0.337 | 0.9946 |
| Alaska | 771 | 160 | 77 | (5, 11) | 0.9 | 0.0081 | 0.0314 | 0.005 | 0.25 | 0.99 | (−74,741.62, 45,222.72) | 0.913 | 0.9977 |
| Arizona | 883 | 147 | 70 | (4, 12) | 0.91 | 0.0209 | 0.0401 | 0.0283 | 0.23 | 0.96 | (−81,270.3, 72,219.87) | 0.928 | 0.9988 |
| Arkansas | 960 | 119 | 28 | (6, 9) | 0.91 | 0.055 | 0.0023 | 0.0111 | 0.36 | 0.97 | (−10,062.42, 73,692.85) | 1.655 | 0.9973 |
| California | 461 | 165 | 37 | (4, 12) | 0.91 | 0.011 | 0.0024 | 0.0676 | 0.28 | 0.92 | (−37,240.04, 78,697.54) | 0.507 | 0.9974 |
| Colorado | 460 | 107 | 45 | (5, 12) | 0.93 | 0.0019 | 0.017 | 0.0488 | 0.13 | 0.97 | (−56,475.89, 14,750.88) | 0.913 | 0.9951 |
| Connecticut | 901 | 195 | 49 | (5, 8) | 0.9 | 0.0005 | 0.0124 | 0.0648 | 0.24 | 0.9 | (−28,905.51, 10,867.32) | 1.129 | 0.9972 |
| Delaware | 511 | 156 | 85 | (4, 12) | 0.9 | 0.0319 | 0.0029 | 0.0034 | 0.59 | 0.98 | (−92,946.76, 90,765.21) | 1.153 | 0.9982 |
| Florida | 930 | 155 | 93 | (5, 11) | 0.91 | 0.014 | 0.0365 | 0.0412 | 0.17 | 0.97 | (−74,763.22, 17,556.85) | 1.631 | 0.9975 |
| Georgia | 710 | 180 | 44 | (4, 10) | 0.91 | 0.0243 | 0.0249 | 0.019 | 0.79 | 0.93 | (−11,923.53, 43,023.78) | 0.781 | 0.9990 |
| Hawaii | 637 | 188 | 39 | (4, 9) | 0.91 | 0.0622 | 0.0177 | 0.0098 | 0.72 | 0.99 | (−84,943.77, 58,918.57) | 0.406 | 0.9978 |
| Idaho | 822 | 185 | 41 | (5, 12) | 0.9 | 0.0043 | 0.0387 | 0.0414 | 0.96 | 0.91 | (−50,998.8, 83,710.65) | 1.441 | 0.9939 |
| Illinois | 820 | 174 | 53 | (6, 8) | 0.91 | 0.0101 | 0.0001 | 0.0025 | 0.4 | 0.97 | (−68,319.97, 77,849.63) | 0.334 | 0.9949 |
| Indiana | 966 | 194 | 22 | (4, 11) | 0.91 | 0.0303 | 0.0415 | 0.0127 | 0.08 | 0.94 | (−73,395.89, 37,738.69) | 1.512 | 0.9966 |
| Iowa | 516 | 116 | 32 | (6, 8) | 0.91 | 0.0008 | 0.0477 | 0.0037 | 0.39 | 0.91 | (−28,074.55, 95,030.32) | 0.332 | 0.9961 |
| Kansas | 277 | 174 | 44 | (6, 9) | 0.9 | 0.0293 | 0.0109 | 0.0411 | 0.67 | 0.91 | (−82,436.08, 59,439.65) | 1.681 | 0.9979 |
| Kentucky | 867 | 111 | 97 | (3, 12) | 0.93 | 0.0046 | 0.0331 | 0.0293 | 0.95 | 0.94 | (−30,555.51, 41,645.64) | 1.202 | 0.9979 |
| Louisiana | 284 | 174 | 91 | (3, 9) | 0.96 | 0.0219 | 0.0108 | 0.0062 | 0.87 | 0.99 | (−95,819.22, 60,443.52) | 1.953 | 0.9924 |
| Maine | 804 | 133 | 86 | (4, 9) | 0.9 | 0.021 | 0.0102 | 0.0025 | 0.02 | 0.99 | (−37,413.71, 42,394.4) | 1.417 | 0.9931 |
| Maryland | 507 | 145 | 25 | (3, 12) | 0.95 | 0.0298 | 0.0023 | 0.0179 | 0.38 | 0.98 | (−15,303.86, 17,295.29) | 0.529 | 0.9933 |
| Massachusetts | 322 | 183 | 98 | (5, 10) | 0.9 | 0.0058 | 0.0568 | 0.0128 | 0.84 | 0.97 | (−31,625.58, 98,448.88) | 1.495 | 0.9948 |
| Michigan | 827 | 100 | 50 | (6, 10) | 0.93 | 0.0167 | 0.0023 | 0.0451 | 0.78 | 0.97 | (−52,357.23, 60,834.5) | 1.081 | 0.9905 |
| Minnesota | 681 | 135 | 20 | (4, 7) | 0.92 | 0.0168 | 0.0206 | 0.0333 | 0.35 | 0.92 | (−94,313.64, 64,670.51) | 1.411 | 0.9957 |
| Mississippi | 324 | 199 | 85 | (6, 7) | 0.9 | 0.0026 | 0.0604 | 0.0122 | 0.89 | 0.91 | (−47,173.58, 27,677.71) | 1.835 | 0.9946 |
| Missouri | 294 | 110 | 100 | (3, 9) | 0.92 | 0.0047 | 0.0619 | 0.0156 | 0.61 | 0.99 | (−48,330.54, 74,375.8) | 0.84 | 0.9959 |
| Montana | 554 | 191 | 85 | (3, 7) | 0.91 | 0.0114 | 0.0101 | 0.0677 | 0.69 | 0.91 | (−82,122.76, 43,188.31) | 0.902 | 0.9950 |
| Nebraska | 948 | 118 | 48 | (3, 10) | 0.9 | 0.0206 | 0.033 | 0.0403 | 0.8 | 0.91 | (−74,393.69, 72,222.09) | 1.612 | 0.9966 |
| Nevada | 736 | 102 | 50 | (3, 8) | 0.91 | 0.0373 | 0.0029 | 0.0491 | 0.27 | 0.91 | (−44,470.01, 81,992.42) | 1.086 | 0.9938 |
| New Hampshire | 987 | 172 | 45 | (6, 7) | 0.91 | 0.0014 | 0.051 | 0.0201 | 0.51 | 0.97 | (−86,428.52, 85,172.59) | 0.538 | 0.9950 |
| New Jersey | 913 | 120 | 51 | (6, 7) | 0.92 | 0.0463 | 0.0086 | 0.0147 | 0.49 | 0.98 | (−98,447.98, 75,736.98) | 0.665 | 0.9976 |
| New Mexico | 549 | 185 | 71 | (6, 8) | 0.92 | 0.038 | 0.004 | 0.0086 | 0.93 | 1 | (−37,868.32, 70,577.25) | 0.525 | 0.9987 |
| New York | 720 | 180 | 79 | (3, 12) | 0.9 | 0.005 | 0.0271 | 0.0407 | 1 | 0.97 | (−37,026.3, 56,065.38) | 1.431 | 0.9992 |
| North Carolina | 905 | 166 | 61 | (3, 9) | 0.93 | 0.0491 | 0.0007 | 0.0086 | 0.85 | 0.97 | (−97,323.84, 12,889.53) | 0.597 | 0.9977 |
| North Dakota | 352 | 168 | 37 | (6, 7) | 0.9 | 0.0379 | 0.0316 | 0.0249 | 0.64 | 0.94 | (−71,924.48, 96,395.39) | 0.322 | 0.9991 |
| Ohio | 827 | 101 | 64 | (4, 12) | 0.92 | 0.0029 | 0.0278 | 0.0308 | 0.9 | 0.96 | (−71,388.35, 16,610.45) | 1.557 | 0.9986 |
| Oklahoma | 975 | 122 | 65 | (6, 9) | 0.92 | 0.0011 | 0.0114 | 0.0469 | 0.52 | 0.9 | (−92,019.71, 79,120.08) | 1.144 | 0.9980 |
| Oregon | 382 | 169 | 96 | (4, 9) | 0.9 | 0.021 | 0.0661 | 0.0089 | 0.72 | 0.91 | (−17,084.62, 57,894.87) | 1.055 | 0.9992 |
| Pennsylvania | 812 | 130 | 28 | (6, 7) | 0.91 | 0.0009 | 0.0276 | 0.0324 | 0.25 | 0.95 | (−15,561.47, 37,619.51) | 1.339 | 0.9939 |
| Rhode Island | 800 | 118 | 79 | (5, 8) | 0.91 | 0.0111 | 0.0406 | 0.009 | 0.69 | 0.93 | (−82,805.13, 96,728.37) | 1.029 | 0.9969 |
| South Carolina | 444 | 114 | 48 | (6, 9) | 0.92 | 0.0041 | 0.0309 | 0.0003 | 0.34 | 0.95 | (−43,420.85, 57,720.71) | 0.618 | 0.9990 |
| South Dakota | 353 | 143 | 51 | (5, 10) | 0.93 | 0.0193 | 0.0115 | 0.0345 | 0.56 | 0.91 | (−51,233.69, 53,021.87) | 0.39 | 0.9958 |
| Tennessee | 746 | 118 | 23 | (4, 11) | 0.92 | 0.049 | 0.0134 | 0.0039 | 0.66 | 0.96 | (−89,010.11, 63,768.4) | 1.438 | 0.9963 |
| Texas | 933 | 124 | 27 | (5, 10) | 0.94 | 0.0187 | 0.024 | 0.0088 | 0.04 | 0.91 | (−94,093.37, 12,518.37) | 1.108 | 0.9960 |
| Utah | 273 | 142 | 56 | (6, 8) | 0.91 | 0.0047 | 0.0092 | 0.0338 | 0.8 | 0.96 | (−74,941.61, 80,716.41) | 0.852 | 0.9975 |
| Vermont | 440 | 136 | 51 | (5, 9) | 0.97 | 0.0024 | 0.01 | 0.0126 | 0.59 | 0.9 | (−17,580.55, 22,768.17) | 1.775 | 0.9406 |
| Virginia | 529 | 134 | 76 | (6, 7) | 0.92 | 0.04 | 0.0303 | 0.0094 | 0.61 | 0.97 | (−52,056.14, 24,414.66) | 1.022 | 0.9992 |
| Washington | 414 | 115 | 91 | (4, 9) | 0.91 | 0.011 | 0.0034 | 0.0216 | 0.58 | 0.91 | (−87,760.78, 65,016.13) | 1.62 | 0.9934 |
| West Virginia | 366 | 194 | 23 | (6, 8) | 0.93 | 0.0361 | 0.0028 | 0.008 | 0.54 | 0.9 | (−37,953.52, 50,863.41) | 0.869 | 0.9992 |
| Wisconsin | 309 | 128 | 32 | (4, 8) | 0.92 | 0.047 | 0.0072 | 0.0118 | 0.64 | 0.95 | (−45,415.23, 20,678.45) | 1.892 | 0.9992 |
| Wyoming | 565 | 167 | 45 | (4, 11) | 0.9 | 0.0317 | 0.0021 | 0.0246 | 0.17 | 0.92 | (−28,663.07, 33,417.43) | 0.69 | 0.9912 |
Appendix A.2. Table of Results and Hyperparameters for Deceased Patients
| State | GP Paramters (Population size, Number of Generations, Tournament Selection, Tree Depth, Crossover Coefficient, Subtree Mutation Coefficient, Point Mutation Coefficient, Hoist Mutation Coefficient, Maximum Samples, Constant Range, Parsimony Coefficeint) | Score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alabama | 1560 | 100 | 197 | (4, 11) | 0.93 | 0.0458 | 0.0119 | 0.0043 | 0.82 | 0.96 | (−59,911.8, 74,719.3) | 0.128 | 0.9951 |
| Alaska | 1807 | 193 | 109 | (3, 7) | 0.91 | 0.0509 | 0.0252 | 0.0043 | 0.23 | 0.92 | (−53,669.79, 47,613.97) | 0.01 | 0.9911 |
| Arizona | 1485 | 101 | 174 | (5, 8) | 0.91 | 0.0385 | 0.0091 | 0.0126 | 0.68 | 0.99 | (−44,062.11, 11,466.03) | 0.151 | 0.9963 |
| Arkansas | 1630 | 102 | 196 | (4, 11) | 0.91 | 0.0027 | 0.0241 | 0.0011 | 0.08 | 0.91 | (−81,559.68, 83,104.24) | 0.053 | 0.9992 |
| California | 1924 | 117 | 172 | (3, 8) | 0.92 | 0.0179 | 0.0342 | 0.0292 | 1 | 0.92 | (−96,904.52, 79,877.88) | 0.162 | 0.9992 |
| Colorado | 1178 | 179 | 175 | (5, 12) | 0.91 | 0.027 | 0.0237 | 0.0184 | 0.2 | 0.93 | (−83,617.77, 25,231.08) | 0.039 | 0.9968 |
| Connecticut | 1858 | 103 | 133 | (6, 8) | 0.96 | 0.0025 | 0.0149 | 0.0034 | 0.51 | 0.96 | (−46,501.8, 88,545.84) | 0.025 | 0.9976 |
| Delaware | 1128 | 157 | 151 | (6, 11) | 0.9 | 0.0185 | 0.0493 | 0.0005 | 0.3 | 0.98 | (−33,858.02, 50,208.99) | 0.197 | 0.9907 |
| Florida | 1969 | 129 | 153 | (6, 8) | 0.91 | 0.003 | 0.0285 | 0.0524 | 0.94 | 0.95 | (−55,101.46, 69,724.53) | 0.068 | 0.9998 |
| Georgia | 1170 | 106 | 139 | (3, 12) | 0.9 | 0.0005 | 0.0101 | 0.0017 | 0.34 | 0.98 | (−13,935.76, 26,427.37) | 0.049 | 0.9977 |
| Hawaii | 1296 | 170 | 138 | (5, 12) | 0.9 | 0.0129 | 0.0222 | 0.0085 | 0.13 | 0.98 | (−28,616.39, 56,164.19) | 0.035 | 0.9906 |
| Idaho | 1083 | 130 | 106 | (3, 7) | 0.93 | 0.0299 | 0.0028 | 0.0015 | 0.86 | 0.95 | (−67,748.18, 45,591.95) | 0.138 | 0.9906 |
| Illinois | 1700 | 123 | 198 | (3, 11) | 0.92 | 0.03 | 0.0173 | 0.0275 | 0.81 | 1 | (−49,294.38, 21,593.25) | 0.161 | 0.9990 |
| Indiana | 1051 | 134 | 102 | (3, 9) | 0.91 | 0.0213 | 0.0414 | 0.0194 | 0.56 | 0.97 | (−19,518.96, 33,483.42) | 0.102 | 0.9940 |
| Iowa | 1667 | 111 | 193 | (3, 7) | 0.94 | 0.0097 | 0.0029 | 0.0144 | 0.28 | 0.97 | (−98,321.14, 41,757.4) | 0.088 | 0.9937 |
| Kansas | 1393 | 108 | 183 | (6, 12) | 0.94 | 0.0019 | 0.0262 | 0.0293 | 0.7 | 0.95 | (−31,926.29, 67,467.88) | 0.024 | 0.9985 |
| Kentucky | 1829 | 131 | 168 | (3, 10) | 0.92 | 0.0658 | 0.0061 | 0.0079 | 0.2 | 0.95 | (−26,869.89, 16,036.16) | 0.195 | 0.9950 |
| Louisiana | 1016 | 114 | 130 | (6, 12) | 0.91 | 0.0024 | 0.0191 | 0.0628 | 0.8 | 0.91 | (−16,806.27, 71,585.89) | 0.135 | 0.9941 |
| Maine | 1869 | 145 | 148 | (6, 7) | 0.92 | 0.0078 | 0.0235 | 0.0464 | 0.04 | 0.98 | (−64,099.38, 46,028.69) | 0.054 | 0.9862 |
| Maryland | 1529 | 172 | 103 | (3, 11) | 0.92 | 0.0352 | 0.0128 | 0.0269 | 0.3 | 0.92 | (−49,603.7, 42,351.06) | 0.156 | 0.9982 |
| Massachusetts | 1487 | 127 | 102 | (4, 10) | 0.93 | 0.0184 | 0.0428 | 0.0078 | 0.92 | 0.97 | (−64,176.94, 12,262.06) | 0.179 | 0.9989 |
| Michigan | 1386 | 129 | 179 | (4, 8) | 0.91 | 0.0033 | 0.0051 | 0.0088 | 0.14 | 0.97 | (−34,562.94, 11,241.83) | 0.111 | 0.9950 |
| Minnesota | 1336 | 181 | 185 | (6, 9) | 0.91 | 0.0432 | 0.0137 | 0.03 | 0.53 | 0.91 | (−16,875.9, 67,235.11) | 0.161 | 0.9953 |
| Mississippi | 1480 | 152 | 188 | (3, 7) | 0.93 | 0.0053 | 0.0105 | 0.0029 | 0.98 | 0.92 | (−67,189.16, 11,351.11) | 0.098 | 0.9977 |
| Missouri | 1173 | 138 | 177 | (6, 9) | 0.92 | 0.0287 | 0.0255 | 0.0082 | 0.99 | 0.94 | (−35,034.14, 45,295.23) | 0.064 | 0.9993 |
| Montana | 1846 | 117 | 137 | (6, 9) | 0.97 | 0.0018 | 0.0058 | 0.0076 | 0.05 | 0.99 | (−14,649.73, 78,214.13) | 0.128 | 0.9956 |
| Nebraska | 1936 | 113 | 174 | (6, 9) | 0.91 | 0.0053 | 0.0317 | 0.0394 | 0.9 | 0.96 | (−89,634.26, 23,529.16) | 0.098 | 0.9928 |
| Nevada | 1626 | 120 | 172 | (4, 10) | 0.92 | 0.0259 | 0.0026 | 0.0011 | 0.71 | 0.94 | (−99,440.0, 84,386.68) | 0.057 | 0.9966 |
| New Hampshire | 1052 | 124 | 164 | (6, 7) | 0.9 | 0.0289 | 0.0132 | 0.008 | 0.68 | 0.94 | (−74,774.46, 60,048.45) | 0.076 | 0.9945 |
| New Jersey | 1555 | 105 | 100 | (6, 7) | 0.91 | 0.0127 | 0.0624 | 0.0133 | 0.72 | 0.99 | (−56,699.21, 11,954.36) | 0.033 | 0.9952 |
| New Mexico | 1113 | 151 | 162 | (4, 12) | 0.91 | 0.0083 | 0.0134 | 0.071 | 0.48 | 0.91 | (−99,066.51, 38,651.75) | 0.06 | 0.9795 |
| New York | 1127 | 175 | 123 | (3, 7) | 0.91 | 0.0105 | 0.0001 | 0.0577 | 0.71 | 0.94 | (−89,053.56, 96,401.32) | 0.141 | 0.9980 |
| North Carolina | 1417 | 115 | 198 | (4, 11) | 0.93 | 0.0288 | 0.0154 | 0.0177 | 0.67 | 0.99 | (−39,717.96, 70,703.02) | 0.058 | 0.9972 |
| North Dakota | 1195 | 141 | 194 | (4, 11) | 0.9 | 0.0301 | 0.0297 | 0.017 | 0.68 | 0.91 | (−46,157.53, 54,882.75) | 0.122 | 0.9907 |
| Ohio | 1701 | 154 | 155 | (3, 8) | 0.9 | 0.0143 | 0.0635 | 0.0054 | 0.13 | 1 | (−29,436.69, 66,004.0) | 0.159 | 0.9976 |
| Oklahoma | 1248 | 102 | 121 | (6, 11) | 0.94 | 0.0079 | 0.0037 | 0.0371 | 0.51 | 0.99 | (−19,528.3, 62,852.77) | 0.053 | 0.9934 |
| Oregon | 1950 | 166 | 134 | (3, 8) | 0.9 | 0.0068 | 0.0248 | 0.062 | 0.61 | 0.94 | (−11,840.52, 71,714.33) | 0.088 | 0.9960 |
| Pennsylvania | 1766 | 149 | 125 | (4, 9) | 0.92 | 0.0065 | 0.0533 | 0.0007 | 0.39 | 0.9 | (−37,853.26, 79,323.8) | 0.16 | 0.9984 |
| Rhode Island | 1313 | 100 | 177 | (4, 9) | 0.91 | 0.0351 | 0.0088 | 0.0303 | 0.58 | 1 | (−91,193.12, 47,731.69) | 0.171 | 0.9904 |
| South Carolina | 1951 | 135 | 129 | (6, 7) | 0.91 | 0.0377 | 0.0189 | 0.0117 | 0.6 | 0.91 | (−36,718.97, 96,189.2) | 0.11 | 0.9982 |
| South Dakota | 1986 | 117 | 149 | (3, 7) | 0.92 | 0.0638 | 0.0014 | 0.0078 | 0.07 | 0.99 | (−18,339.16, 69,218.67) | 0.075 | 0.9972 |
| Tennessee | 1807 | 135 | 113 | (4, 7) | 0.96 | 0.0041 | 0.0195 | 0.001 | 0.07 | 0.97 | (−40,942.66, 76,218.33) | 0.131 | 0.9989 |
| Texas | 1611 | 169 | 163 | (3, 12) | 0.91 | 0.0164 | 0.0459 | 0.0059 | 0.55 | 0.96 | (−30,718.01, 95,378.4) | 0.197 | 0.9986 |
| Utah | 1106 | 123 | 144 | (3, 10) | 0.97 | 0.0058 | 0.0017 | 0.0241 | 0.68 | 0.94 | (−88,621.48, 18,401.85) | 0.175 | 0.9927 |
| Vermont | 1482 | 175 | 180 | (6, 9) | 0.92 | 0.0108 | 0.0295 | 0.0402 | 0.03 | 0.92 | (−95,752.51, 86,013.68) | 0.116 | 0.9925 |
| Virginia | 1153 | 196 | 192 | (6, 9) | 0.9 | 0.0323 | 0.0372 | 0.0284 | 0.47 | 0.95 | (−81,831.35, 83,625.37) | 0.106 | 0.9970 |
| Washington | 1596 | 124 | 125 | (5, 10) | 0.9 | 0.001 | 0.026 | 0.0609 | 0.01 | 0.96 | (−78,735.68, 72,604.06) | 0.144 | 0.9404 |
| West Virginia | 1309 | 165 | 139 | (6, 7) | 0.91 | 0.0543 | 0.0056 | 0.003 | 0.79 | 0.91 | (−20,826.25, 46,189.87) | 0.042 | 0.9976 |
| Wisconsin | 1423 | 144 | 108 | (4, 9) | 0.94 | 0.0176 | 0.0158 | 0.0151 | 0.3 | 0.94 | (−88,808.96, 72,727.52) | 0.013 | 0.9957 |
| Wyoming | 1763 | 107 | 185 | (4, 11) | 0.93 | 0.0449 | 0.0044 | 0.0048 | 0.42 | 0.93 | (−29,862.23, 55,353.33) | 0.136 | 0.9918 |
Appendix A.3. Table of Results and Hyperparameters for Recovered Patients
| State | GP Paramters (Population size, Number of Generations, Tournament Selection, Tree Dept, Crossover Coefficient, Subtree Mutation Coefficient, Point Mutation Coefficient, Hoist Mutation Coefficient, Maximum Samples, Constant Range, Parsimony Coefficeint) | Score | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Alabama | 1692 | 194 | 101 | (5, 11) | 0.94 | 0.0084 | 0.012 | 0.0186 | 0.33 | 0.94 | (−40,687.16, 62,255.12) | 1.175 | 0.997328 |
| Alaska | 1819 | 173 | 101 | (4, 10) | 0.92 | 0.0053 | 0.012 | 0.0061 | 0.24 | 0.91 | (−96,425.9, 52,000.72) | 0.229 | 0.992049 |
| Arizona | 1987 | 109 | 178 | (4, 7) | 0.91 | 0.0308 | 0.012 | 0.0491 | 0.91 | 0.93 | (−31,479.48, 24,361.18) | 1.847 | 0.995554 |
| Arkansas | 1370 | 171 | 187 | (3, 10) | 0.91 | 0.0557 | 0.004 | 0.0128 | 0.78 | 0.98 | (−39,980.95, 93,794.62) | 1.426 | 0.997685 |
| California | 1596 | 167 | 145 | (5, 10) | 0.93 | 0.0062 | 0.0209 | 0.027 | 0.89 | 0.96 | (−75,968.18, 36,861.41) | 0.652 | 0.99833 |
| Colorado | 1742 | 170 | 164 | (5, 7) | 0.91 | 0.0399 | 0.0006 | 0.0487 | 0.94 | 0.98 | (−30,246.91, 92,280.0) | 0.119 | 0.998557 |
| Connecticut | 1777 | 184 | 102 | (6, 8) | 0.92 | 0.0093 | 0.0131 | 0.0307 | 0.04 | 0.92 | (−34,426.08, 15,684.83) | 1.277 | 0.998242 |
| Delaware | 1963 | 196 | 171 | (6, 7) | 0.96 | 0.0047 | 0.0137 | 0.0054 | 0.22 | 0.92 | (−15,778.35, 39,877.09) | 0.1 | 0.99423 |
| Florida | 1957 | 101 | 144 | (6, 12) | 0.93 | 0.0051 | 0.0051 | 0.0278 | 0.74 | 0.91 | (−44,281.68, 36,978.67) | 0.395 | 0.997043 |
| Georgia | 1892 | 119 | 149 | (4, 9) | 0.9 | 0.0482 | 0.0105 | 0.015 | 0.78 | 0.94 | (−64,708.07, 93,322.46) | 0.858 | 0.998556 |
| Hawaii | 1041 | 138 | 177 | (6, 10) | 0.9 | 0.0133 | 0.0453 | 0.0147 | 0.95 | 0.98 | (−43,162.04, 20,225.95) | 0.348 | 0.983491 |
| Idaho | 1967 | 117 | 194 | (3, 10) | 0.94 | 0.0071 | 0.0484 | 0.0058 | 0.68 | 0.98 | (−84,158.66, 36,695.1) | 0.25 | 0.999529 |
| Illinois | 1155 | 114 | 109 | (3, 11) | 0.94 | 0.0114 | 0.0012 | 0.0027 | 0.92 | 1 | (−79,669.27, 92,735.77) | 1.112 | 0.996273 |
| Indiana | 1572 | 109 | 184 | (4, 11) | 0.92 | 0.0121 | 0.0195 | 0.0254 | 0.11 | 0.96 | (−62,380.4, 28,314.4) | 1.691 | 0.996928 |
| Iowa | 1363 | 144 | 196 | (6, 12) | 0.91 | 0.0138 | 0.0489 | 0.0186 | 0.78 | 0.98 | (−81,536.43, 29,347.32) | 0.207 | 0.998156 |
| Kansas | 1750 | 144 | 182 | (5, 9) | 0.91 | 0.0297 | 0.0304 | 0.0213 | 0.95 | 0.93 | (−58,666.97, 75,144.45) | 1.678 | 0.998437 |
| Kentucky | 1293 | 183 | 154 | (6, 10) | 0.9 | 0.0223 | 0.0275 | 0.0162 | 0.83 | 0.96 | (−84,243.44, 82,923.58) | 1.4 | 0.99247 |
| Louisiana | 1597 | 138 | 198 | (4, 12) | 0.93 | 0.0224 | 0.0274 | 0.0024 | 0.75 | 0.91 | (−65,660.45, 51,980.82) | 1.069 | 0.993177 |
| Maine | 1848 | 110 | 102 | (4, 10) | 0.91 | 0.0568 | 0.0239 | 0.0086 | 0.03 | 0.96 | (−94,938.64, 41,857.95) | 0.221 | 0.997116 |
| Maryland | 1983 | 177 | 197 | (4, 7) | 0.9 | 0.0708 | 0.0081 | 0.0174 | 0.98 | 0.91 | (−33,498.91, 75,399.0) | 1.359 | 0.996912 |
| Massachusetts | 1923 | 123 | 117 | (5, 11) | 0.92 | 0.0046 | 0.0013 | 0.0625 | 0.41 | 0.94 | (−53,547.7, 53,068.29) | 0.599 | 0.991613 |
| Michigan | 1957 | 121 | 149 | (4, 7) | 0.92 | 0.0151 | 0.0048 | 0.0427 | 0.27 | 0.99 | (−70,498.48, 76,208.22) | 1.602 | 0.990563 |
| Minnesota | 1474 | 164 | 161 | (4, 7) | 0.95 | 0.0085 | 0.004 | 0.0362 | 0.66 | 0.93 | (−89,378.38, 12,518.38) | 1.27 | 0.999551 |
| Mississippi | 1878 | 157 | 180 | (4, 10) | 0.91 | 0.0078 | 0.0343 | 0.0243 | 0.36 | 0.99 | (−69,080.55, 41,650.59) | 0.148 | 0.998907 |
| Missouri | 1524 | 114 | 189 | (6, 11) | 0.96 | 0.0055 | 0.0083 | 0.0178 | 0.71 | 0.91 | (−58,679.61, 18,090.86) | 1.703 | 0.997492 |
| Montana | 1737 | 171 | 184 | (6, 7) | 0.93 | 0.0248 | 0.004 | 0.0253 | 0.51 | 0.94 | (−29,350.61, 26,050.27) | 1.821 | 0.991147 |
| Nebraska | 1736 | 136 | 151 | (4, 9) | 0.9 | 0.0146 | 0.0373 | 0.0427 | 0.95 | 0.93 | (−88,950.04, 33,806.79) | 0.776 | 0.991462 |
| Nevada | 1178 | 146 | 110 | (3, 7) | 0.91 | 0.0477 | 0.0026 | 0.0347 | 0.1 | 0.95 | (−43,965.03, 72,125.86) | 1.327 | 0.992045 |
| New Hampshire | 1678 | 136 | 159 | (5, 7) | 0.92 | 0.0214 | 0.0116 | 0.0022 | 0.89 | 0.91 | (−28,363.16, 48,743.6) | 0.648 | 0.993274 |
| New Jersey | 1193 | 114 | 200 | (6, 8) | 0.95 | 0.0097 | 0.0031 | 0.0152 | 0.84 | 0.91 | (−38,954.87, 50,274.61) | 0.674 | 0.997067 |
| New Mexico | 1642 | 181 | 199 | (4, 10) | 0.97 | 0.0103 | 0.0008 | 0.016 | 0.43 | 0.94 | (−41,177.27, 26,347.72) | 0.391 | 0.997407 |
| New York | 1779 | 152 | 165 | (5, 12) | 0.9 | 0.0154 | 0.0063 | 0.0552 | 0.27 | 0.94 | (−82,261.02, 85,378.68) | 1.56 | 0.997782 |
| North Carolina | 1406 | 130 | 143 | (5, 11) | 0.93 | 0.0513 | 0.0062 | 0.0054 | 0.69 | 0.98 | (−28,595.52, 66,166.6) | 0.221 | 0.996477 |
| North Dakota | 1573 | 164 | 191 | (5, 10) | 0.91 | 0.0428 | 0.0222 | 0.0164 | 0.87 | 0.96 | (−87,840.07, 16,782.34) | 0.897 | 0.996419 |
| Ohio | 1451 | 141 | 117 | (3, 12) | 0.91 | 0.039 | 0.0257 | 0.0099 | 0.56 | 0.95 | (−13,223.56, 83,042.99) | 1.063 | 0.999314 |
| Oklahoma | 1331 | 188 | 113 | (6, 8) | 0.91 | 0.0017 | 0.0214 | 0.0503 | 0.27 | 0.96 | (−48,918.28, 92,436.69) | 0.484 | 0.996927 |
| Oregon | 1500 | 109 | 115 | (4, 9) | 0.9 | 0.0679 | 0.0109 | 0.0088 | 0.7 | 0.99 | (−18,150.22, 21,135.98) | 0.539 | 0.99823 |
| Pennsylvania | 1650 | 114 | 121 | (3, 9) | 0.93 | 0.0125 | 0.016 | 0.0359 | 0.77 | 1 | (−49,036.36, 57,956.7) | 1.785 | 0.99771 |
| Rhode Island | 1975 | 180 | 196 | (6, 9) | 0.92 | 0.025 | 0.0076 | 0.0072 | 0.94 | 0.94 | (−20,950.37, 87,459.91) | 0.459 | 0.983645 |
| South Carolina | 1239 | 176 | 198 | (3, 9) | 0.91 | 0.0021 | 0.05 | 0.0206 | 0.85 | 0.97 | (−14,444.19, 92,390.17) | 1.381 | 0.99792 |
| South Dakota | 1470 | 166 | 121 | (5, 7) | 0.92 | 0.0028 | 0.0023 | 0.0603 | 0.83 | 0.94 | (−88,393.46, 72,432.92) | 0.929 | 0.998192 |
| Tennessee | 1783 | 131 | 123 | (4, 7) | 0.93 | 0.005 | 0.0171 | 0.0474 | 0.86 | 0.96 | (−58,354.06, 88,482.19) | 1.821 | 0.99929 |
| Texas | 1047 | 133 | 125 | (3, 9) | 0.9 | 0.0501 | 0.0033 | 0.0375 | 0.84 | 0.94 | (−42,111.51, 86,733.0) | 1.057 | 0.999476 |
| Utah | 1253 | 181 | 191 | (5, 10) | 0.93 | 0.0213 | 0.0208 | 0.0163 | 0.12 | 0.92 | (−42,893.54, 61,858.96) | 0.339 | 0.995521 |
| Vermont | 1029 | 177 | 183 | (3, 8) | 0.91 | 0.0179 | 0.0157 | 0.0572 | 0.46 | 0.97 | (−85,678.92, 59,965.71) | 0.324 | 0.979788 |
| Virginia | 1650 | 153 | 151 | (6, 12) | 0.94 | 0.0024 | 0.0227 | 0.0271 | 0.99 | 0.9 | (−23,993.54, 41,056.55) | 1.736 | 0.996561 |
| Washington | 1766 | 134 | 149 | (5, 10) | 0.91 | 0.007 | 0.0135 | 0.0205 | 0.05 | 0.97 | (−47,952.8, 78,162.68) | 1.549 | 0.992944 |
| West Virginia | 1542 | 175 | 198 | (3, 12) | 0.92 | 0.0385 | 0.0084 | 0.0254 | 0.7 | 0.94 | (−81,647.2, 33,925.68) | 1.241 | 0.99826 |
| Wisconsin | 1884 | 158 | 124 | (3, 7) | 0.92 | 0.0078 | 0.0158 | 0.0349 | 0.2 | 0.92 | (−58,100.96, 16,423.25) | 1.548 | 0.998998 |
| Wyoming | 1778 | 117 | 105 | (4, 8) | 0.95 | 0.008 | 0.0054 | 0.0056 | 0.26 | 0.92 | (−45,555.91, 47,028.4) | 1.979 | 0.996617 |
References
- COVID-19 and vascular disease. EBioMedicine 2020, 58, 102966. [CrossRef]
- Apolone, G.; Montomoli, E.; Manenti, A.; Boeri, M.; Sabia, F.; Hyseni, I.; Mazzini, L.; Martinuzzi, D.; Cantone, L.; Milanese, G.; et al. Unexpected detection of SARS-CoV-2 antibodies in the prepandemic period in Italy. Tumori J. 2020, 0300891620974755. [Google Scholar] [CrossRef]
- Coronavirus Disease (COVID-19): How Is It Transmitted? World Health Organization. Available online: https://www.who.int/news-room/q-a-detail/coronavirus-disease-covid-19-how-is-it-transmitted (accessed on 12 December 2020).
- Transmission of COVID-19. European Centre for Disease Prevention and Control. 2020. Available online: https://www.ecdc.europa.eu/en/covid-19/latest-evidence/transmission (accessed on 12 December 2020).
- Grant, M.C.; Geoghegan, L.; Arbyn, M.; Mohammed, Z.; McGuinness, L.; Clarke, E.L.; Wade, R. The Prevalence of Symptoms in 24,410 Adults Infected by the Novel Coronavirus (SARS-CoV-2; COVID-19): A Systematic Review and Meta-Analysis of 148 Studies from 9 Countries. 2020. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3582819 (accessed on 12 December 2020).
- Symptoms of Coronavirus. Centers for Disease Control and Prevention. Available online: https://www.cdc.gov/coronavirus/2019-ncov/symptoms-testing/symptoms.html (accessed on 12 December 2020).
- Lorencin, I.; Baressi Šegota, S.; Anđelić, N.; Blagojević, A.; Šušteršić, T.; Protić, A.; Arsenijević, M.; Ćabov, T.; Filipović, N.; Car, Z. Automatic Evaluation of the Lung Condition of COVID-19 Patients Using X-ray Images and Convolutional Neural Networks. J. Pers. Med. 2021, 11, 28. [Google Scholar] [CrossRef] [PubMed]
- Coronavirus. Available online: https://www.who.int/health-topics/coronavirus (accessed on 12 December 2020).
- Q & A on COVID-19: Basic Facts. European Centre for Disease Prevention and Control. 2020. Available online: https://www.ecdc.europa.eu/en/covid-19/facts/questions-answers-basic-facts (accessed on 12 December 2020).
- Long, C.; Xu, H.; Shen, Q.; Zhang, X.; Fan, B.; Wang, C.; Zeng, B.; Li, Z.; Li, X.; Li, H. Diagnosis of the Coronavirus disease (COVID-19): rRT-PCR or CT? Eur. J. Radiol. 2020, 126, 108961. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.J.; Cao, Y.Y.; Dong, X.; Wang, B.C.; Liao, M.Y.; Lin, J.; Yan, Y.Q.; Akdis, C.A.; Gao, Y.D. Distinct characteristics of COVID-19 patients with initial rRT-PCR-positive and rRT-PCR-negative results for SARS-CoV-2. Allergy 2020. [Google Scholar] [CrossRef] [PubMed]
- Car, Z.; Baressi Šegota, S.; Anđelić, N.; Lorencin, I.; Mrzljak, V. Modeling the Spread of COVID-19 Infection Using a Multilayer Perceptron. Comput. Math. Methods Med. 2020, 2020. [Google Scholar] [CrossRef]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Štifanić, D.; Musulin, J.; Miočević, A.; Baressi Šegota, S.; Šubić, R.; Car, Z. Impact of COVID-19 on Forecasting Stock Prices: An Integration of Stationary Wavelet Transform and Bidirectional Long Short-Term Memory. Complexity 2020. [Google Scholar] [CrossRef]
- Hu, Z.; Ge, Q.; Jin, L.; Xiong, M. Artificial intelligence forecasting of covid-19 in china. arXiv 2020, arXiv:2002.07112. [Google Scholar]
- Ribeiro, M.H.D.M.; da Silva, R.G.; Mariani, V.C.; dos Santos Coelho, L. Short-term forecasting COVID-19 cumulative confirmed cases: Perspectives for Brazil. Chaos Solitons Fractals 2020, 135, 109853. [Google Scholar] [CrossRef]
- Yan, L.; Zhang, H.T.; Goncalves, J.; Xiao, Y.; Wang, M.; Guo, Y.; Sun, C.; Tang, X.; Jing, L.; Zhang, M.; et al. An interpretable mortality prediction model for COVID-19 patients. Nat. Mach. Intell. 2020, 2, 283–288. [Google Scholar] [CrossRef]
- Chimmula, V.K.R.; Zhang, L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks. Chaos Solitons Fractals 2020, 135, 109864. [Google Scholar] [CrossRef] [PubMed]
- Chakraborty, T.; Ghosh, I. Real-time forecasts and risk assessment of novel coronavirus (COVID-19) cases: A data-driven analysis. Chaos Solitons Fractals 2020, 135, 109850. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Pacheco-Vega, A.; Sen, M.; Yang, K.T. Heat transfer correlations by symbolic regression. Int. J. Heat Mass Transf. 2006, 49, 4352–4359. [Google Scholar] [CrossRef]
- Gustafson, S.; Burke, E.K.; Krasnogor, N. On improving genetic programming for symbolic regression. In Proceedings of the 2005 IEEE Congress on Evolutionary Computation, Scotland, UK, 2–5 September 2005; Volume 1, pp. 912–919. [Google Scholar]
- Keijzer, M. Scaled symbolic regression. Genet. Program. Evolvable Mach. 2004, 5, 259–269. [Google Scholar] [CrossRef]
- Raymond, C.; Chen, Q.; Xue, B.; Zhang, M. Adaptive weighted splines: A new representation to genetic programming for symbolic regression. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancún, Mexico, 8–12 July 2020; pp. 1003–1011. [Google Scholar]
- Marko, K.A.; Hampo, R.J. Application of genetic programming to control of vehicle systems. In Proceedings of the Intelligent Vehicles92 Symposium, Detroit, MI, USA, 29 June–1 July 1992; pp. 191–195. [Google Scholar]
- Trujillo, L.; Olague, G. Using evolution to learn how to perform interest point detection. In Proceedings of the IEEE 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 1, pp. 211–214. [Google Scholar]
- Martin, M.C. Evolving visual sonar: Depth from monocular images. Pattern Recognit. Lett. 2006, 27, 1174–1180. [Google Scholar] [CrossRef]
- Hu, X.; Ding, L.; Shang, J.; Fan, H.; Novack, T.; Noskov, A.; Zipf, A. Data-driven approach to learning salience models of indoor landmarks by using genetic programming. Int. J. Digit. Earth 2020, 13, 1–28. [Google Scholar] [CrossRef]
- Chen, S.H.; Duffy, J.; Yeh, C.H. Equilibrium selection via adaptation: Using genetic programming to model learning in a coordination game. In Advances in Dynamic Games; Springer: Berlin, Germany, 2005; pp. 571–598. [Google Scholar]
- Neely, C.J.; Weller, P.A.; Ulrich, J.M. The adaptive markets hypothesis: Evidence from the foreign exchange market. J. Financ. Quant. Anal. 2009, 44, 467–488. [Google Scholar] [CrossRef]
- Agapitos, A.; Brabazon, A.; O’Neill, M. Genetic programming with memory for financial trading. In European Conference on the Applications of Evolutionary Computation; Springer: Berlin, Germany, 2016; pp. 19–34. [Google Scholar]
- Michell, K.; Kristjanpoller, W. Generating trading rules on U.S. Stock Market using strongly typed genetic programming. Soft Comput. 2020, 24, 3257–3274. [Google Scholar] [CrossRef]
- Cpalka, K.; Łapa, K.; Przybył, A. A new approach to design of control systems using genetic programming. Inf. Technol. Control. 2015, 44, 433–442. [Google Scholar] [CrossRef]
- Enríquez-Zárate, J.; Trujillo, L.; de Lara, S.; Castelli, M.; Emigdio, Z.; Mu noz, L.; Popovič, A. Automatic modeling of a gas turbine using genetic programming: An experimental study. Appl. Soft Comput. 2017, 50, 212–222. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, T.; Liang, X.; Ali, M.Z.; Shabbir, M.N.S.K. Fault detection and classification for induction motors using genetic programming. In European Conference on Genetic Programming; Springer: Berlin, Germany, 2019; pp. 178–193. [Google Scholar]
- Dou, T.; Lopes, Y.K.; Rockett, P.; Hathway, E.A.; Saber, E. Model predictive control of non-domestic heating using genetic programming dynamic models. Appl. Soft Comput. 2020, 97, 106695. [Google Scholar] [CrossRef]
- Tan, M.S.; Tan, J.W.; Chang, S.W.; Yap, H.J.; Kareem, S.A.; Zain, R.B. A genetic programming approach to oral cancer prognosis. PeerJ 2016, 4, e2482. [Google Scholar] [CrossRef] [PubMed]
- Brameier, M.; Banzhaf, W. A comparison of linear genetic programming and neural networks in medical data mining. IEEE Trans. Evol. Comput. 2001, 5, 17–26. [Google Scholar] [CrossRef]
- Salgotra, R.; Gandomi, M.; Gandomi, A.H. Time Series Analysis and Forecast of the COVID-19 Pandemic in India using Genetic Programming. Chaos Solitons Fractals 2020, 135, 109945. [Google Scholar] [CrossRef]
- Koza, J.R.; Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992; Volume 1. [Google Scholar]
- Stephens, T. GPLearn (2015). 2019. Available online: https://gplearn.readthedocs.io/en/stable/index.html (accessed on 12 December 2020).
- Anđelić, N.; Šegota, S.B.; Lorencin, I.; Mrzljak, V.; Car, Z. Estimation of COVID-19 epidemic curves using genetic programming algorithm. Health Inform. J. 2021, 27, 1460458220976728. [Google Scholar] [CrossRef]
- Md, J.M. When Did COVID-19 Arrive and Could We Have Spotted It Earlier? 2020. Available online: https://www.medpagetoday.com/infectiousdisease/covid19/86291 (accessed on 12 December 2020).
- Public Health Response to the Initiation and Spread of Pandemic COVID-19 in the United States, 24 February–21 April 2020. Available online: https://www.cdc.gov/mmwr/volumes/69/wr/mm6918e2.htm (accessed on 12 December 2020).
- Alex Horton, M.B. Trump Announces Travel Ban from Most of Europe. 2020. Available online: https://www.washingtonpost.com/world/2020/03/11/coronavirus-live-updates/ (accessed on 12 December 2020).
- Liptak, K. White House Advises Public to Avoid Groups of More Than 10, Asks People to Stay Away from Bars and Restaurants. 2020. Available online: https://edition.cnn.com/2020/03/16/politics/white-house-guidelines-coronavirus/index.html (accessed on 8 January 2021).
- U.S. Embassy Panama City|19 March,..T.E. Global Level 4 Health Advisory—Do Not Travel. 2020. Available online: https://pa.usembassy.gov/globallevel-4-health-advisory-do-not-travel-march-19-2020/ (accessed on 8 January 2021).
- Khazan, O. The 4 Key Reasons the U.S. Is So Behind on Coronavirus Testing. 2020. Available online: https://www.theatlantic.com/health/archive/2020/03/whycoronavirus-testing-us-so-delayed/607954/ (accessed on 7 January 2021).
- Hernandez, S. This Is How a Group Linked to Betsy DeVos Is Organizing Protests to End Social Distancing, Now with Trump’s Support. 2020. Available online: https://www.buzzfeednews.com/article/salvadorhernandez/coronavirus-quarantine-protests-facebook-groups (accessed on 7 January 2021).
- Wu, J.; Chiwaya, N.; Smith, S. Map: Protests and Rallies for George Floyd Spread Across the Country. 2020. Available online: https://www.nbcnews.com/news/us-news/map-protests-rallies-george-floyd-spread-across-country-n1220976 (accessed on 8 January 2021).
- Durkee, A. Medical Experts Tell Government: ’Shut It Down Now, and Start Over. 2020. Available online: https://www.forbes.com/sites/alisondurkee/2020/07/24/medical-experts-tell-government-shut-it-down-now-and-start-over/ (accessed on 8 January 2021).
- Board, T.E. America Could Control the Pandemic by October. Let’s Get to It. 2020. Available online: https://www.nytimes.com/2020/08/08/opinion/testing-lockdown.html (accessed on 8 January 2021).
- Resetting Our Response: Changes Needed in the U.S. Approach to COVID-19. Available online: https://www.centerforhealthsecurity.org/our-work/publications/resetting-our-response-changes-needed-in-the-us-approach-to-covid-19 (accessed on 7 January 2021).
- Walker, M.; Healy, J. A Motorcycle Rally in a Pandemic? We Kind of Knew What Was Going to Happen.2020. Available online: https://www.nytimes.com/2020/11/06/us/sturgis-coronavirus-cases.html (accessed on 8 January 2021).
- COVID-19 Outbreak Associated with a 10-Day Motorcycle Rally in a Neighboring State—Minnesota, August–September 2020. 2020. Available online: https://www.cdc.gov/mmwr/volumes/69/wr/mm6947e1.htm (accessed on 7 January 2021).
- Mansfield, E.; Salman, J.; Pulver, D.V. Trump’s Campaign Made Stops Nationwide. Coronavirus Cases Surged in his Wake in at Least Five Places. USA Today. 2020. Available online: https://eu.usatoday.com/story/news/investigations/2020/10/22/trumps-campaign-made-stops-nationwidethen-coronavirus-cases-surged/3679534001/ (accessed on 7 January 2021).
- Moon, S. A Seemingly Healthy Woman’s Sudden Death Is Now the First Known US Coronavirus-Related Fatality. 2020. Available online: https://edition.cnn.com/2020/04/23/us/california-woman-first-coronavirus-death/index.html (accessed on 7 January 2021).
- Shumaker, L. U.S. Coronavirus Deaths Top 20,000, Highest in World Exceeding Italy: Reuters Tally. 2020. Available online: https://cn.reuters.com/article/health-coronavirus-usa-casualties/u-s-coronavirus-deaths-highest-in-world-exceeding-italy-reuters-tally-idINKCN21T0O2 (accessed on 7 January 2021).
- U.S. Coronavirus Death Toll Surpasses 100,000. 2020. Available online: https://www.washingtonpost.com/graphics/2020/national/100000-deaths-american-coronavirus/ (accessed on 7 January 2021).
- Woolf, S.H.; Chapman, D.A.; Lee, J.H. COVID-19 as the Leading Cause of Death in the United States. JAMA 2020, 325, 123–124. [Google Scholar]
- Sobol, I.M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]

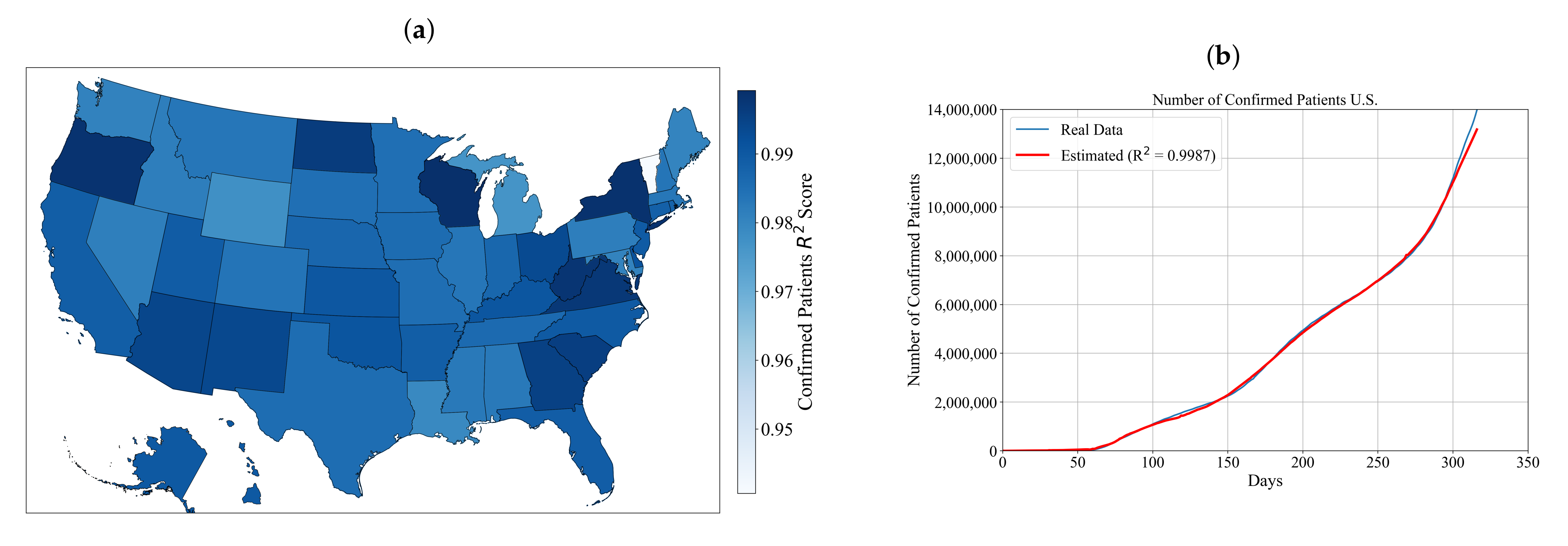
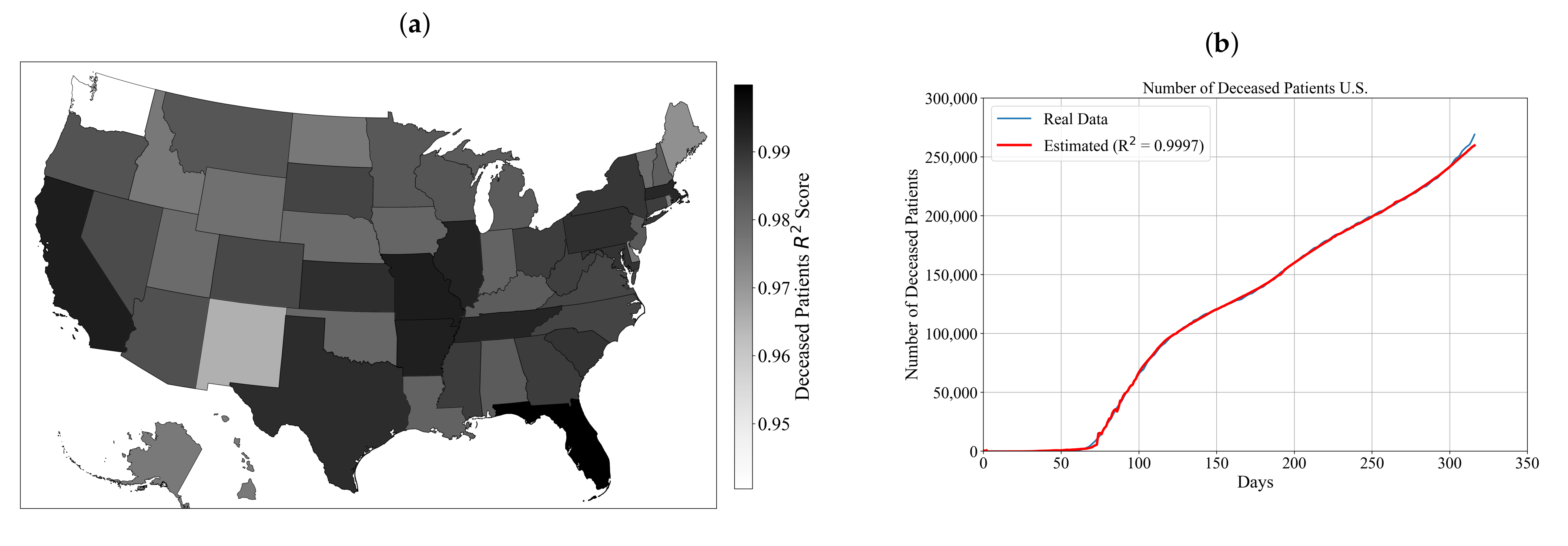
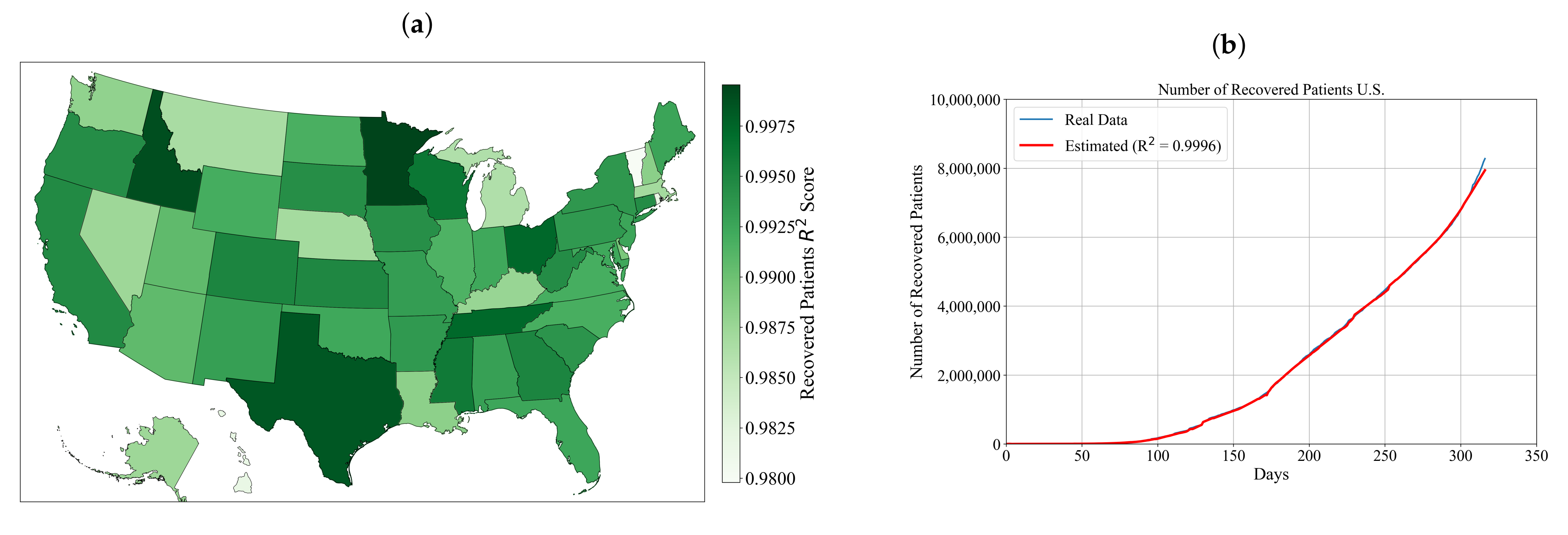
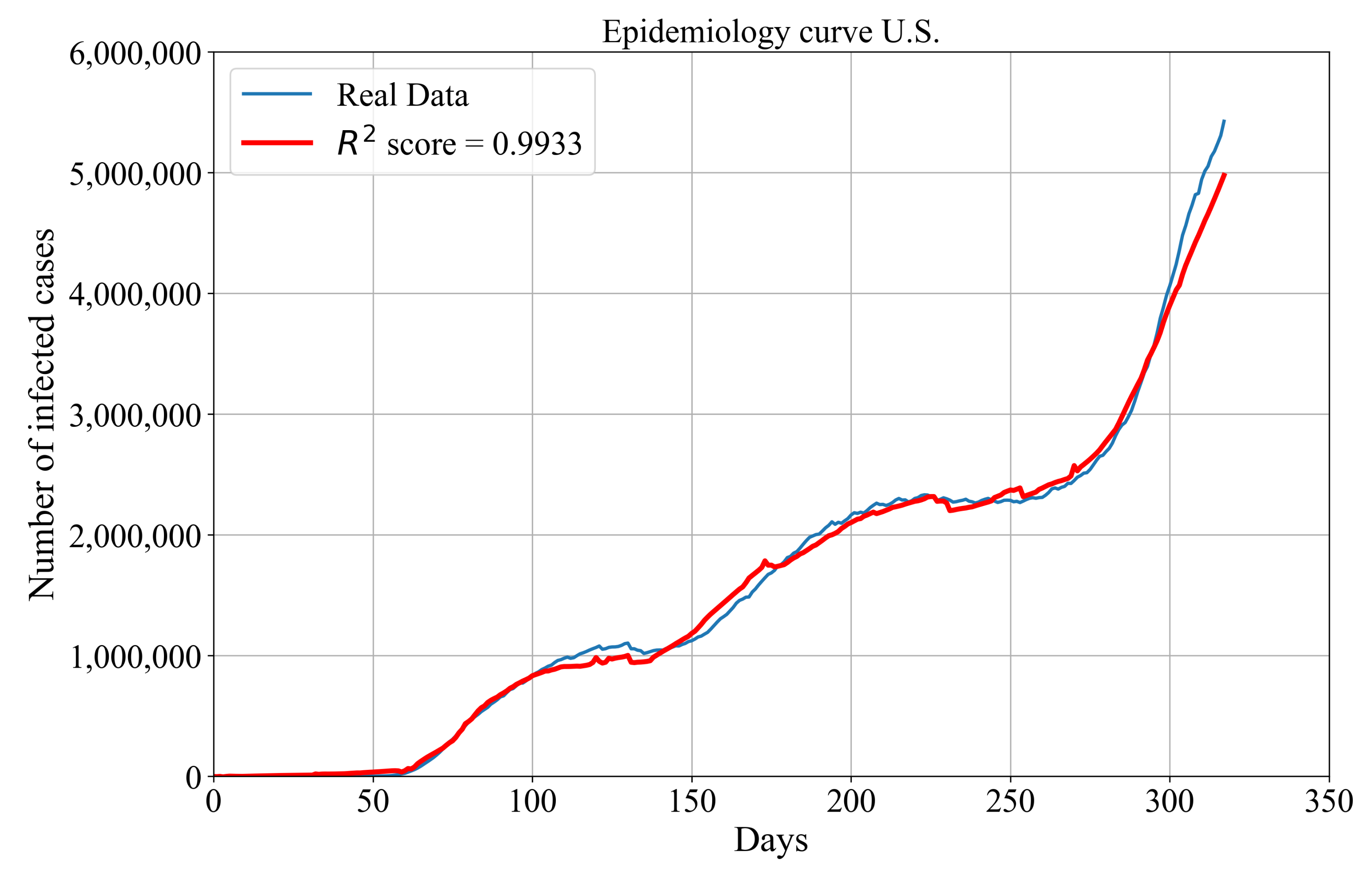
| Instance Number | Latitude | Longitude | Day | Number of Confirmed Patients |
|---|---|---|---|---|
| 308 | 32.318230 | −86.902298 | 308 | 236,865 |
| 309 | 32.318230 | −86.902298 | 309 | 239,318 |
| 310 | 32.318230 | −86.902298 | 310 | 241,957 |
| 311 | 32.318230 | −86.902298 | 311 | 242,874 |
| 312 | 32.318230 | −86.902298 | 312 | 244,993 |
| 313 | 32.318230 | −86.902298 | 313 | 247,229 |
| 314 | 32.318230 | −86.902298 | 314 | 249,524 |
| 315 | 32.318230 | −86.902298 | 315 | 252,900 |
| 316 | 32.318230 | −86.902298 | 316 | 256,828 |
| 317 | 32.318230 | −86.902298 | 317 | 260,359 |
| Parameters | Confirmed Patients Analysis | Deceased Patients Analysis | Recovered Patients Analysis |
|---|---|---|---|
| Latitude | |||
| Longitude | |||
| Day | |||
| Number of patients per day |
| Parameter | Confirmed | Deceased | Recovered | |||
|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | Lower Bound | Upper Bound | |
| Population Size | 200 | 1000 | 1000 | 2000 | 1000 | 2000 |
| Number of generations | 100 | 200 | 100 | 200 | 100 | 200 |
| Tournament Size | 20 | 100 | 100 | 200 | 100 | 200 |
| Tree Depth | 3–6 | 7–12 | 3–6 | 7–12 | 3–6 | 7–12 |
| Crossover coefficient | 0.9 | 1 | 0.9 | 1 | 0.9 | 1 |
| Subtree mutation coefficient | 0.001 | 0.1 | 0.001 | 0.1 | 0.001 | 0.1 |
| Hoist mutation coefficient | 0.001 | 0.1 | 0.001 | 0.1 | 0.001 | 0.1 |
| Point mutation coefficient | 0.001 | 0.1 | 0.001 | 0.1 | 0.001 | 0.1 |
| Stopping criteria | 0.001 | 1 | 0.001 | 1 | 0.001 | 1 |
| Maximum number of samples | 0.9 | 1 | 0.9 | 1 | 0.9 | 1 |
| Constant range | −100,000 | 100,000 | −100,000 | 100,000 | −100,000 | 100,000 |
| Parsimony coefficient | 0.1 | 2 | 0.01 | 0.2 | 0.1 | 2 |
| Variable | Distribution | Sobol Indices | |
|---|---|---|---|
| First-Order | Total-Effect | ||
| 19.74176, 66.16051 | 0.592586 | 1.036779 | |
| −155.844, −69.9722 | 0.00047 | 0.00417 | |
| (0, 317) | 0.367189 | 1.15179916 | |
| Variable | Distribution | Sobol Indices | |
|---|---|---|---|
| First-Order | Total-Effect | ||
| 19.74176, 66.16051 | 0.10282 | 0.124253 | |
| −155.844, −69.9722 | 0.002036 | 0.0127 | |
| (0, 317) | 0.87679 | 0.99746 | |
| Variable | Distribution | Sobol Indices | |
|---|---|---|---|
| First-Order | Total-Effect | ||
| 19.74176, 66.16051 | 0.13976 | 0.010748 | |
| −155.844, −69.9722 | 0.016542 | 0.13089 | |
| (0, 317) | 0.836388 | 0.986203 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anđelić, N.; Šegota, S.B.; Lorencin, I.; Jurilj, Z.; Šušteršič, T.; Blagojević, A.; Protić, A.; Ćabov, T.; Filipović, N.; Car, Z. Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm. Int. J. Environ. Res. Public Health 2021, 18, 959. https://doi.org/10.3390/ijerph18030959
Anđelić N, Šegota SB, Lorencin I, Jurilj Z, Šušteršič T, Blagojević A, Protić A, Ćabov T, Filipović N, Car Z. Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm. International Journal of Environmental Research and Public Health. 2021; 18(3):959. https://doi.org/10.3390/ijerph18030959
Chicago/Turabian StyleAnđelić, Nikola, Sandi Baressi Šegota, Ivan Lorencin, Zdravko Jurilj, Tijana Šušteršič, Anđela Blagojević, Alen Protić, Tomislav Ćabov, Nenad Filipović, and Zlatan Car. 2021. "Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm" International Journal of Environmental Research and Public Health 18, no. 3: 959. https://doi.org/10.3390/ijerph18030959
APA StyleAnđelić, N., Šegota, S. B., Lorencin, I., Jurilj, Z., Šušteršič, T., Blagojević, A., Protić, A., Ćabov, T., Filipović, N., & Car, Z. (2021). Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm. International Journal of Environmental Research and Public Health, 18(3), 959. https://doi.org/10.3390/ijerph18030959











