1. Introduction
Health is universally regarded as one of the most highly appreciated values. Good health is the main factor contributing to people’s well-being, which enhances their opportunities to participate in social life and to benefit from economic and employment growth. Better health is also consistently associated with greater life satisfaction (Ngamaba et al. [
1]). A good health situation is instrumental in achieving good labor market outcomes. By reducing the individual’s capacity to work long hours, a deteriorated health status decreases their chance of getting employed and being productive at work and has a strong impact on the labor market situation (James et al. [
2], OECD [
3]).
For the purpose of this study, the term “health situation” is understood as inhabitants’ health described by the set of selected indicators and healthcare access in their area of residence. According to Penchansky and Thomas [
4], healthcare access can be defined as a multi-faceted concept expressing the “degree of fit” between clients (patients) and the healthcare system according to five important dimensions: availability, accessibility, accommodation, affordability, and acceptability. In our article, we focus mainly on the first dimension, i.e., availability, which represents the “spatial” component of healthcare access. This choice is motivated by the fact that our understanding of availability is the same as that presented by Penchansky and Thomas [
4], i.e., as the relationship between the number and type of existing services (and resources) and the number of patients and types of their needs. In other words, it represents the adequacy of the supply of physicians, dentists, and other providers; of facilities, such as clinics and hospitals; and of specialized programs and services, such as mental health and emergency care. The second dimension highlighted by Penchansky and Thomas [
4], i.e., accessibility, also represents the “spatial” component of healthcare access and is understood as the relationship between the location of supply and the location of clients, while accounting for clients’ transportation resources and travel time, distance and cost. In our approach, however, we do not take this spatial component into account, mainly due to limited data availability. However, it should be emphasized that the literature on accessibility in the context of healthcare access is wide (see, for instance, Wang [
5] and Neutens [
6]). There is also a rich literature devoted to applications of the access concept to various health care services, e.g., regarding health care accessibility analyzed in connection with availability (Barbarisi et al. [
7], Bruno et al. [
8], Lu et al. [
9], Okuyama et al. [
10], Pu et al. [
11]).
The importance attached to health by different organizations is reflected in the way health protection is implemented in public policies, particularly in health policy, which aims to have a positive influence on population health (De Leeuw et al. [
12]). This policy can be understood as government decisions and plans of action to make progress towards achieving the goals of the health system: improved health status of the population, better financial risk protection, and better client satisfaction; or intermediate outcomes for health systems, which include: quality, access, and efficiency (Campos and Reich [
13]). In many countries, the main objective of public health policy is to create the conditions for good and equitable health for the entire population and within specific groups and to eliminate avoidable health inequalities. It should also be underlined that decisions made in sectors outside of public health and health care, such as education, transportation, and criminal justice, strongly affect health and well-being (Pollack et al. [
14]).
As mentioned above, the main objective of activities in the area of health policy is to improve the health of the population, and this improvement is nowadays understood in two ways (Łyszczarz [
15]). First, in terms of improving the average health status, e.g., measured in terms of life expectancy or premature mortality. Second, increasing the importance attached to the issue of inequalities in health. The term ‘health inequality’ refers to differences in the health of individuals or specific subgroups; any measurable aspect of health that varies across individuals or according to socially relevant groupings can be called a health inequality (Boyle [
16], Kawachi et al. [
17], Arcaya et al. [
18]). The aim of actions in the field of health policy is to reduce such inequalities. Large inequalities in health status exist across population groups, countries and specific regions within countries (Wojtyła-Buciora et al. [
19], Wojtyła et al. [
20]). These health inequalities are linked to many factors, including differential exposure to health risk factors and access to health care (Samet [
21]). Inequalities in health are mainly manifested as differences in the health status between socioeconomic groups, but they can also described in terms of employment status, sex or geographic location (Crombie et al. [
22]). The prospect of reducing inequalities seems to be increasingly important in contemporary research trends on the implementation of health policy in the world (see, e.g., Spinakis et al. [
23]). It should also be emphasized that health inequalities have to be considered as a global problem, which not only affects populations of the poorest countries and regions but also those of the richest ones; persistent health inequalities are among the most serious and challenging health problems worldwide (Barreto [
24]). How policies can reduce the main factors of health inequality and promote health equality will be a key challenge for public health in the future.
Monitoring population health and eliminating health inequalities are essential activities aimed at maintaining and improving public health. The main goals of health monitoring involve measuring the extent of health problems, their trends, and the degree of variation between different population groups, including spatial distribution, as well as identifying priority areas for public health (Pizot et al. [
25]). Another objective of monitoring is to track the current health situation at the national and local level. This is especially important today, in the era of the Covid-19 pandemic, when up-to-date information is required at lower levels of spatial aggregation.
The unequal spatial distribution of resources, such as clinics, hospitals, nurses, pharmacies, or doctors, could make entire communities more vulnerable and less resilient to adverse health effects. That is why the health situation needs to be investigated by accounting for spatial differences to gain a deeper understanding of why and how some geographical areas experience different health than others (Ozdenerol [
26]). Understanding the role played by location in shaping the geographic distribution of the health situation within countries is critical for informing appropriate public health policy regarding prevention and treatment (Casper et al. [
27]).
There are numerous articles about the spatial variation in the health situation, health inequalities or health conditions at the local or national level (see, for instance, Gilliland et al. [
28], Wang and Nie [
29], Chen et al. [
30]). In the case of Poland, various analyses have been conducted to investigate regional inequalities in the health status of the population (Wierzbicka [
31], Bem et al. [
32]).
Interestingly, all studies mentioned above were based on data for a specific year or, in some cases where comparative analysis was involved, for two years (e.g., Shi et al. [
33], Hübelová et al. [
34]). If the authors of these articles chose, say,
p variables describing the health situation of a given territorial unit, then the obtained data were
p-dimensional vectors or points in a
p-dimensional Euclidean space.
This article presents a more general approach to investigating the health situation across territorial units, which is based on spatio-temporal data. This kind of data is more general than static vector data as it takes into account changes that happen over time. The statistical methodology involving the use of functional discriminant coordinates and cluster analysis is applied to available data for Poland. However, this approach can be used to investigate the health situation or other phenomena at lower levels of spatial aggregation in other countries. For this reason, its results may be useful for policy-makers in the field of public health. The data to measure the health situation in Poland come from the Local Data Bank (LDB). Several important variables related to the health situation observed at the level of districts (LAU—also called poviats) located within provinces (approximately equivalent to NUTS2 (regions) level and also called voivodships) (see
Section 2) in the period 2013–2018 were taken into account in the analysis. More specifically, each district is described by 8 variables representing the situation over 6 years. The data for 380 districts were arranged in the form of a matrix with 6 rows and 8 columns, containing a total of 18,240 numerical values.
The main aim of this article is to determine whether Polish provinces are homogeneous in terms of spatio-temporal data characterizing their health situation. In order to answer this question, three multivariate statistical methods were used: multivariate functional discriminant coordinates analysis (MFDCA), functional cluster analysis (FCA), and the multivariate functional coefficient of variation (MFCV).
In the first step, spatio-temporal data were transformed into functional data by applying a continuous function of time
t (see, e.g., Górecki and Krzyśko [
35]). Functional data can be regarded as realizations of the random process
. Then, functional discriminant coordinates were constructed in the functional data space, and further calculations were performed in the functional discriminant coordinate space.
At this point, an important question arises: do the functional data recorded as continuous functions really exist and can these multivariate functions actually be derived? This question is critical because, in practice, values of an observed random process are always recorded in discrete moments in time, sparsely or densely distributed in the interval of variability over time. Thus, in this case, we encounter a time series or, in other words, a highly-dimensional vector of observations. However, there are numerous reasons why it is useful to model a time series as a continuous function (elements of a certain functional space); one of them is that functional data have many advantages in comparison to other representations of time series. In particular, the MFDCA derived in the present study has the following statistical advantages:
Firstly, functional data are normally used to cope with the problem of missing observations, which is inevitable in many areas of applied research. Unfortunately, most methods concerning data analysis require complete time series. The removal of a time series with missing observations from a data set is one of popular solutions, but this can lead, and in most cases does lead, to serious data loss. Another possibility is to use one of the many methods of missing data prediction, but, in that case, the results will depend on the interpolation method. Contrary to these approaches, in the case of functional data, the problem of missing observations is resolved by expressing a given time series in the form of a continuous function set.
Secondly, in the statistical development of MFDCA, the structure of observations is naturally retained when using functional data, i.e., the temporal link is maintained and the information regarding any measurement is taken into account. Consequently, results are assumed to be robust.
Thirdly, moments of observation do not have to be equally spaced in a particular time series, which can be a major advantage in online applications.
Fourthly, when using functional data, one avoids the problem of dimensionality. When the total number of time points in which observations are made exceeds the number of time series under analysis, most statistical methods do not provide satisfactory results because of misleading false estimates. In the case of functional data, this problem can be avoided because the time series are replaced by a set of continuous representative functions, which are independent of the time points in which observations are made.
The construction of functional discriminant coordinates is described in Górecki et al. [
36], and their application to fruit data can be found in Hanusz et al. [
37]. Two other proposals are: kernel discriminant coordinates (Krzyśko et al. [
38]) and discriminant coordinates with the additional condition imposed on the covariance matrix (Krzyśko et al. [
39]).
In the second step, cluster analysis was used to distinguish between groups of homogeneous provinces. Ward’s hierarchical clustering method was chosen as a commonly used technique in cluster analysis. Moreover, to determine whether obtained clusters are homogeneous, a functional multivariate coefficient of variation was applied.
The main value of this article, according to its authors, is the proposed statistical methodology. Despite the use of country-specific data for the purpose of spatial analysis of the health situation, the presented methods are universal and can be successfully applied to any territorial unit and spatio-temporal dynamic data connected to other phenomena (e.g., poverty or the labor market situation at lower levels of spatial aggregation).
This article is organized as follows.
Section 2 contains a short description of data used to analyze differences in the health situation across Polish provinces. The section also provides a description of the administrative division of Poland and details of the procedure of data standardization, as well as their transformation into functional data.
Section 3 presents the statistical methodology involving the use of functional discriminant coordinates, cluster analysis, and the functional multivariate coefficient of variation. How this approach was applied to real data describing the health situation in Poland is described in
Section 4. Finally, concluding remarks and further steps to be taken in the future are provided in
Section 5.
2. The Data
The original data set contains values of
variables characterizing the health situation of the population (see
Table 1). All variables come from the LDB, which is Poland’s largest database of information relating to the economy, society and the environment. Data and statistical indicators in the LDB describe entire country, as well as units representing three NUTS levels: macroregions (NUTS1), regions (NUTS2), and subregions (NUTS3).
Table 1 also contains information about variable type, with S denoting the so-called stimulant, where a higher value means a better situation (in terms of health), and D denoting the so-called destimulant, where lower values represent a better situation (Walesiak and Dudek [
40]).
The variables were selected with a view to obtaining a relatively comprehensive description of the health situation of the population and taking into account their availability and completeness. The data cover the period 2013–2018, i.e.,
years and describe
districts located within 16 provinces (see
Table 2).
Provinces are essentially equivalent to NUTS2 units, while districts are the upper level of local administrative units, which are currently not part of the NUTS system. The NUTS classification (Nomenclature of territorial units for statistics) is a geographical standard used for a statistical division of the EU Member States economic territories into three regional levels of specified classes of the population. It was established in order to enable the collection, compilation, and dissemination of harmonized regional statistics in the European Union. More information about the administrative division of Poland can be found at
https://stat.gov.pl/en/regional-statistics/classification-of-territorial-units/administrative-division-of-poland/.
Figure 1 shows the administrative division of Poland into provinces and districts (the left panel) and the division of
opolskie (as an example) into districts (the right panel).
The values of the selected variables, expressed in different measurement units and having different ranges of variation, were standardized using the method of zero unitization (see, for example, Jajuga and Walesiak [
41]).
Subsequently, the unitized data were transformed into functional data using the least squares method (see, e.g., Górecki and Krzyśko [
35]).
Now, let us assume that the
d-th component of the
process can be represented by a finite number of orthonormal basis functions
:
where
are random variables such that
for
and
.
Let
and
where
,
,
. Then,
Individual years (time points) were assigned the following values:
. The
functions are considered on the interval
. The Fourier base of the form
where
,
, was adopted as the orthonormal basis. Górecki and Krzyśko [
35] showed that the Fourier base leads to a minimal number of terms in the expansion of a given function into a series, which is a desirable feature because expansion coefficients play the role of new variables in the functional approach. Given the small number of time points, for each of the 8 variables, the number of expansion terms was the same and equal to 5. Hence,
,
,
. Thus,
and
.
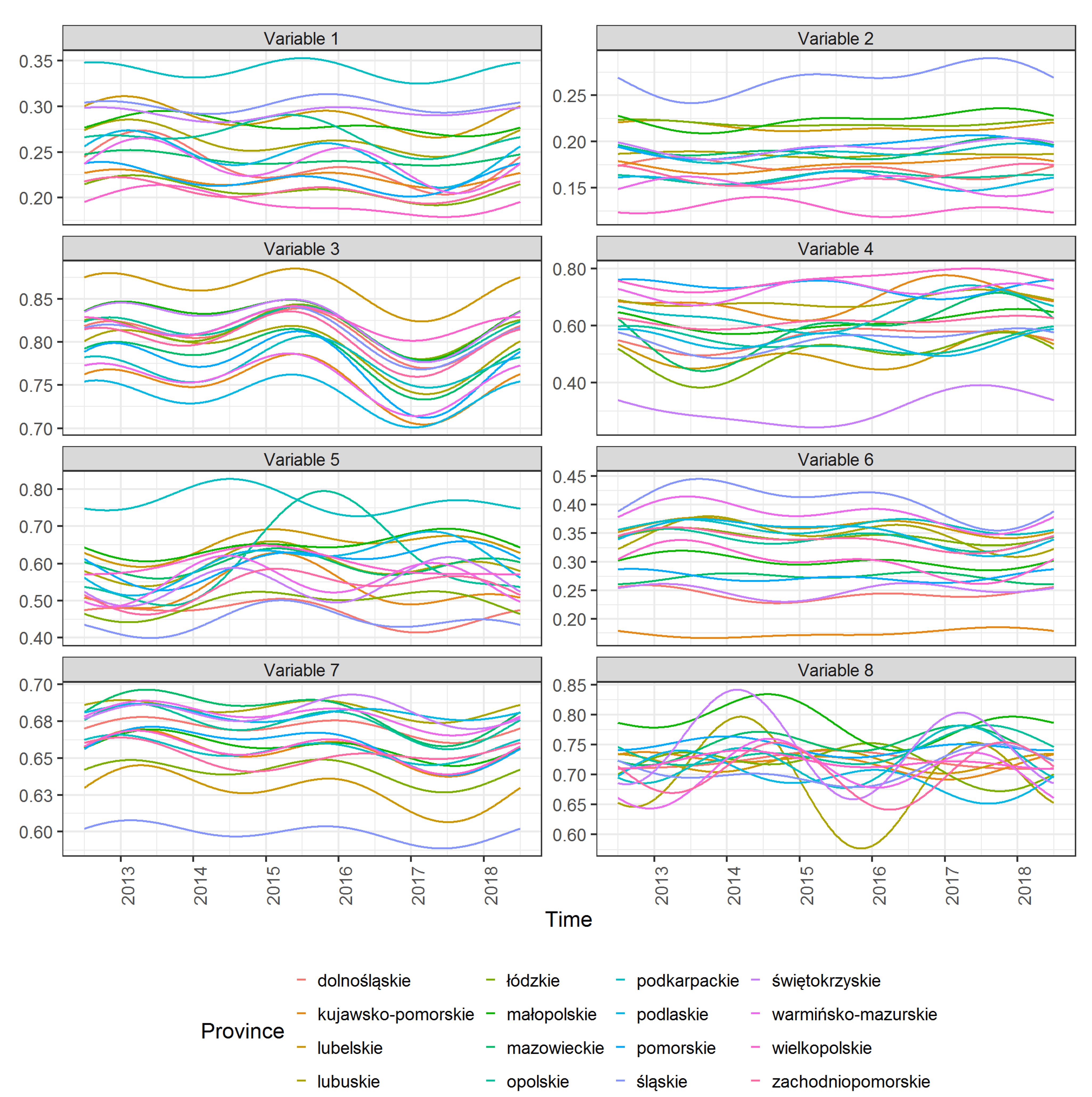
Figure 2 shows the functional data (average values) for 8 variables and 16 provinces. One can see how the values of individual variables vary over time and between provinces.
4. Results
To construct functional discriminant coordinates, we calculated the estimates of the vectors , .
The vectors were then used to construct the estimator of the matrix of between-class variability and the estimator of the matrix of within-class variability. Next, the non-zero eigenvalues of of the matrix and the corresponding eigenvectors , , were calculated.
Multivariate functional discriminant coordinates have the form:
where
are vectors of weight functions.
We treat the resulting multivariate functional discriminant coordinates as indicators (synthetic measures) of the health situation of inhabitants of Polish provinces. These indicators contain full information on the values of 8 diagnostic variables measured over 6 years. They are, therefore, composite indicators of the health situation.
These 15 composite indicators have a different power of differentiating between the provinces (these indicators have different variances (eigenvalues); see
Table 3).
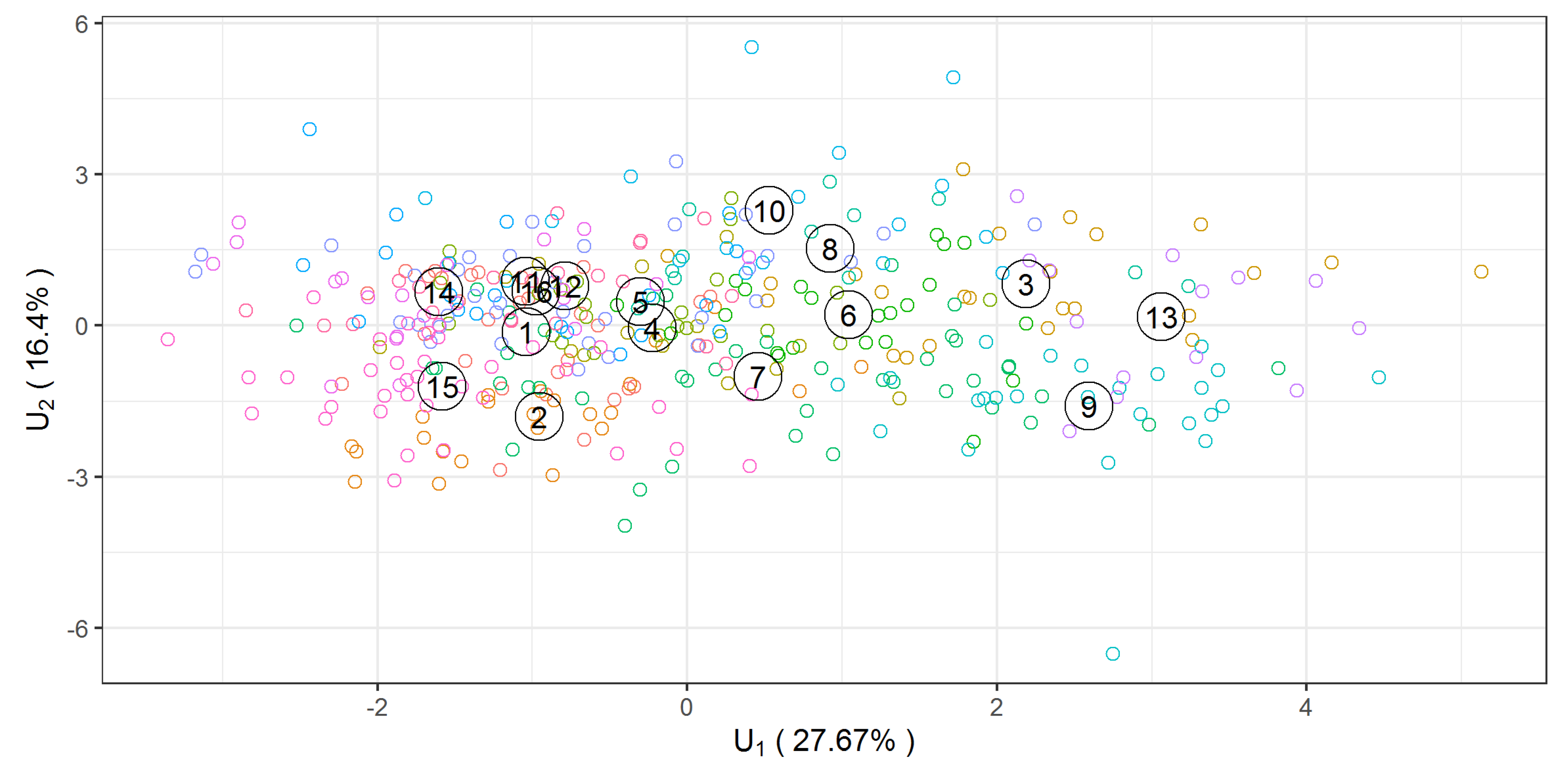
The first indicator is the strongest and the fifteenth is the least powerful. It is not possible to see the mutual position of provinces in the 15-dimensional space of these indicators, but it is possible in the space of the first two composite indicators that differentiate between the provinces most clearly.
It can be noticed that 44.1% of total variability is attributed to the first two multivariate functional coordinates.
The mean values of the 16 provinces in the system of the first two functional discriminant coordinates are presented in
Table 4.
The location of the 16 provinces in the system of the first two functional discriminant coordinates is shown in
Figure 3.
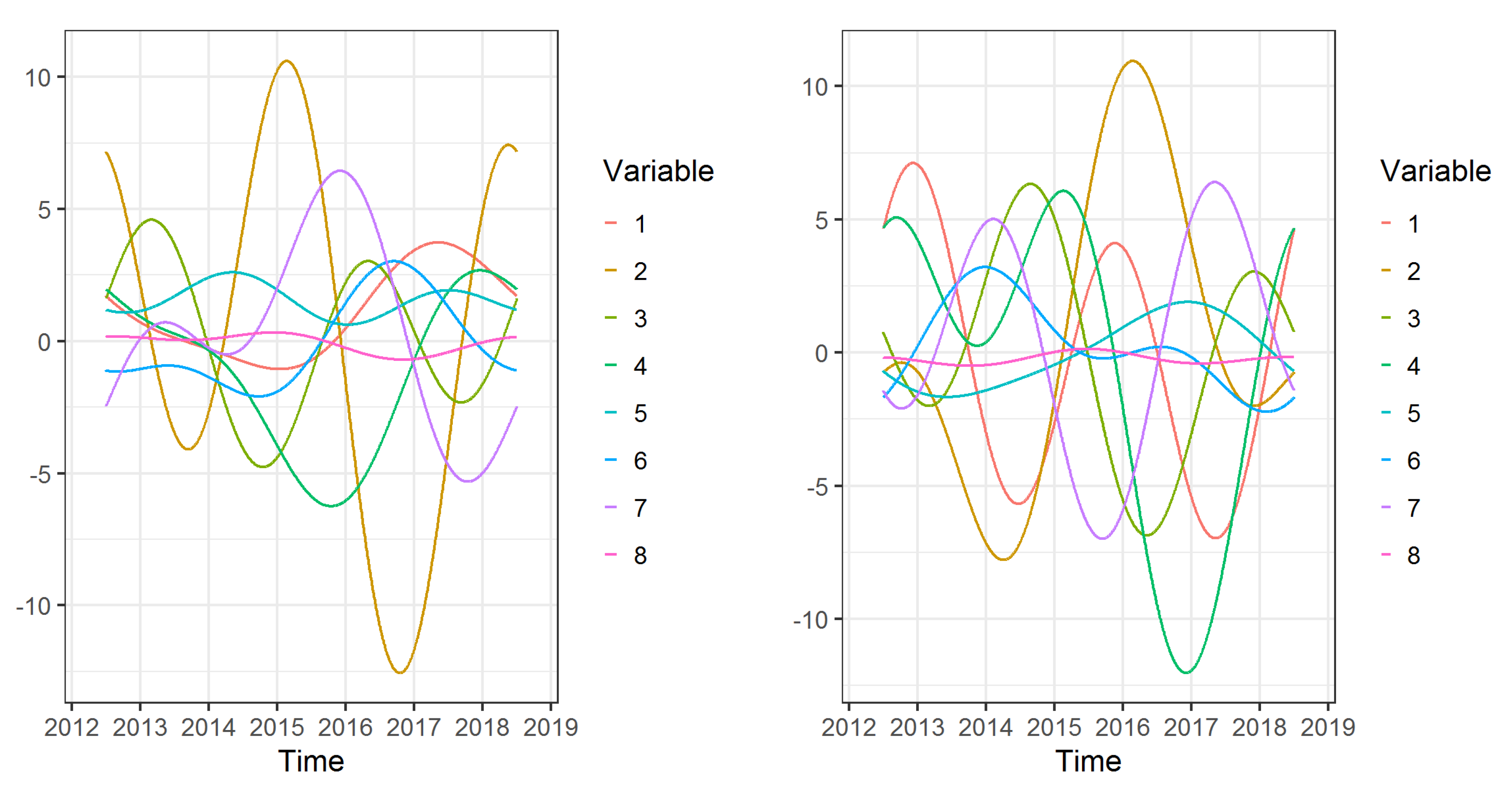
The total contribution of the individual variables to the structure of the particular functional discriminant coordinates can be estimated using the area under the absolute value of the weight functions corresponding to a given variable. The graphs of the eight components of the vector weight function for the first and second functional discriminant coordinates are shown in
Figure 4.
These contributions, for the first and second functional discriminant coordinates for 8 variables are also given in
Table 5.
Table 5 shows that the largest share in the construction of the first functional discriminant coordinate is played by variable No. 2 (Doctors per 10,000 population)—32.0%—and variable No. 7 (Number of doctor consultations per 10,000 population)—14.7%. On the other hand, variable No. 4 (Deaths of people due to cardiovascular disease per 100,000 population)—21.0%—and variable No. 2 (Doctors per 10,000 population)—20.2%—have the greatest share in the construction of the second functional discriminant coordinate. Values of coefficients of the vector weight functions are also presented in
Table 5.
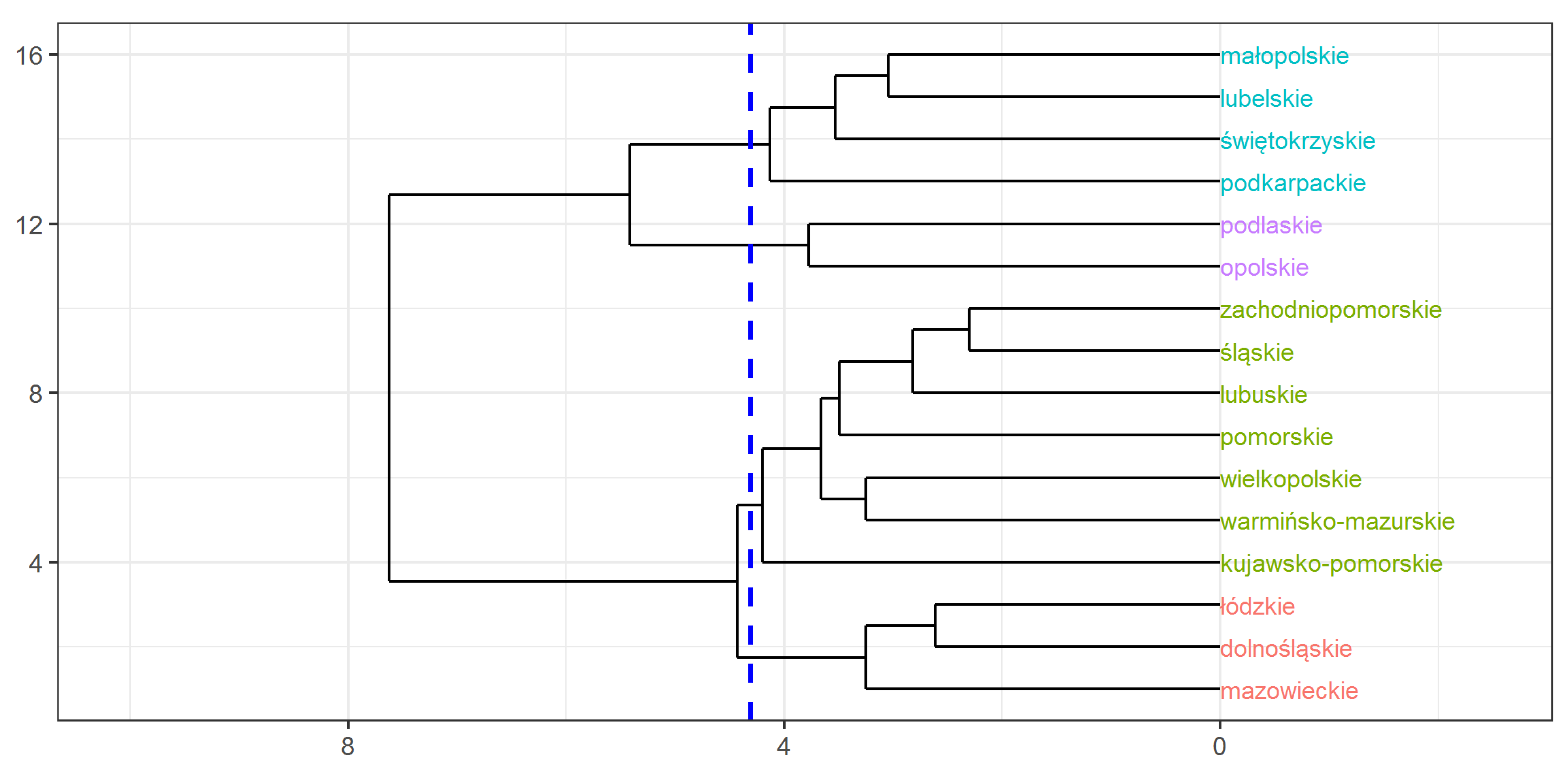
In the next step, cluster analysis was used to select groups of homogeneous provinces in a fifteen-dimensional space of functional discriminant coordinates. The Ward method was selected as a commonly used technique. The Mahalanobis distance was chosen as a measure of the distance between the mean vectors of individual provinces. The obtained dendrogram is presented in
Figure 5.
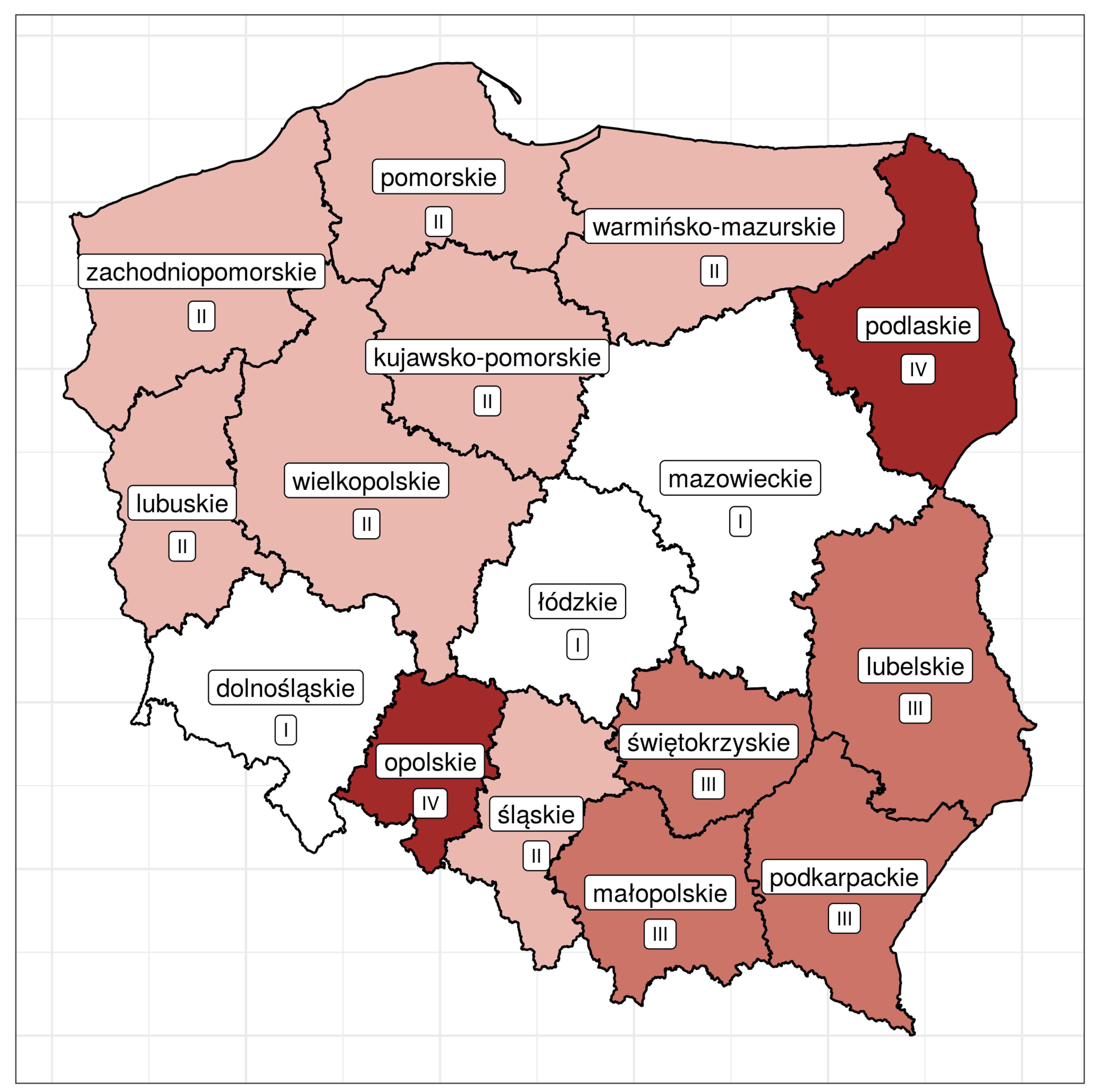
We obtained four homogeneous clusters. Which cluster individual provinces belong to is shown in
Table 6 and in
Figure 6 (spatial distribution).
Taking into account the spatial variation in the health situation of the provinces, it is possible to distinguish four spatial clusters. The first one, denoted as II, consists of six provinces located in the north-western part of Poland. At the opposite end of the country, there are four provinces that make up cluster III. Finally, in the approximate middle belt, one can see cluster I, consisting of three provinces. Cluster IV consists of two non-contiguous provinces (podlaskie and opolskie), located in different parts of Poland.
Figure 6 shows that Poland can be divided into two part: Western Poland (provinces belonging to clusters I and II) and Eastern Poland (provinces belonging to clusters III and IV). The health of inhabitants living in the provinces belonging to cluster I is the best, while that of people living in the provinces belonging to cluster IV is the worst. All the previous studies conducted in Poland show that Western Poland is better developed in socio-economic terms than Eastern Poland (see, for instance, Szymkowiak et al. [
47], Marchetti et al. [
48], Roszka [
49]). Current research shows that this division is also valid as regards the health situation.
Decision-makers at national and local government levels should be advised to redirect more funds to improve the health situation of inhabitants of Easter Poland.
To verify that the obtained four clusters are really homogeneous, a multivariate functional coefficient of variation (MFCV) was calculated for all provinces together and for each cluster separately (see
Table 7).
As can be seen, the coefficients of variation for individual clusters are lower than that for all indeed homogeneous.