Multilevel Zero-One Inflated Beta Regression Model for the Analysis of the Relationship between Exogenous Health Variables and Technical Efficiency in the Spanish National Health System Hospitals
Abstract
1. Introduction
2. Materials and Methods
2.1. Decision Making Units (DMUs)
2.2. Variables
2.3. Sources of Information
2.4. Data Analysis
2.4.1. Data Envelopment Analysis
2.4.2. Second-Stage Analysis
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Hughes, D.; McGuire, A. Stochastic demand. production responses and hospital costs. J. Health Econ. 2003, 22, 999–1010. [Google Scholar] [CrossRef]
- Bagust, A.; Place, M.; Posnett, J.W. Dynamics of bed use in accommodating emergency admissions: Stochastic simulation model. Br. Med. J. 1999, 319, 155–158. [Google Scholar] [CrossRef] [PubMed]
- Almeida, A.S.; Cima, J.F. Demand uncertainty and hospital costs: An application to Portuguese public hospitals. Eur. J. Health Econ. 2015, 16, 35–45. [Google Scholar] [CrossRef] [PubMed]
- Krämer, J.; Schreyögg, J.; Busse, R. Classification of hospital admissions into emergency and elective care: A machine learning approach. Health Care Manag. Sci. 2019, 22, 85–105. [Google Scholar] [CrossRef] [PubMed]
- Johar, M.; Jones, G.S.; Savage, E. Emergency admissions and elective surgery waiting times. Health. Econ. 2013, 22, 749–756. [Google Scholar] [CrossRef] [PubMed]
- Wallace, E.; Smith, S.M.; Fahey, T.; Roland, M. Reducing emergency admissions through community based interventions. Br. Med. J. 2016, 352, h6817. [Google Scholar] [CrossRef] [PubMed]
- Melnick, G.A.; Serrato, C.A.; Mann, J.M. Prospective payments to hospitals: Should emergency admissions have higher rates? Health Care Financ. Rev. 1989, 10, 29–39. [Google Scholar]
- McRae, S.; Brunner, J.O.; Bard, J.F. Analyzing economies of scale and scope in hospitals by use of case mix planning. Health Care Manag. Sci. 2020, 23, 80–101. [Google Scholar] [CrossRef]
- Gaynor, M.; Anderson, G.F. Uncertain demand, the structure of hospital costs, and the cost of empty hospital beds. J. Health Econ. 1995, 14, 291–317. [Google Scholar] [CrossRef]
- Starfield, B.; Shi, L. Policy relevant determinants of health: An international perspective. Health Policy 2002, 60, 201–218. [Google Scholar] [CrossRef]
- Starfield, B.; Chang, H.Y.; Lemke, K.; Weiner, J. Ambulatory specialist use by nonhospitalized patients in US Health Plans: Correlates and consequences. J. Ambul. Care Manag. 2009, 32, 216–225. [Google Scholar] [CrossRef]
- Lee, K.S.; Chun, K.H.; Lee, J.S. Reforming the hospital service structure to improve efficiency: Urban hospital specialization. Health Policy 2008, 87, 41–49. [Google Scholar] [CrossRef]
- Romero, C.P.; Ortega-Díaz, M.I.; Ocaña-Riola, R.; Martín, J.J.M.; Ortega-Díaz, M.I. Análisis de la eficiencia técnica en los hospitales del Sistema Nacional de Salud español. Gac. Sanit. 2017, 31, 108–115. [Google Scholar] [CrossRef]
- Pérez-Romero, C.; Ortega-Díaz, M.I.; Ocaña-Riola, R.; Martín-Martín, J.J. Análisis multinivel de la eficiencia técnica de los hospitales del Sistema Nacional de Salud español por tipo de propiedad y gestión. Gac. Sanit. 2019, 33, 325–332. [Google Scholar] [CrossRef]
- Zhang, L.; Cheng, G.; Song, S.; Yuan, B.; Zhu, W.; He, L.; Ma, X.; Meng, Q. Efficiency performance of China’s health care delivery system. J. Health Plan. Manag. 2017, 32, 254–263. [Google Scholar] [CrossRef]
- Maren Schneider, A.; Oppel, E.M.; Schreyögg, J. Investigating the link between medical urgency and hospital efficiency—Insights from the German hospital market. Health Care Manag. Sci. 2020, 23, 649–660. [Google Scholar] [CrossRef]
- Tynkkynen, L.; Vrangbæk, K. Comparing public and private providers: A scoping review of hospital services in Europe. BMC Health Serv. Res. 2018, 18, 141. [Google Scholar] [CrossRef]
- Kruse, F.M.; Stadhouders, N.W.; Adang, E.M.; Groenewoud, S.; Jeurissen, P.P. Do private hospitals outperform public hospitals regarding efficiency, accessibility, and quality of care in the European Union? A literature review. Int. J. Health Plan. Manag. 2018, 33, e434–e453. [Google Scholar] [CrossRef]
- Barbetta, G.P.; Turati, G.; Zago, A. Behavioral differences between public and private not-for-profit hospitals in the Italian national health service. Health Econ. 2007, 16, 75–96. [Google Scholar] [CrossRef]
- Tiemann, O.; Schreyögg, J. Effects of Ownership on Hospital Efficiency in Germany. Bus. Res. 2009, 2, 115–145. [Google Scholar] [CrossRef]
- Lindlbauer, I.; Schreyögg, J. The relationship between hospital specialization and hospital efficiency: Do different measures of specialization lead to different results? Health Care Manag. Sci. 2014, 17, 365–378. [Google Scholar] [CrossRef]
- Czypionka, T.; Kraus, M.; Mayer, S.; Röhrling, G. Efficiency, ownership, and financing of hospitals: The case of Austria. Health Care Manag. Sci. 2014, 17, 331–347. [Google Scholar] [CrossRef]
- Sommersguter-Reichmann, M.; Stepan, A. The interplay between regulation and efficiency: Evidence from the Austrian hospital inpatient sector. Socio. Econ. Plan. Sci. 2015, 52, 10–21. [Google Scholar] [CrossRef]
- Rego, G.; Nunes, R.; Costa, J. The challenge of corporatisation: The experience of Portuguese public hospitals. Eur. J. Health Econ. 2010, 11, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.-C.; Eggleston, K.; Lau, J.; Schmid, C.H. Hospital Ownership and Financial Performance: What Explains the Different Findings in the Empirical Literature? Inq. J. Health Care Organ. Provis. Financ. 2007, 44, 41–68. [Google Scholar] [CrossRef] [PubMed]
- Roehrich, J.K.; Lewis, M.A.; George, G. Are public–private partnerships a healthy option? A systematic literature review. Soc. Sci. Med. 2014, 113, 110–119. [Google Scholar] [CrossRef] [PubMed]
- Zarei, E.; Moghaddasfar, T.; Eidkhani, V. Challenges and Problems of Public Private Partnership in Health System: A Review Study. Community Health 2018, 5, 386–402. [Google Scholar] [CrossRef]
- Martín, J.J.M. Formas Directa e Indirecta de Gestión Institucional en Centros y Servicios Sanitarios. Tema 5; Escuela Nacional de Sanidad: Madrid, Spain, 2013; Available online: http://e-spacio.uned.es/fez/eserv.php?pid=bibliuned:500622&dsID=n5.4_formas_directas_e_indirectas_de_gesti__n.pdf (accessed on 12 October 2019).
- Martín, J.J.; del Amo, M.D.P.L.; Hita, J.M.C. La empresa pública en la sanidad. Prestación de sanidad pública por hospitales y ambulatorios privados. Presup. Gasto Público 2016, 83, 81–104. [Google Scholar]
- World Bank Institute. Public-Private Partnerships: Reference Guide Version 1; World Bank: Washington, DC, USA, 2012. [Google Scholar]
- Commission of the European Communities. Communication from the Commission to the European Parliament, the Council, the European Economic and Social Committee and the Committee of the Regions. Mobilising Private and Public Investment for Recovery and Long Term Structural Change: Developing Public Private Partnerships. COM(2009) 615 Final; European Union: Brussels, Belgium, 2009. [Google Scholar]
- Sekhri, N.; Feachem, R.; Ni, A. Public-Private Integrated Partnerships Demonstrate the Potential to Improve Health Care Access, Quality, And Efficiency. Health Aff. 2011, 30, 1498–1507. [Google Scholar] [CrossRef]
- Minué-Lorenzo, S.; Martín-Martín, J.J. Gestión privada: ¿más eficiente? An. Med. Fam. 2013, 9, 15–23. [Google Scholar]
- Meneu, R.; Urbanos, R. La colaboración público-privada en sanidad: Hasta dónde y cómo delimitar sus fronteras. Cuad. Econ. ICE 2019, 96, 35–56. [Google Scholar] [CrossRef]
- Nikjoo, R.G.; Beyrami, H.J.; Jannati, A.; Jaafarabadi, M.A. Prioritizing Public- Private Partnership Models for Public Hospitals of Iran Based on Performance Indicators. Health Promot. Perspect. 2012, 2, 251–264. [Google Scholar]
- EPOS Health Management. Health and Economics Analysis for an Evaluation of the Public Private Partnerships in Health Care Delivery across EU; European Union: Brussels, Belgium, 2013. [Google Scholar]
- Sadeghi, A.; Barati, O.; Bastani, P.; Jafari, D.D.; Etemadian, M. Experiences of selected countries in the use of public-private partnership in hospital services provision. J. Pak. Med. Assoc. 2016, 66, 1401–1406. [Google Scholar]
- Barlow, J.; Roehrich, J.K.; Wright, S. Europe Sees Mixed Results from Public-Private Partnerships for Building and Managing Health Care Facilities and Services. Health Aff. 2013, 32, 146–154. [Google Scholar] [CrossRef]
- Sánchez-Martínez, F.I.; Abellan-Perpiñan, J.M.; Oliva-Moreno, J. La privatización de la gestión sanitaria: Efecto secundario de la crisis y síntoma de mal gobierno. Informe SESPAS 2014. Gac. Sanit. 2014, 28, 75–80. [Google Scholar] [CrossRef][Green Version]
- Wong, E.L.; Yeoh, E.-K.; Chau, P.Y.; Yam, C.H.; Cheung, A.W.; Fung, H. How shall we examine and learn about public-private partnerships (PPPs) in the health sector? Realist evaluation of PPPs in Hong Kong. Soc. Sci. Med. 2015, 147, 261–269. [Google Scholar] [CrossRef]
- Comendeiro-Maaløe, M.; López, M.R.; Gorgemans, S.; Bernal-Delgado, E. A comparative performance analysis of a renowned public private partnership for health care provision in Spain between 2003 and 2015. Health Policy 2019, 123, 412–418. [Google Scholar] [CrossRef]
- Cantor, V.J.M.; Poh, K.L. Integrated Analysis of Healthcare Efficiency: A Systematic Review. J. Med. Syst. 2017, 42, 8. [Google Scholar] [CrossRef]
- Kohl, S.; Schoenfelder, J.; Fügener, A.; Brunner, J.O. The use of Data Envelopment Analysis (DEA) in healthcare with a focus on hospitals. Health Care Manag. Sci. 2019, 22, 245–286. [Google Scholar] [CrossRef]
- Goldstein, H. Multilevel Statistical Models, 4th ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Min, A.; Scott, L.D.; Park, C.; Vincent, C.; Ryan, C.; Lee, T.W. Impact of Medicare Advantage penetration and hospital competition on technical efficiency of nursing care in US intensive care units. Int. J. Health Plan. Manag. 2018, 33, 733–745. [Google Scholar] [CrossRef]
- Min, A.; Scott, L.D.; Park, C.; Vincent, C.; Ryan, C.J. Organizational Factors Associated with Technical Efficiency of Nursing Care in US Intensive Care Units. J. Nurs. Care Qual. 2019, 34, 242–249. [Google Scholar] [CrossRef]
- Ortega-Díaz, M.I.; Ocaña-Riola, R.; Pérez-Romero, C.; Martín-Martín, J.J. Multilevel Analysis of the Relationship between Ownership Structure and Technical Efficiency Frontier in the Spanish National Health System Hospitals. Int. J. Environ. Res. Public Health 2020, 17, 5905. [Google Scholar] [CrossRef]
- Ospina, R.; Ferrari, S.L.P. Inflated beta distributions. Stat. Pap. 2010, 51, 111–126. [Google Scholar] [CrossRef]
- Ospina, R.; Ferrari, S.L.P. A general class of zero-or-one inflated beta regression models. Comput. Stat. Data Anal. 2012, 56, 1609–1623. [Google Scholar] [CrossRef]
- Liu, F.; Eugenio, E.C. A review and comparison of Bayesian and likelihood-based inferences in beta regression and zero-or-one-inflated beta regression. Stat. Methods Med. Res. 2018, 27, 1024–1044. [Google Scholar] [CrossRef]
- Khushalani, J.S.; Ozcan, Y.A. Are hospitals producing quality care efficiently? An analysis using Dynamic Network Data Envelopment Analysis (DEA). Socio. Econ. Plan. Sci. 2017, 60, 15–23. [Google Scholar] [CrossRef]
- Emrouznejad, A.; De Witte, K. COOPER-Framework: A Unified Process. (for Nonparametric Projects TIER Working Paper Series 10/05); TIER: Berlin, Germany, 2010; Available online: http://www.tierweb.nl/assets/files/UM/cooper%20framework.final.pdf (accessed on 12 October 2019).
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Banker, R.D.; Cooper, W.W.; Seiford, L.M.; Zhu, J. Returns to Scale in DEA. In Handbook on Data Envelopment Analysis; Cooper, W., Seiford, L., Zhu, J., Eds.; Springer: Boston, MA, USA, 2011; Volume 164, pp. 10–41. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.C. Rank-normalization, folding, and localization: An improved R for assessing convergence of MCMC. Bayesian Anal. 2021, 16, 667–718. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis, 3rd ed.; CRC Press Taylor & Francis Group: New York, NY, USA, 2015. [Google Scholar]
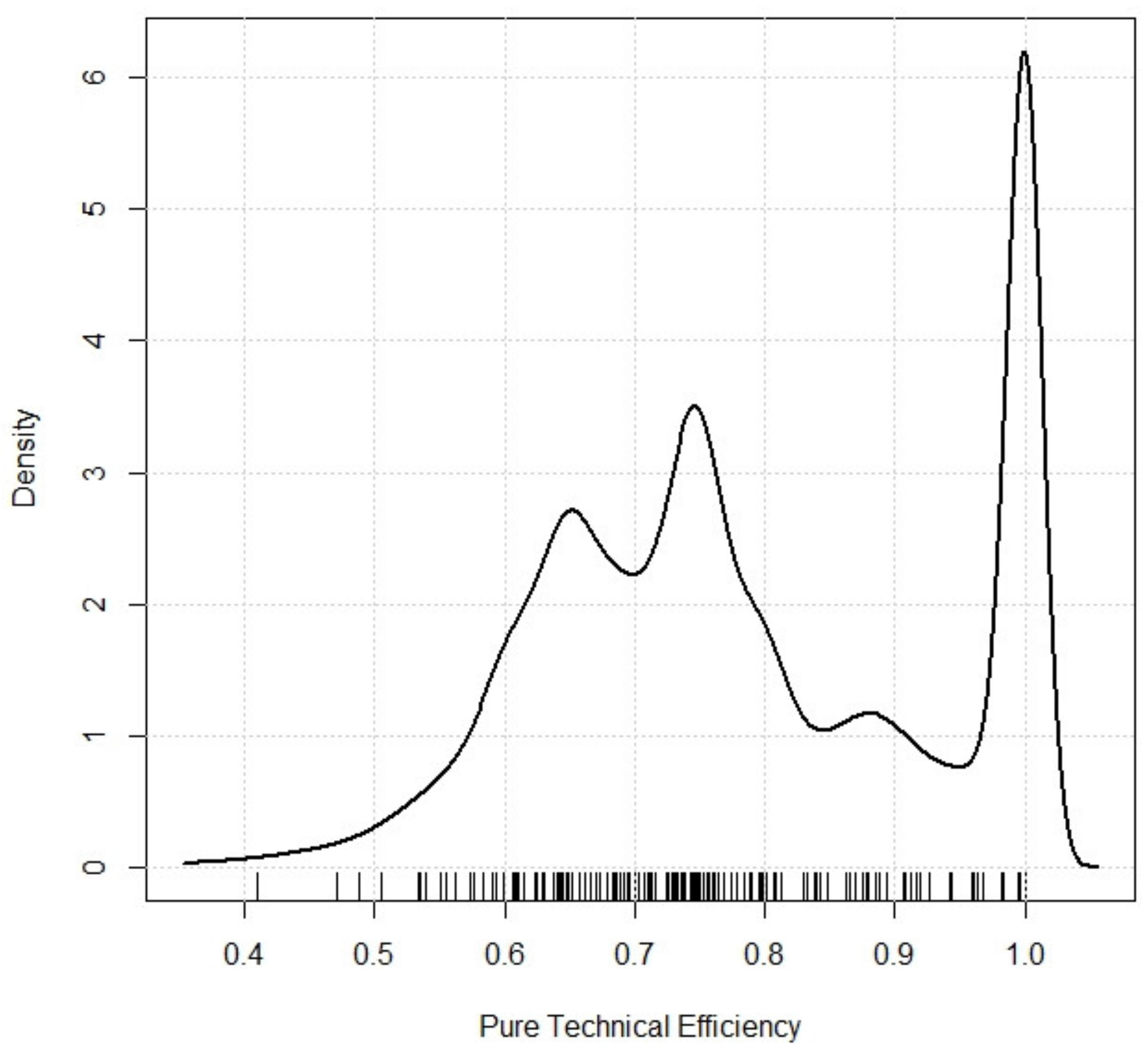
| Mean | Standard Deviation | Maximum | Minimum | |
|---|---|---|---|---|
| Inputs | ||||
| Installed beds a | 484.03 | 331.22 | 1408.00 | 63.00 |
| Healthcare personnel b | 2146.58 | 1669.66 | 7947.00 | 169.50 |
| Non-healthcare personnel b | 517.68 | 456.44 | 2417.50 | 20.00 |
| Adjusted purchases and external services c | 156,561.26 | 53,247.90 | 327,822.98 | 40,261.73 |
| Outputs | ||||
| Total discharges adjusted case by case d | 18,833.02 | 13,578.33 | 59,811.27 | 1503.74 |
| Outpatient activity e | 31,892.54 | 20,207.32 | 108,572.25 | 5720.43 |
| Quantitative Variables | Original Variable | Standardized Variable 1 | ||||||
|---|---|---|---|---|---|---|---|---|
| Minimum | Maximum | Mean | Standard Deviation | Minimum | Maximum | Mean | Standard Deviation | |
| Hospital variables | ||||||||
| Resident physicians per 100 faculty members | 0.00 | 60.78 | 23.75 | 16.08 | −1.48 | 2.30 | 0.00 | 1.00 |
| Emergency physicians per 100 faculty members a | 4.56 | 30.58 | 13.32 | 4.97 | −1.76 | 3.48 | 0.00 | 1.00 |
| % Beds in operation in Intensive Care Units b | 0.84 | 9.36 | 4.30 | 1.62 | −2.15 | 3.13 | 0.00 | 1.00 |
| % Occupation in Intensive Care Units c | 7.12 | 97.06 | 56.32 | 22.27 | −2.21 | 1.83 | 0.00 | 1.00 |
| Regional variables | ||||||||
| Public healthcare spending per inhabitant d | 1153.43 | 1710.08 | 1374.11 | 145.35 | −1.52 | 2.31 | 0.00 | 1.00 |
| Average annual income per household (Thousands of €) e | 24,375.00 | 39,578.00 | 31,705.28 | 4170.42 | −1.76 | 1.89 | 0.00 | 1.00 |
| Installed private beds per 1000 inhabitants f | 0.11 | 1.06 | 0.58 | 0.29 | −1.63 | 1.69 | 0.00 | 1.00 |
| Installed public beds per 1000 inhabitants f | 2.14 | 3.77 | 2.83 | 0.55 | −1.25 | 1.73 | 0.00 | 1.00 |
| Public beds in operation in Intensive Care Units per 1000 inhabitants | 0.07 | 0.09 | 0.08 | 0.01 | −1.09 | 1.74 | 0.00 | 1.00 |
| Emergency physicians per 1000 inhabitants a | 0.16 | 0.30 | 0.20 | 0.03 | −1.56 | 3.89 | 0.00 | 1.00 |
| External emergency centers per 1000 inhabitants g | 0.01 | 0.12 | 0.04 | 0.03 | −1.21 | 2.73 | 0.00 | 1.00 |
| Primary care doctors and nurses per 1000 people allocated h | 1.12 | 2.01 | 1.44 | 0.21 | −1.52 | 2.77 | 0.00 | 1.00 |
| External emergency personnel per 1000 inhabitants i | 0.16 | 1.07 | 0.41 | 0.17 | −1.42 | 3.80 | 0.00 | 1.00 |
| Qualitative variables | Number | Percentage | ||||||
| Exogenous hospital variables | ||||||||
| Hospital type | ||||||||
| Public | 147 | 84.97% | ||||||
| Private | 12 | 6.94% | ||||||
| Public-Private Partnership | 14 | 8.09% | ||||||
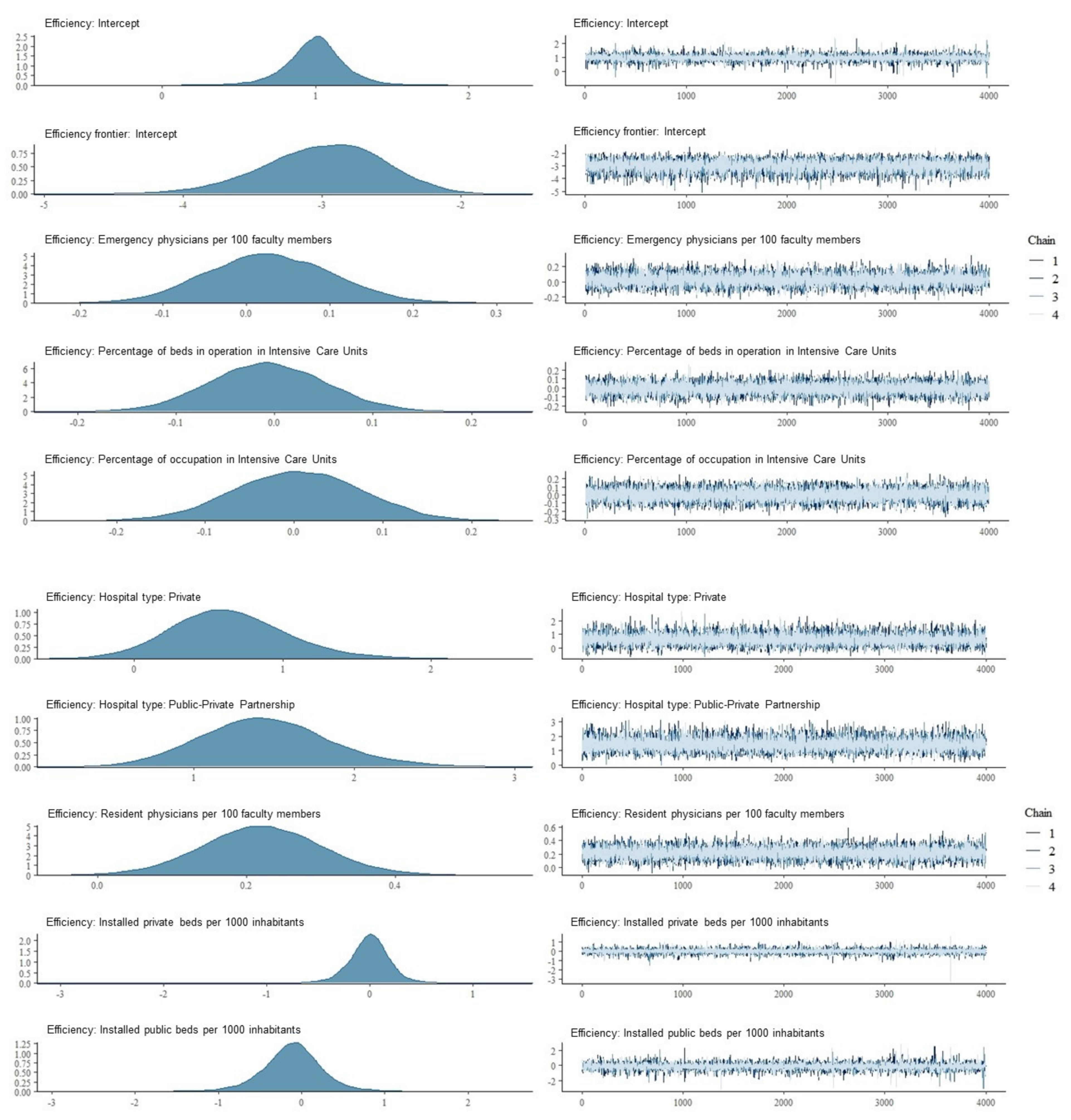
| Variable a | Coefficient | Standard Error | Credibility Interval b | PCP c | NCP c | Bulk-ESS | Tail-ESS | RMAI d | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Average Efficiency Index Model | ||||||||||
| Intercept | 1.00 | 0.21 | 0.58 | 1.40 | 1.00 | 0.00 | 1.00 | 10,710 | 8026 | |
| Hospital type | ||||||||||
| Public | Reference | Reference | Reference | Reference | Reference | Reference | Reference | |||
| Public-Private Partnership | 1.45 | 0.41 | 0.69 | 2.32 | 1.00 | 0.00 | 1.00 | 22,111 | 13,024 | 4.27 |
| Private | 0.64 | 0.39 | −0.08 | 1.48 | 0.96 | 0.04 | 1.00 | 25,642 | 10,668 | 1.90 |
| Resident physicians per 100 faculty members | 0.22 | 0.08 | 0.06 | 0.38 | 1.00 | 0.00 | 1.00 | 16,751 | 12,123 | 1.25 |
| Emergency physicians per 100 faculty members | 0.03 | 0.08 | −0.12 | 0.18 | 0.64 | 0.36 | 1.00 | 19,586 | 12,303 | 1.03 |
| Occupation in Intensive Care Units (%) | 0.00 | 0.07 | −0.14 | 0.14 | 0.52 | 0.48 | 1.00 | 20,699 | 11,979 | 1.00 |
| Beds in operation in Intensive Care Units (%) | −0.01 | 0.06 | −0.12 | 0.11 | 0.45 | 0.55 | 1.00 | 26,946 | 13,022 | 0.99 |
| Public healthcare spending per inhabitant | 0.29 | 0.46 | −0.59 | 1.23 | 0.77 | 0.23 | 1.00 | 6240 | 5652 | 1.33 |
| Average annual income per household (thousand €) | 0.10 | 0.48 | −0.87 | 1.09 | 0.59 | 0.41 | 1.00 | 5279 | 5106 | 1.11 |
| Primary care doctors and nurses per 1000 people allocated | 0.09 | 0.50 | −0.92 | 1.10 | 0.58 | 0.42 | 1.00 | 5313 | 4869 | 1.09 |
| Installed private beds per 1000 inhabitants | 0.00 | 0.22 | −0.45 | 0.41 | 0.51 | 0.49 | 1.00 | 11,941 | 8845 | 1.00 |
| External emergency centres per 1000 inhabitants | −0.02 | 0.52 | −1.08 | 1.00 | 0.49 | 0.51 | 1.00 | 5423 | 5204 | 0.98 |
| External emergency personnel per 1000 inhabitants | −0.10 | 0.40 | −0.91 | 0.71 | 0.37 | 0.63 | 1.00 | 5471 | 5073 | 0.90 |
| Installed public beds per 1000 inhabitants | −0.11 | 0.40 | −0.91 | 0.66 | 0.37 | 0.63 | 1.00 | 7459 | 6470 | 0.90 |
| Emergency physicians per 1000 inhabitants | −0.18 | 0.42 | −1.04 | 0.67 | 0.30 | 0.70 | 1.00 | 5015 | 4809 | 0.83 |
| Public beds in operation in Intensive Care Units per 1000 inhabitants | −0.23 | 0.42 | −1.09 | 0.63 | 0.26 | 0.74 | 1.00 | 5455 | 5540 | 0.80 |
| Probability of Being Situated on the Efficiency Frontier Model | ||||||||||
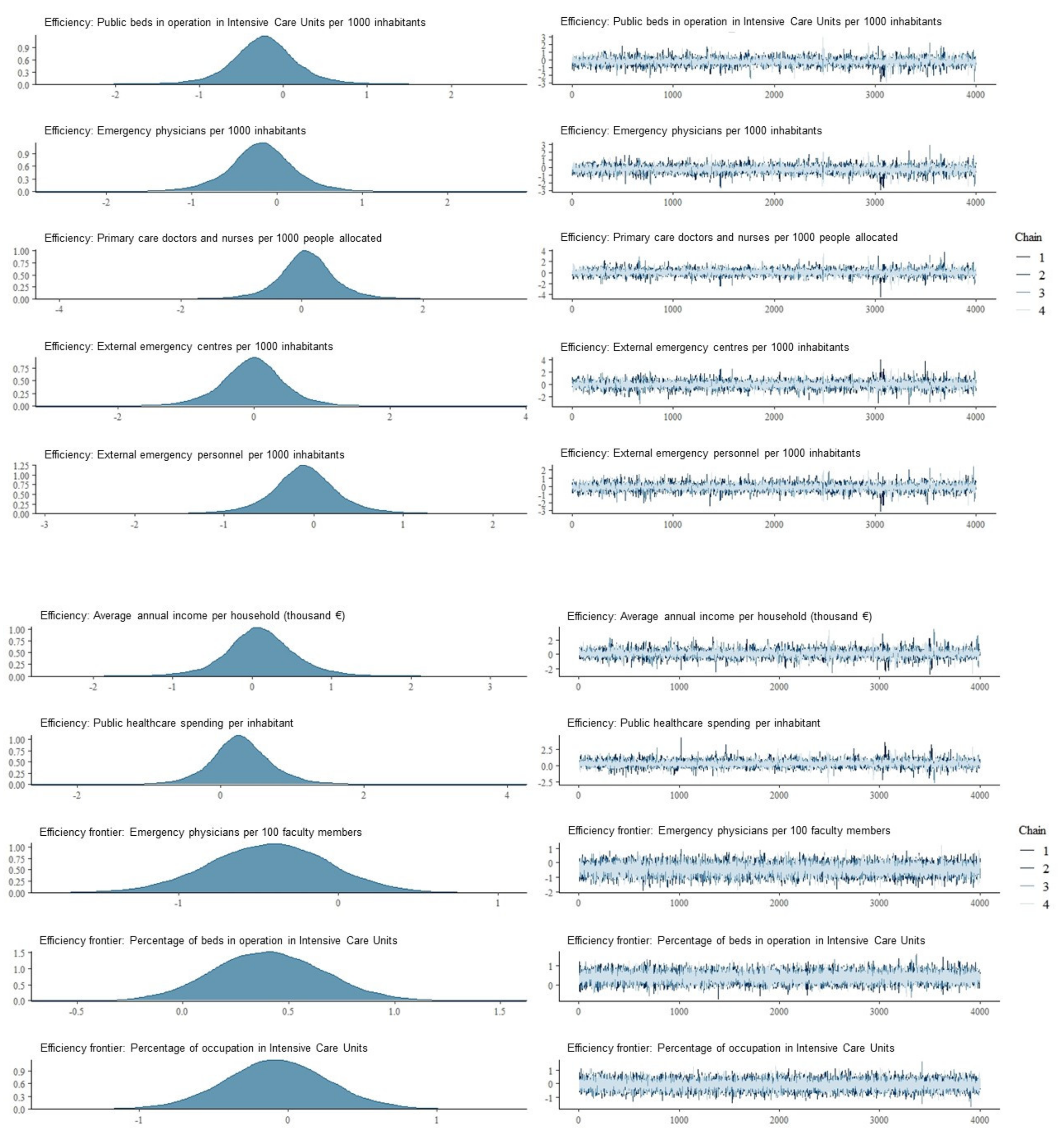
| Intercept | −3.00 | 0.44 | −3.94 | −2.21 | 0.00 | 1.00 | 1.00 | 12,108 | 10,551 | |
| Hospital type | ||||||||||
| Public | Reference | Reference | Reference | Reference | Reference | Reference | Reference | |||
| Public-Private Partnership | 3.74 | 1.22 | 1.57 | 6.37 | 1.00 | 0.00 | 1.00 | 17,875 | 11,484 | 42.06 |
| Private | 2.10 | 1.14 | −0.07 | 4.40 | 0.97 | 0.03 | 1.00 | 20,600 | 11,977 | 8.17 |
| Beds in operation in Intensive Care Units (%) | 0.41 | 0.26 | −0.09 | 0.93 | 0.95 | 0.05 | 1.00 | 25,157 | 11,536 | 1.50 |
| Occupation in Intensive Care Units (%) | −0.08 | 0.35 | −0.76 | 0.61 | 0.42 | 0.58 | 1.00 | 22,315 | 12,218 | 0.93 |
| Resident physicians per 100 faculty members | −0.38 | 0.43 | −1.23 | 0.48 | 0.19 | 0.81 | 1.00 | 14,282 | 12,800 | 0.68 |
| Emergency physicians per 100 faculty members | −0.43 | 0.37 | −1.18 | 0.29 | 0.12 | 0.88 | 1.00 | 20,060 | 12,905 | 0.65 |
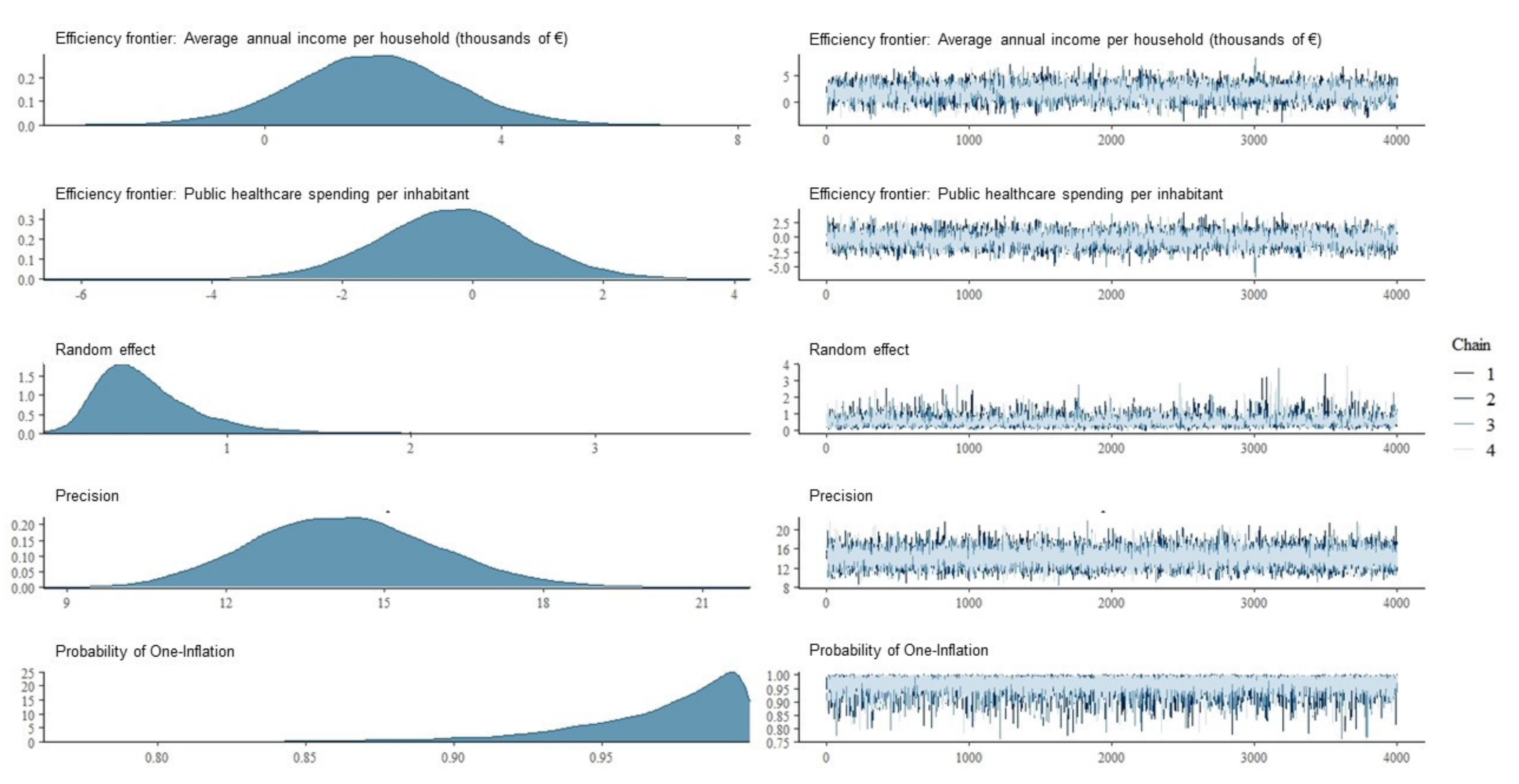
| Average annual income per household (thousands of €) | 1.86 | 1.38 | −0.90 | 4.62 | 0.91 | 0.09 | 1.00 | 4774 | 6823 | 6.43 |
| Primary care doctors and nurses per 1000 people allocated | 1.09 | 1.27 | −1.29 | 3.72 | 0.80 | 0.20 | 1.00 | 5435 | 7190 | 2.97 |
| Public beds in operation in Intensive Care Units per 1000 inhabitants | 0.23 | 1.03 | −1.83 | 2.29 | 0.58 | 0.42 | 1.00 | 5450 | 7804 | 1.26 |
| Emergency physicians per 1000 inhabitants | 0.12 | 1.12 | −2.23 | 2.29 | 0.54 | 0.46 | 1.00 | 5126 | 7031 | 1.13 |
| External emergency personnel per 1000 inhabitants | 0.12 | 1.13 | −2.19 | 2.30 | 0.54 | 0.46 | 1.00 | 5716 | 7733 | 1.12 |
| Public healthcare spending per inhabitant | −0.28 | 1.16 | −2.57 | 2.03 | 0.41 | 0.59 | 1.00 | 5110 | 6895 | 0.75 |
| External emergency centres per 1000 inhabitants | −0.43 | 1.25 | −2.97 | 1.96 | 0.37 | 0.63 | 1.00 | 5775 | 8174 | 0.65 |
| Installed public beds per 1000 inhabitants | −0.84 | 0.91 | −2.63 | 0.98 | 0.18 | 0.82 | 1.00 | 6257 | 8963 | 0.43 |
| Installed private beds per 1000 inhabitants | −0.98 | 0.57 | −2.19 | 0.05 | 0.03 | 0.97 | 1.00 | 17,535 | 11,127 | 0.37 |
| Accuracy. Conditional Probability of Inflation one and Random Effect | ||||||||||
| Precision () | 14.27 | 1.77 | 11.01 | 17.92 | 1.00 | 18,753 | 11,620 | |||
| Probability of One-Inflation () | 0.97 | 0.03 | 0.89 | 1.00 | 1.00 | 19,419 | 7510 | |||
| Random Effect | 0.57 | 0.31 | 0.17 | 1.34 | 1.00 | 3041 | 4251 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ocaña-Riola, R.; Pérez-Romero, C.; Ortega-Díaz, M.I.; Martín-Martín, J.J. Multilevel Zero-One Inflated Beta Regression Model for the Analysis of the Relationship between Exogenous Health Variables and Technical Efficiency in the Spanish National Health System Hospitals. Int. J. Environ. Res. Public Health 2021, 18, 10166. https://doi.org/10.3390/ijerph181910166
Ocaña-Riola R, Pérez-Romero C, Ortega-Díaz MI, Martín-Martín JJ. Multilevel Zero-One Inflated Beta Regression Model for the Analysis of the Relationship between Exogenous Health Variables and Technical Efficiency in the Spanish National Health System Hospitals. International Journal of Environmental Research and Public Health. 2021; 18(19):10166. https://doi.org/10.3390/ijerph181910166
Chicago/Turabian StyleOcaña-Riola, Ricardo, Carmen Pérez-Romero, Mª Isabel Ortega-Díaz, and José Jesús Martín-Martín. 2021. "Multilevel Zero-One Inflated Beta Regression Model for the Analysis of the Relationship between Exogenous Health Variables and Technical Efficiency in the Spanish National Health System Hospitals" International Journal of Environmental Research and Public Health 18, no. 19: 10166. https://doi.org/10.3390/ijerph181910166
APA StyleOcaña-Riola, R., Pérez-Romero, C., Ortega-Díaz, M. I., & Martín-Martín, J. J. (2021). Multilevel Zero-One Inflated Beta Regression Model for the Analysis of the Relationship between Exogenous Health Variables and Technical Efficiency in the Spanish National Health System Hospitals. International Journal of Environmental Research and Public Health, 18(19), 10166. https://doi.org/10.3390/ijerph181910166






