How Important Is Behavioral Change during the Early Stages of the COVID-19 Pandemic? A Mathematical Modeling Study
Abstract
:1. Introduction
2. Materials and Methods
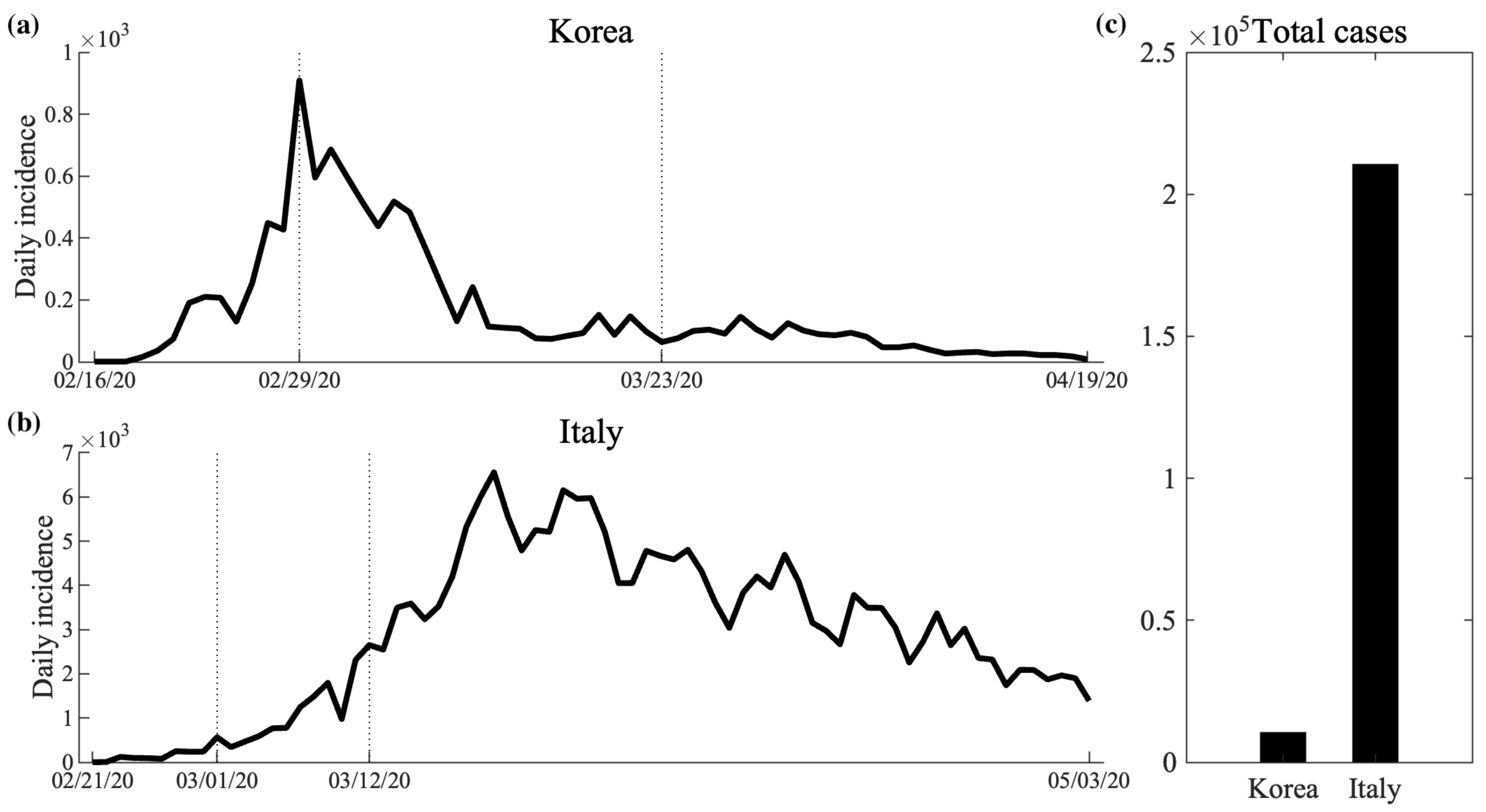
2.1. Epidemic Data
2.2. Social Distancing Strategies in Korea and Italy
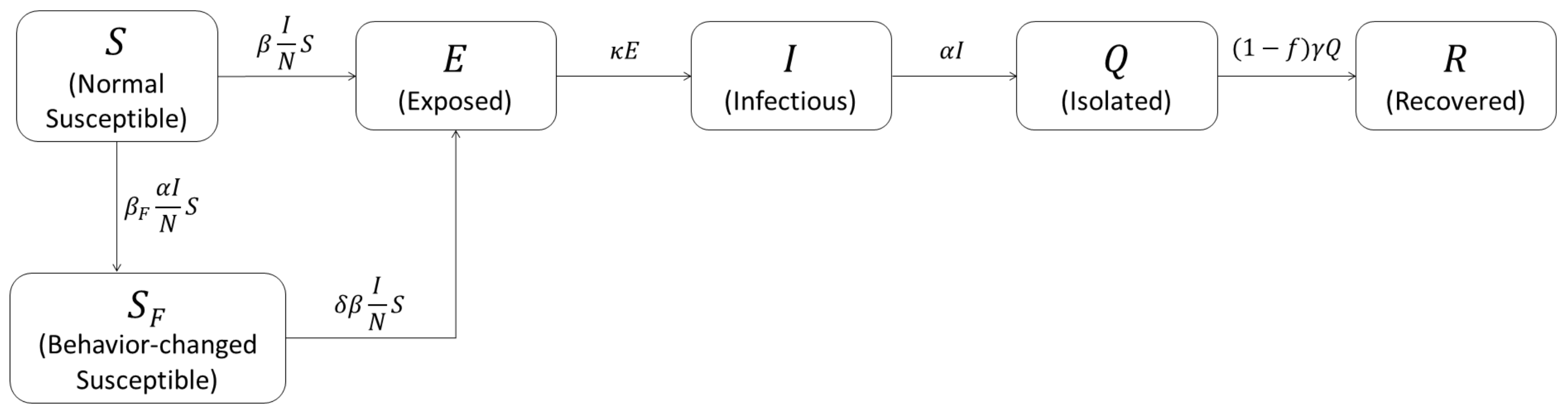
2.3. Mathematical Model Considering Behavioral Change
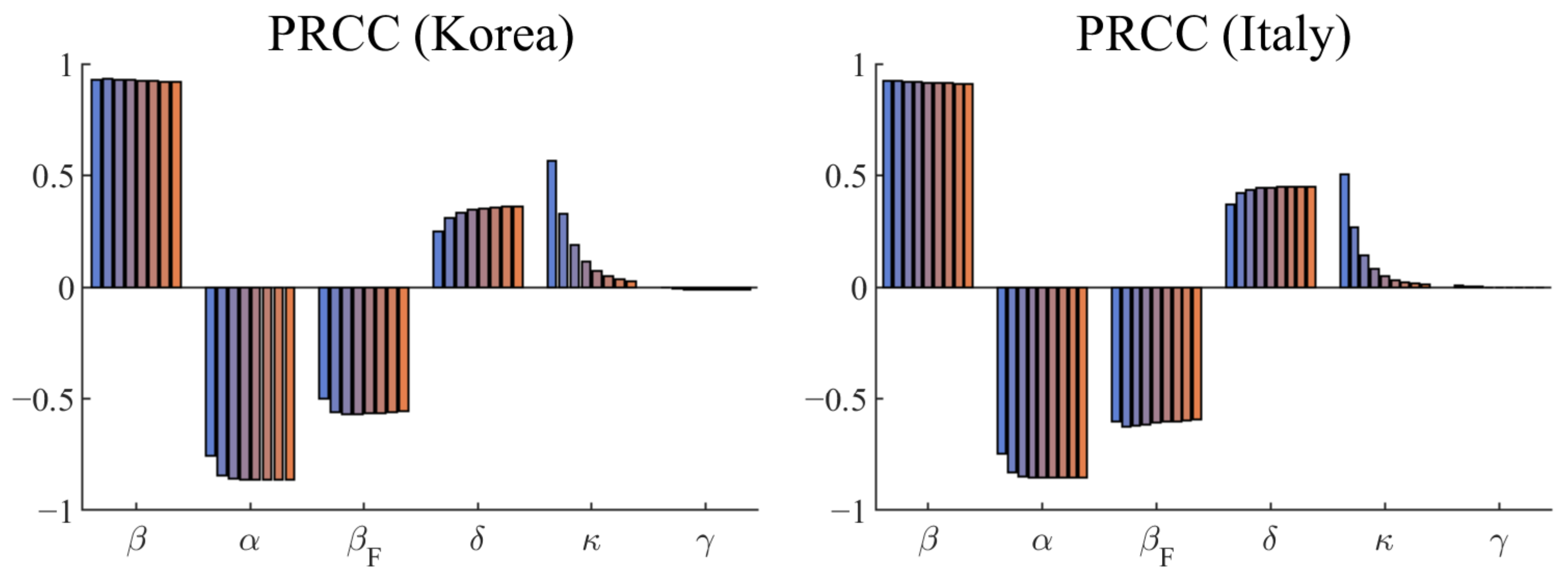
2.4. Sensitivity Analysis: PRCC-LHS
3. Results
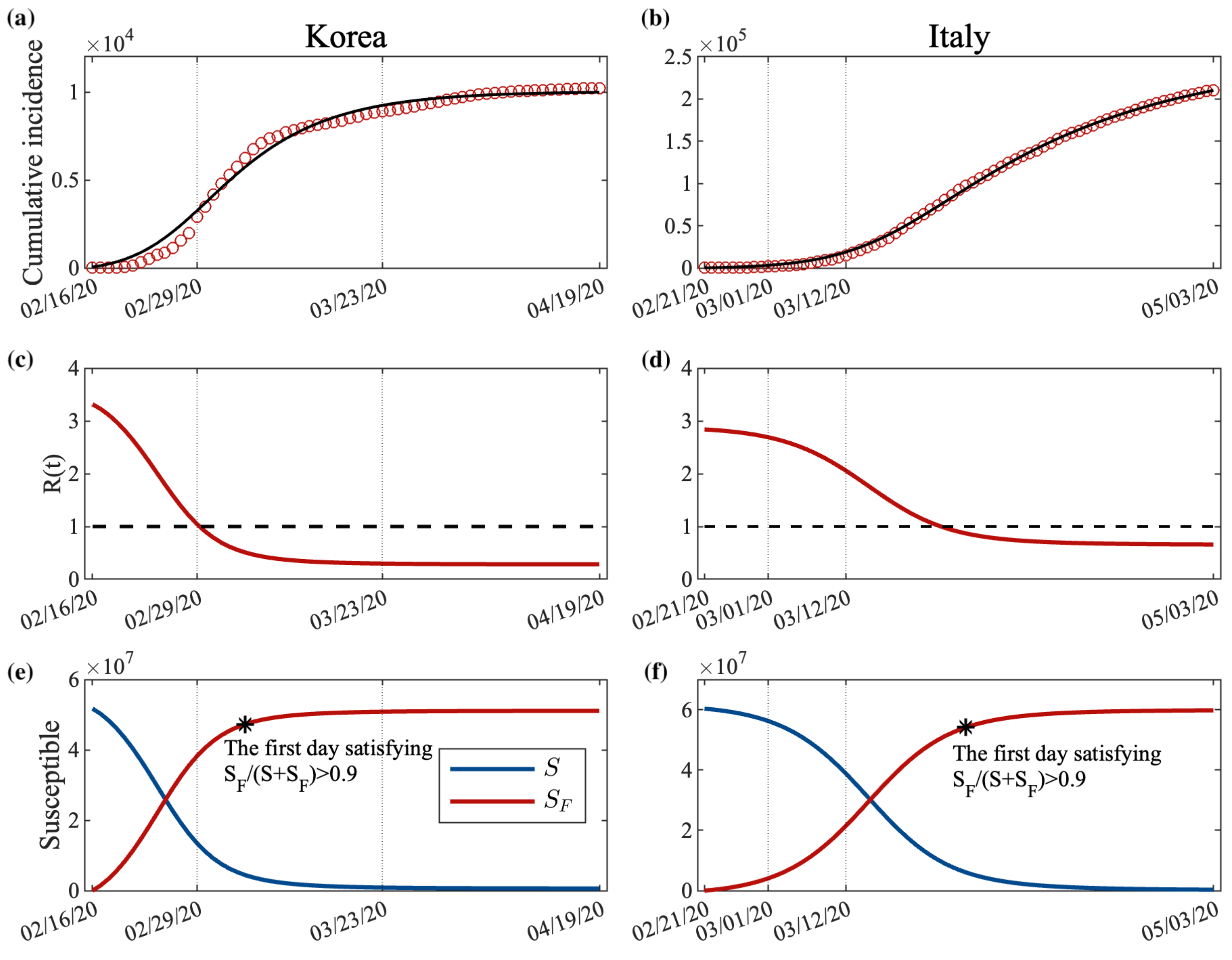
3.1. Data Fitting Result
3.2. Sensitivity Analysis
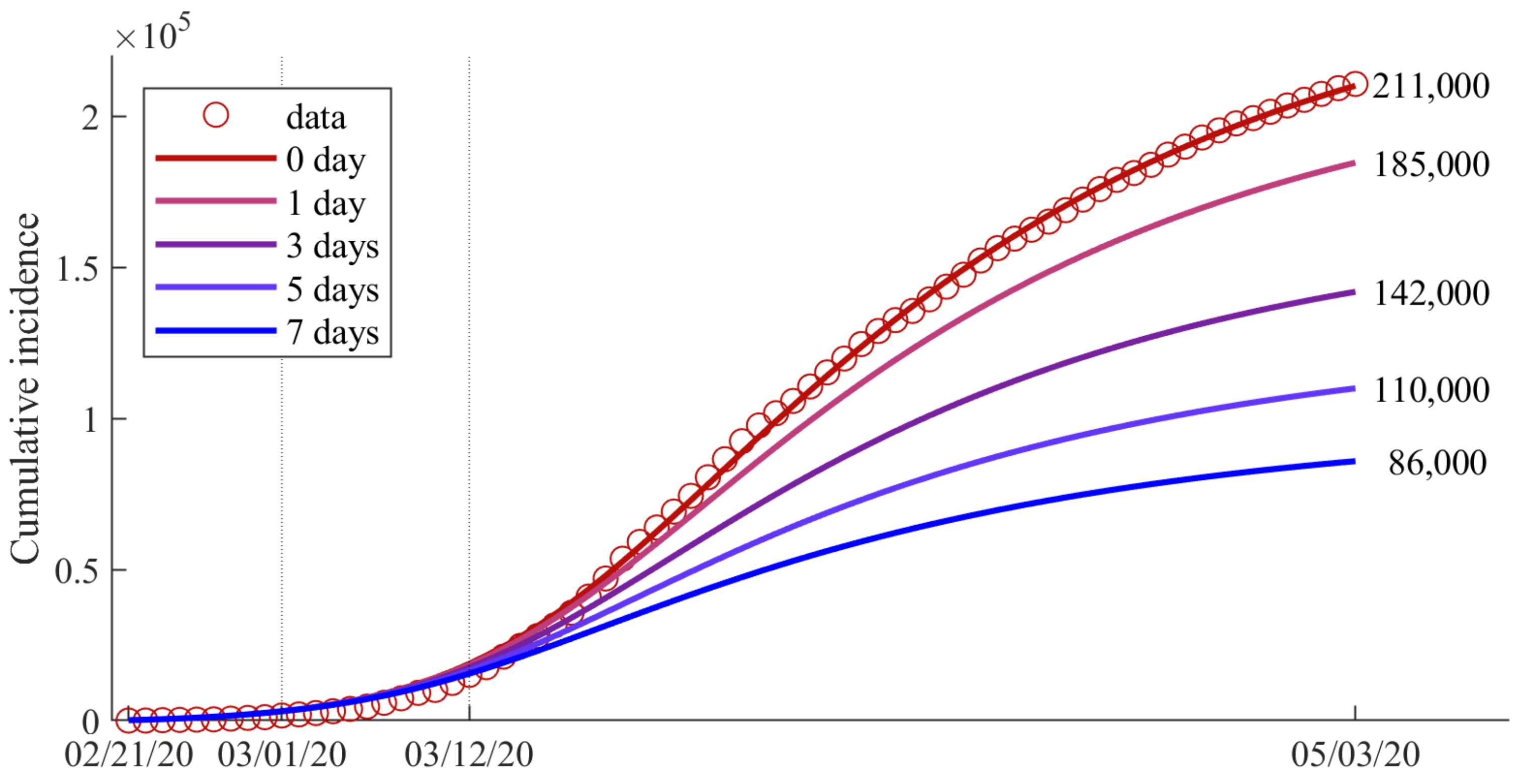
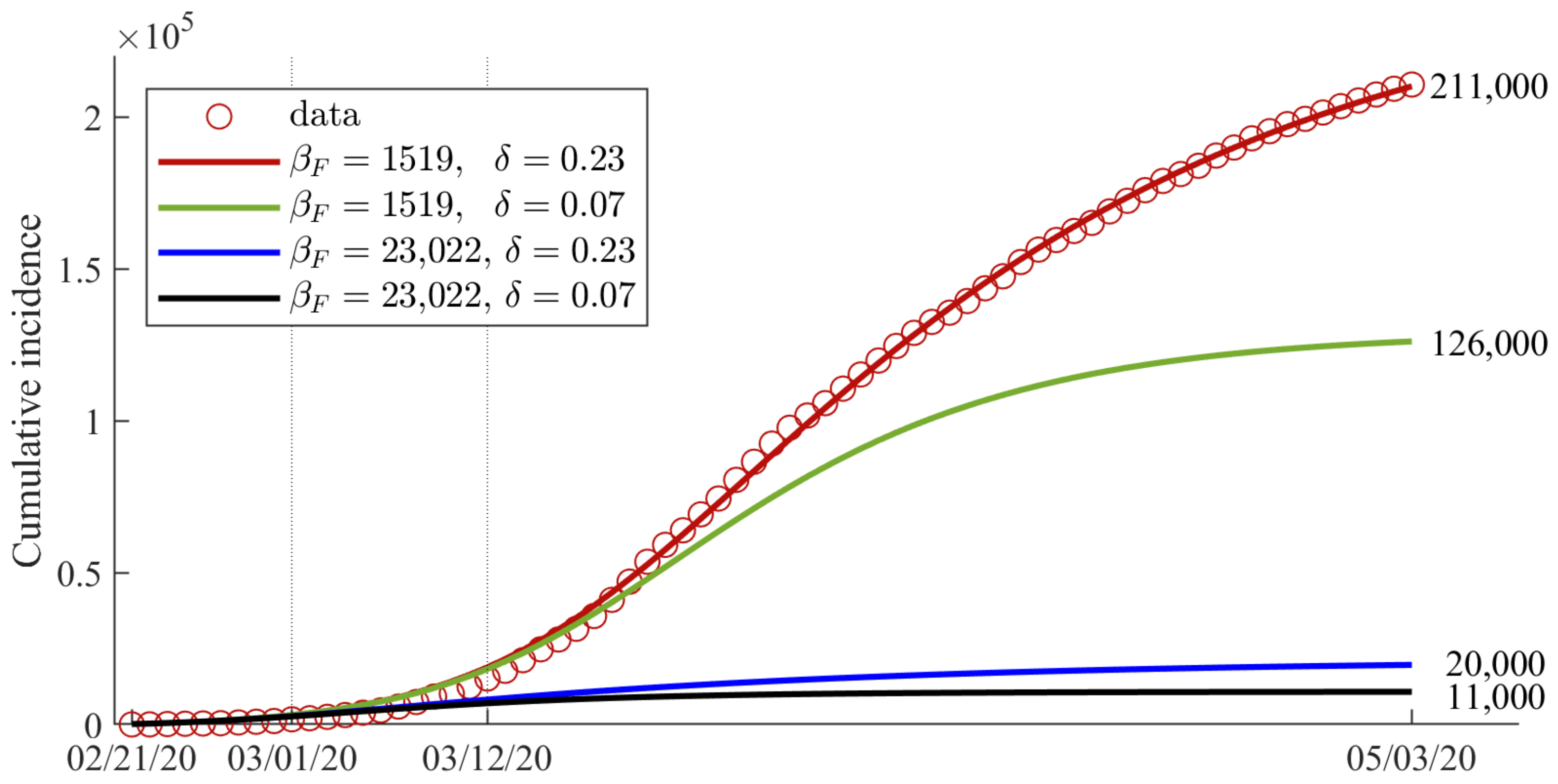
3.3. Analysis of Behavioral Change
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| COVID-19 | Coronavirus disease 2019 |
| NPIs | Nonpharmaceutical interventions |
| WHO | World Health Organization |
| KDCA | Korea Disease Control and Prevention Agency |
| ISS | Italian National Institute of Health |
| CFR | Case fatality ratio |
| PRCC | Partial rank coefficient correlation |
| LHS | Latin hypercube sampling |
| BCT | Behavior change timing |
Appendix A. Reproductive Number R(t)
References
- WHO Coronavirus Disease (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 17 September 2021).
- Palaniappan, A.; Dave, U.; Gosine, B. Comparing South Korea and Italy’s healthcare systems and initiatives to combat COVID-19. Rev. Panam. Salud Pública 2020, 44, e53. [Google Scholar] [CrossRef] [PubMed]
- World Development Indicators: Population Dynamics. Available online: http://wdi.worldbank.org/table/2.1 (accessed on 17 September 2021).
- KDCA Press Release. Available online: https://www.kdca.go.kr/board/board.es?mid=a20501010000&bid=0015 (accessed on 17 September 2021).
- COVID-19 Integrated Surveillance: Key National Data. Available online: https://www.epicentro.iss.it/en/coronavirus/sars-cov-2-integrated-surveillance-data (accessed on 17 September 2021).
- Ferguson, N.M.; Laydon, D.; Nedjati-Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunubá, Z.; Hinsley, W.; et al. Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College COVID-19 Response Team: London, UK, 2020; p. 20. [Google Scholar]
- (US) HSC. National Strategy for Pandemic Influenza; Homeland Security Council: Washington, DC, USA, 2005. [Google Scholar]
- (US) HSC. National Strategy for Pandemic Influenza: Implementation Plan; Executive Office of the President: Washington, DC, USA, 2006. [Google Scholar]
- World Health Organization. Global Influenza Strategy 2019–2030 (2019). Available online: https://www.paho.org/en/documents/global-influenza-strategy-2019-2030 (accessed on 17 September 2021).
- Stevens, H. Why outbreaks like coronavirus spread exponentially, and how to “flatten the curve”. The Washington Post, 14 March 2020. [Google Scholar]
- Ahmed, F.; Zviedrite, N.; Uzicanin, A. Effectiveness of workplace social distancing measures in reducing influenza transmission: A systematic review. BMC Public Health 2018, 18, 1–13. [Google Scholar] [CrossRef]
- Guilbert, J.J. The world health report 2002–reducing risks, promoting healthy life. Educ. Health 2003, 16, 230. [Google Scholar]
- Perra, N.; Balcan, D.; Gonçalves, B.; Vespignani, A. Towards a characterization of behavior-disease models. PLoS ONE 2011, 6, e23084. [Google Scholar]
- Brauer, F. A simple model for behaviour change in epidemics. BMC Public Health 2011, 11, 1–5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.; Seo, Y.B.; Jung, E. Prediction of COVID-19 transmission dynamics using a mathematical model considering behavior changes in Korea. Epidemiol. Health 2020, 42, e2020026. [Google Scholar] [CrossRef]
- Kim, S.; Ko, Y.; Kim, Y.J.; Jung, E. The impact of social distancing and public behavior changes on COVID-19 transmission dynamics in the Republic of Korea. PLoS ONE 2020, 15, e0238684. [Google Scholar] [CrossRef]
- Acuña-Zegarra, M.A.; Santana-Cibrian, M.; Velasco-Hern, J.X. Modeling behavioral change and COVID-19 containment in Mexico: A trade-off between lockdown and compliance. Math. Biosci. 2020, 325, 108370. [Google Scholar] [CrossRef] [PubMed]
- Badr, H.S.; Du, H.; Marshall, M.; Dong, E.; Squire, M.M.; Gardner, L.M. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. Lancet Infect. Dis. 2020, 20, 1247–1254. [Google Scholar] [CrossRef]
- Coronavirus Disease-19 Republic of Korea. Available online: http://ncov.mohw.go.kr/ (accessed on 17 September 2021).
- Kim, S.; Kim, Y.J.; Peck, K.R.; Ko, Y.; Lee, J.; Jung, E. Keeping Low Reproductive Number Despite the Rebound Population Mobility in Korea, a Country Never under Lockdown during the COVID-19 Pandemic. Int. J. Environ. Res. Public Health 2020, 17, 9551. [Google Scholar] [CrossRef]
- Covid-19, in the Official Gazette the Dpcm 1 March 2020. All Containment Measures by Area. Available online: http://www.salute.gov.it/portale/nuovocoronavirus/dettaglioNotizieNuovoCoronavirus.jsp?lingua=italiano&menu=notizie&p=dalministero&id=4137 (accessed on 17 September 2021).
- Covid-19, Non-Essential Businesses Close. Available online: http://www.salute.gov.it/portale/nuovocoronavirus/dettaglioNotizieNuovoCoronavirus.jsp?lingua=italiano&menu=notizie&p=dalministero&id=4212 (accessed on 17 September 2021).
- Lee, J.; Lim, D.S.; Hong, S.O.; Park, M.-J.; Kim, G.; Lim, N.-K.; Lee, S.Y.; Park, J.Y.; Song, D.S.; Chai, H.Y.; et al. KDCA Weekly Report. The primary report of clinical data analysis on the COVID-19 in the Republic of Korea. Available online: https://www.kdca.go.kr/board/board.es?mid=a20602010000&bid=0034&list_no=367744&act=view (accessed on 17 September 2021).
- KDCA Press Reference. Available online: https://www.kdca.go.kr/upload_comm/syview/doc.html?fn=159004743687800.pdf&rs=/upload_comm/docu/0015/ (accessed on 17 September 2021).
- World Health Organization. Transmission of SARS-CoV-2: Implications for Infection Prevention Precautions: Scientific Brief, 9 July 2020; World Health Organization: Geneva, Switzerland, 2020. [Google Scholar]
- Ki, M. Epidemiologic characteristics of early cases with 2019 novel coronavirus (2019-nCoV) disease in Korea. Epidemiol. Health 2020, 42, e2020007. [Google Scholar] [CrossRef]
- Flavia, R.; Xanthi, A.; Antonino, B.; Del Manso, M.; Urdiales, A.M.; Fabiani, M.; Bellino, S.; Boros, S.; D’Ancona, F.; Rota, M.C.; et al. Epidemia COVID-19 Aggiornamento Nazionale; Istituto Superiore di Sanitá: Rome, Italy, 26 May 2020; Available online: https://www.epicentro.iss.it/coronavirus/bollettino/Bollettino-sorveglianza-integrata-COVID-19_26-Maggio-2020.pdf (accessed on 17 September 2021).
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Musa, S.S.; Baba, I.A.; Yusuf, A.; Sulaiman, T.A.; Aliyu, A.I.; Zhao, S.; He, D. Transmission dynamics of SARS-CoV-2: A modeling analysis with high-and-moderate risk populations. Results Phys. 2021, 26, 104290. [Google Scholar] [CrossRef]
- Musa, S.S.; Qureshi, S.; Zhao, S.; Yusuf, A.; Mustapha, U.T.; He, D. Mathematical modeling of COVID-19 epidemic with effect of awareness programs. Infect. Dis. Model. 2021, 6, 448–460. [Google Scholar]
- Adewole, M.O.; Onifade, A.A.; Abdullah, F.A.; Kasali, F.; Ismail, A.I. Modeling the Dynamics of COVID-19 in Nigeria. Int. J. Appl. Comput. Math. 2021, 7, 1–25. [Google Scholar] [CrossRef]
- Buhat, C.A.H.; Torres, M.C.; Olave, Y.H.; Gavina, M.K.A.; Felix, E.F.O.; Gamilla, G.B.; Verano, K.V.B.; Babierra, A.L.; Rabajante, J.F. A mathematical model of COVID-19 transmission between frontliners and the general public. Netw. Model. Anal. Health Inform. Bioinform. 2021, 10, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, J.F.; Jorge, D.C.; Veiga, R.V.; Rodrigues, M.S.; Torquato, M.F.; da Silva, N.B.; Fiaccone, R.L.; Cardim, L.L.; Pereira, F.A.C.; de Castro, C.P.; et al. Mathematical modeling of COVID-19 in 14.8 million individuals in Bahia, Brazil. Nat. Commun. 2021, 12, 1–13. [Google Scholar] [CrossRef]
- Barbarossa, M.V.; Bogya, N.; Dénes, A.; Röst, G.; Varma, H.V.; Vizi, Z. Fleeing lockdown and its impact on the size of epidemic outbreaks in the source and target regions—A COVID-19 lesson. Sci. Rep. 2021, 11, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Nande, A.; Adlam, B.; Sheen, J.; Levy, M.Z.; Hill, A.L. Dynamics of COVID-19 under social distancing measures are driven by transmission network structure. PLoS Comput. Biol. 2021, 17, e1008684. [Google Scholar] [CrossRef] [PubMed]
- Neuwirth, C.; Gruber, C.; Murphy, T. Investigating duration and intensity of Covid-19 social-distancing strategies. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- La Torre, D.; Liuzzi, D.; Marsiglio, S. Epidemics and macroeconomic outcomes: Social distancing intensity and duration. J. Math. Econ. 2021, 93, 102473. [Google Scholar] [CrossRef] [PubMed]
- Alagoz, O.; Sethi, A.K.; Patterson, B.W.; Churpek, M.; Safdar, N. Effect of Timing of and Adherence to Social Distancing Measures on COVID-19 Burden in the United States: A Simulation Modeling Approach. Ann. Intern. Med. 2020, 174, 50–57. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]

| Parameters | Korea | Italy | |||
|---|---|---|---|---|---|
| Symbol | Description | Value (CI) | References | Value (CI) | References |
| Number of people who changed their behavior per the number of daily incidence | 23,000 (15,000, 31,000) | data-fit | 1500 (1400, 1600) | data-fit | |
| Transmission rate in normal susceptible group (per day) | 0.55 (0.49, 0.61) | data-fit | 0.40 (0.39, 0.40) | data-fit | |
| Reduction ratio of transmission in the behavior-changed group | 0.074 (0.023, 0.13) | data-fit | 0.23 (0.023, 0.13) | data-fit | |
| Latent period (days) | 2.1 | [24,25] | 2.1 | [24,25] | |
| Infectious period (days) | 6 | [25,26] | 7.16 | [25,27] | |
| Isolation period (days) | 20.7 | [23] | 20.7 | [23] | |
| f | Case fatality ratio | 0.022 | [4] | 0.14 | [5] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Lee, S.-M.; Jung, E. How Important Is Behavioral Change during the Early Stages of the COVID-19 Pandemic? A Mathematical Modeling Study. Int. J. Environ. Res. Public Health 2021, 18, 9855. https://doi.org/10.3390/ijerph18189855
Lee J, Lee S-M, Jung E. How Important Is Behavioral Change during the Early Stages of the COVID-19 Pandemic? A Mathematical Modeling Study. International Journal of Environmental Research and Public Health. 2021; 18(18):9855. https://doi.org/10.3390/ijerph18189855
Chicago/Turabian StyleLee, Jongmin, Seok-Min Lee, and Eunok Jung. 2021. "How Important Is Behavioral Change during the Early Stages of the COVID-19 Pandemic? A Mathematical Modeling Study" International Journal of Environmental Research and Public Health 18, no. 18: 9855. https://doi.org/10.3390/ijerph18189855






