Modeling of the Long-Term Epidemic Dynamics of COVID-19 in the United States
Abstract
:1. Introduction
2. Methods
2.1. T-SIR Model
2.2. Data Sources and Processing
2.2.1. Epidemiological Data
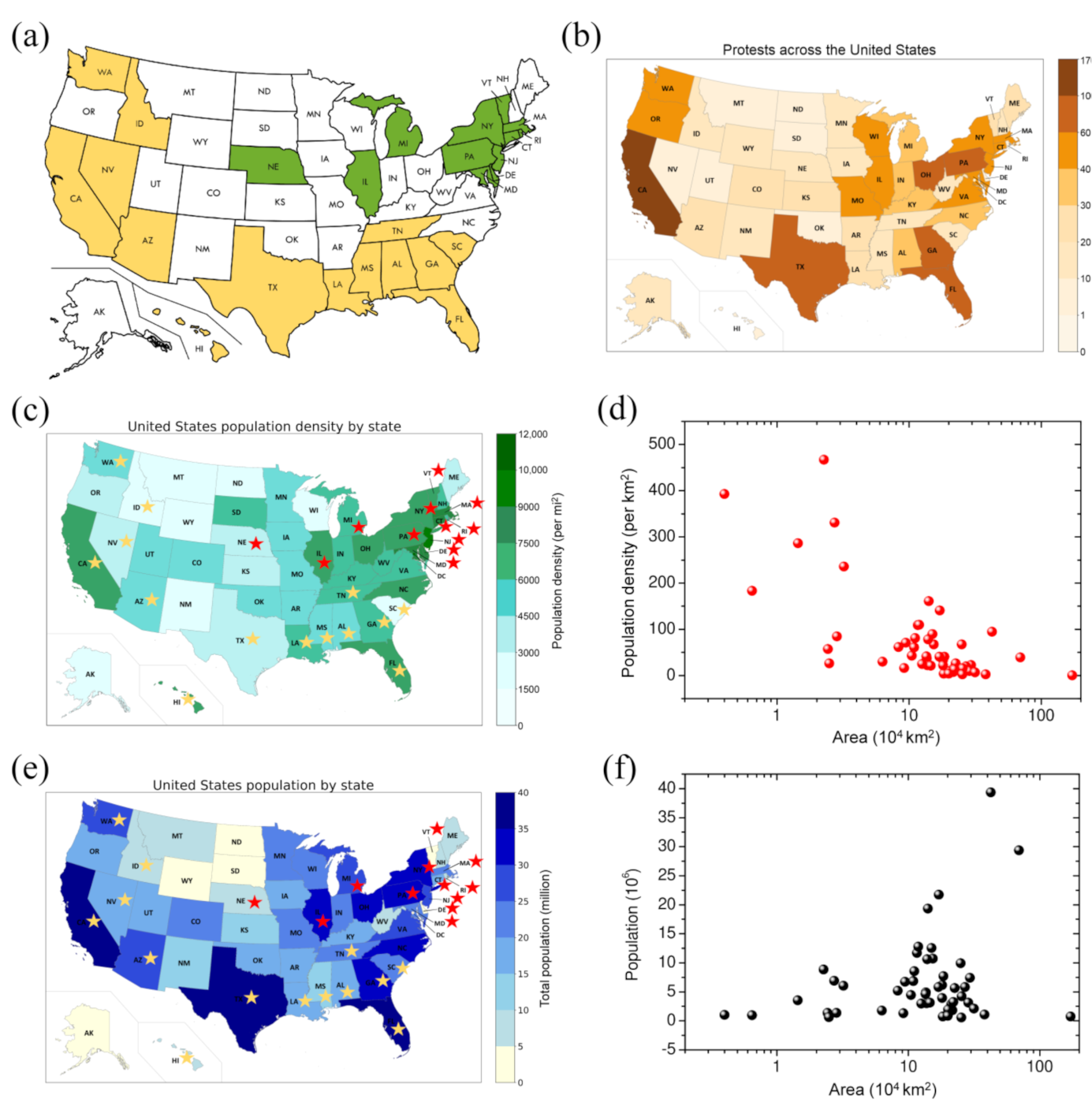
2.2.2. Geographical and Demographic Data
2.2.3. Mobility Data
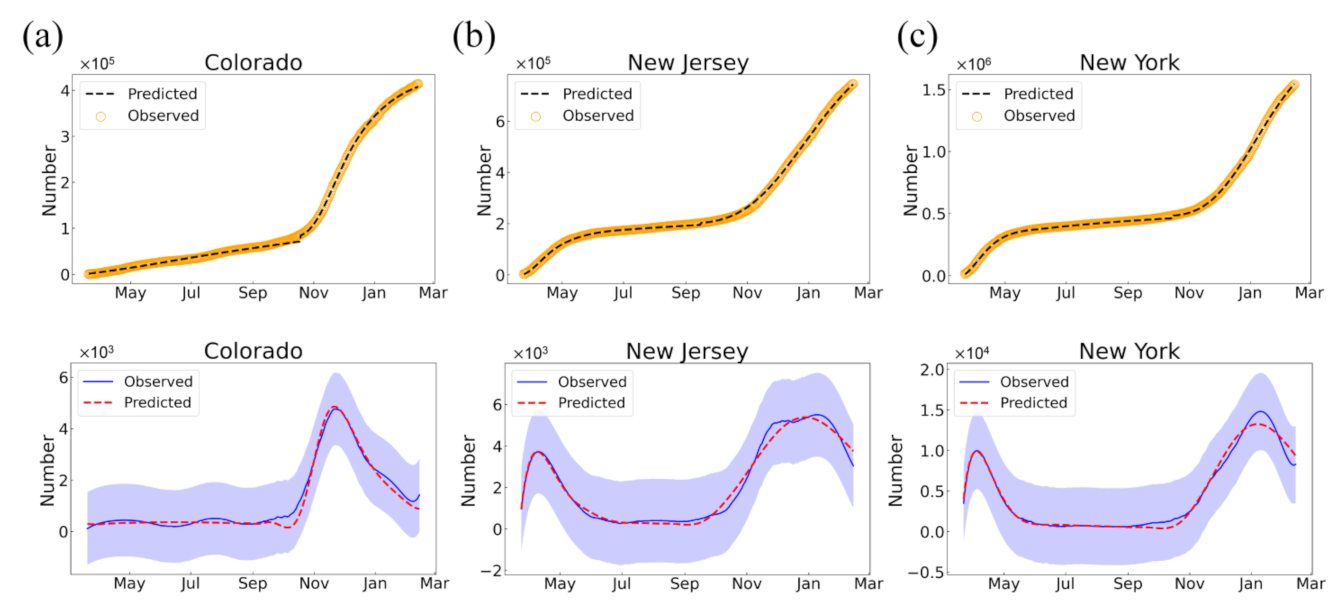
2.3. Fitting
3. Results
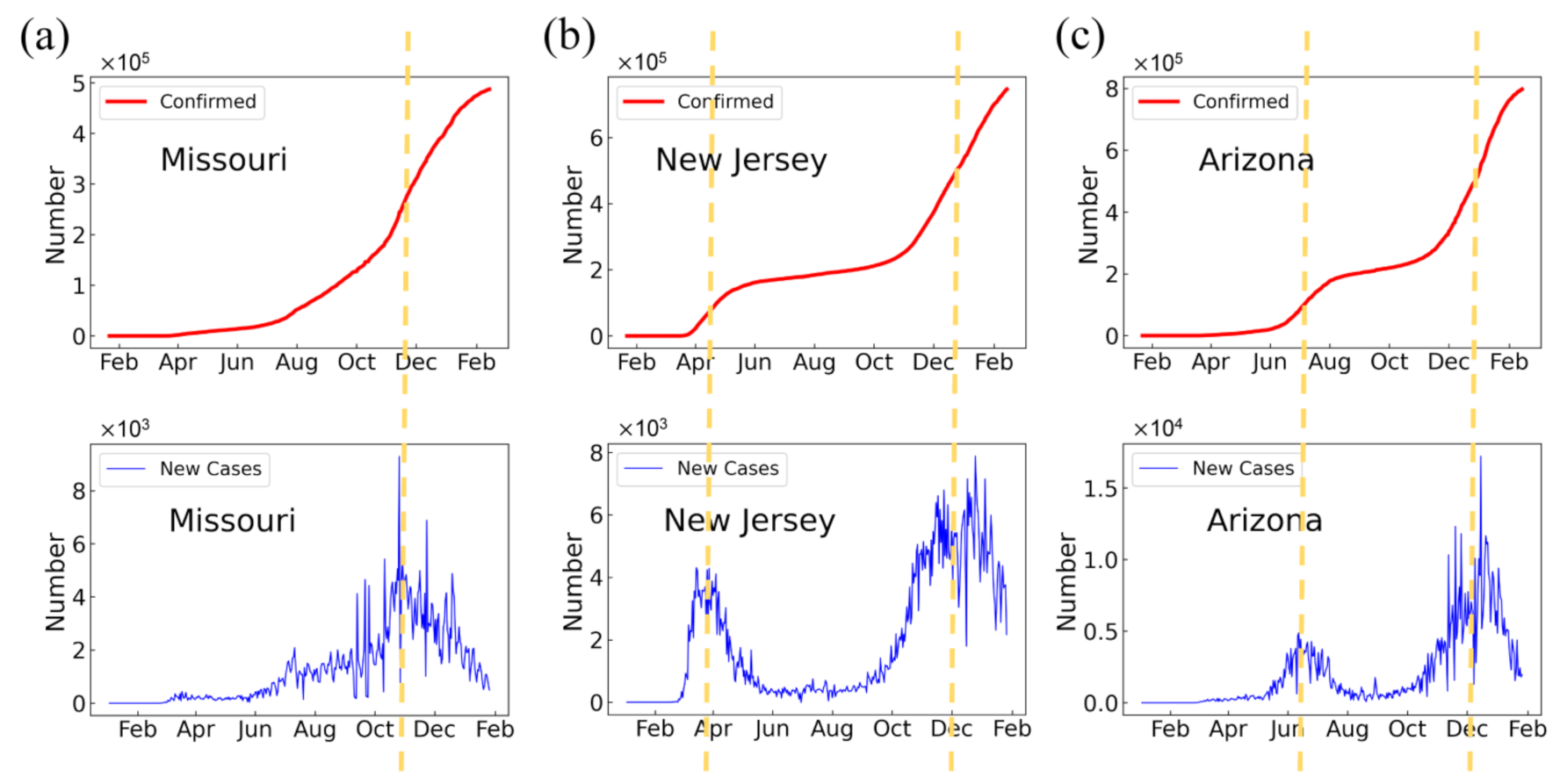
3.1. COVID-19 Epidemics of the 50 States in the US
3.1.1. Times of COVID-19 Outbreaks
3.1.2. Properties of COVID-19 Outbreaks
3.1.3. Demographic Impact on COVID-19 Outbreaks
3.2. Modeling the COVID-19 Dynamics of the US States
3.2.1. Fitting of the T-SIR Model
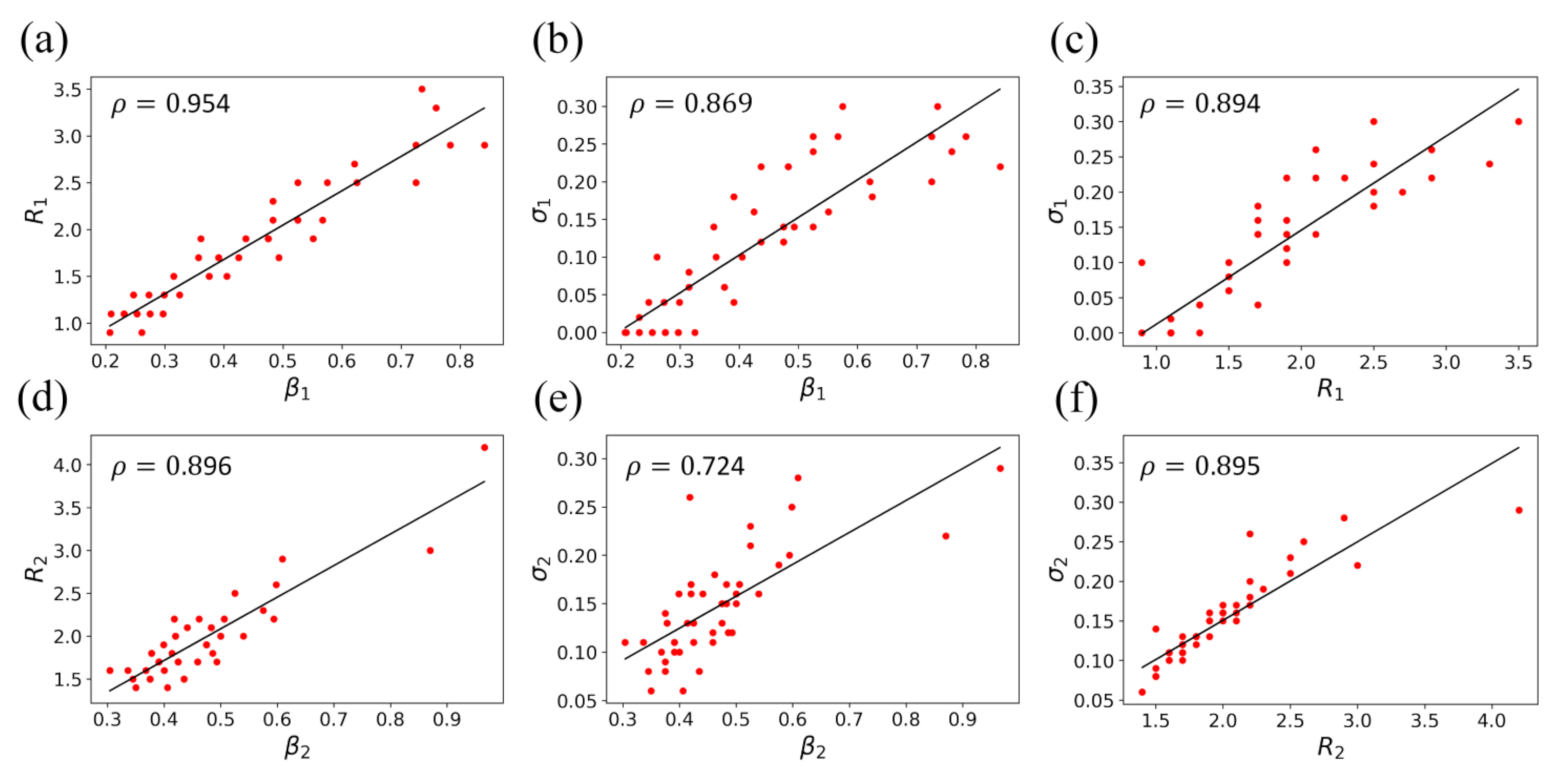
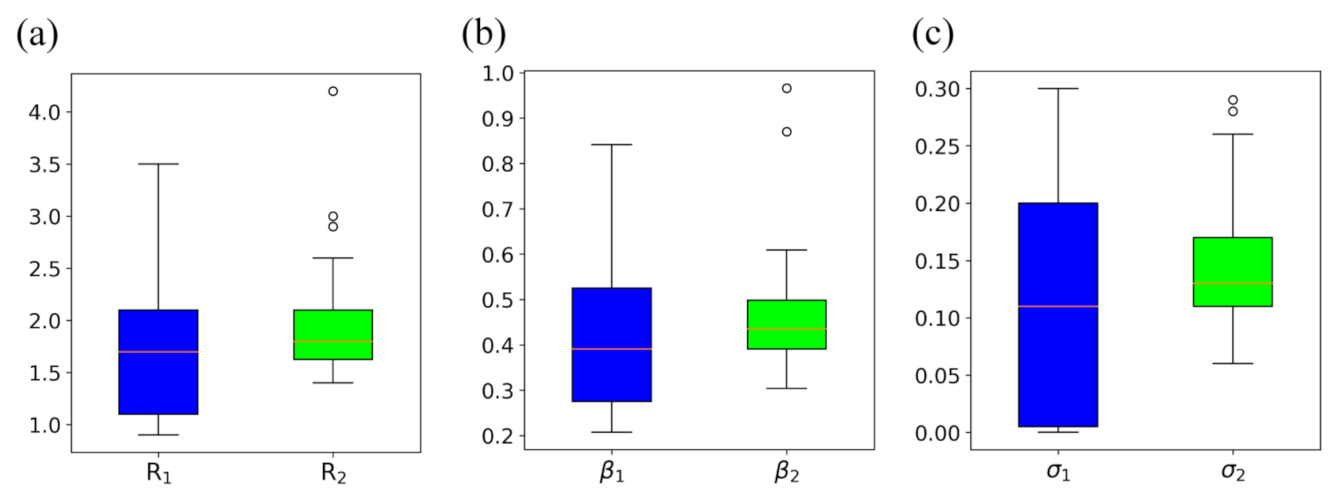
3.2.2. Implications of T-SIR Model Parameters
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WHO Coronavirus (COVID-19) Dashboard. Available online: https://covid19.who.int/ (accessed on 15 July 2021).
- Coronavirus Disease (COVID-19) Situation Reports. Available online: https://www.who.int/emergencies/diseases/novel-coronavirus-2019/situation-reports (accessed on 14 February 2021).
- Anderson, R.M.; Heesterbeek, H.; Klinkenberg, D.; Hollingsworth, T.D. How will country-based mitigation measures influence the course of the COVID-19 epidemic? Lancet 2020, 395, 931–934. [Google Scholar] [CrossRef]
- Ngonghala, C.N.; Iboi, E.; Eikenberry, S.; Scotch, M.; MacIntyre, C.R.; Bonds, M.H.; Gumel, A.B. Mathematical assessment of the impact of non-pharmaceutical interventions on curtailing the 2019 novel Coronavirus. Math. Biosci. 2020, 325, 108364. [Google Scholar] [CrossRef]
- Teslya, A.; Pham, T.M.; Godijk, N.G.; Kretzschmar, M.E.; Bootsma, M.C.J.; Rozhnova, G. Impact of self-imposed prevention measures and short-term government-imposed social distancing on mitigating and delaying a COVID-19 epidemic: A modelling study. PLoS Med. 2020, 17, e1003166. [Google Scholar] [CrossRef]
- Pan, A.; Liu, L.; Wang, C.; Guo, H.; Hao, X.; Wang, Q.; Huang, J.; He, N.; Yu, H.; Lin, X.; et al. Association of Public Health Interventions With the Epidemiology of the COVID-19 Outbreak in Wuhan, China. JAMA 2020, 323, 1915–1923. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hartley, D.M.; Perencevich, E.N. Public Health Interventions for COVID-19: Emerging Evidence and Implications for an Evolving Public Health Crisis. JAMA 2020, 323, 1908–1909. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Chen, C.; Shen, W.; Tang, F.; Lei, H.; Xie, Y.; Cao, Z.; Tang, K.; Bai, J.; Xiao, L.; et al. Impact of population movement on the spread of 2019-nCoV in China. Emerg. Microbes Infect. 2020, 9, 988–990. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Tang, F.; Chen, C.; Zhang, C.; Guo, Y.; Lin, R.; Huang, Z.; Teng, Y.; Xie, T.; Xu, Y.; et al. Impact of Systematic Factors on the Outbreak Outcomes of the Novel COVID-19 Disease in China: Factor Analysis Study. J. Med. Internet. Res. 2020, 22, e23853. [Google Scholar] [CrossRef]
- Gilman, R.T.; Mahroof-Shaffi, S.; Harkensee, C.; Chamberlain, A.T. Modelling interventions to control COVID-19 outbreaks in a refugee camp. BMJ Glob. Health 2020, 5, e003727. [Google Scholar] [CrossRef] [PubMed]
- Alfonso Viguria, U.; Casamitjana, N. Early Interventions and Impact of COVID-19 in Spain. Int. J. Environ. Res. Public Health 2021, 18, 4026. [Google Scholar] [CrossRef] [PubMed]
- Modeling COVID-19 scenarios for the United States. Nat. Med. 2021, 27, 94–105. [CrossRef] [PubMed]
- Hao, X.; Cheng, S.; Wu, D.; Wu, T.; Lin, X.; Wang, C. Reconstruction of the full transmission dynamics of COVID-19 in Wuhan. Nature 2020, 584, 420–424. [Google Scholar] [CrossRef] [PubMed]
- Rader, B.; Scarpino, S.V.; Nande, A.; Hill, A.L.; Adlam, B.; Reiner, R.C.; Pigott, D.M.; Gutierrez, B.; Zarebski, A.E.; Shrestha, M.; et al. Crowding and the shape of COVID-19 epidemics. Nat. Med. 2020, 26, 1829–1834. [Google Scholar] [CrossRef] [PubMed]
- Monod, M.; Blenkinsop, A.; Xi, X.; Hebert, D.; Bershan, S.; Tietze, S.; Baguelin, M.; Bradley, V.C.; Chen, Y.; Coupland, H.; et al. Age groups that sustain resurging COVID-19 epidemics in the United States. Science 2021, 371, 6536. [Google Scholar] [CrossRef] [PubMed]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, 6500. [Google Scholar] [CrossRef]
- Spassiani, I.; Sebastiani, G.; Palù, G. Spatiotemporal Analysis of COVID-19 Incidence Data. Viruses 2021, 13, 463. [Google Scholar] [CrossRef]
- Loeffler-Wirth, H.; Schmidt, M.; Binder, H. Covid-19 Transmission Trajectories-Monitoring the Pandemic in the Worldwide Context. Viruses 2020, 12, 777. [Google Scholar] [CrossRef]
- Röst, G.; Bartha, F.A.; Bogya, N.; Boldog, P.; Dénes, A.; Ferenci, T.; Horváth, K.J.; Juhász, A.; Nagy, C.; Tekeli, T.; et al. Early Phase of the COVID-19 Outbreak in Hungary and Post-Lockdown Scenarios. Viruses 2020, 12, 708. [Google Scholar] [CrossRef]
- Roosa, K.; Lee, Y.; Luo, R.; Kirpich, A.; Rothenberg, R.; Hyman, J.M.; Yan, P.; Chowell, G. Short-term Forecasts of the COVID-19 Epidemic in Guangdong and Zhejiang, China: February 13–23, 2020. J. Clin. Med. 2020, 9, 596. [Google Scholar] [CrossRef] [Green Version]
- Aguas, R.; White, L.; Hupert, N.; Shretta, R.; Pan-Ngum, W.; Celhay, O.; Moldokmatova, A.; Arifi, F.; Mirzazadeh, A.; Sharifi, H.; et al. Modelling the COVID-19 pandemic in context: An international participatory approach. BMJ Glob. Health 2020, 5, e003126. [Google Scholar] [CrossRef]
- Gabutti, G.; d'Anchera, E.; De Motoli, F.; Savio, M.; Stefanati, A. The Epidemiological Characteristics of the COVID-19 Pandemic in Europe: Focus on Italy. Int. J. Environ. Res. Public Health 2021, 18, 2942. [Google Scholar] [CrossRef]
- De Sousa, L.E.; Neto, P.H.O.; Filho, D. Kinetic Monte Carlo model for the COVID-19 epidemic: Impact of mobility restriction on a COVID-19 outbreak. Phys. Rev. 2020, 102, 032133. [Google Scholar] [CrossRef]
- Weitz, J.S.; Park, S.W.; Eksin, C.; Dushoff, J. Awareness-driven behavior changes can shift the shape of epidemics away from peaks and toward plateaus, shoulders, and oscillations. Proc. Natl. Acad. Sci. USA 2020, 117, 32764–32771. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Franco, E.; Mohler, G.; Short, M.B.; Sledge, D. The challenges of modeling and forecasting the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 16732–16738. [Google Scholar] [CrossRef]
- Maugeri, A.; Barchitta, M.; Battiato, S.; Agodi, A. Estimation of Unreported Novel Coronavirus (SARS-CoV-2) Infections from Reported Deaths: A Susceptible-Exposed-Infectious-Recovered-Dead Model. J. Clin. Med. 2020, 9, 1350. [Google Scholar] [CrossRef]
- Reno, C.; Lenzi, J.; Navarra, A.; Barelli, E.; Gori, D.; Lanza, A.; Valentini, R.; Tang, B.; Fantini, M.P. Forecasting COVID-19-Associated Hospitalizations under Different Levels of Social Distancing in Lombardy and Emilia-Romagna, Northern Italy: Results from an Extended SEIR Compartmental Model. J. Clin. Med. 2020, 9, 1492. [Google Scholar] [CrossRef]
- Siraj, A.; Worku, A.; Berhane, K.; Aregawi, M.; Eshetu, M.; Mirkuzie, A.; Berhane, Y.; Siraj, D. Early estimates of COVID-19 infections in small, medium and large population clusters. BMJ Glob. Health 2020, 5, e003055. [Google Scholar] [CrossRef] [PubMed]
- Anđelić, N.; Baressi Šegota, S.; Lorencin, I.; Jurilj, Z.; Šušteršič, T.; Blagojević, A.; Protić, A.; Ćabov, T.; Filipović, N.; Car, Z. Estimation of COVID-19 Epidemiology Curve of the United States Using Genetic Programming Algorithm. Int. J. Environ. Res. Public Health 2021, 18, 959. [Google Scholar] [CrossRef]
- Chowell, G.; Sattenspiel, L.; Bansal, S.; Viboud, C. Mathematical models to characterize early epidemic growth: A review. Phys. Life Rev. 2016, 18, 66–97. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tolles, J.; Luong, T. Modeling Epidemics with Compartmental Models. JAMA 2020, 323, 2515–2516. [Google Scholar] [CrossRef] [PubMed]
- Bootsma, M.C.; Ferguson, N.M. The effect of public health measures on the 1918 influenza pandemic in U.S. cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7588–7593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, Z.J.; Zou, X.W.; Jin, Z.Z. Percolation with long-range correlations for epidemic spreading. Phys. Rev. 2000, 62, 8409–8412. [Google Scholar] [CrossRef]
- Shao, Z.G.; Tan, Z.J.; Zou, X.W.; Jin, Z.Z. Epidemics with pathogen mutation on small-world networks. Phys. Stat. Mech. Appl. 2006, 363, 561–566. [Google Scholar] [CrossRef]
- Leontitsis, A.; Senok, A.; Alsheikh-Ali, A.; Al Nasser, Y.; Loney, T.; Alshamsi, A. SEAHIR: A Specialized Compartmental Model for COVID-19. Int. J. Environ. Res. Public Health 2021, 18, 2667. [Google Scholar] [CrossRef]
- Maugeri, A.; Barchitta, M.; Battiato, S.; Agodi, A. Modeling the Novel Coronavirus (SARS-CoV-2) Outbreak in Sicily, Italy. Int. J. Environ. Res. Public Health 2020, 17, 4964. [Google Scholar] [CrossRef] [PubMed]
- Haushofer, J.; Metcalf, C.J.E. Which interventions work best in a pandemic? Science 2020, 368, 1063–1065. [Google Scholar] [CrossRef] [PubMed]
- Chinazzi, M.; Davis, J.T.; Ajelli, M.; Gioannini, C.; Litvinova, M.; Merler, S.; Pastore, Y.P.A.; Mu, K.; Rossi, L.; Sun, K.; et al. The effect of travel restrictions on the spread of the 2019 novel coronavirus (COVID-19) outbreak. Science 2020, 368, 395–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cabrera, M.; Córdova-Lepe, F.; Gutiérrez-Jara, J.P.; Vogt-Geisse, K. An SIR-type epidemiological model that integrates social distancing as a dynamic law based on point prevalence and socio-behavioral factors. Sci. Rep. 2021, 11, 10170. [Google Scholar] [CrossRef]
- Law, K.B.; Peariasamy, K.M.; Gill, B.S.; Singh, S.; Sundram, B.M.; Rajendran, K.; Dass, S.C.; Lee, Y.L.; Goh, P.P.; Ibrahim, H.; et al. Tracking the early depleting transmission dynamics of COVID-19 with a time-varying SIR model. Sci. Rep. 2020, 10, 21721. [Google Scholar] [CrossRef]
- Sun, J.; Chen, X.; Zhang, Z.; Lai, S.; Zhao, B.; Liu, H.; Wang, S.; Huan, W.; Zhao, R.; Ng, M.T.A.; et al. Forecasting the long-term trend of COVID-19 epidemic using a dynamic model. Sci. Rep. 2020, 10, 21122. [Google Scholar] [CrossRef] [PubMed]
- JHU CSSE COVID-19 Dataset. Available online: https://github.com/CSSEGISandData/COVID-19/tree/master/csse_covid_19_data/ (accessed on 14 February 2021).
- Bereau, U.C. Change in Resident Population of the 50 States, the District of Columbia, and Puerto Rico: 1910 to 2020. Available online: https://www2.census.gov/programs-surveys/decennial/2020/data/apportionment/population-change-data-table.pdf (accessed on 14 February 2021).
- Bureau, U.C. State Area Measurements and Internal Point Coordinates. Available online: https://www.census.gov/geographies/reference-files/2010/geo/state-area.html (accessed on 14 February 2021).
- He, J.; Tao, H.; Yan, Y.; Huang, S.Y.; Xiao, Y. Molecular Mechanism of Evolution and Human Infection with SARS-CoV-2. Viruses 2020, 12, 428. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Jain, V.; Schwarz, L.; Lorgelly, P. A Rapid Review of COVID-19 Vaccine Prioritization in the U.S.: Alignment between Federal Guidance and State Practice. Int. J. Environ. Res. Public Health 2021, 18, 3483. [Google Scholar] [CrossRef] [PubMed]
- Mathieu, E.; Ritchie, H.; Ortiz-Ospina, E.; Roser, M.; Hasell, J.; Appel, C.; Giattino, C.; Rodés-Guirao, L. A global database of COVID-19 vaccinations. Nat. Hum. Behav. 2021. [Google Scholar] [CrossRef]

| Population Density | Population | Area | ||||||
|---|---|---|---|---|---|---|---|---|
| Rank | State | Density (/km2) | Rank | State | Population | Rank | State | Area (km2) |
| 1 | New Jersey | 393.18 | 1 | California | 39,368,078 | 1 | Alaska | 1,723,337 |
| 2 | Rhode Island | 264.22 | 2 | Texas | 29,360,759 | 2 | Texas | 695,662 |
| 3 | Massachusetts | 252.18 | 3 | Florida | 21,733,312 | 3 | California | 423,967 |
| 4 | Connecticut | 247.75 | 4 | New York | 19,336,776 | 4 | Montana | 380,831 |
| 5 | Maryland | 188.47 | 5 | Pennsylvania | 12,783,254 | 5 | New Mexico | 314,917 |
| 6 | Delaware | 153.09 | 6 | Illinois | 12,587,530 | 6 | Arizona | 295,234 |
| 7 | New York | 136.85 | 7 | Ohio | 11,693,217 | 7 | Nevada | 286,380 |
| 8 | Florida | 127.61 | 8 | Georgia | 10,710,017 | 8 | Colorado | 269,601 |
| 9 | Pennsylvania | 107.17 | 9 | North Carolina | 10,600,823 | 9 | Oregon | 254,799 |
| 10 | Ohio | 100.72 | 10 | Michigan | 9,966,555 | 10 | Wyoming | 253,335 |
| 11 | California | 92.86 | 11 | New Jersey | 8,882,371 | 11 | Michigan | 250,487 |
| 12 | Illinois | 83.92 | 12 | Virginia | 8,590,563 | 12 | Minnesota | 225,163 |
| 13 | Virginia | 77.54 | 13 | Washington | 7,693,612 | 13 | Utah | 219,882 |
| 14 | North Carolina | 76.05 | 14 | Arizona | 7,421,401 | 14 | Idaho | 216,443 |
| 15 | Indiana | 71.61 | 15 | Massachusetts | 6,893,574 | 15 | Kansas | 213,100 |
| 16 | Georgia | 69.59 | 16 | Tennessee | 6,886,834 | 16 | Nebraska | 200,330 |
| 17 | Tennessee | 63.09 | 17 | Indiana | 6,754,953 | 17 | South Dakota | 199,729 |
| 18 | South Carolina | 62.92 | 18 | Missouri | 6,151,548 | 18 | Washington | 184,661 |
| 19 | New Hampshire | 56.43 | 19 | Maryland | 6,055,802 | 19 | North Dakota | 183,108 |
| 20 | Hawaii | 49.69 | 20 | Wisconsin | 5,832,655 | 20 | Oklahoma | 181,037 |
| 21 | Kentucky | 42.78 | 21 | Colorado | 5,807,719 | 21 | Missouri | 180,540 |
| 22 | Texas | 42.21 | 22 | Minnesota | 5,657,342 | 22 | Florida | 170,312 |
| 23 | Washington | 41.66 | 23 | South Carolina | 5,218,040 | 23 | Wisconsin | 169,635 |
| 24 | Michigan | 39.79 | 24 | Alabama | 4,921,532 | 24 | Georgia | 153,910 |
| 25 | Alabama | 36.25 | 25 | Louisiana | 4,645,318 | 25 | Illinois | 149,995 |
| 26 | Wisconsin | 34.38 | 26 | Kentucky | 4,477,251 | 26 | Iowa | 145,746 |
| 27 | Louisiana | 34.24 | 27 | Oregon | 4,241,507 | 27 | New York | 141,297 |
| 28 | Missouri | 34.07 | 28 | Oklahoma | 3,980,783 | 28 | North Carolina | 139,391 |
| 29 | West Virginia | 28.44 | 29 | Connecticut | 3,557,006 | 29 | Arkansas | 137,732 |
| 30 | Arizona | 25.14 | 30 | Utah | 3,249,879 | 30 | Alabama | 135,767 |
| 31 | Minnesota | 25.13 | 31 | Iowa | 3,163,561 | 31 | Louisiana | 135,659 |
| 32 | Vermont | 25.03 | 32 | Nevada | 3,138,259 | 32 | Mississippi | 125,438 |
| 33 | Mississippi | 23.65 | 33 | Arkansas | 3,030,522 | 33 | Pennsylvania | 119,280 |
| 34 | Arkansas | 22.00 | 34 | Mississippi | 2,966,786 | 34 | Ohio | 116,098 |
| 35 | Oklahoma | 21.99 | 35 | Kansas | 2,913,805 | 35 | Virginia | 110,787 |
| 36 | Iowa | 21.71 | 36 | New Mexico | 2,106,319 | 36 | Tennessee | 109,153 |
| 37 | Colorado | 21.54 | 37 | Nebraska | 1,937,552 | 37 | Kentucky | 104,656 |
| 38 | Oregon | 16.65 | 38 | Idaho | 1,826,913 | 38 | Indiana | 94,326 |
| 39 | Utah | 14.78 | 39 | West Virginia | 1,784,787 | 39 | Maine | 91,633 |
| 40 | Maine | 14.73 | 40 | Hawaii | 1,407,006 | 40 | South Carolina | 82,933 |
| 41 | Kansas | 13.67 | 41 | New Hampshire | 1,366,275 | 41 | West Virginia | 62,756 |
| 42 | Nevada | 10.96 | 42 | Maine | 1,350,141 | 42 | Maryland | 32,131 |
| 43 | Nebraska | 9.67 | 43 | Montana | 1,080,577 | 43 | Hawaii | 28,313 |
| 44 | Idaho | 8.44 | 44 | Rhode Island | 1,057,125 | 44 | Massachusetts | 27,336 |
| 45 | New Mexico | 6.69 | 45 | Delaware | 986,809 | 45 | Vermont | 24,906 |
| 46 | South Dakota | 4.47 | 46 | South Dakota | 892,717 | 46 | New Hampshire | 24,214 |
| 47 | North Dakota | 4.18 | 47 | North Dakota | 765,309 | 47 | New Jersey | 22,591 |
| 48 | Montana | 2.84 | 48 | Alaska | 731,158 | 48 | Connecticut | 14,357 |
| 49 | Wyoming | 2.30 | 49 | Vermont | 623,347 | 49 | Delaware | 6,446 |
| 50 | Alaska | 0.42 | 50 | Wyoming | 582,328 | 50 | Rhode Island | 4,001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Tao, H.; Wu, Q.; Huang, S.-Y.; Xiao, Y. Modeling of the Long-Term Epidemic Dynamics of COVID-19 in the United States. Int. J. Environ. Res. Public Health 2021, 18, 7594. https://doi.org/10.3390/ijerph18147594
Huang D, Tao H, Wu Q, Huang S-Y, Xiao Y. Modeling of the Long-Term Epidemic Dynamics of COVID-19 in the United States. International Journal of Environmental Research and Public Health. 2021; 18(14):7594. https://doi.org/10.3390/ijerph18147594
Chicago/Turabian StyleHuang, Derek, Huanyu Tao, Qilong Wu, Sheng-You Huang, and Yi Xiao. 2021. "Modeling of the Long-Term Epidemic Dynamics of COVID-19 in the United States" International Journal of Environmental Research and Public Health 18, no. 14: 7594. https://doi.org/10.3390/ijerph18147594
APA StyleHuang, D., Tao, H., Wu, Q., Huang, S.-Y., & Xiao, Y. (2021). Modeling of the Long-Term Epidemic Dynamics of COVID-19 in the United States. International Journal of Environmental Research and Public Health, 18(14), 7594. https://doi.org/10.3390/ijerph18147594






