Perspectives on Complexity, Chaos and Thermodynamics in Environmental Pathology
Abstract
1. Introduction
2. Complexity, Chaos and Thermodynamics in Living Systems
2.1. Complexity
2.2. Chaos
2.3. Thermodynamics
3. Pathology and Environmental Pathology
3.1. General Pathology
3.2. Environmental Pathology
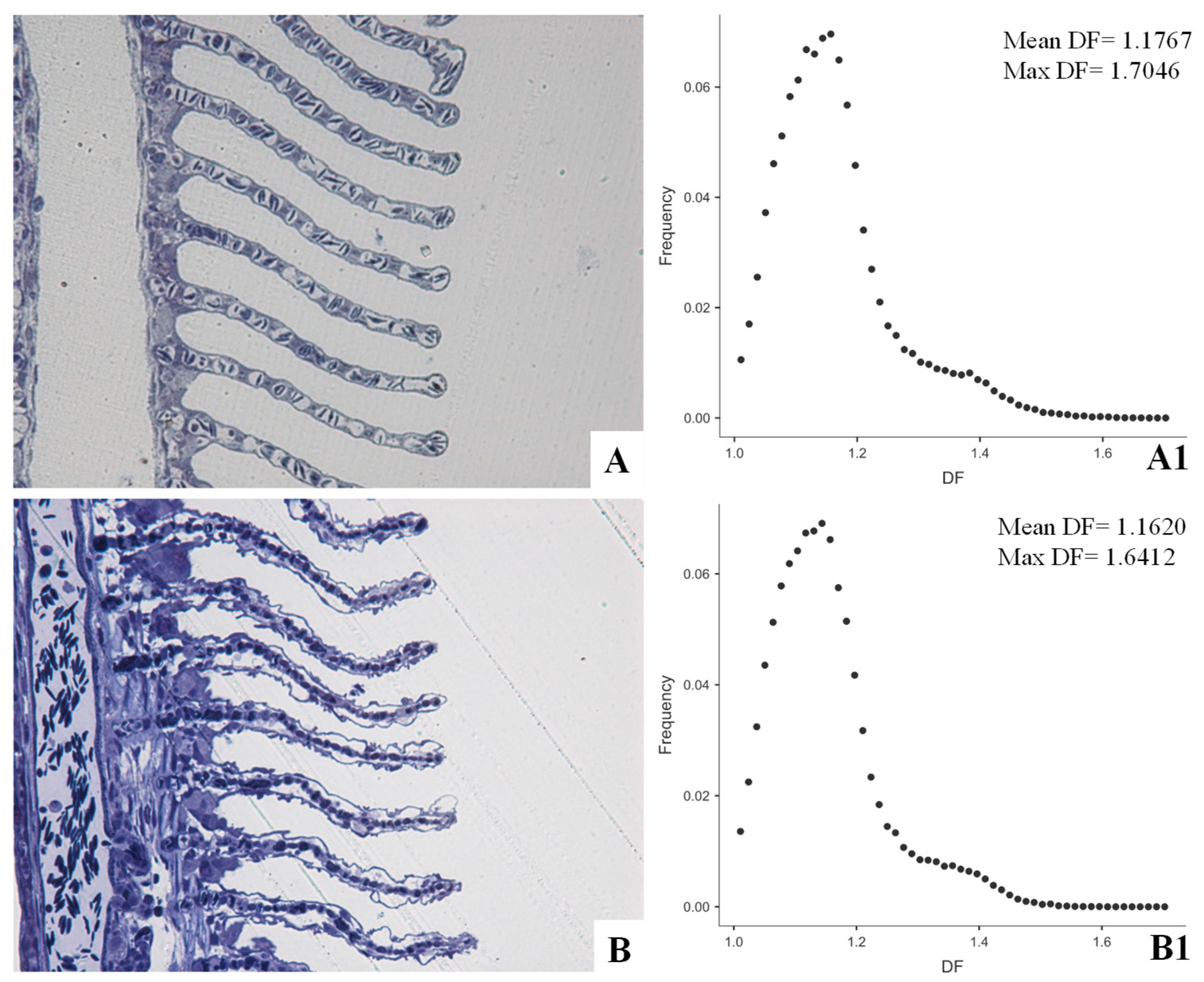
Image Analysis in Environmental Pathology
4. Perspectives
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Martin-Araguz, A.; Ruiz-Alâez, A.; De La Garcia Rocha, M.L.; Fernândez-Armayor, V.; Delgado-Reyes, S.; Moreno-Martincz, J.M. Caos determinista, cinemâtica de fluidos y geometria fractal en el sistema carotideo. Rev. Neurol. 1997, 25, 2021–2031. [Google Scholar]
- Manera, M.; Sayyaf Dezfuli, B.; DePasquale, J.A.; Giari, L. Multivariate approach to gill pathology in European sea bass after experimental exposure to cadmium and terbuthylazine. Ecotoxicol. Environ. Saf. 2016, 129, 282–290. [Google Scholar] [CrossRef]
- Al-Janabi, S.; Huisman, A.; Van Diest, P.J. Digital pathology: Current status and future perspectives. Histopathology 2012, 61, 1–9. [Google Scholar] [CrossRef]
- Goodwin, J.S. A piece of my mind. Chaos, and the limits of modern medicine. JAMA 1997, 278, 1399–1400. [Google Scholar] [CrossRef] [PubMed]
- Oestreicher, C. A history of chaos theory. Dialogues Clin. Neurosci. 2007, 9, 279–289. [Google Scholar]
- Hueso, M.; Cruzado, J.M.; Torras, J.; Navarro, E. ALUminating the path of atherosclerosis progression: Chaos theory suggests a role for alu repeats in the development of atherosclerotic vascular disease. Int. J. Mol. Sci. 2018, 19, 1734. [Google Scholar] [CrossRef] [PubMed]
- Sigston, E.A.W.; Williams, B.R.G. An Emergence Framework of Carcinogenesis. Front. Oncol. 2017, 7, 198. [Google Scholar] [CrossRef]
- Varela, M.; Ruiz-Esteban, R.; Mestre De Juan, M.J. Chaos, Fractals, and Our Concept of Disease. Perspect. Biol. Med. 2010, 53, 584–595. [Google Scholar] [CrossRef]
- Eid, R.A.; Landini, G. Quantification of the Global and Local Complexity of the Epithelial-Connective Tissue Interface of Normal, Dysplastic, and Neoplastic Oral Mucosae Using Digital Imaging. Pathol. Res. Pract. 2003, 199, 475–482. [Google Scholar] [CrossRef] [PubMed]
- Edmonds, B. What is Complexity?—The philosophy of complexity per se with application to some examples in evolution. In The Evolution of Complexity: The Violet Book of “Einstein Meets Magritte”; Heylighen, F., Bollen, J., Riegler, A., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 1–13. [Google Scholar]
- Bar-Yam, Y. Dynamics of Complex Systems; Addison-Wesley: Reading, MA, USA, 1997; ISBN 0201557487. [Google Scholar]
- Adami, C. What is complexity? BioEssays 2002, 24, 1085–1094. [Google Scholar] [CrossRef]
- Kaneko, K. Life: An Introduction to Complex Systems Biology; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2006; ISBN 9783540326663. [Google Scholar]
- Mitchell, M. Complexity A Guided Tour; Oxford University Press: Oxford, MS, USA, 2009; ISBN 9780195124415. [Google Scholar]
- Shannon, C.E. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cross, S.S.; Cotton, D.W.K. Chaos and antichaos in pathology. Hum. Pathol. 1994, 25, 630–637. [Google Scholar] [CrossRef]
- Johnson, B.R.; Lam, S.K. Self-organization, natural selection, and evolution: Cellular hardware and genetic software. Bioscience 2010, 60, 879–885. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; The MacMillan Company: New York, NY, USA, 1945; ISBN 9780521437769. [Google Scholar]
- Chan, S. Complex Adaptive Systems. ESD.83 Res. Semin. Eng. Syst. 2001, 31, 1–9. [Google Scholar]
- Manera, M.; Dezfuli, B.S.; Castaldelli, G.; DePasquale, J.A.; Fano, E.A.; Martino, C.; Giari, L. Perfluorooctanoic Acid Exposure Assessment on Common Carp Liver through Image and Ultrastructural Investigation. Int. J. Environ. Res. Public Health 2019, 16, 4923. [Google Scholar] [CrossRef] [PubMed]
- Manera, M.; Giari, L.; De Pasquale, J.A.; Sayyaf Dezfuli, B. Local connected fractal dimension analysis in gill of fish experimentally exposed to toxicants. Aquat. Toxicol. 2016, 175, 12–19. [Google Scholar] [CrossRef] [PubMed]
- Thomas, S.; Bonchev, D. A survey of current software for network analysis in molecular biology. Hum. Genom. 2010, 4, 353–360. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Oltvai, Z.N. Network biology: Understanding the cell’s functional organization. Nat. Rev. Genet. 2004, 5, 101–113. [Google Scholar] [CrossRef]
- Li, S.; Armstrong, C.M.; Bertin, N.; Ge, H.; Milstein, S.; Boxem, M.; Vidalain, P.O.; Han, J.D.J.; Chesneau, A.; Hao, T.; et al. A Map of the Interactome Network of the Metazoan C. elegans. Science 2004, 303, 540–543. [Google Scholar] [CrossRef]
- Carey, S.S. A beginner’s Guide to Scientific Method, 4th ed.; Wadsworth, Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Goldberger, A.L. Non-linear dynamics for clinicians: Chaos theory, fractals, and complexity at the bedside. Lancet 1996, 347, 1312–1314. [Google Scholar] [CrossRef]
- Marquis de Laplace, P.S. Essai Philosophique sur les Probabilités, 5th ed.; Bachelier: Paris, France, 1825. [Google Scholar]
- Busch, P.; Heinonen, T.; Lahti, P. Heisenberg’s uncertainty principle. Phys. Rep. 2007, 452, 155–176. [Google Scholar] [CrossRef]
- Baclawski, K. The Observer Effect. In Proceedings of the 2018 IEEE International Conference on Cognitive and Computational Aspects of Situation Management, CogSIMA 2018, Boston, MA, USA, 11–14 June 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 83–89. [Google Scholar]
- Sassoli de Bianchi, M. The Observer Effect. Found. Sci. 2013, 18, 213–243. [Google Scholar] [CrossRef]
- Iglesias, A.; Gutiérrez, J.M.; Güémez, J.; Matías, M.A. Chaos suppression through changes in the system variables and numerical rounding errors. Chaos Solitons Fractals 1996, 7, 1305–1316. [Google Scholar] [CrossRef]
- Poincaré, H. Sur les solutions périodiques et le principe de moindre action. CR Acad. Sci. Paris 1896, 123, 915–918. [Google Scholar]
- Schuster, H.G.; Just, W. Deterministic Chaos, 4th ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2005. [Google Scholar]
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Prigogine, I.; Stengers, I. The End of Certainty; The Free Press: New York, NY, USA, 1997; ISBN 0684837056. [Google Scholar]
- Yao, Q.; Tong, H. On prediction and chaos in stochastic systems. Philos. Trans. R. Soc. London. Ser. A Phys. Eng. Sci. 1994, 348, 357–369. [Google Scholar] [CrossRef]
- Timmer, J.; Häussler, S.; Lauk, M.; Lücking, C.H. Pathological tremors: Deterministic chaos or nonlinear stochastic oscillators? Chaos 2000, 10, 278–288. [Google Scholar] [CrossRef]
- Garfinkel, A.; Spano, M.L.; Ditto, W.L.; Weiss, J.N. Controlling cardiac chaos. Science 1992, 257, 1230–1235. [Google Scholar] [CrossRef] [PubMed]
- Chialvo, D.R.; Gilmour, R.F.; Jalife, J. Low dimensional chaos in cardiac tissue. Nature 1990, 343, 653–657. [Google Scholar] [CrossRef]
- Denton, T.A.; Diamond, G.A.; Helfant, R.H.; Khan, S.; Karagueuzian, H. Fascinating rhythm: A primer on chaos theory and its application to cardiology. Am. Heart J. 1990, 120, 1419–1440. [Google Scholar] [CrossRef]
- King, C.C. Fractal and chaotic dynamics in nervous systems. Prog. Neurobiol. 1991, 36, 279–308. [Google Scholar] [CrossRef]
- Babloyantz, A.; Destexhe, A. Low-dimensional chaos in an instance of epilepsy. Proc. Natl. Acad. Sci. USA 1986, 83, 3513–3517. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, M.I.; Abarbanel, H.D.I. The role of chaos in neural systems. Neuroscience 1998, 87, 5–14. [Google Scholar] [CrossRef]
- Sarbadhikari, S.N.; Chakrabarty, K. Chaos in the brain: A short review alluding to epilepsy, depression, exercise and lateralization. Med. Eng. Phys. 2001, 23, 447–457. [Google Scholar] [CrossRef]
- Mangin, L.; Fiamma, M.N.; Straus, C.; Derenne, J.P.; Zelter, M.; Clerici, C.; Similowski, T. Source of human ventilatory chaos: Lessons from switching controlled mechanical ventilation to inspiratory pressure support in critically ill patients. Respir. Physiol. Neurobiol. 2008, 161, 189–196. [Google Scholar] [CrossRef] [PubMed]
- Vena, A.; Conte, E.; Perchiazzi, G.; Federici, A.; Giuliani, R.; Zbilut, J.P. Detection of physiological singularities in respiratory dynamics analyzed by recurrence quantification analysis of tracheal sounds. Chaos Solitons Fractals 2004, 22, 869–881. [Google Scholar] [CrossRef]
- Mackey, M.C.; Glass, L. Oscillation and chaos in physiological control systems. Science 1977, 197, 287–289. [Google Scholar] [CrossRef]
- Otero-Siliceo, E.; Arriada-Mendicoa, N. Is it healthy to be chaotic? Med. Hypotheses 2003, 60, 233–236. [Google Scholar] [CrossRef]
- Poon, C.S.; Merrill, C.K. Decrease of cardiac chaos in congestive heart failure. Nature 1997, 389, 492–495. [Google Scholar] [CrossRef] [PubMed]
- Liu, R.; Li, M.; Liu, Z.P.; Wu, J.; Chen, L.; Aihara, K. Identifying critical transitions and their leading biomolecular networks in complex diseases. Sci. Rep. 2012, 2, 1–9. [Google Scholar] [CrossRef]
- Haynie, D.T. Biological Thermodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008; ISBN 9789896540821. [Google Scholar]
- Schrödinger, E. What Is Life? The Physical Aspect of the Living Cell; Cambridge University Press: Cambridge, UK, 1944. [Google Scholar]
- Gheorghiu, S.; Kjelstrup, S.; Pfeifer, P.; Coppens, M.O. Is the Lung an Optimal Gas Exchanger? In Fractals in Biology and Medicine; Losa, G.A., Merlini, D., Nonnenmacher, T.F., Weibel, E.R., Eds.; Birkhäuser Verlag: Basel, Switzerland, 2005; pp. 31–42. ISBN 978-3-7643-7172-2. [Google Scholar]
- Oliveira, C.L.N.; Araújo, A.D.; Bates, J.H.T.; Andrade, J.S.; Suki, B. Entropy Production and the Pressure–Volume Curve of the Lung. Front. Physiol. 2016, 7, 73. [Google Scholar] [CrossRef]
- Kurakin, A. The self-organizing fractal theory as a universal discovery method: The phenomenon of life. Theor. Biol. Med. Model. 2011, 8, 1–66. [Google Scholar] [CrossRef]
- Majno, G.; Joris, I. Cells, Tissues, and Disease: Principles of General Pathology; Oxford University Press: New York, NY, USA, 2004; ISBN 0199748926. [Google Scholar]
- Zampieri, F.; Zanatta, A.; Thiene, G. An etymological “autopsy” of Morgagni’s title: De sedibus et causis morborum per anatomen indagatis (1761). Hum. Pathol. 2014, 45, 12–16. [Google Scholar] [CrossRef] [PubMed]
- Magner, L.N. A History of Medicine, 2nd ed.; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 3527404139. [Google Scholar]
- Morgagni, J.B. De Sedibus, et Causis Morborum per Anatomen Indagatis; Remondini: Venezia, Italy, 1761. [Google Scholar]
- Virchow, R. Die Cellularpathologie; Verlag von August Hirschwald: Berlin, Germany, 1859. [Google Scholar]
- Epstein, S.S. Environmental pathology. A review. Am. J. Pathol. 1972, 66, 352–374. [Google Scholar] [PubMed]
- Popper, H.; Selikoff, I.J. What is environmental pathology? Am. J. Med. 1981, 70, 218–220. [Google Scholar] [CrossRef]
- Centeno, J.A.; Mullick, F.G.; Ishak, K.G.; Franks, T.J.; Burke, A.P.; Koss, M.N.; Perl, D.P.; Tchounwou, P.B.; Pestaner, J.P. Environmental Pathology. In Essentials of Medical Geology; Revised ed.; Selinus, O., Ed.; Springer: Dordrecht, The Netherlands, 2013; pp. 569–596. ISBN 9789400743755. [Google Scholar]
- Adams, S.M.; Shepard, K.L.; Greeley, M.S.; Jimenez, B.D.; Ryon, M.G.; Shugart, L.R.; McCarthy, J.F.; Hinton, D.E. The use of bioindicators for assessing the effects of pollutant stress on fish. Mar. Environ. Res. 1989, 28, 459–464. [Google Scholar] [CrossRef]
- Manera, M. I Biomarcatori nel Monitoraggio Ambientale—Pesci Ossei ed Ecosistemi Acquatici; Aracne: Rome, Italy, 2013; ISBN 978-88-548-6221-0. [Google Scholar]
- Manera, M.; Giari, L.; Vincenzi, F.; Guerranti, C.; Depasquale, J.A.; Castaldelli, G. Texture analysis in liver of common carp (Cyprinus carpio) sub-chronically exposed to perfluorooctanoic acid. Ecol. Indic. 2017, 81, 54–64. [Google Scholar] [CrossRef]
- Rotondo, J.C.; Giari, L.; Guerranti, C.; Tognon, M.; Castaldelli, G.; Fano, E.A.; Martini, F. Environmental doses of perfluorooctanoic acid change the expression of genes in target tissues of common carp. Environ. Toxicol. Chem. 2018, 37, 942–948. [Google Scholar] [CrossRef]
- Manera, M.; Castaldelli, G.; Fano, E.A.; Giari, L. Perfluorooctanoic acid-induced cellular and subcellular alterations in fish hepatocytes. Environ. Toxicol. Pharmacol. 2021, 81, 103548. [Google Scholar] [CrossRef]
- Shui, L.; Ren, H.; Yang, X.; Li, J.; Chen, Z.; Yi, C.; Zhu, H.; Shui, P. The Era of Radiogenomics in Precision Medicine: An Emerging Approach to Support Diagnosis, Treatment Decisions, and Prognostication in Oncology. Front. Oncol. 2021, 10, 3195. [Google Scholar] [CrossRef] [PubMed]
- Velmovitsky, P.E.; Bevilacqua, T.; Alencar, P.; Cowan, D.; Morita, P.P. Convergence of Precision Medicine and Public Health Into Precision Public Health: Toward a Big Data Perspective. Front. Public Health 2021, 9, 561873. [Google Scholar] [CrossRef]
- Manera, M.; Sayyaf Dezfuli, B.; Depasquale, J.A.; Giari, L. Pigmented macrophages and related aggregates in the spleen of european sea bass dosed with heavy metals: Ultrastructure and explorative morphometric analysis. Microsc. Res. Tech. 2018, 81, 351–364. [Google Scholar] [CrossRef] [PubMed]
- Manera, M.; Sayyaf Dezfuli, B.; Castaldelli, G.; Martino, C.; Giari, L. Grayscale differential box counting as a measure of complexity of liver texture in common carp (Cyprinus carpio) sub-chronically exposed to perfluorooctanoic acid (PFOA). In Proceedings of the Abstracts of the 55th Congress of the European Societies of Toxicology (EUROTOX 2019) TOXICOLOGY SCIENCE PROVIDING SOLUTIONS, Helsinki, Finland, 8–11 September 2019; Toxicology Letters. 2019; Volume 314, p. S186. [Google Scholar] [CrossRef]
- Moore, M.N. Is toxicological pathology characterised by a loss of system complexity? Mar. Environ. Res. 2010, 69, S37–S41. [Google Scholar] [CrossRef]
- Landini, G. Fractals in microscopy. J. Microsc. 2011, 241, 1–8. [Google Scholar] [CrossRef]
- Landini, G.; Murray, P.I.; Misson, G.P. Local connected fractal dimensions and lacunarity analyses of 60 degrees fluorescein angiograms. Investig. Ophthalmol. Vis. Sci. 1995, 36, 2749–2755. [Google Scholar]
- Laurinavicius, A.; Laurinaviciene, A.; Dasevicius, D.; Elie, N.; Plancoulaine, B.; Bor, C.; Herlin, P. Digital image analysis in pathology: Benefits and obligation. Anal. Cell. Pathol. 2012, 35, 75–78. [Google Scholar] [CrossRef]
- Pantanowitz, L. Digital images and the future of digital pathology. J. Pathol. Inform. 2010, 1, 15. [Google Scholar] [CrossRef] [PubMed]
- Kayser, G.; Kayser, K. Quantitative pathology in virtual microscopy: History, applications, perspectives. Acta Histochem. 2013, 115, 527–532. [Google Scholar] [CrossRef]
- Karp, G. Cell and Molecular Biology; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Bernet, D.; Schmidt, H.; Meier, W.; Burkhardt-Holm, P.; Wahli, T. Histopathology in fish: Proposal for a protocol to assess aquatic pollution. J. Fish Dis. 1999, 22, 25–34. [Google Scholar] [CrossRef]
- Manera, M.; Giari, L.; DePasquale, J.A.; Dezfuli, B.S.S. European sea bass gill pathology after exposure to cadmium and terbuthylazine: Expert versus fractal analysis. J. Microsc. 2016, 261, 291–299. [Google Scholar] [CrossRef] [PubMed]
- Mallatt, J. Fish gill structural changes induced by toxicants and other irritants: A statistical review. Can. J. Fish. Aquat. Sci. 1985, 42, 630–648. [Google Scholar] [CrossRef]
- Gomes, I.D.; Nascimento, A.A.; Sales, A.; Araújo, F.G. Can fish gill anomalies be used to assess water quality in freshwater Neotropical systems? Environ. Monit. Assess. 2012, 184, 5523–5531. [Google Scholar] [CrossRef] [PubMed]
- Hawkins, A.D.; Thornton, C.; Kennedy, A.J.; Bu, K.; Cizdziel, J.; Jones, B.W.; Steevens, J.A.; Willett, K.L. Gill histopathologies following exposure to nanosilver or silver nitrate. J. Toxicol. Environ. Health Part A Curr. Issues 2015, 78, 301–315. [Google Scholar] [CrossRef] [PubMed]
- Alvarado, N.E.; Quesada, I.; Hylland, K.; Marigómez, I.; Soto, M. Quantitative changes in metallothionein expression in target cell-types in the gills of turbot (Scophthalmus maximus) exposed to Cd, Cu, Zn and after a depuration treatment. Aquat. Toxicol. 2006, 77, 64–77. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manera, M. Perspectives on Complexity, Chaos and Thermodynamics in Environmental Pathology. Int. J. Environ. Res. Public Health 2021, 18, 5766. https://doi.org/10.3390/ijerph18115766
Manera M. Perspectives on Complexity, Chaos and Thermodynamics in Environmental Pathology. International Journal of Environmental Research and Public Health. 2021; 18(11):5766. https://doi.org/10.3390/ijerph18115766
Chicago/Turabian StyleManera, Maurizio. 2021. "Perspectives on Complexity, Chaos and Thermodynamics in Environmental Pathology" International Journal of Environmental Research and Public Health 18, no. 11: 5766. https://doi.org/10.3390/ijerph18115766
APA StyleManera, M. (2021). Perspectives on Complexity, Chaos and Thermodynamics in Environmental Pathology. International Journal of Environmental Research and Public Health, 18(11), 5766. https://doi.org/10.3390/ijerph18115766





