Re-Thinking the Role of Government Information Intervention in the COVID-19 Pandemic: An Agent-Based Modeling Analysis
Abstract
1. Introduction
2. Methods
2.1. The Model of Information Disclosing
2.2. The Experiments of Information Disclosing
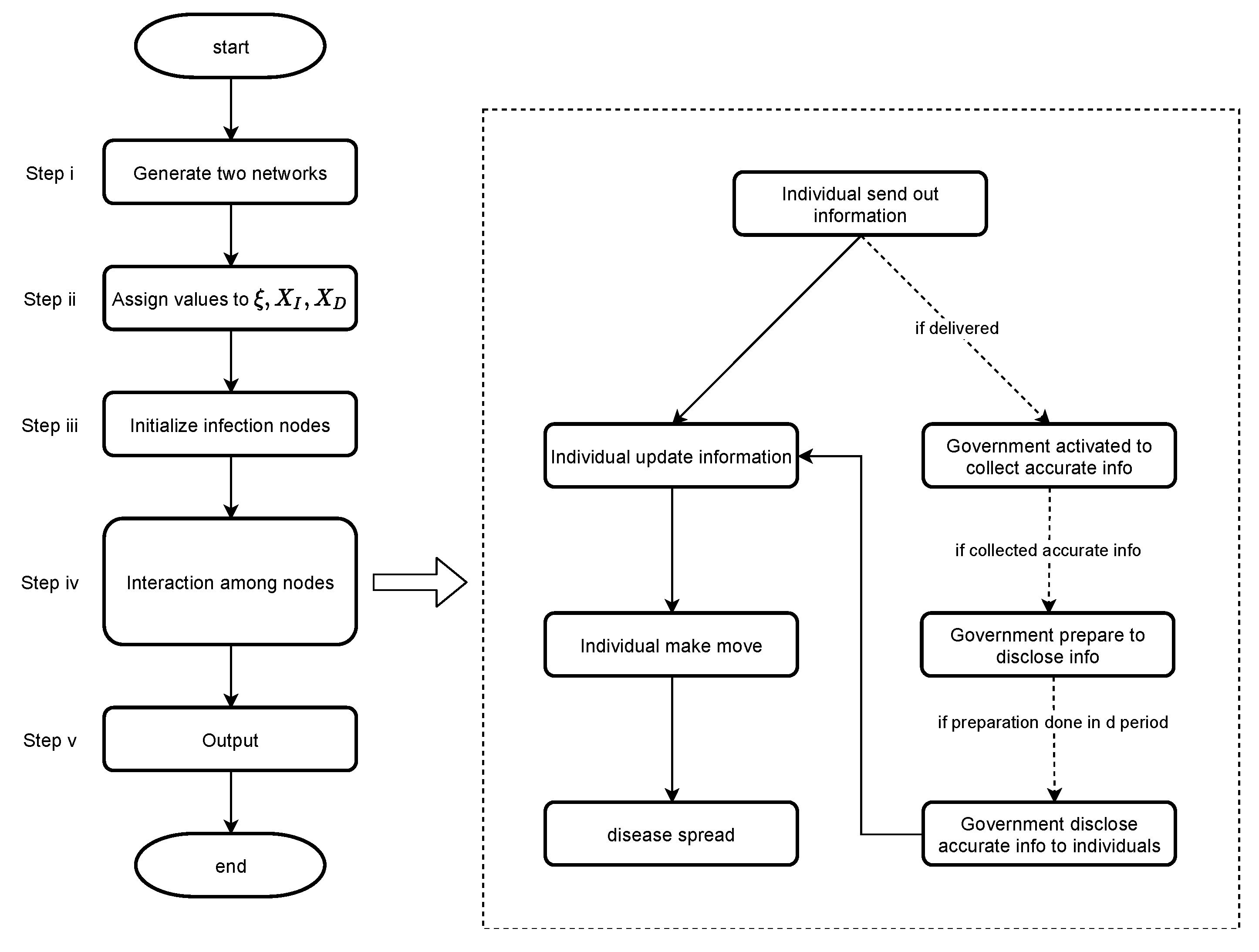
- Generate a random information network and a random physical network, the former illustrates the information relationship between people, and the latter records the coordinates of people and gathering spots on the map.
- Assign values to initial information and individual threshold. The initial information is the source of all information, which denotes the medical awareness of the virus; the individual threshold is a parameter to distinguish the population by groups set above; the smaller it is, the higher the level of public health awareness.
- Assign values to the disclosing threshold. The disclosing threshold, chosen by the government, measures its relative priority to speed and accuracy in information dissemination. One of the objectives of our experiment is to ascertain the optimal disclosing threshold. Government prioritizes speed more as its threshold is lower.
- Generate random individual nodes with initial information and random initial infected nodes.
- Enter period 1.
- (a)
- Each individual node with information sends out information to neighbors.
- (b)
- Each individual node will update its information (weighted) based on Equation (1).
- (c)
- The government initiates a censoring and screening and enters stage d after a lag period, only for the first time does it receive the above-threshold information. If the government never receives above-threshold information, skip c, d, and go to e.
- (d)
- Government discloses information to the public, which induces another round of information update for individual nodes based on Equation (2).
- (e)
- The population is grouped into infected and healthy people by health status, and into panic-prone and non panic-prone by how much information one has compared with the individual threshold.
- (f)
- Each individual node moves in a physical layer following the routine of the subgroup it is in with probability based on its final information.
- (g)
- Reset the infection status of healthy individual within the transmission radius of an infected one according to the infection probability.
- Return to step 5, initiate a new round for 50 times, that is, run the experiment for 50 periods. The data show a stability after 40 periods, so we stopped at 50.
- Output the final overall infection rate at the end of period 50.
- Repeat steps 4–7 for 50 times to reduce the randomness, record the mean, and standard deviation of the final infection rate.
- Reassign for the disclosing threshold discrete values that equally divide the interval into 11 parts, and repeat steps 3–8 for each value, that is, 11 times, to find the final infection rates for different disclosing threshold scenarios.
- Reassign for initial information a discrete array , and reassign for an individual threshold the same values reassigned for the disclosing threshold in the previous step. Then, repeat steps 2–9, that is, 44 times.
2.3. The Model and Experiments of Information Blocking
3. Results and Discussion
3.1. Modeling Framework
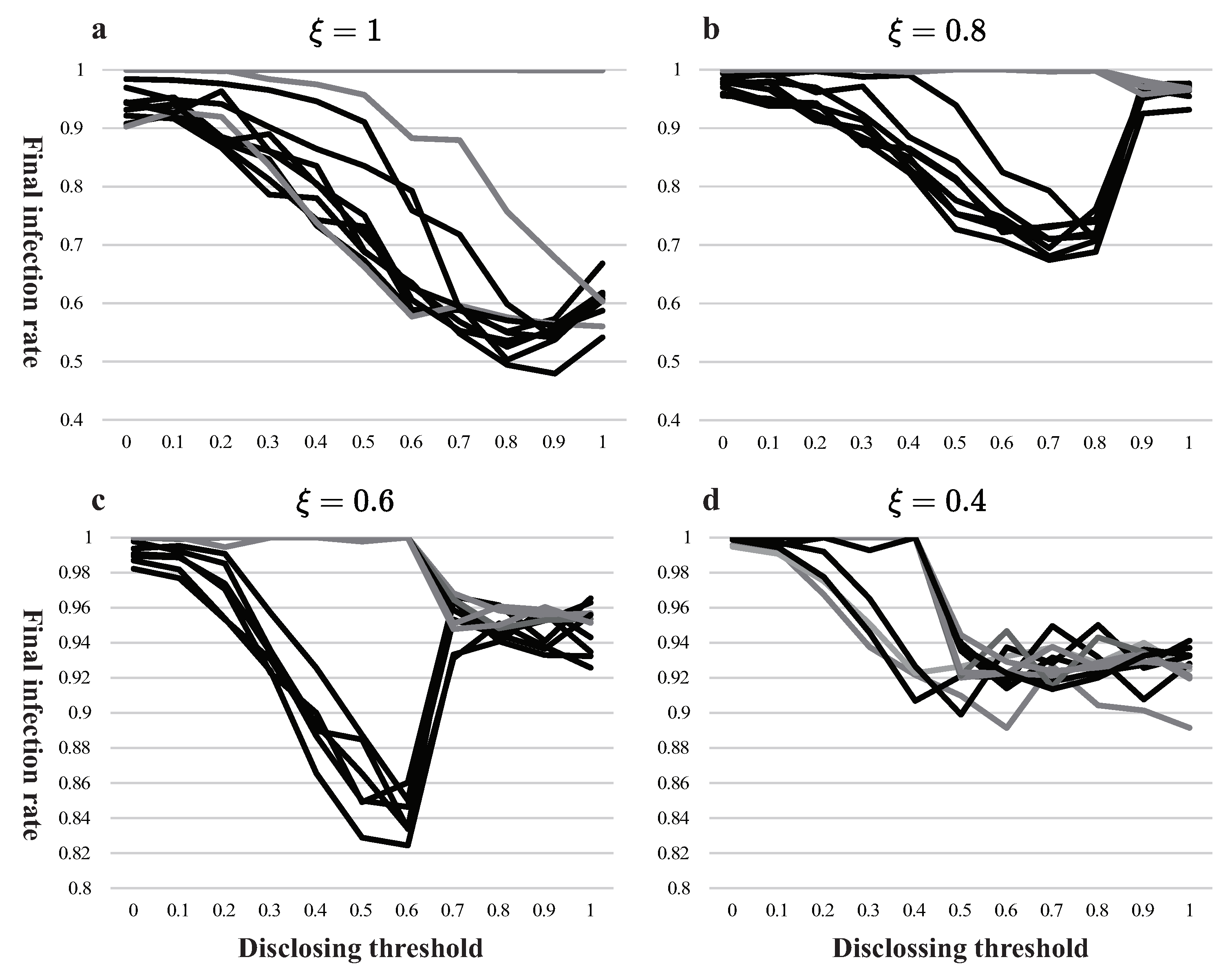
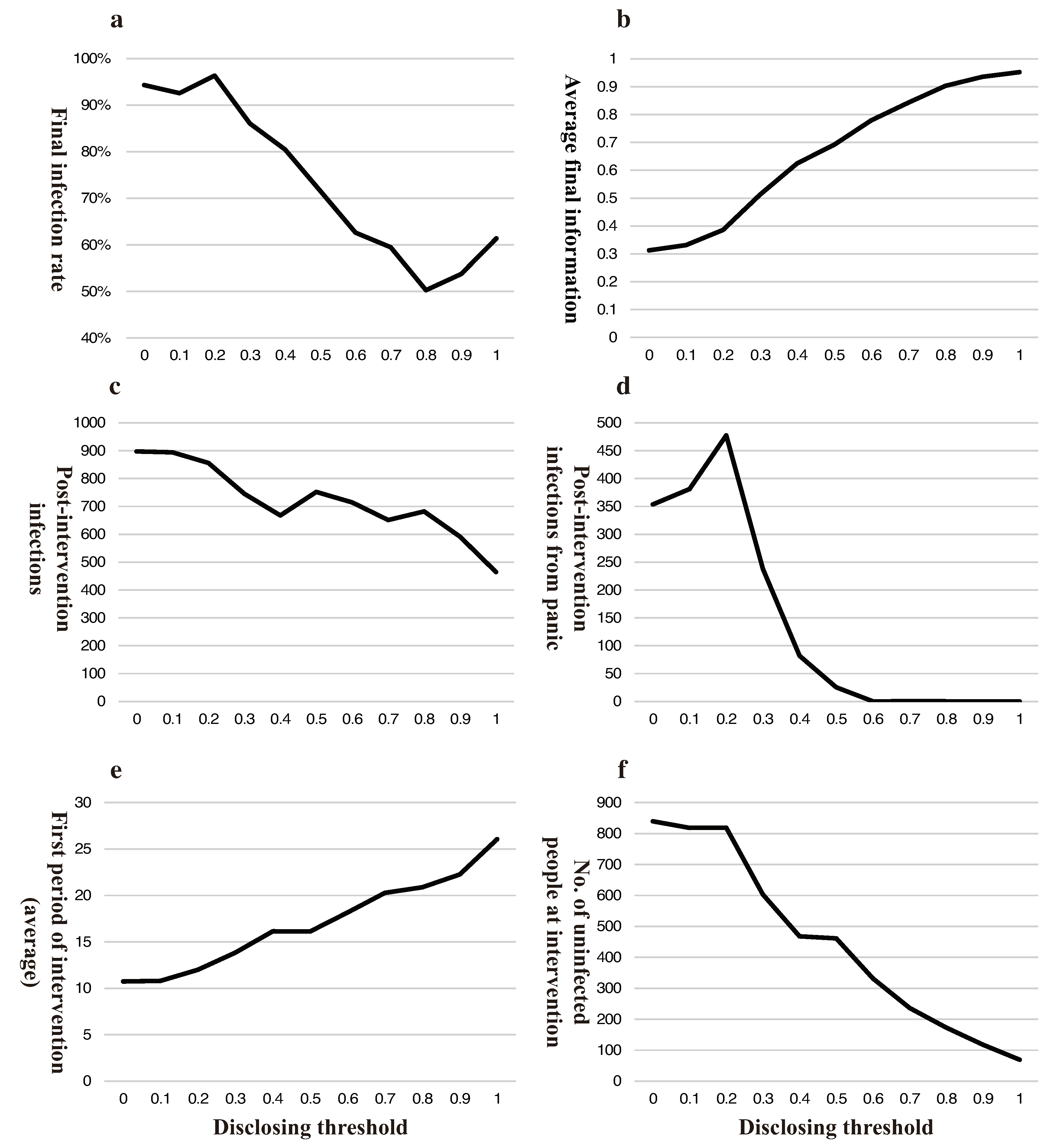
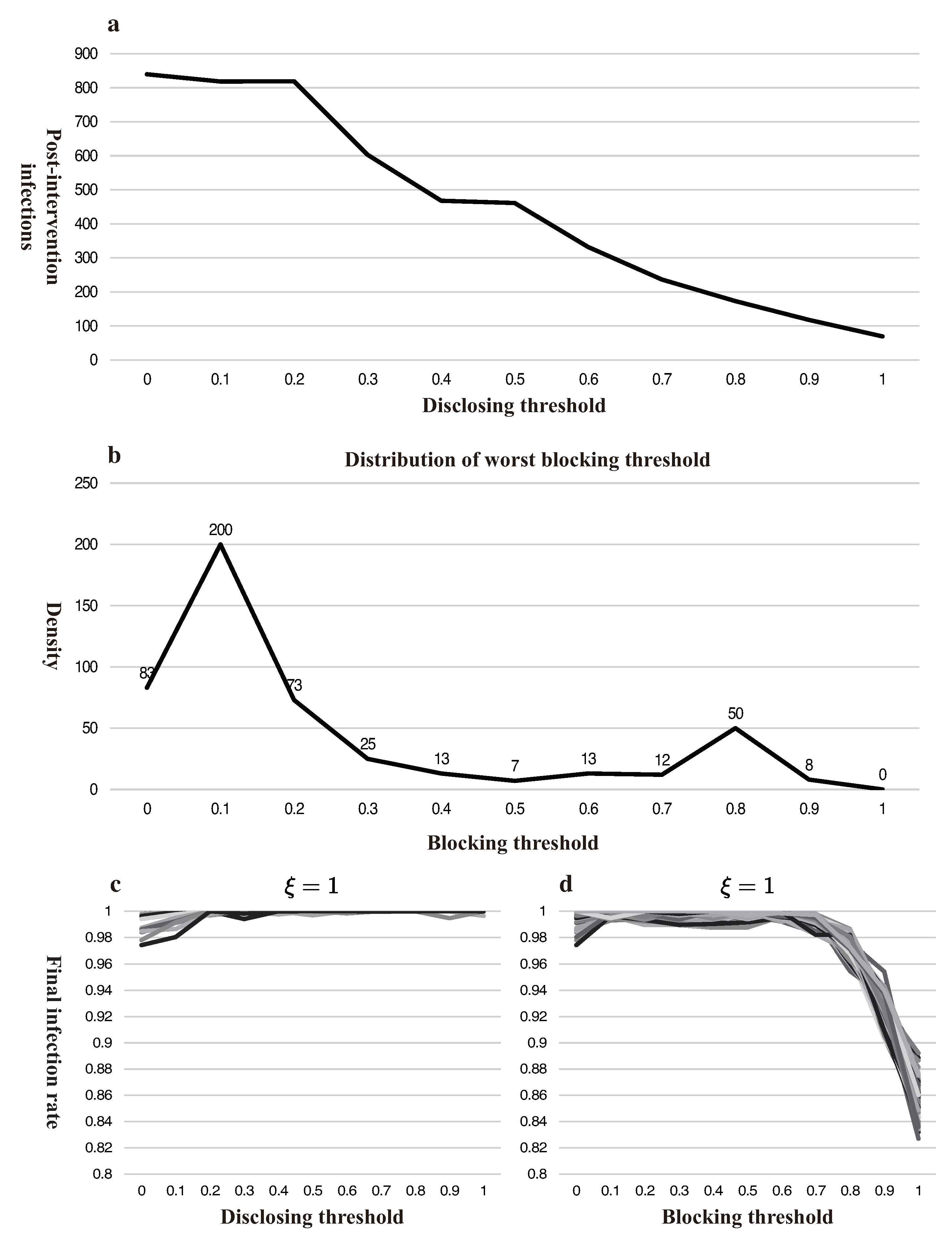
3.2. Intervention Dilemma in Disclosing Information
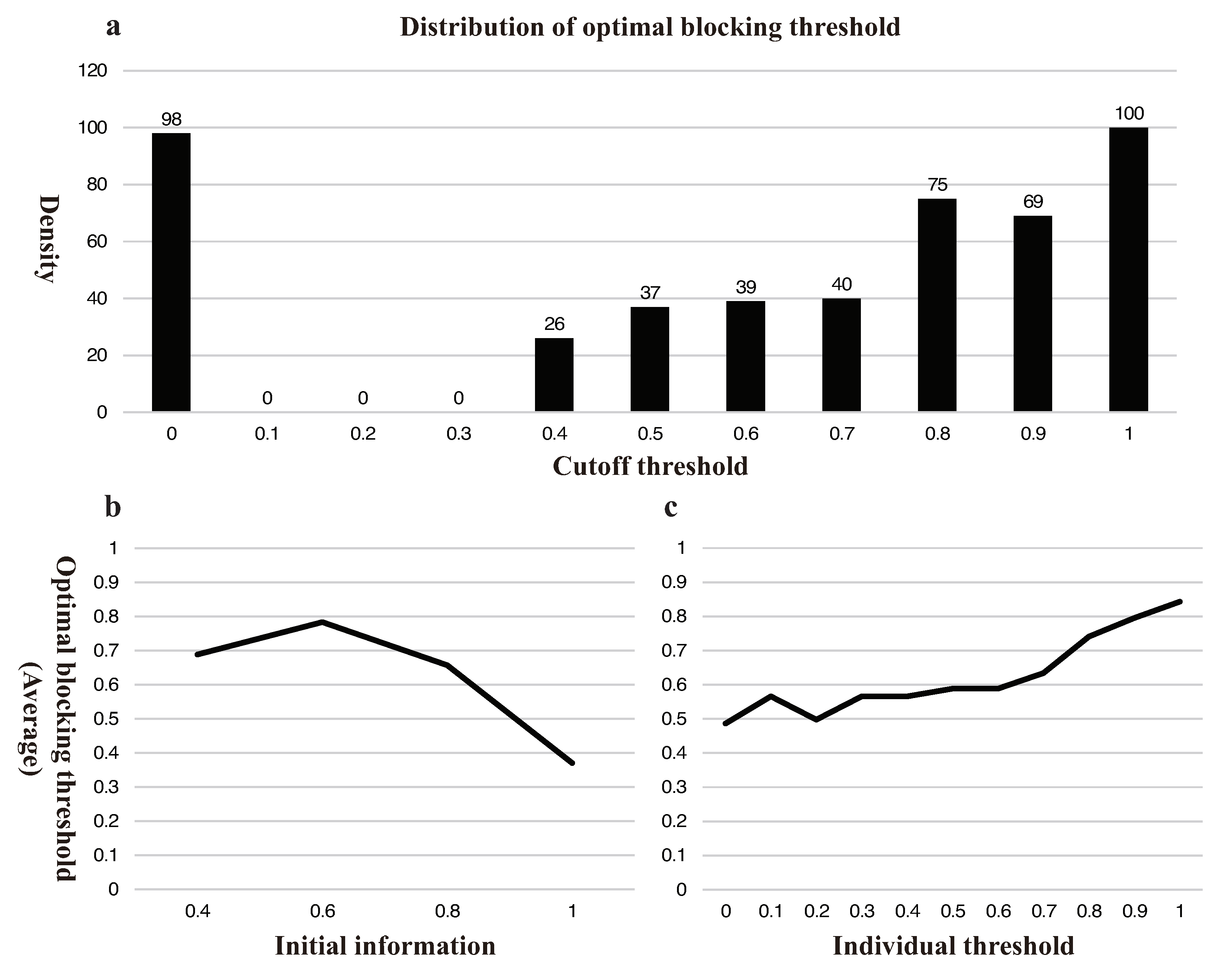
3.3. Intervention Dilemma in Blocking Information
3.4. Optimal Intervention under Different Government Types
4. Conclusions
- For information disclosing, governments face a trade-off between speed and accuracy. A better medical understanding of the virus and an inadequate public health awareness make accuracy outweigh speed; otherwise, a quick one is better.
- For information blocking, the optimal strategy is contingent on varying conditions: no blocking is usually optimal for a well-known virus and a higher public health awareness; otherwise, blocking is preferred.
- The optimal combination of disclosing and blocking is highly sensitive to the government preference and its governance capability. A government that is only responsible for the outcome of intervention will focus unilaterally on accuracy at the expense of speed; a risk-averse government that intends to minimize the maximum infection rate in uncertain scenarios will impose a more restrictive blocking; and the most restrictive blocking strategy might be best for governments with lower capability and credibility.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Heymann, D.L.; Shindo, N. COVID-19: What Is next for Public Health? Lancet 2020, 395, 542–545. [Google Scholar] [CrossRef]
- Mizumoto, K.; Kagaya, K.; Zarebski, A.; Chowell, G. Estimating the Asymptomatic Proportion of Coronavirus Disease 2019 (COVID-19) Cases on Board the Diamond Princess Cruise Ship, Yokohama, Japan, 2020. Eurosurveillance 2020, 25, 2000180. [Google Scholar] [CrossRef] [PubMed]
- Qiu, J. Covert Coronavirus Infections Could Be Seeding New Outbreaks. Nature 2020. [Google Scholar] [CrossRef] [PubMed]
- Zou, L.; Ruan, F.; Huang, M.; Liang, L.; Huang, H.; Hong, Z.; Yu, J.; Kang, M.; Song, Y.; Xia, J.; et al. SARS-CoV-2 Viral Load in Upper Respiratory Specimens of Infected Patients. N. Engl. J. Med. 2020, 382, 1177–1179. [Google Scholar] [CrossRef] [PubMed]
- Terpstra, T.; Lindell, M.K.; Gutteling, J.M. Does Communicating (Flood) Risk Affect (Flood) Risk Perceptions? Results of a Quasi-Experimental Study. Risk Anal. Int. J. 2009, 29, 1141–1155. [Google Scholar] [CrossRef] [PubMed]
- Van Der Bles, A.M.; van der Linden, S.; Freeman, A.L.; Spiegelhalter, D.J. The Effects of Communicating Uncertainty on Public Trust in Facts and Numbers. Proc. Natl. Acad. Sci. USA 2020, 117, 7672–7683. [Google Scholar] [CrossRef]
- Wang, Z.; Andrews, M.A.; Wu, Z.X.; Wang, L.; Bauch, C.T. Coupled Disease–Behavior Dynamics on Complex Networks: A Review. Phys. Life Rev. 2015, 15, 1–29. [Google Scholar] [CrossRef]
- Kasperson, R.E.; Renn, O.; Slovic, P.; Brown, H.S.; Emel, J.L.; Goble, R.; Kasperson, J.X.; Ratick, S.J. The Social Amplification of Risk: A Conceptual Framework. Risk Anal. 1988, 8, 177–187. [Google Scholar] [CrossRef]
- Azizi, A.; Montalvo, C.; Espinoza, B.; Kang, Y.; Castillo-Chavez, C. Epidemics on Networks: Reducing Disease Transmission Using Health Emergency Declarations and Peer Communication. Infect. Dis. Model. 2020, 5, 12–22. [Google Scholar] [CrossRef]
- Lynch, A. Thought Contagion as Abstract Evolution. J. Ideas 1991, 2, 3–10. [Google Scholar]
- Pastor-Satorras, R.; Castellano, C.; Van Mieghem, P.; Vespignani, A. Epidemic Processes in Complex Networks. Rev. Mod. Phys. 2015, 87, 925. [Google Scholar] [CrossRef]
- Tai, Z.; Sun, T. Media Dependencies in a Changing Media Environment: The Case of the 2003 SARS Epidemic in China. New Media Soc. 2007, 9, 987–1009. [Google Scholar] [CrossRef]
- Ferguson, N. Capturing Human Behaviour. Nature 2007, 446, 733. [Google Scholar] [CrossRef] [PubMed]
- Ruan, Z.; Tang, M.; Liu, Z. Epidemic Spreading with Information-Driven Vaccination. Phys. Rev. E 2012, 86, 036117. [Google Scholar] [CrossRef] [PubMed]
- Granell, C.; Gómez, S.; Arenas, A. Dynamical Interplay between Awareness and Epidemic Spreading in Multiplex Networks. Phys. Rev. Lett. 2013, 111, 128701. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Tang, M.; Yang, H.; Do, Y.; Lai, Y.C.; Lee, G. Asymmetrically Interacting Spreading Dynamics on Complex Layered Networks. Sci. Rep. 2014, 4, 5097. [Google Scholar] [CrossRef]
- Lynch, K.; Hunter, S. Conflicting Authority. Ref. Serv. Rev. 2020. [Google Scholar] [CrossRef]
- Wineburg, S.; McGrew, S.; Breakstone, J.; Ortega, T. Evaluating Information: The Cornerstone of Civic Online Reasoning. Stanf. Digit. Repos. 2016, 8, 2018. [Google Scholar]
- Allport, G.; Postman, L. The Psychology of Rumor: Gordon w. Allport, Leo Postman; Henry Holt: New York, NY, USA, 1947. [Google Scholar]
- Ng, Y.J.; Yang, Z.J.; Vishwanath, A. To Fear or Not to Fear? Applying the Social Amplification of Risk Framework on Two Environmental Health Risks in Singapore. J. Risk Res. 2018, 21, 1487–1501. [Google Scholar] [CrossRef]
- Slovic, P. Perception of Risk. Science 1987, 236, 280–285. [Google Scholar] [CrossRef]
- Bordia, P.; Rosnow, R.L. Rumor Rest Stops on the Information Highway: Transmission Patterns in a Computer-Mediated Rumor Chain. Hum. Commun. Res. 1998, 25, 163–179. [Google Scholar] [CrossRef]
- Taha, S.A.; Matheson, K.; Anisman, H. H1N1 Was Not All That Scary: Uncertainty and Stressor Appraisals Predict Anxiety Related to a Coming Viral Threat. Stress Health 2014, 30, 149–157. [Google Scholar] [CrossRef] [PubMed]
- Jones, N.M.; Thompson, R.R.; Schetter, C.D.; Silver, R.C. Distress and Rumor Exposure on Social Media during a Campus Lockdown. Proc. Natl. Acad. Sci. USA 2017, 114, 11663–11668. [Google Scholar] [CrossRef] [PubMed]
- Meijer, A.; Webster, C.W.R. The COVID-19-crisis and the information polity: An overview of responses and discussions in twenty-one countries from six continents. Inf. Polity 2020, 25, 243–274. [Google Scholar] [CrossRef]
- Gao, X.; Yu, J. Public governance mechanism in the prevention and control of the COVID-19: Information, decision-making and execution. J. Chin. Gov. 2020, 5, 178–197. [Google Scholar] [CrossRef]
- Pisano, G.P.; Sadun, R.; Zanini, M. Lessons from Italy’s Response to Coronavirus. Available online: https://hbr.org/2020/03/lessons-from-italys-response-to-coronavirus (accessed on 26 December 2020).
- Huo, L.a.; Huang, P.; Fang, X. An Interplay Model for Authorities’ Actions and Rumor Spreading in Emergency Event. Phys. A Stat. Mech. Appl. 2011, 390, 3267–3274. [Google Scholar] [CrossRef]
- Mukkamala, A.; Beck, R. The Role of Social Media for Collective Behavior Development in Response to Natural Disasters. In Proceedings of the ECIS 2018, Portsmouth, UK, 23–28 June 2018. [Google Scholar]
- Garfin, D.R.; Silver, R.C.; Holman, E.A. The Novel Coronavirus (COVID-2019) Outbreak: Amplification of Public Health Consequences by Media Exposure. Health Psychol. 2020, 39, 355–357. [Google Scholar] [CrossRef]
- Tang, B.; Wang, X.; Li, Q.; Bragazzi, N.L.; Tang, S.; Xiao, Y.; Wu, J. Estimation of the Transmission Risk of the 2019-nCoV and Its Implication for Public Health Interventions. J. Clin. Med. 2020, 9, 462. [Google Scholar] [CrossRef]
- Li, A.; Zhou, L.; Su, Q.; Cornelius, S.P.; Liu, Y.Y.; Wang, L.; Levin, S.A. Evolution of Cooperation on Temporal Networks. Nat. Commun. 2020, 11, 2259. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Q.; Cai, S.; Tang, M.; Braunstein, L.A.; Stanley, H.E. Suppressing Disease Spreading by Using Information Diffusion on Multiplex Networks. Sci. Rep. 2016, 6, 29259. [Google Scholar] [CrossRef]
- Ball-Rokeach, S.J.; DeFleur, M.L. A Dependency Model of Mass-Media Effects. Commun. Res. 1976, 3, 3–21. [Google Scholar] [CrossRef]
- Christensen, T.; Lægreid, P. Balancing governance capacity and legitimacy-how the Norwegian government handled the COVID-19 crisis as a high performer. Public Adm. Rev. 2020, 80, 774–779. [Google Scholar] [CrossRef]
- Sibley, C.G.; Greaves, L.M.; Satherley, N.; Wilson, M.S.; Overall, N.C.; Lee, C.H.; Milojev, P.; Bulbulia, J.; Osborne, D.; Milfont, T.L.; et al. Effects of the COVID-19 pandemic and nationwide lockdown on trust, attitudes toward government, and well-being. Am. Psychol. 2020, 75, 618–630. [Google Scholar] [CrossRef] [PubMed]
- Erikson, S. Pandemics show us what government is for. Nat. Hum. Behav. 2020, 4, 441–442. [Google Scholar] [CrossRef] [PubMed]
- Gentzkow, M.; Shapiro, J.M. What Drives Media Slant? Evidence from US Daily Newspapers. Econometrica 2010, 78, 35–71. [Google Scholar] [CrossRef]
- Besley, T.; Prat, A. Handcuffs for the Grabbing Hand? Media Capture and Government Accountability. Am. Econ. Rev. 2006, 96, 720–736. [Google Scholar] [CrossRef]
- Milgrom, P.; Roberts, J. Relying on the Information of Interested Parties. RAND J. Econ. 1986, 17, 18–32. [Google Scholar] [CrossRef]
- Mullainathan, S.; Shleifer, A. The Market for News. Am. Econ. Rev. 2005, 95, 1031–1053. [Google Scholar] [CrossRef]
- Djankov, S.; McLiesh, C.; Nenova, T.; Shleifer, A. Who Owns the Media? J. Law Econ. 2003, 46, 341–382. [Google Scholar] [CrossRef]
- Gentzkow, M.; Shapiro, J.M. Media Bias and Reputation. J. Political Econ. 2006, 114, 280–316. [Google Scholar] [CrossRef]
- Kirkpatrick, D.D.; Fabrikant, G. Changes at the Times: Reactions; Advertisers and Wall St. See an End to Turmoil. New York Times, 6 June 2003. [Google Scholar]
- Gentzkow, M.; Shapiro, J.M. Competition and Truth in the Market for News. J. Econ. Perspect. 2008, 22, 133–154. [Google Scholar] [CrossRef]
- Mao, L.; Yang, Y. Coupling Infectious Diseases, Human Preventive Behavior, and Networks—A Conceptual Framework for Epidemic Modeling. Soc. Sci. Med. 2012, 74, 167–175. [Google Scholar] [CrossRef] [PubMed]
- Zhou, T.; Liu, J.G.; Bai, W.J.; Chen, G.; Wang, B.H. Behaviors of Susceptible-Infected Epidemics on Scale-Free Networks with Identical Infectivity. Phys. Rev. E 2006, 74, 056109. [Google Scholar] [CrossRef] [PubMed]
- DiResta, R. Of Virality and Viruses: The Anti-Vaccine Movement and Social Media. Nautilus Institute for Security and Sustainability. 2018. Available online: https://nautilus.org/napsnet/napsnet-special-reports/of-virality-and-viruses-the-anti-vaccine-movement-and-social-media/ (accessed on 26 December 2020).
- Johnson, N.F.; Velásquez, N.; Restrepo, N.J.; Leahy, R.; Gabriel, N.; El Oud, S.; Zheng, M.; Manrique, P.; Wuchty, S.; Lupu, Y. The Online Competition between Pro- and Anti-Vaccination Views. Nature 2020, 582, 230–233. [Google Scholar] [CrossRef] [PubMed]
- Starbird, K. Disinformation’s Spread: Bots, Trolls and All of Us. Nature 2019, 571, 449–450. [Google Scholar] [CrossRef]
- Depoux, A.; Martin, S.; Karafillakis, E.; Preet, R.; Wilder-Smith, A.; Larson, H. The Pandemic of Social Media Panic Travels Faster than the COVID-19 Outbreak. J. Travel Med. 2020, 27, taaa031. [Google Scholar] [CrossRef]
- Duong, V.; Pham, P.; Yang, T.; Wang, Y.; Luo, J. The Ivory Tower Lost: How College Students Respond Differently than the General Public to the COVID-19 Pandemic. arXiv 2020, arXiv:2004.09968. [Google Scholar]
- James, A.; Eagle, L.; Phillips, C.; Hedges, D.S.; Bodenhamer, C.; Brown, R.; Wheeler, J.G.; Kirking, H. High COVID-19 Attack Rate Among Attendees at Events at a Church—Arkansas, March 2020. MMWR Morb. Mortal. Wkly. Rep. 2020, 69, 632–635. [Google Scholar] [CrossRef]
- Ho, C.S.; Chee, C.Y.; Ho, R.C. Mental Health Strategies to Combat the Psychological Impact of COVID-19 Beyond Paranoia and Panic. Ann. Acad. Med. 2020, 49, 155–160. [Google Scholar]
- Wang, D.; Hu, B.; Hu, C.; Zhu, F.; Liu, X.; Zhang, J.; Wang, B.; Xiang, H.; Cheng, Z.; Xiong, Y.; et al. Clinical Characteristics of 138 Hospitalized Patients with 2019 Novel Coronavirus–Infected Pneumonia in Wuhan, China. JAMA 2020, 323, 1061–1069. [Google Scholar] [CrossRef]

| Variable | Definition | Values/Distributions |
|---|---|---|
| initial information | ||
| individual threshold | ||
| disclosing threshold | ||
| blocking threshold | ||
| maximum moving radius | 2 | |
| maximum infection radius | 1 | |
| N | population | 1024 |
| population that can send information to government | 5 | |
| numbers of gathering spots | 10 | |
| population with initial information | 1 | |
| initial infections | 3 | |
| M | numbers of nodes (area of the whole map) | 2500 |
| infection rate of one-time contact | ||
| information decay rate | ||
| government’s credibility |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Ji, Z.; Zhang, X.; Zheng, Y.; Liang, H. Re-Thinking the Role of Government Information Intervention in the COVID-19 Pandemic: An Agent-Based Modeling Analysis. Int. J. Environ. Res. Public Health 2021, 18, 147. https://doi.org/10.3390/ijerph18010147
Lu Y, Ji Z, Zhang X, Zheng Y, Liang H. Re-Thinking the Role of Government Information Intervention in the COVID-19 Pandemic: An Agent-Based Modeling Analysis. International Journal of Environmental Research and Public Health. 2021; 18(1):147. https://doi.org/10.3390/ijerph18010147
Chicago/Turabian StyleLu, Yao, Zheng Ji, Xiaoqi Zhang, Yanqiao Zheng, and Han Liang. 2021. "Re-Thinking the Role of Government Information Intervention in the COVID-19 Pandemic: An Agent-Based Modeling Analysis" International Journal of Environmental Research and Public Health 18, no. 1: 147. https://doi.org/10.3390/ijerph18010147
APA StyleLu, Y., Ji, Z., Zhang, X., Zheng, Y., & Liang, H. (2021). Re-Thinking the Role of Government Information Intervention in the COVID-19 Pandemic: An Agent-Based Modeling Analysis. International Journal of Environmental Research and Public Health, 18(1), 147. https://doi.org/10.3390/ijerph18010147





