A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases
Abstract
:1. Introduction
1.1. Medical Evaluation Process
- Search for information on the patient’s health status.
- Assessment of the collected information.
- Development of a treatment plan.
- -
- Subjective data: symptoms.
- -
- Objective data: signals.
1.2. Use of Expert Systems in Decision-Support Tools
1.3. Expert Systems in Health Applications
1.4. Current Approaches for the Detection of Hypoxemic Clinical Cases
1.4.1. Measurement Instruments Used in the Determination of Hypoxemic Clinical Cases
1.4.2. Clinical Decision Support Systems Applied to the Detection and Monitoring of Hypoxemic Cases
1.5. Prior Considerations
2. Materials and Methods
2.1. Definition of the Methodology
2.1.1. Previous Considerations
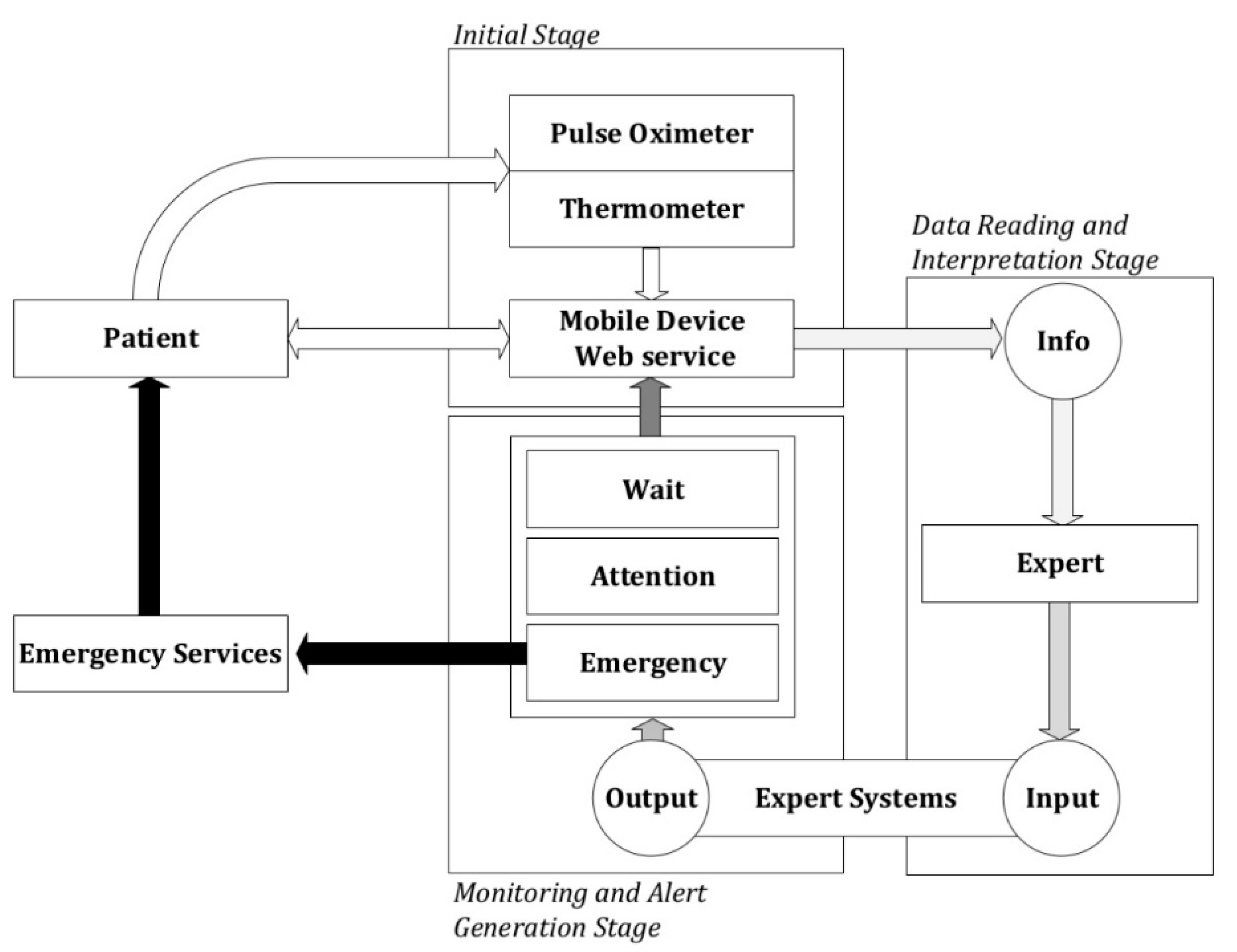
2.1.2. Conceptual Design and Description of the Methodology
Initial Stage
- Personal information: name, identifier, date of birth, race, and sex.
- Respiratory diseases: respiratory conditions the patient has been diagnosed with, such as for example chronic obstructive pulmonary disease (COPD), asthma, etc.
- Harmful habits: If she is/is not a smoker, and in the former case for how long and how many cigarettes she usually smokes per day.
Data Reading and Interpretation Stage
Monitoring and Alert Generation Stage
- Wait: It is not required to assist the patient, as it is considered that her health status does not demand it.
- Warning: It is recommended to carry out new measurements within a pre-determined period of time by the system in order to reassess the patient’s health status. The healthcare professional might provide indications about the care to be given to the patient if it is necessary.
- Emergency: It is recommended to send the emergency systems immediately to assist the patient.
2.2. Implementation of the Methodology
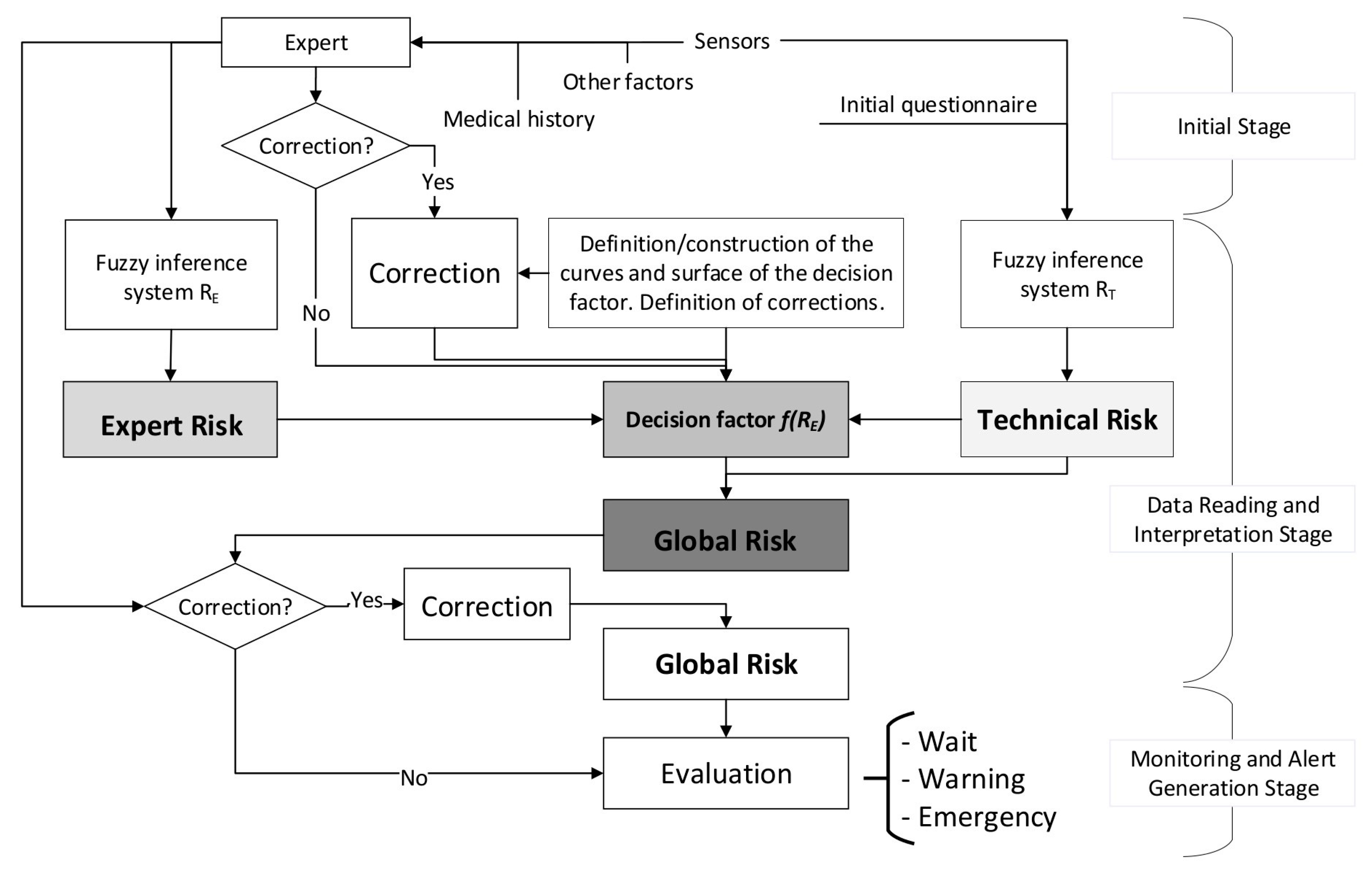
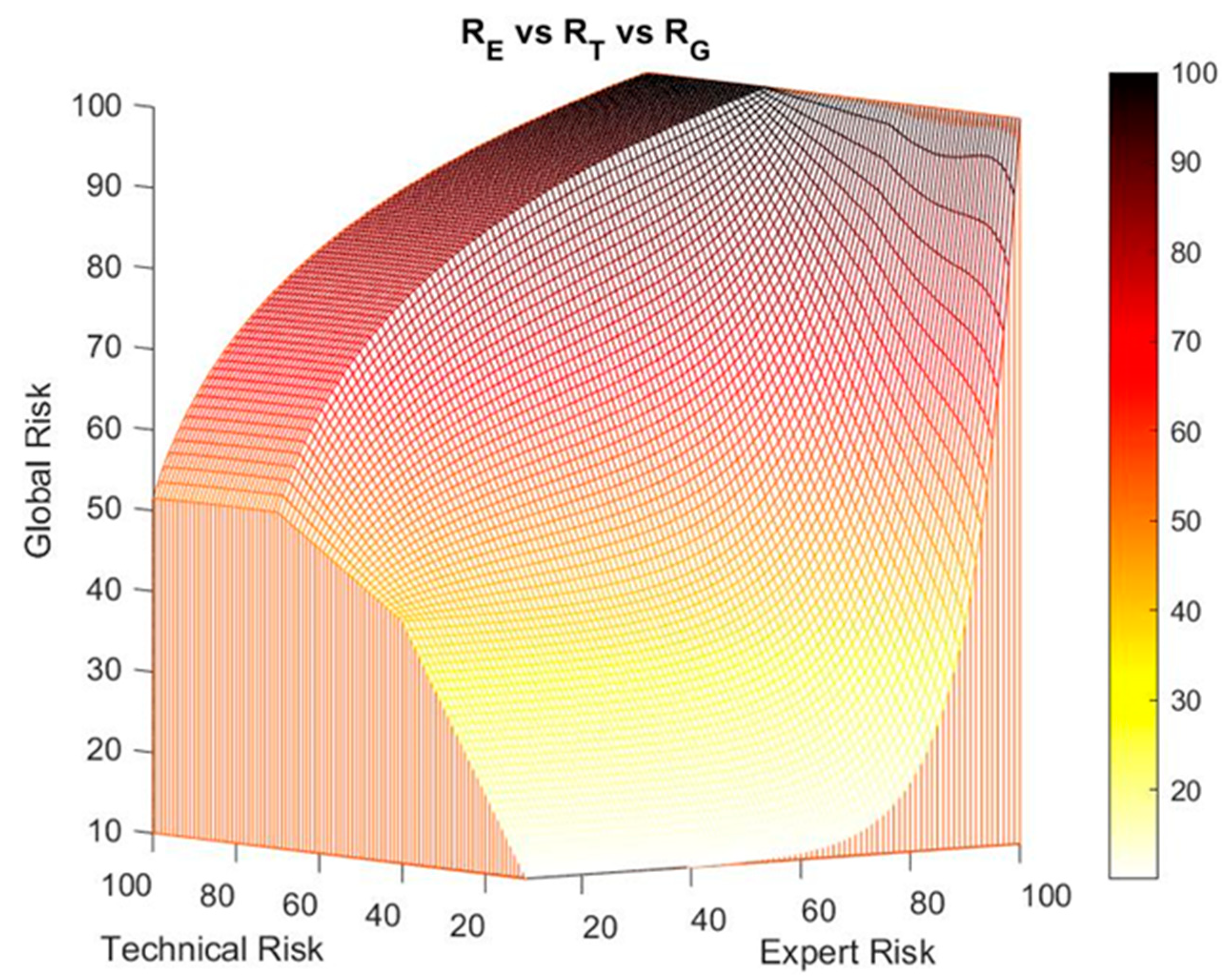
2.2.1. Definition of the Global Hypoxemia Risk Concept
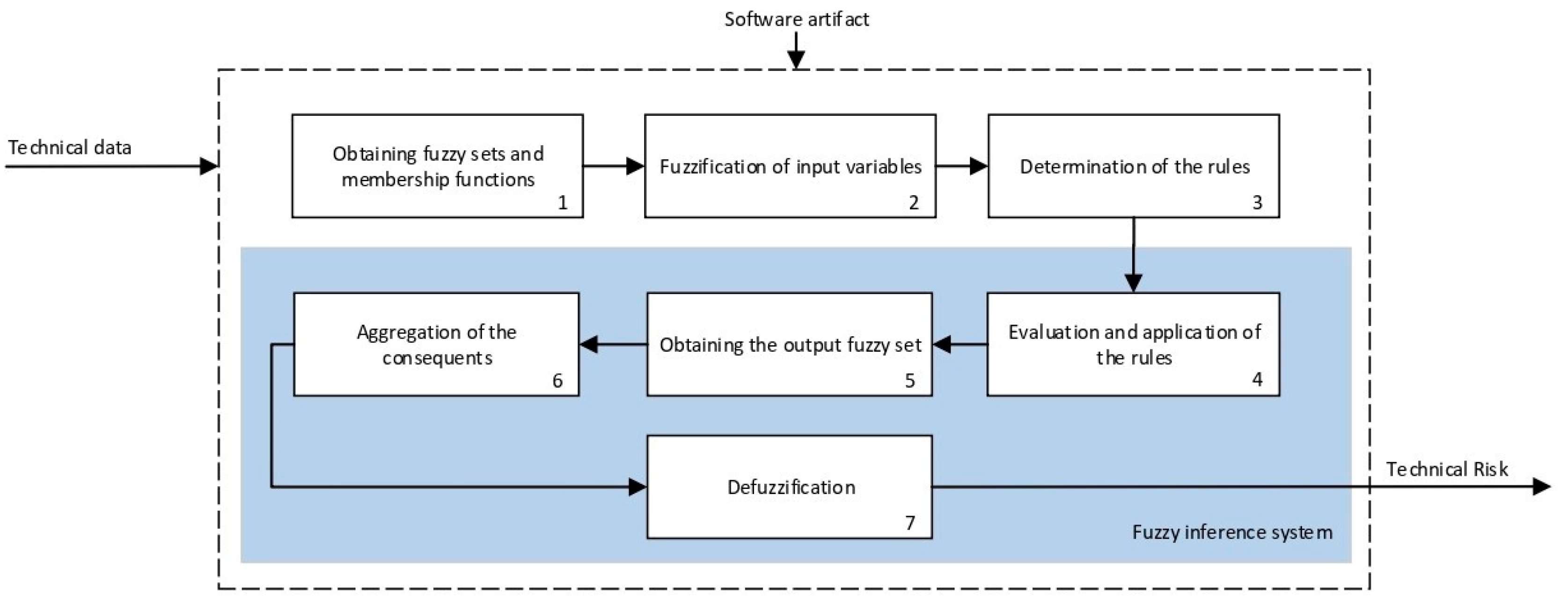
2.2.2. Definition and Calculation of Technical and Expert Risk
Calculation
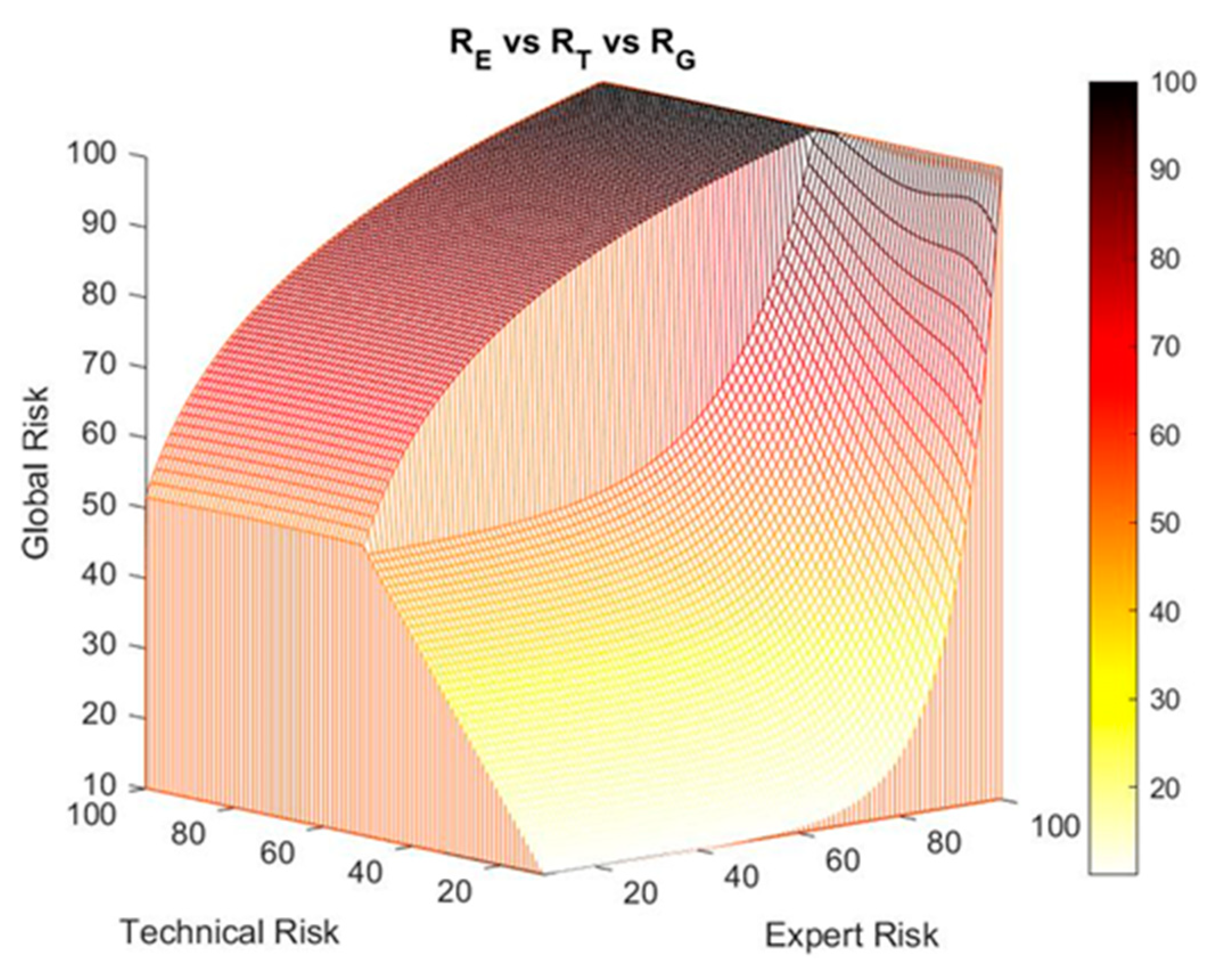
Behavior of the Expert Risk Parameter
- When the technical risk value is less than or equal to 50, a high decision factor value will be required to obtain a high global value risk, as a result of applying Equation (1). That is why as the expert risk value raises, the decision factor value must also grow fast. This means that if the technical risk values do not indicate an alert, the expert will be responsible in exclusive of raising her valuation of the hypoxemic seriousness level by means of her assessment, which directly will result in a high expert risk value.
- If the technical risk value is greater than 50, then it will not be required the decision factor value to be as high as before to obtain a high global hypoxemic risk value, and thus high global hypoxemic risk values may be obtained with smaller expert risk values. From this, it is derived that, in situations where the technical risk value is high, the alert will prevail on the expert’s considerations, thus forcing her to justify any low evaluation results that reduce the potential alert level.
Corrections
Corrections on the Decision Factor Definition Curves
- Exponential zone: This zone applies to technical risk values less than or equal to 50. As it was explained before, while the exponential growth zone is not reached the decision factor value is almost constant. After that, once the exponential growth zone is reached, the decision factor grows fast. It might be the case that the expert wishes the growth zone to be reached before, or that a growth rate is produced that is higher than the one provided by the exponential function. In this way, the expert is allowed to perform modifications on the decision factor within a range of values of the expert risk. A new correction is proposed in this case, so that the expert has the capability to change the growth rate of the exponential function by establishing a linear transition zone in the equation that defines the decision factor. To do so, an expert risk value must be defined from which the decision factor values are intended to be modified and the desired growth rate is to be established, this rate being at all times delimited in the interval defined by . For example, in the case that the expert wishes to perform a correction starting for expert risk values higher than 30 with a maximum growth rate, the expression to be used is shown in Equation (8), that in essence represents a straight line.
- Logarithmic zone: In the first segment of the expert risk, for values up to 30–40, decision factor values are produced that cause the global hypoxemic value to be lower than the technical risk. That is why a correction is proposed aiming to avoid a potential undervaluation on the side of the expert that might avoid the generation of warning or emergency alert levels when the expert is not fully convinced of it. When percentage variations exist between the technical risk and the global hypoxemic risk larger than a threshold value, for example a 15%, the expert will be asked about how sure she is about her assessment, and the decision factor value will be corrected according to Equation (9).
2.2.3. Determination of the Global Hypoxemic Risk and the Alert Level
Corrections on the Exponential–Logarithmic Transition Zone of the Global Risk Surface
2.2.4. Alert Evaluation
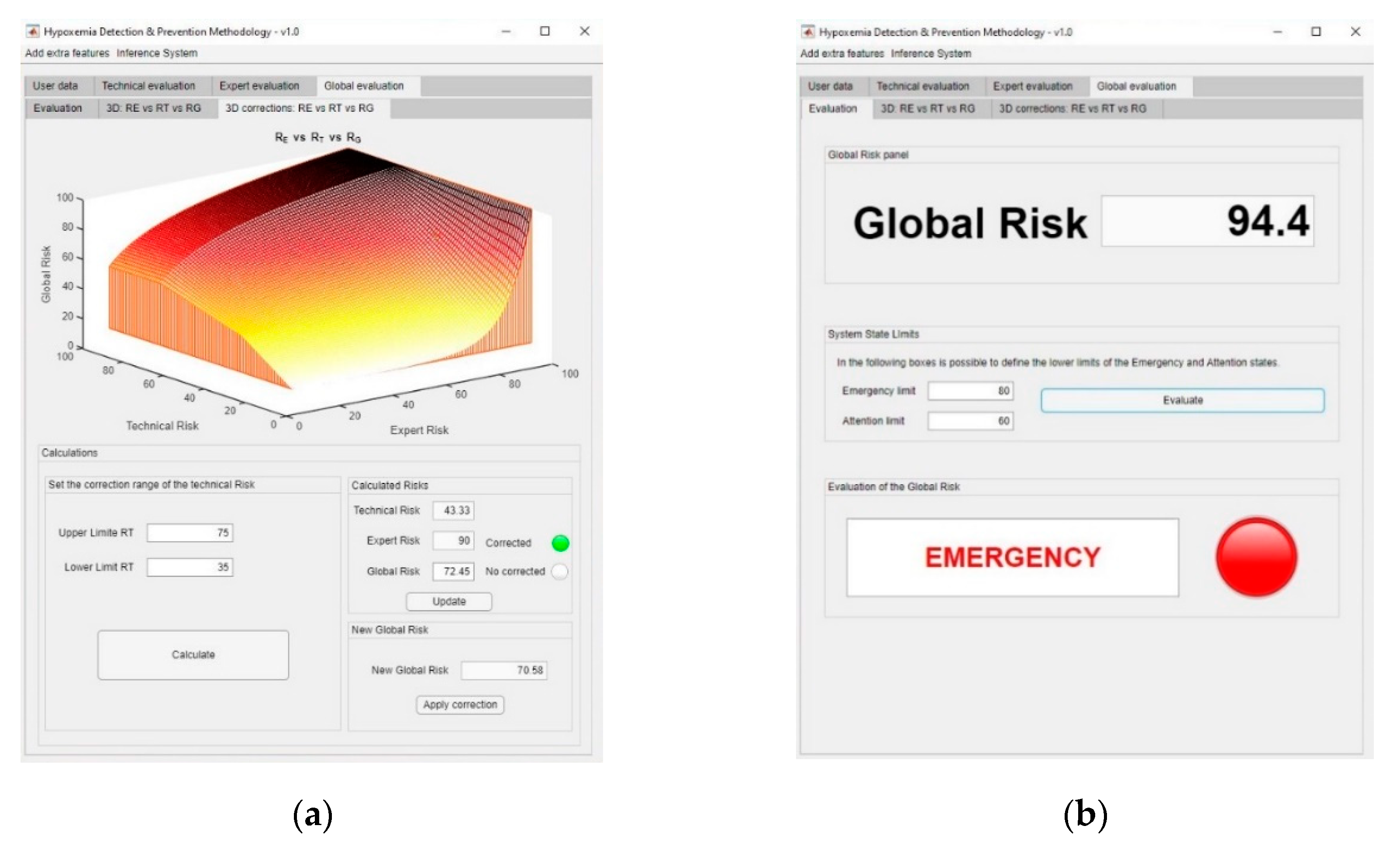
- Wait: when the global risk value is contained in (0–60).
- Warning: when the global risk value is contained in (60–80).
- Emergency: when the global risk value is contained in (80–100).
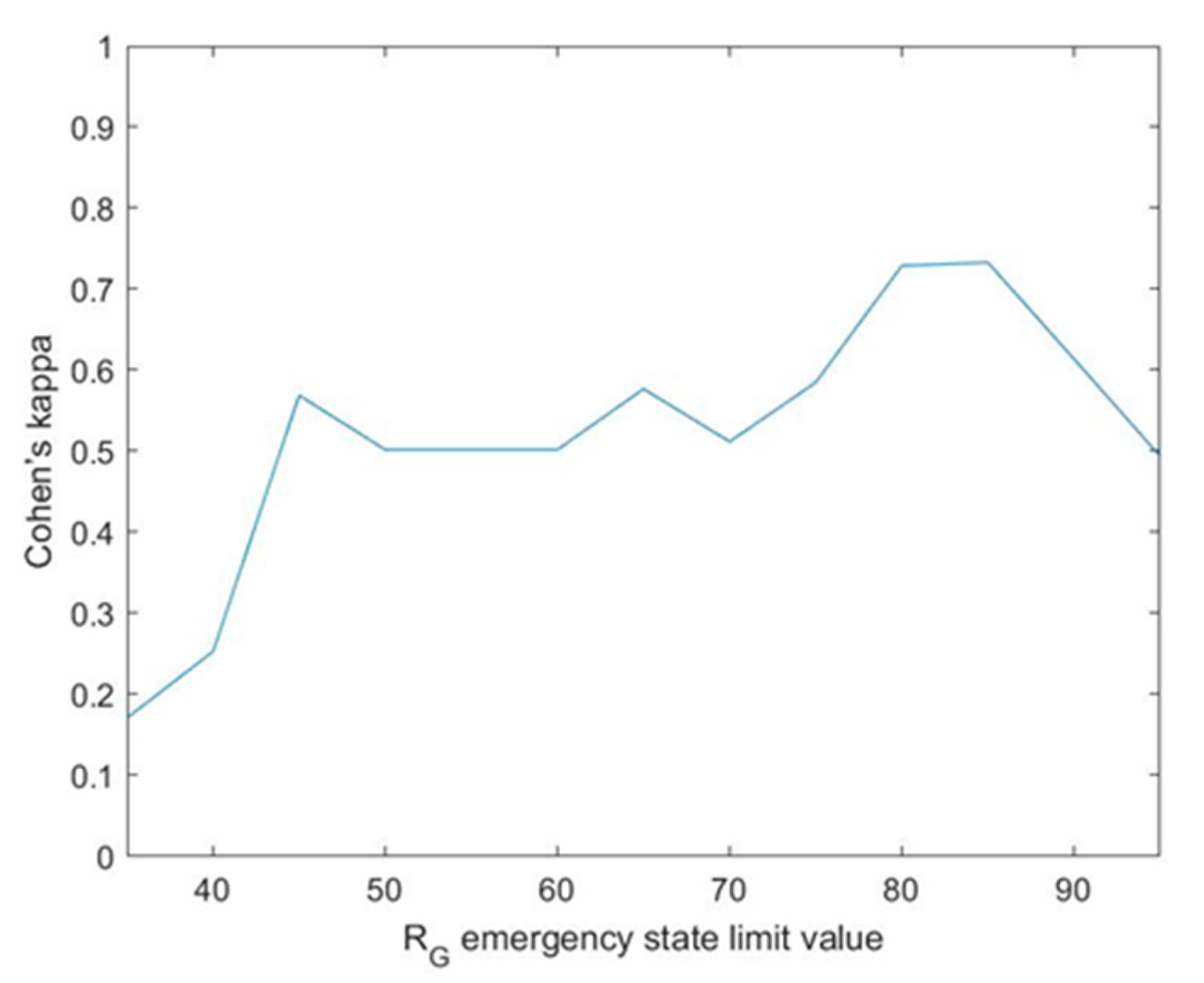
3. Simulation and Results
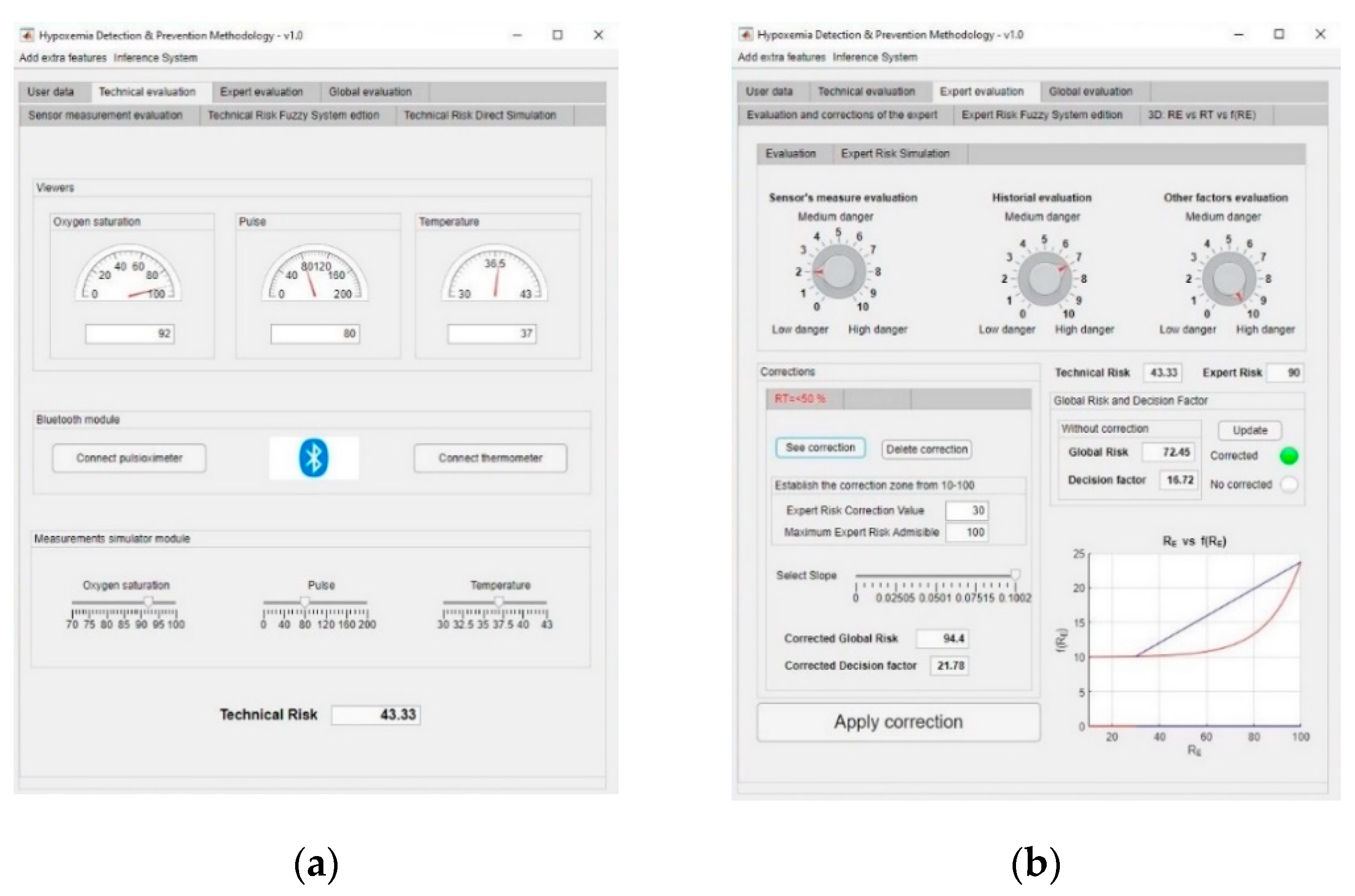
3.1. Simulation
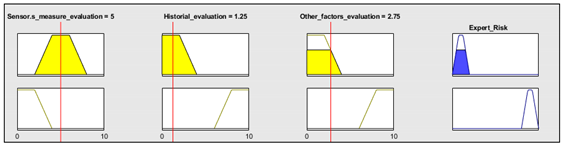
- Oxygen blood level: 92%.
- Heart rate: 80 beat/min.
- Temperature: 37 °C.
- Assessment of measurements: medium-low risk level (3/10).
- Assessment of the patient’s medical history: In this case the risk level is medium-high, as the patient is affected by sleep apnea and chronical obstructive pulmonary disease (COPD) (7/10).
- Assessment of any other potential risk factors: The risk is high, as the patient has an at-risk job (10/10).
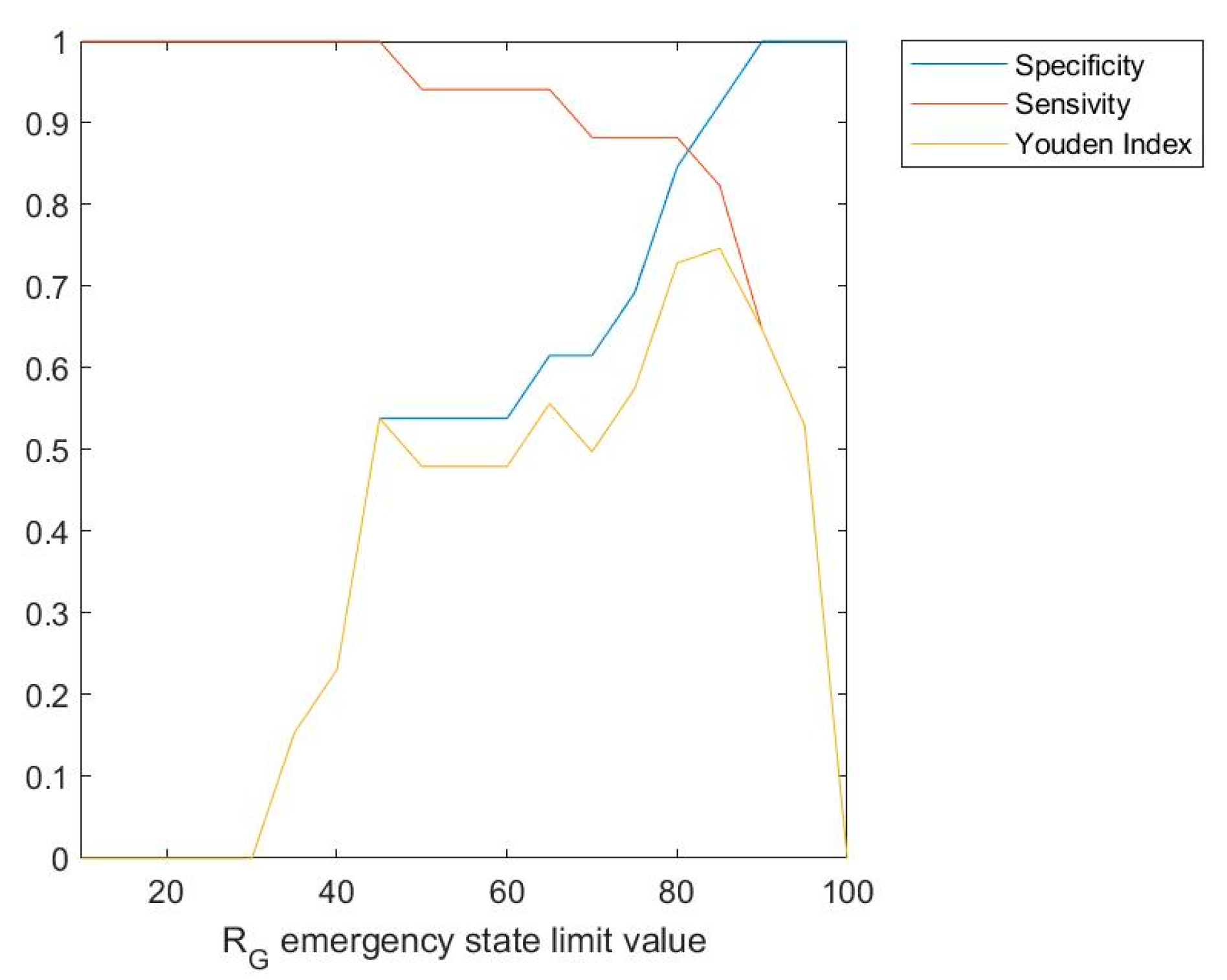
3.2. Results
Interpretation of the Results
4. Discussion
- The proposed methodology allows to integrate all those aspects related with improvements in the reliability, placement and interpretation of the pulse-oximeter readings. In this case, the integration of this device is carried out by means of an inference system that fuzzifies its measurements. This makes possible to improve its qualitative interpretation. In the same way, suggestions related to its placement or to the threshold values may be directly implemented in the membership functions of the technical and expert risk antecedents, by means of the assessment of the information collected in all the related studies. They can even be reflected on the definition of the global risk ranges associated to the definition of the recommendations.
- All the works analyzed related to decision support systems aimed to the detection of hypoxemic cases are based on the integration of data and the determination of values for warning and alert thresholds. According to this approach, the determination of the global risk in the presented methodology is similar to those with the following considerations:
- ○
- The global risk is a function calculated from the inference of the technical risk and the expert risk, which allows to integrate quantitative and qualitative variables into the calculation process, thus incorporating the assessment of the healthcare team.
- ○
- The global risk ranges associated to the recommendations can always be modified by the healthcare team, being liable to alterations or modifications adapted to the collected dataset.
- ○
- The processing of the initial data of both inference systems is performed by means of the definition of membership functions, reducing the uncertainty in the process of quantification of its qualitative expression.
- ○
- The use of expert systems, a key feature of this methodology, makes possible as already explained the diversification and formalization of the information related to the detection of hypoxemic conditions, thus allowing the methodology to be used by different experts possessing different training and experience.
- ○
- The incorporation of corrections, as indicated in the results section, significantly extends the usefulness of the methodology. It has already been argued in this section that the benefits of this type of support tools to the decision process is currently under question. The presence of corrections reinforces its character to support and to help the diagnosis process, but always leaving the final decision to the healthcare team, which always may re-interpret the results provided by the expert systems.
- ○
- The interface, same as happens in the works by Karlen et al. [45], Keerthika and Ganesan [46], Isik and Güler [47], and Merone et al. [48], makes possible to implement a system for the application of the methodology. Even if it is has not being incorporated yet into mobile devices, such a realization would be simple. Additionally, the software artifact developed was conceived for its incorporation into clinical information systems, therefore being useful at times in which, either because of the large number of patients, or because of the widespread dissemination of a disease, said systems work at saturation conditions. A clear example of this is the health system collapse caused in many areas by the COVID-19 pandemic that has circulated worldwide in 2020.
- ○
- Both the concurrence in the inference of the expert systems and the global risk calculation and the corrections, provide an effective supervision of the uncertainty. It is convenient to highlight that, further away from the risk that is evaluated here, a more essential risk exists associated to this uncertainty that measures what is unknown or what cannot be assessed. It is clear that, for all expert systems, to evaluate what is uncertain is a key point that, in this case, gets even bigger because of the particular importance of the specific topic dealt with. The methodology does not only reduce the uncertainty from the collection and interpretation of the input data, but also makes possible to handle what is uncertain by means of the correction, thus building trust in the processes.
- ○
- Lastly, it must be highlighted that the presented methodology is modular, meaning that it will always be possible to incorporate it into other inference engines or prediction algorithms. This integrating capability, derived from its own design, allows other developments in the field of study to be integrated into it, if that is the case.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ferkol, T.; Schraufnagel, D. The global burden of respiratory disease. Ann. Am. Thorac. Soc. 2014, 11, 404–406. [Google Scholar] [CrossRef] [PubMed]
- Forum of International Respiratory Societies. The Global Impact of Respiratory Disease, 2nd ed.; European Respiratory Society: Sheffield, UK, 2017; ISBN 9781849840873. [Google Scholar]
- Organización Mundial de la Salud-COVID-19. Available online: https://www.who.int/es/emergencies/diseases/novel-coronavirus-2019/advice-for-public/q-a-coronaviruses (accessed on 17 September 2020).
- García-Iglesias, J.J.; Gómez-Salgado, J.; Martín-Pereira, J.; Fagundo-Rivera, J.; Ayuso-Murillo, D.; Martínez-Riera, J.R.; Ruiz-Frutos, C. Impacto del SARS-CoV-2 (Covid-19) en la salud mental de los profesionales sanitarios: Una revisión sistemática. Rev. Esp. Salud Publica 2020, 94, 23–24. [Google Scholar]
- Sedes, P.R.; Sanz, M.Á.B.; Saera, M.A.B.; RodríguezRey, L.F.C.; Ortega, Á.C.; González, M.C.; de López, C.H.; Santos, E.D.; Barcena, A.E.; Mera, M.J.F.; et al. Plan de contingencia para los servicios de medicina intensiva frente a la pandemia COVID-19. Enfermería Intensiva 2020, 31, 82–89. [Google Scholar] [CrossRef]
- Thornett, A.M. Computer decision support systems in general practice. Int. J. Inf. Manage. 2001. [Google Scholar] [CrossRef]
- Turban, E.; Aronson, J.E.; Liang, T.-P. Decision Support Systems and Intelligent Systems; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 2007; ISBN 9788578110796. [Google Scholar]
- Liao, S.H. Expert system methodologies and applications-a decade review from 1995 to 2004. Expert Syst. Appl. 2005, 28, 93–103. [Google Scholar] [CrossRef]
- Casal-Guisande, M.; Comesaña-Campos, A.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. Design and development of a methodology based on expert systems, applied to the treatment of pressure ulcers. Diagnostics 2020, 10, 614. [Google Scholar] [CrossRef]
- Papadakis, M.A.; Mcphee, S.J. Current Medical Diagnosis & Treatment; McGraw-Hill Education: New York, NY, USA, 2019; ISBN 978-1260117431. [Google Scholar]
- Des Jardins, T.R.; Burton, G.G.; Phelps, T.H. Clinical Manifestations and Assessment of Respiratory Disease, 7th ed.; Elsevier Health Sciences: London, UK, 2015; ISBN 9780323244794. [Google Scholar]
- Hess, D.R.; MacIntyre, N.R.; Galvin, W.F.; Mishoe, S.C. Respiratory Care: Principles and Practice, 3rd ed.; Jones & Bartlett Learning: Burlington, VT, USA, 2015; ISBN 978-1-284-05000-4. [Google Scholar]
- Hevner, A.R.; Chatterjee, S. Design Research in Information Systems: Theory and Practice; Springer: New York, NY, USA, 2010; ISBN 978-1-4419-6107-5. [Google Scholar]
- Lucas, P.J.F.; van der Gaag, L.C. Principles of Expert Systems; Addison-Wesley: Wokingham, UK, 1991; ISBN 0-201-41640-9. [Google Scholar]
- Krishnamoorthy, C.S.; Rajeev, S. Artificial Intelligence and Expert Systems for Engineers; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Kumar, Y.; Jain, Y. Research aspects of expert system. Int. J. Comput. Bus. Res. 2012, 1, 1–11. [Google Scholar]
- Merritt, D. Building Expert Systems in Prolog; Springer: New York, NY, USA, 1989; ISBN 978-1-4613-8913-2. [Google Scholar]
- Nebendahl, D. Expert Systems: Introduction to the Technology and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 1988; ISBN 0471919667. [Google Scholar]
- Beynon-Dames, P. Database and expert systems applications. Eng. Appl. Artif. Intell. 1996, 9, 575. [Google Scholar] [CrossRef]
- Henrion, M.; Breese, J.S.; Horvitz, E. Decision analysis and expert systems. AI Mag. 1991, 12, 64. [Google Scholar]
- Jackson, P. Introduction to Expert Systems; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1998. [Google Scholar]
- Leondes, C.T. Expert Systems The Technology of Knowledge Management and Decision Making for the 21st Century; Academic Press: San Diego, CA, USA, 2002; ISBN 978-0-12-443880-4. [Google Scholar]
- Marston, M.; Allen, J.; Mistree, F. The decision support problem technique: Integrating descriptive and normative approaches in decision based design. Eng. Valuat. Cost Anal. 2000, 3, 107–129. [Google Scholar]
- Allen, J.K.; Seepersad, C.C.; Choi, H.-J.; Panchal, J.H.; McDowell, D.L.; Mistree, F. Decision Making in Engineering Design. In Integrated Design of Multiscale, Multifunctional Materials and Products; Elsevier: Burlington, MA, USA, 2010. [Google Scholar]
- Mistree, F.; Smith, W.F.; Bras, B.; Allen, J.K.; Muster, D. Decision-based Design: A Contemporary Paradigm for Ship Design. Trans. Soc. Nav. Archit. Mar. Eng. 1990, 98, 565–597. [Google Scholar]
- Chien, C.F.; Kim, K.H.; Liu, B.; Gen, M. Advanced decision and intelligence technologies for manufacturing and logistics. J. Intell. Manuf. 2012, 23, 2133–2135. [Google Scholar] [CrossRef] [Green Version]
- Hazelrigg, G.A. A framework for decision-based engineering design. J. Mech. Des. 1998, 120, 653–658. [Google Scholar] [CrossRef]
- Lewis, K.; Chen, W.; Schmidt, L. Decision Making in Engineering Design; ASME Press: New York, NY, USA, 2006; ISBN 978-0791802465. [Google Scholar]
- Myers, W. Introduction to Expert Systems. IEEE Expert 1986, 1, 100–109. [Google Scholar] [CrossRef]
- Buchanan, B.G. Expert systems: Working systems and the research literature. Expert Syst. 1986, 3, 32–50. [Google Scholar] [CrossRef]
- Todd, B.S. An Introduction to Expert Systems; Oxford University Computing Laboratory: Oxford, UK, 1992. [Google Scholar]
- Berzal, F. Redes Neuronales & Deep Learning; 2018; ISBN 1731265387. [Independently published]. [Google Scholar]
- Schröder, T. Use of Decision Support Systems for Medical Diagnosis and Treatment Selection-Volumen 85 de Schriften zur Gesundheitsökonomie. In Crossing Borders–Digital Transformation and the U.S. Health Care System; Schmid, A., Fried, B., Eds.; Verlag, P.C.O.: Bayreuth, Germany, 2020; pp. 219–234. [Google Scholar]
- Nazari, S.; Fallah, M.; Kazemipoor, H.; Salehipour, A. A fuzzy inference-fuzzy analytic hierarchy process-based clinical decision support system for diagnosis of heart diseases. Expert Syst. Appl. 2018, 95, 261–271. [Google Scholar] [CrossRef]
- Malmir, B.; Amini, M.; Chang, S.I. A medical decision support system for disease diagnosis under uncertainty. Expert Syst. Appl. 2017, 88, 95–108. [Google Scholar] [CrossRef]
- Hamedan, F.; Orooji, A.; Sanadgol, H.; Sheikhtaheri, A. Clinical decision support system to predict chronic kidney disease: A fuzzy expert system approach. Int. J. Med. Inform. 2020, 138, 104134. [Google Scholar] [CrossRef]
- Test Utilization Management, LDS, LDS Analytics, MedicalDatabase.com | Medical Database. Available online: https://www.medicaldatabase.com/ (accessed on 21 January 2020).
- Campos, M.; Jimenez, F.; Sanchez, G.; Juarez, J.M.; Morales, A.; Canovas-Segura, B.; Palacios, F. A methodology based on multiple criteria decision analysis for combining antibiotics in empirical therapy. Artif. Intell. Med. 2020, 102, 101751. [Google Scholar] [CrossRef]
- Qu, Y.; Yue, G.; Shang, C.; Yang, L.; Zwiggelaar, R.; Shen, Q. Multi-criterion mammographic risk analysis supported with multi-label fuzzy-rough feature selection. Artif. Intell. Med. 2019, 100. [Google Scholar] [CrossRef]
- DeMeulenaere, S. Pulse Oximetry: Uses and Limitations. J. Nurse Pract. 2007, 3, 312–317. [Google Scholar] [CrossRef]
- Jubran, A. Pulse oximetry. Intensive Care Med. 2004, 30, 2017–2020. [Google Scholar] [CrossRef]
- Fanconi, S. Pulse oximetry for hypoxemia: A warning to users and manufacturers. Intensive Care Med. 1989, 15, 540–542. [Google Scholar] [CrossRef] [PubMed]
- Hamber, E.A.; Bailey, P.L.; James, S.W.; Wells, D.T.; Lu, J.K.; Pace, N.L. Delays in the detection of hypoxemia due to site of pulse oximetry probe placement. J. Clin. Anesth. 1999, 11, 113–118. [Google Scholar] [CrossRef]
- Davidson, J.A.H.; Hosie, H.E. Limitations of pulse oximetry: Respiratory insufficiency-A failure of detection. Br. Med. J. 1993, 307, 372–373. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Karlen, W.; Dumont, G.A.; Petersen, C.; Gow, J.; Lim, J.; Sleiman, J.; Ansermino, J.M. Human-centered Phone Oximeter Interface Design for the Operating Room. In Proceedings of the International Conference on Health Informatics (HEALTHINF), Rome, Italy, 26–29 January 2011; pp. 433–438. [Google Scholar]
- Keerthika, A.; Ganesan, R. Pervasive health care system for monitoring oxygen saturation using pulse oximeter sensor. In Proceedings of the 2013 IEEE Conference on Information and Communication Technologies, ICT 2013, Thuckalay, Tamil Nadu, India, 11–12 April 2013; pp. 819–823. [Google Scholar]
- Işik, A.H.; Güler, I. Pulse oximeter based mobile biotelemetry application. Stud. Health Technol. Inform. 2012, 181, 197–201. [Google Scholar] [CrossRef] [PubMed]
- Merone, M.; Pedone, C.; Capasso, G.; Incalzi, R.A.; Soda, P. A Decision Support System for Tele-Monitoring COPD-Related Worrisome Events. IEEE J. Biomed. Heal. Informatics 2017, 21, 296–302. [Google Scholar] [CrossRef] [PubMed]
- Hassan, O.; Shamsir, S.; Islam, S.K. Machine Learning Based Hardware Model for a Biomedical System for Prediction of Respiratory Failure. In IEEE Medical Measurements and Applications, MeMeA 2020-Conference Proceedings; Institute of Electrical and Electronics Engineers Inc.: Bari, Italy, 2020. [Google Scholar]
- Ghazal, S.; Sauthier, M.; Brossier, D.; Bouachir, W.; Jouvet, P.A.; Noumeir, R. Using machine learning models to predict oxygen saturation following ventilator support adjustment in critically ill children: A single center pilot study. PLoS ONE 2019, 14, e0198921. [Google Scholar] [CrossRef] [Green Version]
- Al-Taee, M.; Zayed, A.Z.; Abood, S.N.; Al-Ani, M.A.; Al-Taee, A.M.; Hassani, H.A. Mobile-based interpreter of arterial blood gases using knowledge-based expert system. Int. J. Pervasive Comput. Commun. 2013, 9, 270–288. [Google Scholar] [CrossRef]
- Hevner, A.R.; March, S.T.; Park, J.; Ram, S. Design science in information systems research. MIS Q. Manag. Inf. Syst. 2004, 28, 75–105. [Google Scholar] [CrossRef] [Green Version]
- Ulrich, K.T.; Eppinger, S.D. Product Design and Development: Fifth Edition; McGraw-Hill Education: New York, NY, USA, 2012; ISBN 9780071086950. [Google Scholar]
- Comesaña-Campos, A.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J. The Value Index as a decision support tool applied to a new system for evaluating and selecting design alternatives. Expert Syst. Appl. 2018, 113. [Google Scholar] [CrossRef]
- Mamdani, E.H. Advances in the linguistic synthesis of fuzzy controllers. Int. J. Man. Mach. Stud. 1976, 8, 669–678. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man. Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Mamdani, E.H. Application of Fuzzy Logic to Approximate Reasoning Using Linguistic Synthesis. IEEE Trans. Comput. 1977, C-26, 1182–1191. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications, 3rd ed.; John Wiley & Sons: Chichester, UK, 2010; ISBN 9780470743768. [Google Scholar]
- Thunnissen, D.P. Propagating and Mitigating Uncertainty in the Design of Complex Multidisciplinary Systems; California Institute of Technology: Pasadena, CA, USA, 2005. [Google Scholar]
- MATLAB-MathWorks-MATLAB & Simulink. Available online: https://www.mathworks.com/products/matlab.html (accessed on 29 May 2020).
- Billo, E.J. Excel for Scientists and Engineers: Numerical Methods; Wiley-Interscience: Hoboken, NJ, USA, 2007; ISBN 9780471387343. [Google Scholar]
- Baratloo, A.; Hosseini, M.; Negida, A.; El Ashal, G. Part 1: Simple Definition and Calculation of Accuracy, Sensitivity and Specificity. Emerg 2015, 3, 48–49. [Google Scholar] [CrossRef]
- Youden, W.J. Index for rating diagnostic tests. Cancer 1950, 3, 32–35. [Google Scholar] [CrossRef]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Viera, A.J.; Garrett, J.M. Understanding interobserver agreement: The kappa statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar]
- Miller, R.A.; Geissbuhler, A. Diagnostic Decision Support Systems. In Clinical Decision Support Systems; Springer: New York, NY, USA, 2007; pp. 99–125. [Google Scholar]
- Pawloski, P.A.; Brooks, G.A.; Nielsen, M.E.; Olson-Bullis, B.A. A systematic review of clinical decision support systems for clinical oncology practice. JNCCN J. Natl. Compr. Cancer Netw. 2019, 17, 331–338. [Google Scholar] [CrossRef] [Green Version]

| Rule 1: Design an artifact (presented methodology) |
| The artifact, i.e., the methodology detailed in Section 2.2, is a tool aimed to help in the process for assessing the health status of patients prone to developing respiratory diseases. |
| Rule 2: Relevance of the problem |
| The assessment of the health status of patients liable to develop potential medical hypoxemia cases is nowadays a topic of vital importance, of undoubtable relevance because respiratory diseases are globally the fifth most relevant cause of death [1,2], and more especially during 2020 due to the pandemic situation caused by COVID-19. |
| Rule 3: Design evaluation |
| The application of a new methodology is demonstrated in the practical case shown in Section 3.1. |
| Rule 4: Contributions to the field of research |
| The contributions to the field of new expert systems applied in the context of decision-making support in medicine are presented in Section 4 and Section 5 of this article. |
| Rule 5: Rigor in the research |
| The conceptual development of the presented methodology has been defined in Section 2.1, as was its classification within the field of research. In the same way, the mathematical groundings of this work are supported on the use of fuzzy-logic inference systems, and the definition of the risk functions and their combinations has adhered at all times to the appropriate mathematical rigor. |
| Rule 6: Design as a search process |
| In Section 1, the methodology was framed within the state of the art of similar applications, observing its differential aspects. These differences are discussed in Section 4. |
| Rule 7: Communication of the research |
| In Section 4 and Section 5, the main contributions of the new method are presented, as well as the future lines of work. |
| Name: | Identifier: | ||
|---|---|---|---|
| Date of Birth: | Race: | Sex(M/F): | |
| Questions to Be Answered: | Yes | No | |
| Have you been abroad in the last month? | |||
| If yes, please, name the region where have you been. | |||
| If yes, for how long, in months, have you been abroad? | |||
| Have you had any risk contact with people affected by—or that might be affected of—COVID-19? | |||
| Have you suffered—or are you suffering now—of fever, dry cough, or fatigue? | |||
| Have you had—or do you have now—breathing difficulties or a shortness of breath feeling? | |||
| Have you been—or are you now—affected by loss of smell or taste, headache, or any other discomfort or pain? | |||
| Do you have an occupation that involves risk to the respiratory system—for example, participation in mining operations? | |||
| If yes, please, explain which occupation it is | |||
| Technical Risk Fuzzy Inference System. | |||
|---|---|---|---|
| Input data | Range | Output data | Range |
| Oxygen saturation | 70–100% | Technical Risk | 0–100 1 |
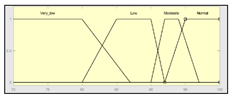 |  1 Actual range is 10–100, for more details see Section 2.2.1. | ||
| Temperature | 33–41 °C | Initial configuration | |
 | Fuzzy structure: Mamdani–type. Membership function type: trapezoidal. Defuzzification method: centroid [58]. | Implication method: MIN. Aggregation method: MAX. Number of fuzzy rules: 45. | |
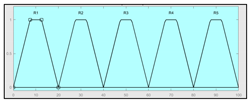
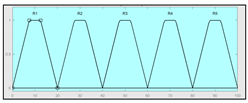
| Heart rate | 15–180 b.p.m | Subset of the 45 fuzzy rules 1. IF (O2_Saturation is Very_Low) AND (Pulse is Normal) THEN (Technical_Risk is R5) 2. IF (O2_Saturation is not Very_Low) AND (Temperature is Normal) AND (Heart_Rate is Normal) THEN (Technical_Risk is R1) 3. IF (O2_Saturation is not Very_Low) AND (Temperature is Normal) AND (Heart_Rate is High) THEN (Technical_Risk is R1) | |
 | |||
| Example of combination of fuzzy rules 2 and 3 | |||
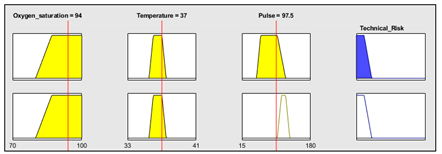 | |||
| Expert Risk Fuzzy Inference System | |||
|---|---|---|---|
| Input data | Range | Output data | Range |
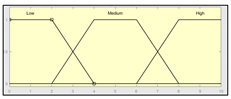
| Sensors’ measurement assessment | 0–10 | Expert Risk | 0–100 2 |
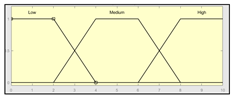 |  2 Actual range is 10–100, for more details see Sub-Section 2.2.1. | ||
| History assessment | 0–10 | Initial configuration | |
 | Fuzzy structure: Mamdani–type. Membership function type: trapezoidal. Defuzzification method: centroid [58]. | Implication method: MIN. Aggregation method: MAX. Number of fuzzy rules: 29. | |
| Assessment of other factors | 0–10 | Subset of the 29 fuzzy rules 1. IF (Sensors_Measurement_Assessment is Medium) AND (History_Assessment is Low) AND (Assessment_Other_Factors is Low) THEN (Expert_Risk is R1) 2. IF (Sensors_Measurement_Assessment is Low) AND (History_Assesment is High) AND (Assessment_Other_Factors is High) THEN (Expert_Risk is R5) | |
 | |||
| Example of combination of fuzzy rules 1 and 2 | |||
 | |||
| Patient | O2 Conc. | Heart Rate (beat/min) | Temp. (°C) | History | Other Factors |
|---|---|---|---|---|---|
| 1 | 92 | 80 | 37 | 55 y.o., sleep apnea and COPD | Mining job |
| 2 | 87 | 50 | 38.5 | 60 y.o., smoker and sedentary | - |
| 3 | 80 | 60 | 37.1 | 47 y.o., lung cancer | - |
| 4 | 93 | 140 | 38 | 18 y.o., obesity and asthma | - |
| 5 | 83 | 80 | 39 | 78 y.o., ex-smoker | - |
| 6 | 91 | 96 | 37.8 | 24 y.o. | - |
| 7 | 95 | 56 | 36.5 | 15 y.o., asthma | - |
| 8 | 90 | 72 | 36 | 35 y.o., smoker | Stone work job |
| 9 | 89 | 55 | 35.9 | 93 y.o., ex-smoker | - |
| 10 | 75 | 50 | 38.5 | 70 y.o., lung oedema | - |
| 11 | 96 | 64 | 36.5 | 25 y.o. | - |
| 12 | 89 | 74 | 36.6 | 26 y.o., smoker | Risky contacts |
| 13 | 92 | 56 | 37 | 45 y.o., sporty | - |
| 14 | 87 | 83 | 37.1 | 44 y.o., post-surgery | - |
| 15 | 80 | 63 | 35.8 | 92 y.o. | - |
| 16 | 65 | 50 | 35.8 | 87 y.o., palliative care | - |
| 17 | 86 | 92 | 37.2 | 17 y.o., obesity | - |
| 18 | 95 | 72 | 36.6 | 49 y.o. | - |
| 19 | 74 | 63 | 35.9 | 50 y.o., alcoholic and smoker | - |
| 20 | 93 | 89 | 37 | 23 y.o. | - |
| 21 | 89 | 66 | 36.7 | 67 y.o., ex-smoker and sedentary | - |
| 22 | 82 | 70 | 37.2 | 52 y.o., post-surgery | - |
| 23 | 92 | 68 | 36.3 | 84 y.o., sporty | - |
| 24 | 70 | 51 | 35.8 | 77 y.o., lung cancer | - |
| 25 | 89 | 66 | 36.3 | 36 y.o., asthma | - |
| 26 | 89 | 66 | 36.3 | 36 y.o., asthma | - |
| 27 | 87 | 94 | 37.2 | 59 y.o., COPD | - |
| 28 | 90 | 56 | 36.9 | 43 y.o. | - |
| 29 | 96 | 71 | 36.7 | 38 y.o., smoker | - |
| 30 | 82 | 84 | 36.4 | 66 y.o., sleep apnea | - |
| Patient | RT | RE | RG | Recommended State | Actual State |
|---|---|---|---|---|---|
| 1 | 43.33 | 90.00 | 72.45 | Emergency | Non-emergency |
| 2 | 80.00 | 74.40 | 94.00 | Emergency | Emergency |
| 3 | 90.00 | 90.00 | 97.92 | Emergency | Emergency |
| 4 | 61.84 | 53.62 | 87.01 | Emergency | Non-emergency |
| 5 | 81.47 | 90.00 | 98.01 | Emergency | Emergency |
| 6 | 45.11 | 10.00 | 45.25 | Non-emergency | Emergency |
| 7 | 38.59 | 10.00 | 38.67 | Non-emergency | Non-emergency |
| 8 | 57.21 | 40.16 | 80.84 | Emergency | Emergency |
| 9 | 55.93 | 69.08 | 92.28 | Emergency | Emergency |
| 10 | 90.00 | 90.00 | 97.92 | Emergency | Emergency |
| 11 | 34.10 | 34.13 | 34.13 | Non-emergency | Non-emergency |
| 12 | 56.67 | 90.00 | 97.85 | Emergency | Emergency |
| 13 | 43.72 | 40.46 | 44.59 | Non-emergency | Non-emergency |
| 14 | 56.67 | 90.00 | 97.85 | Emergency | Emergency |
| 15 | 90.00 | 90.00 | 97.90 | Emergency | Emergency |
| 16 | 90.00 | 90.00 | 97.90 | Emergency | Emergency |
| 17 | 57.62 | 40.00 | 80.76 | Emergency | Non-emergency |
| 18 | 40.68 | 10.00 | 40.75 | Non-emergency | Non-emergency |
| 19 | 90.00 | 90.00 | 97.90 | Emergency | Emergency |
| 20 | 43.33 | 10.00 | 43.43 | Non-emergency | Non-emergency |
| 21 | 56.67 | 31.33 | 75.59 | Emergency | Non-emergency |
| 22 | 65.67 | 56.06 | 87.98 | Emergency | Emergency |
| 23 | 43.33 | 29.66 | 43.72 | Non-emergency | Non-emergency |
| 24 | 90.00 | 90.00 | 97.70 | Emergency | Emergency |
| 25 | 56.67 | 22.51 | 68.61 | Emergency | Emergency |
| 26 | 56.59 | 40.00 | 87.74 | Emergency | Emergency |
| 27 | 55.92 | 16.33 | 61.82 | Emergency | Non-emergency |
| 28 | 33.47 | 20.00 | 33.54 | Non-emergency | Non-emergency |
| 29 | 64.63 | 56.78 | 88.24 | Emergency | Emergency |
| 30 | 52.83 | 35.94 | 78.41 | Emergency | Non-emergency |
| Binary classification groups | Classification state | Number of Cases |
|---|---|---|
| Correctly classified patients | True positive (tp) | 16 |
| True negative (tn) | 7 | |
| Wrongly classified patients | False positive (fp) | 6 |
| False negative (fn) | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Comesaña-Campos, A.; Casal-Guisande, M.; Cerqueiro-Pequeño, J.; Bouza-Rodríguez, J.-B. A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases. Int. J. Environ. Res. Public Health 2020, 17, 8644. https://doi.org/10.3390/ijerph17228644
Comesaña-Campos A, Casal-Guisande M, Cerqueiro-Pequeño J, Bouza-Rodríguez J-B. A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases. International Journal of Environmental Research and Public Health. 2020; 17(22):8644. https://doi.org/10.3390/ijerph17228644
Chicago/Turabian StyleComesaña-Campos, Alberto, Manuel Casal-Guisande, Jorge Cerqueiro-Pequeño, and José-Benito Bouza-Rodríguez. 2020. "A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases" International Journal of Environmental Research and Public Health 17, no. 22: 8644. https://doi.org/10.3390/ijerph17228644
APA StyleComesaña-Campos, A., Casal-Guisande, M., Cerqueiro-Pequeño, J., & Bouza-Rodríguez, J.-B. (2020). A Methodology Based on Expert Systems for the Early Detection and Prevention of Hypoxemic Clinical Cases. International Journal of Environmental Research and Public Health, 17(22), 8644. https://doi.org/10.3390/ijerph17228644






