A Gravity-Based Food Flow Model to Identify the Source of Foodborne Disease Outbreaks
Abstract
1. Introduction
2. Gravity Model
2.1. Method
2.2. Model Inputs
2.2.1. Area of Analysis and Zone Delineation
2.2.2. Inter-Zonal Distance Estimation
2.2.3. Intra-Zonal Distance Estimation
2.2.4. Retailer Revenue Estimation
2.2.5. Consumption Potential Estimation
2.2.6. Observed Trip Data
2.3. Model Calibration
2.4. Gravity Model Results
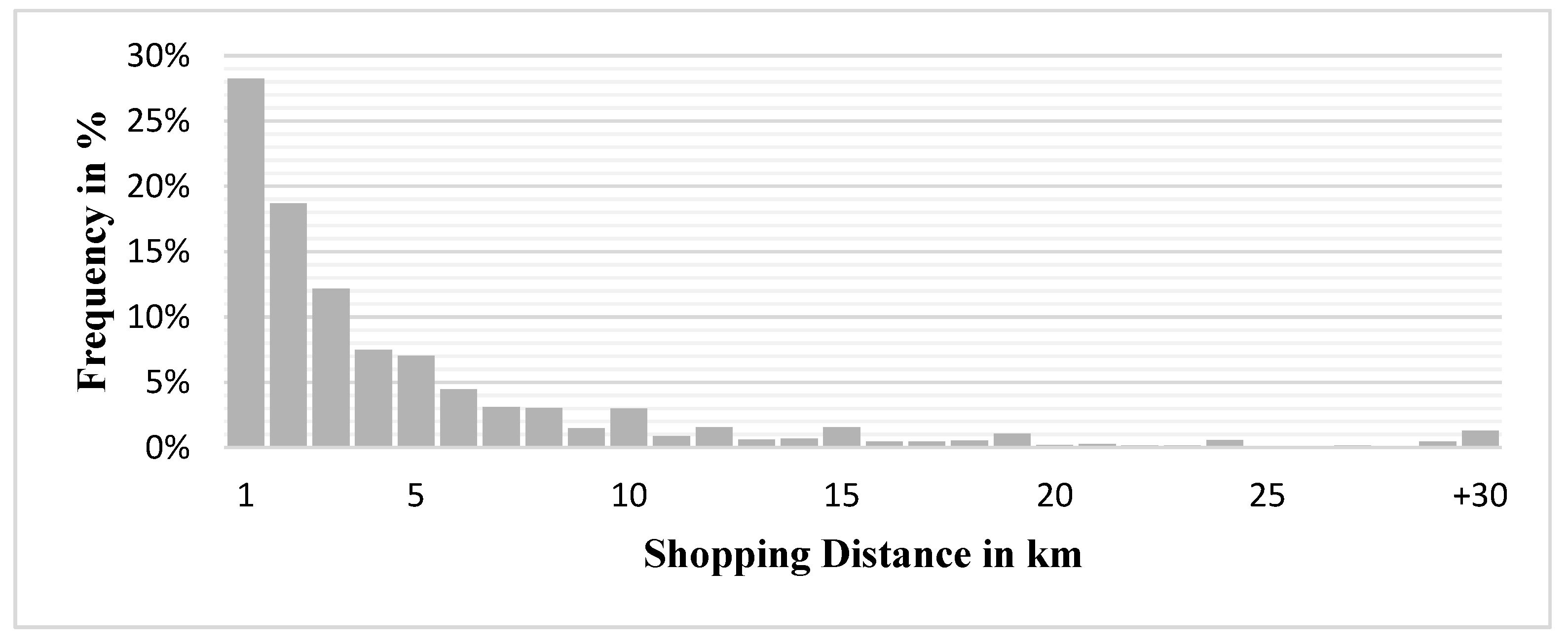
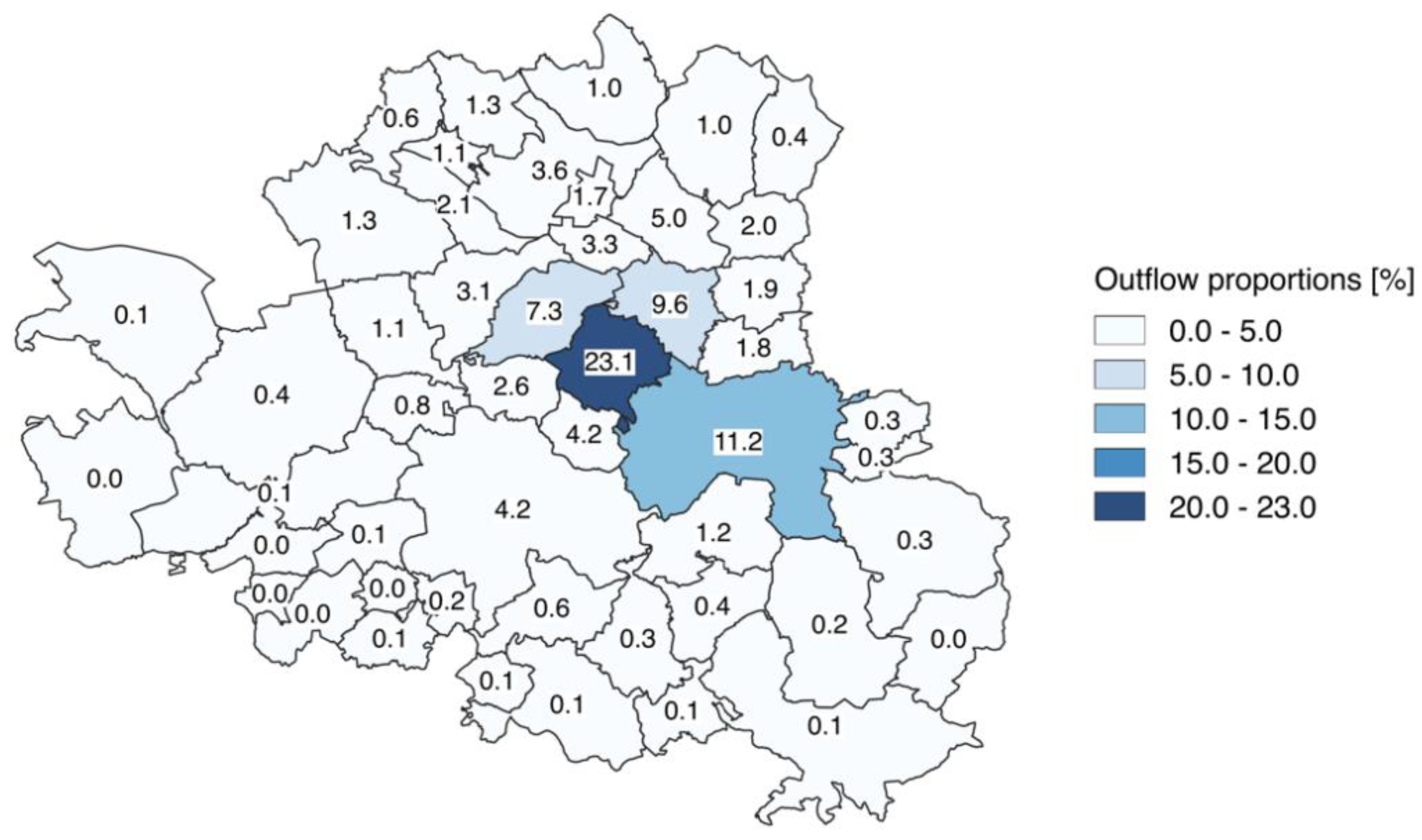
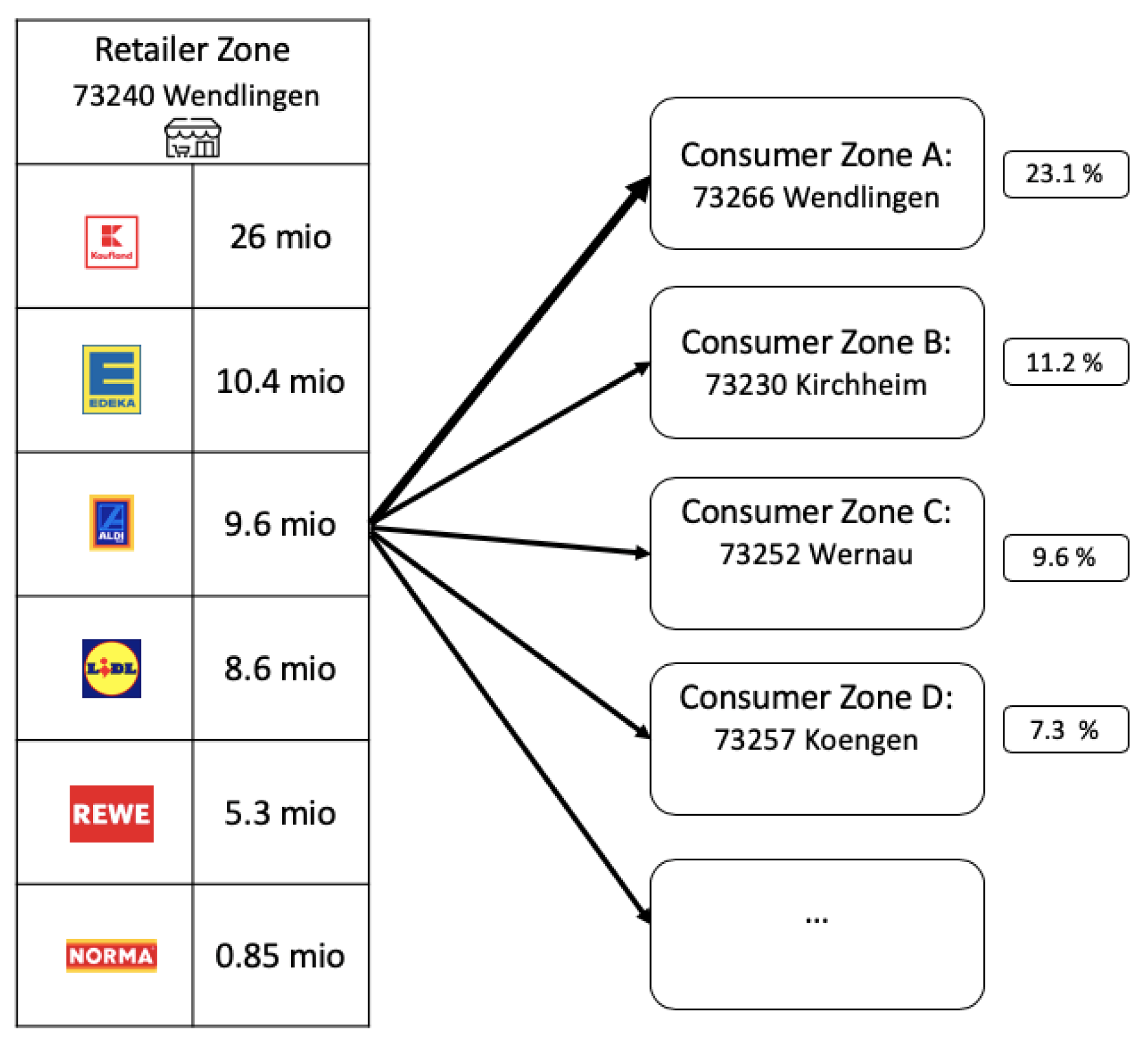
2.4.1. Food Flow Distribution
- (i)
- How many postal zones are supplied by a retailer zone?
- (ii)
- What proportion of goods are expected to be sold intra-zonally to consumers?
2.4.2. Revenue Estimation of Food Retailers in Affected Regions
2.4.3. Implication of Gravity Model Results
3. Application: Retailer Brand Identification
3.1. Retail Brand Source Identification Model
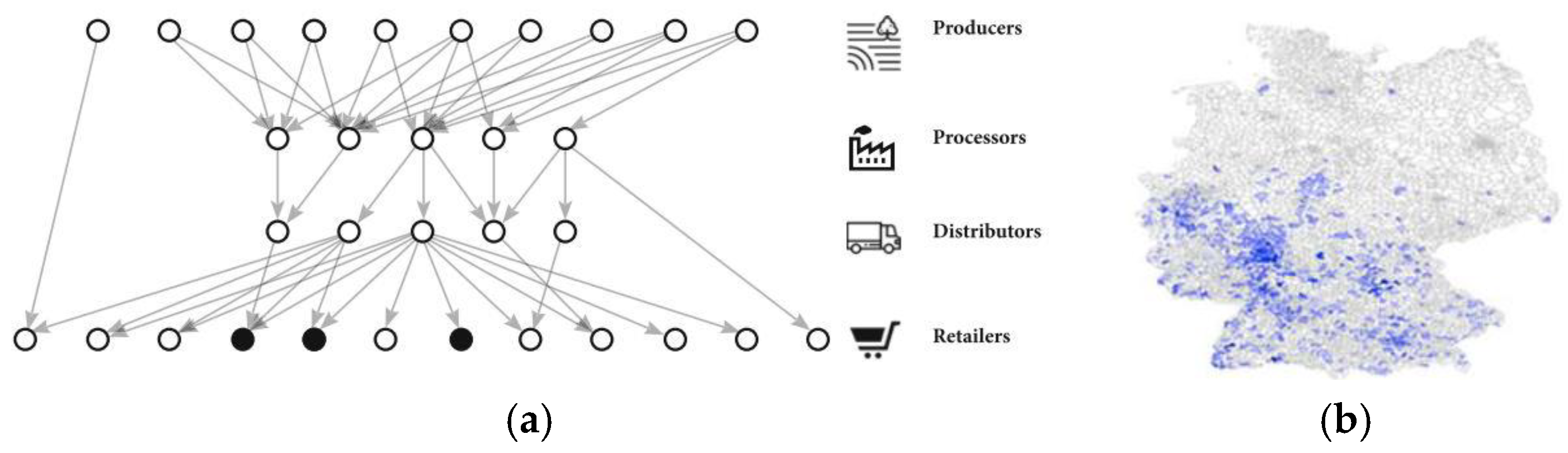
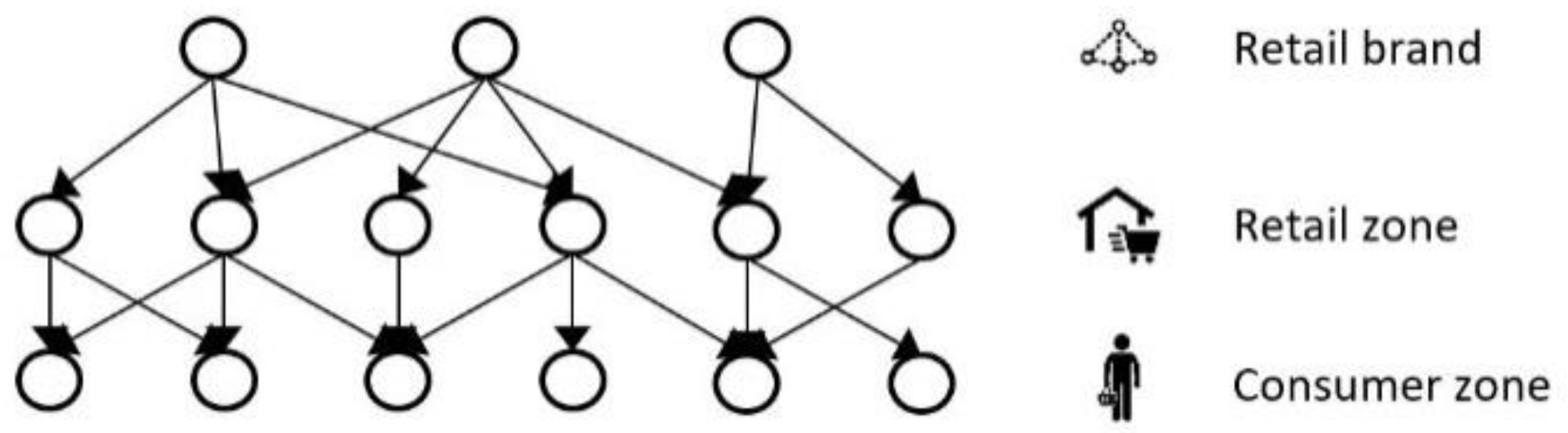
3.1.1. Network Model
3.1.2. Transmission Model
- The contaminated quantity is fixed and is composed of individual contaminated units that neither spread nor recover from contamination as they travel through the supply network.
- Each unit travels independently through the supply network.
- Each transition of a unit from one node to the next entails an independent transmission direction.
3.1.3. Traceback Algorithm: Bayesian Inference
3.2. Model Evaluation
3.2.1. Food Network Models
Food Network A (with Gravity Model)
Food Network B (without Gravity Model)
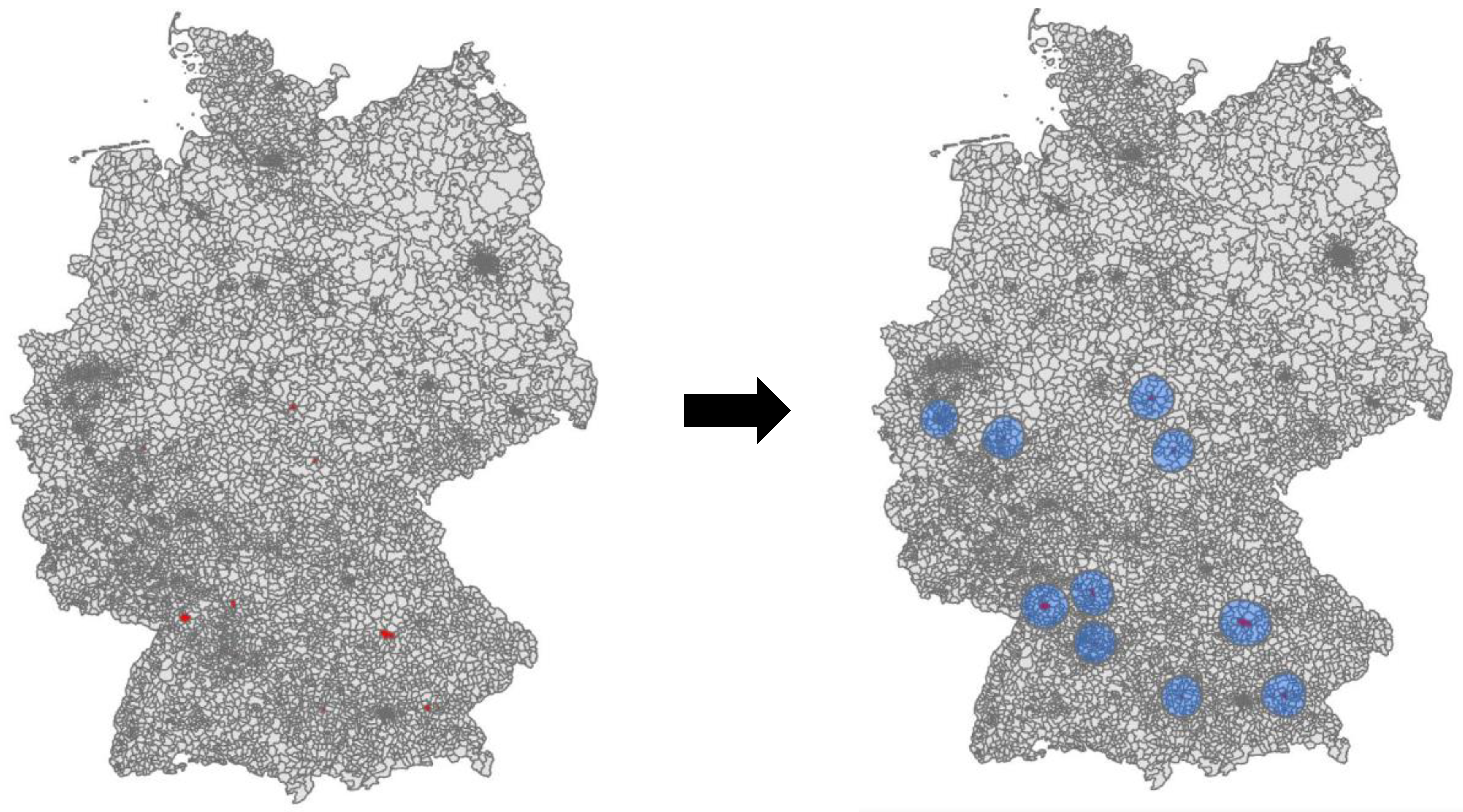
3.2.2. Outbreak Simulation
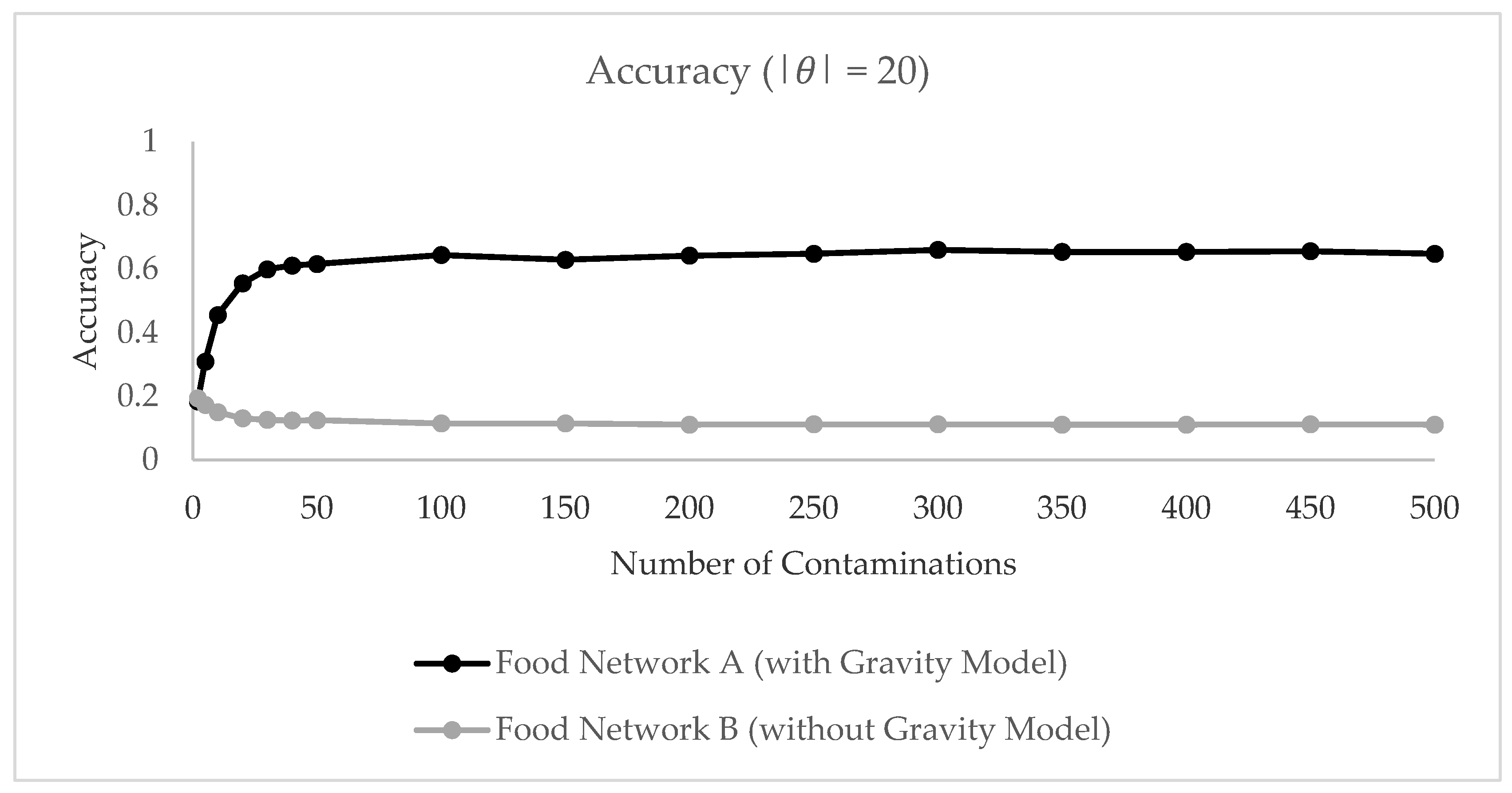
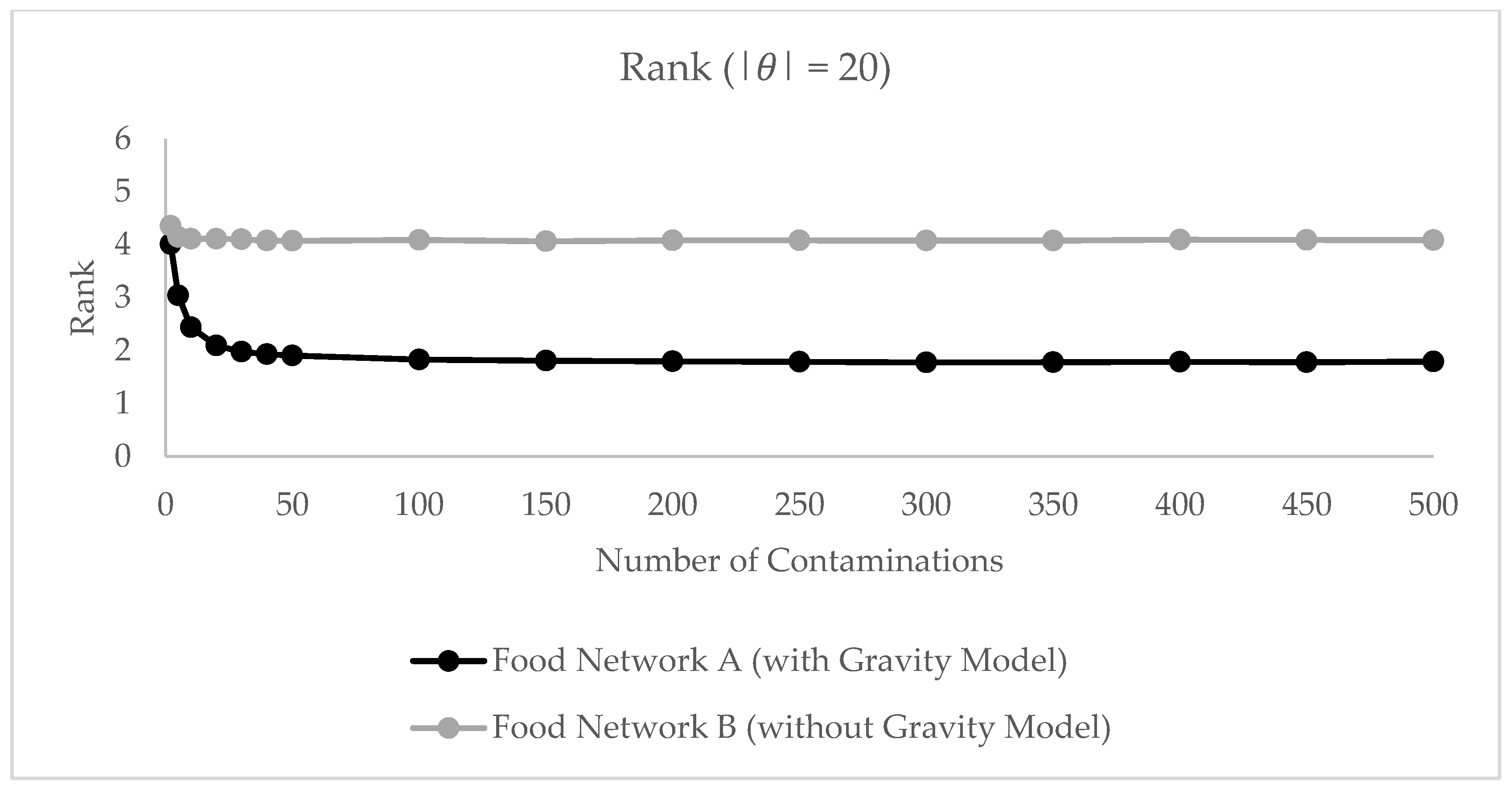
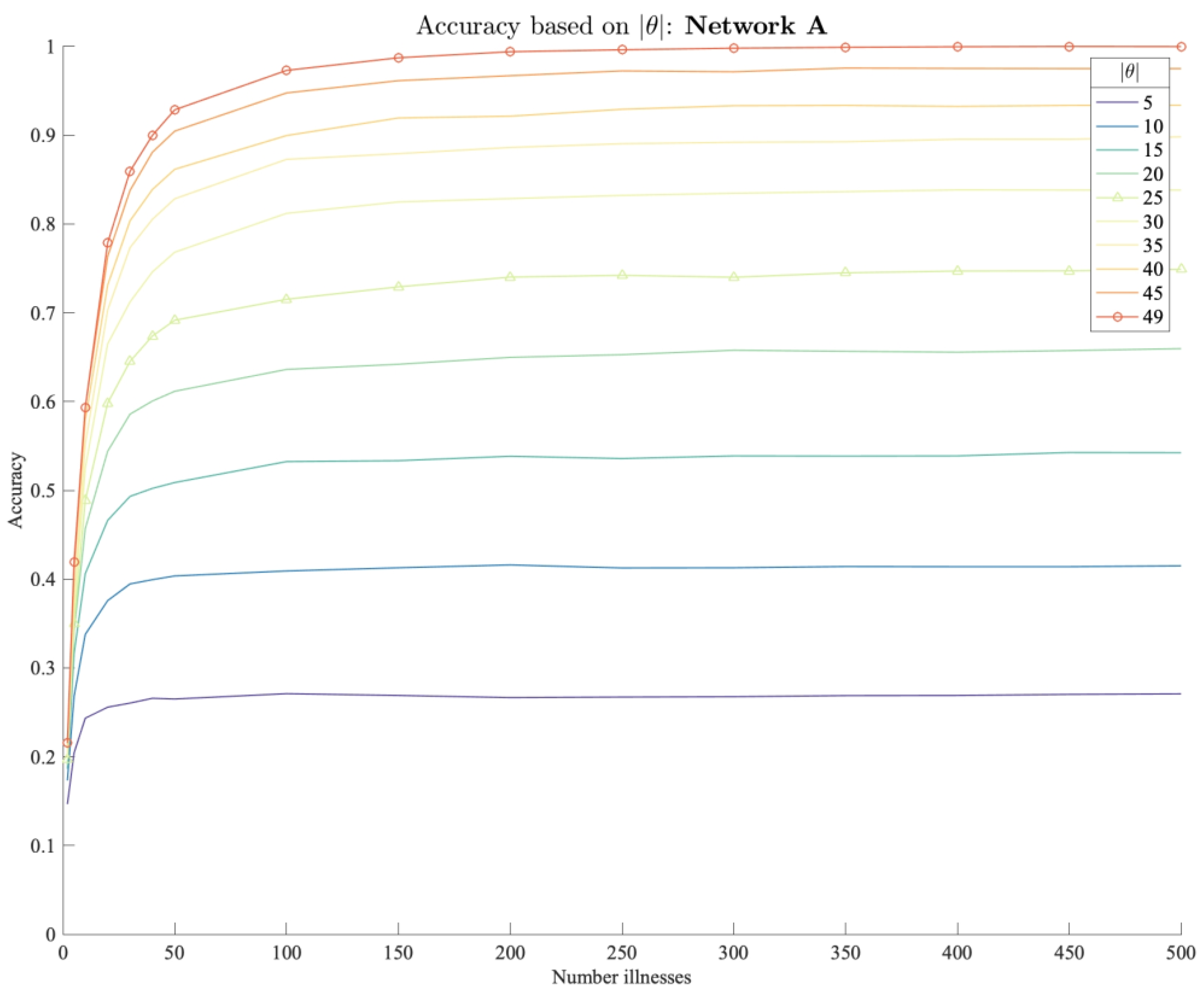
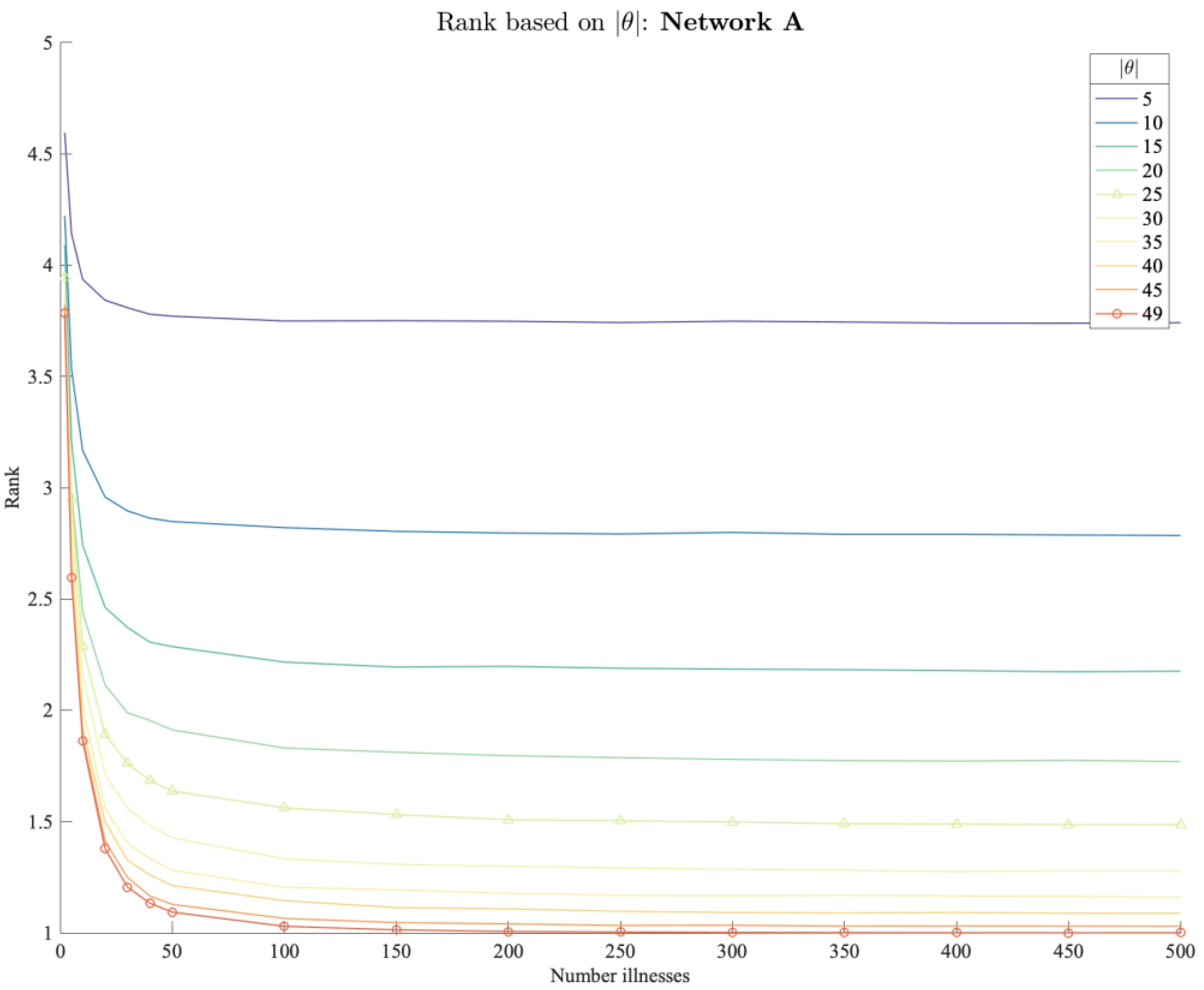
3.2.3. Modeling Results
3.2.4. Interpretation of Results
4. Conclusions
Author Contributions
Funding

Acknowledgments
Conflicts of Interest
References
- World Health Organisation. WHO Estimates of the Global Burden of Foodborne Diseases; World Health Organization: Geneva, Switzerland, 2015. [Google Scholar]
- Scallan, E.; Hoekstra, R.M.; Angulo, F.J.; Tauxe, R.V.; Widdowson, M.-A.; Roy, S.L.; Jones, J.L.; Griffin, P.M. Foodborne Illness Acquired in the United States—Major Pathogens. Emerg. Infect. Dis. 2011, 17, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Ärztezeitung. RKI Meldet Dritten Listerien-Todesfall. Available online: https://www.aerztezeitung.de/Medizin/RKI-meldet-dritten-Listerien-Todesfall-402360.html (accessed on 1 December 2019).
- Robert Koch Institut. RKI-Archiv 2019—Listeriose-Ausbruch mit Listeria Monocytogenes Sequenz-Cluster-Typ 2521 (Sigma1) in Deutschland. Available online: https://www.rki.de/DE/Content/Infekt/EpidBull/Archiv/2019/41/Art_02.html (accessed on 1 December 2019).
- Tinga, C.; TODD, E.; Cassidy, M.; Pollari, F.; Marshall, B.; Greig, J.; Campbell, G.; Ravel, A. Exploring Historical Canadian Foodborne Outbreak Data Sets for Human Illness Attribution. J. Food Prot. 2016, 72, 1963–1976. [Google Scholar] [CrossRef]
- National Center for Emerging; Zoonotic Infectious Diseases; Division of Foodborne, Waterborne; Environmental Diseases. Surveillance for Foodborne Disease Outbreaks United States, 2017. Annual Report; 2017. Available online: https://www.cdc.gov/fdoss/pdf/2016_FoodBorneOutbreaks_508.pdf (accessed on 7 January 2020).
- Marvin, H.J.P.; Janssen, E.M.; Bouzembrak, Y.; Hendriksen, P.J.M.; Staats, M. Big Data in Food Safety: An Overview. Crit. Rev. Food Sci. Nutr. 2017, 57, 2286–2295. [Google Scholar] [CrossRef] [PubMed]
- Horn, A.L.; Friedrich, H. Locating the Source of Large-Scale Diffusion of Foodborne Contamination. J. R. Soc. Interface 2019, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Manitz, J.; Kneib, T.; Schlather, M.; Helbing, D.; Brockmann, D. Origin Detection During Food-Borne Disease Outbreaks—A Case Study of the 2011 EHEC/HUS Outbreak in Germany. PLoS Curr. 2014. [Google Scholar] [CrossRef] [PubMed]
- Kaufman, J.; Lessler, J.; Harry, A.; Edlund, S.; Hu, K.; Douglas, J.; Thoens, C.; Appel, B.; Käsbohrer, A.; Filter, M. A Likelihood-Based Approach to Identifying Contaminated Food Products Using Sales Data: Performance and Challenges. PLoS Comput. Biol. 2014, 10, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Norström, M.; Kristoffersen, A.B.; Görlach, F.S.; Nygård, K.; Hopp, P. An Adjusted Likelihood Ratio Approach Analysing Distribution of Food Products to Assist the Investigation of Foodborne Outbreaks. PLoS ONE 2015, 10, 1–13. [Google Scholar] [CrossRef]
- Hu, K.; Renly, S.; Edlund, S.; Davis, M.; Kaufman, J. A Modeling Framework to Accelerate Food-Borne Outbreak Investigations. Food Control 2016, 59, 53–58. [Google Scholar] [CrossRef]
- Infas. Mobilität in Deutschland—Ergebnisbericht; Infas: Brrlin, Germany, 2017. [Google Scholar]
- Veenstra, S.A.; Thomas, T.; Tutert, S.I.A. Trip Distribution for Limited Destinations: A Case Study for Grocery Shopping Trips in the Netherlands. Transportation (Amst.) 2010, 37, 663–676. [Google Scholar] [CrossRef][Green Version]
- Jonker, N.J.; Venter, C.J. Modeling Trip-Length Distribution of Shopping Center Trips from GPS Data. J. Transp. Eng. Part A Syst. 2019, 145, 04018079. [Google Scholar] [CrossRef]
- McFadden, D. Disaggregate Behavioral Travel Demand’s RUM Side A 30-Year Retrospective; University of Sydney: Sydney, Australia, 2000. [Google Scholar]
- Suhara, Y.; Bahrami, M.; Bozkaya, B.; Pentland, A. Validating Gravity-Based Market Share Models Using Large-Scale Transactional Data; MIT Media Lab: Cambridge, MA, USA, 2019. [Google Scholar]
- Cascetta, E.; Pagliara, F.; Papola, A. Alternative Approaches to Trip Distribution Modelling: A Retrospective Review and Suggestions for Combining Different Approaches. Pap. Reg. Sci. 2007, 86, 597–620. [Google Scholar] [CrossRef]
- Drezner, T. Derived Attractiveness of Shopping Malls. IMA J. Manag. Math. 2006, 17, 349–358. [Google Scholar] [CrossRef]
- Hyman, G.M. The Calibration of Trip Distribution Models. Environ. Plan. 1969, 1, 105–112. [Google Scholar] [CrossRef]
- Furness, K.P. Time Function Iteration. Traffic Eng. Control 1965, 7, 458–460. [Google Scholar]
- Huff, D.L. A Probabilistic Analysis of Shopping Center Trade Areas. Land Econ. 1963, 39, 81. [Google Scholar] [CrossRef]
- Nakanishi, M.; Cooper, L. Parameter Estimation for a Multiplicative Competitive Interaction Model—Least Squares Approach. J. Mark. Res. 1974, 11, 303–311. [Google Scholar] [CrossRef]
- Bawa, K.; Ghosh, A. A Model of Household Grocery Shopping Behavior; Springer: Berlin, Germany, 1999; Volume 10. [Google Scholar]
- De Beule, M.; Van den Poel, D.; Van de Weghe, N. An Extended Huff-Model for Robustly Benchmarking and Predicting Retail Network Performance. Appl. Geogr. 2014, 46, 80–89. [Google Scholar] [CrossRef]
- Baviera-Puig, A.; Buitrago-Vera, J.; Escriba-Perez, C. Geomarketing Strategies in Supermarkt Location Strategies. J. Bus. Econ. Manag. 2016, 17, 1205–1221. [Google Scholar] [CrossRef]
- Suel, E.; Polak, J.W. Development of Joint Models for Channel, Store, and Travel Mode Choice: Grocery Shopping in London. Transp. Res. Part A Policy Pract. 2017, 99, 147–162. [Google Scholar] [CrossRef]
- Wilson, A.G. The Use of the Concept of Entropy in System Modelling. Oper. Res. Q. 1970, 21, 247–265. [Google Scholar] [CrossRef]
- Schlaich, T.; Friedrich, H.; Horn, A. A Gravity-Based Approach to Connect Food Retailers with Consumers for Traceback Models of Food-Borne Diseases. In Complex Networks and Their Applications VIII.; Cherifi, H., Gaito, S., Mendes, J.F., Moro, E., Rocha, R.L., Eds.; Springer: Berlin, Germany, 2020; pp. 363–375. [Google Scholar] [CrossRef]
- De Ortúzar, J.D.; Willumsen, L.G. Modelling Transport; John Wiley & Sons, Ltd.: Chichester, UK, 2011. [Google Scholar] [CrossRef]
- Open Street Map. OpenStreetMap Deutschland: Die freie Wiki-Weltkarte. Available online: https://www.openstreetmap.de/ (accessed on 9 April 2019).
- Statistische Ämter des Bundes und der Länder. ZENSUS2011—Homepage. Available online: https://www.zensus2011.de/EN/Home/home_node.html;jsessionid=8A55DF20B6CB474A1DB6DEFDD94B4949.1_cid389 (accessed on 9 April 2019).
- Mekky, A. A Direct Method for Speeding up the Convergence of the Furness Biproportional Method. Transp. Res. Part B 1983, 17B, 1–11. [Google Scholar] [CrossRef]
- Chang, K.-T.; Khatib, Z.; Ou, Y. Effects of Zoning Structure and Network Detail on Traffic Demand Modeling. Environ. Plan. B Plan. Des. 2002, 29, 37–52. [Google Scholar] [CrossRef]
- Kordi, M.; Kaiser, C.; Fotheringham, A.S. A Possible Solution for the Centroid-to-Centroid and Intra-Zonal Trip Length Problems. In Multidisciplinary Research on Geographical Information in Europe and Beyond; Gense, J., Josselin, D., Vandenbroucke, D., Eds.; Centre for GeoInformatics (CGI): Avignon, France, 2012; pp. 147–152. [Google Scholar]
- Bhatta, B.P.; Larsen, O.I. Are Intrazonal Trips Ignorable? Transp. Policy 2010, 18, 13–22. [Google Scholar] [CrossRef]
- Manout, O.; Bonnel, P. The Impact of Ignoring Intrazonal Trips in Assignment Models: A Stochastic Approach. Transportation (Amst.) 2018, 46, 1–21. [Google Scholar] [CrossRef]
- Zhu, J.; Ye, X. Development of Destination Choice Model with Pairwise District-Level Constants Using Taxi GPS Data. Transp. Res. Part C Emerg. Technol. 2018, 93, 410–424. [Google Scholar] [CrossRef]
- US Bureau of Public Roads. Calibrating and Treating a Gravity Model for Any Size Urban Area; US Bureau of Public Roads: Washington, DC, USA, 1965. [Google Scholar]
- CZuber, E. Geometrische Wahrscheinlichkeiten Und Mittelwerte; T.B. Teubner: Leipzig, Germany, 1884. [Google Scholar]
- Balster, A.; Friedrich, H. Dynamic Freight Flow Modelling for Risk Evaluation in Food Supply. Transp. Res. Part E Logist. Transp. Rev. 2019, 121, 4–22. [Google Scholar] [CrossRef]
- Friedrich, H. Simulation of Logistics in Food Retailing for Freight Transportation Analysis; Karlsruher Institut für Technologie: Karlsruhe, Germany, 2010. [Google Scholar]
- Larson, R.; Odoni, A. Chapter 3.8.3: Application to Facility Location and Districting. In Urban Operations Research; Prentice Hall: New Jersey, NJ, USA, 1981. [Google Scholar]
- Lebensmittel Zeitung. Ranking: Top 30 Lebensmittelhandel Deutschland 2018. Available online: https://www.lebensmittelzeitung.net/handel/Ranking-Top-30-Lebensmittelhandel-Deutschland-2018-134606 (accessed on 6 May 2019).
- REWE Group. REWE Markttypen. Available online: https://www.rewe-group.com/de/unternehmen/vertriebslinien/rewe (accessed on 1 July 2019).
- Edeka. EDEKA Markttypen. Available online: https://verbund.edeka/südbayern/über-uns/märkte-vertrieb/markttypen/ (accessed on 1 July 2019).
- Infas. Mobilität in Deutschland—Wissenschaftlicher Hintergrund. Available online: http://www.mobilitaet-in-deutschland.de/ (accessed on 10 April 2019).
- KNIME. KNIME Analytics Platform|KNIME. Available online: https://www.knime.com/knime-software/knime-analytics-platform (accessed on 14 June 2019).
- Infectious Intestinal Disease Study Team. A Report of the Study of Infectious Intestinal Disease in England; Infectious Intestinal Disease Study Team: London, UK, 2000. [Google Scholar]
- World Health Organization. Foodborne Disease Outbreaks: Guidelines for Investigation and Control WHO Library Cataloguing-in-Publication Data; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Statista. Marktanteil von Eigenmarken in Deutschland bis 2018|Statista. Available online: https://de.statista.com/statistik/daten/studie/184142/umfrage/umsatzanteil-von-handelsmarken-im-deutschen-einzelhandel/ (accessed on 17 December 2019).
- Baratloo, A.; Hosseini, M.; Negida, A.; El Ashal, G. Part 1: Simple Definition and Calculation of Accuracy, Sensitivity and Specificity. Emergency (Tehran, Iran) 2015, 3, 48–49. [Google Scholar] [CrossRef]
- Rhone, A.; Ploeg, M.V.; Dicken, C.; Williams, R.; Breneman, V. Low-Income and Low-Supermarket-Access Census Tracts, 2010-2015; Economic Research Service: Washington, DC, USA, 2017. [Google Scholar]


| Parameter | Flow Threshold | ||
|---|---|---|---|
| >0% | >5% | >10% | |
| Number of supplied consumer zones | 49 | 5.3 | 2.6 |
| Proportion of intra-zonal flows | 28.5% | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schlaich, T.; Horn, A.L.; Fuhrmann, M.; Friedrich, H. A Gravity-Based Food Flow Model to Identify the Source of Foodborne Disease Outbreaks. Int. J. Environ. Res. Public Health 2020, 17, 444. https://doi.org/10.3390/ijerph17020444
Schlaich T, Horn AL, Fuhrmann M, Friedrich H. A Gravity-Based Food Flow Model to Identify the Source of Foodborne Disease Outbreaks. International Journal of Environmental Research and Public Health. 2020; 17(2):444. https://doi.org/10.3390/ijerph17020444
Chicago/Turabian StyleSchlaich, Tim, Abigail L. Horn, Marcel Fuhrmann, and Hanno Friedrich. 2020. "A Gravity-Based Food Flow Model to Identify the Source of Foodborne Disease Outbreaks" International Journal of Environmental Research and Public Health 17, no. 2: 444. https://doi.org/10.3390/ijerph17020444
APA StyleSchlaich, T., Horn, A. L., Fuhrmann, M., & Friedrich, H. (2020). A Gravity-Based Food Flow Model to Identify the Source of Foodborne Disease Outbreaks. International Journal of Environmental Research and Public Health, 17(2), 444. https://doi.org/10.3390/ijerph17020444





