Implications of Projected Hydroclimatic Change for Tularemia Outbreaks in High-Risk Areas across Sweden
Abstract
1. Introduction
2. Methods
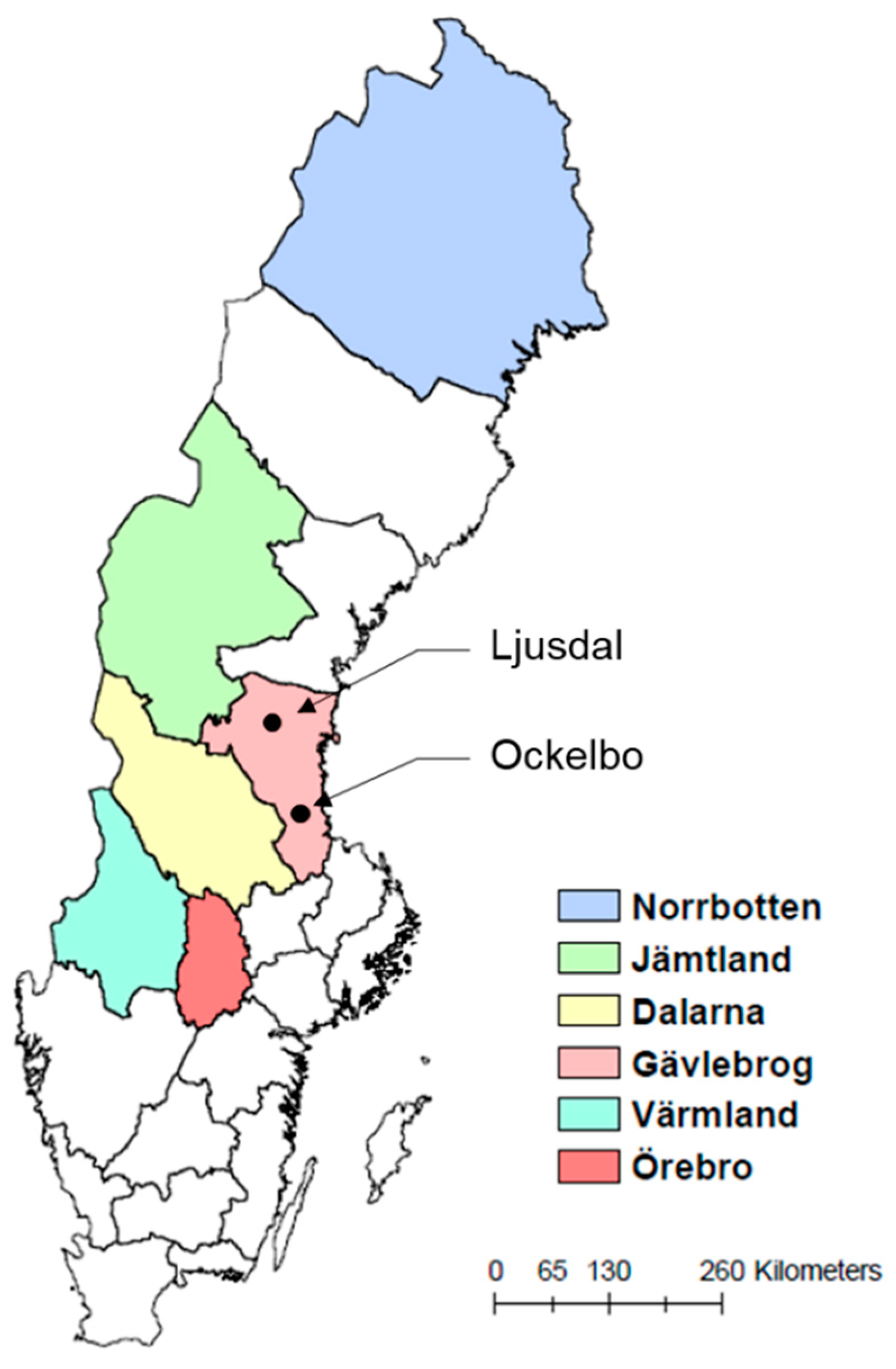
2.1. Six High-Risk Counties with Established Statistical Models of Tularemia
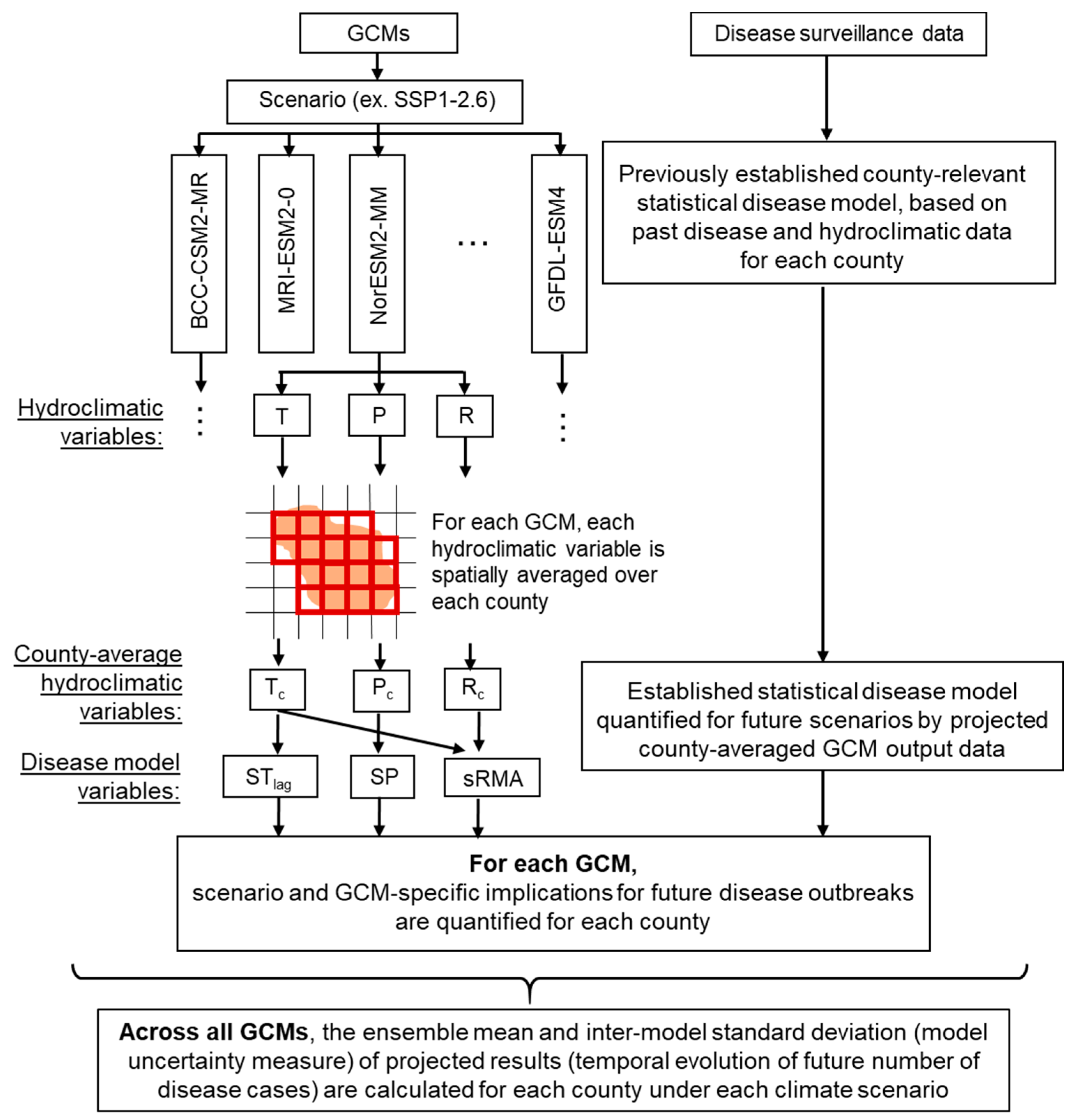
2.2. Climate Change Scenario Data, Human Tularemia Data, and Projection of Annual Cases
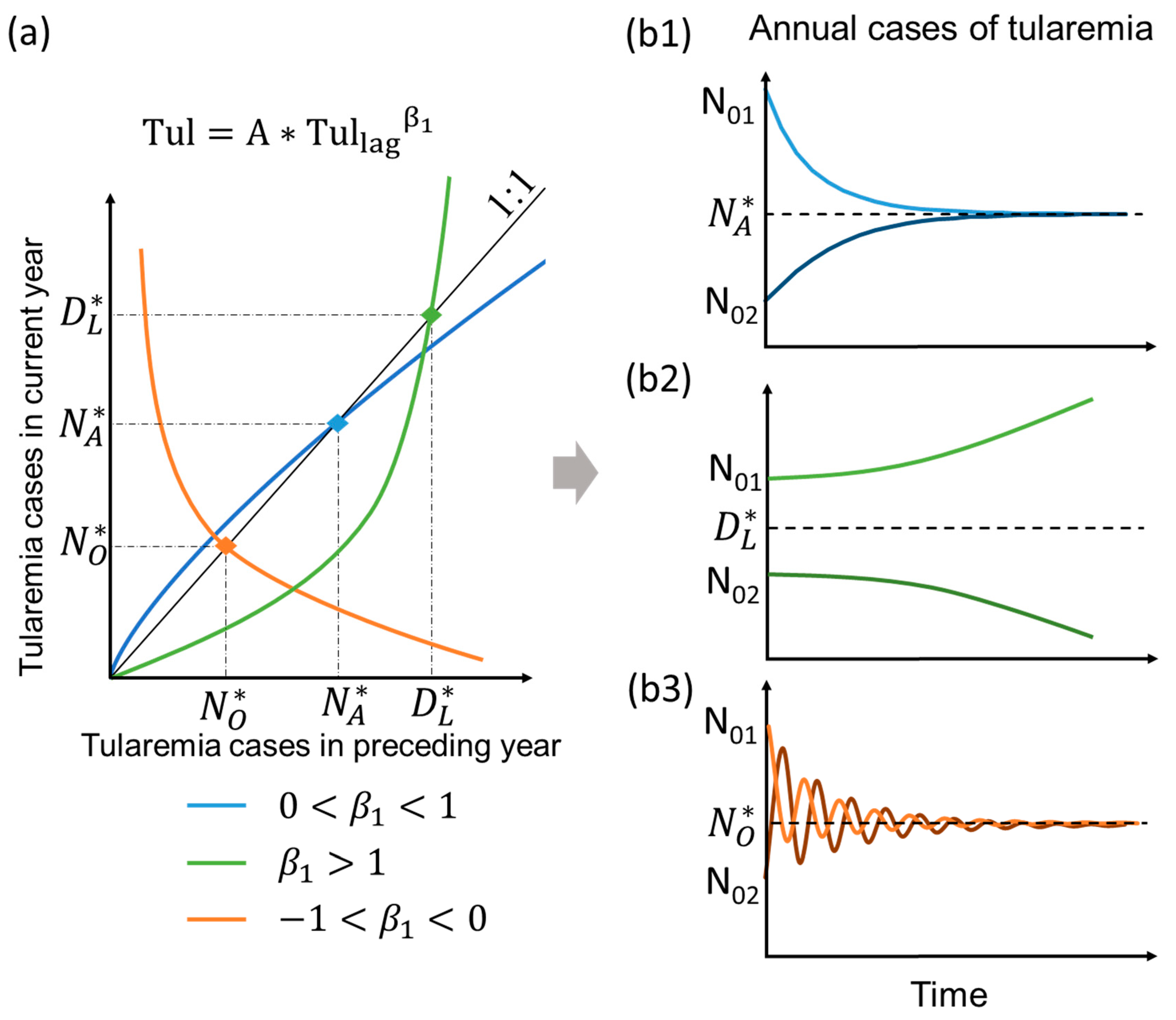
2.3. Typology of Model Behavior Under Mean Climate State in the Long-Term
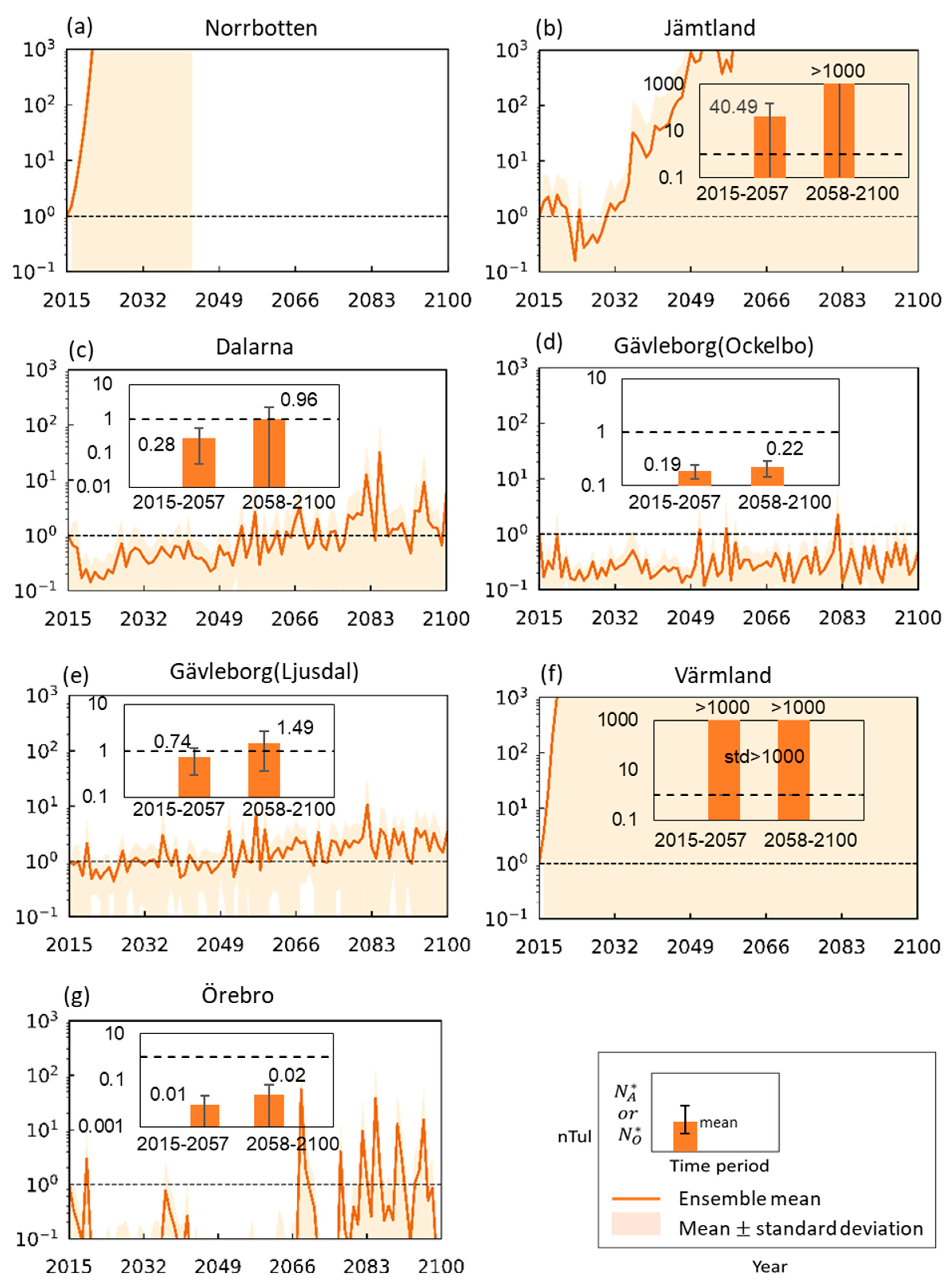
3. Results
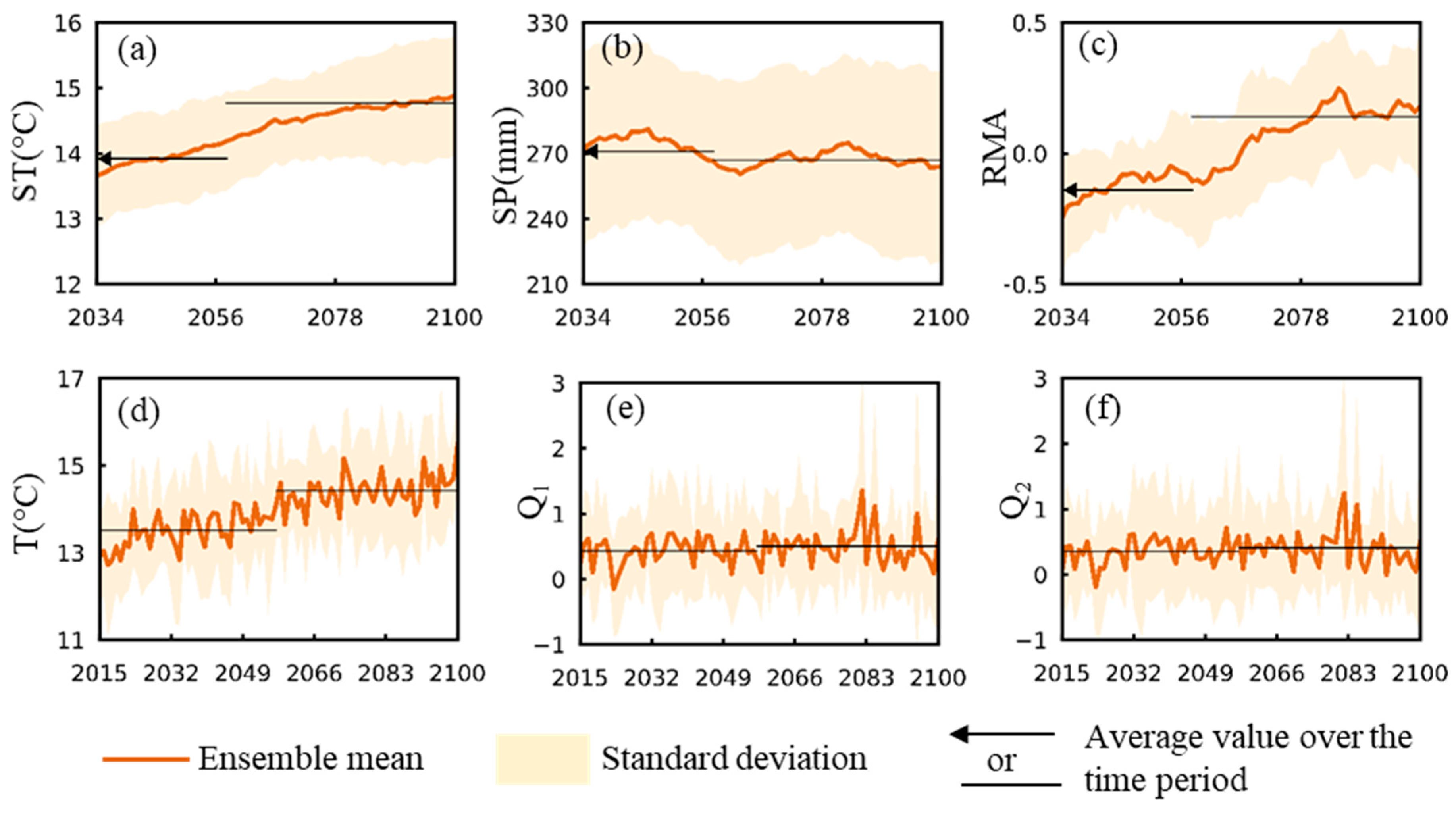
3.1. Change Trends for Hydroclimatic and Related Mosquito Abundance Variables
3.2. Tularemia Change Trends Under Projected Future Hydroclimatic Conditions
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Baker-Austin, C.; Trinanes, J.A.; Taylor, N.G.H.; Hartnell, R.; Siitonen, A.; Martinez-Urtaza, J. Emerging Vibrio risk at high latitudes in response to ocean warming. Nat. Clim. Chang. 2013, 3, 73–77. [Google Scholar] [CrossRef]
- Burge, C.A.; Mark Eakin, C.; Friedman, C.S.; Froelich, B.; Hershberger, P.K.; Hofmann, E.E.; Petes, L.E.; Prager, K.C.; Weil, E.; Willis, B.L.; et al. Climate change influences on marine infectious diseases: Implications for management and society. Ann. Rev. Mar. Sci. 2014, 6, 249–277. [Google Scholar] [CrossRef]
- Garrett, K.A.; Dobson, A.D.M.; Kroschel, J.; Natarajan, B.; Orlandini, S.; Tonnang, H.E.Z.; Valdivia, C. The effects of climate variability and the color of weather time series on agricultural diseases and pests, and on decisions for their management. Agric. For. Meteorol. 2013, 170, 216–227. [Google Scholar] [CrossRef]
- Harvell, D.; Altizer, S.; Cattadori, I.M.; Harrington, L.; Weil, E. Climate change and wildlife diseases: When does the host matter the most? Ecology 2009, 90, 912–920. [Google Scholar]
- Rodó, X.; Pascual, M.; Doblas-Reyes, F.J.; Gershunov, A.; Stone, D.A.; Giorgi, F.; Hudson, P.J.; Kinter, J.; Rodríguez-Arias, M.-À.; Stenseth, N.C.; et al. Climate change and infectious diseases: Can we meet the needs for better prediction? Clim. Chang. 2013, 118, 625–640. [Google Scholar] [CrossRef]
- Ma, Y.; Bring, A.; Kalantari, Z.; Destouni, G. Potential for Hydroclimatically Driven Shifts in Infectious Disease Outbreaks: The Case of Tularemia in High-Latitude Regions. Int. J. Environ. Res. Public Health. 2019, 16, 3717. [Google Scholar] [CrossRef]
- Waits, A.; Emelyanova, A.; Oksanen, A.; Abass, K.; Rautio, A. Human infectious diseases and the changing climate in the Arctic. Environ. Int. 2018, 121, 703–713. [Google Scholar] [CrossRef]
- Malkhazova, S.; Mironova, V.; Shartova, N.; Orlov, D. Mapping Russia’s Natural Focal Diseases: History and Contemporary Approaches; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Petersen, J.M.; Mead, P.S.; Schriefer, M.E. Francisella tularensis: An arthropod-borne pathogen. Vet. Res. 2009, 40, 1. [Google Scholar] [CrossRef]
- Rydén, P.; Sjöstedt, A.; Johansson, A. Effects of climate change on tularaemia disease activity in Sweden. Glob. Health Action 2009, 2, 2063. [Google Scholar] [CrossRef]
- Hestvik, G.; Warns-Petit, E.; Smith, L.A.; Fox, N.J.; Uhlhorn, H.; Artois, M.; Hannant, D.; Hutchings, M.R.; Mattsson, R.; Yon, L.; et al. The status of tularemia in Europe in a one-health context: A review. Epidemiol. Infect. 2015, 143, 2137–2160. [Google Scholar] [CrossRef]
- Desvars, A.; Furberg, M.; Hjertqvist, M.; Vidman, L.; Sjöstedt, A.; Rydén, P.; Johansson, A. Epidemiology and Ecology of Tularemia in Sweden, 1984–2012. Emerg. Infect. Dis. 2015, 21, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Balci, E.; Borlu, A.; Kilic, A.U.; Demiraslan, H.; Oksuzkaya, A.; Doganay, M. Tularemia outbreaks in Kayseri, Turkey: An evaluation of the effect of climate change and climate variability on tularemia outbreaks. J. Infect. Public Health 2014, 7, 125–132. [Google Scholar] [CrossRef]
- Desvars-Larrive, A.; Liu, X.; Hjertqvist, M.; Sjöstedt, A.; Johansson, A.; Rydén, P. High-risk regions and outbreak modelling of tularemia in humans. Epidemiol. Infect. 2017, 145, 482–490. [Google Scholar] [CrossRef]
- Nakazawa, Y.; Williams, R.; Peterson, A.T.; Mead, P.; Staples, E.; Gage, K.L. Climate Change Effects on Plague and Tularemia in the United States. Vector Borne Zoonotic Dis. 2007, 7, 529–540. [Google Scholar] [CrossRef]
- Palo, T.R.; Ahlm, C.; Tärnvik, A. Climate variability reveals complex events for tularaemia dynamics in man and mammals. Ecol. Soc. 2005, 10, 1. [Google Scholar] [CrossRef]
- Rydén, P.; Björk, R.; Schäfer, M.L.; Lundström, J.O.; Petersén, B.; Lindblom, A.; Forsman, M.; Sjöstedt, A.; Johansson, A. Outbreaks of Tularemia in a Boreal Forest Region Depends on Mosquito Prevalence. J. Infect. Dis. 2012, 205, 297–304. [Google Scholar] [CrossRef] [PubMed]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model. Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Lafferty, K.D. The ecology of climate change and infectious diseases. Ecology 2009, 90, 888–900. [Google Scholar] [CrossRef]
- Eisen, R.J.; Mead, P.S.; Meyer, A.M.; Pfaff, L.E.; Bradley, K.K.; Eisen, L. Ecoepidemiology of Tularemia in the Southcentral United States. Am. J. Trop. Med. Hyg. 2008, 78, 586–594. [Google Scholar] [CrossRef]
- Eliasson, H.; Lindbäck, J.; Nuorti, J.P.; Arneborn, M.; Giesecke, J.; Tegnell, A. The 2000 Tularemia Outbreak: A Case-Control Study of Risk Factors in Disease-Endemic and Emergent Areas, Sweden. Emerg. Infect. Dis. 2002, 8, 956–960. [Google Scholar] [CrossRef]
- Keim, P.; Johansson, A.; Wagner, D.M. Molecular Epidemiology, Evolution, and Ecology of Francisella. Ann. N. Y. Acad. Sci. 2007, 1105, 30–66. [Google Scholar] [CrossRef]
- Gidden, M.J.; Riahi, K.; Smith, S.J.; Fujimori, S.; Luderer, G.; Kriegler, E.; van Vuuren, D.P.; van den Berg, M.; Feng, L.; Klein, D.; et al. Global emissions pathways under different socioeconomic scenarios for use in CMIP6: A dataset of harmonized emissions trajectories through the end of the century. Geosci. Model Dev. 2019, 12, 1443–1475. [Google Scholar] [CrossRef]
- CLINF Project—Climate Change Effects on the Epidemiology of Infectious Diseases and the Impacts on Northern Societies, 2020. The CLINF Data Repository, WP3: Depicting the Geographic Spread of Climate-Sensitive Infections in the Nordic Region. Available online: https://clinf.org (accessed on 25 January 2019).
- Hales, S.; de Wet, N.; Maindonald, J.; Woodward, A. Potential effect of population and climate changes on global distribution of dengue fever: An empirical model. Lancet 2002, 360, 830–834. [Google Scholar] [CrossRef]
- Rogers, D.J.; Randolph, S.E. The Global Spread of Malaria in a Future, Warmer World. Science 2000, 289, 1763–1766. [Google Scholar] [CrossRef]
- Reiter, P. Climate change and mosquito-borne disease. Environ. Health Perspect. 2001, 109, 141–161. [Google Scholar] [CrossRef]
- Rohr, J.R.; Dobson, A.P.; Johnson, P.T.J.; Kilpatrick, A.M.; Paull, S.H.; Raffel, T.R.; Ruiz-Moreno, D.; Thomas, M.B. Frontiers in climate change–disease research. Trends Ecol. Evol. 2011, 26, 270–277. [Google Scholar] [CrossRef]
- Bring, A.; Goldenberg, R.; Kalantari, Z.; Prieto, C.; Ma, Y.; Jarsjö, J.; Destouni, G. Contrasting Hydroclimatic Model-Data Agreements Over the Nordic-Arctic Region. Earth’s Future 2019, 7, 1270–1282. [Google Scholar] [CrossRef]
| High-Risk County | |||||
|---|---|---|---|---|---|
| Norrbotten | −5.73 | 1.16 | 0.20 | 0.35 | 0.005 |
| Jämtland | −11.47 | 0.93 | 0.75 | 0.84 | 0.003 |
| Gävleborg (Ockelbo) | −2.86 | −0.19 | 0.36 | 0.10 | 0.010 |
| Gävleborg (Ljusdal) | −7.60 | 0.09 | 0.29 | 0.50 | 0.009 |
| Dalarna | −10.74 | 0.37 | 0.43 | 0.67 | 0.008 |
| Värmland | 10.11 | 0.99 | 0.82 | −0.39 | −0.014 |
| Örebro | −9.19 | 0.73 | 0.75 | 0.18 | 0.023 |
| Model | SSP1-2.6 | SSP2-4.5 | SSP5-8.5 |
|---|---|---|---|
| BCC-CSM2-MR | X | X | X |
| MRI-ESM2-0 | X | X | X |
| NorESM2-MM | X | X | X |
| EC-Earth3 | X | X | X |
| * INM-CM5-0 | X | X | X |
| * INM-CM4-8 | X | X | X |
| MPI-ESM1-2-HR | X | X | X |
| GFDL-ESM4 | X | X | X |
| GFDL-CM4 | X | X |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Y.; Vigouroux, G.; Kalantari, Z.; Goldenberg, R.; Destouni, G. Implications of Projected Hydroclimatic Change for Tularemia Outbreaks in High-Risk Areas across Sweden. Int. J. Environ. Res. Public Health 2020, 17, 6786. https://doi.org/10.3390/ijerph17186786
Ma Y, Vigouroux G, Kalantari Z, Goldenberg R, Destouni G. Implications of Projected Hydroclimatic Change for Tularemia Outbreaks in High-Risk Areas across Sweden. International Journal of Environmental Research and Public Health. 2020; 17(18):6786. https://doi.org/10.3390/ijerph17186786
Chicago/Turabian StyleMa, Yan, Guillaume Vigouroux, Zahra Kalantari, Romain Goldenberg, and Georgia Destouni. 2020. "Implications of Projected Hydroclimatic Change for Tularemia Outbreaks in High-Risk Areas across Sweden" International Journal of Environmental Research and Public Health 17, no. 18: 6786. https://doi.org/10.3390/ijerph17186786
APA StyleMa, Y., Vigouroux, G., Kalantari, Z., Goldenberg, R., & Destouni, G. (2020). Implications of Projected Hydroclimatic Change for Tularemia Outbreaks in High-Risk Areas across Sweden. International Journal of Environmental Research and Public Health, 17(18), 6786. https://doi.org/10.3390/ijerph17186786







