Decisive Factors for a Greater Performance in the Change of Direction and Its Angulation in Male Basketball Players
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Procedure
2.3. Anthropometric Measurements
2.4. Weight-Bearing Dorsiflexion Test (WB-DF)
2.5. Star Excursion Balance Test (SEBT) and Y Balance Test (YBT)
2.6. The 30-M Sprint Test (30S)
2.7. Triple Hop Test for Distance Unilateral (THTU)
2.8. Countermovement Jump (CMJ) Test
2.9. Drop Jump Unilateral (DJU) Test
2.10. Vertical Force–Velocity Profile
2.11. Change of Direction (COD)
2.12. Statistical Analysis
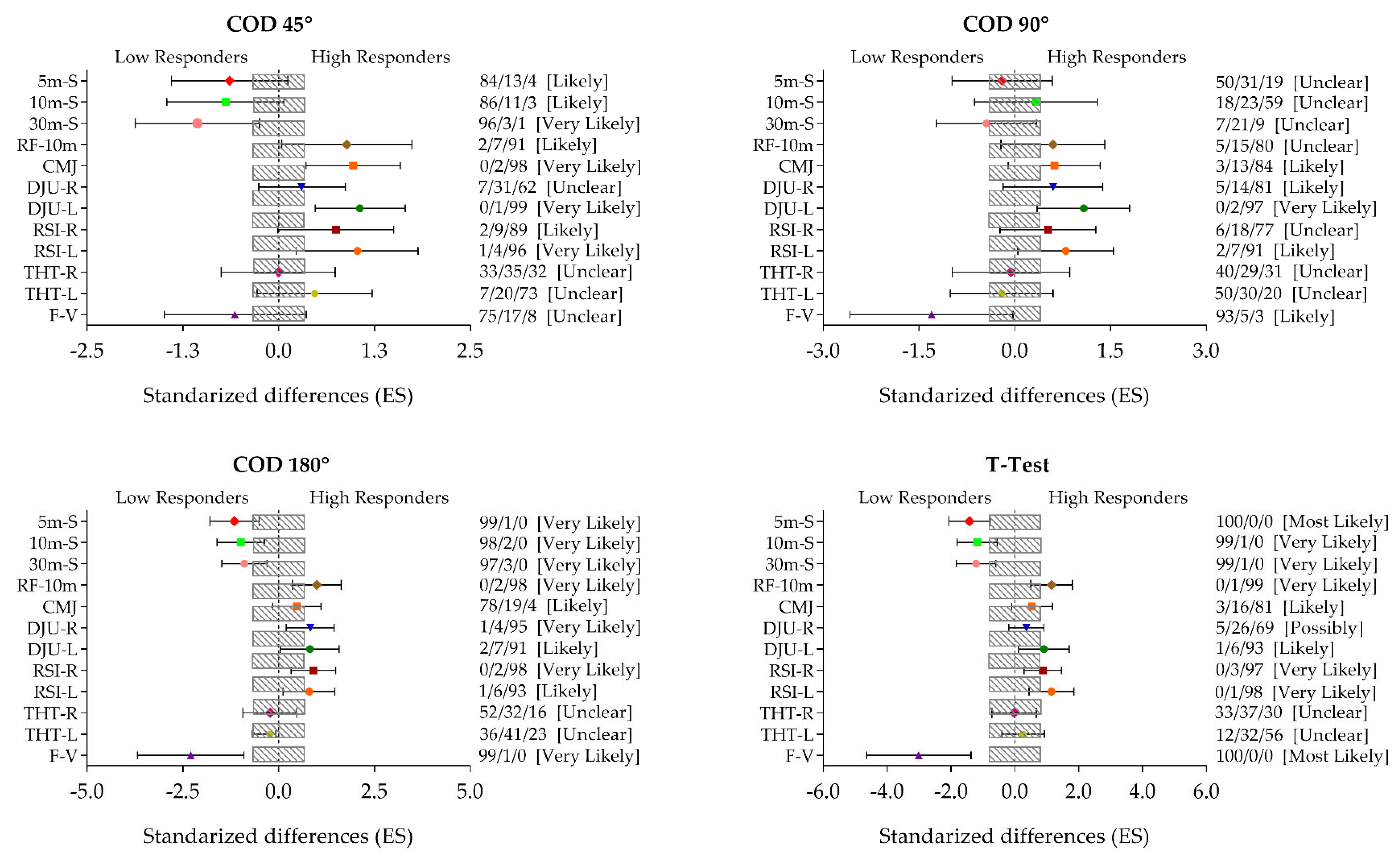
3. Results
4. Discussion
4.1. Influence of Age Category on Sport Performance-Related Variables
4.2. Influence of Sport Performance-Related Variables on the Time Execution COD and Angles
5. Conclusions
6. Practical Application
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Abdelkrim, N.B.; Chaouachi, A.; Chamari, K.; Chtara, M.; Castagna, C. Positional role and competitive-level differences in elite-level men’s basketball players. J. Strength Cond. Res. 2010, 24, 1346–1355. [Google Scholar] [CrossRef] [PubMed]
- Abdelkrim, N.B.; El Fazaa, S.; El Ati, J. Time-motion analysis and physiological data of elite under-19-year-old basketball players during competition. Br. J. Sports Med. 2007, 41, 69–75. [Google Scholar] [CrossRef] [PubMed]
- Conte, D.; Favero, T.G.; Lupo, C.; Francioni, F.M.; Capranica, L.; Tessitore, A. Time-Motion Analysis of Italian Elite Womenʼs Basketball Games. J. Strength Cond. Res. 2015, 29, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, J.; Young, W. Agility literature review: Classifications, training and testing. J. Sports Sci. 2006, 24, 919–932. [Google Scholar] [CrossRef] [PubMed]
- Paul, D.J.; Gabbett, T.J.; Nassis, G.P. Agility in Team Sports: Testing, Training and Factors Affecting Performance. Sport. Med. 2016, 46, 421–442. [Google Scholar] [CrossRef]
- Young, W.B.; Dawson, B.; Henry, G.J. Agility and Change-of-Direction Speed are Independent Skills: Implications for Training for Agility in Invasion Sports. Int. J. Sports Sci. Coach. 2015, 10, 159–169. [Google Scholar] [CrossRef]
- Brughelli, M.; Cronin, J.; Levin, G.; Chaouachi, A. Understanding change of direction ability in sport: A review of resistance training studies. Sport. Med. 2008, 38, 1045–1063. [Google Scholar] [CrossRef]
- Hojka, V.; Stastny, P.; Rehak, T.; Gołas, A.; Mostowik, A.; Zawart, M.; Musálek, M. A systematic review of the main factors that determine agility in sport using structural equation modeling. J. Hum. Kinet. 2016, 52, 115–123. [Google Scholar] [CrossRef]
- Lockie, R.G.; Callaghan, S.J.; Berry, S.P.; Cooke, E.R.A.; Jordan, C.A.; Luczo, T.M.; Jeffriess, M.D. Relationship between unilateral jumping ability and asymmetry on multidirectional speed in team-sport athletes. J. Strength Cond. Res. 2014, 28, 3557–3566. [Google Scholar] [CrossRef]
- Sekulic, D.; Pehar, M.; Krolo, A.; Spasic, M.; Uljevic, O.; Calleja-González, J.; Sattler, T. Evaluation of basketball-specific agility: Applicability of preplanned and nonplanned agility performances for differentiating playing positions and playing levels. J. Strength Cond. Res. 2017, 31, 2278–2288. [Google Scholar] [CrossRef]
- Young, W.B.; McDowell, M.H.; Scarlett, B.J. Specificity of Sprint and Agility Training Methods. J. Strength Cond. Res. 2001, 15, 315–319. [Google Scholar] [CrossRef] [PubMed]
- Zamparo, P.; Zadro, I.; Lazzer, S.; Beato, M.; Sepulcri, L. Energetics of shuttle runs: The effects of distance and change of direction. Int. J. Sports Physiol. Perform. 2014, 9, 1033–1039. [Google Scholar] [CrossRef] [PubMed]
- Zagatto, A.M.; Ardigò, L.P.; Barbieri, F.A.; Milioni, F.; Dello Iacono, A.; Camargo, B.H.F.; Padulo, J. Performance and Metabolic Demand of a New Repeated-Sprint Ability Test in Basketball Players: Does the Number of Changes of Direction Matter? J. Strength Cond. Res. 2017, 31, 2438–2446. [Google Scholar] [CrossRef] [PubMed]
- DosʼSantos, T.; Thomas, C.; Jones, P.A.; Comfort, P. Mechanical Determinants of Faster Change of Direction Speed Performance in Male Athletes. J. Strength Cond. Res. 2017, 31, 696–705. [Google Scholar] [CrossRef] [PubMed]
- Castillo-Rodríguez, A.; Fernández-García, J.C.; Chinchilla-Minguet, J.L.; Carnero, E.Á. Relationship Between Muscular Strength and Sprints with Changes of Direction. J. Strength Cond. Res. 2012, 26, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Salaj, S.; Markovic, G. Specificity of jumping, sprinting, and quick change-of-direction motor abilities. J. Strength Cond. Res. 2011, 25, 1249–1255. [Google Scholar] [CrossRef]
- Barnes, J.L.; Schilling, B.K.; Falvo, M.J.; Weiss, L.W.; Creasy, A.K.; Fry, A.C. Relationship of jumping and agility performance in female volleyball athletes. J. Strength Cond. Res. 2007, 21, 1192–1196. [Google Scholar] [CrossRef]
- Spiteri, T.; Nimphius, S.; Hart, N.H.; Specos, C.; Sheppard, J.M.; Newton, R.U. Contribution of Strength Characteristics to Change of Direction and Agility Performance in Female Basketball Athletes. J. Strength Cond. Res. 2014, 28, 2415–2423. [Google Scholar] [CrossRef]
- Spiteri, T.; Newton, R.U.; Binetti, M.; Hart, N.H.; Sheppard, J.M.; Nimphius, S. Mechanical Determinants of Faster Change of Direction and Agility Performance in Female Basketball Athletes. J. Strength Cond. Res. 2015, 29, 2205–2214. [Google Scholar] [CrossRef]
- Sassi, R.H.; Dardouri, W.; Yahmed, M.H.; Gmada, N.; Mahfoudhi, M.E.; Gharbi, Z. Relative and Absolute Reliability of a Modified Agility T-test and Its Relationship With Vertical Jump and Straight Sprint. J. Strength Cond. Res. 2009, 23, 1644–1651. [Google Scholar] [CrossRef]
- Mancha-Triguero, D.; García-Rubio, J.; Calleja-González, J.; Ibáñez, S.J. Physical fitness in basketball players: A systematic review. J. Sports Med. Phys. Fit. 2019, 59, 1513–1525. [Google Scholar] [CrossRef] [PubMed]
- Balsalobre-Fernández, C.; Romero-Franco, N.; Jiménez-Reyes, P. Concurrent validity and reliability of an iPhone app for the measurement of ankle dorsiflexion and inter-limb asymmetries. J. Sports Sci. 2019, 37, 249–253. [Google Scholar] [CrossRef] [PubMed]
- Onofrei, R.R.; Amaricai, E.; Petroman, R.; Suciu, O. Relative and absolute within-session reliability of the modified Star Excursion Balance Test in healthy elite athletes. Peer J. 2019, 7, e6999. [Google Scholar] [CrossRef]
- Gonzalo-Skok, O.; Tous, J. La Velocidad en el Cambio de Dirección en los Deportes de Equipo: Evaluación, Especificidad y Entrenamiento. Disertation Thesis, Universidad de Zaragoza, Zaragoza, Spain, 2015. [Google Scholar]
- Gonzalo-Skok, O.; Serna, J.; Rhea, M.R.; Marín, P.J. Relationships between functional movement tests and performance tests in young elite male basketball players. Int. J. Sports Phys. Ther. 2015, 10, 628. [Google Scholar]
- Romero-Franco, N.; Jiménez-Reyes, P.; Castaño-Zambudio, A.; Capelo-Ramírez, F.; Rodríguez-Juan, J.J.; González-Hernández, J.; Toscano-Bendala, F.J.; Cuadrado-Peñafiel, V.; Balsalobre-Fernández, C. Sprint performance and mechanical outputs computed with an iPhone app: Comparison with existing reference methods. Eur. J. Sport Sci. 2017, 17, 386–392. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Rabita, G.; Dorel, S.; Slawinski, J.; Peyrot, N.; Saez de Villarreal, E.; Morin, J.-B. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running. Scand. J. Med. Sci. Sports 2016, 26, 648–658. [Google Scholar] [CrossRef] [PubMed]
- Rogers, S.M.; Winkelmann, Z.K.; Ebermann, L.E.; Games, K.E. Triple Hop for Distance as a Predictor of Lower Extremity Performance in Firefighter Equipment. Int. J. Exerc. Sci. 2019, 12, 515–525. [Google Scholar]
- Hamilton, R.T.; Shultz, S.J.; Schmitz, R.J.; Perrin, D.H. Triple-hop distance as a valid predictor of lower limb strength and power. J. Athl. Train. 2008, 43, 144–151. [Google Scholar] [CrossRef]
- Munro, A.G.; Herrington, L.C. Between-session reliability of four hop tests and the Agility T-test. J. Strength Cond. Res. 2011, 25, 1470–1477. [Google Scholar] [CrossRef]
- Stolberg, M.; Sharp, A.; Comtois, A.S.; Lloyd, R.S.; Oliver, J.L.; Cronin, J. Triple and Quintuple Hops: Utility, Reliability, Asymmetry, and Relationship to Performance. Strength Cond. J. 2016, 38, 18–25. [Google Scholar] [CrossRef]
- De Blas, X.; Padullés, J.M.; Del Amo, J.L.L.; Guerra-Balic, M. Creación y validación de Chronojump-Boscosystem: Un instrumento libre para la medición de saltos verticales. RICYDE Rev. Int. Cienc. Del Deport. 2012, 8, 334–356. [Google Scholar] [CrossRef]
- García-Ramos, A.; Pérez-Castilla, A.; Jaric, S. Optimisation of applied loads when using the two-point method for assessing the force-velocity relationship during vertical jumps. Sport. Biomech. 2018, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Balsalobre-Fernández, C.; Glaister, M.; Lockey, R.A. The validity and reliability of an iPhone app for measuring vertical jump performance. J. Sports Sci. 2015, 33, 1574–1579. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Morin, J.B.; Hintzy, F.; Belli, A. A simple method for measuring force, velocity and power output during squat jump. J. Biomech. 2008, 41, 2940–2945. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Rejc, E.; Di Prampero, P.E.; Belli, A.; Morin, J.-B. Optimal Force–Velocity Profile in Ballistic Movements—Altius. Med. Sci. Sport. Exerc. 2012, 44, 313–322. [Google Scholar] [CrossRef] [PubMed]
- Samozino, P.; Edouard, P.; Sangnier, S.; Brughelli, M.; Gimenez, P.; Morin, J.B. Force-velocity profile: Imbalance determination and effect on lower limb ballistic performance. Int. J. Sports Med. 2014, 35, 505–510. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Routledge: London, UK, 1988. [Google Scholar]
- Chtourou, H.; Hammouda, O.; Souissi, H.; Chamari, K.; Chaouachi, A.; Souissi, N. Diurnal variations in physical performances related to football in young soccer players. Asian J. Sports Med. 2012, 3, 139–144. [Google Scholar] [CrossRef]
- Webb, P.; Lander, J.L. An economical fitness testing battery for high school and college rugby teams. Sport. Coach 1983, 44–46. [Google Scholar]
- Hopkins, W.G.; Marshall, S.W.; Batterham, A.M.; Hanin, J. Progressive Statistics for Studies in Sports Medicine and Exercise Science. Med. Sci. Sport. Exerc. 2009, 41, 3–13. [Google Scholar] [CrossRef]
- Hopkins, W.G. Spreadsheets for analysis of controlled trials, with adjustment for a subject characteristic. Sportscience 2006, 10, 46–50. [Google Scholar]
- Sisic, N.; Jelicic, M.; Pehar, M.; Spasic, M.; Sekulic, D. Agility performance in high-level junior basketball players: The predictive value of anthropometrics and power qualities. J. Sports Med. Phys. Fit. 2016, 56, 884. [Google Scholar]
- Calleja-González, J.; Mielgo-Ayuso, J.; Lekue, J.A.; Leibar, X.; Erauzkin, J.; Jukic, I.; Ostojic, S.M.; Ponce-González, J.G.; Fuentes-Azpiroz, M.; Terrados, N. Anthropometry and performance of top youth international male basketball players in spanish national academy. Nutr. Hosp. 2018, 35, 1331–1339. [Google Scholar] [CrossRef] [PubMed]
- Nikolaidis, P.; Calleja-González, J.; Padulo, J. The effect of age on positional differences in anthropometry, body composition, physique and anaerobic power of elite basketball players. Sport Sci. Health 2014, 10, 225–233. [Google Scholar] [CrossRef]
- Peterson, M.D.; Alvar, B.A.; Rhea, M.R. The contribution of maximal force production to explosive movement among young collegiate athletes. J. Strength Cond. Res. 2006, 20, 867–873. [Google Scholar] [CrossRef]
- Chaouachi, A.; Brughelli, M.; Chamari, K.; Levin, G.T.; Ben Abdelkrim, N.; Laurencelle, L.; Castagna, C. Lower limb maximal dynamic strength and agility determinants in elite basketball players. J. Strength Cond. Res. 2009, 23, 1570–1577. [Google Scholar] [CrossRef]
- Meylan, C.; McMaster, T.; Cronin, J.; Mohammad, N.I.; Rogers, C.; Deklerk, M. Single-leg lateral, horizontal, and vertical jump assessment: Reliability, interrelationships, and ability to predict sprint and change-of-direction performance. J. Strength Cond. Res. 2009, 23, 1140–1147. [Google Scholar] [CrossRef]
- Bourgeois, F.; McGuigan, M.; Gill, N.; Gamble, G. Physical characteristics and performance in change of direction tasks: A brief review and training considerations. J. Aust. Strength 2017, 25, 104–117. [Google Scholar]
- Lockie, R.G.; Schultz, A.B.; Callaghan, S.J.; Jeffriess, M.D. The Relationship Between Dynamic Stability and Multidirectional Speed. J. Strength Cond. Res. 2016, 30, 3033–3043. [Google Scholar] [CrossRef]
- Plisky, P.J.; Rauh, M.J.; Kaminski, T.W.; Underwood, F.B. Star excursion balance test as a predictor of lower extremity injury in high school basketball players. J. Orthop. Sports Phys. Ther. 2006, 36, 911–919. [Google Scholar] [CrossRef]
- Havens, K.L.; Sigward, S.M. Joint and segmental mechanics differ between cutting maneuvers in skilled athletes. Gait Posture 2015, 41, 33–38. [Google Scholar] [CrossRef]
- Nimphius, S.; Callaghan, S.J.; Spiteri, T.; Lockie, R.G. Change of Direction Deficit: A More Isolated Measure of Change of Direction Performance Than Total 505 Time. J. Strength Cond. Res. 2016, 30, 3024–3032. [Google Scholar] [CrossRef] [PubMed]
- Cuthbert, M.; Thomas, C.; DosʼSantos, T.; Jones, P.A. Application of Change of Direction Deficit to Evaluate Cutting Ability. J. Strength Cond. Res. 2019, 33, 2138–2144. [Google Scholar] [CrossRef] [PubMed]
- DosʼSantos, T.; Thomas, C.; Jones, P.A.; Comfort, P. Assessing Asymmetries in Change of Direction Speed Performance: Application of Change of Direction Deficit. J. Strength Cond. Res. 2019, 33, 2953–2961. [Google Scholar] [CrossRef] [PubMed]
- Dos’Santos, T.; Thomas, C.; Comfort, P.; Jones, P.A. The Effect of Angle and Velocity on Change of Direction Biomechanics: An Angle-Velocity Trade-Off. Sports Med. 2018, 48, 2235–2253. [Google Scholar] [CrossRef]
- DosʼSantos, T.; McBurnie, A.; Thomas, C.; Comfort, P.; Jones, P.A. Biomechanical Determinants of the Modified and Traditional 505 Change of Direction Speed Test. J. Strength Cond. Res. 2019, 1. [Google Scholar] [CrossRef]
- Nygaard Falch, H.; Guldteig Rædergård, H.; van den Tillaar, R. Effect of Different Physical Training Forms on Change of Direction Ability: A Systematic Review and Meta-analysis. Sport. Med. Open 2019, 5, 53. [Google Scholar] [CrossRef]
- Nygaard Falch, H.; Guldteig Rædergård, H.; Van den Tillaar, R. Relationship of Performance Measures and Muscle Activity between a 180° Change of Direction Task and Different Countermovement Jumps. Sports 2020, 8, 47. [Google Scholar] [CrossRef]
- Bishop, C.; Turner, A.; Read, P. Effects of inter-limb asymmetries on physical and sports performance: A systematic review. J. Sports Sci. 2018, 36, 1135–1144. [Google Scholar] [CrossRef]
| Variables | JUNIOR | SENIOR | % (CL 90%) | ES (CL 90%) | Chances (%) | Outcome | ||
|---|---|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | |||||
| Body Composition | ||||||||
| BMI (kg/cm2) | 21.8 | 2.90 | 24.1 | 2.87 | −9.65 (−17.81; −0.68) | −0.81 (−1.57; −0.05) | 91/7/2 | Likely |
| Lean mass (kg) | 35.9 | 4.12 | 42.8 | 4.45 | 15.83 (−22.44; −8.67) | −1.58 (−2.33; −0.83) | 100/0/0 | Most likely |
| Fat mass (%) | 11.9 | 6.61 | 11.4 | 5.08 | −5.77 (−36.02; 38.77) | −0.13 (−0.95; 0.70) | 44/31/25 | Unclear |
| Mobility | ||||||||
| WB-DF R (°) | 40.7 | 5.65 | 37.1 | 4.31 | 9.86 (0.19; 20.45) | 0.78 (0.02; 1.54) | 2/8/90 | Likely |
| WB-DF L (°) | 40.1 | 5.60 | 38.4 | 3.77 | 3.77 (−5.68; 14.15) | 0.34 (−5.54; 1.22) | 15/24/61 | Unclear |
| Dynamic Balance | ||||||||
| SEBT R (cm) | 57.6 | 7.31 | 63.5 | 4.97 | −8.77 (−15.67; −1.30) | −1.08 (−2.00; −0.15) | 94/4/1 | Likely |
| SEBT L (cm) | 57.3 | 7.60 | 63.2 | 6.27 | −8.80 (−16.62; −0.25) | −0.85 (−1.67; −0.02) | 90/7/2 | Likely |
| YBT R (cm) | 62.9 | 7.05 | 69.0 | 6.34 | −7.94 (−14.69; −0.66) | −0.81 (−1.56; −0.06) | 91/7/2 | Likely |
| YBT L (cm) | 62.8 | 7.97 | 67.9 | 7.79 | −6.73 (−14.93; 2.26) | −0.56 (−1.29; 0.18) | 79/16/5 | Likely |
| Linear Sprint | ||||||||
| 5 m sprint (s) | 0.89 | 0.04 | 0.88 | 0.04 | 0.87 (−2.46; 4.31) | 0.17 (−0.49; 0.84) | 17/36/47 | Unclear |
| 10 m sprint (s) | 1.48 | 0.06 | 1.47 | 0.08 | 0.87 (−2.69; 4.57) | 0.15 (−0.48; 0.78) | 17/38/45 | Unclear |
| 30 m sprint (s) | 4.31 | 0.14 | 4.16 | 0.19 | 3.18 (−0.23; 6.71) | 0.58 (−0.04; 1.20) | 2/13/85 | Likely |
| RF-10M | 0.30 | 0.01 | 0.31 | 0.02 | −2.33 (−5.87; 1.33) | −0.41 (−1.04; 0.23) | 71/23/6 | Unclear |
| Strength | ||||||||
| CMJ (cm) | 34.9 | 5.14 | 35.6 | 4.78 | −0.51 (−10.45; 10.54) | −0.03 (−0.72; 0.65) | 34/38/28 | Unclear |
| DJU R (cm) | 17.5 | 3.41 | 17.6 | 1.00 | −1.93 (−12.55; 9.97) | −0.32 (−2.21; 1.57) | 55/14/32 | Unclear |
| DJU L (cm) | 17.1 | 3.45 | 16.3 | 3.40 | 5.63 (−10.06; 24.05) | 0.23 (−0.45; 0.91) | 14/33/53 | Unclear |
| RSI R | 0.93 | 0.28 | 0.99 | 0.21 | 7.78 (−25.03; 13.42) | −0.32 (−1.13; 0.50) | 60/26/14 | Unclear |
| RSI L | 0.93 | 0.31 | 0.87 | 0.25 | 4.79 (−16.89; 32.14) | 0.15 (−0.59; 0.89) | 21/33/45 | Unclear |
| THT R (cm) | 566.3 | 42.4 | 566.1 | 59.5 | 1.64 (−4.90; 8.62) | 0.14 (−0.43; 0.70) | 16/42/42 | Unclear |
| THT L (cm) | 570.3 | 58.2 | 598.5 | 63.9 | −2.96 (−9.70; 4.29) | −0.26 (−0.87; 0.36) | 56/33/11 | Unclear |
| F-V | 61.8 | 17.3 | 51.0 | 20.5 | 27.89 (−10.70; 83.16) | 0.37 (−0.17; 0.91) | 4/25/71 | Possibly |
| COD | ||||||||
| COD45° R (s) | 2.01 | 0.09 | 2.03 | 0.11 | −1.81 (−4.96; 1.44) | −0.33 (−0.91; 0.26) | 65/29/7 | Unclear |
| COD45° L (s) | 2.02 | 0.08 | 2.05 | 0.16 | −1.52 (−5.94; 3.09) | −0.19 (−0.74; 0.37) | 48/40/12 | Unclear |
| COD90° R (s) | 2.37 | 0.13 | 2.26 | 0.12 | 4.40 (0.24; 8.73) | 0.77 (0.04; 1.49) | 2/8/90 | Likely |
| COD90° L (s) | 2.35 | 0.09 | 2.27 | 0.10 | 3.00 (−0.14; 6.23) | 0.63 (−0.03; 1.28) | 2/12/86 | Likely |
| COD180° R (s) | 2.75 | 0.16 | 2.61 | 0.10 | 4.68 (0.90; 8.59) | 1.12 (0.22; 2.02) | 1/4//95 | Very likely |
| COD180° L (s) | 2.77 | 0.18 | 2.58 | 0.14 | 7.05 (2.33; 11.99) | 1.19 (0.40; 1.97) | 0/2/98 | Very likely |
| COD T-test (s) | 6.75 | 0.39 | 6.49 | 0.34 | 3.48 (−0.67; 7.80) | 0.61 (−0.12; 1.35) | 4/14/83 | Likely |
| Variables | LR | HR | % (CL 90%) | ES (CL 90%) | ||
|---|---|---|---|---|---|---|
| Mean | SD | Mean | SD | |||
| COD45° | ||||||
| 5 m sprint (s) | 0.90 | 0.04 | 0.87 | 0.04 | −2.43 (−5.23; 0.46) | −0.64 (−1.40; 0.12) |
| 10 m sprint (s) | 1.50 | 0.07 | 1.45 | 0.07 | −2.66 (−5.52; 0.29) | −0.69 (−1.46; 0.07) |
| 30 m sprint (s) | 4.15 | 0.17 | 4.33 | 0.13 | −3.86 (−6.73; −0.91) | −1.06 (−1.87; −0.25) |
| RF-10M | 0.30 | 0.01 | 0.31 | 0.02 | 3.53 (0.16; 7.02) | 0.89 (0.04; 1.74) |
| CMJ (cm) | 32.6 | 4.41 | 37.7 | 4.00 | 15.97 (5.57; 27.39) | 0.97 (0.36; 1.59) |
| DJU R (cm) | 17.1 | 2.97 | 17.9 | 2.04 | 6.21 (−5.10; 18.87) | 0.30 (−0.26; 0.87) |
| DJU L (cm) | 14.6 | 2.77 | 18.6 | 2.74 | 26.81 (11.22; 44.59) | 1.06 (0.48; 1.65) |
| RSI R | 0.86 | 0.19 | 1.04 | 0.27 | 20.04 (−0.30; 44.52) | 0.75 (−0.01; 1.50) |
| RSI L | 0.77 | 0.17 | 1.03 | 0.30 | 29.20 (5.92; 57.58) | 1.03 (0.23; 1.82) |
| THT R (cm) | 564.9 | 45.8 | 567.4 | 55.7 | −0.02 (−6.76; 7.21) | 0.00 (−0.75; 0.74) |
| THT L (cm) | 569.2 | 50.7 | 597.1 | 69.0 | 5.03 (−2.87; 13.57) | 0.47 (−0.28; 1.22) |
| F-V | 61.5 | 18.0 | 52.2 | 20.0 | −19.95 (−44.29; 15.05) | −0.57 (−1.49; 0.36) |
| COD90° | ||||||
| 5 m sprint (s) | 0.88 | 0.04 | 0.88 | 0.04 | −0.93 (−4.56; 2.84) | −0.20 (−0.98; 0.59) |
| 10 m sprint (s) | 1.47 | 0.06 | 1.48 | 0.08 | 1.35 (–2.54; 5.40) | 0.33 (−0.63; 1.29) |
| 30 m sprint (s) | 4.29 | 0.16 | 4.19 | 0.18 | −2.19 (−5.96; 1.73) | −0.44 (−1.23; 0.34) |
| RF-10M | 0.30 | 0.01 | 0.31 | 0.02 | 3.06 (−1.09; 7.38) | 0.60 (−0.22; 1.41) |
| CMJ (cm) | 33.7 | 5.51 | 36.6 | 3.94 | 12.25 (−1.93; 28.48) | 0.62 (−0.10; 1.34) |
| DJU R (cm) | 16.5 | 2.22 | 18.5 | 2.41 | 9.83 (−2.72; 24.01) | 0.60 (−0.18; 1.38) |
| DJU L (cm) | 15.3 | 3.40 | 18.0 | 2.91 | 30.40 (8.97; 56.05) | 1.08 (0.35; 1.80) |
| RSI R | 0.84 | 0.25 | 1.06 | 0.20 | 17.03 (−6.83; 47.00) | 0.52 (−0.23; 1.27) |
| RSI L | 0.81 | 0.29 | 0.99 | 0.25 | 34.59 (2.05; 77.50) | 0.80 (0.05; 1.55) |
| THT R (cm) | 563.1 | 43.7 | 569.1 | 57.1 | −0.53 (−8.05; 7.62) | −0.06 (−0.98; 0.86) |
| THT L (cm) | 581.2 | 64.3 | 586.1 | 61.1 | −2.41 (−11.37; 7.45) | −0.20 (−1.01; 0.60) |
| F-V | 64.9 | 15.7 | 49.0 | 19.5 | −30.84 (−51.75; −0.88) | −1.30 (−2.58; −0.03) |
| COD180° | ||||||
| 5 m sprint (s) | 0.90 | 0.04 | 0.86 | 0.03 | −4.39 (−6.74; −1.99) | −1.15 (−1.79; −0.51) |
| 10 m sprint (s) | 1.51 | 0.07 | 1.44 | 0.05 | −4.84 (−7.74; −1.86) | −0.99 (−1.60; −0.37) |
| 30 m sprint (s) | 4.35 | 0.19 | 4.13 | 0.10 | −4.47 (−7.31; −1.54) | −0.89 (−1.48; −0.30) |
| RF-10M | 0.30 | 0.01 | 0.31 | 0.01 | 5.05 (1.83; 8.38) | 1.00 (0.37; 1.64) |
| CMJ (cm) | 33.82 | 5.11 | 36.54 | 4.46 | 8.36 (−2.46; 20.37) | 0.48 (−0.15; 1.11) |
| DJU R (cm) | 16.39 | 2.18 | 18.60 | 2.39 | 13.69 (3.23; 25.22) | 0.83 (0.20; 1.45) |
| DJU L (cm) | 15.32 | 2.65 | 17.99 | 3.55 | 16.61 (0.97; 34.68) | 0.82 (0.05; 1.58) |
| RSI R | 0.84 | 0.23 | 1.06 | 0.22 | 27.61 (9.17; 49.18) | 0.91 (0.33; 1.49) |
| RSI L | 0.79 | 0.20 | 1.00 | 0.31 | 25.44 (3.46; 52.09) | 0.80 (0.12; 1.47) |
| THT R (cm) | 572.4 | 47.8 | 560.6 | 53.5 | −2.14 (−8.61; 4.78) | −0.22 (−0.93; 0.48) |
| THT L (cm) | 586.9 | 66.4 | 580.8 | 59.0 | −0.91 (−8.75; 7.60) | −0.07 (−0.68; 0.55) |
| F-V | 69.2 | 12.7 | 45.1 | 17.0 | −40.19 (−56.19; −18.33) | −2.29 (−3.68; −0.90) |
| T-Test | ||||||
| 5 m sprint (s) | 0.91 | 0.03 | 0.86 | 0.03 | −4.88 (−7.02; −2.68) | −1.42 (−2.06; −0.77) |
| 10 m sprint (s) | 1.52 | 0.06 | 1.44 | 0.05 | −5.29 (−7.98; −2.52) | −1.18 (−1.80; −0.55) |
| 30 m sprint (s) | 4.37 | 0.16 | 4.11 | 0.11 | −5.29 (−7.88; −2.63) | −1.21 (−1.83; −0.60) |
| RF-10M | 0.30 | 0.01 | 0.31 | 0.01 | 5.46 (2.34; 8.68) | 1.16 (0.50; 1.81) |
| CMJ (cm) | 33.7 | 4.96 | 36.7 | 4.52 | 9.15 (−1.65; 21.14) | 0.54 (−0.10; 1.18) |
| DJU R (cm) | 17.0 | 3.07 | 18.1 | 1.84 | 7.55 (−3.88; 20.34) | 0.36 (−0.19; 0.91) |
| DJU L (cm) | 15.2 | 2.49 | 18.1 | 3.58 | 17.69 (2.16; 35.59) | 0.91 (0.12; 1.70) |
| RSI R | 0.84 | 0.23 | 1.06 | 0.22 | 26.87 (8.31; 48.61) | 0.88 (0.29; 1.46) |
| RSI L | 0.76 | 0.17 | 1.03 | 0.30 | 32.20 (11.56; 56.66) | 1.15 (0.45; 1.85) |
| THT R (cm) | 566.5 | 47.7 | 566.0 | 54.3 | −0.17 (−6.67; 6.79) | −0.02 (−0.72; 0.68) |
| THT L (cm) | 573.9 | 60.3 | 592.8 | 63.4 | 3.28 (−4.75; 11.99) | 0.26 (−0.40; 0.92) |
| F-V | 70.2 | 11.0 | 44.2 | 16.6 | −42.39 (−57.37; −22,16) | −3.01 (−4.65; −1.37) |
| Variables | COD45° | COD90° | COD180° | COD | |||
|---|---|---|---|---|---|---|---|
| L (s) | R (s) | L (s) | R (s) | L (s) | R (s) | T-Test (s) | |
| Body Composition | |||||||
| BMI (kg/height) | 0.165 | 0.278 | −0.075 | −0.052 | −0.048 | −0.203 | −0.226 |
| Lean mass (kg) | 0.167 | −0.076 | −0.341 | −0.300 | −0.380 | −0.374 | −0.370 |
| Fat mass (%) | 0.193 | 0.527 ** | 0.246 | 0.154 | 0.384 | 0.184 | 0.100 |
| Mobility | |||||||
| WB-DF R (°) | −0.056 | −0.128 | 0.089 | −0.008 | −0.011 | 0.058 | 0.055 |
| WB-DF L (°) | −0.121 | 0.144 | 0.316 | 0.196 | 0.085 | 0.132 | 0.128 |
| Dynamic Balance | |||||||
| SEBT L (cm) | 0.222 | −0.187 | −0.394 | −0.086 | −0.237 | −0.193 | −0.171 |
| SEBT R (cm) | 0.132 | −0.226 | −0.403 | −0.187 | −0.334 | −0.262 | −0.148 |
| YBT L (cm) | 0.211 | −0.144 | −0.414 * | −0.139 | −0.231 | −0.153 | −0.141 |
| YBT R (cm) | 0.099 | −0.240 | −0.430 * | −0.251 | −0.383 | −0.269 | −0.178 |
| Linear Sprint | |||||||
| 5 m sprint (s) | 0.176 | 0.125 | 0.227 | −0.050 | 0.382 | 0.476 * | 0.456 * |
| 10 m sprint (s) | 0.153 | 0.104 | 0.233 | −0.037 | 0.404 | 0.461 * | 0.427 * |
| 30 m sprint (s) | 0.164 | 0.355 * | 0.441 * | 0.214 | 0.498 * | 0.537 ** | 0.501 * |
| RF-10M | −0.180 | −0.339 | −0.433 * | −0.169 | −0.470 * | −0.514 * | −0.472 * |
| Strength | |||||||
| CMJ (cm) | −0.215 | −0.668 ** | −0.340 | −0.226 | −0.462 * | −0.443 * | −0.314 |
| DJU L (cm) | −0.293 | −0.632 ** | −0.532 ** | −0.273 | −0.451 * | −0.400 | −0.541 ** |
| DJU R (cm) | −0.261 | −0.162 | −0.294 | −0.170 | −0.451 * | −0.515 * | −0.360 |
| RSI L | −0.368 | −0.446 * | −0.427 * | −0.246 | −0.504 * | −0.420 * | −0.626 ** |
| RSI R | −0.265 | −0.378 | −0.465 * | −0.339 | −0.546 ** | −0.579 ** | −0.656 ** |
| THT R (cm) | 0.232 | −0.295 | −0.289 | 0.057 | 0.107 | 0.053 | −0.129 |
| THT L (cm) | −0.284 | −0.196 | −0.311 | −0.245 | −0.034 | −0.036 | −0.121 |
| F-V Profile | |||||||
| F-V Imbalance | 0.183 | 0.255 | 0.603 ** | 0.407 | 0.523 * | 0.589 ** | 0.784 ** |
| F-V V0 | 0.219 | 0.171 | 0.379 | 0.330 | 0.441 * | 0.530 ** | 0.680 ** |
| F-V F0 | −0.344 | −0.330 | −0.711 ** | −0.555 ** | −0.605 ** | −0.621 ** | −0.778 ** |
| F-V Pmax | 0.097 | 0.065 | 0.193 | 0.166 | 0.244 | 0.342 | 0.468 * |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrera-Domínguez, F.J.; Almagro, B.J.; Tornero-Quiñones, I.; Sáez-Padilla, J.; Sierra-Robles, Á.; Molina-López, J. Decisive Factors for a Greater Performance in the Change of Direction and Its Angulation in Male Basketball Players. Int. J. Environ. Res. Public Health 2020, 17, 6598. https://doi.org/10.3390/ijerph17186598
Barrera-Domínguez FJ, Almagro BJ, Tornero-Quiñones I, Sáez-Padilla J, Sierra-Robles Á, Molina-López J. Decisive Factors for a Greater Performance in the Change of Direction and Its Angulation in Male Basketball Players. International Journal of Environmental Research and Public Health. 2020; 17(18):6598. https://doi.org/10.3390/ijerph17186598
Chicago/Turabian StyleBarrera-Domínguez, Francisco J., Bartolomé J. Almagro, Inmaculada Tornero-Quiñones, Jesús Sáez-Padilla, Ángela Sierra-Robles, and Jorge Molina-López. 2020. "Decisive Factors for a Greater Performance in the Change of Direction and Its Angulation in Male Basketball Players" International Journal of Environmental Research and Public Health 17, no. 18: 6598. https://doi.org/10.3390/ijerph17186598
APA StyleBarrera-Domínguez, F. J., Almagro, B. J., Tornero-Quiñones, I., Sáez-Padilla, J., Sierra-Robles, Á., & Molina-López, J. (2020). Decisive Factors for a Greater Performance in the Change of Direction and Its Angulation in Male Basketball Players. International Journal of Environmental Research and Public Health, 17(18), 6598. https://doi.org/10.3390/ijerph17186598









